Delegated Proof of Secret Sharing: A Privacy-Preserving Consensus Protocol Based on Secure Multiparty Computation for IoT Environment
 ^†

Abstract

With the rapid advancement and wide application of blockchain technology, blockchain consensus protocols, which are the core part of blockchain systems, along with the privacy issues, have drawn much attention from researchers. A key aspect of privacy in the blockchain is the sensitive content of transactions in the permissionless blockchain. Meanwhile, some blockchain applications, such as cryptocurrencies, are based on low-efficiency and high-cost consensus protocols, which may not be practical and feasible for other blockchain applications. In this paper, we propose an efficient and privacy-preserving consensus protocol, called Delegated Proof of Secret Sharing (DPoSS), which is inspired by secure multiparty computation. Specifically, DPoSS first uses polynomial interpolation to select a dealer group from many nodes to maintain the consensus of the blockchain system, in which the dealers in the dealer group take turns to pack the new block. In addition, since the content of transactions is sensitive, our proposed design utilizes verifiable secret sharing to protect the privacy of transmission and defend against the malicious attacks. Extensive experiments show that the proposed consensus protocol achieves fairness during the process of reaching consensus.

1. Introduction

In a distributed system, the consensus is the task of reaching an agreement on some specific values among a group of processes. Consensus is helpful in the following application scenarios: leader electing, synchronizing replicated state machines, deciding to commit or abort for distributed transactions, etc. As one realization of the distributed system, a blockchain network is dependent on the consensus protocol to achieve a common status for all nodes in the network [1]. Consensus protocols are designed to maintain the reliability in a network involving multiple unreliable nodes; therefore, it is necessary to assume that some communications are not available, and the consensus protocol must be fault-tolerant.

To maintain the integrity of the blockchain network, various consensus protocols have been proposed, and many of them have been employed extensively. Proof of Work (PoW) has the main idea of producing a cryptographic hash, and the concept was invented by Dwork and Naor in 1993 to deter denial-of-service attacks and other service abuses, such as email spam [2]. PoW was then introduced by Satoshi Nakamoto for describing the design of Bitcoin as the foundation of its consensus [3]. In PoW, participants are required to perform some time-consuming and complex computation, such as the hashing in Bitcoin, and the result of the computation can be validated quickly. The consumed time, device wear, and energy are considered as the guarantees that can prevent the abuse of the blockchain network service. Meanwhile, the consumption brought by the complex computation, typically called “mining” in Bitcoin, overwhelms the usage of electricity in some countries with a population of more than 10 million, such as Argentina, Netherlands, and United Arab Emirates [4].

Unlike the PoW protocol, Proof of Stake (PoS) does not prompt extreme amounts of energy consumption. In PoS, the production of a new block is based on the amount of stake (coins in cryptocurrency) a participant holds [5]. The principle in the back is that the participant that holds the most stakes cherishes the worth of the blockchain network the most and is not willing to lose the wealth, so the probability that this participant is honest is quite high. However, an often discussed point about PoS is that it probably leads to the centralization of the blockchain network since the blockchain network utilizing PoS favors participants with a higher amount of stakes, and a more substantial participant will use the profit to increase the production ability of new blocks; thus, a more substantial participant grows faster than a participant with a smaller stake. After some point, the cost of entering the group of block producers becomes too high, causing many other participants to quit, resulting in centralization [6].

In addition to these two most popular consensus protocols, there are some other competitive ones, including Proof of Elapsed Time (PoET), Proof of Luck (PoL), and Delegated Proof of Stake (DPoS). Both PoET and PoL utilize the capacity of a Trusted Execution Environment (TEE), such as Intel’s Software Guard Extension, to achieve consensus. PoET generates a random waiting time for each participant in the blockchain network, in which the one whose waiting time expires first will win the selection and obtain the privilege of producing a new block [7]. PoL makes all participants generate a random number in each round of block producing, and the participant with the largest time is the winner [8]. DPoS is a hybrid consensus protocol that utilizes the representative democratic. Nodes in the blockchain network can vote for a few delegates who are responsible for the network maintenance and new block packing.

The Internet of Things (IoT) network has evolved because of the advancement of multiple techniques, including embedded systems, wireless sensors, and automation. IoT devices are widely adopted in the market of smart homes, healthcare systems, manufacturing, etc. However, there are many serious issues exposed along with the development of IoT ecology, especially in the areas of security and scalability. Security is a major concern for the center server and sensors at the edge of the IoT network. The center server of the IoT network is an obvious target of DDoS attacks, which have the potential to cause the paralysis of the entire network. Another issue is about the scalability. Along with the fast increase in the number of connected devices, the overhead of the authentication process, address assignment, and frequent communications will impose growing pressure on the center server.

Meanwhile, the sensors and edge devices in the IoT network may become the breaking point of malicious attackers due to the following reasons of lacking compliance on manufacturers and the complicated upgrade management [9]. Many IoT devices come out with undiscovered vulnerabilities in the hardware and software. For example, a group of hackers discovered one security vulnerability that can be used to perform a man-in-the-middle attack and gain the user’s Gmail login credential [10]. Since there is no standard for the IoT connection module and interface, these security issues can not be upgraded and fixed easily, especially on the hardware side.

Blockchain can help mitigate the security and scalability concerns associated with IoT in the way of security and scalability. The transformation from centralization to decentralization brought by the integration of blockchain avoids the risk of single-point failure and alleviates the pressure of communication over the entire network, such that the scalability is improved. At the same time, the maintenance of the network does not rely on the center server; therefore, the influence of the targeted DDoS attack can be reduced. The key idea of integrating IoT with blockchain is simple, but the implementation raises many challenges, and the most serious one is the choice of consensus protocol since consensus protocol forms the backbone of the blockchain network and affects efficiency and security.

As we mentioned above, PoW is the most well-known consensus protocol, and it has been shown that it is an effective approach for the operation of the cryptocurrency system. However, it is not suitable for the IoT network due to the high energy consumption. PoET has significantly lower energy consumption, but reaching a consensus relies on the specific hardware platform, which is not practical for the large-scale deployment in the IoT environment. Proof of Capacity (PoC) is also similar to PoW, but the complex computation is replaced by the capacity of storage. It is well known that IoT devices are constrained by their small storage capacity and slow storage speed, which makes PoC not a viable choice. Other consensus protocols, such as the variants of PoS and Byzantine Agreement Methods, have higher efficiency and lower energy consumption than PoW, but few of them focus on the privacy of communication within the blockchain network. In most consensus protocols, the built blockchain network provides transparency by allowing all the authorized participants to review the content of the transaction and track the past blocks. This can help track the malicious actions and source but may leak sensitive information in some special application scenarios.

Most of the current existing consensus protocols have some common shortcomings, such as low efficiency, centralization trend, high energy consumption, and privacy issues. The problems of low efficiency and high energy consumption make them impractical for the application of blockchain networks in the IoT environment. These issues motivate us to propose a privacy-preserving and efficient consensus protocol, which enables the blockchain network to be deployed in resource-constrained IoT networks.

In this work, we present a consensus protocol that provides fairness during the election of nodes to pack the new block and preserves privacy during information transmission while maintaining efficiency. Our contributions can be summarized as follows:

• To achieve the fairness of the election, we propose a random algorithm to randomly choose several nodes as the packers based on all of the nodes’ given parameters.
• The feature of privacy-preserving is implemented with verifiable secret sharing, in which the information is split and then encrypted so as to protect the sensitive information during transmission.
• We propose one method to keep the efficiency of the election when the number of nodes in the blockchain network is very large.
• Evaluation results and analysis show the efficiency and security of our scheme.

The remainder of the paper is organized as follows. In Section 2, we give a description about secret sharing and an overview of existing consensus protocols used in the IoT environment. In Section 3, we introduce the design assumptions and ideas of the proposed DPoSS consensus protocol, and then present it with pseudocode. In Section 4, we give an analysis on security and privacy. In Section 5, we discuss the possible application scenarios and compare our scheme with some existing blockchain systems, which are integrated with secure multi-party computations. In Section 6, we conclude the paper and discuss the future work.

2. Background and Related Work

In this section, we provide a high-level overview of the core technologies we use in the design of the DPoSS consensus protocol. We first introduce the secure multi-party computation (MPC) technique used in our design: secret sharing, mainly Shamir’s Secret Sharing and Verifiable Secret Sharing. Then, we discuss some prior works on the consensus protocols in the IoT blockchain network.

2.1. Secret Sharing

Secret sharing is a technique that first splits one secret into multiple shares and distributes them. Typically, there is one dealer and n players from a collection $\Delta$ in secret sharing, and the dealer distributes the secret to each player. The secret can be reconstructed only when k (for threshold) or more shares are provided by the players in the collection $\Delta$. Such a cryptographic system is called a $(k,n)—$threshold secret sharing system [11]. A secret sharing scheme is practical for storing and distributing confidential and sensitive information, such as the private key of a Certificate Authority. Secret sharing schemes are also effective in a distributed network system, but the split pieces make it harder for the eavesdropper to gain valuable information. The implementation of secret sharing was proposed by Adi Shamir and George Blakley independently in 1979.

In the implementation made by Shamir [12], the scheme Shamir Secret Sharing (SSS) was described as follows: the secret is some data D that are divided into n pieces $D_1,\dots ,D_n$ in such a way that:

• knowledge of any k or more $D_i$ pieces makes D easily computable;
• knowledge of any $k-1$ or fewer $D_i$ pieces leaves D completely undetermined.

By using the $(k,n)—$ threshold secret sharing, the original secret can be reconstructed if no more than $\lfloor n/2\rfloor =k-1$ of the n pieces are destroyed. The key idea of SSS is based on the Lagrange interpolation theorem that k points are enough to uniquely identify a polynomial of degree less than or equal to $k-1$.

Theorem 1

(Lagrange interpolation). Let $\mathcal{F}$ be a finite field. Then k pairs $(x_i,y_i)$ uniquely determine a polynomial $f\left(x\right)$ of degree $\le k-1$, such that $f\left(x_i\right)=y_i$. We assume that $k-1<\left|\mathcal{F}\right|$ so that all $x_i$’s can be distinct. $f\left(x\right)$ is determined by:

$$f\left(x\right)=\sum _{i=1}^k{y}_i\prod _{\begin{array}{c}1\le j\le k\\ i\ne j\end{array}}\frac{x-x_j}{x_i-x_j}$$

(1)

To share the secret D as $D\Rightarrow (D_1,\dots ,D_n)$, the distribution of the secret is conducted by the following steps:

• Choose a large prime number p and let $\mathcal{F}=\mathcal{Z}/p\mathcal{Z}$.
• Choose coefficients $f_1,\dots ,f_{k-1}\in \mathcal{F}$, which are to be the coefficients of degree $k-1$ polynomial f.
• Let $f\left(z\right)=f_0+f_{1}z+\dots f_{k-1}{z}^{k-1}$, where $f_0=D$.
• Evaluate the value of each $f\left(i\right)$ and distribute them to player i, $i=1\dots n$.

The reconstruction of SSS is also based on the Lagrange interpolation theorem described in Theorem 1. If there are k players and each player has the corresponding $f\left(i\right)$, then we have k points on the curve of a polynomial whose degree is less than (k − 1), and we can evaluate unique coefficients to a polynomial whose degree is (k − 1). The secret D is the coefficient $f_0$ in the polynomial. With the following equation, given any k pieces of share, we can obtain $f_0$ using interpolation:

$$f\left(x\right)=\sum _{i=1}^k{y}_i\prod _{\begin{array}{c}1\le j\le k\\ i\ne j\end{array}}\frac{x-x_j}{x_i-x_j}\Rightarrow f\left(0\right)=\sum _{i=1}^k{y}_i\prod _{\begin{array}{c}1\le j\le k\\ i\ne j\end{array}}\frac{x_j}{x_j-x_i}$$

(2)

2.2. Verifiable Secret Sharing (VSS)

Earlier secret sharing schemes, including the above-mentioned Shamir’s Secret Sharing and Blakley’s Secret Sharing, share one common hypothesis, which is that the dealer and the players of the secret are honest. However, it is not always realistic for the employment of secret sharing in the real world. Therefore, one secure secret sharing scheme for the purpose of cryptography should put the participants in an adversarial position and try to imagine what would happen if they jump out of the rules and stray away from the instructions. The security concerns of earlier secret sharing schemes mainly come from two directions: adversary dealer and malicious player. First, the dealer is possible to distribute maliciously tampered shares or even random information as pieces of shares instead of truly split shares. The players cannot figure out the impossibility of reconstruction until they try to perform the task of reconstruction. The other main problem is that when one or more players contribute the incorrect share $\widehat{D_i}\ne D_i$, the reconstruction of the polynomial will be a failure (taking Shamir’s Secret Sharing as the example). Even worse, if $n-k$ or more players refuse to contribute their shares, the reconstruction cannot be continued.

Chor et al. proposed the conception of Verifiable Secret Sharing [13]. Same as earlier secret sharing schemes, there are two stages in the protocol of VSS: distribution stage and reconstruction. However, to make the shares verifiable, extra commitments for verification must be provided. Informally, the VSS has two requirements as follows [14]:

• Verifiability constraint: upon receiving a piece of secret share, a player must be able to validate the piece. If k or more (k for threshold) pieces of a secret share are valid, there exists one unique result for the reconstruction of the original secret.
• Unpredictability: there is no polynomial-time strategy for picking less than k pieces of shares such that they can be used to predict the original secret.

From the perspective of interactions between players and the interactions between dealers and players, the VSS can be divided into interactive ones and non-interactive ones. The first work on VSS proposed by Chor et al. belongs to the type of interactive verifiable secret sharing, which is based on the difficulty of factorization of large numbers and oblivious transfer. Goldreich et al. proposed their work based on a zero-knowledge proofs system and one-way function, and the system can be used to build an interactive verifiable secret sharing scheme [14].

Feldman presented an efficient noninteractive protocol for VSS [14] based on Shamir’s Secret Sharing and the discrete logarithm problem in finite fields, which can tolerate up to $(n-1)/2$ dishonest players. According to the paper’s definition, a VSS is non-interactive if there exists a polynomial-time algorithm that verifies the validity of the pieces. In [15], Pedersen presented a commitment solution with the property of homomorphism and then one non-interactive VSS based on Lagrange interpolation. His solution has demonstrated and established three important features for the later VSS research: (1) if the dealer is honest, then all honest players can determine one unique polynomial of degree $k-1$ (k for threshold); (2) any subset of k valid pieces of the secret share can be used for the reconstruction, even if there exist some malicious players; (3) no set of, at most, $k-1$ players obtain any information about the secret. Gennaro et al. [16] proposed one solution of VSS with a simple structure based on fast cryptographic primitives so as to avoid the high cost on the zero-knowledge proofs, and then the efficiency of secret sharing has a huge improvement.

2.3. Consensus Protocols Based on Verifiable Random Function

During the development of consensus protocols from PoW-based to PoS-based, one critical problem is that how PoS-based consensus protocols, whose energy consumption is much lower, guarantee fairness and justice when choosing the node to generate a new block while maintaining the robustness of the system after abandoning the competition scheme, such as hash computing in PoW-based consensus protocols. Under the circumstances that PoS comes under heavy criticism on the trend of centralization, verifiable random function (VRF) was introduced into the building of consensus protocols by Gilad et al. in the description of Algorand [17]. The conception of VRF was proposed by Micali, Rabin, and Vadhan for the purpose of combing unpredictability and verifiability [18]. VRF is a cryptographic function that maps inputs to verifiable pseudorandom outputs and has the following three properties: pseudorandomness, verifiability, and uniqueness. These properties will be explained along with the introduction of the algorithms of VRF.

• Key pair generation algorithm: $G\left(i\right)\to (K_v,K_s)$.
  For a random input i, a pair of a verification key $K_v$ and a secret key $K_s$ will be produced.
• Evaluation algorithm: $E(K_s,X)\to (Y,\pi )$.
  The evaluation algorithm takes the secret key $K_s$ and message X as inputs, and it will produce a random output Y and a proof $\pi$. The random output here indicates the unpredictability and uniqueness since the output will not change if the input and key pair do not alter.
• Verification algorithm: $V(K_v,X,Y,\pi )\to True/False$.
  The verification algorithm takes the verification key $K_v$, message X, output Y, and the proof $\pi$ as inputs, then the result True or False shows the verification result of whether the output Y is actually produced by the evaluation algorithm with message X and the corresponding secret key $K_s$. This asserts the property of verifiability that the output can be validated by anyone who has the necessary information.

Generally, VRF provides a random data generator in which the random producing is associated with the private secret key and the producing can be verified by the public verification key, and the VRF is used for the random picking of the block producer or block producer group.

Based on the properties of VRF, the Algorand network implemented cryptographic sortition, which allows a collection of users to secretly participate in reaching consensus, without them being known to anyone else [17]. The cryptographic sortition can be described as a combination of local sortition, winner broadcast, and public verification. The participants in the procedure of consensus need to perform the sortition locally such that a verifiable deterministic random number Y will be produced, and this local sortition will indicate if the participant is selected, which means whether the produced Y locates in the range. Since this produced Y can be verified by every participant in the network, it is impossible for the existence of impostors. Afterward, the selected participant broadcasts the result of the sortition and submits the candidate for the new block.

Another consensus protocol called Dfinity is also based on the VRF but is designed for the permissioned blockchain model [19]. In the Dfinity network, all participants, called clients, are registered for a permanent and pseudonymous identity, and the registration has an advantage on the prevention of misbehavior over the network without registration due to the penalty and the possible stake deposit. All the clients will be assigned into different groups based on the output of the VRF, and VRF is also used to randomly choose one group from all groups to perform the Boneh–Lynn–Shacham threshold signature scheme (BLS) [20]. In each group of the entire Dfinity network, there is a pair of a public key $PK$ and a private key $SK$, but every member of the group can only be acquainted with a part of the private key, denoted as $S{K}_i$, instead of the complete $SK$. Each member can sign one message X with its piece of signature and produce the corresponding short signature $SI{G}_i\left(X\right)$. With at least k short signatures, the complete signature $SIG\left(X\right)$ for that message X can be computed, and the $SIG\left(X\right)$ here is exactly the same as the signature signed directly with the private key $SK$.

2.4. Consensus Protocols in IoT

Due to the existing concerns on the computational and communication capabilities of the IoT devices, especially those edge devices, they cannot be deployed with many types of blockchain networks that are based on those traditional consensus protocols, such as PoW. Most embedded IoT devices are equipped with low-power processors with low frequency and small caches, and the memory and storage are both very limited for cost and design. Many IoT devices are connected with low-powered wireless techniques, such as LPWANs, Zigbee, and RFID. These constraints stimulate the development of new types of consensus protocols. In this subsection, we will give an overview of some consensus protocols designed specifically for IoT networks.

Different from regular consensus protocols in the blockchain network, many consensus protocols designed for the IoT blockchain network have exclusive application scenarios, such as Industrial Internet of Things (IIoT), secure IoT, and IoT for smart monitoring. Uddin et al. proposed one efficient selective miner consensus protocol using miners’ performance parameters for smart home/city monitoring IoT [21]. The gateway, which connects the IoT devices to the blockchain network, assesses the bandwidth, propagation speed, energy consumption, communication speed, and CPU performance of prospective miners, then chooses the node with the highest score as the selected miner to produce the new block. This protocol runs like PoW, but there are two obvious differences: (1) one same node will not be selected twice within a period, and (2) part of the stake held by the node competitors will be locked temporarily so that they cannot lie when reporting their performance parameters. However, the malicious node may be nominated to produce a new block in the above design. Lao et al. [22] proposed one consensus protocol called G-PBFT or Geographic-PBFT that leverages the geographic information of IoT devices during the running of the blockchain network. The geographic information is used to determine if the IoT node is fixed or mobile, and their design is based on the following assumptions: (1) fixed IoT devices typically have higher computational power than mobile IoT devices, and (2) fixed IoT devices are well-maintained, with a lower possibility of being a malicious node. All the nodes are divided into endorsers and clients, and endorsers are in charge of validation. All the endorsers participating in the miner election have historical geographic information, including the coordinate hashing and timestamp. The first endorser who does not move in the past 72 h will be elected to maintain the consensus. They also argue that the proposed G-PBFT consensus protocol can defend the Sybil attacks while reducing the communication and validating overhead. However, there are several concerns about this protocol. Not only that the above-mentioned assumptions do not always hold, but also that it requires that all the IoT nodes work within a small physical area. One lightweight and sustainable consensus protocol called PoAh (Proof-of-Authentication) proposes an authentication mechanism during block validation [23], in which one trusted node is introduced for block authentication. The process begins by compiling a list of transactions into an individual block that is not linked with other blocks yet. This individual block has a device identifier; if the identifier is valid, then the trusted node will append the individual block into the chain. This PoAh consensus protocol is based on one trusted node for validation; therefore, a private blockchain must be built for the consensus protocol.

Meanwhile, there are several regular consensus protocols designed for IoT blockchain networks. PoEWAL (Proof of Elapsed Work Furthermore, Luck) is a consensus protocol for a noncooperative blockchain environment, and the authors argue that PoEWAL has low energy consumption, low latency, and a short time for reaching consensus [24]. PoEWAL used a PoW-like method to do the miner election, but the idea is similar to PoET. During the election, each participant will run a cryptographic puzzle for a fixed time, and the result of the puzzle will be broadcast to the network for comparison. The node whose puzzle result has the highest number of consecutive zeros is the winner. However, more than one node may win the puzzle competition. To prevent collision and forking, the node with lower nonce used in the puzzle computation will be assigned the rights to pack a new block. SLPoW (Secure and Low latency Proof of Work) [25] is another consensus protocol inspired by PoW and committed to reduce energy consumption. They move the computation of PoW to the FPGA platform since the FPGA hardware platform can increase the processing speed and provide a more secure environment. Makhdoom et al. [26] proposed “Pledge”, a PoH (Proof of Honesty)-based consensus protocol. Pledge is designed to reduce the participation of faulty, malicious, and unresponsive nodes in order to increase the capability of tolerating the fault. Attributes such as the number of valid blocks proposed, number of transactions in previous valid blocks, number of sent transactions, number of received transactions, and number of connected peers, are cumulatively considered based on each corresponding weight. As a result, each node has one cumulative score, and the block producer will be randomly chosen from a list of nodes whose score is higher than the dynamic threshold value.

One work from Dorri and Jurdak [27] introduced a fast and lightweight consensus protocol based on random hash function output. Each validator will be assigned one “consensus code” based on the public key. In the level of transactions, the validator of each transaction is randomly chosen based on the hash value of the transaction content by matching the first few characters with the validators’ consensus code. If one transaction’s hash function output is the same as one validator’s consensus code, then the transaction will be committed by that validator. As for the structure of the blockchain network, the network has many ledgers as the branches, and each ledger is maintained by one validator. Basically, the Tree-Chain consensus protocol makes the blockchain network more like an acyclic graph instead of a linear data structure.

3. Design

In this section, we present the design of our novel consensus protocol. From the above description about consensus protocol, we found three existing problems of the current popular consensus protocols: efficiency, centralization, and privacy issues. Therefore, we ask the following research questions:

Q1.

How to improve the efficiency of the blockchain system from the perspective of consensus protocol and reduce the waste of energy?

Q2.

How to guarantee the democracy or fairness during the selection of the new block packer to avoid the centralized control by one or a small group of nodes while reducing the ratio of malicious nodes being selected?

Q3.

How to protect the privacy of the blockchain network participants when the information being transmitted is sensitive?

To answer these questions, we proposed a novel consensus protocol called Delegated Proof of Secret Sharing (DPoSS), which is suitable for the application scenario of an IoT environment. DPoSS is designed based on the following assumptions:

• The IoT network includes many edge devices and more sensors connected to the edge devices. The blockchain network consists of only those edge devices; sensors are not included as the nodes of the blockchain network.
• Each node in the blockchain network has it own pair of a public key and a private key. The node’s public key is available to all other nodes, and its private key is known only to itself and the control center, if established.
• Our proposed DPoSS relies on one group of delegate nodes in the blockchain network instead of all nodes, as in the case of PoW. With DPoSS, every node has the opportunity to be elected as a delegate, denoted as “teller”; all other unelected nodes are called “fishers”.
• Sensors are not able to vote for delegates due to the constraints on the abilities of computation power, battery, and transmission bandwidth.

Basically, there are two kinds of nodes in the blockchain network during the processing of consensus: regular nodes (fishers) and delegate nodes (tellers). We do not define and confine the principle to choose or screen the tellers for the various applications of the IoT network because there are many options available, such as random choosing and PoW-like method, in which the first several nodes successfully figure out one simple problem will be the tellers. Meanwhile, there is also no requirement of the number of tellers. The appropriate number of tellers depends on the threshold of secret sharing. For the convenience of discussion, we denote the number of all nodes (fishers and tellers) as m and denote the number of tellers as n.

3.1. Election

Assume that there are some connected nodes already, and every node has its own pair of public and private keys. To prevent the 51% attack, the first block of the blockchain network is produced by the system maintainer, such as the control center, instead of the first connected node. Before the proceeding of any transaction, the election must be finished since the responsibilities of the tellers include both the packing of a new block and the spreading of transactions.

In general, the election is implemented by a verifiable random number generation based on the polynomial interpolation. If there are $m+1$ running nodes in the blockchain network, and each node contributes one data point $P_i:(x_i,y_i)$ of the polynomial interpolation of m degree such that no two data points are the same, one equation of the polynomial can be deduced from the data points provided by the running nodes. All $m+1$ coefficients can be used to build one random number by performing the xor operations. For example, there are four running nodes in the blockchain network, and the provided data points are $P_0(-1.5,-1.2),P_1(-0.2,0),P_2(1,0.5),P_3(5,1)$, so the deduced equation of the polynomial would be

$$f\left(x\right)=2.2535\times {10}^{-2}\times x^3-1.8679\times {10}^{-1}\times x^2+5.4717\times {10}^{-1}\times x+1.1709\times {10}^{-1}$$

(3)

and the coefficients, such as $2.2535\times {10}^{-2}$ and $1.1709\times {10}^{-1}$, are the factors used to build the random number.

The steps for the general election can be described as follows:

• All the nodes randomly pick one data point $P_i:(x_i,y_i)$ and broadcast the data point with a timestamp. If two or more nodes pick a conflicting data point such that they share the same x value or they share the same x and y values, the node whose timestamp is later will be asked to pick another data point until there is no conflict.
• Build the polynomial of the form $f\left(x\right)=a_0+a_{1}x+...+a_n{x}^n$ based on all received data points and generate the random number result r.
• Choose first k nodes whose data point has the value of $|x-y|$ is closest to the generated random number r.
• These k nodes form the group of dealers and dealers take turns to pack the new block. The dealer that has already packed the new block loses the identity and the permission of the dealer until the dealer group is empty; at that time, a new round of election will be initiated.

In step 2, the random number is computed by bitwise xor operation on all coefficients of the interpolated polynomial. Since most of the coefficients are not integers and some of them are very big or very small, we concatenate all the coefficients together into a long string $\mathcal{C}$ according to the degree order, and then split the concatenated string $\mathcal{C}$ into an array $A\left(n\right)$ of n number based on the globally consistent value range of data points from all nodes in order to make the final random number close to data points from all nodes. For example, if the range of all nodes’ data points are within $(0,100)$, then $\mathcal{C}$ will be cut as one integer every two digits so that all elements of array $A\left(n\right)$ stand in the same plane with all data points, and the result of bitwise xor stands in it.

Each data point has two values $x_i$ and $y_i$, but the calculation of bitwise xor can only yield one single value instead of one pair. To solve this problem, the separated array $A\left(n\right)$ needs some changes, for example, reducing by 1 for all numbers in array $A\left(n\right)$. Thus, we obtain two random numbers to form a random point as the reference to choose k closest data points, and their senders form the dealer group to pack the new block. The algorithm to generate the random point is presented in Algorithm 1.

Algorithm 1: Algorithm to generate random data points. The parameters X and Y are the collections of data points such that X contains all $x_i$ and Y contains all $y_i$.

1: procedure BITWISE($X,Y$) 2:     $degree=X.size\left(\right)$ 3:     $poly=FuncPolynomialFit(X,Y,degree)$   ▹ Polynomial interpolation 4:     $coes=poly.coefficients\left(\right)$            ▹ Return all coefficients 5:     for $coe$ in $coes$ do 6:         Make all coefficient value positive 7:         Delete the decimal point 8:         Concatenate them together as one string S 9:     Split S as an array of integers A 10:     Substract each element in $A\left(n\right)$ by one number to form another array B 11:     $x=bitwiseXOR\left(A\right)$ 12:     $y=bitwiseXOR\left(B\right)$ 13:     return $x,y$

Interpolation is a method to discover more data points based on the known data points. In other words, interpolation can help to obtain the unique mathematical expression that can cover all given data points. The method we used is Lagrange’s interpolation formula such that if $y=L\left(x\right)$ takes the values $y_0,y_1,\dots ,y_n$ corresponding to $x=x_0,x_1,\dots ,x_n$, then the Lagrange form polynomial $L\left(x\right)$ is

$$L\left(x\right)=\sum _{j=0}^n{y}_j{l}_j\left(x\right)$$

(4)

of Lagrange basic polynomials

$$l_j\left(x\right)=\prod _{i=0,i\ne j}^n\frac{x-x_i}{x_j-x_i}$$

(5)

If any of the nodes have doubts about the validation of the built polynomial, the verification can be conducted individually. The node has the polynomial of the form $f\left(x\right)=a_0+a_{1}x+\dots +a_n{x}^n$ and its own data point $(x_i,y_i)$ and verifies if $y_i=f\left(x_i\right)$ is correct or not. If $y_i=f\left(x_i\right)$, this indicates that this node’s data point participates in the building of the polynomial that yields the random number; otherwise, the generated random number is not valid.

3.2. Election on Large Network

The time complexity of the election solution is $O\left(n^2\right)$ and auxiliary space is $O\left(1\right)$, which means that when the number of nodes in the blockchain network becomes large to a certain extent, the action to build the polynomial for all nodes is no longer efficient. For extremely large blockchain networks, one extra cryptographic sortition step is necessary for the election. Based on the VRF’s properties of pseudo-randomness, uniqueness, and verifiability, each node can calculate a random number within the predefined range, such as $[0,1)$, and according to the total number of nodes in the blockchain network, a value k can be set as the number of groups to separate all the nodes. For example, all the nodes need to be divided into four groups, the predefined range $[0,1)$ can be partitioned into $[0,0.25)$, $[0.25,0.5)$, $[0.5,0.75)$, and $[0.75,1)$. Then, each group will build one polynomial for selecting dealers in each group, and the selected dealers in each group will form a larger group of dealers. Because of the existing of multiple groups, the total number of dealers should be adjusted in each group in order to maintain the balance between the number of dealers and the number of nodes.

3.3. Transactions

In the IoT network, the information may flow from the sensor to the control center through the blockchain network, and the control center can also send messages to one or more sensors. The information flow in both directions is achieved through the employment of the lightweight communication protocol designed specifically for the IoT network, such as MQTT and CoAP [28]. In the IoT network integrated with blockchain, the smallest unit of communication is called a transaction. The tellers are in charge of packing a new block of transactions, and all the nodes help to spread the transactions just like in the regular blockchain network.

If the control center requests data from one or more target sensors, this transaction will be directly sent to the blockchain network. Each node in the blockchain network will check if the target sensors are connected to itself; if so, the node will send the transaction to the connected sensors.

If the transaction is initiated from a sensor, no matter if it is a publish message or response message, the transaction will be sent to the connected edge nodes. This transaction will be split into n pieces (n is the number of tellers), and then spread through the blockchain network. These split n pieces will be encrypted using the public key of tellers. Therefore, except for the node that splits the transaction and the control center, no other node can merge these encrypted pieces and fetch the sensitive information. Because the control center is aware of the tellers’ private key, the control center is able to recover the original information sent by the sensors. In this way, even if one or some nodes are controlled by a malicious attacker, the attacker still cannot break the protection of the information; thus, the privacy is preserved.

3.4. Security

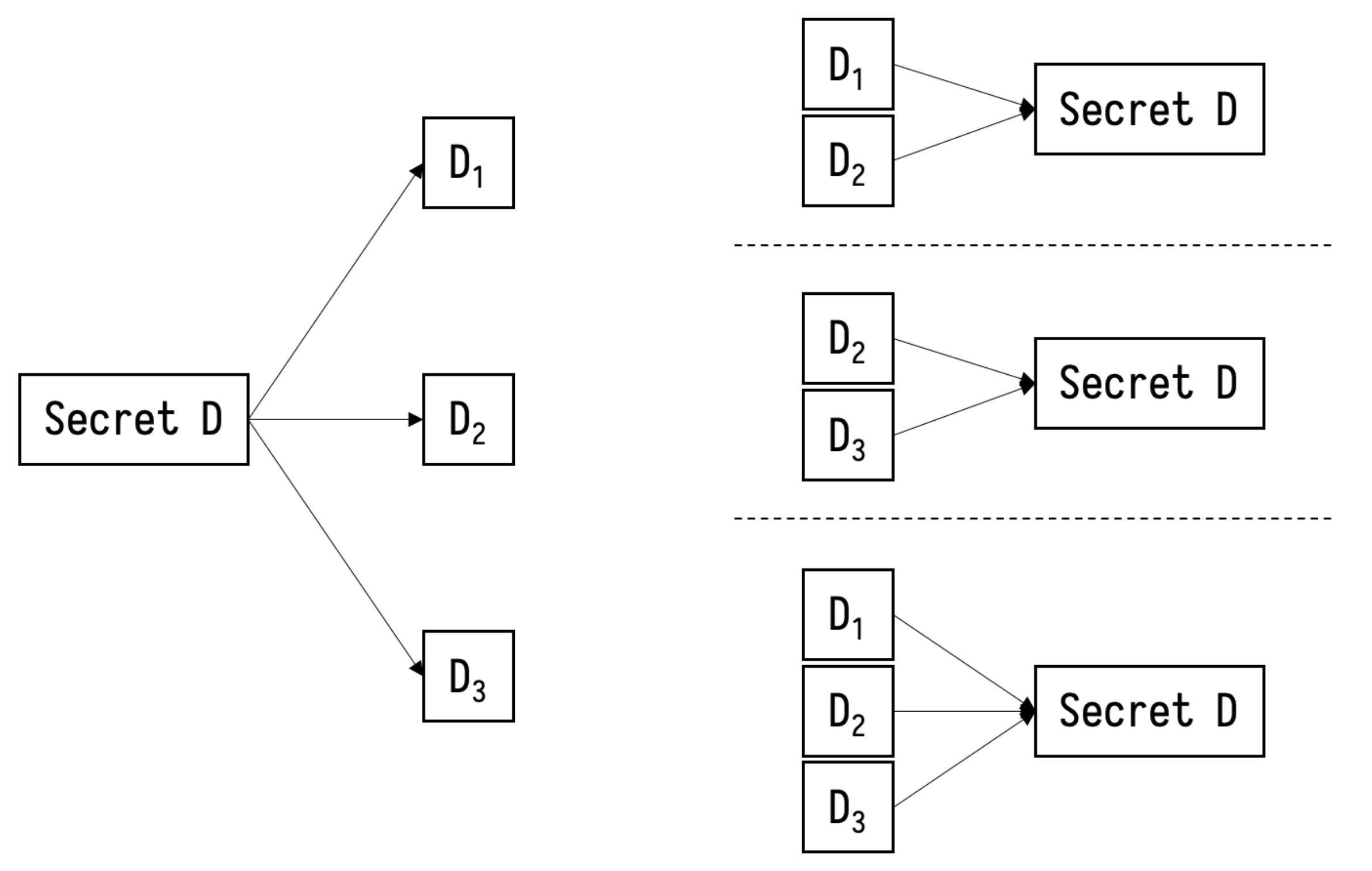
With the scheme of secret sharing, the secret sent to the control center through the blockchain network can be privacy-preserved. However, there is one special case in which the node in charge of the job of splitting and distributing is not honest anymore, which may cause the transaction information to be garbled from the very beginning. As shown in Figure 1, they indicate a $(2,3)$-threshold secret sharing system in which any two shares can reconstruct the secret, but there exists at least one security issue: the dealer is malicious so that the secret shares sent to three players are not incorrect. For example, the share sent to the third player is garbled, and it is possible that the reconstruction will fail. To solve this problem, we choose to integrate the Verifiable Secret Sharing instead of the basic secret sharing, such as Shamir’s Secret Sharing.

4. Analysis and Evaluation

In this section, we provide some analysis about the proposed consensus protocol in terms of security, fault tolerance, and efficiency.

4.1. Fault Tolerance

A blockchain is essentially a distributed and decentralized network that shares a common state. However, even though various consensus protocols have been designed to maintain the agreement on all nodes, it is still possible that this agreement does not occur due to some fault. The endeavor to achieve and maintain this agreement under possible faults is called fault tolerance.

We note that our proposed consensus protocol is based on secret sharing, which refers to splitting one secret S to m shares $(S_1,S_2,\dots ,S_m)$ and distributing shares to m participants, and one important feature of secret sharing is that the secret can be reconstructed with t (t stands for a threshold and $t<m$) or more shares presented. Such a $(t,n)$-threshold secret sharing system can be used to implement the fault tolerance in the following way:

• Information of any t or more $S_i$ shares makes S easily computable. This means that the secret S can be easily reconstructed from any combination of t shares.
• Information of any $t-1$ or fewer $S_i$ shares will leave the secret S completely undetermined. This means that the secret S cannot be reconstructed with fewer than t shares.
• One extreme case of such a secret sharing system is that $t=m$ so that all shares are required to build the original secret.

With the $(t,n)$-threshold secret sharing system, the fault tolerance depends on a majority of the tellers, so the tolerance rate is less than 51% of tellers. For instance, if the transaction was split into 12 shares, then setting $t=6$ cannot make sure the reconstruction of the secret since these 6 tellers could be all controlled by the attacker, even though the possibility of device failure still exists. If the value of t is set to be larger than 6, then the secret can be recovered, and the consensus can still be reached.

4.2. Random Number Distribution

In cryptography, confusion and diffusion are two critical properties in the processing of secure cipher [29], and diffusion indicates the connection between the plaintext and ciphertext. In our design, the distribution of generated random numbers should have no obvious connection with any data point given by the nodes in the blockchain network. To show the randomness of the generated random data points and scattered distribution, we simulate the distribution using several rounds of polynomial interpolation of degree 1000 and plot all rounds’ data points in the coordinate plane. As shown in Figure 2, the red dots represent the data points in 1000 rounds of polynomial interpolation. We can see that there is no obvious pattern, which shows the randomness of k data points selection and the fairness of dealer selection.

4.3. Efficiency

We experiment to show the approximate time used to build the polynomial, as shown in

Table 1. Running time used to build the polynomial with Lagrange form.

Degree	10	50	100	500	1000	5000	10,000	20,000	50,000
Time	513 ns	0.012 ms	0.05 ms	1.25 ms	5.20 ms	0.12 s	0.49 s	1.99 s	12.38 s

. With a prototype implemented on a machine with Intel Core i7 10700f CPU, we can see that building a polynomial with a Lagrange form for 20,000 degrees needs around 2 s, while the polynomial with degree 10,000 only takes less than 0.5 s. These experimental results show that our scheme is quite efficient. Although some nodes in the blockchain network may be equipped with lower end processors, it should be capable of handling the work of building a polynomial with thousands of nodes according to our results.

5. Discussion

In this section, we present some application scenarios of our proposed consensus protocol. The comparison between our design and some similar consensus protocols based on secure multi-party computations is given as follows.

5.1. Application Scenarios

Blockchain technology produces a structure of data with inherent security qualities since it is based on cryptography. In most blockchain and distributed ledger applications, the data are structured into multiple blocks, and each block can be used to carry information. The encryption and protection on the blocks make our proposed design especially suitable for blockchain systems that transmit sensitive information, such as cloud computing and financial systems.

Individuals and small companies tend to deploy their services on the cloud instead of purchasing and maintaining their own servers because of many benefits, including cost-saving, fast deployment, scalability, etc. However, confidentiality and integrity of the data in a remote cloud computing environment are some of the security concerns. If the cloud service, or a connected device, is breached, sensitive data could be accessed [30]. The data including personal health information, personally identifiable information, trade secrets, and intellectual property are often the targets of data breaches and require robust security protection in cloud computing [31]. Even though cloud computing and blockchain seem to be deceptively in conflict from the perspective of infrastructure that cloud computing is representative of centralized computing and the blockchain typically stands for decentralization, but there are many fields on which blockchain and cloud computing can be integrated [32]. For example, the storage of the cloud computing environment can be built based on blockchain with our design so that the stored data are split and individually encrypted. The advantage of our design over encryption on undivided data is risk diversification. Meanwhile, the inherent features of blockchain including parallel throughput bandwidth and data tamper resistance are also retained in our design.

Blockchain technology has supported multiple cryptocurrency ecosystems and has inspired the interest of the financial sectors. The financial industry has already started the experiment with blockchain to see how the distributed ledger techniques can leverage financial transactions. However, due to the characteristics of sensitivity in the financial transactions, the blockchain system applied in the financial industry tends to be a private blockchain. In the private blockchain, only a few participants can read and write on the distributed ledger to prevent data leakage. With our design, the public blockchain can also be used to build the transaction systems based on blockchain such that the communication between nodes is split and encrypted, and the decryption can only occur when the number of recipients agreed on is more than a predefined threshold value.

5.2. Comparison

Luo et al. [33] proposed a consensus algorithm based on secure MPC, which incorporates Yao’s millionaire algorithm. Specifically, one candidate group of 101 nodes is selected first, and then the election process is conducted within the group. During the election process, Yao’s millionaire algorithm, one of the secure MPC, permits the comparison between different nodes’ stake to be qualified as the “proxy” node of the generation block. By contrast, our design does not need extra communication if the blockchain network scale is not extraordinary large. Moreover, our design uses the secure MPC in both the election process and the communication process, which enhances the overall security.

Zhong et al. [34] introduced the overview on how secure MPC can be performed using blockchain techniques. Secure MPC and blockchain are both of distributed form, so they are compatible with each other. There are many other practical applications that benefit from the integration of secure MPC and blockchain, such as smart city [35], health record system [36], electronic voting [37], and storage system [38]. However, all these applications of secure MPC are based on blockchain, while we use secure MPC to improve the security, efficiency, and equity of the blockchain system.

Through the above-mentioned comparison, we show that our contribution lies in the novel use of secure MPC and the combination of blockchain and secure MPC.

6. Conclusions

This paper proposes an improved consensus protocol, which is integrated with verifiable secret sharing, the polynomial interpolation, and verifiable random function when the blockchain network is very large. We have combined these ideas into a new consensus protocol that not only takes charge of the packing of new blocks but also maintains the privacy of information transmission. The distribution experiment shows the randomness of the node selection using polynomial interpolation, which provides fairness for every node in the blockchain network. The observed running time demonstrates the efficiency of our approach.

Our future work will focus on two aspects. First, we plan to conduct a larger experiment to verify the efficiency of our consensus protocol. Second, we plan to improve our design on the modularization so that different types of secret sharing schemes can be changed under different application scenarios.