Locally Odd-Parity Hybridization Induced by Spiral Magnetic Textures
Abstract
1. Introduction
2. Model
3. Active Multipole
4. Density Waves
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Matrix Elements of Multipoles
Appendix B. Real-Space Multipole Configurations
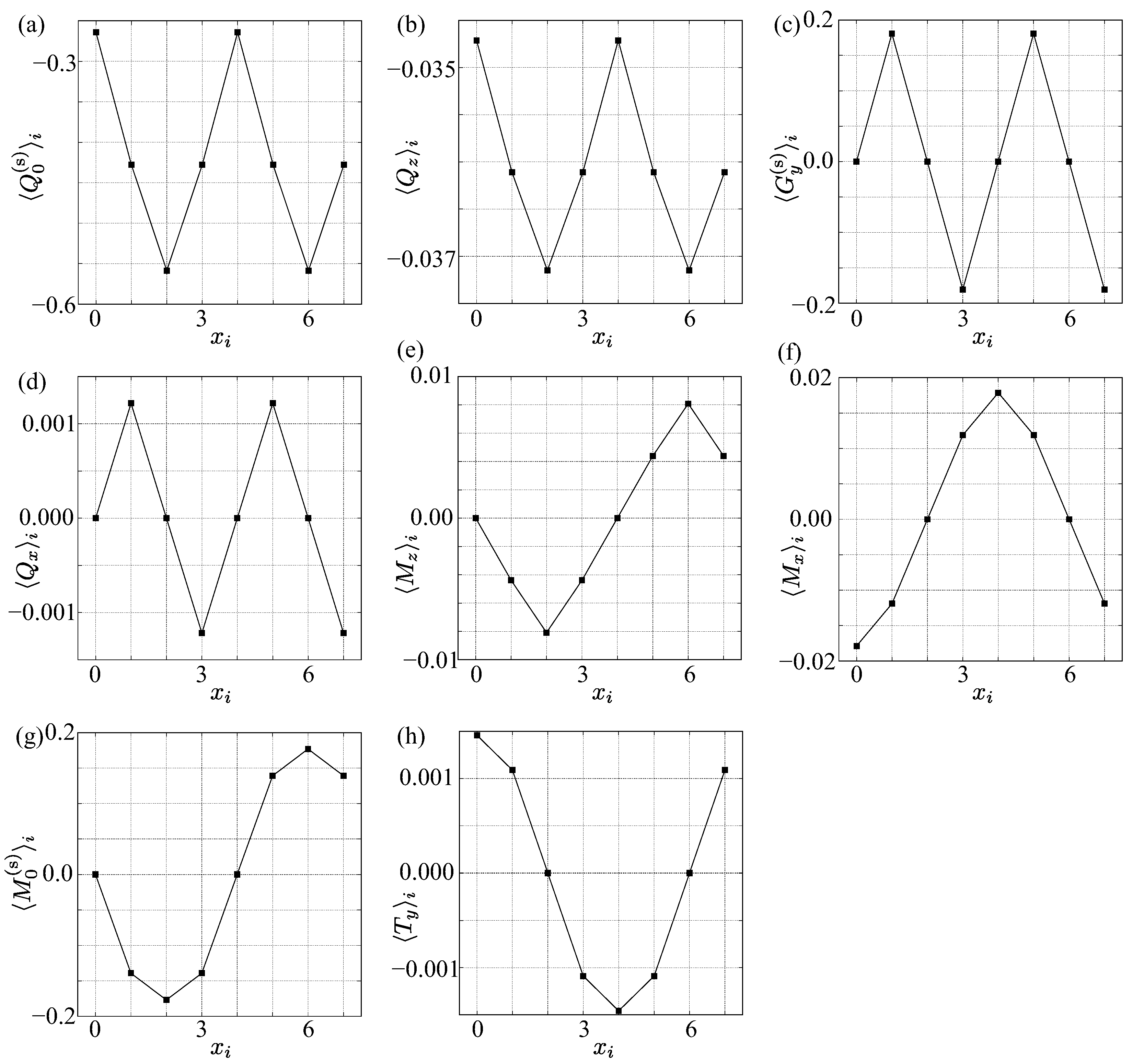
References
- Santini, P.; Carretta, S.; Amoretti, G.; Caciuffo, R.; Magnani, N.; Lander, G.H. Multipolar interactions in f-electron systems: The paradigm of actinide dioxides. Rev. Mod. Phys. 2009, 81, 807–863. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Kusunose, H.; Kiss, A. Multipole orders and fluctuations in strongly correlated electron systems. J. Phys. Soc. Jpn. 2009, 78, 072001. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Ikeda, H.; Oppeneer, P.M. First-principles theory of magnetic multipoles in condensed matter systems. J. Phys. Soc. Jpn. 2018, 87, 041008. [Google Scholar] [CrossRef]
- Takigawa, M.; Yasuoka, H.; Tanaka, T.; Ishizawa, Y. NMR Study on the Spin Structure of CeB6. J. Phys. Soc. Jpn. 1983, 52, 728–731. [Google Scholar] [CrossRef]
- Lüthi, B.; Blumenröder, S.; Hillebrands, B.; Zirngiebl, E.; Güntherodt, G.; Winzer, K. Elastic and magnetoelastic effects in CeB6. J. Magn. Magn. Mater. 1985, 47–48, 321–322. [Google Scholar] [CrossRef]
- Effantin, J.; Rossat-Mignod, J.; Burlet, P.; Bartholin, H.; Kunii, S.; Kasuya, T. Magnetic phase diagram of CeB6. J. Magn. Magn. Mater. 1985, 47–48, 145–148. [Google Scholar] [CrossRef]
- Erkelens, W.; Regnault, L.; Burlet, P.; Rossat-Mignod, J.; Kunii, S.; Kasuya, T. Neutron scattering study of the antiferroquadrupolar ordering in CeB6 and Ce0.75La0.25B6. J. Magn. Magn. Mater. 1987, 63–64, 61–63. [Google Scholar] [CrossRef]
- Nakamura, S.; Goto, T.; Kunii, S.; Iwashita, K.; Tamaki, A. Quadrupole-strain interaction in rare earth hexaborides. J. Phys. Soc. Jpn. 1994, 63, 623–636. [Google Scholar] [CrossRef]
- Sakai, O.; Shiina, R.; Shiba, H.; Thalmeier, P. A new interpretation of NMR in quadrupolar ordering phase of CeB6-Consistency with neutron scattering. J. Phys. Soc. Jpn. 1997, 66, 3005–3007. [Google Scholar] [CrossRef]
- Shiina, R.; Shiba, H.; Thalmeier, P. Magnetic-field effects on quadrupolar ordering in a Γ 8-quartet system CeB6. J. Phys. Soc. Jpn. 1997, 66, 1741–1755. [Google Scholar] [CrossRef]
- Shiina, R.; Sakai, O.; Shiba, H.; Thalmeier, P. Interplay of Field-Induced Multipoles in CeB6. J. Phys. Soc. Jpn. 1998, 67, 941–949. [Google Scholar] [CrossRef]
- Nakao, H.; Magishi, K.i.; Wakabayashi, Y.; Murakami, Y.; Koyama, K.; Hirota, K.; Endoh, Y.; Kunii, S. Antiferro-quadrupole ordering of CeB6 studied by resonant X-ray scattering. J. Phys. Soc. Jpn. 2001, 70, 1857–1860. [Google Scholar] [CrossRef]
- Cameron, A.S.; Friemel, G.; Inosov, D.S. Multipolar phases and magnetically hidden order: Review of the heavy-fermion compound Ce1-xLaxB6. Rep. Prog. Phys. 2016, 79, 066502. [Google Scholar] [CrossRef]
- Morin, P.; Schmitt, D.; du Tremolet de Lacheisserie, E. Magnetic and quadrupolar properties of PrPb3. J. Magn. Magn. Mater. 1982, 30, 257–264. [Google Scholar] [CrossRef]
- Tayama, T.; Sakakibara, T.; Kitami, K.; Yokoyama, M.; Tenya, K.; Amitsuka, H.; Aoki, D.; Ōnuki, Y.; Kletowski, Z. Antiferro-Quadrupolar Ordering and Multipole Interactions in PrPb3. J. Phys. Soc. Jpn. 2001, 70, 248–258. [Google Scholar] [CrossRef]
- Onimaru, T.; Sakakibara, T.; Harita, A.; Tayama, T.; Aoki, D.; Ōnuki, Y. Angle-resolved Magnetization Measurements on Antiferroquadrupolar Ordering System PrPb3: Evidence for Anisotropic Quadrupolar Interaction. J. Phys. Soc. Jpn. 2004, 73, 2377–2380. [Google Scholar] [CrossRef]
- Onimaru, T.; Sakakibara, T.; Aso, N.; Yoshizawa, H.; Suzuki, H.S.; Takeuchi, T. Observation of Modulated Quadrupolar Structures in PrPb3. Phys. Rev. Lett. 2005, 94, 197201. [Google Scholar] [CrossRef]
- Sato, Y.; Morodomi, H.; Ienaga, K.; Inagaki, Y.; Kawae, T.; S. Suzuki, H.; Onimaru, T. New Phase Diagram of PrPb3 in [100] Magnetic Filed Direction. J. Phys. Soc. Jpn. 2010, 79, 093708. [Google Scholar] [CrossRef]
- Kubo, K.; Hotta, T. Influence of lattice structure on multipole interactions in Γ3 non-Kramers doublet systems. Phys. Rev. B 2017, 95, 054425. [Google Scholar] [CrossRef]
- Onimaru, T.; Matsumoto, K.T.; Inoue, Y.F.; Umeo, K.; Sakakibara, T.; Karaki, Y.; Kubota, M.; Takabatake, T. Antiferroquadrupolar Ordering in a Pr-Based Superconductor PrIr2Zn20. Phys. Rev. Lett. 2011, 106, 177001. [Google Scholar] [CrossRef] [PubMed]
- Ishii, I.; Muneshige, H.; Suetomi, Y.; K. Fujita, T.; Onimaru, T.; T. Matsumoto, K.; Takabatake, T.; Araki, K.; Akatsu, M.; Nemoto, Y.; et al. Antiferro-Quadrupolar Ordering at the Lowest Temperature and Anisotropic Magnetic Field-Temperature Phase Diagram in the Cage Compound PrIr2Zn20. J. Phys. Soc. Jpn. 2011, 80, 093601. [Google Scholar] [CrossRef]
- Sakai, A.; Nakatsuji, S. Kondo Effects and Multipolar Order in the Cubic PrTr2Al20 (Tr= Ti, V). J. Phys. Soc. Jpn. 2011, 80, 063701. [Google Scholar] [CrossRef]
- Onimaru, T.; Nagasawa, N.; Matsumoto, K.; Wakiya, K.; Umeo, K.; Kittaka, S.; Sakakibara, T.; Matsushita, Y.; Takabatake, T. Simultaneous superconducting and antiferroquadrupolar transitions in PrRh2Zn20. Phys. Rev. B 2012, 86, 184426. [Google Scholar] [CrossRef]
- Ishii, I.; Muneshige, H.; Kamikawa, S.; Fujita, T.K.; Onimaru, T.; Nagasawa, N.; Takabatake, T.; Suzuki, T.; Ano, G.; Akatsu, M.; et al. Antiferroquadrupolar ordering and magnetic-field-induced phase transition in the cage compound PrRh2Zn20. Phys. Rev. B 2013, 87, 205106. [Google Scholar] [CrossRef]
- Tsujimoto, M.; Matsumoto, Y.; Tomita, T.; Sakai, A.; Nakatsuji, S. Heavy-Fermion Superconductivity in the Quadrupole Ordered State of PrV2Al20. Phys. Rev. Lett. 2014, 113, 267001. [Google Scholar] [CrossRef]
- Onimaru, T.; Kusunose, H. Exotic Quadrupolar Phenomena in Non-Kramers Doublet Systems—The Cases of PrT2Zn20 (T= Ir, Rh) and PrT2Al20 (T= V, Ti)—. J. Phys. Soc. Jpn. 2016, 85, 082002. [Google Scholar] [CrossRef]
- Iwasa, K.; Matsumoto, K.T.; Onimaru, T.; Takabatake, T.; Mignot, J.M.; Gukasov, A. Evidence for antiferromagnetic-type ordering of f-electron multipoles in PrIr2Zn20. Phys. Rev. B 2017, 95, 155106. [Google Scholar] [CrossRef]
- Andres, K.; Davidov, D.; Dernier, P.D.; Hsu, F.S.L.; Reed, W.A.; Nieuwenhuys, G. Anomalous behavior in the low temperature properties of UPd3. Solid State Commun. 1978, 28, 405–408. [Google Scholar] [CrossRef]
- Walker, M.; Kappler, C.; McEwen, K.; Steigenberger, U.; Clausen, K. Triple-Q quadrupolar order in UPd3. J. Phys. Condens. Matter 1994, 6, 7365. [Google Scholar] [CrossRef]
- McEwen, K.; Steigenberger, U.; Clausen, K.; Kulda, J.; Park, J.G.; Walker, M. Quadrupolar and magnetic transitions in UPd3. J. Magn. Magn. Mater. 1998, 177, 37–40. [Google Scholar] [CrossRef]
- Lingg, N.; Maurer, D.; Müller, V.; McEwen, K.A. Ultrasound investigations of orbital quadrupolar ordering in UPd3. Phys. Rev. B 1999, 60, R8430–R8433. [Google Scholar] [CrossRef]
- McMorrow, D.F.; McEwen, K.A.; Steigenberger, U.; Rønnow, H.M.; Yakhou, F. X-Ray Resonant Scattering Study of the Quadrupolar Order in UPd3. Phys. Rev. Lett. 2001, 87, 057201. [Google Scholar] [CrossRef] [PubMed]
- Walker, H.C.; McEwen, K.A.; McMorrow, D.F.; Wilkins, S.B.; Wastin, F.; Colineau, E.; Fort, D. Determination of the Antiferroquadrupolar Order Parameters in UPd3. Phys. Rev. Lett. 2006, 97, 137203. [Google Scholar] [CrossRef]
- Kawarasaki, Y.; Matsumura, T.; Sera, M.; Ochiai, A. Pressure-Induced Antiferroquadrupole Order in CeTe. J. Phys. Soc. Jpn. 2011, 80, 023713. [Google Scholar] [CrossRef]
- Takaguchi, H.; Hayashi, Y.; Matsumura, T.; Umeo, K.; Sera, M.; Ochiai, A. Anomalous Magnetic Phase Diagram of CeTe under High Pressure. J. Phys. Soc. Jpn. 2015, 84, 044708. [Google Scholar] [CrossRef]
- Yamauchi, H.; Onodera, H.; Ohoyama, K.; Onimaru, T.; Kosaka, M.; Ohashi, M.; Yamaguchi, Y. Antiferroquadrupolar Ordering and Magnetic Properties of the Tetragonal DyB2C2 Compound. J. Phys. Soc. Jpn. 1999, 68, 2057–2066. [Google Scholar] [CrossRef]
- Hirota, K.; Oumi, N.; Matsumura, T.; Nakao, H.; Wakabayashi, Y.; Murakami, Y.; Endoh, Y. Direct Observation of Antiferroquadrupolar Ordering: Resonant X-Ray Scattering Study of DyB2C2. Phys. Rev. Lett. 2000, 84, 2706–2709. [Google Scholar] [CrossRef]
- Staub, U.; Mulders, A.M.; Zaharko, O.; Janssen, S.; Nakamura, T.; Lovesey, S.W. Orbital Dynamics of the 4f Shell in DyB2C2. Phys. Rev. Lett. 2005, 94, 036408. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Goto, T.; Nemoto, Y.; Watanuki, R.; Suzuki, K.; Suzuki, O.; Kido, G. Magnetic phase diagram of antiferroquadrupole ordering in HoB2C2. Phys. Rev. B 2005, 71, 104416. [Google Scholar] [CrossRef]
- Hirai, D.; Sagayama, H.; Gao, S.; Ohsumi, H.; Chen, G.; Arima, T.h.; Hiroi, Z. Detection of multipolar orders in the spin-orbit-coupled 5d Mott insulator Ba2MgReO6. Phys. Rev. Res. 2020, 2, 022063. [Google Scholar] [CrossRef]
- Mansouri Tehrani, A.; Spaldin, N.A. Untangling the structural, magnetic dipole, and charge multipolar orders in Ba2MgReO6. Phys. Rev. Mater. 2021, 5, 104410. [Google Scholar] [CrossRef]
- Lovesey, S.W.; Khalyavin, D.D. Magnetic order and 5d1 multipoles in a rhenate double perovskite Ba2MgReO6. Phys. Rev. B 2021, 103, 235160. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys.: Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef]
- Ikhlas, M.; Tomita, T.; Koretsune, T.; Suzuki, M.T.; Nishio-Hamane, D.; Arita, R.; Otani, Y.; Nakatsuji, S. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 2017, 13, 1085. [Google Scholar] [CrossRef]
- Kuroda, K.; Tomita, T.; Suzuki, M.T.; Bareille, C.; Nugroho, A.; Goswami, P.; Ochi, M.; Ikhlas, M.; Nakayama, M.; Akebi, S.; et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 2017, 16, 1090. [Google Scholar] [CrossRef]
- Higo, T.; Man, H.; Gopman, D.B.; Wu, L.; Koretsune, T.; van’t Erve, O.M.; Kabanov, Y.P.; Rees, D.; Li, Y.; Suzuki, M.T.; et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics 2018, 12, 73. [Google Scholar] [CrossRef]
- Yamasaki, Y.; Nakao, H.; Arima, T.h. Augmented Magnetic Octupole in Kagomé 120-degree Antiferromagnets Detectable via X-ray Magnetic Circular Dichroism. J. Phys. Soc. Jpn. 2020, 89, 083703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 2021, 103, L180407. [Google Scholar] [CrossRef]
- Kimata, M.; Sasabe, N.; Kurita, K.; Yamasaki, Y.; Tabata, C.; Yokoyama, Y.; Kotani, Y.; Ikhlas, M.; Tomita, T.; Amemiya, K.; et al. X-ray study of ferroic octupole order producing anomalous Hall effect. Nat. Commun. 2021, 12, 5582. [Google Scholar] [CrossRef]
- Sasabe, N.; Kimata, M.; Nakamura, T. Presence of X-Ray Magnetic Circular Dichroism Signal for Zero-Magnetization Antiferromagnetic State. Phys. Rev. Lett. 2021, 126, 157402. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I. On the magneto-electrical effect in antiferromagnets. Sov. Phys. JETP 1960, 10, 628–629. [Google Scholar]
- Astrov, D. The magnetoelectric effect in antiferromagnetics. Sov. Phys. JETP-USSR 1960, 11, 708–709. [Google Scholar]
- Astrov, D. Magnetoelectric effect in chromium oxide. Sov. Phys. JETP 1961, 13, 729–733. [Google Scholar]
- Folen, V.J.; Rado, G.T.; Stalder, E.W. Anisotropy of the Magnetoelectric Effect in Cr2O3. Phys. Rev. Lett. 1961, 6, 607–608. [Google Scholar] [CrossRef]
- Shitade, A.; Watanabe, H.; Yanase, Y. Theory of orbital magnetic quadrupole moment and magnetoelectric susceptibility. Phys. Rev. B 2018, 98, 020407(R). [Google Scholar] [CrossRef]
- Fischer, E.; Gorodetsky, G.; Hornreich, R. A new family of magnetoelectric materials: A2M4O9 (A= Ta, Nb; M= Mn, Co). Solid State Commun. 1972, 10, 1127–1132. [Google Scholar] [CrossRef]
- Khanh, N.D.; Abe, N.; Sagayama, H.; Nakao, A.; Hanashima, T.; Kiyanagi, R.; Tokunaga, Y.; Arima, T. Magnetoelectric coupling in the honeycomb antiferromagnet Co4Nb2O9. Phys. Rev. B 2016, 93, 075117. [Google Scholar] [CrossRef]
- Khanh, N.D.; Abe, N.; Kimura, S.; Tokunaga, Y.; Arima, T. Manipulation of electric polarization with rotating magnetic field in a honeycomb antiferromagnet Co4Nb2O9. Phys. Rev. B 2017, 96, 094434. [Google Scholar] [CrossRef]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Yamaura, J.i.; Hiroi, Z. Crystal structure and magnetic properties of the 5d transition metal oxides AOsO4(A = K, Rb, Cs). Phys. Rev. B 2019, 99, 155113. [Google Scholar] [CrossRef]
- Saito, H.; Uenishi, K.; Miura, N.; Tabata, C.; Hidaka, H.; Yanagisawa, T.; Amitsuka, H. Evidence of a New Current-Induced Magnetoelectric Effect in a Toroidal Magnetic Ordered State of UNi4B. J. Phys. Soc. Jpn. 2018, 87, 033702. [Google Scholar] [CrossRef]
- Gitgeatpong, G.; Zhao, Y.; Avdeev, M.; Piltz, R.O.; Sato, T.J.; Matan, K. Magnetic structure and Dzyaloshinskii-Moriya interaction in the S=12 helical-honeycomb antiferromagnet α-Cu2V2O7. Phys. Rev. B 2015, 92, 024423. [Google Scholar] [CrossRef]
- Gitgeatpong, G.; Suewattana, M.; Zhang, S.; Miyake, A.; Tokunaga, M.; Chanlert, P.; Kurita, N.; Tanaka, H.; Sato, T.J.; Zhao, Y.; et al. High-field magnetization and magnetic phase diagram of α-Cu2V2O7. Phys. Rev. B 2017, 95, 245119. [Google Scholar] [CrossRef]
- Gitgeatpong, G.; Zhao, Y.; Piyawongwatthana, P.; Qiu, Y.; Harriger, L.W.; Butch, N.P.; Sato, T.J.; Matan, K. Nonreciprocal Magnons and Symmetry-Breaking in the Noncentrosymmetric Antiferromagnet. Phys. Rev. Lett. 2017, 119, 047201. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Magnetic hexadecapole order and magnetopiezoelectric metal state in Ba1-xKxMn2As2. Phys. Rev. B 2017, 96, 064432. [Google Scholar] [CrossRef]
- Shiomi, Y.; Watanabe, H.; Masuda, H.; Takahashi, H.; Yanase, Y.; Ishiwata, S. Observation of a Magnetopiezoelectric Effect in the Antiferromagnetic Metal EuMnBi2. Phys. Rev. Lett. 2019, 122, 127207. [Google Scholar] [CrossRef]
- Kusunose, H.; Hayami, S. Generalization of microscopic multipoles and cross-correlated phenomena by their orderings. J. Phys. Condens. Matter 2022, 34, 464002. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Day, P.; Moore, M.W.; Wilkinson, C.; Ziebeck, K.R.A. Neutron diffraction study of the incommensurate magnetic phase of Ni0.92Zn0.08Br2. J. Phys. C Solid State Phys. 1981, 14, 3423. [Google Scholar] [CrossRef]
- Regnault, L.; Rossat-Mignod, J.; Adam, A.; Billerey, D.; Terrier, C. Inelastic neutron scattering investigation of the magnetic excitations in the helimagnetic state of NiBr2. J. Phys. 1982, 43, 1283–1290. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Nambu, Y.; Tonomura, H.; Sakai, O.; Jonas, S.; Broholm, C.; Tsunetsugu, H.; Qiu, Y.; Maeno, Y. Spin disorder on a triangular lattice. Science 2005, 309, 1697–1700. [Google Scholar] [CrossRef]
- Ghimire, N.; Ronning, F.; Williams, D.; Scott, B.; Luo, Y.; Thompson, J.; Bauer, E. Investigation of the physical properties of the tetragonal CeMAl4Si2 (M= Rh, Ir, Pt) compounds. J. Phys. Condens. Matter 2014, 27, 025601. [Google Scholar] [CrossRef] [PubMed]
- Gunasekera, J.; Harriger, L.; Dahal, A.; Maurya, A.; Heitmann, T.; Disseler, S.M.; Thamizhavel, A.; Dhar, S.; Singh, D.J.; Singh, D.K. Electronic nature of the lock-in magnetic transition in CeXAl4Si2. Phys. Rev. B 2016, 93, 155151. [Google Scholar] [CrossRef]
- Yoshimori, A. A new type of antiferromagnetic structure in the rutile type crystal. J. Phys. Soc. Jpn. 1959, 14, 807–821. [Google Scholar] [CrossRef]
- Kaplan, T.A. Some Effects of Anisotropy on Spiral Spin-Configurations with Application to Rare-Earth Metals. Phys. Rev. 1961, 124, 329–339. [Google Scholar] [CrossRef]
- Elliott, R.J. Phenomenological Discussion of Magnetic Ordering in the Heavy Rare-Earth Metals. Phys. Rev. 1961, 124, 346–353. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Katsura, H.; Nagaosa, N.; Balatsky, A.V. Spin Current and Magnetoelectric Effect in Noncollinear Magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef] [PubMed]
- Mostovoy, M. Ferroelectricity in Spiral Magnets. Phys. Rev. Lett. 2006, 96, 067601. [Google Scholar] [CrossRef] [PubMed]
- Sergienko, I.A.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef]
- Harris, A.B.; Yildirim, T.; Aharony, A.; Entin-Wohlman, O. Towards a microscopic model of magnetoelectric interactions in Ni3V2O8. Phys. Rev. B 2006, 73, 184433. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Cardias, R.; Szilva, A.; Bezerra-Neto, M.; Ribeiro, M.; Bergman, A.; Kvashnin, Y.O.; Fransson, J.; Klautau, A.; Eriksson, O.; Nordström, L. First-principles Dzyaloshinskii–Moriya interaction in a non-collinear framework. Sci. Rep. 2020, 10, 20339. [Google Scholar] [CrossRef]
- Hayami, S. Mechanism of antisymmetric spin polarization in centrosymmetric multiple-Q magnets based on effective chiral bilinear and biquadratic spin cross products. Phys. Rev. B 2022, 105, 024413. [Google Scholar] [CrossRef]
- Sukhachov, P.; Linder, J. Impurity-induced Friedel oscillations in altermagnets and p-wave magnets. Phys. Rev. B 2024, 110, 205114. [Google Scholar] [CrossRef]
- Brekke, B.; Sukhachov, P.; Giil, H.G.; Brataas, A.; Linder, J. Minimal Models and Transport Properties of Unconventional p-Wave Magnets. Phys. Rev. Lett. 2024, 133, 236703. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Complete Multipole Basis Set for Single-Centered Electron Systems. J. Phys. Soc. Jpn. 2020, 89, 104704. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Kusunose, H.; Hayami, S. Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena. Phys. Rev. B 2021, 104, 054412. [Google Scholar] [CrossRef]
- Rashba, E.I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Ishizaka, K.; Bahramy, M.; Murakawa, H.; Sakano, M.; Shimojima, T.; Sonobe, T.; Koizumi, K.; Shin, S.; Miyahara, H.; Kimura, A.; et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 2011, 10, 521–526. [Google Scholar] [CrossRef] [PubMed]
- Bahramy, M.S.; Arita, R.; Nagaosa, N. Origin of giant bulk Rashba splitting: Application to BiTeI. Phys. Rev. B 2011, 84, 041202(R). [Google Scholar] [CrossRef]
- Sunko, V.; Rosner, H.; Kushwaha, P.; Khim, S.; Mazzola, F.; Bawden, L.; Clark, O.; Riley, J.; Kasinathan, D.; Haverkort, M.; et al. Maximal Rashba-like spin splitting via kinetic-energy-coupled inversion-symmetry breaking. Nature 2017, 549, 492–496. [Google Scholar] [CrossRef]
- Edelstein, V.M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Charge density waves in multiple-Q spin states. Phys. Rev. B 2021, 104, 144404. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. USA 2013, 110, 3738–3742. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Kishine, J.i.; Kusunose, H.; Yamamoto, H.M. On the definition of chirality and enantioselective fields. Isr. J. Chem. 2022, 62, e202200049. [Google Scholar] [CrossRef]
- Inda, A.; Oiwa, R.; Hayami, S.; Yamamoto, H.M.; Kusunose, H. Quantification of chirality based on electric toroidal monopole. J. Chem. Phys. 2024, 160, 184117. [Google Scholar] [CrossRef]
- Rikken, G.; Raupach, E. Observation of magneto-chiral dichroism. Nature 1997, 390, 493–494. [Google Scholar] [CrossRef]
- Rikken, G.L.J.A.; Fölling, J.; Wyder, P. Electrical Magnetochiral Anisotropy. Phys. Rev. Lett. 2001, 87, 236602. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, T.; Shimokawa, Y.; Kobayashi, K.; Itou, T. Observation of current-induced bulk magnetization in elemental tellurium. Nat. Commun. 2017, 8, 954. [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H.; Motome, Y. Electric Toroidal Quadrupoles in the Spin-Orbit-Coupled Metal Cd2Re2O7. Phys. Rev. Lett. 2019, 122, 147602. [Google Scholar] [CrossRef] [PubMed]

| Basis | |||||
|---|---|---|---|---|---|
| s-s | |||||
| p-p | |||||
| s-p | |||||
| Irrep. | MP | Peak Positions w/SOC | w/o SOC |
|---|---|---|---|
| , , , , , , | 0, , | 0 | |
| , , | — | — | |
| , , | — | ||
| , , | — | — | |
| , , | — | — | |
| , , | 0, , | — | |
| , , | — | — | |
| , , | — | ||
| , , | — | — | |
| , , , , , , | , | ||
| , , , , , , | — | — | |
| , , , , , , | , | ||
| , , | , | ||
| , , | — | — | |
| , , | , | 1Q | |
| , , | — | — |
| Irrep. | MP | Peak Positions w/SOC | w/o SOC |
|---|---|---|---|
| , , , , , , | 0, | 0 | |
| , , | — | — | |
| , , | — | — | |
| , , | — | ||
| , , | 0, | — | |
| , , | — | — | |
| , , | — | — | |
| , , | — | ||
| , , | — | — | |
| , , , , , , | , | ||
| , , , , , , | , | ||
| , , , , , , | — | — | |
| , , | — | — | |
| , , | , | ||
| , , | , | 1Q | |
| , , | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Locally Odd-Parity Hybridization Induced by Spiral Magnetic Textures. Magnetism 2025, 5, 24. https://doi.org/10.3390/magnetism5040024
Hayami S. Locally Odd-Parity Hybridization Induced by Spiral Magnetic Textures. Magnetism. 2025; 5(4):24. https://doi.org/10.3390/magnetism5040024
Chicago/Turabian StyleHayami, Satoru. 2025. "Locally Odd-Parity Hybridization Induced by Spiral Magnetic Textures" Magnetism 5, no. 4: 24. https://doi.org/10.3390/magnetism5040024
APA StyleHayami, S. (2025). Locally Odd-Parity Hybridization Induced by Spiral Magnetic Textures. Magnetism, 5(4), 24. https://doi.org/10.3390/magnetism5040024






