Modelling the Elliptical Instability of Magnetic Skyrmions
Abstract
1. Introduction
2. The Chiral Magnet Model
3. Methods
3.1. The Zero-Energy Stripe Domain Method
3.2. The Diverging Lengthscale Method
4. Results
4.1. Skyrmions in the Symmetry-Breaking Phase of the Chiral Magnet
4.2. Skyrmions and Antiskyrmions in the Chiral Magnet with Tilted Applied Field and Anisotropy
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Minima of the General Chiral Magnet Potential
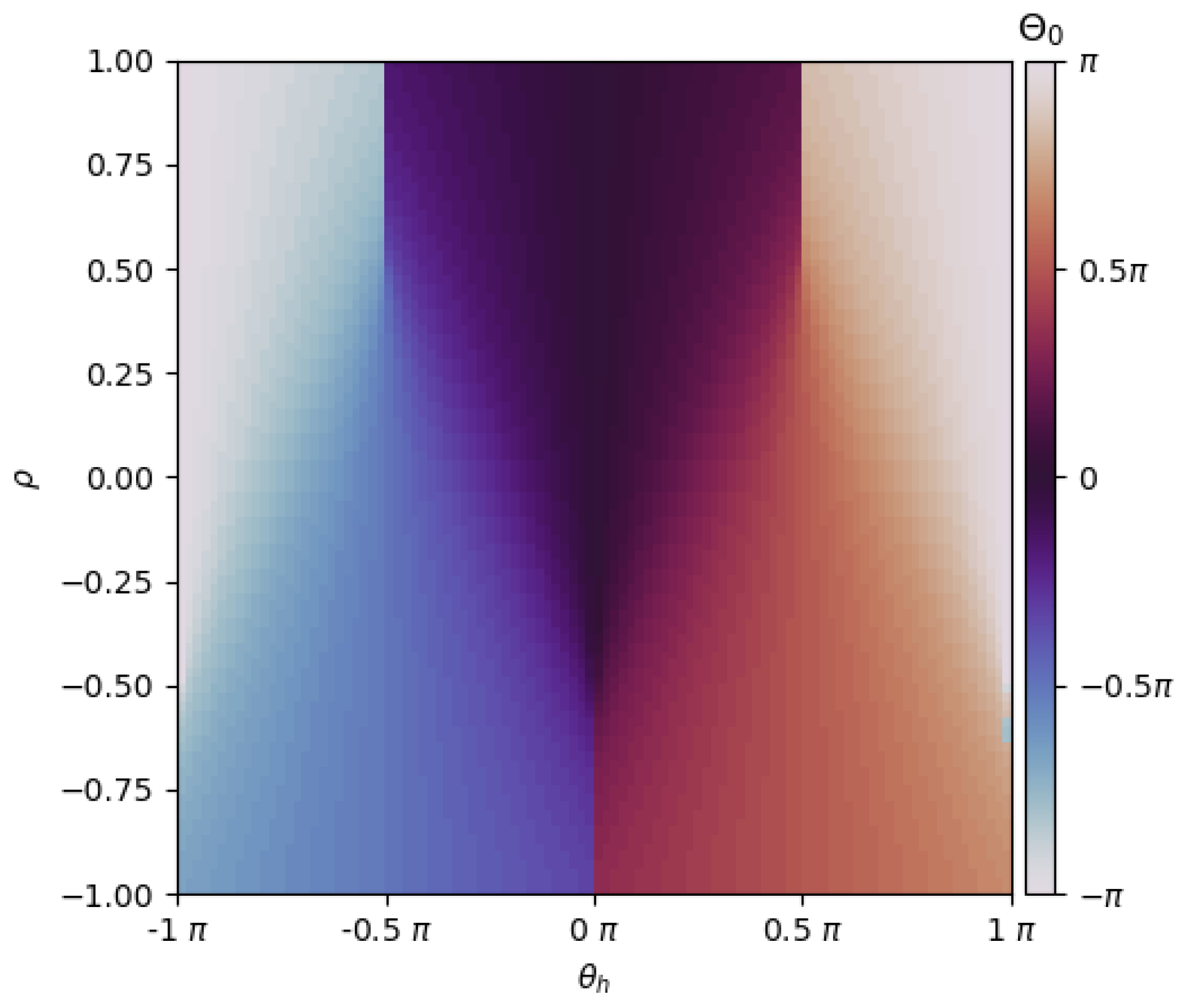
Appendix B. Decay Lengthscale of the General Linearised Euler–Lagrange Equations
References
- Bogdanov, A.N.; Yablonskii, D. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Zh. Eksp. Teor. Fiz 1989, 95, 178. [Google Scholar]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Onose, Y.; Kanazawa, N.; Park, J.; Han, J.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Papanicolaou, N.; Tomaras, T. Dynamics of magnetic vortices. Nucl. Phys. B 1991, 360, 425–462. [Google Scholar] [CrossRef]
- Bogdanov, A. New localized solutions of the nonlinear field equations. ZhETF Pisma Redaktsiiu 1995, 62, 231. [Google Scholar]
- Foster, D.; Kind, C.; Ackerman, P.J.; Tai, J.S.B.; Dennis, M.R.; Smalyukh, I.I. Two-dimensional skyrmion bags in liquid crystals and ferromagnets. Nat. Phys. 2019, 15, 655–659. [Google Scholar] [CrossRef]
- Huang, P.; Schönenberger, T.; Cantoni, M.; Heinen, L.; Magrez, A.; Rosch, A.; Carbone, F.; Rønnow, H.M. Melting of a skyrmion lattice to a skyrmion liquid via a hexatic phase. Nat. Nanotechnol. 2020, 15, 761–767. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Müller, J. Magnetic Skyrmions on a Two-Lane Racetrack. New J. Phys. 2017, 19, 025002. [Google Scholar] [CrossRef]
- Zheng, F.; Rybakov, F.N.; Borisov, A.B.; Song, D.; Wang, S.; Li, Z.A.; Du, H.; Kiselev, N.S.; Caron, J.; Kovács, A.; et al. Experimental observation of chiral magnetic bobbers in B20-type FeGe. Nat. Nanotechnol. 2017, 13, 451–455. [Google Scholar] [CrossRef]
- Zhang, X.; Ezawa, M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef]
- Song, K.; Jeong, J.S.; Pan, B.; Zhang, X.; Xia, J.; Cha, S.; Park, T.E.; Kim, K.; Finizio, S.; Raabe, J.; et al. Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 2020, 3, 148. [Google Scholar] [CrossRef]
- Yokouchi, T.; Sugimoto, S.; Rana, B.; Seki, S.; Ogawa, N.; Shiomi, Y.; Kasai, S.; Otani, Y. Pattern recognition with neuromorphic computing using magnetic field–induced dynamics of skyrmions. Sci. Adv. 2022, 8, eabq5652. [Google Scholar] [CrossRef]
- Rybakov, F.N.; Kiselev, N.S. Chiral magnetic skyrmions with arbitrary topological charge. Phys. Rev. B 2019, 99, 064437. [Google Scholar] [CrossRef]
- Kuchkin, V.M.; Barton-Singer, B.; Rybakov, F.N.; Blügel, S.; Schroers, B.J.; Kiselev, N.S. Magnetic skyrmions, chiral kinks, and holomorphic functions. Phys. Rev. B 2020, 102, 144422. [Google Scholar] [CrossRef]
- Kuchkin, V.M.; Chichay, K.; Barton-Singer, B.; Rybakov, F.N.; Blügel, S.; Schroers, B.J.; Kiselev, N.S. Geometry and symmetry in skyrmion dynamics. Phys. Rev. B 2021, 104, 165116. [Google Scholar] [CrossRef]
- Barton-Singer, B.; Schroers, B.J. Stability and asymptotic interactions of chiral magnetic skyrmions in tilted magnetic field. arXiv 2023, arXiv:2211.08017. [Google Scholar] [CrossRef]
- Göbel, B.; Mertig, I.; Tretiakov, O.A. Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles. Phys. Rep. 2021, 895, 1–28. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjet. 1935, 8, 153. [Google Scholar]
- Hubert, A.; Bogdanov, A. The Properties of Isolated Magnetic Vortices. Phys. Status Solidi (b) 1994, 186, 527–543. [Google Scholar] [CrossRef]
- Bogdanov, A.; Hubert, A. The stability of vortex-like structures in uniaxial ferromagnets. J. Magn. Magn. Mater. 1999, 195, 182–192. [Google Scholar] [CrossRef]
- Li, X.; Melcher, C. Stability of axisymmetric chiral skyrmions. J. Funct. Anal. 2018, 275, 2817–2844. [Google Scholar] [CrossRef]
- Kuchkin, V.M.; Kiselev, N.S. Turning a chiral skyrmion inside out. Phys. Rev. B 2020, 101, 064408. [Google Scholar] [CrossRef]
- Kharkov, Y.A.; Sushkov, O.P.; Mostovoy, M. Bound States of Skyrmions and Merons near the Lifshitz Point. Phys. Rev. Lett. 2017, 119, 207201. [Google Scholar] [CrossRef]
- Leonov, A.; Kézsmárki, I. Asymmetric isolated skyrmions in polar magnets with easy-plane anisotropy. Phys Rev B. Solid State 2017, 96, 014423. [Google Scholar] [CrossRef]
- Leonov, A.O.; Kézsmárki, I. Skyrmion robustness in noncentrosymmetric magnets with axial symmetry: The role of anisotropy and tilted magnetic fields. Phys. Rev. B 2017, 96, 214413. [Google Scholar] [CrossRef]
- Büttner, F.; Lemesh, I.; Beach, G.S. Theory of isolated magnetic skyrmions: From fundamentals to room temperature applications. Sci. Rep. 2018, 8, 4464. [Google Scholar] [CrossRef]
- Gioia, G.; James, R.D. Micromagnetics of Very Thin Films. Proceedings Math. Phys. Eng. Sci. 1997, 453, 213–223. [Google Scholar] [CrossRef]
- Davoli, E.; Di Fratta, G.; Praetorius, D.; Ruggeri, M. Micromagnetics of thin films in the presence of Dzyaloshinskii—Moriya interaction. Math. Model. Methods Appl. Sci. 2022, 32, 911–939. [Google Scholar] [CrossRef]
- Fratta, G.D.; Muratov, C.B.; Slastikov, V.V. Reduced energies for thin ferromagnetic films with perpendicular anisotropy. Math. Model. Methods Appl. Sci. 2023, 34, 1861–1904. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Schroers, B. Gauged sigma models and magnetic Skyrmions. SciPost Phys. 2019, 7, 030. [Google Scholar] [CrossRef]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 13, L881–L885. [Google Scholar] [CrossRef]
- Han, J.H.; Zang, J.; Yang, Z.; Park, J.H.; Nagaosa, N. Skyrmion lattice in a two-dimensional chiral magnet. Phys. Rev. B 2010, 82, 094429. [Google Scholar] [CrossRef]
- Barton-Singer, B.; Ross, C.; Schroers, B.J. Magnetic skyrmions at critical coupling. Commun. Math. Phys. 2020, 375, 2259–2280. [Google Scholar] [CrossRef]
- Palais, R. The principle of symmetric criticality. Commun. Math. Phys. 1979, 69, 19–30. [Google Scholar] [CrossRef]
- Ross, C.; Sakai, N.; Nitta, M. Exact ground states and domain walls in one dimensional chiral magnets. J. High Energy Phys. 2021, 2021, 163. [Google Scholar] [CrossRef]
- Kosevich, A.; Ivanov, B.; Kovalev, A. Magnetic Solitons. Phys. Rep. 1990, 194, 117–238. [Google Scholar] [CrossRef]
- Jin, C.; Song, C.; Wang, J.; Liu, Q. Dynamics of antiferromagnetic skyrmion driven by the spin Hall effect. Appl. Phys. Lett. 2016, 109, 182404. [Google Scholar] [CrossRef]
- Komineas, S.; Papanicolaou, N. Traveling skyrmions in chiral antiferromagnets. SciPost Phys. 2020, 8, 86. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barton-Singer, B. Modelling the Elliptical Instability of Magnetic Skyrmions. Magnetism 2024, 4, 305-321. https://doi.org/10.3390/magnetism4040020
Barton-Singer B. Modelling the Elliptical Instability of Magnetic Skyrmions. Magnetism. 2024; 4(4):305-321. https://doi.org/10.3390/magnetism4040020
Chicago/Turabian StyleBarton-Singer, Bruno. 2024. "Modelling the Elliptical Instability of Magnetic Skyrmions" Magnetism 4, no. 4: 305-321. https://doi.org/10.3390/magnetism4040020
APA StyleBarton-Singer, B. (2024). Modelling the Elliptical Instability of Magnetic Skyrmions. Magnetism, 4(4), 305-321. https://doi.org/10.3390/magnetism4040020





