An Update to The Demagnetizing Factor Dataset Calculated for The General Ellipsoid by Osborn

Abstract

The exact formulae for calculating the demagnetizing factors of a general ellipsoid along the three main axes a ≥ b ≥ c have been long known. According to these formulae, the demagnetizing factors depend only on the axial ratios b/a and c/a. Although the calculation of the demagnetizing factors is a straightforward task, the calculation itself is not a simple one. Therefore, tabular and graphical representations of these demagnetizing factor data have also been presented which can then be used for approximating the demagnetizing factors of a rectangular ferromagnetic slab with the same axial ratios. It turned out in our recent study, however, that, in some ranges of axial ratios (e.g., for very small c/a values), the available tables and graphs do not provide sufficient resolution for obtaining the demagnetizing factors with reasonable accuracy. It was decided to calculate these missing values, and they are presented here in both tabular and graphical form by giving instructions for how to obtain conveniently further interpolated data. In addition, the previous and current demagnetizing factor data have been replotted and fitted to a polynomial function with high accuracy. The functional form of these fitting polynomials is presented in a table for the whole range of the axial ratios b/a and c/a. By graphically displaying these functions, one can obtain, in a relatively simple manner, the demagnetizing factors of a general ellipsoid with known axial ratios without the need to directly calculate through the exact formulae. This may be helpful in obtaining a quick estimate for the demagnetizing factors of any rectangular ferromagnetic slab of interest.

1. Introduction

The determination of the anisotropic magnetoresistance (AMR) [1,2] requires the measurement of the field dependence of the resistivity in the configurations when the magnetic field H is parallel to the measuring current (this is called longitudinal magnetoresistance, LMR) and when H is perpendicular to the current (this is the transverse magnetoresistance, TMR). The measurement of the MR(H) curves can be conveniently carried out on thin strip-shaped samples with a current flowing along the long axis of the strip, and the magnetic field H is oriented in the strip plane either parallel or perpendicular to the current flow direction [3].

It turned out, in some recent MR studies of various ferromagnetic materials [4,5,6,7,8], that the shape and width of the low-field LMR(H) and TMR(H) curves were similar for some of the samples whereas they were distinctly different for other samples. The strip-shaped foil samples for the MR(H) measurements were typically 5 to 10 mm long, 1 to 2 mm wide, and 10 to 50 μm thick. In order to reveal the origin of the observed differences in the LMR(H) and TMR(H) curves, magnetization (M) measurements have been subsequently performed [9] on similar strip-shaped samples. These M(H) studies [9] revealed that the differences between the longitudinal and transverse configurations can be well explained by demagnetizing field effects. Two examples are shown in Figure 1 where the magnetization is displayed as a function of the external magnetic field for a cold-rolled Ni₅₀Co₅₀ strip and an electrodeposited nanocrystalline (nc) Ni strip, with the magnetic field oriented in the strip plane parallel (M_L) and transverse (M_T) to the longest edge. These samples have the largest and smallest thickness/length ratio, respectively, showing the huge effect of sample geometry on the transverse magnetization curves. The detailed evaluation of the M(H) study to be published elsewhere [9] necessitated a thorough consideration of the demagnetizing factors for such strip-shaped samples, and this was a major motivation for the present work.

From the viewpoint of the demagnetizing effects, the strip-shaped thin foil samples can be considered as a rectangular ferromagnetic slab which, on the other hand, can be approximated by a general ellipsoid. The exact formulae for calculating the demagnetizing factors of a general ellipsoid along the three main axes a ≥ b ≥ c have been long known [10,11]. According to these formulae, the demagnetizing factors depend only on the axial ratios b/a and c/a. Osborn [10] presented a tabular and graphical representation of the demagnetizing factor data for the general ellipsoid which was then complemented with some further data by Cronemeyer [12].

It should be noted that, following the work of Osborn [10], Stoner [11], and Cronemeyer [12], numerous further studies (see, e.g., Refs. [13,14,15,16,17,18,19,20,21]) have been carried out for calculating the demagnetizing factors of both the general ellipsoid and its specific forms and also various rectangular or circular ferromagnetic slabs, such as rods and disks, by accounting in numerous cases also for the fact that, in not perfectly ellipsoidal objects, the magnetization distribution within the specimen is not homogeneous, in contrast to the general ellipsoid. However, by looking at these reports [13,14,15,16,17,18,19,20,21], it turned out that, whereas they are really useful for the specific cases considered, e.g., for infinite cylinders or rods, the results cannot be straightforwardly applied to the strip-shaped samples with the axial ratios of our interest.

Therefore, we have found it more useful to follow the scheme to rely on the formulae of Osborn [10] and Stoner [11] to directly calculate the required demagnetizing factors of interest for our study. Namely, it turned out that the approximation of a rectangular ferromagnetic slab with a general ellipsoid having the same axial ratios is a fairly good approach since direct experimental determinations of the demagnetizing factors of rectangular slab samples [9,14] have demonstrated a not-too-large deviation. As noted above, such a deviation arises due to the fact that, even in a homogeneous external magnetic field, the magnetization orientation is homogeneous only in a body having the shape of a general ellipsoid. Therefore, in a rectangular slab, the magnetization orientation is inhomogeneous to some extent around the edges [14] as a result of which the effective demagnetizing factor will be somewhat different [9,14] than that calculated for a general ellipsoid having the same axial ratios. The recent magnetic measurements [9] revealed that the experimental demagnetizing factor N_b when the magnetic field is oriented along the slab edge b is about 8% larger only than the N_b value calculated for the corresponding general ellipsoid.

It is, therefore, useful to have available detailed data for the demagnetizing factors of the general ellipsoid for the whole range of axial ratios. It turned out, however, in our recent study [9], that, in some ranges of axial ratios (e.g., for very small c/a values), the available tables and graphs [10,12] do not provide sufficient resolution for obtaining the demagnetizing factors with reasonable accuracy. The two samples shown in Figure 1 correspond to the smallest and largest c/a values (c/a = 0.00074 for nc-Ni and c/a = 0.01533 for Ni₅₀Co₅₀) in our recent work [9]. Thus, the c/a values for our samples fall just in the range where the demagnetizing factors cannot be obtained with reasonable accuracy from previously existing sources.

It was decided, therefore, to calculate these missing values, and they are presented here in both tabular and graphical form by giving instructions for how to conveniently obtain further interpolated data. In addition, the previous and current demagnetizing factor data [10,12] have been replotted and fitted to a polynomial function with high accuracy. The functional form of these fitting polynomials is presented in a table for the whole range of the axial ratios b/a and c/a. By graphically displaying these functions, one can obtain, in a relatively simple manner, the demagnetizing factors of a general ellipsoid with known axial ratios without the need to directly calculate through the exact formulae. This may be helpful in obtaining a quick estimate for the demagnetizing factors of any rectangular ferromagnetic slab of interest.

2. Demagnetizing Factors of the General Ellipsoid

The magnetic induction inside a ferromagnetic specimen is given by the general expression [22]

B = H − NM + 4πM

(1)

where H is the external magnetic field and N is the demagnetizing factor (we use here the CGS system). Strictly speaking, this expression is valid only for a homogeneously magnetized specimen in the form of a general ellipsoid. In this case, the demagnetizing field H_d is also uniform within the specimen and is proportional to the magnetization: H_d = −NM; and this appears in Expression (1). The demagnetizing factor is a scalar quantity along the three main axes a ≥ b ≥ c of the ellipsoid, and for the three demagnetizing factors, the relation

N_a + N_b + N_c = 4π

(2)

holds. Osborn [10] and Stoner [11] have provided exact formulae for the calculation of the demagnetizing factors of the general ellipsoid.

As outlined in the Introduction, a general ellipsoid will be used for approximating the demagnetizing factors of a rectangular slab shown in Figure 2. In this approach, we will approximate the slab with a corresponding inscribed general ellipsoid having the same full axis lengths as the edges of the rectangular slab. (Since the demagnetizing factors depend only on the axial ratios b/a and c/a, any general ellipsoid with the same axial ratios is an equally appropriate approximation, the term “inscribed“ does not represent any restriction, and the same is valid whether the parameters a, b and c are defined as full axes or semiaxes.)

3. New Calculated Data for the Demagnetizing Factors of the General Ellipsoid

As noted in the Introduction, Osborn [10] and Cronemeyer [12] presented tabular values and graphical representations of the dependence of the demagnetizing factors of the general ellipsoid on the axial ratios c/a and b/a for a wide range of the axial ratios. Unfortunately, no useful data were included in these works [10,12] for axial ratios c/a < 0.1. For completing these missing data, by using formulae (2.1)–(2-3) from Osborn [10], we have calculated a set of N/4π values in this c/a range for b/a values of integer multiples of 0.1, and these values are collected in

Table 1. Demagnetizing factors of the general ellipsoid as calculated in the present work from formulae (2.1)–(2.3) from Osborn [10] for selected b/a and c/a values. The N/4π values for c/a = 0.1 were taken from Refs. [10,12] in the case of b/a = 0.1 to 0.9. For b/a = 1.0, we obtained the N/4π values from the formulae for oblate spheroids [10,11,22].

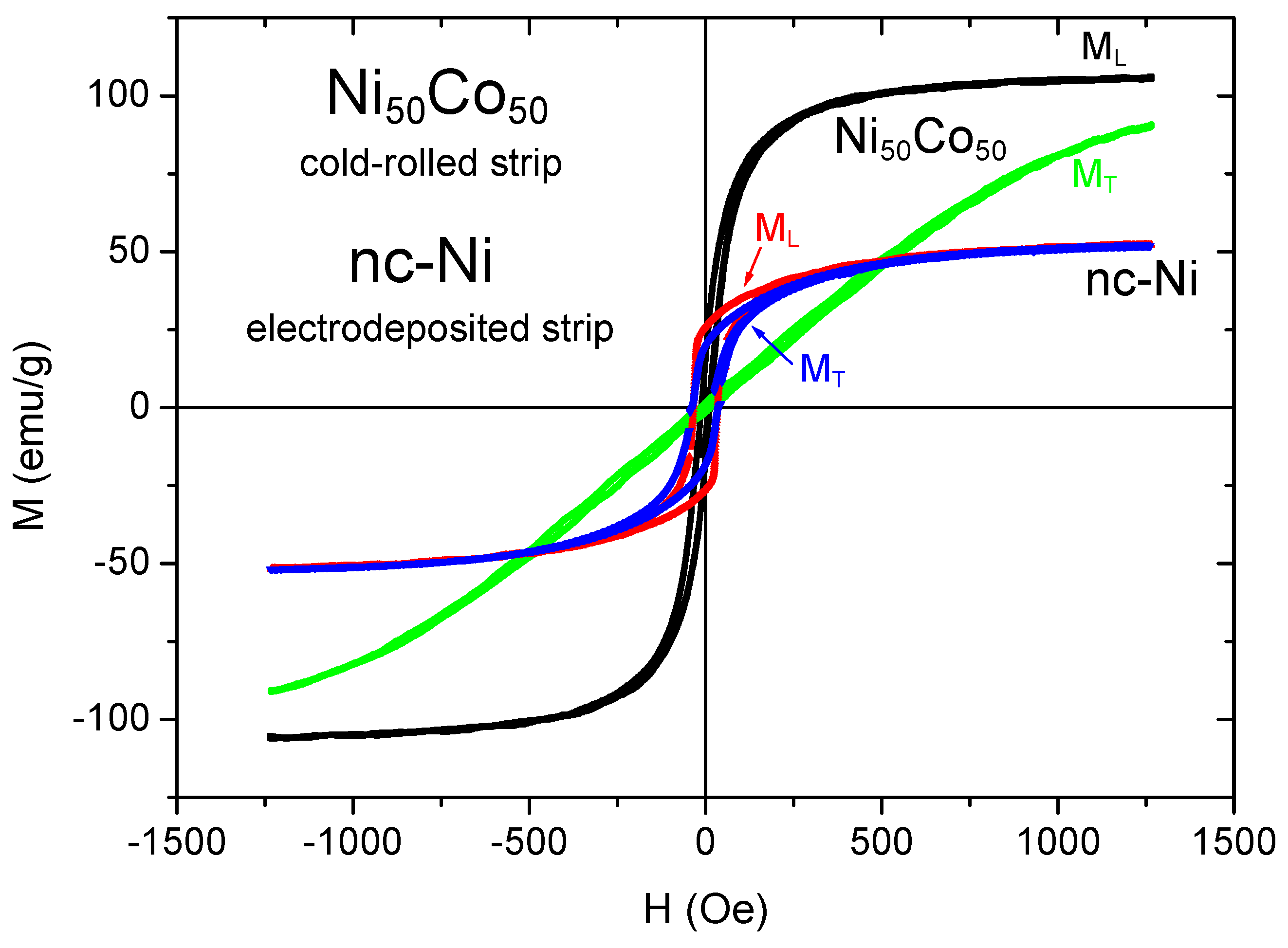
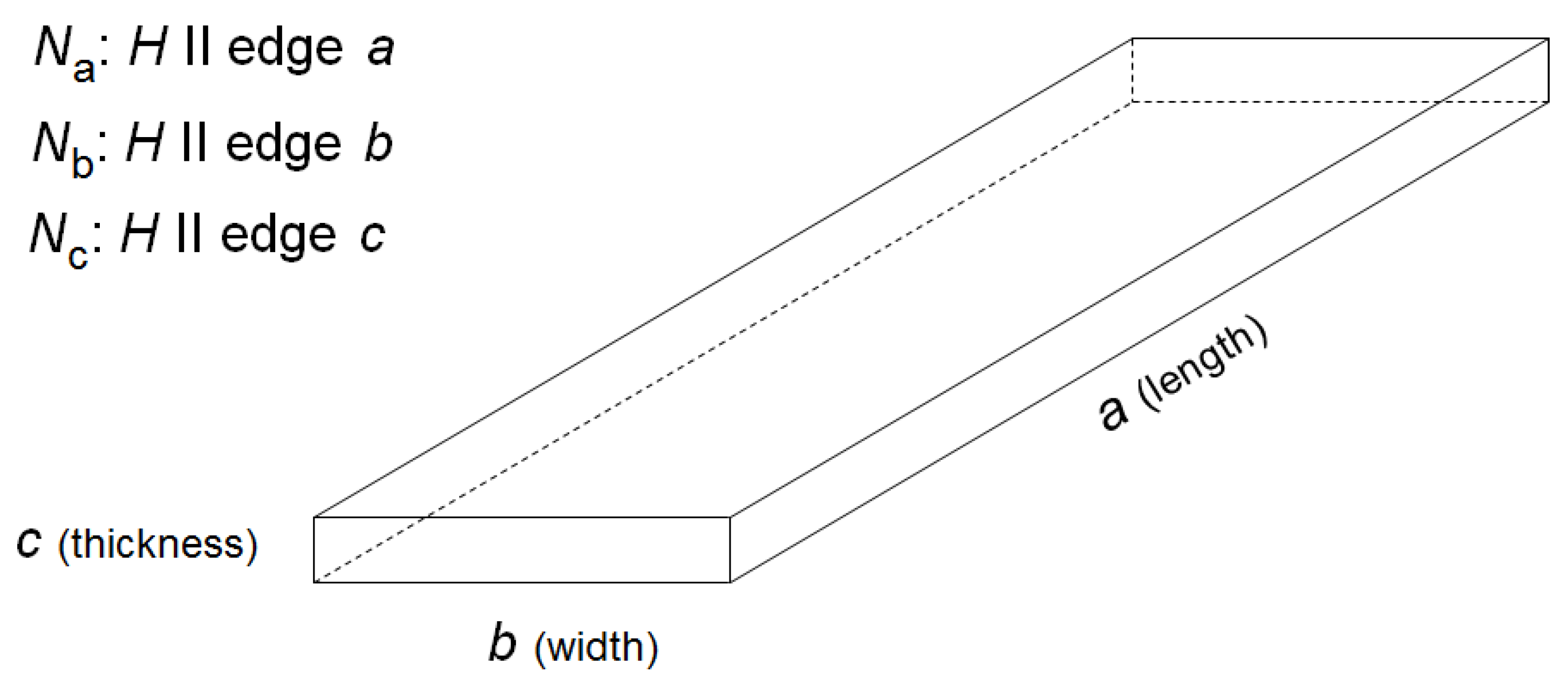
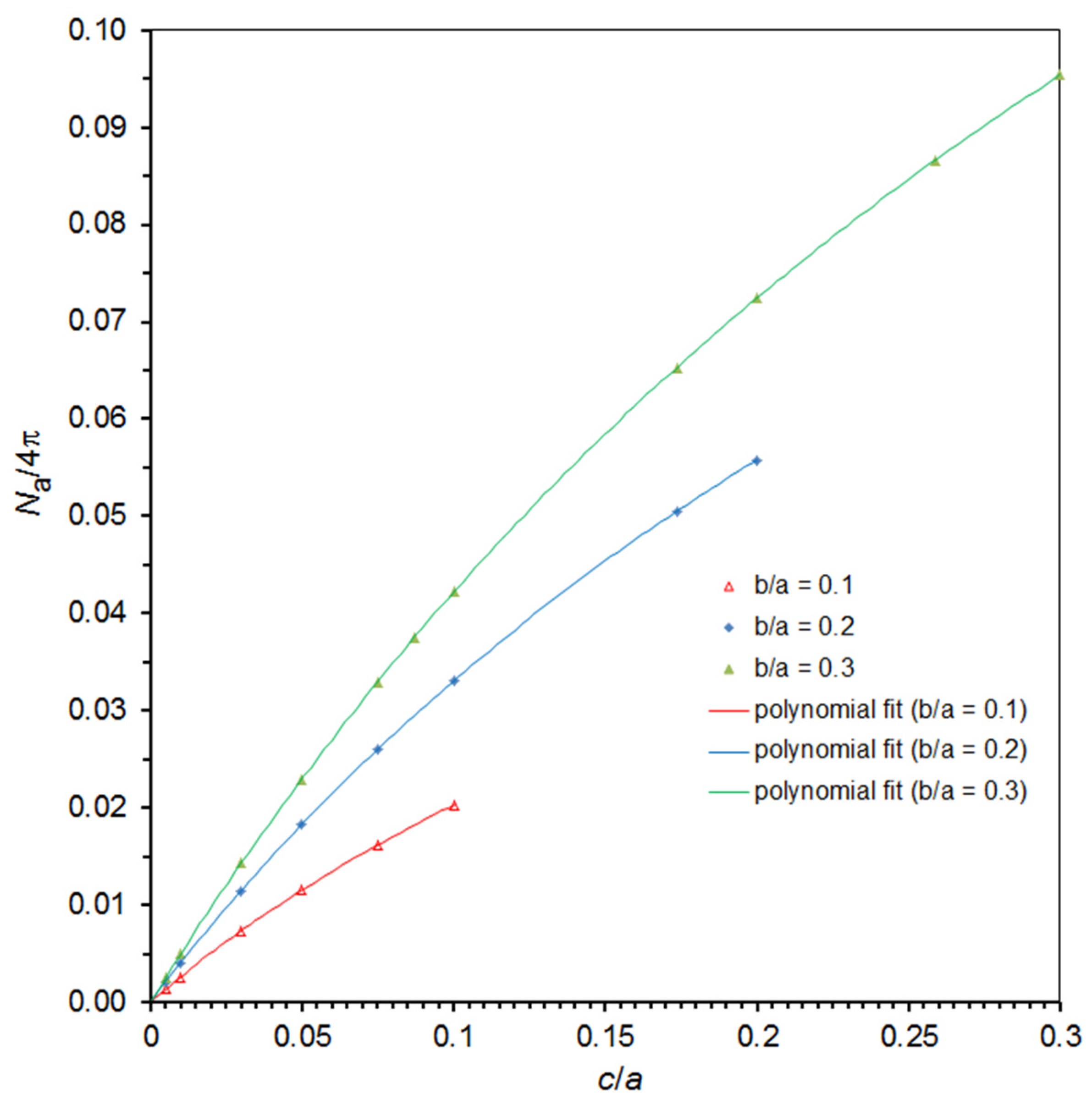
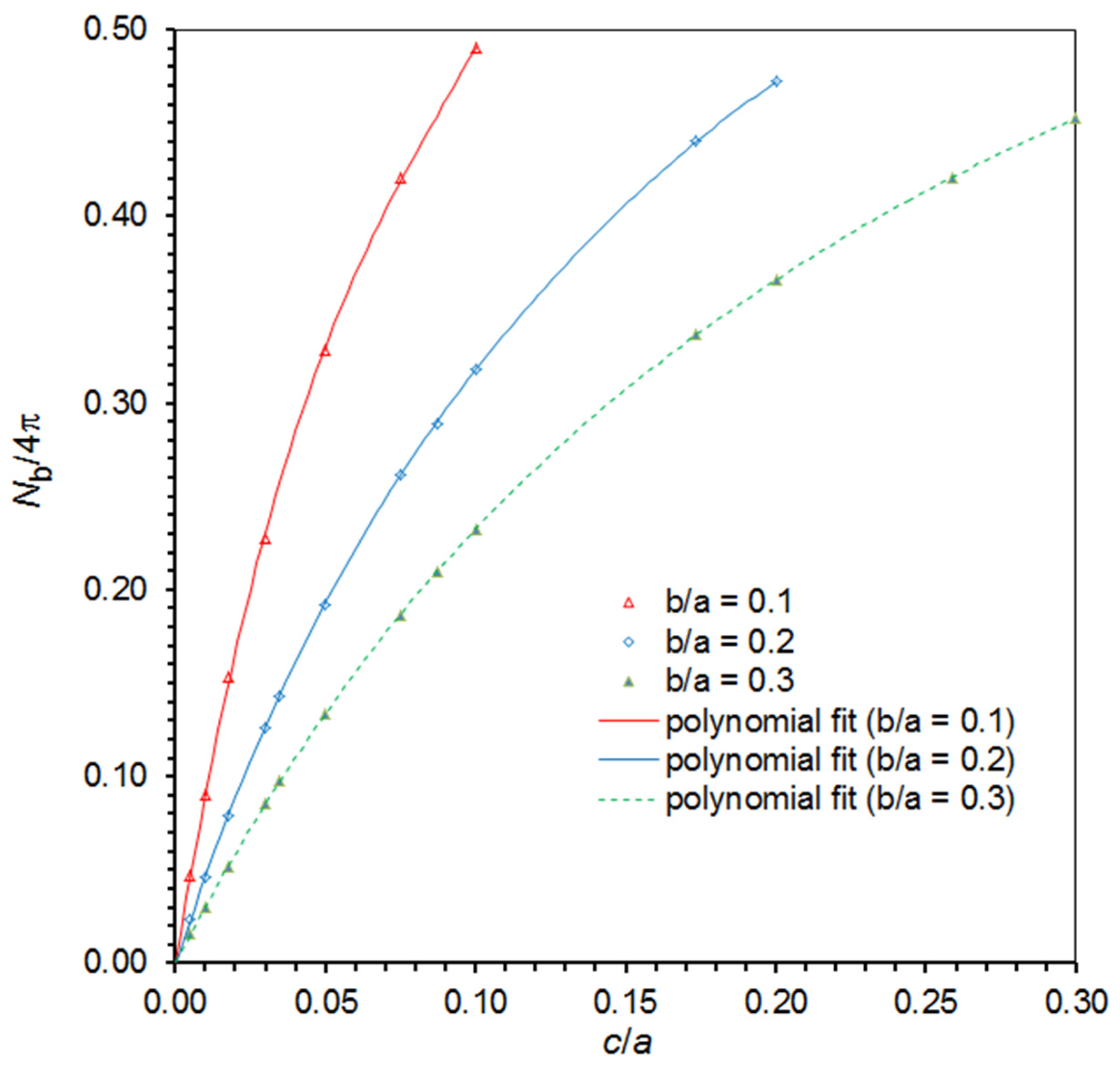
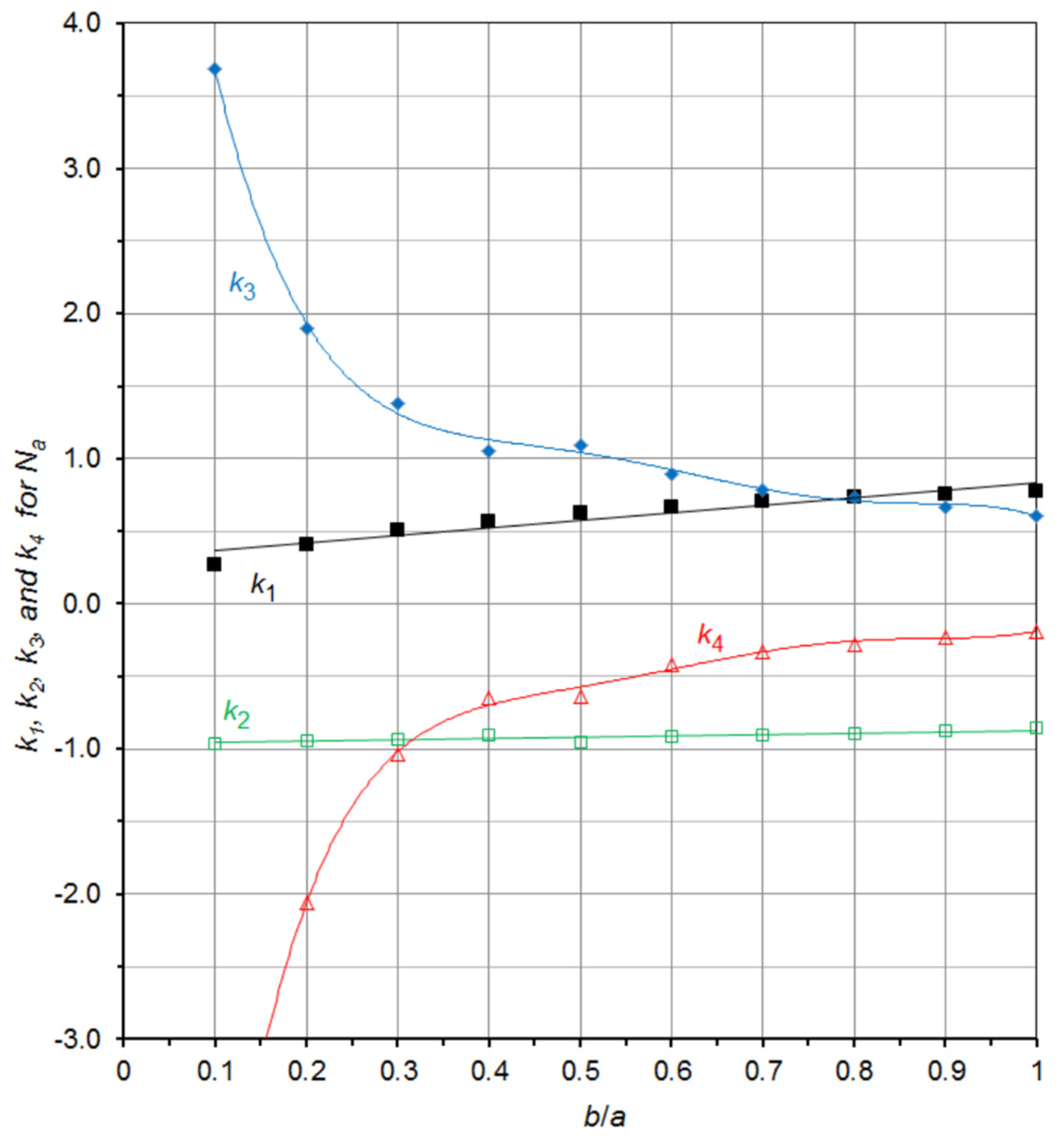
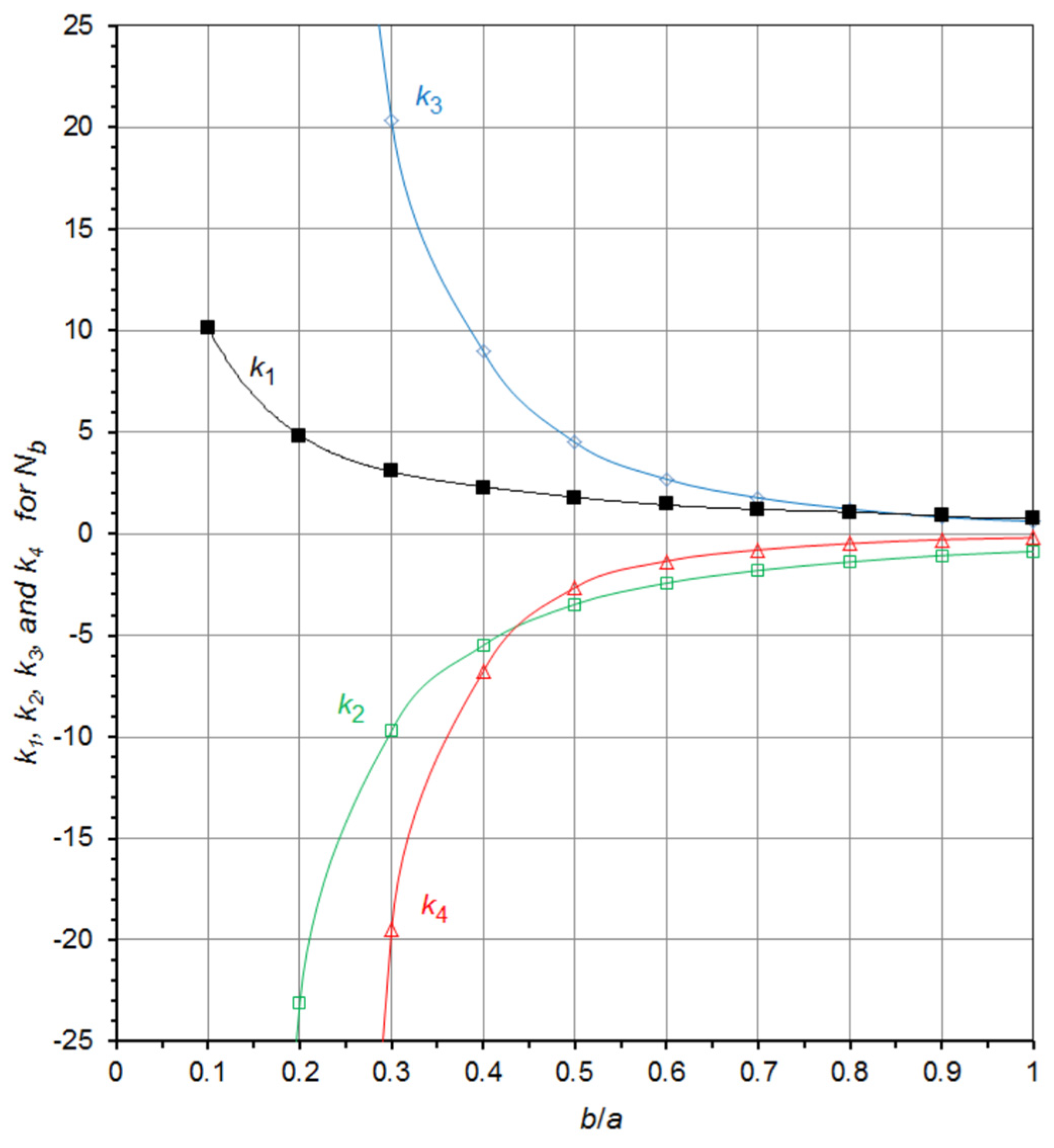
b/a	c/a	Na/4π	Nb/4π	Nc/4π	b/a	c/a	Na/4π	Nb/4π	Nc/4π
0.1	0.005	0.001329	0.047066	0.951605	0.6	0.005	0.003345	0.007197	0.989457
	0.01	0.002612	0.089804	0.907585		0.01	0.006642	0.014259	0.979099
	0.03	0.007338	0.227495	0.765167		0.03	0.019357	0.041225	0.939419
	0.05	0.011528	0.327974	0.660498		0.05	0.031364	0.066289	0.902346
	0.075	0.016171	0.420749	0.563080		0.075	0.045462	0.095223	0.859315
	0.1	0.0203	0.4899	0.4898		0.1	0.0586	0.1218	0.8196
0.2	0.005	0.002023	0.023606	0.974372	0.7	0.005	0.003524	0.006012	0.990464
	0.01	0.003998	0.046050	0.949952		0.01	0.006998	0.011925	0.981077
	0.03	0.011455	0.125752	0.862793		0.03	0.020424	0.034624	0.944952
	0.05	0.018279	0.192259	0.789461		0.05	0.033138	0.055900	0.910962
	0.075	0.026049	0.261274	0.712676		0.075	0.048107	0.080677	0.871216
	0.1	0.0331	0.3183	0.6486		0.1	0.0621	0.1036	0.8343
0.3	0.005	0.002499	0.015477	0.982023	0.8	0.005	0.003671	0.005128	0.991201
	0.01	0.004950	0.030426	0.964623		0.01	0.007294	0.010179	0.982527
	0.03	0.014297	0.085430	0.900273		0.03	0.021311	0.029650	0.949039
	0.05	0.022975	0.133772	0.843253		0.05	0.034611	0.048018	0.917371
	0.075	0.032988	0.186493	0.780519		0.075	0.050305	0.069552	0.880143
	0.1	0.0422	0.2322	0.7256		0.1	0.0651	0.0896	0.8453
0.4	0.005	0.002853	0.011351	0.985796	0.9	0.005	0.003796	0.004444	0.991760
	0.01	0.005657	0.022402	0.971941		0.01	0.007543	0.008829	0.983629
	0.03	0.016410	0.063814	0.919776		0.03	0.022058	0.02578	0.952162
	0.05	0.026474	0.101225	0.872300		0.05	0.035853	0.041849	0.922298
	0.075	0.038182	0.143158	0.818660		0.075	0.052157	0.060793	0.887050
	0.1	0.049	0.1805	0.7705		0.1	0.0675	0.0786	0.8539
0.5	0.005	0.003127	0.008860	0.988013	1	0.005	0.003902	0.003902	0.992196
	0.01	0.006205	0.017526	0.976269		0.01	0.007755	0.007755	0.98449
	0.03	0.018049	0.050368	0.931583		0.03	0.022693	0.022693	0.954615
	0.05	0.029193	0.080545	0.890262		0.05	0.036909	0.036909	0.926181
	0.075	0.042225	0.114965	0.842810		0.075	0.053738	0.053738	0.892524
	0.1	0.0544	0.1462	0.7994		0.1	0.069598	0.069598	0.860804

.

4. A Useful Graphical Representation of the Demagnetizing Factor Data for the General Ellipsoid

In order to provide help for obtaining N values for more c/a and b/a values than available in the published tables and graphs [10,12] and in the present Table 1, it was found useful to replot the available data. Therefore, we have prepared graphs of N_a/4π and N_b/4π as a function of c/a for all values of b/a for which data are available. The datasets N/4π vs. c/a obtained in this manner were fitted for each available value of b/a to a polynomial under the constraint that the polynomial should be zero (N = 0) at c/a = 0.

Examples of these graphs are shown in Figure 3 for the demagnetizing factor N_a/4π and in Figure 4 for N_b/4π. These graphs demonstrate that the available N_a and N_b data for b/a = 0.1, 0.2, and 0.3 can be fitted to a fourth-order polynomial with a very good fit quality. The same order of polynomial was sufficient to obtain similarly good fits for N_a and N_b with b/a = 0.4 to 1.0. The fit quality R2 was at least 0.9999 or even higher for all the fits. The parameters of the polynomial fitting functions are collected in

Table 2. Fit functions y = f(x) = k₄x⁴ + k₃x³ + k₂x²+ k₁x obtained by fitting a fourth-order polynomial to the N/4π vs. c/a data from Refs. [10,12] as well as from Table 1 and graphs shown in Figure 3 and Figure 4 for various fixed values of b/a. The N_c/4π values can then be obtained from Equation (2).

Demagnetizing Factor	b/a	Fitted Polynomials for Na/4π and Nb/4π vs. c/a Data
Na/4π	0.1	y = −8.213325x4 + 3.683730x3 − 0.959648x2 + 0.270340x
	0.2	y = −2.056457x4 + 1.893922x3 − 0.943486x2 + 0.408386x
	0.3	y = −1.036537x4 + 1.383364x3 − 0.937688x2 + 0.502749x
	0.4	y = −0.649740x4 + 1.058068x3 − 0.901723x2 + 0.570613x
	0.5	y = −0.634477x4 + 1.093231x3 − 0.950133x2 + 0.628057x
	0.6	y = −0.416283x4 + 0.892748x3 − 0.918148x2 + 0.669353x
	0.7	y = −0.323111x4 + 0.789552x3 − 0.901536x2 + 0.703562x
	0.8	y = −0.277554x4 + 0.737396x3 − 0.896990x2 + 0.732554x
	0.9	y = −0.226527x4 + 0.664125x3 − 0.875293x2 + 0.754415x
	1.0	y = −0.190013x4 + 0.607244x3 − 0.857422x2 + 0.773218x
Nb/4π	0.1	y = −2725.800x4 + 797.2283x3 − 104.9405x2 + 10.14657x
	0.2	y = −122.1111x4 + 78.27606x3 − 23.08401x2 + 4.822780x
	0.3	y = −19.49980x4 + 20.34586x3 − 9.691984x2 + 3.109993x
	0.4	y = −6.783389x4 + 8.992644x3 − 5.484144x2 + 2.269712x
	0.5	y = −2.650351x4 + 4.504643x3 − 3.476309x2 + 1.769546x
	0.6	y = −1.337034x4 + 2.687582x3 − 2.427738x2 + 1.436237x
	0.7	y = −0.782321x4 + 1.770638x3 − 1.798673x2 + 1.199285x
	0.8	y = −0.475207x4 + 1.211208x3 − 1.377362x2 + 1.022217x
	0.9	y = −0.278778x4 + 0.814805x3 − 1.057882x2 + 0.880707x
	1.0	y = −0.190013x4 + 0.607244x3 − 0.857422x2 + 0.773218x

.

By using these fitting functions, one can now display the demagnetizing factors as a function of c/a for several fixed values of b/a which fall close to the b/a value of the rectangular slab sample of interest. Such plots can now be easily created even for the range of extremely small c/a values which cannot be resolved properly in the graphs presented by Osborn [10]. The good quality of fits ensures that we can reliably estimate the N data in the whole range of c/a values.

Since the b/a values of actual samples are always somewhat different from the fixed b/a values selected as integral multiples of 0.1 only, one should make a non-linear interpolation for actual b/a values in between the displayed polynomial curves in order to obtain a good N value for a given c/a value. We can see, for example, from Table 1, that for c/a = 0.1, we find that N_b/4π = 0.4899 for b/a = 0.1, N_b/4π = 0.3183 for b/a = 0.2, and N_b/4π = 0.2322 for b/a = 0.3. One easily finds that the difference in the N_b/4π values between b/a = 0.1 and b/a = 0.2 is almost precisely a factor of two larger than that between b/a = 0.2 and b/a = 0.3 (0.1716 and 0.0861, respectively). This implies that the N_b/4π value for b/a = 0.15 can be safely obtained by taking a subdivision at a ratio of 2:1 between the N values for b/a = 0.1 and b/a = 0.2, and then we end up with N_b/4π = 0.3755 for b/a = 0.15 at c/a = 0.1. With a similar non-linear interpolation, one can straightforwardly obtain N_b data for any further intermediate b/a values by using Figure 4. The same procedure can also be used for interpolating N_a data with the help of graphs like Figure 3.

Furthermore, the data summarized in Table 2 can be utilized in another manner. Namely, an inspection of the coefficients k₁, k₂, k₃, and k₄ quickly reveals that each coefficient varies fairly smoothly and monotonously with the axial ratio b/a, and this gives us a chance to easily obtain demagnetizing factors for any arbitrary b/a value. For this purpose, we have plotted the coefficients k₁, k₂, k₃, and k₄ as a function of b/a in Figure 5 for N_a and in Figure 6 for N_b. With the help of the gridlines, from these plots, one can make a fairly good reading of all four coefficients for the actual b/a value of the sample of interest. Then, by inserting these values into the fitting equation y = f(x) = k₄x⁴ + k₃x³ + k₂x²+ k₁x together with the actual x = c/a value of the sample, one can directly obtain the N_a and N_b values for any b/a and c/a values with sufficient accuracy.

5. Summary

In the present paper, demagnetizing factor data are reported for the general ellipsoid, which were missing in previous works [10,12]. In addition, all available demagnetizing factor data of the general ellipsoid were displayed as a function of the axial ratio c/a and fitted by a polynomial for each b/a value. The parameters of the fitting polynomials are provided here from which a graphical representation of the demagnetizing factors can be easily created. Some hints were also provided for obtaining interpolated values not displayed. An advantage of the suggested procedure is that one can obtain a good value for the demagnetizing factor values also in axial ratio ranges not available in previous reports [10,12]. It is hoped that the present paper will be useful for quickly obtaining a reliable estimate of the demagnetizing factors for a rectangular slab of interest.