1. Introduction
A precise estimation of the air gap field inside electrical machines is really important in order to properly estimate local and integral quantities and thus predict machine performance. Most of the methods used in the literature start with the study of the air gap field between smooth ferromagnetic surfaces (slotless approach) [
1,
2,
3,
4,
5,
6] and subsequently, the effect on the field due to the presence of slotting is introduced, making use of a slotting function which can also be called the air gap relative permeance function.
The air gap relative permeance function was initially introduced by [
7,
8] using magnetic circuit theories. Magnetomotive force (m.m.f.) and the concept of permeance were used together with conformal mapping in order to retrieve the aforementioned function, which was developed only for a normal flux density component. Making use of a similar approach, Ref. [
9] also studied the behaviour of the tangential component introducing the concept of a complex relative permeability function, useful for calculating quantities like the cogging torque throughout the integration of the Maxwell stress tensor [
10]. Other topologies of the slot opening function were later developed solving the Laplace equations inside the air gap in terms of Fourier series, by assuming the flux density distributions in some region of it, in particular, using approximate functions [
11,
12,
13]. However, most of the approaches present in the literature that refer to these methods, describing the slot opening function, do not consider the effect of adjacent slots [
11,
12,
13,
14,
15,
16], which, in certain circumstances, cannot be neglected. Inside the following work, a procedure to retrieve the slotting function will be introduced, also considering the effects of adjacent slots.
The air gap field of a slotted surface facing a smooth one has been studied for a few decades: the first, classical analysis was based on a conformal mapping method, as developed by Carter, by solving the Schwarz–Christoffel equation [
17,
18].
The air gap relative permeance function was introduced in [
9], where the air gap flux density distribution was obtained by numerically inverting the conformal mapping solution in the complex domain. However, this analysis, as it has already been pointed out previously, did not consider the presence of adjacent slots, being based on a single-slot approach. Thus, it is only sufficiently accurate if the single-slot flux density distributions of adjacent slots do not interfere with each other; this occurs if the equivalent air gap
g is “small” compared to the slot opening
bs and the slot pitch
τs, for example, in induction machines. However, when the equivalent air gap
g is not “small” anymore compared to the slot opening
bs and the slot pitch
τs, the precision of the method gets degraded, due to the effect of adjacent slots being stronger and not negligible anymore.
The approach adopted here is based on the field solution of the Laplace equation in the air gap, for a multi-slot disposition, expressed in terms of Fourier series. To obtain the Fourier coefficients, at first, the single-slot field analytical solution was considered, along a smooth surface, as obtained in [
18]. As for the multi-slot disposition, the calculation was based on the principle of superposition of the lost flux density distribution of each slot. This made the result correct also in the case of a “high” magnetic air gap width, for example, if the machine is a surface mounted permanent magnet (SPM) synchronous machine.
The paper consists of the following: in
Section 2, the formulation of the Laplace equation in the air gap is outlined for a multi-slot disposition, and the symmetry and periodicity field properties are analysed; in
Section 3, the single-slot air gap field was studied by conformal transformation, and the normal component of the flux density distribution along the smooth surface was obtained; in
Section 4, the single-slot lost flux density function is introduced and its distribution was superimposed with those of the other slots, from which the multi-slot opening function was obtained, along the smooth surface; in
Section 5, the integrals for the Fourier coefficient calculation, written for a multi-slot disposition, are reformulated in terms of single-slot Fourier integrals;
Section 6 shows how the slotting function can be expressed in complex form; in
Section 7, a few slot opening function distributions are plotted, for different geometric parameters (with “high” and “small” air gap widths) and for different exploration lines in the air gap, comparing the results with FEM simulations;
Section 8 discusses some numerical convergence and accuracy limits; and in
Section 9, some conclusions and perspectives are drawn.
In all the diagrams illustrated in the following sections, the units of the variables along the axes are omitted, because they are all expressed as pu quantities.
2. Laplace Equation for a Multi-Slot Disposition: Solution Structure and Properties
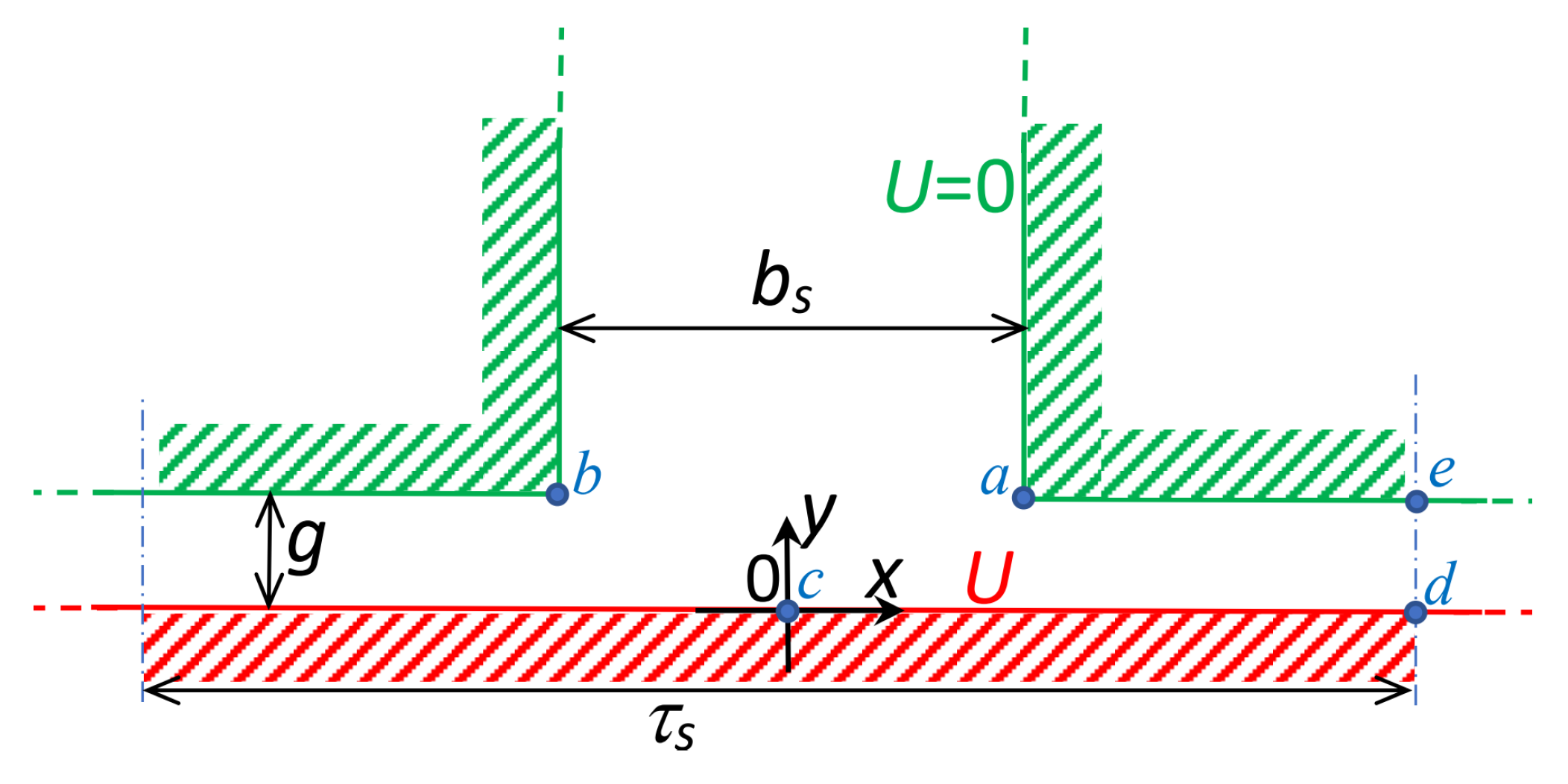
Figure 1 shows the considered air gap geometry, the main dimensions and the reference frame adopted for the analysis of the magnetic field in a slotted air gap.
Let us consider a multi-slot upper surface facing a smooth lower one, where τs is the slot pitch; for this situation, the adopted reference frame xy is centred at the point c.
In the air gap, the magnetic field is described by the vector potential component
A(
x,
y), perpendicular to the
xy plane, as the solution to the Laplace equation:
The generic point (
x,
y) inside the air gap can also be defined by using a complex variable
z that in the
xy reference frame of
Figure 1 can be written as the following:
z =
x +
j·
y.
By adopting the method of separation of the variables,
A(
x,
y) can be written in terms of a series, according to the following expression:
It is easy to verify that (2) satisfies (1).
Considering that the
x and
y flux density components are given by
from (2), we obtain
with
In (2) and in (4),
Bo is the average flux density, calculated within the slot pitch
τs:
while the
By(
x,
y) distribution shape depends on the position
y chosen for the horizontal exploration line in the air gap, it is possible to show that
Bo does not depend on
y.
If the upper surface would have been smooth like the lower one, the flux density in the air gap would possess just the
y component which would be uniform; referring to it as the ideal flux density
Bi, its value can be calculated as
where
U is the magnetic voltage drop across the two surfaces.
If we divide the air gap flux density components in (4) by
Bi, the pu flux density components
βx and
βy can be written as
with
and
where
KC is the Carter’s factor [
17]
From the inspection of (8), the following properties can be recognized, for any value of y (0 ≤ y ≤ g). Of course, the same properties are also valid also for (4):
- -
Equation (8) is periodic in space, along the x axis, with a period equal to the slot pitch τs:
- -
The functions βx and βy are symmetrical with respect to the origin O of the xy reference frame:
- -
For x = ±τs/2, the βx component is zero:
Thus, the solution of (1) was reduced to calculate the coefficients βk (or Ak, from (5) and (9)), for k = 1, 2… ∞. In practice, the series should be extended up to a maximum suited term kM, as will be discussed later.
3. Single-Slot Air Gap Field Analysis by Conformal Transformation
In order to calculate the coefficients
βk, at first, the field of the single-slot system must be studied using conformal transformations [
18], as resumed in this section.
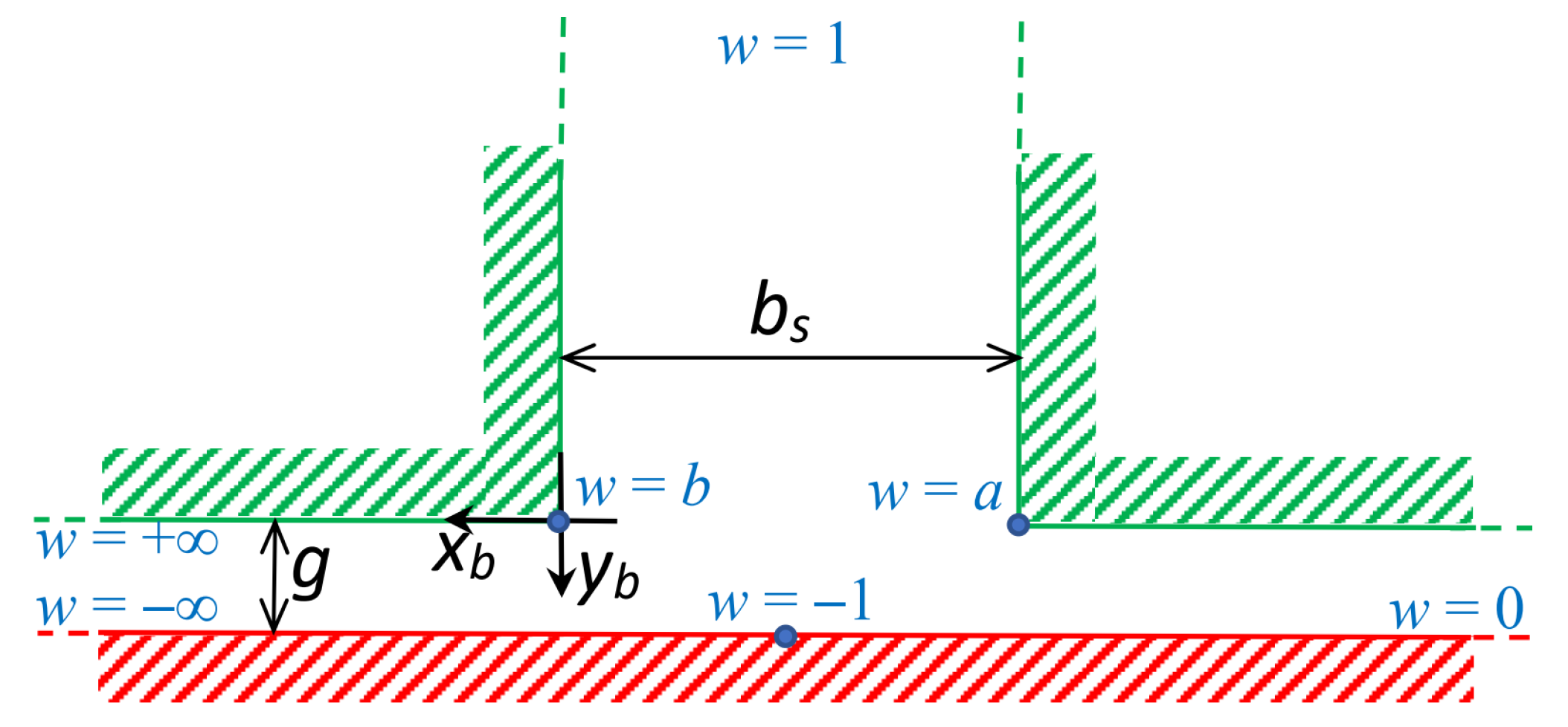
Figure 2 shows the single-slot disposition, with the same air gap and slot opening dimensions considered in
Figure 1.
Here, in order to apply the conformal transformation procedure, a corner of the Schwarz–Christoffel polygon should be chosen as the origin of the plane; thus, the corner
b of
Figure 2 was chosen as the origin of the reference frame
xbyb. The new complex position variable was
zb =
xb +
j·
yb.
By writing the Schwarz–Christoffel equation, the transformation from the
zb plane (
zb =
xb +
j·
yb) to the
w plane (
w =
u +
j·
v) is represented by the following equation [
18]:
where
Then, by integrating (15), the function
zb(
w) was retrieved as
with
As regards the flux density vector in the air gap, for a single-slot configuration (subscript
s), referred to the ideal flux density
Bi, the following expression was obtained, as a function of the complex variable
w [
18]:
from which the
xb and
yb components followed as
In principle, the elimination of the variable w in putting together (17) and (20) would give the slotting opening functions βsx(zb) and βsy(zb) for the single-slot disposition but unfortunately, (17) could not be inverted in closed form.
Moreover, if a generic position
zb =
xb +
j·
yb was considered inside the air gap (with
xb as the exploring variable and
yb <
g kept constant during exploration), the numerical inversion of (18) in the complex domain, as described in [
9], exhibited some convergence issues.
An alternative approach to obtain the Fourier series coefficients
βk of (8) is described in [
12]. It is based on an approximated formulation of the field along the slot opening segment; however, the accuracy of the obtained distributions could be critical, depending on the air gap geometry and on the exploring line position in the air gap.
4. Single-Slot and Multi-Slot Normal Slotting Function along a Smooth Surface
The numerical inversion of (17) was easier along the smooth surface (where yb = g), because the calculation involved just real variables (xb and u); in fact, along the smooth surface, where we had zb = xb + j·g, w = u occurred.
Due to the slotting function symmetry with respect to the slot axis, the interval of interest for
xb was −
bs/2 ≤
xb < ∞, corresponding to −1 ≥
u > −∞ for
w =
u (see
Figure 2); in practice,
ulim = 1013 can be adopted, from which, by (17), it follows that
xlim = Re[
zb(−
ulim)].
For example, with g = 5 mm, bs = 5 mm, τs = 10 mm, we obtained xlim = 45.5 mm = 4.55·τs.
For any sampling point
xb +
j·
g along the smooth surface in the interval −
bs/2 ≤
xb <
xlim, the numerical inversion of (17) gives the corresponding
w values:
where the function “
root” looks for the zero condition of the first argument inside square brackets and
wg is a guess value, here set to −1, corresponding to the point
c present in
Figure 1.
To ensure suitably accurate results from (21), the convergence tolerance, TOL, should be set to the smallest value compatible with a stable numerical solution (here TOL = 10−15).
Coming back to the
xy reference frame shown in
Figure 1, by applying a displacement equal to
bs/2, and considering the 2nd of (13), it follows that
Thus, from (19), the normal component
βsy0(
x) of the single-slot slotting function along the smooth surface (subscript 0, because
y = 0) can be written as the following:
The single-slot slotting function of the slot positioned h slot pitches at the left of the original one could be easily obtained by displacing the slotting function (23): βsy0(x − h·τs). Of course, if h was negative, the displaced slot was positioned at the right of the original one.
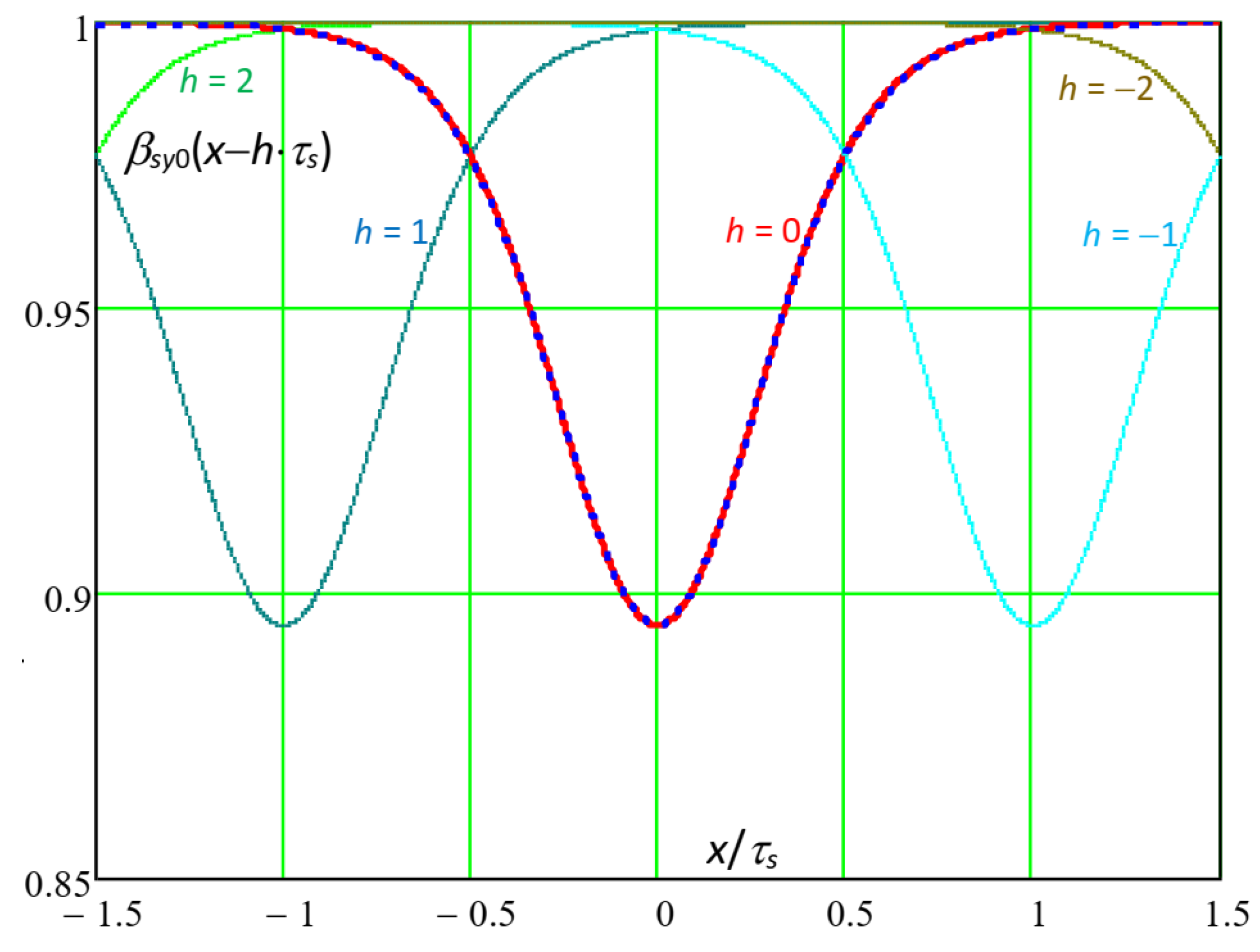
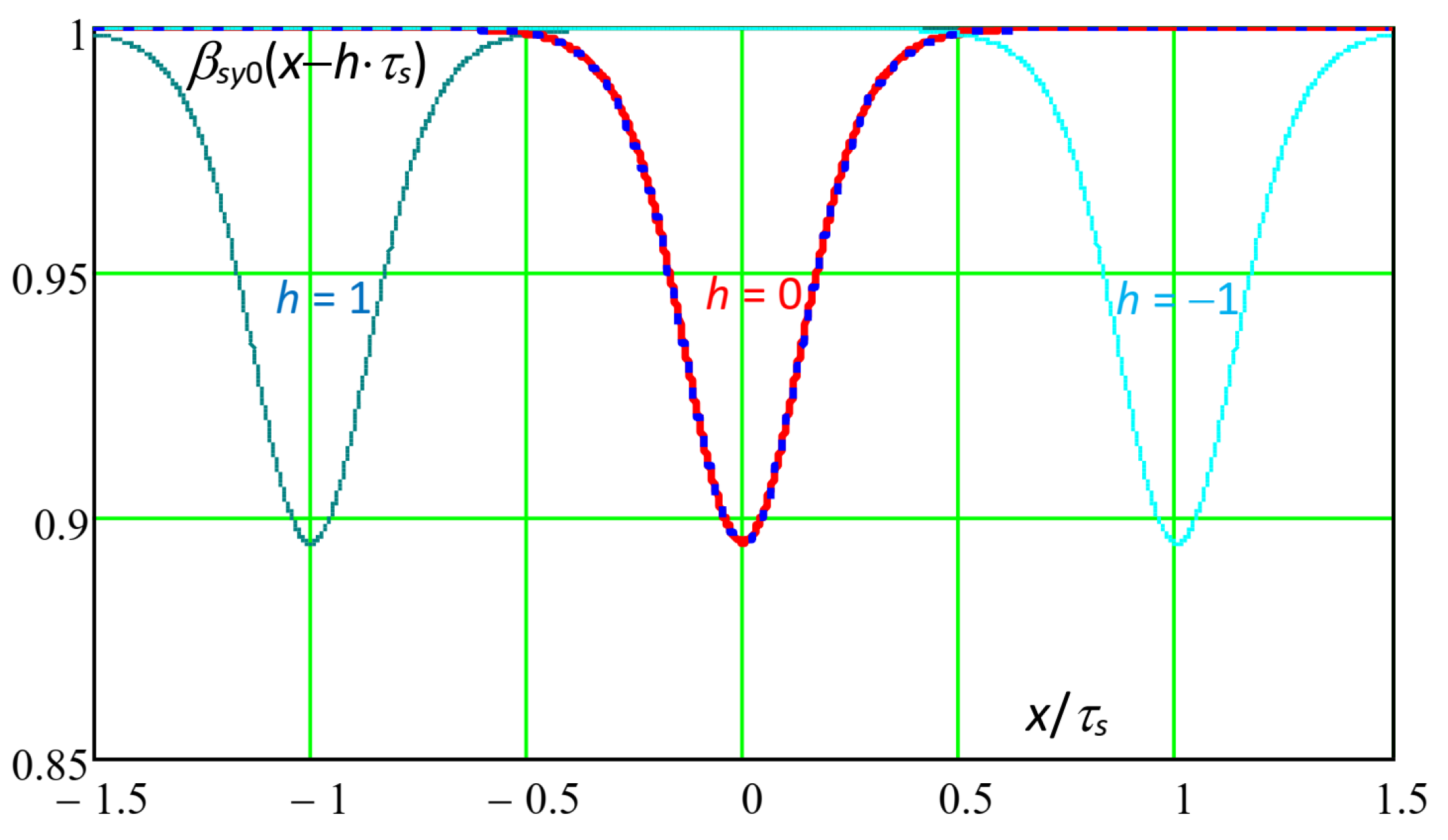
Figure 3 shows the single-slot slotting functions
βsy0(
x −
h·
τs) with h = −2, −1, 0, 1, 2, again for
g = 5 mm,
bs = 5 mm,
τs = 10 mm.
For
h = 0, the analytical curve is shown together with the FEM curve [
19], with bold lines.
For x/τs = ±0.5, βsy0(±τs/2) appears significantly lower than 1. This means that the single-slot slotting functions of adjacent slots interfered among each other; in this situation, the air gap width could be qualified as “high”.
The complement to 1 of the single-slot slotting function can be called the single-slot lost flux density function; for the central slot we can write
and for a generic slot positioned
h slots at the left of the central one:
In the case of a multi-slot configuration, the total lost flux density function
βℓy0(
x) can be expressed as the following:
Equation (26) corresponds to the formulation of the so-called principle of superposition of the distributions of the single-slot lost flux density functions: the lost flux density along a smooth structure, due to an infinite number of slots in the faced structure, can be expressed by means of a sequence of single-slot flux density distributions, separately evaluated for every slot as if they would be present on their own. This principle is valid even in the case that the lost flux density curves of adjacent slots interfere among them.
Finally, the multi-slot slotting function
βy0(x) is given by the following:
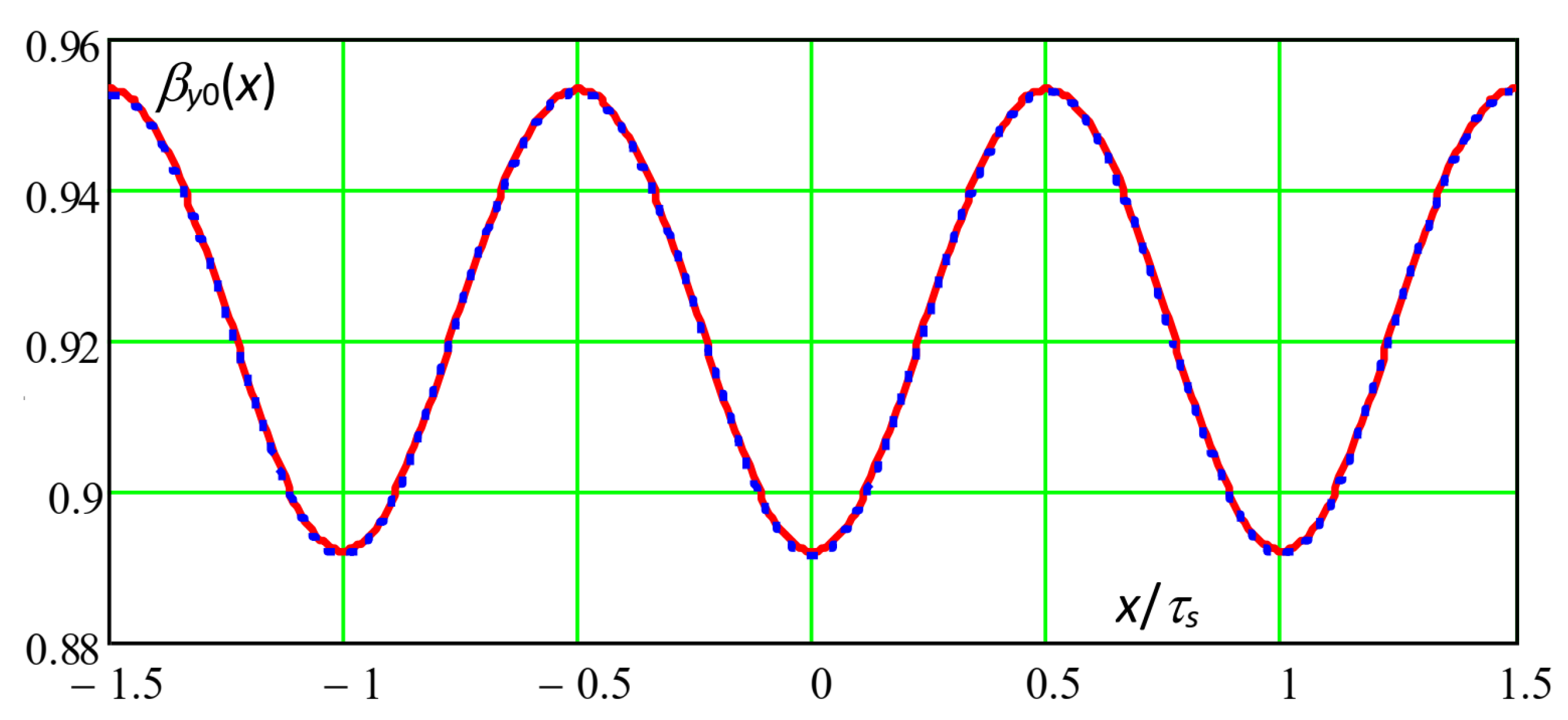
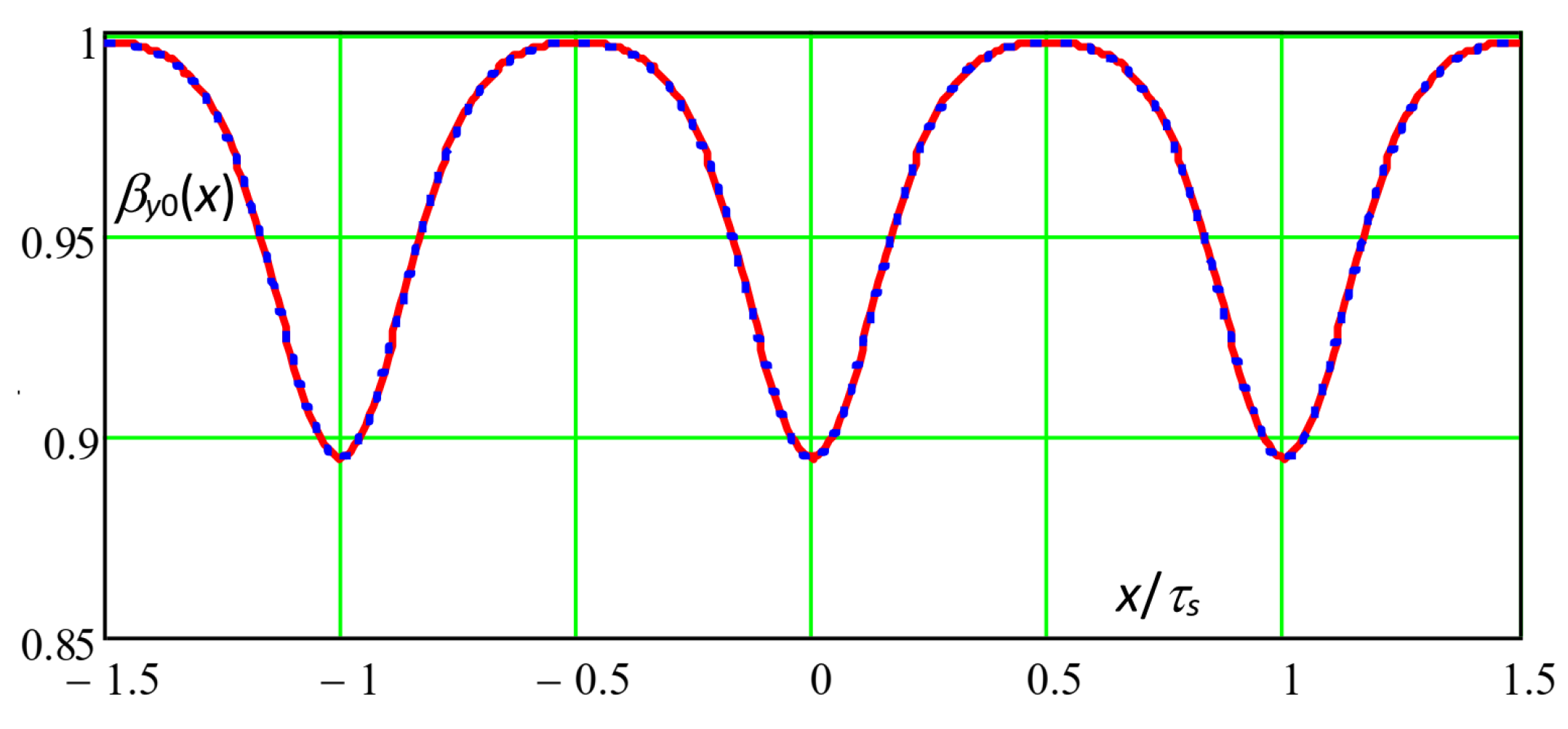
Figure 4 shows the distribution of the multi-slot slotting function
βy0(x) along the smooth surface, according to (27) (red continuous curve), together with the FEM 2D calculated one (blue dotted curve, [
19]), for
g = 5 mm,
bs = 5 mm,
τs = 10 mm. The agreement is excellent, confirming the correctness of the superposition principle of the single-slot lost flux density functions’ distribution; moreover,
βy0(±
τs) is considerably lower than 1, confirming the appreciable interference between adjacent single-slot slotting distributions.
The same agreement was also verified for several different air gap geometry parameters, confirming the general validity of the cited principle.
5. Calculation of the Fourier Coefficients of the Multi-Slot Slotting Function βy0(x)
The Fourier series expression of
βy0(
x) followed from the 2nd of (8), for y = 0:
The calculation of
βo by the analytical formulation (10) and by the numerical expression ∫
τs βy0(
x)d
x/
τs, for
g = 5 mm,
bs = 5 mm,
τs = 10 mm, gave, respectively,
confirming the accuracy of (27).
As regards the Fourier coefficients
βk, they were calculated by using the multi-slot flux density function
βy0(
x), as the following:
However, substituting (27) in (29) led to a more simple, significant and direct result:
In fact, by exchanging the order of the integration and summation operators, by observing that cos[
k·2
π·(
x −
h·
τs)/
τs] = cos(
k·2
π·
x/
τs) for any
h integer, and considering that
we could write
and finally (thanks to the symmetry of the integrand with respect to the origin),
Thus, the Fourier coefficients of the multi-slot flux density function βy0(x) could be calculated by using a formulation involving the single-slot flux density function, provided that the integration was extended to infinity; in practice, it can be extended to an extreme xmax = nτ·τs, multiple of τs, where βℓsy0(x) becomes negligible (for example nτ = 10).
6. Complex Formulation of the Slotting Function in the Air Gap
By inserting the results from (33) into (8), the slotting function’s
x and
y components were obtained. Expressing the generic
kth term of (8) in complex form, we could write
where
is the complex conjugate of
z =
x +
j·
y.
Thus, the complex slotting function
β(
z) can be written as
and the
x and
y components of the slotting function can be evaluated as
7. Distribution of the Slotting Functions Compared with FEM
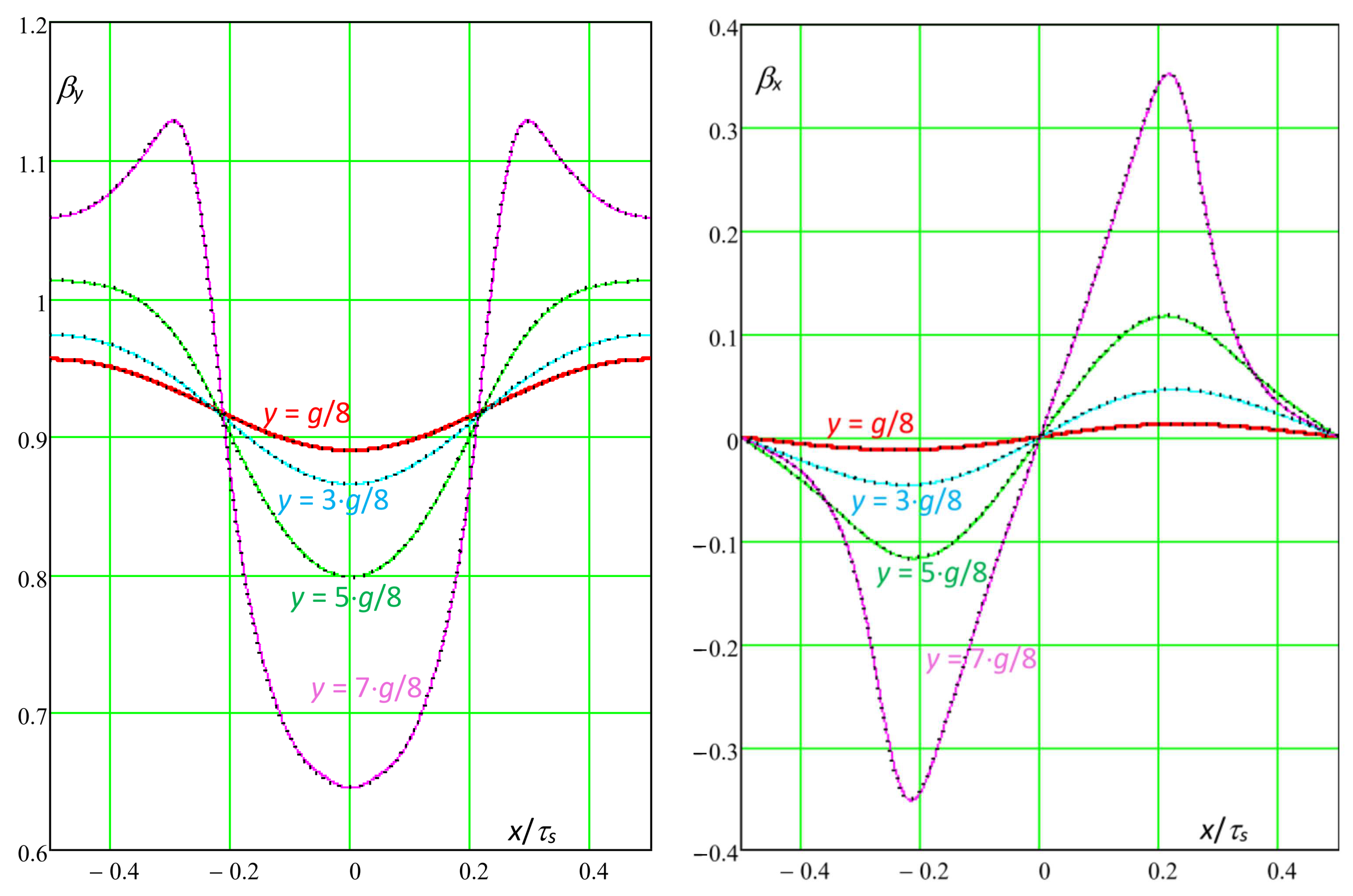
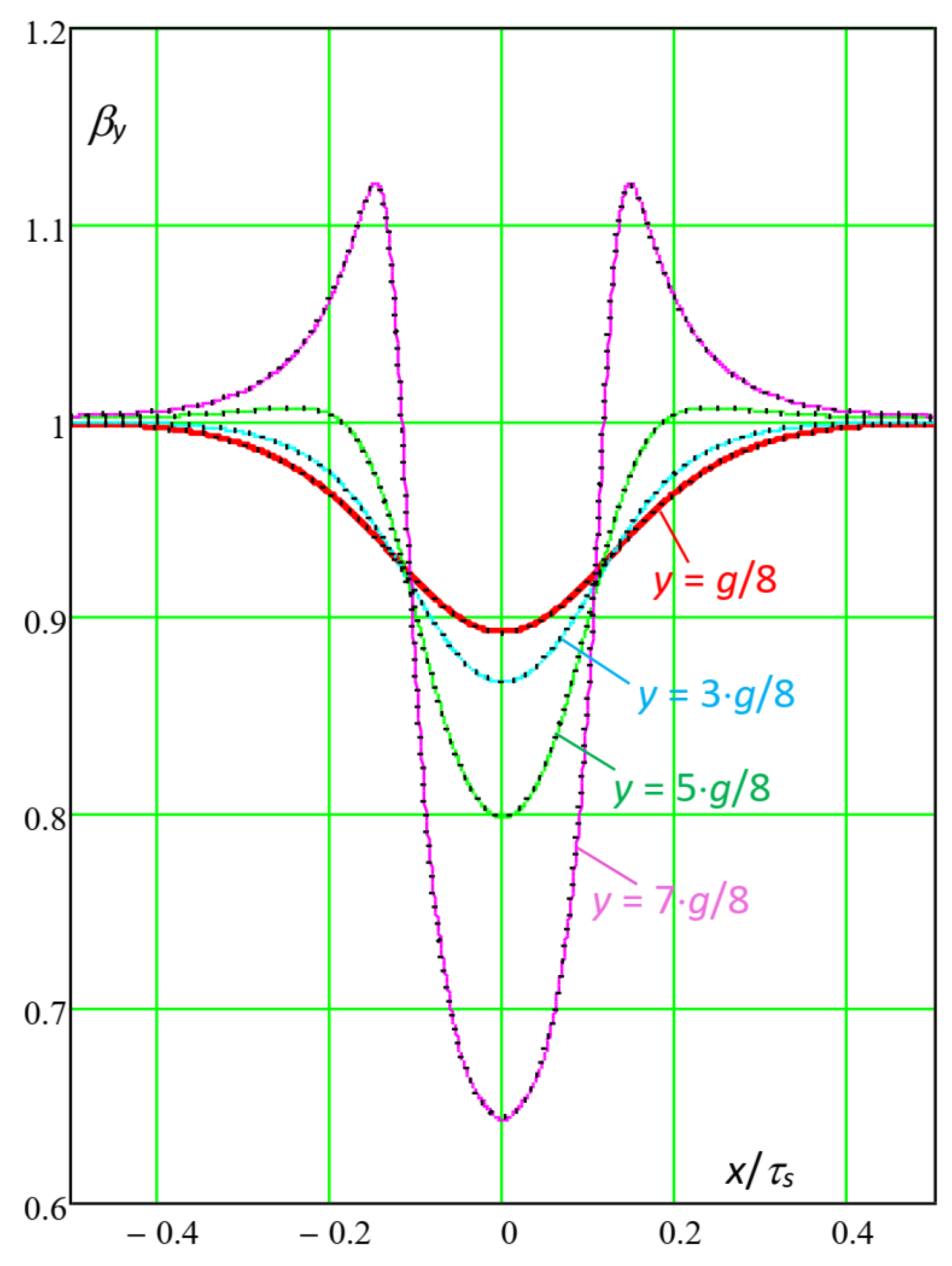
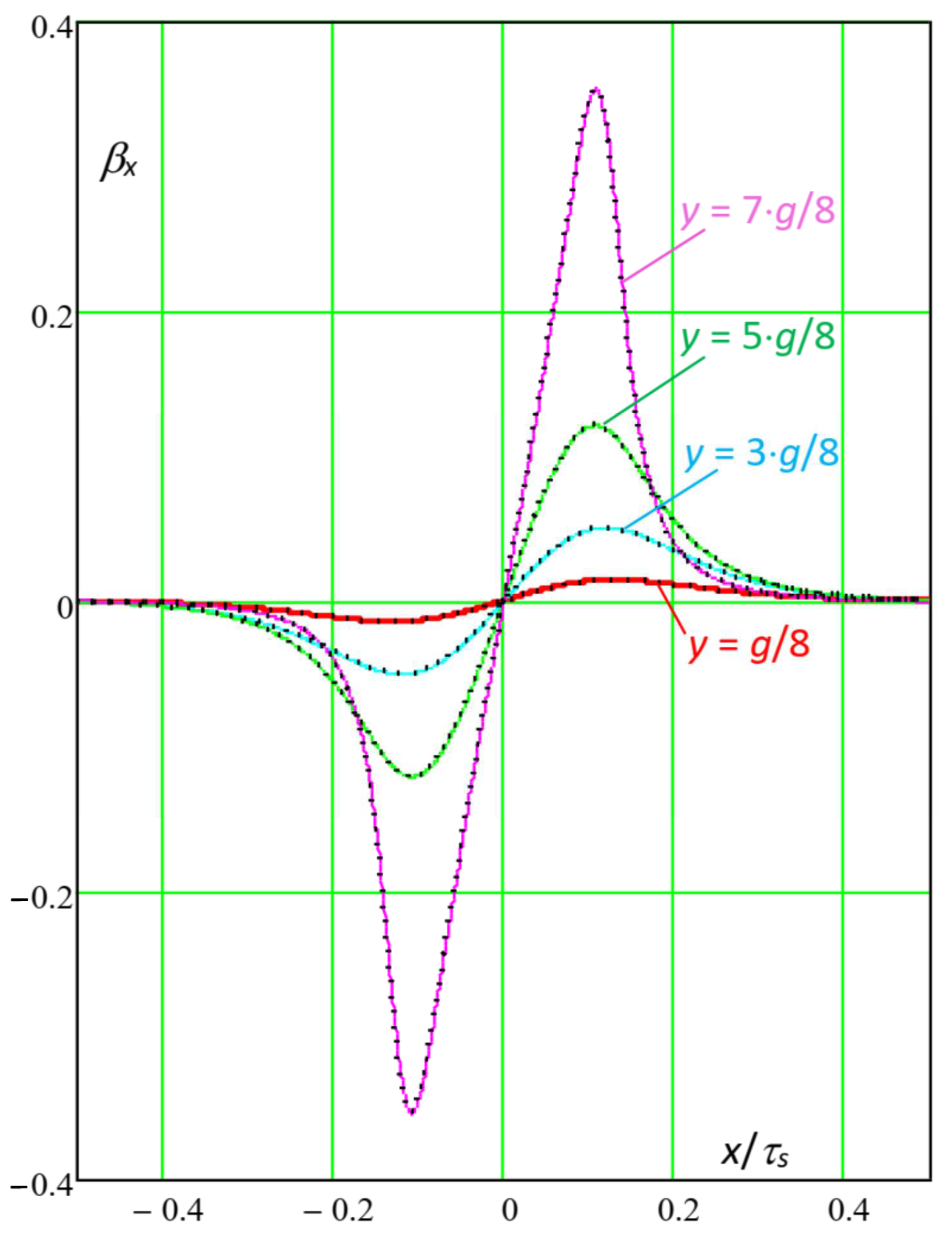
7.1. Slotting Functions for “High” Air Gap Width
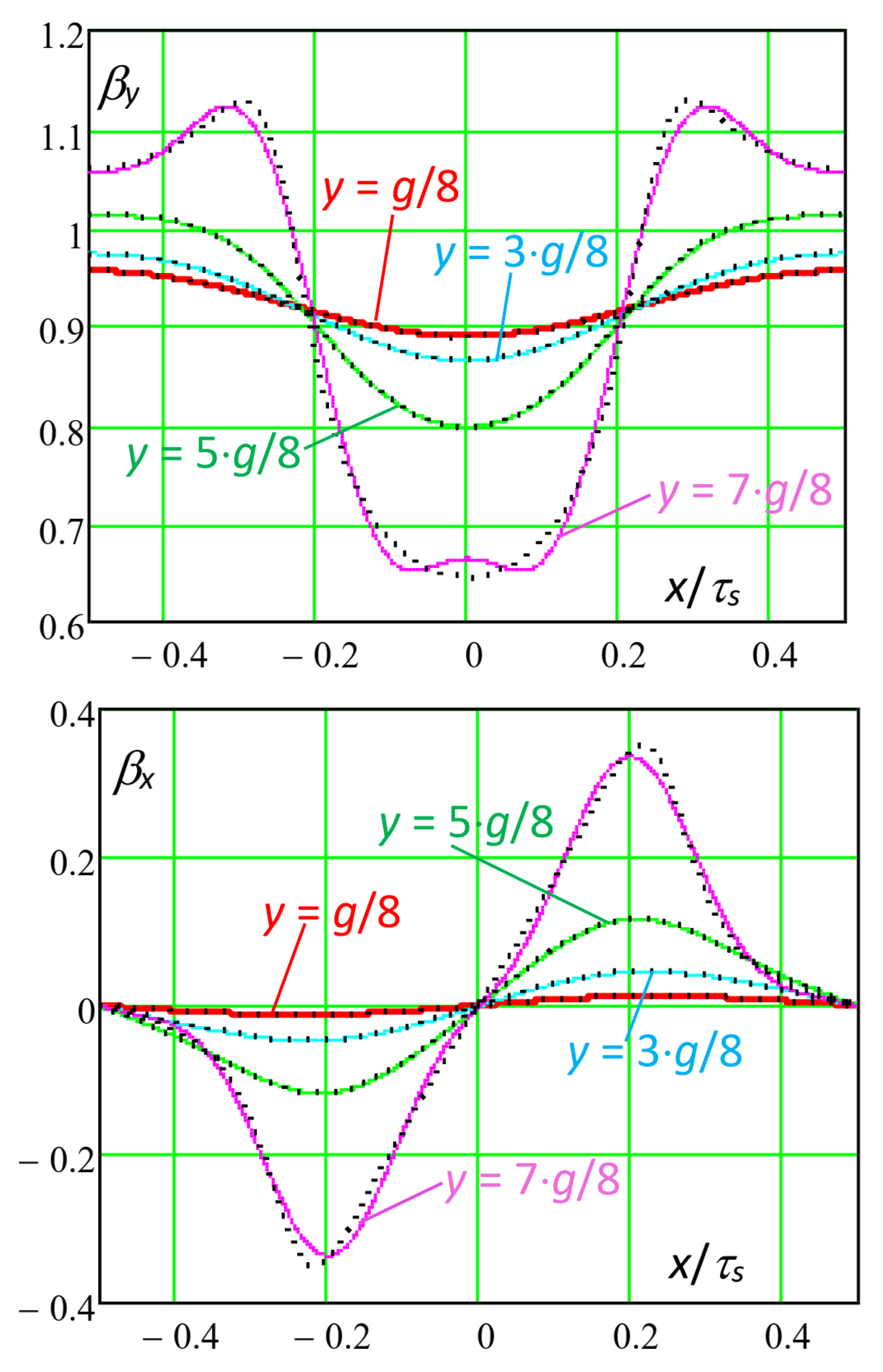
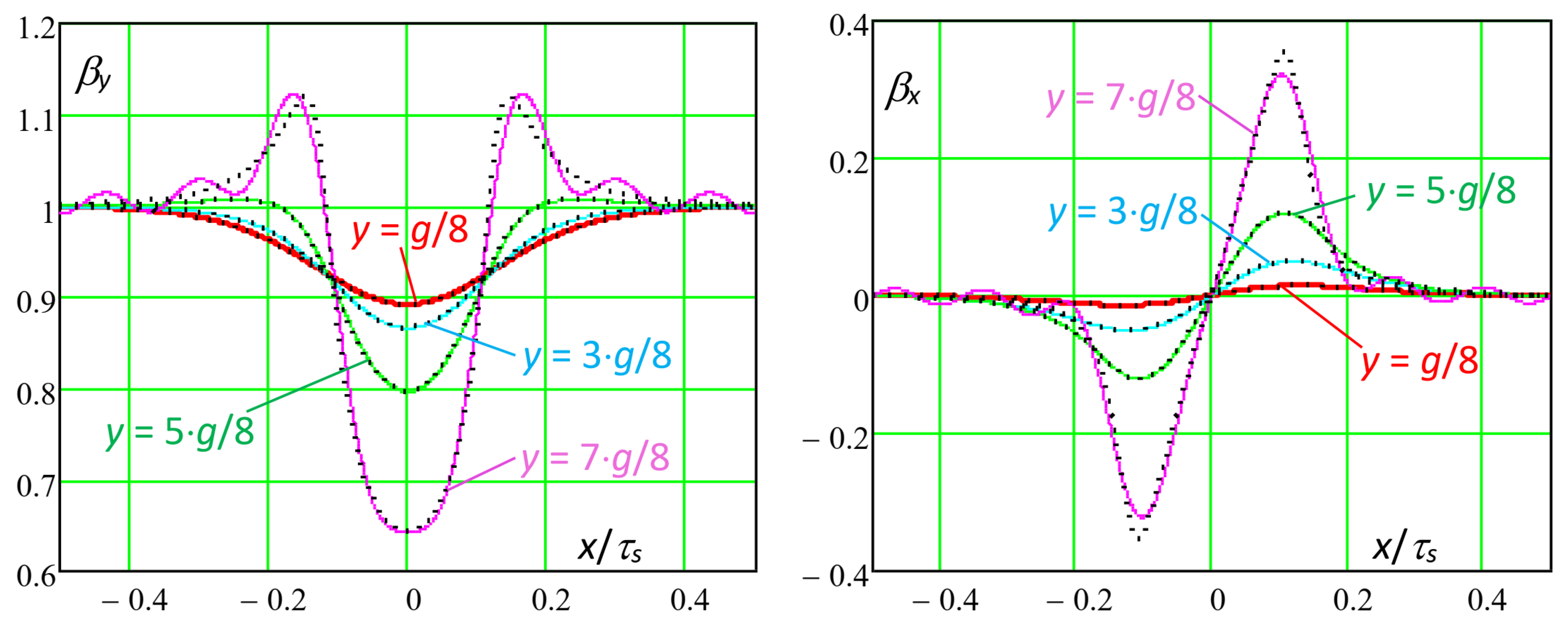
In the following, the multi-slot slotting function x and y components were evaluated as a function of the position x in the slot pitch τs, for different values of the exploring line y position in the air gap. At first, the considered geometry was g = 5 mm, bs = 5 mm, τs = 10 mm; as observed before, this was a “high” air gap width and in this case, the maximum considered harmonic order in (35) was kM = 10.
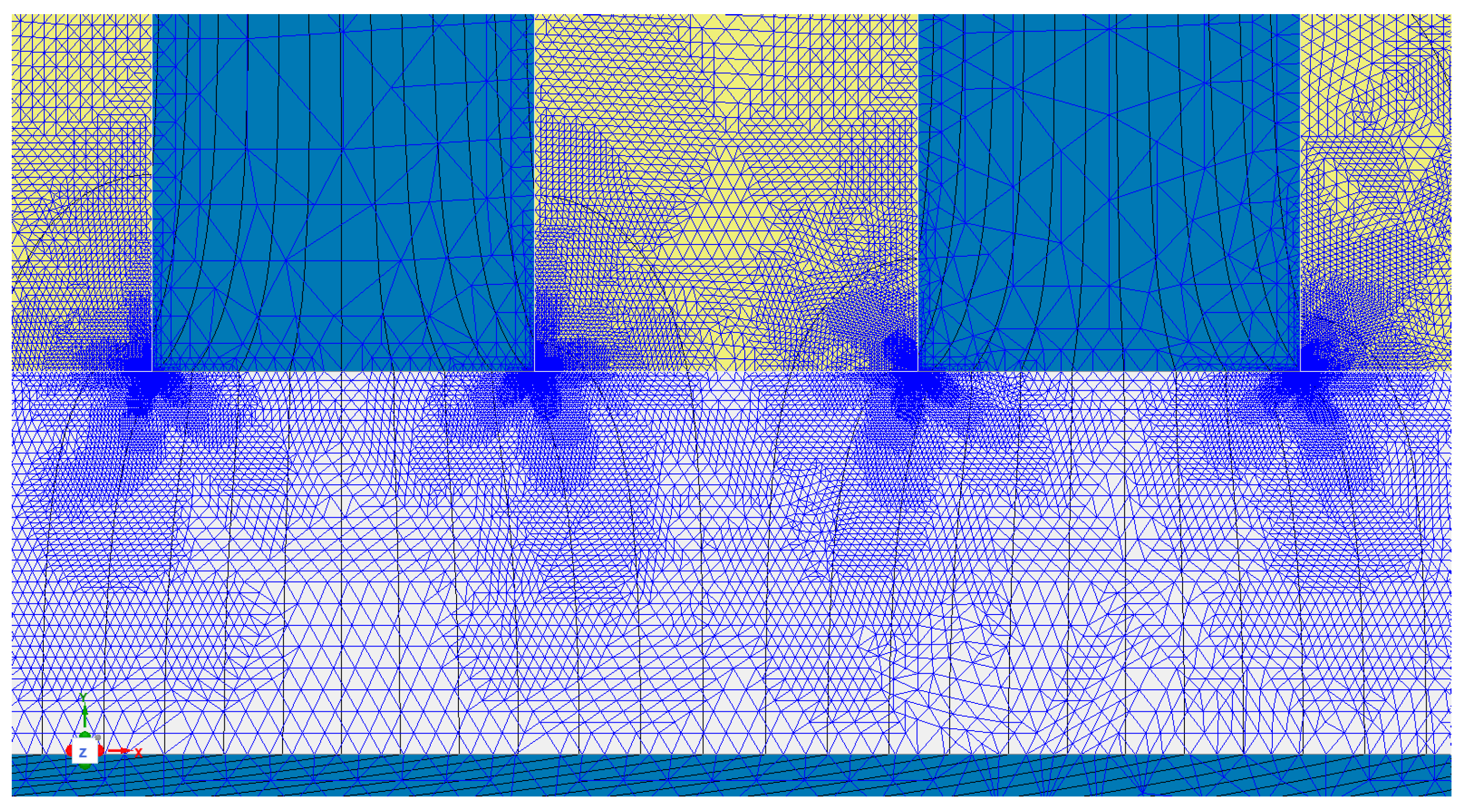
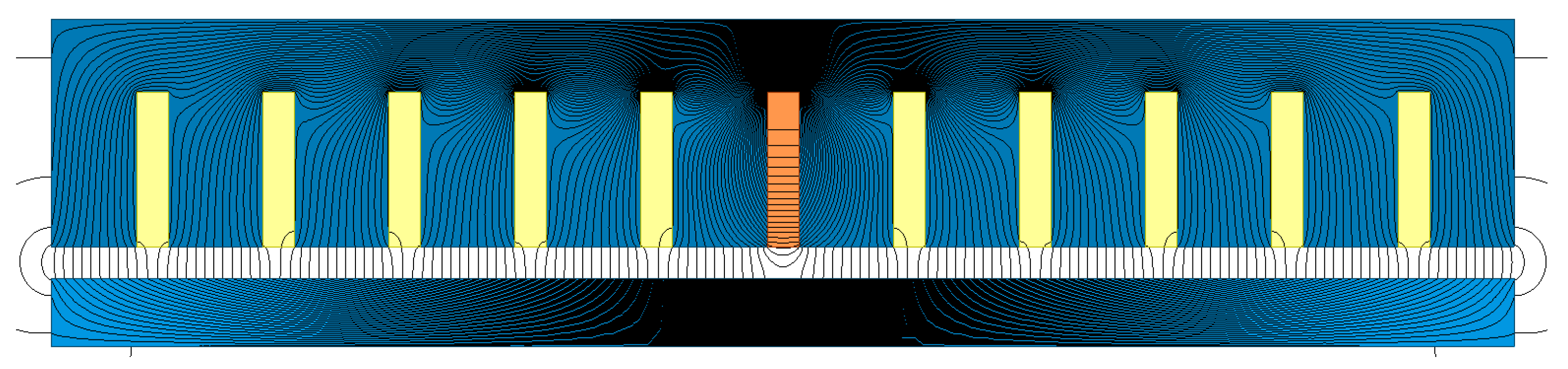
The complete FEM model adopted for a comparison with the analytical calculation of the slotting functions is shown in
Figure 5;
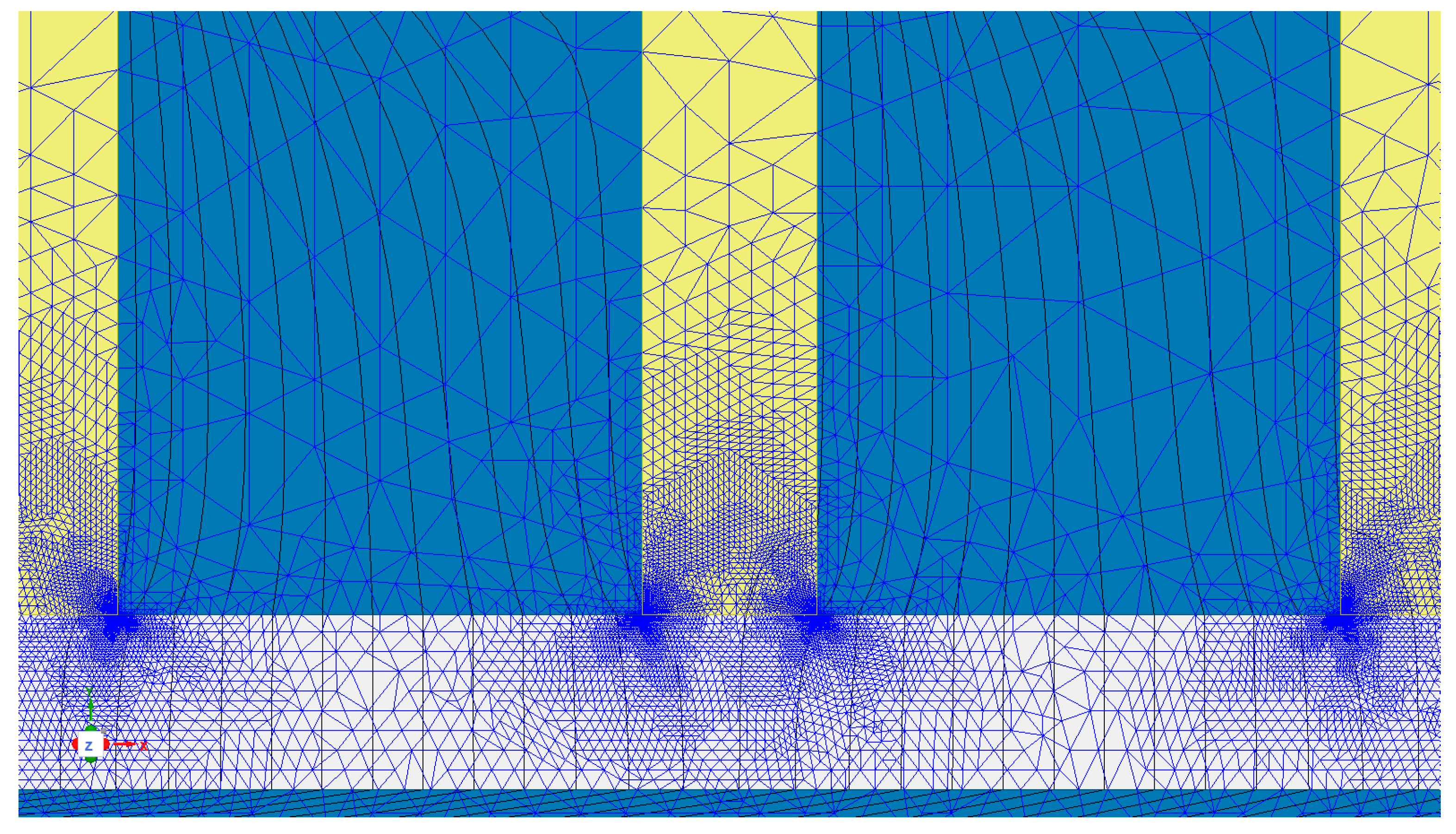
Figure 6 shows the detail of the mesh around the central slot at the right of the conductor; and
Figure 7 shows the analytical and FEM slotting functions curves for different positions of the exploring lines. In the FEM model, the ferromagnetic cores were assumed as ideal (
μfe = 10
6 pu).
With the conductor current Ic considered in the FEM model, the ideal normal component Bi of the flux density, occurring in case of a smooth upper core, equals Bi = μ0·Ic/(2·g); thus, from the actual FEM-calculated distributions BFEMx(x) and BFEMy(x), the corresponding FEM slotting functions are βFEMx(x) = BFEMx(x)/Bi and βFEMy(x) = BFEMy(x)/Bi.
In order to ensure accurate and regular distributions of x and y flux density inside the air gap, the following salient data of FEM simulation were adopted: 27 adaptive mesh refinement iterations; energy error = 4.92·10−6%; Δenergy = 1.22·10−5%; CPU simulation time = 508 s; total number of mesh triangles (thousands) = 422; in the conductor = 13.5; in each slot = 10.5; and in the air-gap = 277. The particularly high mesh refinement around the tooth corners is evident, where the field changes quickly in space.
Some remarks can be proposed as the following:
- -
by using (35) and (36), the position
y inside the air gap along which the slotting function was to be calculated could be defined at any time, while, according to [
9] and [
12],
y had to be predefined at half the air gap width and could not be changed;
- -
as can be observed, continuous analytical curves and dashed FEM 2D curves were well superposed for any chosen y position of the exploration line.
7.2. Slotting Functions for “Small” Air Gap Width
Figure 8 shows the single-slot slotting functions
βsy0(
x −
h·
τs) with h = −1, 0, 1, for
g = 2.5 mm,
bs = 2.5 mm,
τs = 10 mm. For
h = 0, the analytical curve is shown together with the FEM curve [
19], with bold lines.
For x/τs = ±0.5, βsy0(±τs/2) appears very close to 1. This means that in practice, the single-slot slotting functions of adjacent slots do not interfere by superposition significantly, almost without reciprocal interference; in this situation, the air gap width can be qualified as “small”.
Figure 9 shows the multi-slot slotting function
βy0(
x) along the smooth surface (y = 0), for the considered “small” air gap geometry (
g = 2.5 mm,
bs = 2.5 mm,
τs = 10 mm): the red curve was analytically calculated (by (28) and the blue dashed curve, by FEM 2D [
19]. Moreover,
βy0(±
τs/2) is very close to 1, confirming the negligible interference between adjacent single-slot slotting distributions.
Again, for
g = 2.5 mm,
bs = 2.5 mm,
τs = 10 mm,
Figure 10 shows the multi-slot slotting function
x and
y components, as a function of the peripheral position
x in the slot pitch
τs, for different values of the exploring line
y position in the air gap: here, the maximum considered harmonic order in (35) was
kM = 21. Also in this case, continuous analytical curves and dashed FEM 2D curves are well superposed, for any
y position of the exploration line.
Figure 11 shows the complete FEM model for a “small” air gap (
g = 2.5 mm,
bs = 2.5 mm,
τs = 10 mm:), adopted for a comparison with the analytically calculated slotting functions shown in
Figure 10, while
Figure 12 shows the detail of the mesh around the central slot at the right of the conductor.
Also for this “small” air gap situation, in order to ensure accurate and regular distributions of x and y flux densities inside the air gap, the following salient data of FEM simulation were adopted: 23 adaptive mesh refinement iterations; energy error = 2.54·10−5%; Δenergy = 5.76·10−5%; CPU simulation time = 218 s; total number of mesh triangles (thousands) = 165; in the conductor = 4.6; in each slot = 3.8; and in the air gap = 106.
By observing
Figure 12, the particularly high mesh refinement around the tooth corners is evident, where the field changes quickly in space.
However, by comparing these FEM data with the corresponding ones adopted for the “high” air gap simulation, here, the FEM calculation burden was lower than that needed in the case of a “high” air gap.
8. Accuracy of the Slotting Functions with the Choice of the Maximum Harmonic Order kM
In the following, some accuracy considerations were made about the calculation of the Fourier coefficients, the maximum order kM of the Fourier series and their consequences on the slotting function distributions.
8.1. Slotting Function Accuracy for “High” Air Gap Width
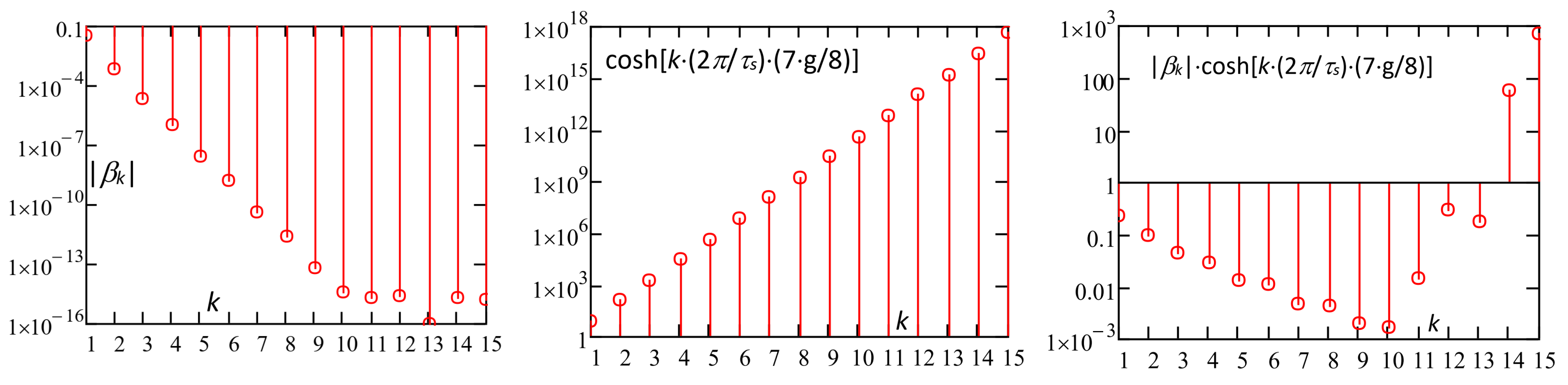
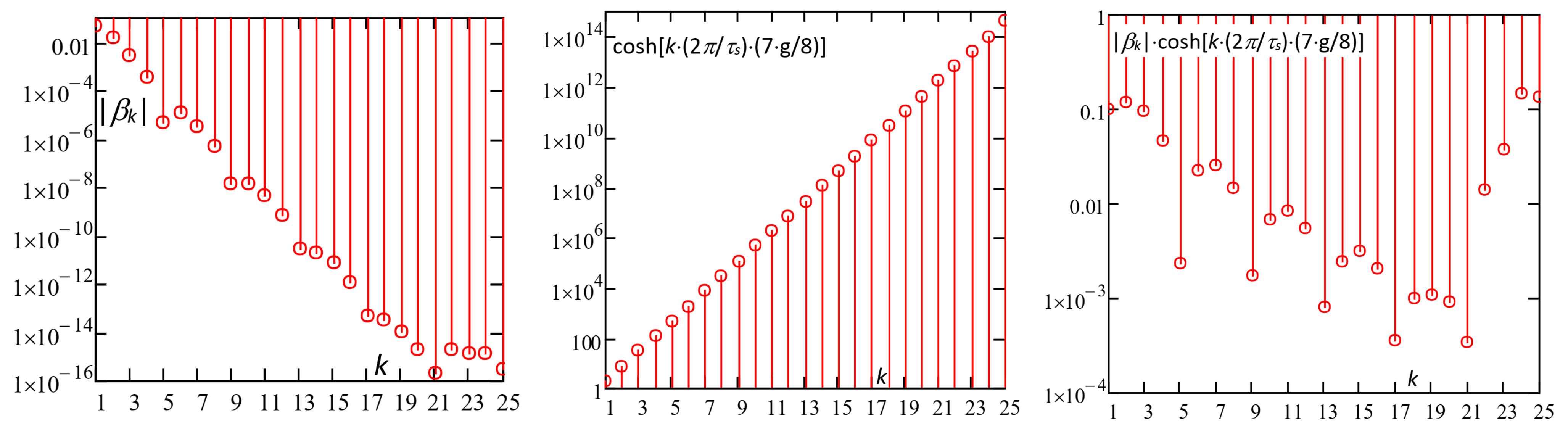
Figure 13 shows a histogram of the |
βk| coefficients of the Fourier series (28), calculated by (33), of the “cosh” factors and of the total factors |
βk|·cosh[
k·(2
π/
τs)·(7·
g/8)] as a function of harmonic order
k, for
g = 5 mm,
bs = 5 mm,
τs = 10 mm (“high” air gap width).
We could make the following remarks:
- -
|βk| decreases with k increasing up to k = 10, while above this order, apparently the amplitude remains almost stationary; however, by observing the |βk| values for k > 10, it appears that a level around the convergence tolerance TOL = 10−15 was reached and thus, above k > 10 the |βk| values were inaccurate.
- -
As regards the factor cosh[k·(2π/τs)·y], for y = 7·g/8 it greatly increases with the increase in the harmonic order k, while the increase is lower for smaller y values.
- -
Up to the order k = 10, the total factor|βk|·cosh[k·(2π/τs)·(7·g/8)] decreases, but with a reduction trend much lower than that of |βk|.
- -
For k < 10, the factor |βk|·cosh[k·(2π/τs)·(7·g/8)] shows the typical decreasing behaviour of any Fourier series, while for k > 10, the total harmonic factor tends to suddenly increase; however, this is caused by the numerical error in the estimation of |βk|, when it falls into the convergence tolerance range.
The following remarks are valid:
- -
for limited values of the y position of the exploring line (y = g/8, 3·g/8, or 5·g/8), the value of kM has a weak effect on the distribution shape, and the analytically calculated slotting functions appear well superposed with the FEM 2D distributions;
- -
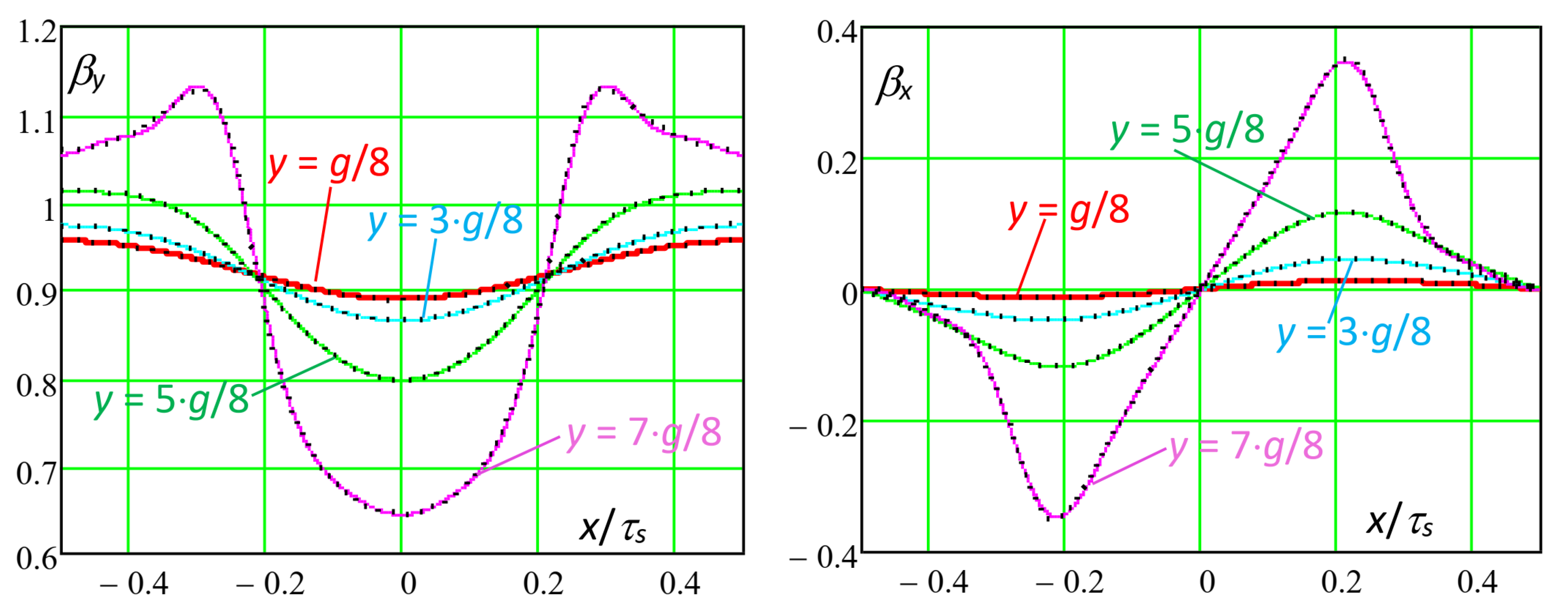
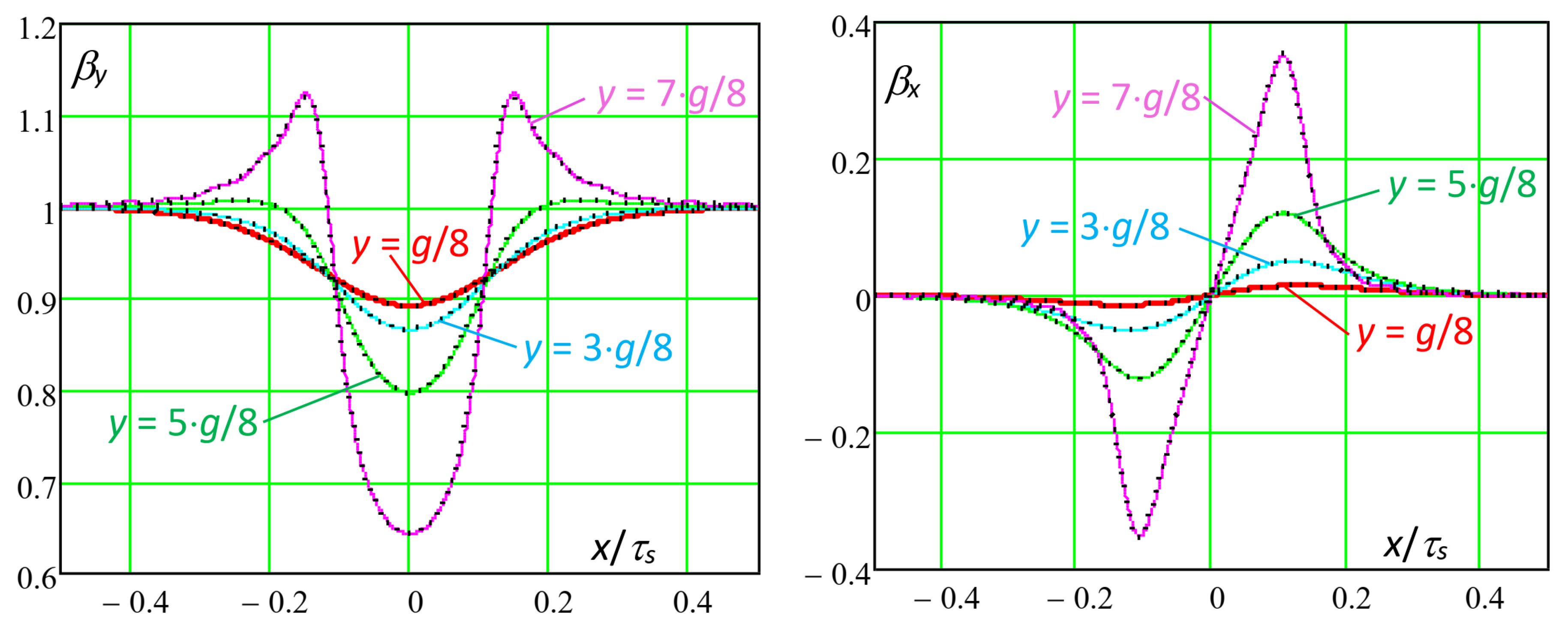
if the exploration line inside the air gap is close to the slotted surface (as for y = 7·g/8), the analytically calculated slotting function shape depends on the choice of kM;
- -
if the
kM is too low (
kM = 4,
Figure 14), the distribution for
y = 7·
g/8 is distorted, because the number of harmonics is not enough to reproduce the correct distribution;
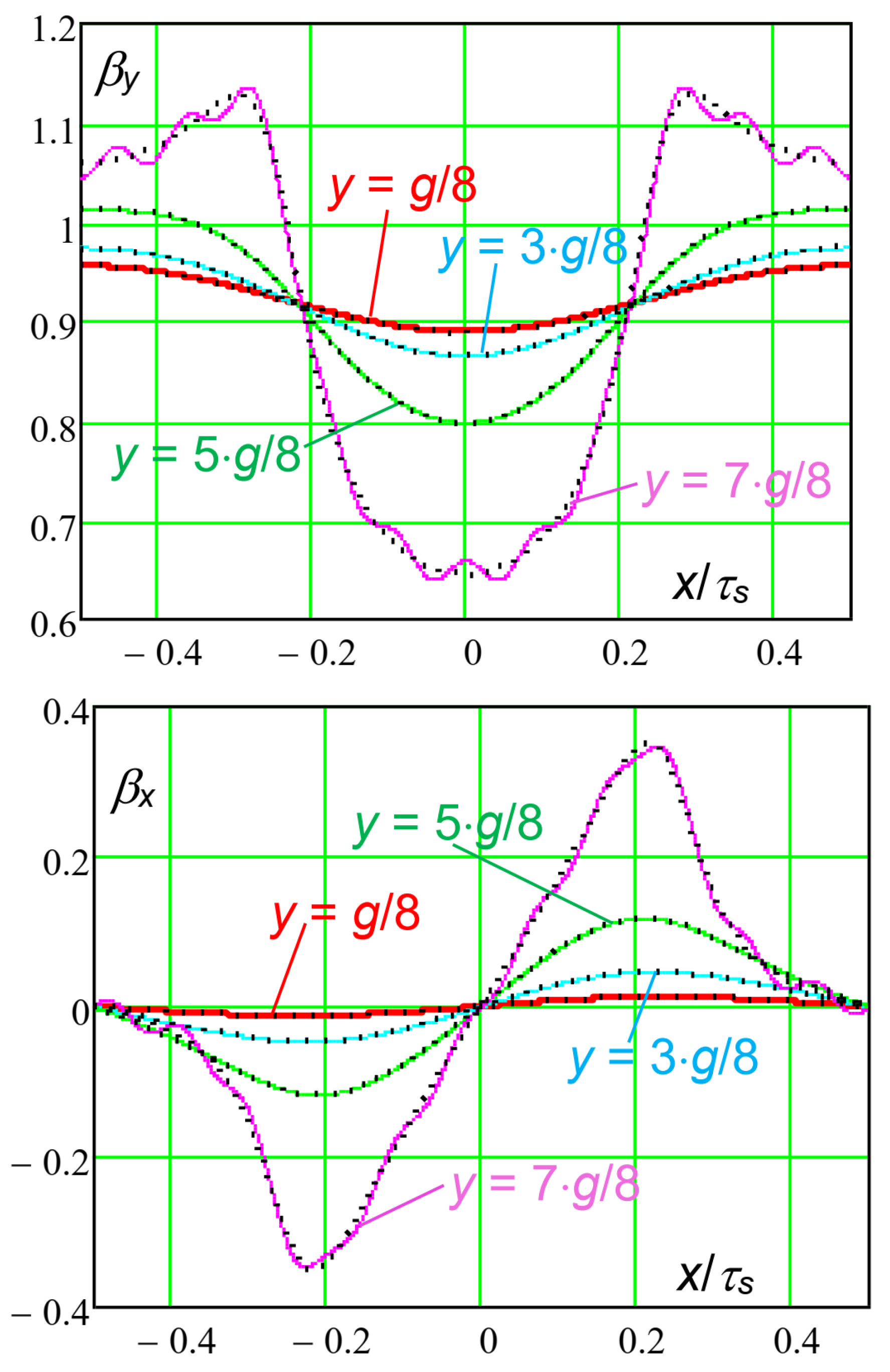
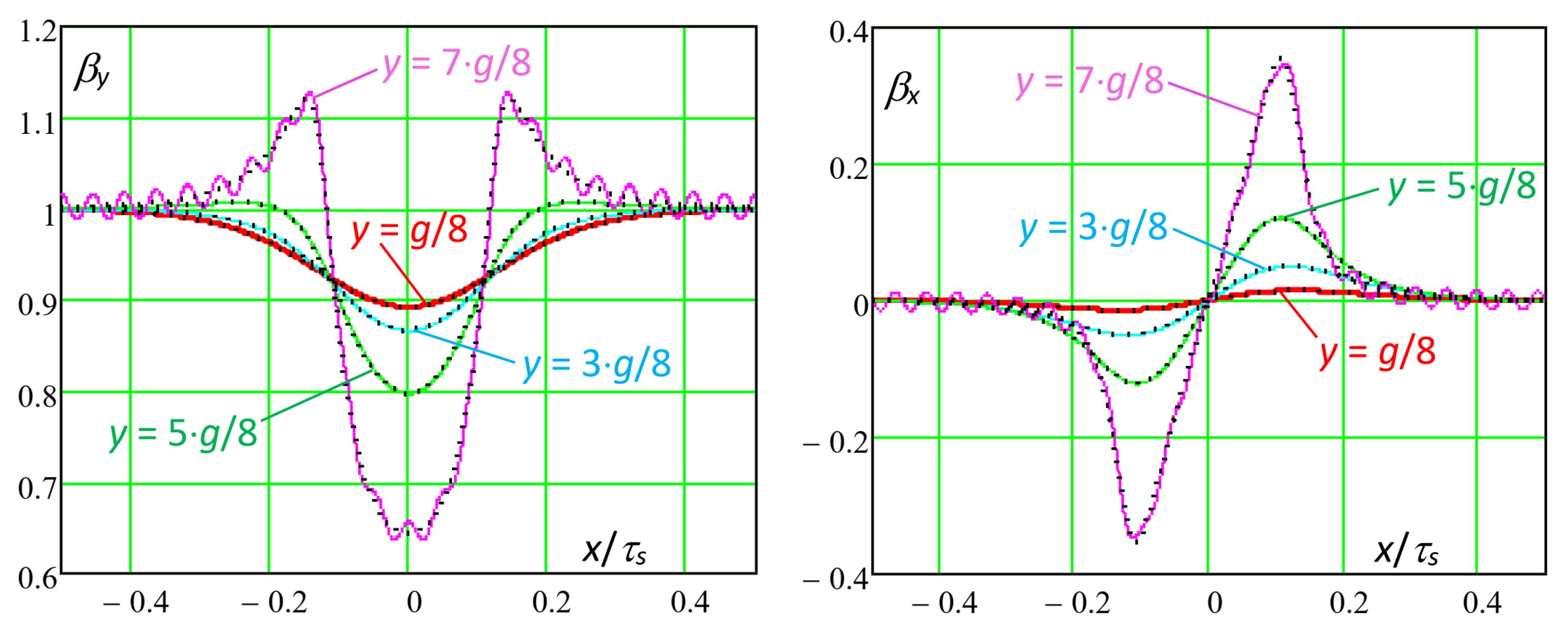
- -
if the
kM is intermediate (
kM = 7,
Figure 15), the distribution for
y = 7·
g/8 is less distorted, because the number of included harmonics is higher, although not enough to avoid some oscillations;
- -
with a
kM = 10 (
Figure 7), the distribution for
y = 7·
g/8 appears well superposed to the FEM distribution and in fact,
kM = 10 is the maximum
kM with a reliable
βkM value (see
Figure 9);
- -
if the
kM = 11 (
Figure 16), the distribution for
y = 7·
g/8 appears highly distorted, due to the incorrect
βkM value (see
Figure 9).
8.2. Slotting Function Accuracy for “Small” Air Gap Width
Figure 17 shows a histogram of the |
βk| coefficients of the Fourier series (28), calculated by (33), of the “cosh” factors and of the total factors |
βk|·cosh[
k·(2
π/
τs)·(7·
g/8)] as a function of harmonic order
k, for
g = 2.5 mm,
bs = 2.5 mm,
τs = 10 mm.
We could make the following remarks:
- -
|βk| decreases with k increases up to k = 21, while above this order, apparently the amplitude increases again or remains almost stationary; however, by observing the |βk| values for k > 21, it appears that a level around the convergence tolerance TOL = 10−15 was reached and thus, above k > 21 the |βk| values were inaccurate.
- -
As regards the factor cosh[k·(2π/τs)·y], for y = 7·g/8, it greatly increases with the increase in the harmonic order k, while the increase is lower for smaller y values.
- -
Up to the order k = 21, the total factor|βk|·cosh[k·(2π/τs)·(7·g/8)] generally decreases, but with a reduction trend much lower than that of |βk|.
- -
For k < 21, the factor |βk|·cosh[k·(2π/τs)·(7·g/8)] shows the typical decreasing behaviour of any Fourier series, while for k > 21, the total harmonic factor tends to suddenly increase; however, this is the wrong effect of the inaccurate estimation of |βk| when it falls into the convergence tolerance range.
- -
for limited values of the y position of the exploring line (y = g/8, 3·g/8, or 5·g/8), the value of kM has a weak effect on the distribution shape, and the analytically calculated slotting functions appear well superposed with the FEM 2D distributions;
- -
if the exploration line inside the air gap is close to the slotted surface (as for y = 7·g/8), the analytically calculated slotting function shape depends on the choice of kM;
- -
if the
kM is too low (
kM = 7,
Figure 18), the distribution for
y = 7·
g/8 is distorted because the number of harmonics is not enough to reproduce the correct distribution;
- -
if the
kM is intermediate (
kM = 15,
Figure 19)), the distribution for
y = 7·
g/8 is less distorted, because the number of harmonics is higher, although not enough to avoid oscillations;
- -
with a
kM = 21 (
Figure 10), the distribution for
y = 7·
g/8 appears well superposed to the FEM distribution and in fact,
kM = 21 is the maximum
kM with a reliable
βkM value (see
Figure 17);
- -
if the
kM = 22 (
Figure 20), the distribution for
y = 7·
g/8 appears highly distorted, due to the incorrect
βkM value (see
Figure 17).
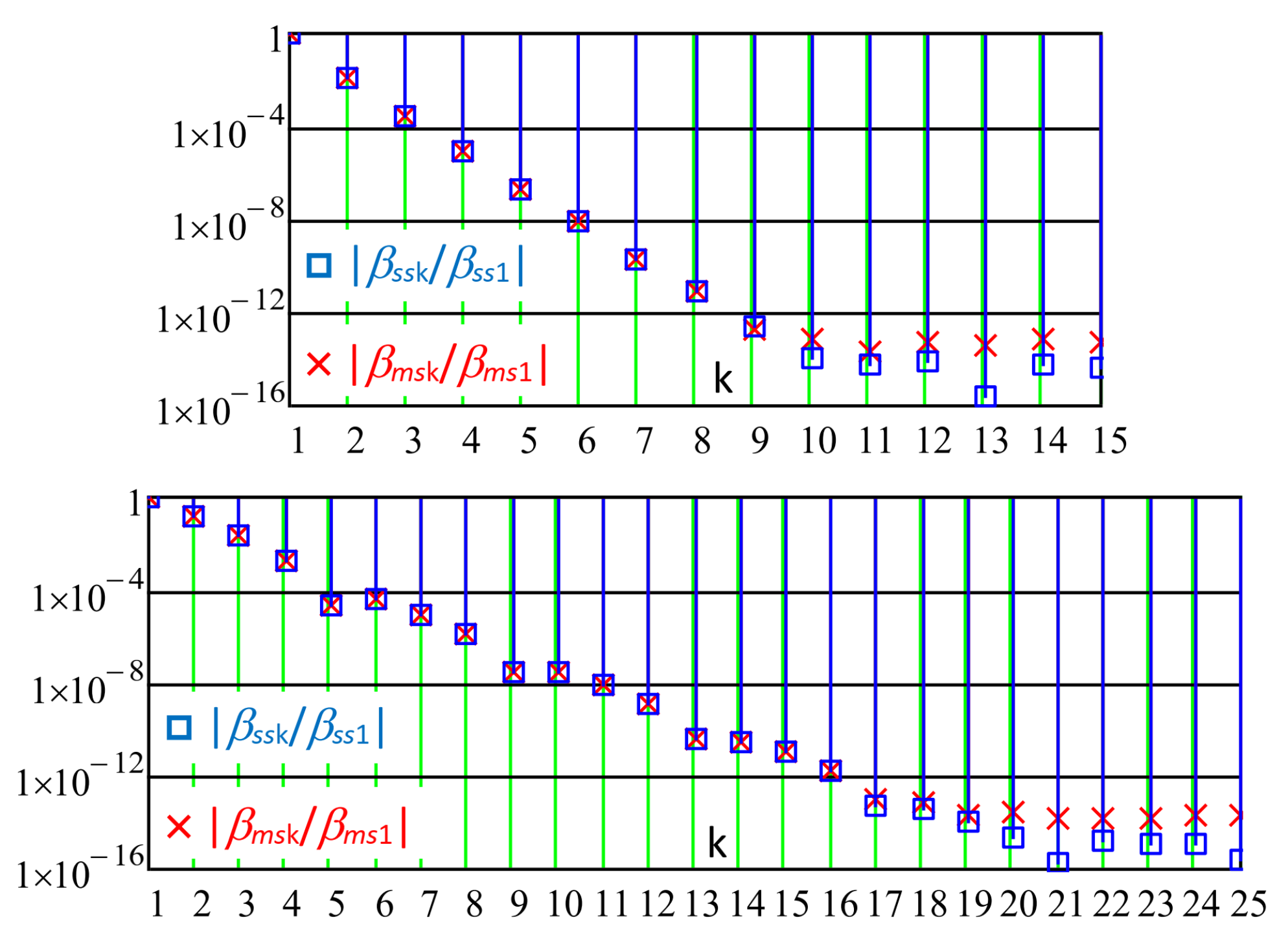
Figure 21 shows the histograms of the harmonic amplitudes of the slotting function Fourier series (28), calculated with a multi-slot approach (Equation (30), subscript
ms,
×) and with a single-slot approach (Equation (33), subscript
ss,
□). On the left is a histogram for the case of
g = 5 mm,
bs = 5 mm,
τs = 10 mm (“high” air gap width) and on the right is a histogram for the case of
g = 2.5 mm,
bs = 2.5 mm,
τs = 10 mm (“small” air gap width). All the harmonic amplitudes are referred to as the amplitude of the fundamental components.
We could make the following remarks:
- -
In the low harmonic order range (below kM), the coefficients calculated with the multi-slot approach (Equation (30)) and with the single-slot approach (Equation (33)) had the same values, confirming the correctness of (33).
- -
For orders approaching kM, the two formulas started to give different results, due to the numerical issues about the TOL limit; these issues appeared more critical for the multi-slot approach, because of the superposition of several single-slot distributions in (33), although each distribution had its own inaccuracies.
- -
The Fourier coefficients calculated by (33) were accurate up to the
kM order, as shown in the diagrams of
Figure 7 and
Figure 10.
- -
However, above
kM, both the calculation methods ((30) and (33)) gave inaccurate results, as already observed in the histograms of
Figure 13 and
Figure 17.
9. Conclusions and Perspectives
A method was developed, using the Laplace equation solution in terms of variable separation and Fourier series, for the accurate calculation of multi-slot slotting functions, valid for any geometric air gap parameters, with or without interference among single-slot distributions.
The obtained slotting functions can be used for different y positions of the exploration line in the air gap, and are also quite close to the toothed structure, as needed in the case of surface-mounted permanent magnetic machines.
The calculation of the Fourier series coefficients of the multi-slot configuration were reformulated by transforming the Fourier integrals in terms of a single-slot solution, obtained by conformal transformation.
The accuracy of the slotting functions was studied and the best value for the maximum harmonic order of the Fourier series was obtained by analysing the numerical issues regarding the convergence tolerance limits.
Some slotting function distributions were considered, showing satisfactory correspondence with FEM 2D calculated distributions.
Future studies will concern accuracy improvement in the Fourier series extension and accuracy improvement in the analysis of the magnetic field in the air gap, under no-load and loaded operating conditions, for slotted peripheral configurations.