Abstract
Magnetic hopfions are three-dimensional topological solitons embedded into a homogeneously magnetized background. The internal structure of hopfions is distinguished by the linked preimages—closed loops with a single orientation of the magnetization on the target space —and is thus characterized by the integer Hopf index . Alternatively, hopfions can be visualized as a result of the swirling of two-dimensional bimerons around the direction of an applied magnetic field. Since the bimeron consists of a circular core and an anti-skyrmion crescent, two hopfion varieties can be achieved with either bimeron constituent facing the hopfion interior. In bulk cubic helimagnets, however, the applied magnetic field leads to a spontaneous collapse of hopfions, i.e., the eigen-energy of hopfions has the minimum for zero hopfion radius R. Anti-hopfions with , in this case, pass through the intermediate toron state with two-point defects. Here, we demonstrate that the competing cubic and exchange anisotropies inherent in cubic non-centrosymmetric magnets (e.g., in the Mott insulator CuOSeO) as a third level of the hierarchy of energy scales following the exchange and Dzyaloshinskii–Moriya interactions, may shift the energy minimum into the region of finite hopfion radii.
PACS:
75.30.Kz; 12.39.Dc; 75.70.-i
1. Introduction
Isolated magnetic skyrmions are particle-like topological solitons with complex non-coplanar spin structure [1,2,3,4] stabilized in noncentrosymmetric magnetic materials by specific Dzyaloshinskii–Moriya interactions (DMI) [5]. Phenomenologically, DMIs are expressed as the first derivatives of the magnetization with respect to the spatial coordinates, the so called Lifshitz invariants (LI):
The skyrmion “knots” are robust against small perturbations and cannot be continuously unwound, i.e., DMI provides a viable stabilization mechanism, protecting skyrmions from radial instability [1,2] and overcoming the constraints of the Hobart–Derrick theorem [6].
The skyrmion field configurations are elements of second homotopy group and can be characterized by a topological charge or skyrmion number [7]:
describing how many times the magnetization field within the single skyrmion wraps around the sphere .
Chiral interactions having the same functional form as (1) may appear also in many other systems: in ferroelectrics with a non-centrosymmetric parent paraelectric phase, non-centrosymmetric superconductors, multiferroics [8,9,10], or even in metallic supercooled liquids and glasses [11]. Localized states in these systems are also named skyrmions by analogy with the Skyrme model for mesons and baryons [12]. Chiral liquid crystals (CLC) are considered as ideal model systems for probing the behavior of different modulated structures on the mesoscopic scale [13].
The current focus of skyrmionics revolves around axisymmetric skyrmions within the saturated ferromagnetic state of non-centrosymmetric magnets [2]. The magnetization twist is localized in two spatial directions (2D) and the axes of skyrmions are co-aligned with an applied magnetic field (in the present manuscript, the field is applied along x), i.e., the magnetization in the center is opposite to the field and gradually rotates to the field-aligned state at the outskirt. Homogeneous extension of such magnetic textures into the third direction along the field forms skyrmionic filaments or strings. Recently, hexagonal skyrmion lattices (SkL) and isolated skyrmions (IS) of such a “standard” skyrmion variety were discovered in bulk chiral magnets near the Curie temperature [14,15,16] and in nanolayered geometries over larger temperature intervals [17,18,19,20]. The internal structure of such axisymmetric skyrmions, which is generally characterized by the repulsive inter-skyrmion potential, has been systematically investigated theoretically [1,2] and experimentally by spin-polarized scanning tunneling microscopy in PdFe bilayers with induced Dzyaloshinskii–Moriya interactions and strong easy-axis anisotropy [4,21]. It was found that the existence region of axisymmetric ISs is restricted by strip-out instabilities at low fields and a collapse at high fields. Due to the nanometer size of skyrmions, their topological stability, and possibility to manipulate by electric currents, the magnetic skyrmions are considered promising objects for the next-generation memory and logic devices [22,23,24].
In Ref. [25], however, it was contended that the saturated state may permit yet another type of isolated skyrmions with their axes oriented perpendicular to the field. Such 2D skyrmions are compelled to develop a non-axisymmetric shape in order to blend into the spin pattern of the homogeneous state and to preserve their total topological charge computed in the plane (Figure 1a,c). Alternatively, the skyrmion cross-section can be thought of as a pair of merons with the topological charges . For example, starting from the upper side of the depicted bimeron in the plane (Figure 1a), the magnetization makes the full swing from 0 to : it passes through the points A and B with the magnetization parallel to the z axis, and , which can be considered as centers of a circular skyrmion core and an anti-skyrmion crescent, respectively. Unlike the repulsive axisymmetric ISs, such non-axisymmetric skyrmions develop anisotropic skyrmion–skyrmion interaction [25,26]. Depending on the relative orientation of two individual skyrmions, this potential can be attractive, leading to the formation of biskyrmion or multiskyrmion chains, aligned along the axis connecting points A and B, as well as repulsive in the perpendicular direction (i.e., along y) [25]. Figure 1c exhibits the repulsive potential of two bimerons with opposite topological charges oriented inward either with their crescents (red curve) or with their cores (blue curve). Since the distorted crescent part is less spacious, the interaction potential in the first case shows pronounced repulsion at much smaller distances between bimerons (red curve). The distance d is measured at the magnetization value opposite to the field.
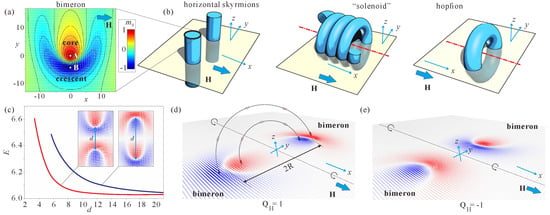
Figure 1.
(color online) (a) Magnetic structure of an isolated bimeron formed in the plane and surrounded by the homogeneous state . The field is applied along the x axis. The color indicates -component whereas the white arrows show the magnetization projections onto the plane . The composite parts of the bimeron structure are the circular core and the crescent. (b) Schematic representation of different 3D structures formed by the proliferation of bimerons: horizontal skyrmions (first panel) are bimeron tubes running perpendicular to the field direction (along z axis in the present case); “solenoids” or “springs” (second panel) are the intermediate states between the horizontal skyrmions and ordinary ISs with their axes along the field. They exist in two varieties and may have a variable radius, which subsequently squeeze into ordinary skyrmions with both polarities: hopfions (third panel) are torus-shaped 3D solitons obtained by the rotation of bimerons around the field direction. (c) Interaction potential of two bimerons with the opposite topological charges (inset shows the corresponding spin structures). Due to the strong deformations of the bimeron cores facing the interior, such a bimeron pair exhibits a stronger repulsion (blue curve) as compared with its counterpart (red curve). (d,e) Schematics showing how to obtain the initial states for the relaxation procedures in mumax3. The characteristic points within the bimeron pair at the distance between them are connected by circular paths with the suitable magnetization alignment. Then, two hopfion varieties with opposite Hopf indices and variable radii can easily be prepared.
Interestingly, propagation of such skyrmion filaments into the third direction may give rise to a number of exotic spin textures (Figure 1b). First of all, such skyrmions may run perpendicular to the field (along the z axis in the present case, first panel in Figure 1b). Such filaments were dubbed horizontal skyrmions in Ref. [27]. It was shown that isolated horizontal skyrmions may attract/couple with ordinary skyrmions oriented along the field and thus form clusters with mutually orthogonal orientations of constituent skyrmions. In Ref. [28], the horizontal skyrmions were shown to swirl into “solenoids”/“springs” with their axes parallel to the field (second panel in Figure 1b). Such spin “solenoids” may exist in two varieties depending on which part of a curled 2D bimeron faces the interior. Subsequently, the solenoids may squeeze into ordinary skyrmions with both polarities (and therefore, opposite topological charges): within the homogeneous state, however, only the ISs with the negative polarity maintain although within the conical phase—both skyrmion varieties are feasible [28]. The attraction between two skyrmion varieties may also lead to a family of so-called target-skyrmions [28]: in this sense, the topological charge of the horizontal skyrmion may either add or subtract from the topological charge of the skyrmion along the field, i.e., “massive” targets with the multiple charges Q can also be created.
In the present manuscript, we consider the swirling of horizontal skyrmions into the doughnut-shaped hopfions, i.e., we just wind the 2D bimeron texture around the x axis (the field direction) until it forms a localized object. We show that two types of hopfions obtained by such a procedure (and thus having opposite Hopf indices (4)) have quite distinct spin textures and internal properties. Most importantly, we pose the question of whether hopfions represent metastable states (local energy minima) in bulk chiral helimagnets, inevitably contract and transform into torons, or collapse altogether. We argue that competing cubic and exchange anisotropies constitute a valid mechanism behind hopfion metastability in chiral magnets. This would pave the way for possible applications of hopfions in spintronic devices.
2. Phenomenological Model
The standard model for magnetic states in bulk cubic non-centrosymmetric ferromagnets is based on the energy density functional [5,29]
including the principal interactions essential to stabilize modulated states: the exchange stiffness with constant A, Dzyaloshinskii–Moriya coupling energy with constant D, and the Zeeman energy; is the unity vector along the magnetization vector , and is the magnetic field applied exclusively along x-axis. The polar angle of the magnetization is measured from the x axis, the azimuthal angle —from the y axis.
For the forthcoming calculations, we use non-dimensional variables. The lengths are expressed in units of , i.e., the length scales are related to the period of the spiral state in zero field , and reflect the fact that the ground state of the system in the form of a single-harmonic mode is yielded as a result of the competition between the counter-acting exchange and DM interactions in Equation (3). Thus, introduces a fundamental length characterizing the magnitude of chiral modulations in non-centrosymmetric magnets. , where , is the reduced magnitude of the applied magnetic field. Within the isotropic model (3), a conical single-harmonic spiral with the wave vector along the field represents the global energy minimum. The critical field value marks the saturation of the conical phase into the ferromagnetic state. Since we aim at hopfions surrounded by the homogeneous state, the field value is taken, .
As a main numerical tool to minimize the functional (3), we use the MuMax3 software package (version 3.10), which calculates magnetization dynamics by solving the Landau–Lifshitz equation using the finite-difference discretization technique (see for details Ref. [30]). The grid size is and the cell size is equal along all coordinate axes, . As an initial “seed” for numerical procedures, we use 2D bimeron pairs (as those depicted in Figure 1d,e) with opposite topological charges/polarities. We prepared a set of such pairs with different distances d between them: first, we use default initial states in the form of ordinary skyrmions with their axes along z; then, by applying the field along x, we obtain bimeron configurations (this is the reason why we have chosen the x direction for the magnetic field also for three-dimensional (3D) spin textures). To prepare a 3D hopfion, we align the magnetization along circular trajectories connecting the characteristic magnetization points in the plane ; for example, , which correspond to the centers of bimeron cores and crescents; additionally, we pin the magnetization along the circle with the radius R, which later will be referred to as a hopfion radius (Figure 1d). After the relaxation procedure, we obtain hopfions of two varieties with variable radii R. As compared with the methods based on the Ansatz solutions for hopfions [31], the present approach has a number of advantages: (i) a trajectory along which one replicates bimerons can be entangled and encompass, for example, different knotted structures; thus, the search for multidimensional solitons can be systematized; it is often impossible to write an appropriate Ansatz for such particle-like states; (ii) one can investigate addition and subtraction of hopfions and investigate “nested” spin distributions, i.e., around a hopfion with one could wind another hopfion with the opposite or the same Hopf index [31]; (iii) one could obtain a smooth transformation between horizontal and vertical skyrmions and thus speculate about hopfions located in other coordinate planes.
3. Internal Structure of Hopfions
The structure of obtained hopfions is characterized by the Hopf invariant , which can be calculated from the Whitehead integral expression [32,33]:
The components of the emergent magnetic field are given by and cyclic permutations for and [34]. is the corresponding vector potential, . To find the components of , one usually exploits the fact that the vector potential is far from unique, i.e., one can choose a differentiable scalar function f on to make zero one of the components of , e.g., [35]. Then, the other two components can easily be obtained by integrating . By performing the integration according to (4), we find that two types of hopfions have Hopf indices of opposite sign, . In the following, the soliton with will be called hopfion, whereas its counterpart – anti-hopfion.
Plots of the preimages of hopfions and anti-hopfions are shown in Figure 2. Preimage is the spatial region of the ferromagnet’s 3D space with a single -orientation corresponding to a point on [31]. Preimages in Figure 2a,c correspond to and varying azimuthal angle . The color scheme indicates the value of the component varying from −1 (blue) to 1 (red) with the step . Preimages in Figure 2b,d correspond to the varying polar angle and ; the color reflects the magnetization component along the field with the same step . Any pair of preimage curves links times (in our case, just once), corroborating the interpretation of as a linking number. Still, the network of preimages is obviously different.
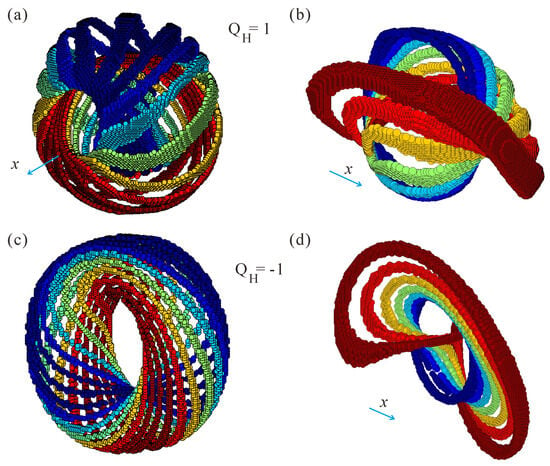
Figure 2.
Characteristic preimages for hopfions (a,b) and anti-hopfions (c,d). The toroids are formed by the isosurfaces of the spin direction (a,c). The color indicates magnetization components varying from −1 (blue) to 1 (red). The hopfion normals are co-aligned with the field (x direction). Since the hopfions and anti-hopfions have Hopf invariants and , respectively, each pair of preimages is linked exactly once. Preimages are also linked for and varying with the step from the direction along the field to the opposite direction (b,d). The color codes -component in this case.
The internal spin patterns of hopfions and anti-hopfions are depicted in Figure 3 for two cross-sections (Figure 3a,e) and (Figure 3b,f). Whereas in the former case, hopfions look as pairs of coupled bimerons with opposite polarities and can be differentiated whether the crescent faces exterior or the interior of a hopfion, in the latter case, hopfions represent so-called target skyrmions [36,37] (alternatively called skyrmioniums [38]), in which the magnetization undergoes a rotation by the angle . Note that the magnetization rotation occurs in accordance with the DMI, which prescribes the relation between the azimuthal angle of the magnetization and the cylindrical coordinate system, i.e., .
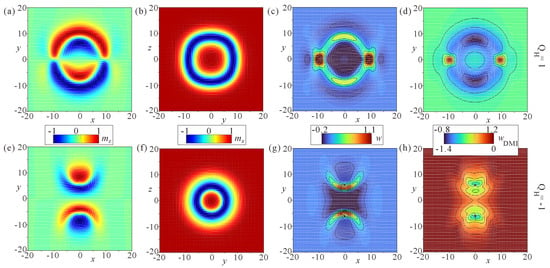
Figure 3.
(color online) Internal structure of hopfions (upper row) and anti-hopfions (bottom row) in bulk cubic helimagnets, . (a,e) Magnetization distribution in the cross-section . Color indicates -component with white arrows being the magnetization projections onto the plane . (b,f) Hopfion cross-section in the plane perpendicular to the field direction . Hopfions, in this case, represent target-skyrmions with the magnetization rotation by the angle from the center to the outskirt. (c,g) The contour plots of the total energy density in the plane . For hopfions, the positive energy density, which is computed with respect to the homogeneous state, is localized within the “egg”-like shell. For anti-hopfions, the positive energy density forms a belt-like pattern around the magnetization opposite to the field. (d,h) The contour plots of the DMI energy density for the 2D cross-section . Hopfions clearly exhibit parts with the reverse rotational sense against one chosen by the DMI, whereas anti-hopfions preserve only one rotational fashion.
Distribution of the total energy density (Figure 3c,g) and the energy density of the DMI (Figure 3d,h) provide even more insight into distinct properties of hopfions. The hopfions (Figure 3c,d) exhibit the parts with the unfavorable rotational sense against the DMI (red regions in Figure 3d). The total energy density in Figure 3c acquires an “egg”-like pattern with the positive energy density forming a shell. On the contrary, the anti-hopfion exhibits only one sense of rotation as shown by its DMI energy density (Figure 3h). The positive energy density is also localized to quite narrow parts surrounding the crescents.
4. Metastability of Hopfions in Bulk Helimagnets
Within the isotropic model (3), the total energy W of hopfions computed with respect to the homogeneous state, , represents almost a straight line (dashed black line in Figure 4a): as a result, both hopfion varieties contract and decrease their radii to reduce the positive eigen-energy. Interestingly, the eigen-energies are degenerate and stay the same up to quite small hopfion sizes for both hopfion types. In this case, constituent bimerons (first and third panels in Figure 4b) are spatially localized and do not significantly deform their internal structure. During the contraction process, the anti-hopfion transforms into a toron (Figure 4c), which represents a localized particle consisting of two Bloch points at a finite distance and a convex-shaped skyrmion stretching between them [39,40]. In the transversal cross-section, the magnetization rotates from the state in the center till the state at the outskirt as it would be in ordinary 2D skyrmions (second panel in Figure 4c). The energy density distribution reflects a great energy penalty associated with point defects (third panel in Figure 4c). The topological transition between the hopfion and the toron states was recently studied in a chiral magnet nanodisk sandwiched by two films with perpendicular magnetic anisotropy [41].
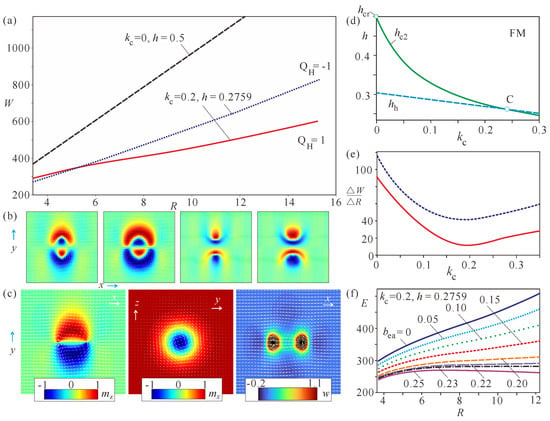
Figure 4.
(color online) (a) The eigen-energies of hopfions and anti-hopfions in dependence on the hopfion radii within the isotropic model (3) (dashed black line) and including the cubic anisotropy (dotted blue and solid red lines). The slope of curves is obviously modified by the decreasing magnetic field and the cubic anisotropy. (b) The spin structures of hopfions without (first and third panels) and with (second and fourth panels) the cubic anisotropy, which leads to spatial extension of hopfions. With the pinning removed, the anti-hopfions transform into torons with two point defects. (c) Toron internal structure is shown as the magnetization and energy density distributions in different 2D cross-sections. (d) The simplified phase diagram including the cubic anisotropy shows the drastic decrease in the saturation field of the conical phase. is a field of the phase transition between the helical and the FM state. In the search for the hopfion metastability, one should avoid the regions of the conical and/or helical spirals. In the former case, hopfions transform into heliknotons; in the latter one, undergo elliptical instability and elongate into helicoids. (e) The slope of the energy curves along the line is dependent on the cubic anisotropy value. Rather flat energy curves are reached in the vicinity of . (f) Modification of the energy curves by the additional exchange anisotropy. For some critical anisotropy values, the minimum corresponding to metastable hopfion appears.
The ()-hopfion, however, simply collapses into the homogeneous state, the behavior being consistent with the transformation of “solenoids” considered in Ref. [28].
To realize hopfions in bulk chiral ferromagnets, therefore, one should find a parameter range/region where static hopfions emerge as local or global minima of the free energy. Here, we notice that alternatively. hopfions can be embedded into a helical or conical background of chiral magnets and are called heliknotons [42]. We, however, concentrate on the areas of phase diagrams with the homogeneous ferromagnetic background.
To make the search more systematic, we first pose the question, of whether the slope of the energy curve in Figure 4a can be affected by additional anisotropies, which are inherent in cubic helimagnets. In particular, it is known that the cubic anisotropy
plays a significant role in bulk cubic helimagnets and may even lead to the thermodynamical stability of skyrmions far from the ordering temperatures [43]. Recently, low-temperature skyrmions have been observed in the Mott insulator CuOSeO, accompanied by tilted spirals. The theoretical explanation of SkL stability by the cubic anisotropy rather hinges on the effect imposed on one-dimensional spiral states than on skyrmions. In fact, the ideal magnetization rotation in the conical state is considerably impaired by the easy and hard anisotropy axes, e.g., for the field along crystallographic directions. Through this mechanism, skyrmions, which are more resilient to anisotropy-induced deformations, due to their two-dimensional nature, gain stability. For our purpose of searching for metastable hopfions, this effect of cubic anisotropy on the conical state would also become helpful: we would like to decrease the field value (to avoid any possible hopfion collapse as observed for isolated skyrmions [2]) but still stay within the homogeneous state. In CuOSeO, the easy cubic axes are (the anisotropy constant ), and the field co-aligned with one of these axes leads to the first-order phase transition between the conical and homogeneous states with the field value much lower than in the isotropic case [43]. The green line in Figure 4d shows the critical field in dependence on the cubic anisotropy. In the following simulations, we will look for metastable hopfions exactly along this line. Furthermore, indeed, we find that the slope of the hopfion eigen-energy decreases by the simultaneous effect of the weaker magnetic field and the cubic anisotropy. In particular, ()-hopfion acquires the smallest slope possible in this case for (red line in Figure 4a): to relax such a hopfion with mumax3 no additional pinning is needed, the relaxation procedure reaches some satisfactory accuracy and preserves hopfions; we believe that in the experiments the observation of hopfions for these anisotropy values would also become possible owing to larger relaxation times.
The anti-hopfion exhibits a slightly larger energy slope (dotted blue line in Figure 4a), but the lower energy at smaller radii. This can be explained by the larger hopfion sizes for the included cubic anisotropy (second and fourth panels in Figure 4b) and distortions of bimeron cores. The field value for both curves corresponds to the line for .
The blue dashed line in Figure 4d signifies the phase transition between the FM state and a helicoid with the wave vector perpendicular to the field. For relatively large anisotropy values (to the right of the intersection point C), this field value becomes higher than the field of the cone saturation . Below the line , hopfions are found to undergo elliptical distortions and elongations along the x direction as was pointed out for isolated skyrmions: in this sense, ISs/hopfions serve as nuclei of the more energetically favorable helical phase.
Figure 4e shows the variation in the slope of the curves , , depending on the cubic anisotropy. At first, the slope drastically decreases following the tendency of the critical field . Then, it reaches the minimum and starts to grow again, which is consistent with the inflection point of the line .
As the second important step, to find the metastability region of hopfions, we engage the exchange anisotropy. In CuOSeO, the exchange anisotropy
has easy axes (i.e., ) and therefore competes with the cubic anisotropy (5). Interestingly, neither the conical state nor the helicoid “feel” the exchange anisotropy: energy of the exchange anisotropy is zero for the conical phase, since the magnetization derivatives in (6) all vanish. Magnetization rotation in hopfions, on the contrary, acquires the negative energy. At larger values, an energy minimum corresponding to metastable hopfions appears (Figure 4f). The mechanism is based on the energy balance between the cubic anisotropy and the exchange interaction, which make hopfions smaller, and the exchange anisotropy trying to inflate hopfions in order to increase the extension of rotational regions. We notice that the relatively large anisotropy values leading to hopfion metastability correspond to low temperatures in the bulk chiral host CuOSeO. In Ref. [43], the values were found to reproduce the experimental results. Isolated hopfions, in this case, will be surrounded by the clusters of skyrmions and the domains of the tilted spiral states, which were experimentally shown to coexist in the low-temperature interval [43]. This fact may impede direct and unambiguous observation of hopfions in this bulk helimagnet.
5. Discussion and Conclusions
Nowadays, 3D hopfions are of great interest due to their potential application in three-dimensional spintronic devices, the reason for this being the emergent electromagnetic response and non-trivial dynamic properties under external stimuli. Hopfions have recently been observed in magnetic [44], ferroelectric [45] and liquid crystals [31,39], and have been studied in Bose–Einstein condensates [46]. Usually, one has to “create” some “special” conditions to observe hopfions: (i) in chiral liquid crystals, the difference in elastic constants alongside with the surface anchoring facilitate hopfion stability; (ii) in different nanostructures [41] or multilayers [44], one modifies the perpendicular magnetic anisotropy to create some energy barrier and prevent hopfion collapse; (iii) in frustrated systems [47,48] with the competing exchange interactions, both senses of the magnetization rotation are energetically equivalent and thus promote hopfions. Anyway, in these material systems, one may create even more complicated hopfions with the bimeron pattern rotating along the circular trajectory. In this case, the cross-section would exhibit target-skyrmions with the anti-skyrmion fashion of rotation but no additional energy “penalty” due to the Lifshitz invariants. In the cross-sections and , different bimeron parts will face the hopfion interior.
In the present manuscript, we, however, use the standard Dzyaloshinskii model for bulk cubic helimagnets. The hopfion texture can be conventionally characterized by the linked set of preimages: the preimages corresponding to any point on a sphere densely fill the surface of an associated withrus The calculated Hopf invariant equals 1 for hopfions and −1 for anti-hopfions. We, however, give another perspective on the internal structure of hopfions. Hopfions are considered a result of the swirling of 2D bimerons formed perpendicular to the applied magnetic field. Such a method allows us to obtain not only the aforementioned -hopfions, but also speculate about more exotic spin textures as “solenoids” and/or horizontal skyrmions. In particular, the smooth connection of solenoids (which are essentially ordinary skyrmion filaments oriented along the field) and the horizontal skyrmions can easily be imagined and, thus, one may attempt to construct versatile 3D solitons. Moreover, the internal properties of hopfions can be analyzed starting from the 2D bimeron patterns or 2D target-skyrmions, i.e., the stability of 2D solitons is vital for the stability of 3D hopfions as well. In particular, we avoid spin patterns obtained in a 2D hopfion cross-section, which do not comply with the Lifshitz invariants for cubic helimagnets.
To find metastable hopfions surrounded by the homogeneous state, we supplement the model by the cubic and exchange anisotropies, which are innate in B20 systems such as CuOSeO. The experiments invoked to indicate the hopfion presence in this bulk helimagnet should, however, take into account skyrmion clusters and tilted spiral states, which coexist with the homogeneous state in the suggested parameter range. At the same time, the inhomogeneous magnetic environment may induce hopfion nucleation. A similar strategy on hopfion observation was recently pursued in a cubic helimagnet FeGe [49], in which the cubic anisotropy and the temperature-induced change in easy axes contribute to the hopfion metastability. The fractional hopfions and their ensembles have been created by flipping the external field or flowing a pulsed current.
At the same time, we admit that the influence of small anisotropic energy terms (cubic and exchange anisotropies) on the hopfion structures and the related question of hopfion stability are far from being completely answered in the present paper. Indeed, depending on the control parameters, one may encounter many degenerate homogeneous states stabilized by the cubic anisotropy as well as a multitude of local energy minima with states oblique with respect to the field (see for details Ref. [50]). Thus, by varying the direction of the applied magnetic field with respect to the easy anisotropic axes, one may “strengthen” some parts of a hopfion (will be performed elsewhere).
Funding
This research was funded by JSPS grant number 21K03406 for A.O.L.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
A.O.L. acknowledges JSPS Grant-in-Aid (C).
Conflicts of Interest
The author declares no conflict of interest.
References
- Bogdanov, A.N.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Rößler, U.K.; Leonov, A.A.; Bogdanov, A.N. Chiral skyrmionic matter in non-centrosymmetric magnets. J. Phys. Conf. Ser. 2011, 303, 012105. [Google Scholar] [CrossRef]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636. [Google Scholar] [CrossRef] [PubMed]
- Dzyaloshinskii, I.E. Theory of helicoidal structures in antiferromagnets. I. nonmetals. Sov. Phys. JETP 1964, 19, 960. [Google Scholar]
- Rajaraman, R. Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory; North-Holland Publishing Company: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, A.N.; Roessler, U.K. Chiral Symmetry Breaking in Magnetic Thin Films and Multilayers. Phys. Rev. Lett. 2001, 87, 037203. [Google Scholar] [CrossRef]
- Bode, M.; Heide, M.; von Bergmann, K.; Ferriani, P.; Heinze, S.; Bihlmayer, G.; Kubetzka, A.; Pietzsch, O.; Blügel, S.; Wiesendanger, R. Chiral magnetic order at surfaces driven by inversion asymmetry. Nature 2007, 447, 190. [Google Scholar] [CrossRef]
- Wright, D.C.; Mermin, N.D. Crystalline liquids: The blue phases. Rev. Mod. Phys. 1989, 61, 385. [Google Scholar] [CrossRef]
- Sethna, J.P. Frustration and Curvature: Glasses and the Cholesteric Blue Phase. Phys. Rev. Lett. 1983, 51, 2198. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A Nonlinear field theory. Proc. Roy. Soc. Lon. 1961, 260, 127. [Google Scholar]
- Oswald, P.; Pieranski, P. Nematic and Cholesteric Liquid Crystals: Concepts and Physical Properties Illustrated by Experiments; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, H.; Baenitz, M.; Schmidt, M.; Roessler, U.K.; Leonov, A.A.; Bogdanov, A.N. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 2011, 107, 127203. [Google Scholar] [CrossRef] [PubMed]
- Kezsmarki, I.; Bordacs, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Ronnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Neel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106. [Google Scholar] [CrossRef]
- Du, H.; Liang, D.; Jin, C.; Kong, L.; Stolt, M.J.; Ning, W.; Yang, J.; Xing, Y.; Wang, J.; Che, R.; et al. Electrical probing of field-driven cascading quantized transitions of skyrmion cluster states in MnSi nanowires. Nat. Commun. 2015, 6, 7637. [Google Scholar] [CrossRef]
- Liang, D.; DeGrave, J.P.; Stolt, M.J.; Tokura, Y.; Jin, S. Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect. Nat. Commun. 2015, 6, 8217. [Google Scholar] [CrossRef]
- Romming, N.; Kubetzka, A.; Hanneken, C.; von Bergmann, K.; Wiesendanger, R. Field-Dependent Size and Shape of Single Magnetic Skyrmions. Phys. Rev. Lett. 2015, 114, 177203. [Google Scholar] [CrossRef]
- Tomasello, E.M.R.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef]
- Kang, W.; Huang, Y.; Zheng, C.; Lv, W.; Lei, N.; Zhang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Voltage Controlled Magnetic Skyrmion Motion for Racetrack Memory. Sci. Rep. 2016, 6, 23164. [Google Scholar] [CrossRef] [PubMed]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A.O.; Kezsmarki, I. Asymmetric isolated skyrmions in polar magnets with easy-plane anisotropy. Phys. Rev. B 2017, 96, 014423. [Google Scholar] [CrossRef]
- Barton-Singer, B.; Schroers, B.J. Stability and asymptotic interactions of chiral magnetic skyrmions in a tilted magnetic field. SciPost Phys. 2023, 15, 011. [Google Scholar] [CrossRef]
- Sohn, H.R.O.; Vlasov, S.M.; Uzdin, V.M.; Leonov, A.O.; Smalyukh, I.I. Real-space observation of skyrmion clusters with mutually orthogonal skyrmion tubes. Phys. Rev. B 2019, 100, 104401. [Google Scholar] [CrossRef]
- Leonov, A.O.; Pappas, C.; Smalyukh, I. Field-driven metamorphoses of isolated skyrmions within the conical state of cubic helimagnets. Phys. Rev. B 2021, 104, 064432. [Google Scholar] [CrossRef]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 13, L881. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Smalyukh, I.I. Static three-dimensional topological solitons in fluid chiral ferromagnets and colloids. Nat. Mater. 2017, 16, 426. [Google Scholar] [CrossRef]
- Whitehead, J.H.C. An Expression of Hopf’s Invariant as an Integral. Proc. Natl. Acad. Sci. USA 1947, 33, 117. [Google Scholar] [CrossRef]
- Gladikowski, J.; Helmund, M. Static solitons with nonzero Hopf number. Phys. Rev. D 1997, 56, 5194. [Google Scholar] [CrossRef]
- Balakrishnan, R.; Dandoloff, R.; Saxena, A. Exact hopfion vortices in a 3D Heisenberg ferromagnet. Phys. Lett. A 2023, 480, 128975. [Google Scholar] [CrossRef]
- Guslienko, K. Emergent Magnetic Field and Vector Potential of the Toroidal Magnetic Hopfions. Chaos Solitons Fractals 2023, 174, 113840. [Google Scholar] [CrossRef]
- Leonov, A.O.; Roessler, U.K.; Mostovoy, M. Target-skyrmions and skyrmion clusters in nanowires of chiral magnets. EPJ Web Conf. 2014, 75, 05002. [Google Scholar] [CrossRef]
- Zheng, F.; Li, H.; Wang, S.; Song, D.; Jin, C.; Wei, W.; Kovacs, A.; Zang, J.; Tian, M.; Zhang, Y.; et al. Direct Imaging of a Zero-Field Target Skyrmion and Its Polarity Switch in a Chiral Magnetic Nanodisk. Phys. Rev. Lett. 2017, 119, 197205. [Google Scholar] [CrossRef]
- Komineas, S.; Papanicolaou, N. Skyrmion dynamics in chiral ferromagnets. Phys. Rev. B 2015, 92, 064412. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Smalyukh, I.I. Diversity of Knot Solitons in Liquid Crystals Manifested by Linking of Preimages in Torons and Hopfions. Phys. Rev. X 2017, 7, 011006. [Google Scholar] [CrossRef]
- Leonov, A.O.; Inoue, K. Homogeneous and heterogeneous nucleation of skyrmions in thin layers of cubic helimagnets. Phys. Rev. B 2018, 98, 0544404. [Google Scholar] [CrossRef]
- Liu, Y.; Lake, R.K.; Zang, J. Binding a hopfion in a chiral magnet nanodisk. Phys. Rev. B 2018, 98, 174437. [Google Scholar] [CrossRef]
- Voinescu, R.; Tai, J.-S.B.; Smalyukh, I. Hopf Solitons in Helical and Conical Backgrounds of Chiral Magnetic Solids. Phys. Rev. Lett. 2020, 125, 057201. [Google Scholar] [CrossRef]
- Crisanti, M.; Leonov, A.O.; Cubitt, R.; Labh, A.; Wilhelm, H.; Schmidt, M.P.; Pappas, C. Tilted spirals and low-temperature skyrmions in Cu2OSeO3. Phys. Rev. Res. 2023, 5, 033033. [Google Scholar] [CrossRef]
- Kent, N.; Reynolds, N.; Raftrey, D.; Campbell, I.T.G.; Virasawmy, S.; Dhuey, S.; Chopdekar, R.V.; Hierro-Rodriguez, A.; Sorrentino, A.; Pereiro, E.; et al. Creation and observation of Hopfions in magnetic multilayer systems. Nat. Commun. 2021, 12, 1562. [Google Scholar] [CrossRef] [PubMed]
- Luk’yanchuk, I.; Tikhonov, Y.; Razumnaya, A.; Vinokur, V.M. Hopfions emerge in ferroelectrics. Nat. Commun. 2020, 11, 2433. [Google Scholar] [CrossRef] [PubMed]
- Bidasyuk, Y.M.; Chumachenko, A.V.; Prikhodko, O.O.; Vilchinskii, S.I.; Weyrauch, M.; Yakimenko, A.I. Stable Hopf solitons in rotating Bose–Einstein condensates. Phys. Rev. A 2015, 92, 053603. [Google Scholar] [CrossRef]
- Sutcliffe, P. Hopfions in chiral magnets. J. Phys. A Math. Theor. 2018, 51, 375401. [Google Scholar] [CrossRef]
- Sallermann, M.; Jonsson, H.; Blügel, S. Stability of hopfions in bulk magnets with competing exchange interactions. Phys. Rev. B 2023, 107, 104404. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Y.; Iakoubovskii, K.V.; Nakajima, K.; Kanazawa, N.; Nagaosa, N.; Tokura, Y. Realization and Current-Driven Dynamics of Fractional Hopfions and Their Ensembles in a Helimagnet FeGe. Adv. Mater. 2023, 35, 2210646. [Google Scholar] [CrossRef]
- Leonov, A.; Roessler, U.K.; Bogdanov, A. Phenomenological theory of magnetization reversal in nanosystems with competing anisotropies. J. Appl. Phys. 2008, 104, 084304. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).