Constructal Design Method Applied to Wave Energy Converters: A Systematic Literature Review

Abstract

The energy potential of sea waves has gained relevance, leading to extensive research on converters. The present work analyzes the contribution of Constructal Design to the development of wave energy converters. Constructal Design utilizes performance indicators to enhance system efficiency by varying the degrees of freedom where flow occurs. Thus, the systematic literature review methodology was applied to gather a collection of documents focused on the research topic. This study identified articles published between 2014 and 2024 by 40 authors affiliated with institutions in Brazil, Italy, and Portugal. The oscillating water column (OWC) converter received the most research attention, followed by the overtopping converter. Analyzing the documents collected for this study, the performance indicators revealed improvements ranging from 1.19 to 839 times, indicating the lowest and highest enhancements observed, respectively. The Constructal Design method has proven highly effective in identifying specific architectures or geometric arrangements that enhance flow configuration and improve the performance of wave energy converters. However, relatively few studies have applied the Constructal Design method to wave energy converters in comparison to other methodologies, presenting a significant opportunity for future research.

1. Introduction

Countries are increasingly incorporating renewable energy sources into their energy portfolios to address the growing energy demand and facilitate a smooth transition to a clean energy future [1,2,3,4]. Oceans cover approximately 71% of the Earth’s surface and present substantial renewable energy reserves, e.g., kinetic and potential energy from waves and tides [5]. The estimated global theoretical wave energy potential is approximately 29,500 TWh/year, and the total tidal energy potential is about 26,000 TWh/year [6,7,8,9]. Exploring ocean energy sources could help achieve net-zero emissions by 2050, which is an important objective given that global electricity demand is expected to increase from around 23,000 TWh in 2015 to roughly 49,000 TWh by 2050 due to population and economic growth [10]. In addition, incorporating ocean energy into the energy matrix can reduce the dependence on fossil fuels and greenhouse gas emissions from traditional thermoelectric power plants.

In the Brazilian context, the country’s total energy demand was met by 50% from fossil sources in 2024, with 34% derived from oil and its derivatives [11]. However, when analyzing Brazil’s electricity matrix, which consists solely of sources used for electricity generation, 86.8% of the energy was sourced from renewable sources. This matrix is predominantly driven by hydropower, accounting for 55.3% of the total electricity generated, followed by wind (14.1%), biomass (8.1%), and solar (9.3%) sources [11]. This underscores the need to diversify energy sources and technologies to lessen reliance on finite resources and ensure a secure energy matrix during periods of limited availability of the dominant source [12,13]. In this regard, ocean energy can play an interesting role in diversifying countries’ energy matrices. The effective utilization of wave, tidal, and current energy can provide reliable electricity, generate socio-economic benefits, and ensure an environmentally friendly energy source [14,15,16].

Despite significant benefits and abundant energy availability, ocean energy contributed only 1.6 TWh globally in 2020, compared to the approximately 23,000 TWh of electricity consumed [5,17]. This minimal contribution can be attributed to various challenges, including materials and manufacturing issues, hydrodynamics, concerns about survivability and reliability, environmental impacts, array configurations, power conversion and control systems, grid connections and infrastructure, maritime safety, socio-economic implications, and governance [18,19,20]. These factors result in low power density, high costs, and low reliability, which hinder the full utilization of ocean energy technologies.

Oceanic renewable energy technologies are vital in decarbonizing the energy sector and addressing climate change [21]. Additionally, the population density and industrial activity in coastal areas are substantial, making the exploration of these energy sources a significant public interest [22]. However, these technologies still require development and investment to become commercially viable.

A review paper by Khojasteh et al. [5] on wave energy from 2003 to 2021 highlights a wide range of ongoing research. The review identifies five main research subgroups: environmental resource assessment, impacts and benefits, wave energy converters and hybrid systems, energy from flow-induced vibrations and oscillations, and flow dynamics and tidal turbines. Among the various technologies, the present work focused on three types of wave energy converters (WECs), as presented in Figure 1: the oscillating water column (OWC) (Figure 1a), the overtopping (Figure 1b), and the submerged horizontal plate (SHP) (Figure 1c).

The oscillating water column (Figure 1a) can be a floating or fixed structure, such as one found on a breakwater. It generates energy using a turbine installed at the top of a partially submerged hydropneumatic chamber, which is driven by air circulation resulting from wave impact and, consequently, pressure variations inside the chamber [23]. The overtopping device (Figure 1b) converts energy from wave impact into its reservoir via a ramp, with the stored water returning to the sea through turbines connected to generators [23]. Finally, the submerged horizontal plate (Figure 1c) was initially developed as a submerged breakwater to reduce wave height [24]. However, the energy flow generated beneath the plate can drive a hydraulic turbine, thus functioning as an energy conversion device.

In the past decade, the optimization of wave energy converters has been a primary focus for researchers, aiming for feasibility, efficiency, and cost-effectiveness [5]. Some review papers addressed in detail the wave energy converter geometry and layout optimization [25,26,27,28]. In particular, López et al. [29] evaluated different oscillating water columns in a case study for the Port of Vigo (Spain). The authors found that the L-shaped column was the best option. Ramezanzadeh et al. [30] improved the OWC efficiency by about 4.3% by studying the best geometry for three wave periods. In experimental and numerical work, Zandi et al. [31] identified the optimal geometry from different primary geometries of floating bodies for wave energy converters. Shadmani et al. [32] explored different multi-objective optimization techniques to obtain the best geometry for multi-axis WECs (MA-WECs). The results indicated that the choice of optimization techniques has a considerable influence on the MA-WEC’s optimal design and efficiency. Another recent work that explored different geometries and optimization techniques to improve the efficiency of WECs can be found in the literature [33,34,35,36].

Despite several studies in the literature evaluating the geometry of different wave energy converters, only a few of them applied the Constructal Design method to maximize the performance of these systems. The Constructal Design method is based on Constructal Law, which considers that for a system to evolve, it must facilitate access to the flow of its currents [37,38]. Thus, Constructal Design seeks architecture or a geometric arrangement that achieves a better flow configuration and uses the system’s performance as an indicator [39,40]. Even though the Constructal Law was born in the realm of thermodynamics, the Constructal Design has been applied in various research fields, including vascular flow design [41], natural flows [42,43], and biological systems [44]. In engineering applications, the Constructal Design has been widely used in many studies, such as composite materials [45], internal combustion engines [46], carbon capture technologies [47], steam turbines [48], battery thermal management systems [49,50], and several heat transfer and fluid flow studies [51,52,53].

Applying the Constructal Design method shows that changing the flow configuration is the key to developing more efficient systems. Nevertheless, the application of this methodology in wave energy converters is relatively new, as the first work dates back to 2014. This paper presents a systematic literature review of applying the Design Constructal method to wave energy converters, shedding light on this research topic and focusing on the development of wave energy converters. Our review compiles the findings and ideas from relevant research, providing an outline of future developments in this research topic. In addition, this paper presents a bibliometric analysis of the growth in the application of the Constructal Design method in wave energy converters over the years, highlighting the most important research groups and the most relevant works. It is also important to emphasize that the other review papers in the literature on the development and optimization of wave energy converters differ from this work, as they focus on general studies and optimization techniques applied to WEC.

2. Methodological Procedures

A systematic literature review (SLR) is a robust tool designed to map a research area through systematic and well-defined procedures. The primary objective of a systematic literature review is to conduct a meticulous and unbiased synthesis of evidence within a specific field or research topic, as well as to identify gaps and opportunities for further development [54]. Unlike other types of reviews, a systematic review defines a specific research question and establishes a detailed protocol [54]. The systematic literature review was initially utilized in medical research to evaluate existing studies. However, it has also been widely adopted in engineering applications to draw reliable conclusions [55,56]. All decisions and steps taken during the systematic literature review must be transparently documented, ensuring clarity regarding the methodology employed [57]. Following specific steps to collect, map, and synthesize information from previous studies helps minimize the risk of bias [58].

This work follows the Preferred Reporting Items for Systematic Reviews and Meta-Analysis (PRISMA) guidelines to present the results of the literature searches and article selection procedure [59]. The PRISMA technique was employed to ensure that the data selection process was transparent and reproducible for other researchers. The first stage of the systematic literature review was the planning stage. The review objective, protocols, and criteria were clearly defined during this step. The second stage involved implementing the plan, which included screening and selecting relevant studies to insert in the review. Finally, the results were processed and analyzed, involving the summarization of the studies and the application of statistical metrics.

Generally, a systematic literature review seeks to find all evidence that matches predefined inclusion criteria to address a specific research question or hypothesis [60]. The present work was conducted to identify the state of the art and address the primary question, “How has the constructal design method been applied to improve the performance of wave energy converters?”

-

Additionally, secondary questions are answered through the systematic literature review:

-

How has the application of the Constructal Design method been growing and expanding over the years in the wave energy converter research field?

-

What types of wave energy converters are studied by the Constructal Design method?

-

What are the leading countries, researchers, and their collaborations in this research field?

-

What are the benefits of applying the Constructal Design method to wave energy converters?

Figure 2 illustrates the research protocol for conducting the systematic literature review of this work, outlining the planning and execution steps. This research was conducted using the Scopus and Web of Science databases to identify articles that employed the Constructal Design method in wave energy converters. The decision to use these two databases is due to their relevance in the engineering field. The search was filtered to include articles containing the term “Constructal Design” in the title, abstract, or keywords, along with “wave energy converter,” or “Oscillating water column,” or “Overtopping,” or “Submerged horizontal plate”. The search was conducted on 26 March 2025. The PRISMA flow diagram for this work is presented in Figure 3.

It is important to note that only journal articles were considered, while other types of work were excluded from this research. Only journal articles were considered, as they are generally more complete than conference papers, and most conference papers are not indexed in the Scopus and Web of Science databases. Additionally, a filter was applied to the year of publication, considering articles published up to the year 2024. As a result of the search described above, 23 articles were obtained from the Scopus database and 15 articles from the Web of Science database. However, this study was developed solely with the data extracted from Scopus. Among the 15 articles found in the Web of Science search, 12 were already included in the Scopus results, representing 80% of the Web of Science documents found. The remaining three, accounting for the other 20%, did not meet the criteria for this research, which focused on the application of Constructal Design in wave energy devices, and were therefore excluded from the present study.

The search data were then exported and processed using Rayyan, VOSviewer (version 1.6.20), and Bibliometrix software (version 5.1.0) to access, quantify, and map the data from the selected articles [61,62]. All documents were categorized and analyzed according to the wave converter type: oscillating water column, overtopping, and submerged horizontal plate, as described in Figure 2. To minimize the risk of bias, all reviewers assessed each study and worked independently. The quality assessment of the primary studies collected was performed manually, checking if they met our eligibility criteria and contributed to answering our research questions [63]. Annual productivity by affiliation and journal was quantified using the Bibliometrix tool. The analysis of authorship, keywords, and correlations among the articles was conducted using VOSviewer, which is recognized for its capabilities in creating correlation networks. In this study, authorship networks, keyword co-occurrence, and bibliographic coupling were analyzed. Additionally, the filtered articles were analyzed in terms of their objectives, methodology, and results regarding the use of Constructal Design.

It is important to highlight that a limitation of this systematic literature review is its exclusive focus on wave energy converter studies that apply the Constructal Design method to improve system performance. Other studies on wave energy converters that do not incorporate this method were not considered.

3. Bibliometric Analyses

The execution of the research protocol outlined in Figure 2 resulted in a collection of 23 articles that apply the Constructal Design method to wave energy converters. These studies were conducted by 40 different researchers affiliated with institutions from three countries: Brazil, Italy, and Portugal. This research field began in 2014 with the application of Constructal Design to an overtopping converter model and has evolved since then. The years with the highest number of publications were 2021 and 2024, with four and five articles, respectively (Figure 4). It is worth noting that in 2015, a total of three articles were published, one of which addresses all three types of converters discussed in this study; however, the Constructal Design method was applied only to the overtopping and oscillating water column converters [64].

The application of Constructal Design specifically to wave energy converters remains a relatively small research area, especially compared to the broader, global application of the method across various fields, which aims to optimize geometric arrangements to facilitate the flow of currents within a system [40]. A search in the Scopus database for the term ‘Constructal Design’ in the title, abstract, or keywords published up to 2024 yielded a total of 441 publications, authored by researchers from 40 countries. Among these, Brazil and China stand out as the countries with the highest number of publications. This research field began to emerge in 2001; Bejan and Lorente [65] published a review on Constructal Design in thermodynamics, while Neagu and Bejan [66], Vargas and Bejan [67], and Wechsatol, Lorente, and Bejan [68] applied Constructal Design to systems involving heat transfer.

Regarding the countries developing work on wave energy converters, an analysis by Khojasteh et al. [5] on wave and tidal energy research identified 8174 publications from 2003 to 2021, spanning 98 countries. The leading countries in this research area are China, the United Kingdom, and the United States. In the context of this study, the researchers are based in Brazil, Italy, and Portugal. Among the 23 documents, all have Brazilian authors affiliated with five different universities, seven documents have Italian authors affiliated with two distinct universities, and two documents have Portuguese authors affiliated with two other universities. The universities that most contributed to this research field are shown in Figure 5. The Universidade Federal do Rio Grande (Brazil) contributed 22 documents, followed by the Instituto Federal de Educação, Ciência e Tecnologia do Paraná (Brazil) and Universidade Federal do Rio Grande do Sul (Brazil) with 19 documents each.

As of the date of this research, the selected articles have received a total of 226 citations.

Table 1. Most cited documents.

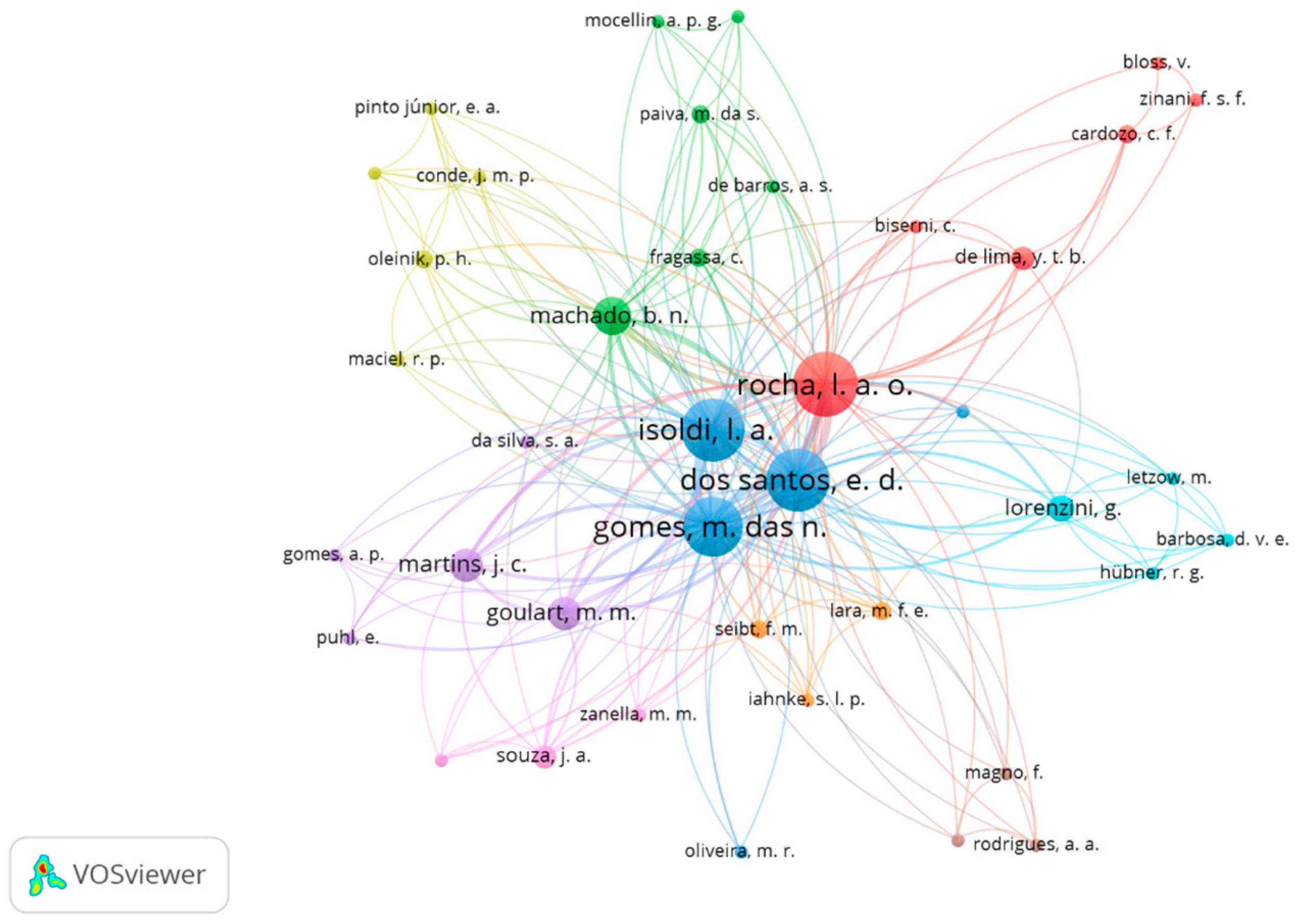
Documents	Journal	Citations	Wave Energy Converter
Martins et al. 2018 [69]	Renewable Energy	68	Overtopping
Gomes et al. 2018 [70]	Journal of Engineering Thermophysics	30	Oscillating water column
dos Santos et al. 2014 [71]	Defect and Diffusion Forum	24	Overtopping

presents the five most cited documents over the years. The first is the work conducted by Martins et al. [69], which has 68 citations, focusing on the optimization of an overtopping wave energy converter, followed by Gomes et al. [70] and Dos Santos et al. [71], with 30 and 24 citations, respectively. The documents collected are from nine different sources, as shown in Figure 6. The journal Defect and Diffusion Forum contributed eight documents, followed by the Journal of Marine Science and Engineering, which contributed four documents.

Using the VOSViewer software, a collaboration network among the contributing authors was generated, as shown in Figure 7. The size of the circle accompanying each researcher’s name corresponds to the number of articles they have authored. At the same time, the thickness of the connecting lines indicates the extent of their co-authorships. Among the 40 researchers, 16 have authored at least two documents included in this study. The collaboration network is centered around four key researchers who are interconnected with others. Rocha L. A. O. is the most prolific, having authored all 23 target articles, followed by Dos Santos E. D. and Isoldi L. A. with 22 articles each, and Gomes M. N. with 20 articles. Accordingly, the researchers with the highest number of publications are positioned at the center of the network, as they are present and connected to all other research groups that form the periphery of the collaboration network.

The authors described 47 different terms in the keywords, with the most frequently cited being “constructal design” (17 occurrences), “numerical simulation” (7 occurrences), and both “overtopping device” and “wave energy” (mentioned six times each). Figure 8 presents the keyword co-occurrence network. The keyword co-occurrence network reveals that, among the 47 identified terms, 44 are interconnected (Figure 8a). In this network, the size of each circle represents the frequency with which the term appears, while the connecting lines indicate terms that are mentioned together in one or more articles. The terms cited two or more times (Figure 8b) are primarily related to the methodology, the type of converter, and geometric configurations. From the most frequent keywords, it can be seen that the Constructal Design method applied to wave energy conversion systems focuses on developing more efficient designs for the systems by enhancing their performance through changes in geometry according to specific degrees of freedom.

Bibliographic coupling indicates the relationship between articles based on the similarity of their references, thereby reinforcing research lines and their respective contributions [72,73]. Consequently, the coupling network generated by the VOSViewer software illustrates the connections between documents. It divides them into three groups with greater similarity between their respective reference lists, as shown in Figure 9. The group of articles, represented in green and located on the middle of the network, consists of studies focused on overtopping-type converters. The blue-colored group on the right side of the network comprises research on oscillating water column (OWC) converters. Finally, the red group at the left side of the network includes articles that address all three types of wave energy converters (WECs). It is worth noting that, in the bibliographic coupling network developed using the VosViewer software, each article is represented by the name of the first author and the year of publication (Figure 9). However, the articles in this collection have four or more authors, with an average of 6.65 authors per article.

4. Synthesis and Interpretation

The articles analyzed in this study applied the Constructal Design to enhance flow access within devices by utilizing their geometric architecture, varying degrees of freedom, maintaining constant constraints, and assessing their impacts on a performance indicator. It is important to emphasize that the Constructal Design is not considered an optimization method but rather a method of geometric analysis. Many authors combine it with optimization techniques to achieve geometric optimization of wave energy converters, typically aiming to maximize their performance.

In general, these studies focus on the operational principles of the devices and the hydrodynamics of wave incidence, applying a geometric analysis accordingly. These works involve both mathematical and numerical modeling. Given the multiphase nature of the systems, the authors in this research field employ the volume of fluid (VOF) method to address the air–water interaction, along with the finite volume method (FVM) for solving the conservation equations of mass, momentum, and volume fraction transport [83,84]. Based on the selected articles and the specific type of converter addressed in each, the summary and discussion of studies related to overtopping devices, oscillating water columns, and submerged horizontal plates are presented in Section 4.1, Section 4.2, and Section 4.3, respectively.

4.1. Overtopping

A total of nine articles were selected that address overtopping devices and apply the Constructal Design method through numerical or experimental research. Generally, these studies aim to identify, through geometric configuration, a design that yields the best performance. In these cases, maximizing the volume of water that overtops the ramp and reaches the reservoir is the goal.

Table 2. Summary of the works that addressed the Constructal Design method in overtopping WECs.

Works	Objective	Performance Indicator	Main Results
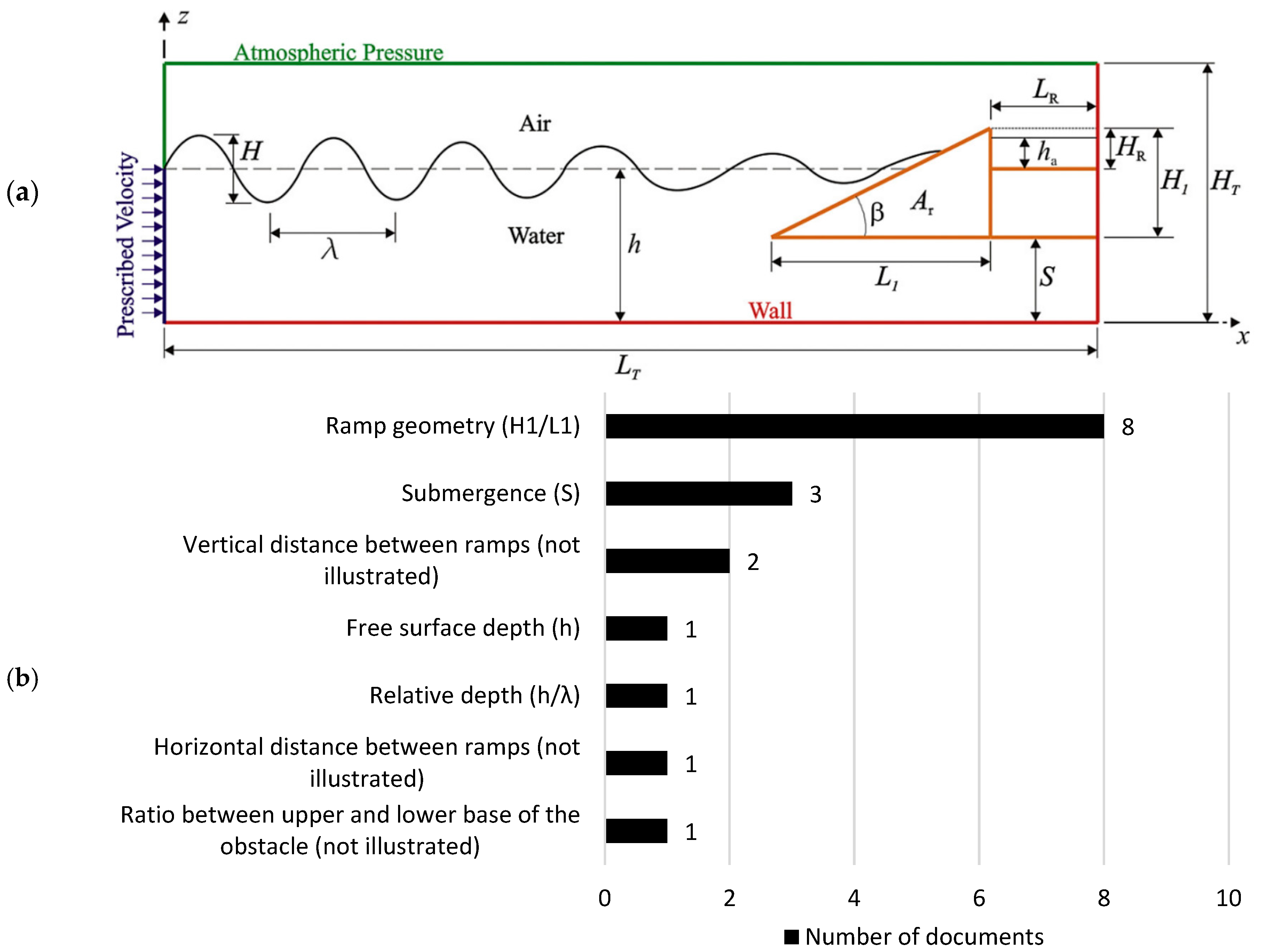
Goulart et al. 2024 [74]	To investigate and compare experimental and numerical results of the effect of ramp geometry and free surface water depth on the device’s performance.	Water accumulated level in the reservoir	The experimental and numerical results showed excellent agreement, validating and recommending the respective computational model for future research. Less steep ramps exhibit better performance, consistent with findings reported in the literature. Different water depths correspond to different ranges of ramp inclinations at which overtopping occurs.
Goulart et al. 2015 [75]	To explore the ramp geometry of the device under different water depths.	Mass of water	Lower height-to-length ratio (less steep ramps) demonstrated better performance. Submergence can increase the amount of overtopped water by up to five times for ramps with the same geometry.
Martins et al. 2022 [76]	To investigate the hydrodynamic performance of devices with one and two sequential ramps, considering their geometry and positioning, in conjunction with a breakwater.	Average dimensionless overtopping flow	The device with two ramps exhibited a performance indicator approximately 6% higher than that of the device with a single ramp.
Martins et al. 2022 [76]	To explore the influence of the vertical distance between the two ramps on the hydrodynamic performance of the device.	Average dimensionless overtopping flow	A greater vertical distance resulted in lower overtopping flow performance. A spacing of 1 m yielded the best performance indicator.
Martins et al. 2018 [69]	To analyze ramp geometry under varying water depths and wave periods.	Dimensionless available power	Wave characteristics, along with parameters such as area, depth, and ramp geometry, are strongly interrelated and influence the available power of the device.
Gomes et al. 2015 [64]	To investigate the effect of ramp geometry on device performance across different water depths.	Mass of water	Less steep ramps and devices placed at greater depths demonstrated better performance.
Dos Santos et al. 2014 [71]	To investigate the impact of relative depth on ramp geometry and its influence on the device’s hydrodynamic performance.	Mass of water	The lowest relative depth analyzed resulted in the best performance. Ramp geometry and device depth are strongly interrelated, both significantly influencing the performance indicator.

presents a summarized analysis of how Constructal Design has been applied in studies focusing on overtopping converters, highlighting the purpose of applying the method, the performance indicators used, and the main results obtained.

Goulart et al. [76], Martins et al. [69], Goulart et al. [75], Gomes et al. [64], and Dos Santos et al. [71] analyzed ramp inclination (H/L) in combination with another system variable and its effects on the performance indicator. Dos Santos et al. [71] explored the relationship with relative depth, defined as the ratio between free surface depth and wavelength. Gomes et al. [64], Goulart et al. [75], and Martins et al. [69] focused on device submergence, defined as the vertical distance from the seabed to the base of the ramp. Goulart et al. [74] investigated the ramp geometry and its relationship exclusively with free surface depth.

Among the nine articles reviewed in this section, eight adopted H/L as a degree of freedom. To analyze the behavior of ramp geometry as a degree of freedom, Figure 10 presents the range of H/L ratios studied across the literature (minimum and maximum point analyses), indicating within this range the intervals in which overtopping occurs (illustrated as a gray box in Figure 10) and the specific H/L value at which maximum performance was achieved (the maximum performance point). The results from Martins et al. [69] were not included in Figure 10 due to the large number of simulations performed. This study varied ramp geometry and device depth as degrees of freedom for three ramp area fractions and two wave periods, resulting in a total of 348 simulated cases.

In the work by Dos Santos et al. [71], a wide range of ramp inclination ratios (H/L from 0 to 1.4) was studied. The authors observed that, within the range where overtopping occurs, extreme H/L values result in low device performance. A very shallow ramp (H/L = 0.1), characterized by a long and sloped profile, behaves similarly to a “beach”, where water rarely reaches the reservoir due to the ramp’s length. Conversely, a steep and short ramp (H/L = 1.2) produces a breakwater effect, which dissipates wave energy and hinders overtopping; in both cases, more wave energy is required for the water to reach the reservoir.

Although using different performance indicators, studies by Gomes et al. [64], Goulart et al. [75], Martins et al. [69], and Goulart et al. [74] similarly reported that higher H/L ratios lead to reduced performance, as the steeper geometry causes a breakwater effect that prevents water from entering the reservoir. These results support the conclusions of Dos Santos et al. [71]. These studies reveal a consistent trend, where the maximum performance is achieved at the lowest H/L ratios analyzed, followed by a decline as the ramp becomes steeper. An exception is found in Da Silva et al., where the maximum performance occurs at an intermediate H/L value, which the authors attribute to the device’s height aligning more closely with the mean water level when the ramp angle is reduced.

In the studies by Gomes et al. [64], Goulart et al. [75], and Martins et al. [69], the effect of device submergence is addressed. More submerged devices require steeper ramps to achieve overtopping. However, Goulart et al. [74] demonstrated that submergence allows overtopping to occur even at higher H/L ratios. Comparing cases where only the submergence varies, the most submerged configurations consistently showed better performance [64,74,75].

Several studies also analyzed the instantaneous mass flow rate into the reservoir, which is the amount of water entering the reservoir through the ramp at any given moment over the analyzed period, as presented in Figure 1b. Dos Santos et al. [71] investigated the effects of ramp geometry and relative depth, while Gomes et al. [64] and Goulart et al. [75] focused exclusively on submergence. Dos Santos et al. [71] performed 20 s simulations where overtopping occurred between 4.5 and 15 s. For each relative depth (0.3, 0.5, and 0.62), different wavelengths were used, revealing that wave characteristics directly influence ramp geometry and overtopping dynamics. At a relative depth of 0.3 and longer wavelengths, more overtopping peaks were observed, with H/L = 1.14 reaching a peak flow rate of 15 kg/s. At an intermediate depth (0.5), fewer peaks occurred, but the maximum rate reached 27 kg/s for H/L = 0.6. The highest relative depth (0.62) with shorter wavelengths showed fewer and smaller overtopping peaks, with a maximum of about 4 kg/s for H/L = 0.4.

In contrast, Gomes et al. [64], Goulart et al. [75], and Martins et al. [69] maintained a fixed relative depth of 0.153 and conducted 100 s simulations, where overtopping began at 45 s. Gomes et al. [64] and Goulart et al. [75] compared 5 m and 6 m submergence for H/L = 0.22. The more submerged device (S = 5 m) yielded higher magnitudes and more overtopping peaks, with a maximum of 790.29 kg/s, while the less submerged case peaked at 154.69 kg/s. Martins et al. [69], with a fixed depth of 6 m, tested H/L ratios of 0.14, 0.18, and 0.22. The lowest H/L ratio (the less inclined ramp) produced the highest flow magnitudes, and overtopping occurred more frequently.

To improve hydrodynamic performance, Martins et al. [76] introduced geometric modifications to the device using the Constructal Design. Barros et al. investigated a bottom-mounted trapezoidal structure placed before the ramp, intended to optimize fluid dynamics by reducing flow resistance. The study explored variations in ramp inclination (H/L) and obstacle geometry, ranging from triangular (top base = 0) to rectangular (top and bottom bases equal, ratio = 1). The authors also compared the performance of the device with the obstacle to the same configuration without any attached structure. Their results showed that H/L had a greater influence on performance than the obstacle’s shape. In line with earlier studies, lower H/L ratios led to a better performance across all configurations. Among the studied configurations (triangular, trapezoidal, rectangular, and without obstacle), the authors found that the trapezoidal structure achieved the best performance, maximizing water volume in the reservoir. The triangular obstacle acted to dissipate the wave, causing dispersion of the flow, while the rectangular shape reflected the wave. In both cases, a reduction in mass flow intensity was observed. The trapezoidal geometry, when optimally arranged, improved performance by 30% compared to the configuration without any structure.

Martins et al. [76] investigated the geometric configuration of an overtopping device with two sequential ramps, integrated into a real breakwater structure located in the state of Rio Grande do Sul, Brazil. The main objective of the authors was to enhance the hydrodynamic performance. The authors defined the dimensionless average overtopping flow rate as the performance indicator and compared it to an empirical dimensionless average overtopping rate. In other words, they measured the volume of water that overtopped the ramp and entered the reservoir. They compared it to reference values based on local environmental conditions, calculating the relative error to assess the reliability of the results.

Martins et al. [76] examined two scenarios. The first involved a single-ramp device, where ramp geometry (H/L) was the degree of freedom. The second scenario incorporates an additional ramp with four degrees of freedom, upper and lower ramp geometries (H/L), as well as the vertical and horizontal distances between the ramps, resulting in a total of 75 simulated cases. The single-ramp configuration coupled with the breakwater achieved the best overtopping performance at the lowest ramp inclination analyzed (H/L = 0.508). In the second case, which included a second ramp in sequence, the optimal geometric configuration was obtained with intermediate inclinations for both ramps (H/L = 0.667). A comprehensive analysis of the degrees of freedom revealed that the lower ramp allowed a greater mass of water to overtop when the horizontal distance between the ramps was larger and the vertical distance was smaller. Conversely, the upper ramp offered less flow resistance when the horizontal spacing was reduced and the vertical spacing increased. Overall, the two-ramp configuration demonstrated an approximately 6% higher performance compared to the single-ramp design [76].

Martins et al. considered the optimal geometry identified in [76], focusing specifically on a more detailed analysis of the vertical spacing between the ramps. While Martins et al. [76] examined two values for vertical distance, Martins et al. evaluated eight different values, aiming to identify the configuration that minimizes flow resistance. The tested values ranged from 0.02 m to 0.35 m. The best performance indicator was achieved with a vertical distance of 0.1 m, consistent with the results of [76]. However, it is noteworthy that the largest vertical spacing analyzed (0.35 m) resulted in the worst performance, as it introduced higher resistance to the overtopping flow.

4.2. Oscillating Water Column

This study compiled a collection of 14 articles focused on oscillating water column (OWC) converters, applying the Constructal Design method to investigate the geometric arrangement of the device. These investigations addressed parameters such as the geometric arrangement of the hydropneumatic chamber, given by the ratio of its height to its length (H/L), the shape of the hydropneumatic chamber, the inclusion of sequential chambers or additional structures, and the device’s submergence.

Table 3. Summary of the works that addressed the Constructal Design method in oscillating water column WECs.

Works	Objective	Performance Indicator	Main Results
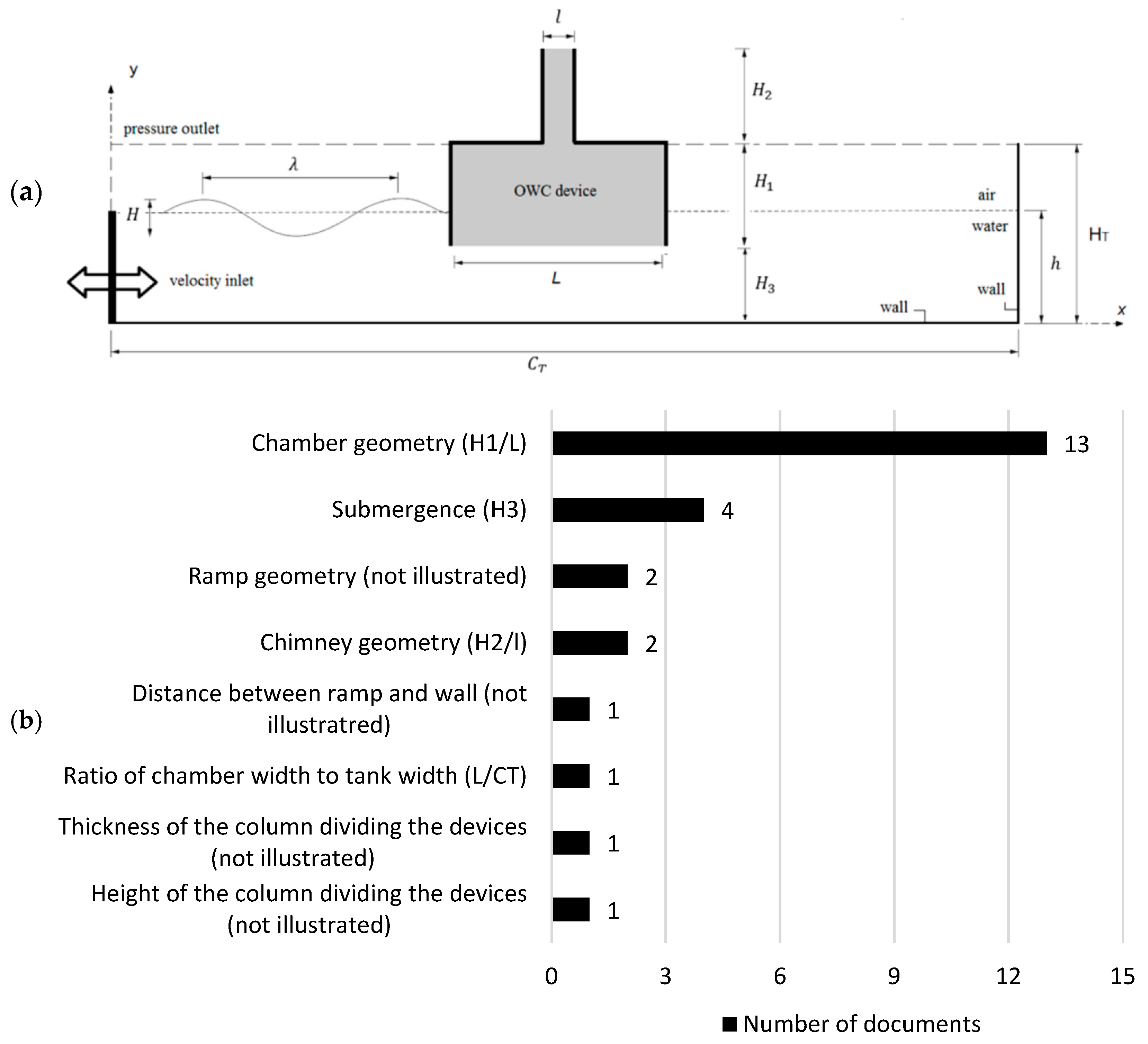
Mocellin et al. 2024 [77]	To evaluate the influence of the hydropneumatic chamber geometry (H/L) on the performance of the device.	Hydropneumatic power	The optimal geometry demonstrated a performance 101% higher than the worst geometry analyzed. Regular wave simulations tend to overestimate performance results when compared to simulations with irregular waves.
Maciel et al. 2023 [78]	To analyze the device geometry under real sea wave conditions and its effect on the performance indicator.	Hydropneumatic power	The chamber with the lowest height-to-width ratio yielded the best performance, while the chamber with the highest ratio resulted in the worst. When compared to regular wave simulations, noticeable differences were observed in the device’s hydrodynamic performance under real wave conditions.
Lima et al. 2024 [79]	To determine the optimal geometry for a WEC equipped with five hydropneumatic chambers.	Hydropneumatic power	The mass flow rate and hydropneumatic power achieved their maximum value at the same geometry. The maximum performance indicator was approximately 74 times higher than that of the lowest-performing case.
Lima et al. 2021 [80]	To evaluate the influence of the number and geometry of hydropneumatic chambers on the performance of the OWC.	Hydropneumatic power	The configuration with five chambers showed the highest available power. However, the design with three chambers achieved a higher maximum performance indicator than the four-chamber configuration.
Pinto Junior et al. 2024 [81]	To identify the hydropneumatic chamber geometry that maximizes the performance indicator by varying its shape from trapezoidal to rectangular.	Available power	The base geometry of the chamber has a greater impact on the performance indicator as it directly influences the device’s inlet area. A difference of up to 795 times was observed between the worst- and best-performing configurations.
Gomes et al. 2018 [70]	To analyze the effect of device geometry under the incidence of regular waves with varying periods.	Hydropneumatic power	An optimal correlation was identified, capable of maximizing hydropneumatic power across all analyzed wave periods. This occurred when the chamber’s height-to-length ratio was four times the height-to-length ratio of the incident wave.
Gomes et al. 2015 [64]	To analyze the effect of geometric configurations on wave energy efficiency.	Hydropneumatic power	Higher submergence levels resulted in poorer performance compared to the other cases. Across all simulated submergence conditions, the highest hydropneumatic power values were observed within the chamber H/L ratio range of 0.0598 to 0.2019.

provides a concise summary of each article’s objective in applying the Constructal Design, the performance indicator used, and the main findings.

Most of the articles listed in Table 3 conducted simulations using regular waves. Mocellin et al. [77] and Maciel et al. [78] specifically investigated the influence of the hydropneumatic chamber geometry (H/L) on the hydropneumatic power and compared the results obtained under different wave types to assess their impact. Mocellin et al. [77] conducted simulations using regular waves representative of the sea state in Tramandaí city (RS) and compared them with the WEC under the same conditions but with realistic irregular waves. In contrast, Maciel et al. [78] carried out their study using irregular waves based on the sea state of Praia do Cassino (RS) and subsequently compared the results with simulations using representative regular waves.

Mocellin et al. [77] reported a performance overestimation when using representative regular wave simulations, with discrepancies ranging from 10% to 260% compared to results obtained with irregular wave simulations. The smallest difference was observed for the smallest geometric configuration analyzed (H/L = 0.1985), while the most significant difference occurred for the largest configuration (H/L = 2.2789). In the comparison conducted by Maciel et al. [78], the hydrodynamic behavior was analyzed for a fixed geometry, which yielded the maximum performance indicator under irregular waves, specifically at H/L = 0.1985, which was the same optimal value identified under irregular wave conditions by [77]. Maciel et al. [78] also highlighted the contrast between a uniform behavior under regular waves and an unstable behavior under irregular waves. However, both produced similar magnitudes, with a difference of approximately 3%. It is important to emphasize that different wave types lead to different optimal geometries and result in distinct behaviors in response to variations in geometric configuration [77]. The optimal configuration, as determined by Mocellin et al. [77], was H/L = 0.1985, which was found to be the worst-performing case under representative regular wave conditions in the study by [77].

Except for Oliveira et al., the geometry of the hydropneumatic chamber, which is the height-to-width ratio (H/L), was defined as a degree of freedom in all studies involving the oscillating water column device. In several cases, it was analyzed independently or in combination with other variables as additional degrees of freedom. To better visualize the behavior of this ratio as a degree of freedom in relation to performance indicators, Figure 11 illustrates the range of H/L values investigated in the selected studies, as well as the H/L ratios corresponding to the maximum and minimum performance indicators identified in each work. Other studies were excluded from the figure due to the larger number of degrees of freedom considered, which made individual illustrations impractical.

From Figure 11, it is evident that the behavior of the performance indicator as a function of H/L variation exhibits similar trends in several studies reviewed, including those by Mocellin et al. [77], Lima et al. [79,80], Gomes et al. [64], and Gomes et al. [70]. In general, the lowest H/L values correspond to the lowest performance. As H/L increases, device performance improves until it reaches a peak. Beyond this point, further increases in H/L result in a decline in performance (Figure 11). On the other hand, the study by Maciel et al. [78] showed a strictly decreasing trend, where the lowest H/L value yielded the maximum performance indicator, which continued to decline steadily up to the highest H/L value analyzed (Figure 11).

Lima et al. [79,80] investigated the effect of the integration of additional hydropneumatic chambers into the hydropneumatic power. In Lima et al. [79,80], the authors proposed a design with five chambers and evaluated the geometric H/L configuration of each. Lima et al. [80] analyzed five cases involving devices with one to five chambers in sequence, examining the H/L ratios for each configuration, and in another work, the authors focused on a two-chamber system, analyzing the H/L ratios along with the height and thickness of the wall separating the chambers.

Lima et al. [79,80] studied the same range of H/L ratios, from 0.0153 to 0.8817, and both studies identified the highest performance within the H/L interval of 0.25 to 0.5. The H/L = 0.2613 was the geometric configuration associated with maximum performance in the studies by Lima et al. [79] and Lima et al. as well as across all cases in Lima et al. [80]. It is worth noting that these studies simulated waves with identical characteristics. Lima et al. highlighted the influence of the wall thickness between chambers, specifically the horizontal distance between them. The lowest performance was recorded for a thickness of 0.1 m, while the highest performance occurred at 2.22 m, representing an approximate 18% increase in the device’s hydropneumatic power. Lima et al. [80] also proposed a theoretical recommendation for geometric configuration in relation to wave characteristics for systems with coupled devices, suggesting that maximum energy conversion occurs when the H/L ratios range from 16 to 32 times the ratio between wave height and wavelength. For single-device systems, Gomes et al. [70] offered a theoretical recommendation based on an analysis of chamber geometry and submergence under different wave periods, indicating that the optimal geometry corresponds to an H/L value four times the wave height-to-wavelength ratio.

From the literature, it is clear that variations in wave characteristics and device design lead to different optimal geometries and performance levels, which highlights the relevance of applying Constructal Design in these studies. Gomes et al. [70] demonstrated that, when comparing simulations with wave periods of 6 and 12 s, the H/L ratio that maximizes available hydropneumatic power varies between 0.04 and 0.23 and 0.01 and 0.03, respectively. In addition to the height and width parameters, chamber submergence must also be considered. Gomes et al. [64] showed that, for the same geometric configuration, increasing the submergence from 9 m to 9.25 m can result in a threefold increase in hydrodynamic power. The studies by Gomes et al. [64,69] explored device submergence within the range of 9 m to 10.25 m, under identical wave conditions (wave propagation depth, period, height, and wavelength). All reported that the best device performance occurred between 9 m and 9.75 m, even in Gomes et al. [70], which included simulations for waves with different periods, and all optimal cases were within this submergence range.

The geometric shape of the hydropneumatic chamber has also been investigated in terms of the energy performance of OWC devices [81]. Gomes et al. proposed four geometric configurations for the chamber (rectangular, trapezoidal, inverted trapezoidal, and double trapezoidal) and studied the influence of the H/L ratio for each case. All shapes exhibited their best performance within the same H/L range. Among them, the rectangular and trapezoidal configurations stood out, with the rectangular chamber achieving the highest performance. The trapezoidal shape reached a maximum hydropneumatic power approximately 16% lower than that of the rectangular chamber, while the double trapezoidal configuration achieved a maximum performance of 47% lower than the rectangular case. It is important to highlight that all proposed design configurations demonstrated a performance improvement of over 90% between their worst and best cases when Constructal Design was applied.

Pinto Junior et al. [81] explored the geometric arrangement of the OWC device by dividing its total area into three sections: the chimney area, which was maintained at a constant H/L ratio, and the chamber region, which was divided into two parts. The lower part, corresponding to the inlet area, had its H/L ratio varied from 0.1 to 1. The upper part, in contact with the chimney, had its width varied between that of the inlet area and the chimney, thereby altering the chamber’s overall shape from rectangular to trapezoidal. The variation in the H/L ratio of the lower chamber region had a significant impact on the improvement in the device’s performance compared to the variation in the upper chamber region. The authors attribute this result to the fact that the lower part of the chamber corresponds to the converter’s inlet area. At the same time, the upper region represents the transition zone leading to the duct, which primarily affects pressure sensitivity in the turbine region. When the upper area of the chamber is held constant, matching the chimney’s width, and the inlet geometry is varied from H/L = 1 to H/L = 0.1, a 795-fold increase in the device’s hydropneumatic power was achieved. On the other hand, when the inlet geometry is held constant at H/L = 0.7 and the upper region is varied from H/L = 0.23 to H/L = 1.91, the available power increases by 6%.

To facilitate the access of the incoming flow into the OWC device, Oliveira et al. proposed the inclusion of a ramp positioned on the seabed upstream of the hydropneumatic chamber. The study evaluated the influence of ramp height and width, as well as the horizontal distance between the ramp and the chamber’s front wall. Under the imposed conditions, a larger horizontal spacing between the structures and steeper ramps (lower H/L ratios) led to better device performance. In this context, the optimal geometric configuration achieved nearly twice the hydropneumatic power compared to the worst-performing setup, which featured a smoother ramp and shorter horizontal spacing.

Also addressing the integration of a ramp in the system, Letzow et al. investigated a configuration in which the ramp is placed beneath the hydropneumatic chamber, simulating an inclined seabed. The study evaluated the geometric configurations (H/L ratios) of both the chamber and the ramp, as well as the submergence depth of the chamber’s front wall. The authors found that when the front wall was submerged at a shallower depth (2.5 m), the maximum performance occurred with the least steep ramp (higher H/L ratio) and lower H/L values for the chamber geometry. However, when a deeper submergence was applied (5 m), which narrows the flow passage into the device, configurations without a ramp performed better in most cases. The geometric arrangement that maximized available power under the shallower submergence condition outperformed the deeper submergence case by 50.7% and exceeded the reference case without a ramp by 37.3%.

4.3. Submerged Horizontal Plate

The submerged horizontal plate device remains a converter model with relatively few published studies compared to overtopping and oscillating water column systems. This review includes only one article that applies the Constructal Design exclusively to this type of converter. Seibt et al. [82] investigated the effect of the plate height relative to the free surface level. The study indicates that, among the analyzed cases, higher relative plate heights and lower relative plate lengths result in higher magnitudes of maximum axial velocity. Accordingly, the optimal geometry was defined as the configuration with the highest relative plate height (90%) and the shortest simulated relative length (L/λ = 0.25). Furthermore, the authors highlighted the similarity between the results obtained in the model-scale study and those from their full-scale analysis. The locations of both global and local maximum and minimum efficiency occurred in the same geometry, with an average difference of only 1.15% in efficiency values.

As previously mentioned, Gomes et al. [64] also investigated the submerged horizontal plate (SHP) in their comprehensive study. However, the Constructal Design approach was applied only to the overtopping and oscillating water column converters. For SHP devices, the authors conducted a numerical analysis focused on the influence of geometry, evaluating the effect of plate length on the efficiency of the SHP device.

According to the research protocol, only the work by Seibt et al. [82] meets the criteria, which involves applying the Constructal Design to SHP devices. However, other works in the literature explored the SHP device and can be found in [85,86,87,88,89]. It is worth highlighting the recent work by Motta et al., who conducted a geometric analysis focusing on the inclination of the plate, evaluating its effect on the device’s efficiency as a wave energy converter through the axial velocity in the region below the plate, as well as its performance as a breakwater, based on the free surface height before and after the device. The authors emphasized that there is a disparity in optimal geometry depending on whether the primary objective is energy conversion or wave attenuation, making it necessary to define the primary purpose of the design and then reconcile it with the device’s secondary functionality.

5. Considerations and Opportunities for Future Research

In the documents collected for this systematic review, the Constructal Design has been widely adopted by researchers to facilitate the flow of currents within the studied system. In other words, the Constructal Design is employed either to maximize energy conversion when combined with optimization methods or to investigate geometric configurations. Constructal Design enables a comprehensive assessment of a system’s geometric arrangement. In the context of wave energy converters, it has allowed the authors to analyze geometries under different wave conditions [69,70], develop theoretical design recommendations [70,80], and propose or assess alternative shapes and structural configurations within the system [76,81].

Among the studies included in this systematic review, all identified an optimal geometry that maximized some performance indicators. Moreover, the significant differences between the maximum and minimum values of performance indicators highlight the critical importance of geometric configuration in wave energy converter systems.

Table 4. Maximum and minimum values of performance indicators reported in the studies that applied Constructal Design.

Performance Indicator	Works	Maximum Value	Minimum Value	Max/Min Ratio
Oscillating Water Column
Available power	Pinto Junior et al. 2024 [81]	16,954.8 kW	20.2 kW	839.35
Hydropneumatic power	Mocellin et al. 2024 [77]	56.66 W	28.19 W	2.01
	Lima et al. 2024 [79]	30.8 kW	0.4168 kW	73.90
	Maciel et al. 2023 [78]	29.63 W	6.83 W	4.34
	Lima et al. 2021 [80]	30.8 kW	0.2 kW	154.00
	Gomes et al. 2018 [70]	214.85 W	14.4 W	14.92
	Gomes et al. 2015 [64]	116.43 W	11.88 W	9.80
Overtopping
Water accumulated level in the reservoir	Goulart et al. 2024 [74]	0.248 m	-	-
Dimensionless available power	Martins et al. 2018 [69]	0.018	-	-
Average dimensionless overtopping flow	Martins et al. 2022 [76]	0.044	0.03	1.47
	Martins et al. 2022 [76]	0.044	0.031	1.42
	Goulart et al. 2015 [75]	8686.73 kg	-	-
	Gomes et al. 2015 [64]	8686.73 kg	-	-
	dos Santos et al. 2014 [71]	9.5 kg	-	-
Submerged Horizontal Plate
Theoretical efficiency	Seibt et al. 2023 [82]	37.15%	1.54%	24.12

summarizes the performance indicators used in each study, along with their respective maximum and minimum values. It is evident that modifications to the geometric configuration of OWC-type devices led to performance improvements ranging from 1.19 to 839.35 times. The study by Pinto Junior et al. [81] presented the most considerable disparity among the OWC devices, with the best-performing configuration achieving a performance 839 times greater than the worst case. In the case of overtopping converters, several studies reported configurations in which no overtopping occurred, resulting in no energy conversion. For overtopping-type converters, variations in geometric configuration show a wide performance range, from scenarios with no energy conversion, resulting in a zero-performance indicator, to those reaching their maximum value [64,69,71,74,75].

Constructal Design enables the analysis of the interaction between different degrees of freedom and their effect on the performance indicator. Figure 12 and Figure 13 present the degrees of freedom and the frequency with which they are analyzed in studies related to the overtopping converter model and the oscillating water column model, respectively. It is observed that the height-to-length ratio of the ramp (in OVT studies—Figure 12b) and of the chamber (in OWC studies—Figure 13b) are the most frequently used degrees of freedom, followed by the submergence depth of the device. Some variables are not illustrated because they are specific to distinct structural configurations, such as OWC devices with multiple chambers or with an added ramp [79,80], and OVT devices with multiple ramps or an obstacle positioned before the ramp [76].

Finally, future studies could consider the turbine to understand its effect on the system and potential head loss, as none of the reviewed articles addressed this point. Another recommendation is to apply and investigate wave characteristics using the most realistic data possible, considering the potential impact on the research outcomes. Regarding the degrees of freedom, there is also an opportunity to explore underutilized variables, or even those commonly treated as constant constraints. Some works presented in Table 4 studied the influence of values defined as geometric constraints. Through variations in both the geometric configuration and chamber volume, an 18-fold improvement in device performance was achieved.

In particular, for oscillating water column (OWC) research, it is recommended to address the geometry of the turbine duct and its influence on energy performance, as only 2 out of the 14 reviewed studies analyzed the geometry of this region. For overtopping device studies, it is recommended that future work analyze the reservoir and turbine together to better understand factors such as emptying time and frequency, particularly in light of overflow risks and the potential for water to return via the device’s ramp. Thus, regarding the Constructal Design method specifically, there is an opportunity to apply it to other types of wave energy converters. This article indicates that most reviewed papers applied the Constructal Design method to OWC devices, although it has been less frequently used on SHP devices. Another area where Constructal Design should be further explored is in experimental research, where, among the 23 articles reviewed, only 1 employed an experimental test, with the vast majority relying on numerical simulations. Based on the literature presented in this work, it is expected that Constructal Design can improve the performance of other wave energy converters and not be limited to those discussed here. Therefore, it is recommended to study the application of the Constructal Design in alternative wave energy converters [90,91,92,93,94]. Finally, future research should compare the Constructal Design method with other geometric analysis methods, considering its scope and applicability. Additionally, combining the Constructal Design with optimization techniques could improve the efficiency of wave energy converters.

6. Conclusions

This work presents a systematic literature review on the application of the Constructal Design method in wave energy converters. The Constructal Design method is widely used in several research fields. However, only a few papers were found about the combination of Constructal Design and wave energy converters. The systematic literature review mapped the works that applied the Constructal Design method and identified its benefits. The main findings are as follows:

The systematic literature review conducted on the application of Constructal Design in wave energy converters collected and reviewed 23 articles authored by 40 different authors and published in 11 scientific journals. The application of this method for improving the performance of wave energy converter devices has been studied since 2014, which is relatively recent compared to its application in other research fields. Consequently, the number of papers that applied the Constructal Design method to wave energy converters remains low compared to the literature that studies the geometry and design of wave energy converters.

The Constructal Design method proved to be a helpful tool for improving the performance of wave energy converters. In all studies reported, it was possible to determine optimal geometry configurations for specific wave energy converters. Among the cases analyzed, the studies reported an increase in the performance indicator ranging from 1.19 to 839 times, representing the lowest and highest improvements observed, respectively.

The oscillating water column (OWC) converter is the most studied device in this literature review, being the focus of fourteen analyzed articles, followed by overtopping devices, which were the subject of nine articles. The submerged horizontal plate device was studied in two articles, with the Constructal Design being applied in only one of them.

In conclusion, the positive contribution of the Constructal Design method to the development of wave energy converters is evident. In all the studies analyzed, the technique identified how the design influenced the system performance, considering the degrees of freedom, constraints, and conditions imposed on the system. For future research, the primary challenges and opportunities lie in incorporating the turbine into simulations and investigating its effects on the system, as none of the studies reviewed in this work addressed these aspects. Additionally, exploring different degrees of freedom than those commonly adopted in the literature is also recommended for future work. Finally, regarding future opportunities, it is worth highlighting the application of the Constructal Design method to other types of WECs beyond those addressed in this study, as well as the use of geometric analysis in experimental investigations, considering that 22 of the 23 analyzed articles are numerical studies.