Coupled Nonlinear Dynamic Modeling and Experimental Investigation of Gear Transmission Error for Enhanced Fault Diagnosis in Single-Stage Spur Gear Systems
Abstract
1. Introduction
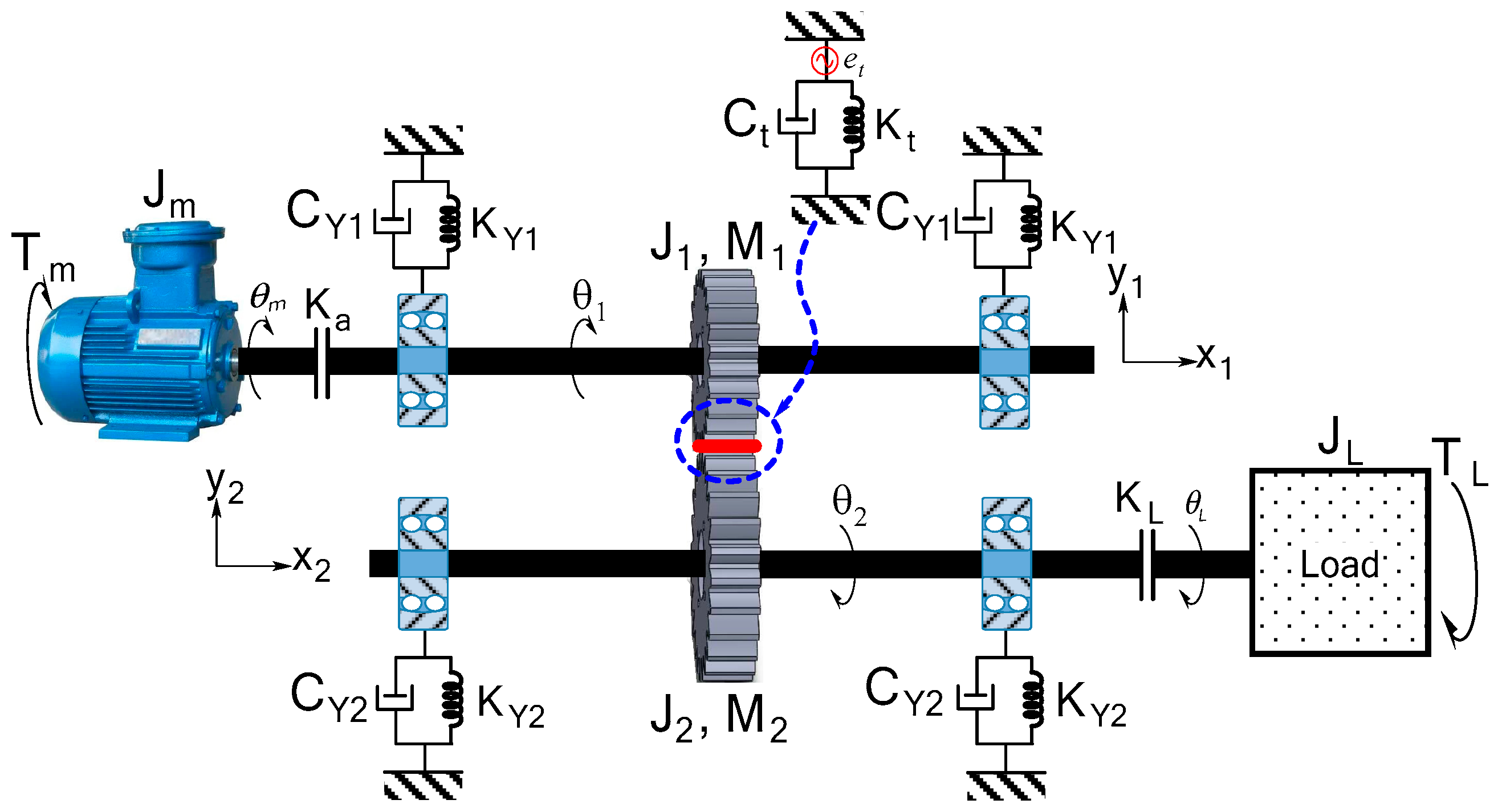
2. Mathematical Modeling of a Spur Gear
2.1. Establishment of a Mathematical Single Stage of a Spur Gear Model
2.2. Kinetic Energy Expression
2.3. Potential Energy Expression
2.4. Rayleigh Dissipation Function
2.5. Modeling the Transmission Error Term
2.6. Equation of Motion Governing the System
3. Configuration and Instrumentation of the Coupled Spur Gear Test Rig
4. Results and Discussion
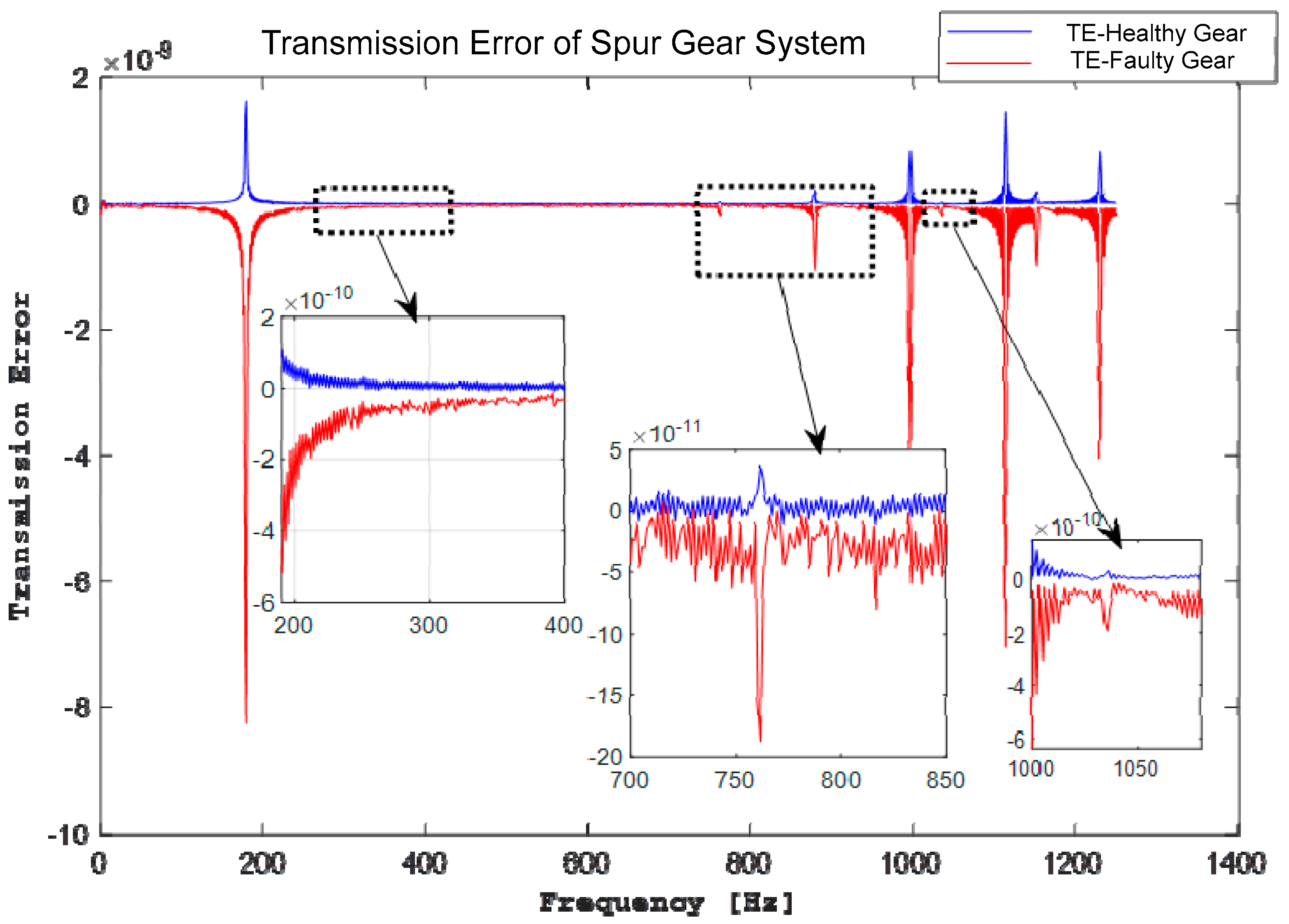
4.1. Waveform of Spur Geared System
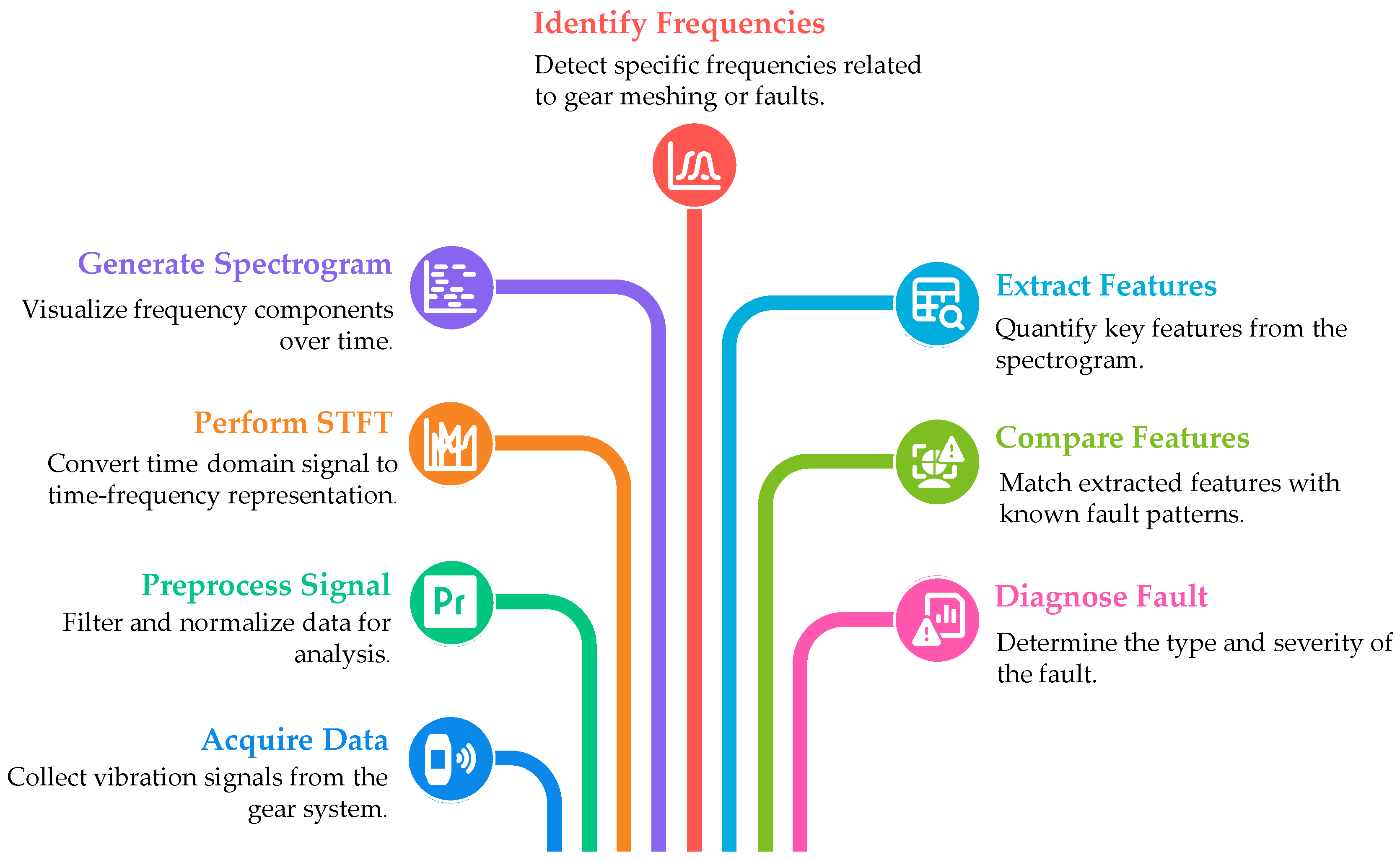
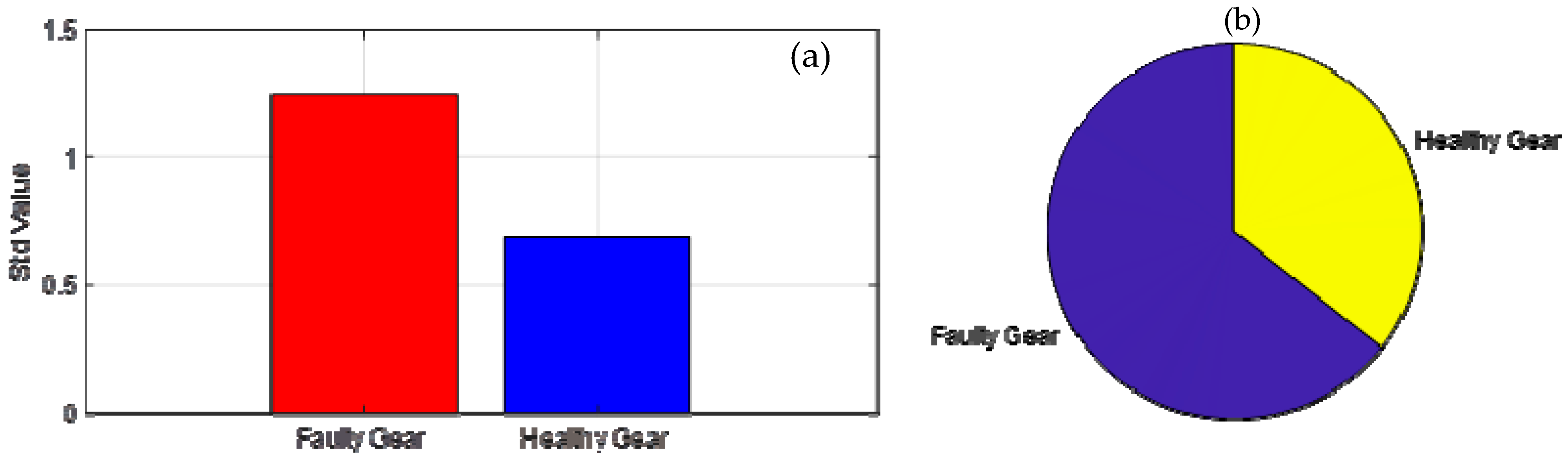
4.2. Feature Extraction of Time–Frequency Representation of Spur Geared System
4.3. Spur Gear Analysis Through Short-Time Fourier Transform
5. Physical Meaning of Results in Terms of System Dynamics
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Definition |
| GTE | Gear Transmission Error |
| STE | Static Transmission Error |
| DTE | Dynamic Transmission Error |
| STFT | Short-Time Fourier Transform |
| M1, M2 | Translational masses of the pinion and gear shafts [kg] |
| Y1, Y2 | Lateral displacements of the pinion and gear shafts [m] |
| K1, K2 | Lateral stiffness of the bearings [N/m] |
| Ka, Kc | Torsional stiffness of input and output couplings [N·m/rad] |
| Kt | Gear mesh stiffness [N/m] |
| C1, C2 | Lateral damping coefficients of bearings [N·s/m] |
| Ca, Cc | Torsional damping coefficients of couplings [N·m·s/rad] |
| e(t) | Transmission error function [m] |
| e₀ | Static transmission error [m] |
| eₙ | Amplitude of nth harmonic component of transmission error [m] |
| ωₘ | Excitation frequency [rad/s] |
| ϕn | Phase of nth harmonic component [rad] |
| θ1 | Angular displacement of the input shaft or pinion [rad] |
| θ2 | Angular displacement of the output shaft or driven gear [rad] |
| θL | Angular displacement of the load side [rad] |
| θm | Angular displacement of the motor side [rad] |
| Tm | Motor input torque [N·m] |
| TL | Load torque [N·m] |
| R1, R2 | Base circle radius of the pinion and gear shafts [m] |
| I | Area moment of inertia of the gear tooth cross-section [m4] |
| M | Bending moment distribution along the gear tooth [Nm] |
| P | Applied load along the line of action [N] |
| x | Coordinate along the tooth length |
| E | Young’s modulus of gear material [GPa] |
| ν | Poisson’s ratio of gear material [-] |
| Z | Number of teeth (pinion or gear) [-] |
References
- Horváth, K.; Feszty, D. The Impact of Pitch Error on the Dynamics and Transmission Error of Gear Drives. Appl. Sci. 2025, 15, 7851. [Google Scholar] [CrossRef]
- Sigonde, V.C.; Koueiou, X.T.; Alugongo, A.A. Enhancing fault diagnosis of gear transmission error based on experimental analysis. In Proceedings of the 2022 IEEE 13th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 25–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 135–140. [Google Scholar]
- Li, J.; Zhao, H.; Ren, Y.; Yang, J. Calculation of Time-Varying Mesh Stiffness of Internal Mesh Transmission and Analysis of Influencing Factors. Appl. Sci. 2025, 15, 4599. [Google Scholar] [CrossRef]
- Masmoudi, W.; Wojtowicki, J.L.; Petrone, G.; Franco, F.; De Rosa, S. Evaluating lightweight gear transmission error: A novel nonlinear finite element approach using direct constraint contact algorithm. Front. Mech. Eng. 2023, 9, 1228696. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Wang, K.; Zhai, W. Dynamic characteristics analysis of gear transmission and its support bearings of high-speed train on the curve. Veh. Syst. Dyn. 2024, 62, 623–650. [Google Scholar] [CrossRef]
- Ding, J.; Jin, G. Modeling and dynamic analysis of split torsion transmission system considering backlash and center distance errors. Sci. Rep. 2025, 15, 1229. [Google Scholar] [CrossRef] [PubMed]
- Sheng, D.; Lu, F. Dynamic Behavior and Double-Parameter Self-Adaptive Stability Control of a Gear Transmission System. Int. J. Bifurc. Chaos 2023, 33, 2350055. [Google Scholar] [CrossRef]
- Liu, S.; Hu, A.; Zhang, Y.; Xiang, L. Nonlinear dynamics analysis of a multistage planetary gear transmission system. Int. J. Bifurc. Chaos 2022, 32, 2250096. [Google Scholar] [CrossRef]
- Wang, M.; Ma, X.; Hu, Y.; Wang, Y. Gear fault diagnosis based on variational modal decomposition and wide+ narrow visual field neural networks. IEEE Trans. Autom. Sci. Eng. 2021, 19, 3288–3299. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, X.; Xiang, J. Fault detection in gears using fault samples enlarged by a combination of numerical simulation and a generative adversarial network. IEEE/ASME Trans. Mechatron. 2021, 27, 3798–3805. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Li, X.; Yao, L.; Liu, X. Lateral-Torsional-Coupled Model Based Dynamic Analyses of Spur Gears Under Time-Varying External Load Conditions with Surface Wear. In Dynamics and Fault Diagnosis of Nonlinear Rotors and Impellers; Springer International Publishing: Cham, Switzerland, 2022; pp. 107–133. [Google Scholar]
- Xie, S.; Du, Q.; Hu, Y. Nonlinear dynamics of spur gear systems with time-varying misalignment errors. J. Vib. Control 2024, 30, 3997–4009. [Google Scholar] [CrossRef]
- Happi, K.H.Y.; Kouejou, B.X.T.; Alugongo, A.A. Pitting and Crack Coexistence in a Model-Based Gear Dynamic System (Part I). In Proceedings of the 2022 IEEE 13th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 25–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 120–126. [Google Scholar]
- Stefani, F.A.; Niccolini Marmont Du Haut Champ, C.A.; Silvestri, P.; Massardo, A.F. Experimental and Numerical Analysis of Torsional—Lateral Vibrations in Drive Lines Supported by Hydrodynamic Journal Bearings. Lubricants 2024, 12, 82. [Google Scholar] [CrossRef]
- Jin, B.; Bian, Y.; Liu, X.; Gao, Z. Dynamic modeling and nonlinear analysis of a spur gear system considering a nonuniformly distributed meshing force. Appl. Sci. 2022, 12, 12270. [Google Scholar] [CrossRef]
- Majeed, R.; Haddar, M.; Chaari, F.; Haddar, M. A wavelet-based statistical control chart approach for monitoring and detection of spur gear system faults. In Proceedings of the International Conference on Acoustics and Vibration, Sousse, Tunisia, 19–21 December 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 140–152. [Google Scholar]
- Raghav, M.S.; Patel, S. Fault diagnosis of spur gearbox by image classification using deep CNN. In Proceedings of the 2024 1st International Conference on Robotics, Engineering, Science, and Technology (RESTCON), Chonburi, Thailand, 16–18 February 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 201–206. [Google Scholar]
- Hashim, S.; Shakya, P. A spectral kurtosis based blind deconvolution approach for spur gear fault diagnosis. ISA Trans. 2023, 142, 492–500. [Google Scholar] [CrossRef]
- Cao, P.; Li, Q.; Feng, K.; Qin, Y. Dynamic modeling of spur gear transmission system with evolutive coupling fault of fatigue crack and wear. Eng. Fail. Anal. 2024, 156, 107820. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, K.; Xu, F.; Yi, Y.; Sang, M.; Zhai, H. Research on the influence of backlash on mesh stiffness and the nonlinear dynamics of spur gears. Appl. Sci. 2019, 9, 1029. [Google Scholar] [CrossRef]
- Ren, F.; Wang, D.; Shi, G.; Wu, X. Investigation on dynamic characteristics of spur gear transmission system with crack fault. Machines 2022, 10, 664. [Google Scholar] [CrossRef]
- Maraş, S.; Arslan, H.; Birgören, B. Detection of gear wear and faults in spur gear systems using statistical parameters and univariate statistical process control charts. Arab. J. Sci. Eng. 2021, 46, 12221–12234. [Google Scholar] [CrossRef]
- Happi, K.H.Y.; Kouejou, B.X.T.; Alugongo, A.A. Influence of Coexistence of Pitting and Cracking Faults on a Two-Stage Spur Gear System. Vibration 2023, 6, 195–217. [Google Scholar] [CrossRef]
- Cheng, Z.; Huang, K.; Xiong, Y.; Sang, M. Dynamic analysis of a high-contact-ratio spur gear system with localized spalling and experimental validation. Machines 2022, 10, 154. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, L. An intelligent fault diagnosis method of rolling bearings based on short-time Fourier transform and convolutional neural network. J. Fail. Anal. Prev. 2023, 23, 795–811. [Google Scholar] [CrossRef]







| Parameter | Pinion | Wheel | Unit |
|---|---|---|---|
| Lateral meshing stiffness of bearings | KY1 = 5.0 × 107 | KY2 = 5.0 × 107 | N/m |
| Lateral damping coefficient of bearings | C1 = 1.2 × 103 | C2 = 1.2 × 103 | Ns/m |
| Torsional stiffness of coupling | Ka = 4.0 × 102 | Kc = 4.0 × 102 | Nm/rad |
| Torsional damping coefficient of coupling | Ca = 5 × 105 | Cc = 5 × 105 | Nms/rad |
| Main gearing parameters | |||
| Mass | 0.198 | 2.417 | kg |
| Number of teeth | 30 | 90 | - |
| Pressure angle | 20 | 20 | o |
| Poisson’s ratio | 0.3 | 0.3 | - |
| Youngs modulus | 207 | 207 | GPa |
| Base circle radius | R1 = R3 = 32 | R2 = R4 = 92 | mm |
| Parameter | FFT | STFT | Unit |
|---|---|---|---|
| Sampling frequency (Fs) | 2500 | 1000 | Hz |
| Window type | Rectangular (default in FFT) | Kaiser (β = 10) | – |
| Window length | 1600 samples | 256 samples | Samples |
| Overlap | – | 255 (≈99%) | Samples |
| Frequency resolution (Δf) | 1.56 | 3.91 | Hz |
| Normalization | Amplitude normalized by signal length | Spectrogram, energy-normalized | – |
| Indicator | Formula | Physical Meaning | Fault Implication |
|---|---|---|---|
| Root Mean Square (RMS) | Represents effective vibration energy or magnitude | Higher RMS indicates stronger and more persistent vibration due to gear faults | |
| Standard Deviation (σ) | Quantifies signal variability around its mean; reflects fluctuation level | Higher σ indicates irregular meshing and instability introduced by defects |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigonde, V.C.; Sozinando, D.F.; Tchomeni, B.X.; Alugongo, A.A. Coupled Nonlinear Dynamic Modeling and Experimental Investigation of Gear Transmission Error for Enhanced Fault Diagnosis in Single-Stage Spur Gear Systems. Dynamics 2025, 5, 37. https://doi.org/10.3390/dynamics5030037
Sigonde VC, Sozinando DF, Tchomeni BX, Alugongo AA. Coupled Nonlinear Dynamic Modeling and Experimental Investigation of Gear Transmission Error for Enhanced Fault Diagnosis in Single-Stage Spur Gear Systems. Dynamics. 2025; 5(3):37. https://doi.org/10.3390/dynamics5030037
Chicago/Turabian StyleSigonde, Vhahangwele Colleen, Desejo Filipeson Sozinando, Bernard Xavier Tchomeni, and Alfayo Anyika Alugongo. 2025. "Coupled Nonlinear Dynamic Modeling and Experimental Investigation of Gear Transmission Error for Enhanced Fault Diagnosis in Single-Stage Spur Gear Systems" Dynamics 5, no. 3: 37. https://doi.org/10.3390/dynamics5030037
APA StyleSigonde, V. C., Sozinando, D. F., Tchomeni, B. X., & Alugongo, A. A. (2025). Coupled Nonlinear Dynamic Modeling and Experimental Investigation of Gear Transmission Error for Enhanced Fault Diagnosis in Single-Stage Spur Gear Systems. Dynamics, 5(3), 37. https://doi.org/10.3390/dynamics5030037






