The In Silico Optimization of a Batch Reactor for D-Fructose Production Using the Cetus Process with In Situ Cofactor Quick Regeneration
Abstract
1. Introduction
2. The Experimental Enzymatic Reactor
3. Kinetic Model of Biocatalytic Process
4. Dynamic Model of Enzymatic Batch Reactor
5. BR Simulation and Optimization
5.1. Nominal BR Simulation and Selection of Control Variables
5.2. Single-Objective Function Optimization (NLP) of the BR
Max Ω, where Ω = [P(t)]
5.3. Optimization Problem Constraints
- (a)
- The BR model in Equation (1);
- (b)
- To limit the excessive consumption of raw materials (especially the costly enzymes), feasible searching limits are imposed on the control/decision variables (Table 2), based on the previous trials of Maria et al. [47,73], and on literature information [74,75,76]. In mathematical terms, the constraints (b) translate toindex ‘i’ = KDG, NADPH, ALR, FDH
6. Optimization Results and Discussion
- -
- -
- -
- A comparison of all BR operating alternatives in terms of P production and consumption of raw materials (based on the initial load) is presented in Table 7.
- (1)
- The non-optimal DS1–DS4 BR experimental runs defined in Table 2 perform much better if the NADPH is regenerated in situ. Thus, the realized yields (4.9/35, 11/35, 7.8/15 in Table 7) are very low if NADPH is not regenerated, though the yields are 100% if NADPH is regenerated. This is a major reason to use the in situ cofactor regeneration for this process.
- (2)
- The non-optimal BR operation (DS1–DS3) using in situ NADPH regeneration resulted in the high consumption of enzymes as a result of the operating alternatives in Table 7. This sub-optimal operation can be improved by applying an NLP procedure using the optimization objective in Equation (2), subjected to the constraints in Section 5.3. Thus, one obtains the optimal BR operation in Table 7 (last row), with the species dynamics plotted in Figure 3. Compared to the experimental nominal, non-optimal BR operation (DS1–DS4), with or without cofactor regeneration, the optimized BR with cofactor regeneration resulted in a 25% lower consumption of NADPH, though the amount of the processed substrate is approximately 3× higher. Moreover, the consumption of costly enzymes (ALR, FDH) is roughly half.
- (3)
- By analyzing the NLP optimal operating policy of the BR, shown in Table 7 and Figure 3, the following conclusion can be derived: the P-productivity increases with the initial substrate [kDG, NADPH] concentrations if enough enzymes (ALR, FDH) are present and if ALR (and FDH) is not deactivated too fast. To better fulfill such a condition, the best alternative could be to use more stable enzymes, that is, immobilized on suitable porous supports [86,87,88] (not investigated here).
- (4)
- For sufficiently stable (immobilized) enzymes (ALR, FDH), DF production maximization clearly depends on the available amount of substrate (kDG) and cofactor (NADPH). As the kDG results from Step 1 of the Cetus process [73], a more realistic optimization must concomitantly consider both linked Cetus processes. Some trials have already been conducted [89].
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Notations
| Cj, | Species j concentration |
| Kj, kj, y, kc2, KM2 | Kinetic model constants |
| k | Rate constants vector |
| Species j reaction rate | |
| Temperature | |
| Time | |
| Batch time | |
| Ω | Optimization objective function |
| [x] | Concentration of species “x” |
| Index | |
| 0,o | Initial |
| Abbreviations | |
| A, A* | NADPH, NADP+ |
| ALR | Aldose reductase |
| BR | Batch reactor |
| DG | D-glucose |
| DF | D-fructose |
| DS1–DS4 | The data sets obtained by Maria and Ene [2013] in batch experiments aimed at investigating the kDG conversion to D-fructose |
| E, ENZ | ALR enzyme |
| Ein, E*Ay | Inactive forms of the enzyme E |
| FBR | Fed-batch reactor |
| FDH | Formate dehydrogenase |
| GMO | Genetically modified organisms |
| HFCS | High-fructose/glucose syrup |
| HFS | High-fructose syrup |
| kDG | Keto D-glucose |
| Max | Maximum |
| Min | Minimum |
| NADPH | Nicotinamide adenine dinucleotide phosphate—reduced form |
| NLP | Nonlinear programming |
| P | Product (D-fructose) |
| P2Ox | Pyranose 2-oxidase |
| R1, R2 | Main reactions of the second step of the Cetus process (Figure 1) |
| S | Substrate (kDG) |
References
- Moulijn, J.A.; Makkee, M.; van Diepen, A. Chemical Process Technology; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Wang, P. Multi-scale features in recent development of enzymic biocatalyst systems. Appl. Biochem. Biotechnol. 2009, 152, 343–352. [Google Scholar] [CrossRef]
- Vasic-Racki, D.; Findrik, Z.; Presecki, A.V. Modelling as a tool of enzyme reaction engineering for enzyme reactor development. Appl. Microbiol. Biotechnol. 2011, 91, 845–856. [Google Scholar] [CrossRef]
- Maria, G. A review of algorithms and trends in kinetic model identification for chemical and biochemical systems. Chem. Biochem. Eng. Q. 2004, 18, 195–222. [Google Scholar]
- Gernaey, K.V.; Lantz, A.E.; Tufvesson, P.; Woodley, J.M.; Sin, G. Application of mechanistic models to fermentation and biocatalysis for next-generation processes. Trends Biotechnol. 2010, 28, 346–354. [Google Scholar] [CrossRef]
- Moser, A. Bioprocess Technology-Kinetics and Reactors; Springer Verlag: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Straathof, A.J.J.; Adlercreutz, P. Applied Biocatalysis; Harwood Academic Publ.: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Dutta, R. Fundamentals of Biochemical Engineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Lübbert, A.; Jørgensen, S.B. Bioreactor performance: A more scientific approach for practice. J. Biotechnol. 2001, 85, 187–212. [Google Scholar] [CrossRef] [PubMed]
- Engasser, J.M. Bioreactor engineering: The design and optimization of reactors with living cells. Chem. Eng. Sci. 1988, 43, 1739–1748. [Google Scholar] [CrossRef]
- Maria, G.; Peptanaru, I.M. Model-based optimization of mannitol production by using a sequence of batch reactors for a coupled bi-enzymatic process–A dynamic approach. Dynamics 2021, 1, 134–154. [Google Scholar] [CrossRef]
- Gijiu, C.L.; Maria, G.; Renea, L. Pareto optimal operating policies of a batch bi-enzymatic reactor for mannitol production. Chem. Eng. Technol. 2024, 48, e202300555. [Google Scholar] [CrossRef]
- Maria, G. Enzymatic reactor selection and derivation of the optimal operation policy by using a model-based modular simulation platform. Comput. Chem. Eng. 2012, 36, 325–341. [Google Scholar] [CrossRef]
- Maria, G. Model-based optimization of a fed-batch bioreactor for mAb production using a hybridoma cell culture. Molecules 2020, 25, 5648. [Google Scholar] [CrossRef] [PubMed]
- Bonvin, D.; Srinivasan, B.; Hunkeler, D. Control and optimization of batch processes. IEEE Control Syst. Mag. 2006, 26, 34–45. [Google Scholar] [CrossRef]
- Srinivasan, B.; Primus, C.J.; Bonvin, D.; Ricker, N.L. Run-to-run optimization via control of generalized constraints. Control Eng. Pract. 2001, 9, 911–919. [Google Scholar] [CrossRef]
- Dewasme, L.; Amribt, Z.; Santos, L.O.; Hantson, A.L.; Bogaerts, P.; Wouwer, A.V. Hybridoma cell culture optimization using nonlinear model predictive control. In The International Federation of Automatic Control, Proceedings of the 12th IFAC Symposium on Computer Applications in Biotechnology, Mumbai, India, 16–18 December 2013; Elsevier: Amsterdam, The Netherlands, 2013; Volume 46, pp. 60–65. [Google Scholar] [CrossRef]
- Dewasme, L.; Cote, F.; Filee, P.; Hantson, A.L.; Wouwer, A.V. Macroscopic dynamic modeling of sequential batch cultures of hybridoma cells: An experimental validation. Bioengineering 2017, 4, 17. [Google Scholar] [CrossRef]
- Mendes, R.; Rocha, I.; Pinto, J.P.; Ferreira, E.C.; Rocha, M. Differential evolution for the offline and online optimization of fed-batch fermentation processes. In Advances in Differential Evolution. Studies in Computational Intelligence; Chakraborty, U.K., Ed.; Springer Verlag: Berlin/Heidelberg, Germany, 2008; pp. 299–317. [Google Scholar]
- Liu, Y.; Gunawan, R. Bioprocess optimization under uncertainty using ensemble modeling. J. Biotechnol. 2017, 244, 34–44. [Google Scholar] [CrossRef]
- Amribt, Z.; Dewasme, L.; Wouwer, A.V.; Bogaerts, P. Optimization and robustness analysis of hybridoma cell fed-batch cultures using the overflow metabolism model. Bioprocess Biosyst. Eng. 2014, 37, 1637–1652. [Google Scholar] [CrossRef]
- Ruppen, D.; Bonvin, D.; Rippin, D.W.T. Implementation of adaptive optimal operation for a semi-batch reaction system. Comput. Chem. Eng. 1998, 22, 185–199. [Google Scholar] [CrossRef]
- Bonvin, D. Optimal operation of batch reactors—A personal view. J. Process Control 1998, 8, 355–368. [Google Scholar] [CrossRef]
- Smets, I.Y.; Claes, J.E.; November, E.J.; Bastin, G.P.; van Impe, J.F. Optimal adaptive control of (bio)chemical reactors: Past, present and future. J. Process Control 2004, 14, 795–805. [Google Scholar] [CrossRef]
- Bonvin, D. Realtime Optimization; MDPI: Basel, Switzerland, 2017. [Google Scholar]
- Srinivasan, B.; Bonvin, D.; Visser, E.; Palanki, S. Dynamic optimization of batch processes: II. Role of measurements in handling uncertainty. Comput. Chem. Eng. 2003, 27, 27–44. [Google Scholar] [CrossRef]
- DiBiasio, D. Introduction to the control of biological reactors. In Chemical Engineering Problems in Biotechnology; Shuler, M.I., Ed.; American Institute of Chemical Engineers: New York, NY, USA, 1989; pp. 351–391. [Google Scholar]
- Martinez, E. Batch-to-batch optimization of batch processes using the STATSIMPLEX search method. In Proceedings of the 2nd Mercosur Congress on Chemical Engineering, Rio de Janeiro, Brazil, 16–18 August 2005. paper #20. [Google Scholar]
- Abel, O.; Marquardt, W. Scenario-integrated on-line optimisation of batch reactors. J. Process Control 2003, 13, 703–715. [Google Scholar] [CrossRef]
- Von Weymarn, N. Process Development for Mannitol Production by Lactic Acid Bacteria. Ph.D. Dissertation, Helsinki University of Technology, Laboratory of Bioprocess Engineering, Espoo, Finland, 2002. Available online: http://lib.tkk.fi/Diss/2002/isbn9512258854/ (accessed on 7 August 2021).
- Song, K.H.; Lee, J.K.; Song, J.Y.; Hong, S.G.; Baek, H.; Kim, S.Y.; Hyun, H.H. Production of mannitol by a novel strain of Candida magnoliae. Biotechnol. Lett. 2002, 24, 9–12. [Google Scholar] [CrossRef]
- Loesche, W.J.; Kornman, K.S. Production of mannitol by Streptococcus mutans. Arch. Oral Biol. 1976, 21, 551–553. [Google Scholar] [CrossRef]
- Bäumchen, C.; Roth, A.H.F.J.; Biedendieck, R.; Malten, M.; Follmann, M.; Sahm, H.; Bringer-Meyer, S.; Jahn, D. D-Mannitol production by resting state whole cell biotransformation of D-fructose by heterologous mannitol and formate dehydrogenase gene expression in Bacillus megentarium. Biotechnol. J. 2007, 2, 1408–1416. [Google Scholar] [CrossRef]
- Binette, J.C.; Srinivasan, B. On the use of nonlinear model predictive control without parameter adaptation for batch processes. Processes 2016, 4, 27. [Google Scholar] [CrossRef]
- Franco-Lara, E.; Weuster-Botz, D. Estimation of optimal feeding strategies for fed-batch bioprocesses, Estimation of optimal feeding strategies for fed-batch bioprocesses. Bioprocess Biosyst. Eng. 2005, 28, 71–77. [Google Scholar] [CrossRef][Green Version]
- Avili, M.G.; Fazaelipoor, M.H.; Jafari, S.A.; Ataei, S.A. Comparison between batch and fed-batch production of rhamnolipid by Pseudomonas aeruginosa. Iran. J. Biotechnol. 2012, 10, 263–269. [Google Scholar][Green Version]
- Loeblein, C.; Perkins, J.; Srinivasan, B.; Bonvin, D. Performance analysis of on-line batch optimization systems. Comput. Chem. Eng. 1997, 21, S867–S872. [Google Scholar] [CrossRef][Green Version]
- Lee, J.; Lee, K.S.; Lee, J.H.; Park, S. An on-line batch span minimization and quality control strategy for batch and semi-batch processes. Control Eng. Pract. 2001, 9, 901–909. [Google Scholar] [CrossRef]
- Rao, M.; Qiu, H. Process Control Engineering: A Textbook for Chemical, Mechanical and Electrical Engineers; Gordon and Breach Science Publ.: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Akinterinwa, O.; Khankal, R.; Cirino, P.C. Metabolic engineering for bioproduction of sugar alcohols. Curr. Opin. Biotechnol. 2008, 19, 461–467. [Google Scholar] [CrossRef]
- Fu, Y.; Ding, L.; Singleton, M.L.; Idrissi, H.; Hermans, S. Synergistic effects altering reaction pathways: The case of glucose hydrogenation over Fe-Ni catalysts. Appl. Catal. B Environ. 2021, 288, 119997. [Google Scholar] [CrossRef]
- Kanagasabai, M.; Elango, B.; Balakrishnan, P.; Jayabalan, J. Ethanol and Glycerol Chemistry-Production, Modelling, Applications, and Technological Aspects; Pandey, R., Pala-Rosas, I., Contreras, J.L., Salmones, J., Eds.; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Akbas, M.Y.; Stark, B.C. Recent trends in bioethanol production from food processing byproducts. J. Ind. Microbiol. Biotechnol. 2016, 43, 1593–1609. [Google Scholar] [CrossRef]
- Liese, A.; Seelbach, K.; Wandrey, C. (Eds.) Industrial Biotransformations; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Ju, Z.; Zhang, Y.; Zhao, T.; Xiao, W.; Yao, X. Mechanism of glucose–fructose isomerization over aluminum-based catalysts in methanol media. ACS Sustain. Chem. Eng. 2019, 7, 14962–14972. [Google Scholar] [CrossRef]
- Ricca, E.; Calabro, V.; Curcio, S.; Iorio, G. The state of the art in the production of fructose from inulin enzymatic hydrolysis. Crit. Rev. Biotechnol. 2007, 27, 129–145. [Google Scholar] [CrossRef]
- Maria, G.; Ene, M.D. Modelling enzymatic reduction of 2-keto-D-glucose by suspended aldose reductase. Chem. Biochem. Eng. Q. 2013, 27, 385–395. [Google Scholar]
- Leitner, C.; Neuhauser, W.; Volc, J.; Kulbe, K.D.; Nidetzky, B.; Haltrich, D. The Cetus process revisited: A novel enzymatic alternative for the production of aldose-free D-fructose. Biocatal. Biotransform. 1998, 16, 365–382. [Google Scholar] [CrossRef]
- Shaked, Z.; Wolfe, S. Stabilization of pyranose 2-oxidase and catalase by chemical modification. Methods Enzymol. 1988, 137, 599–615. [Google Scholar] [CrossRef]
- Leskovac, V.; Trivic, S.; Wohlfahrt, G.; Kandrac, J.; Pericin, D. Glucose oxidase from Aspergillus niger: The mechanism of action with molecular oxygen, quinones, and one-electron acceptors. Int. J. Biochem. Cell Biol. 2005, 37, 731–750. [Google Scholar] [CrossRef] [PubMed]
- Slatner, M.; Nagl, G.; Haltrich, D.; Kulbe, K.D.; Nidetzky, B. Enzymatic production of pure D-mannitol at high productivity. Biocatal. Biotransform. 1998, 16, 351–363. [Google Scholar] [CrossRef]
- Parmentier, S.; Arnaut, F.; Soetaert, W.; Vandamme, E.J. Enzymatic production of D-mannitol with the Leuconostoc pseudomesenteroides mannitol dehydrogenase coupled to a coenzyme regeneration system. Biocatal. Biotransform. 2005, 23, 1–7. [Google Scholar] [CrossRef]
- Liu, W.; Wang, P. Cofactor regeneration for sustainable enzymatic biosynthesis. Biotechnol. Adv. 2007, 25, 369–384. [Google Scholar] [CrossRef]
- Berenguer-Murcia, A.; Fernandez-Lafuente, R. New trends in the recycling of NAD(P)H for the design of sustainable asymmetric reductions catalyzed by dehydrogenases. Curr. Org. Chem. 2010, 14, 1000–1021. [Google Scholar] [CrossRef]
- Maria, G. Model-based optimization of a batch reactor with a coupled bi-enzymatic process for mannitol production. Comput. Chem. Eng. 2020, 133, 106628–106635. [Google Scholar] [CrossRef]
- Slatner, M.; Nagl, G.; Haltrich, D.; Kulbe, K.D.; Nidetzky, B. Enzymatic synthesis of mannitol. Reaction engineering for a recombinant mannitol dehydrogenase. Ann. N. Y. Acad. Sci. 1998, 864, 450–453. [Google Scholar] [CrossRef]
- Laos, K.; Harak, M. The viscosity of supersaturated aqueous glucose, fructose and glucose-fructose solutions. J. Food Phys. 2014, 27, 27–30. Available online: http://www.foodphysics.net/journal/2014/paper_4.pdf (accessed on 7 July 2025).
- Roberfroid, M. Inulin-Type Fructans; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Rocha, J.R.; Catana, R.; Ferreira, B.S.; Cabral, J.M.S.; Fernandes, P. Design and characterisation of an enzyme system for inulin hydrolysis. Food Chem. 2006, 95, 77–82. [Google Scholar] [CrossRef]
- Ricca, E.; Calabro, V.; Curcio, S.; Iorio, G. Fructose production by chicory inulin enzymatic hydrolysis: A kinetic study and reaction mechanism. Process Biochem. 2009, 44, 466–470. [Google Scholar] [CrossRef]
- Ricca, E.; Calabro, V.; Curcio, S.; Iorio, G. Optimization of inulin hydrolysis by inulinase accounting for enzyme time- and temperature-dependent deactivation. Biochem. Eng. J. 2009, 48, 81–86. [Google Scholar] [CrossRef]
- Tewari, Y.B.; Goldberg, R.N. Thermodynamics of the conversion of aqueous glucose to fructose. Appl. Biochem. Biotechnol. 1985, 11, 17–24. [Google Scholar] [CrossRef]
- Illanes, A.; Zuniga, M.E.; Contreras, S.; Guerrero, A. Reactor design for the enzymatic isomerization of glucose to fructose. Bioprocess Biosyst. Eng. 1992, 7, 199–204. [Google Scholar] [CrossRef]
- Lee, H.S.; Hong, J. Kinetics of glucose isomerization to fructose by immobilized glucose isomerase: Anomeric reactivity of D-glucose in kinetic model. J. Biotechnol. 2000, 84, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Dehkordi, A.M.; Safari, I.; Karima, M.M. Experimental and modeling study of catalytic reaction of glucose isomerization: Kinetics and packed-bed dynamic modelling. AIChE J. 2008, 54, 1333–1343. [Google Scholar] [CrossRef]
- Myande Comp., Fructose Syrup Production, China. 2024. Available online: https://www.myandegroup.com/starch-sugar-technology?ad_account_id=755-012-8242&gad_source=1 (accessed on 22 March 2025).
- Marianou, A.A.; Michailof, C.M.; Pineda, A.; Iliopoulou, E.F.; Triantafyllidis, K.S.; Lappas, A.A. Glucose to fructose isomerization in aqueous media over homogeneous and heterogeneous catalysts. ChemCatChem 2016, 8, 1100–1110. [Google Scholar] [CrossRef]
- Hanover, L.M.; White, J.S. Manufacturing, composition, and applications of fructose. Am. J. Clin. Nutr. 1993, 58, 724S–732S. [Google Scholar] [CrossRef]
- Bastian, S.; Rekowski, M.J.; Witte, K.; Heckmann-Pohl, D.M.; Giffhorn, F. Engineering of pyranose 2-oxidase from Peniophora gigantean towards improved thermostability and catalytic efficiency. Appl. Microbiol. Biotechnol. 2005, 67, 654–663. [Google Scholar] [CrossRef]
- Chenault, H.K.; Whitesides, G.M. Regeneration of nicotinamide cofactors for use in organic synthesis. Appl. Biochem. Biotechnol. 1987, 14, 147–197. [Google Scholar] [CrossRef]
- Leonida, M.D. Redox enzymes used in chiral syntheses coupled to coenzyme regeneration. Curr. Med. Chem. 2001, 8, 345–369. [Google Scholar] [CrossRef]
- Bachosz, K.; Zdarta, J.; Bilal, M.; Meyer, A.S.; Jesionowski, T. Enzymatic cofactor regeneration systems: A new perspective on efficiency assessment. Sci. Total Environ. 2023, 868, 161630. [Google Scholar] [CrossRef]
- Maria, G.; Ene, M.D.; Jipa, I. Modelling enzymatic oxidation of D-glucose with pyranose 2-oxidase in the presence of catalase. J. Mol. Catal. B Enzym. 2012, 74, 209–218. [Google Scholar] [CrossRef]
- Partipilo, M.; Ewins, E.J.; Frallicciardi, J.; Robinson, T.; Poolman, B.; Slotboom, D.J. Minimal pathway for the regeneration of redox cofactors. JACS 2021, 1, 2280–2293. [Google Scholar] [CrossRef]
- BioIVT, Rapid-Start, NADPH RapidStart Regeneration System for Extended Metabolism, Woodbury, New York, May 30, 2018. Available online: https://bioivt.com/blogs/nadph-rapidstart-regeneration-system-for-extended-metabolism (accessed on 11 August 2025).
- Kuhn, A.; Yu, S.; Giffhorn, F. Catabolism of 1,5-Anhydro-D-Fructose in Sinorhizobium morelense S-30.7.5: Discovery, Characterization, and Overexpression of a New 1,5-Anhydro-D-Fructose Reductase and Its Application in Sugar Analysis and Rare Sugar Synthesis. Appl. Environ. Microbiol. 2006, 72, 1248–1257. [Google Scholar] [CrossRef]
- Bishop, M. An Introduction to Chemistry; Chiral Publ.: San Ramon, CA, USA, 2013; Available online: https://preparatorychemistry.com/Bishop_contact.html (accessed on 7 July 2025).
- Carroll, J.J.; Mather, A.E. The system carbon dioxide-water and the Krichevsky-Kasarnovsky equation. J. Solut. Chem. 1992, 21, 607–621. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw-Hill: Boston, FL, USA, 1987. [Google Scholar]
- Zaykovskaya, A.; Amano, B.; Louhi-Kultanen, M. Influence of viscosity on variously scaled batch cooling crystallization from aqueous erythritol, glucose, xylitol, and xylose solutions. Cryst. Growth Des. 2024, 24, 2700–2712. [Google Scholar] [CrossRef]
- Chenault, H.K.; Simon, E.S.; Whitesides, G.M. Cofactor regeneration for enzyme-catalysed synthesis. Biotechnol. Genet. Eng. Rev. 2013, 6, 221–270. [Google Scholar] [CrossRef]
- Jiang, H.W.; Chen, Q.; Pan, J.; Zheng, G.W.; Xu, J.H. Rational engineering of formate dehydrogenase substrate/cofactor affinity for better performance in NADPH regeneration. Appl. Biochem. Biotechnol. 2020, 192, 530–543. [Google Scholar] [CrossRef]
- Ansorge-Schumacher, M.B.; Steinsiek, S.; Eberhard, W.; Keramidas, N.; Erkens, K.; Hartmeier, W.; Buechs, J. Assaying CO2 release for determination of formate dehydrogenase activity in entrapment matrices and aqueous-Organic two-phase systems. Biotechnol. Bioeng. 2006, 95, 199–203. [Google Scholar] [CrossRef]
- Wang, X.; Saba, T.; Yiu, H.H.P.; Howe, R.F.; Anderson, J.A.; Shi, J. Cofactor NAD(P)H regeneration inspired by heterogeneous pathways. Chem 2017, 2, 621–654. [Google Scholar] [CrossRef]
- Brenda. Enzyme Database. 2025. Available online: www.brenda-enzymes.org (accessed on 25 March 2025).
- Nasliyan, M.V.; Bereketoglu, S.; Yildirim, O. Optimization of immobilized aldose reductase isolated from bovine liver. Turk. J. Pharm. Sci. 2019, 16, 206–210. [Google Scholar] [CrossRef]
- Tanaka, A.; Tosa, T.; Kobayashi, T. (Eds.) Industrial Applications of Immobilized Catalysts; Marcel Dekkwer: New York, NY, USA, 1993. [Google Scholar]
- Guisan, J.M. (Ed.) Immobilization of Enzymes and Cells; Humana Press: Totowa, NJ, USA, 2006. [Google Scholar]
- Maria, G.; Crisan, M. Operation of a mechanically agitated semi-continuous multi-enzymatic reactor by using the Pareto-optimal multiple front method. J. Process Control 2017, 53, 95–105. [Google Scholar] [CrossRef]
- Fotopoulos, J.; Georgakis, C.; Stenger, H.G., Jr. Uncertainty issues in the modeling and optimization of batch reactors with tendency models. Chem. Eng. Sci. 1994, 49, 5533–5547. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization—Theory and Practice; Wiley: New York, NY, USA, 1993. [Google Scholar]
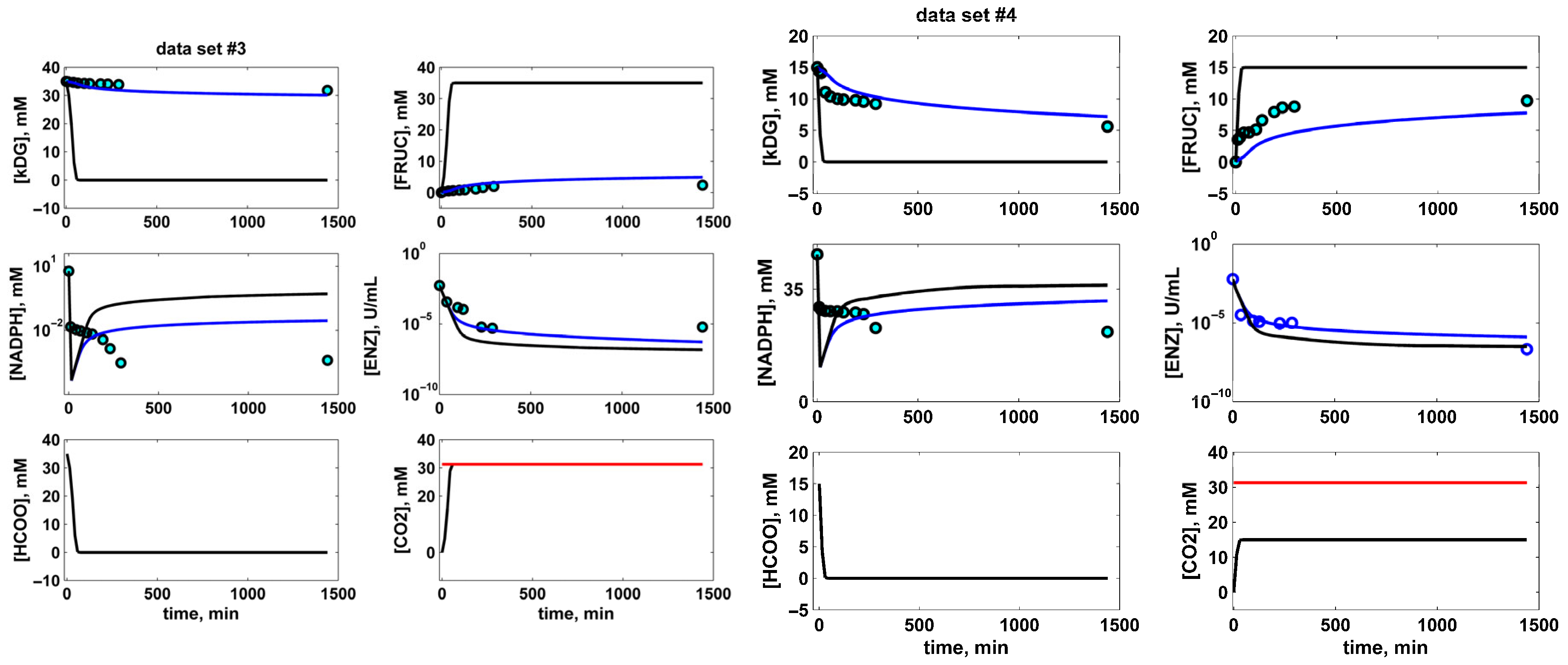
 ) without NADPH regeneration [47] vs. experimental kinetic data (blue circles ο) and vs. kinetic model predictions that also consider in situ NADPH regeneration (this study, FDH = 1000 U/L) (black continuous line
) without NADPH regeneration [47] vs. experimental kinetic data (blue circles ο) and vs. kinetic model predictions that also consider in situ NADPH regeneration (this study, FDH = 1000 U/L) (black continuous line  ). Species dynamics concern the observable key species concentrations, that is, for kDG (S), NADPH (A), D-fructose (P), and suspended ALR (enzyme ENZ). The red line in the CO2 plots indicates the saturation concentration under the running conditions. The initial experimental BR loads are as follows (phosphate buffer, pH = 7; 25 °C, Table 2): Data set # 1 (DS1): 35 mM kDG, 35 mM NADPH, 0.0048 U/mL ALR. Data set # 2 (DS2): 35 mM kDG, 35 mM NADPH, 0.00257 U/mL ALR. Data set # 3 (DS3): 35 mM kDG, 6 mM NADPH, 0.0055 U/mL ALR. Data set # 4 (DS4): 15 mM kDG, 35 mM NADPH, 0.006 U/mL ALR. The experimental curves reproduced from [47] courtesy of CABEQ Jl.
). Species dynamics concern the observable key species concentrations, that is, for kDG (S), NADPH (A), D-fructose (P), and suspended ALR (enzyme ENZ). The red line in the CO2 plots indicates the saturation concentration under the running conditions. The initial experimental BR loads are as follows (phosphate buffer, pH = 7; 25 °C, Table 2): Data set # 1 (DS1): 35 mM kDG, 35 mM NADPH, 0.0048 U/mL ALR. Data set # 2 (DS2): 35 mM kDG, 35 mM NADPH, 0.00257 U/mL ALR. Data set # 3 (DS3): 35 mM kDG, 6 mM NADPH, 0.0055 U/mL ALR. Data set # 4 (DS4): 15 mM kDG, 35 mM NADPH, 0.006 U/mL ALR. The experimental curves reproduced from [47] courtesy of CABEQ Jl.
 ) without NADPH regeneration [47] vs. experimental kinetic data (blue circles ο) and vs. kinetic model predictions that also consider in situ NADPH regeneration (this study, FDH = 1000 U/L) (black continuous line
) without NADPH regeneration [47] vs. experimental kinetic data (blue circles ο) and vs. kinetic model predictions that also consider in situ NADPH regeneration (this study, FDH = 1000 U/L) (black continuous line  ). Species dynamics concern the observable key species concentrations, that is, for kDG (S), NADPH (A), D-fructose (P), and suspended ALR (enzyme ENZ). The red line in the CO2 plots indicates the saturation concentration under the running conditions. The initial experimental BR loads are as follows (phosphate buffer, pH = 7; 25 °C, Table 2): Data set # 1 (DS1): 35 mM kDG, 35 mM NADPH, 0.0048 U/mL ALR. Data set # 2 (DS2): 35 mM kDG, 35 mM NADPH, 0.00257 U/mL ALR. Data set # 3 (DS3): 35 mM kDG, 6 mM NADPH, 0.0055 U/mL ALR. Data set # 4 (DS4): 15 mM kDG, 35 mM NADPH, 0.006 U/mL ALR. The experimental curves reproduced from [47] courtesy of CABEQ Jl.
). Species dynamics concern the observable key species concentrations, that is, for kDG (S), NADPH (A), D-fructose (P), and suspended ALR (enzyme ENZ). The red line in the CO2 plots indicates the saturation concentration under the running conditions. The initial experimental BR loads are as follows (phosphate buffer, pH = 7; 25 °C, Table 2): Data set # 1 (DS1): 35 mM kDG, 35 mM NADPH, 0.0048 U/mL ALR. Data set # 2 (DS2): 35 mM kDG, 35 mM NADPH, 0.00257 U/mL ALR. Data set # 3 (DS3): 35 mM kDG, 6 mM NADPH, 0.0055 U/mL ALR. Data set # 4 (DS4): 15 mM kDG, 35 mM NADPH, 0.006 U/mL ALR. The experimental curves reproduced from [47] courtesy of CABEQ Jl.

| Characteristics | Glucose Isomerization [a,d] | Cetus Two-Step Process [b] | Inulin Hydrolysis [c] |
|---|---|---|---|
| Number of steps | 1 | 2 | 1 |
| Conversion (%) | 50 (limited by the equilibrium) [d] | 99 | 99.5 |
| Raw material availability | Glucose from the starch of crops, molasses, cellulose, and food processing byproducts [42,43] | Genetically modified chicory crop; cultures of Aspergillus sp. | |
| Impurities in the product | Yes | Traces | Negligible amounts |
| Reaction type | Enzymatic isomerization | Enzymatic oxidation (step 1), followed by enzymatic reduction (step 2) | Enzymatic hydrolysis |
| Enzyme mobility | Immobilized [d] | Free (suspended) | Immobilized |
| Enzyme stability and other additives | Intracellular glucose-isomerase (e.g., Streptomyces murinus) of low stability; metal (Al) salts | Pyranose 2-oxidase (P2Ox) and catalase (step 1); aldose reductase and NAD(P)H (step 2); enzymes are costly | Inulinase |
| Temperature | 50–60 °C | 25–30 °C/ 25–30 °C | 55 °C (40–60 °C) |
| Reaction time (h) | 7 | 3–20 (step 1); 25 (step 2) | 13 |
| pH | 7–8.5 | 6.5–7(–8.5); 7–8.5 | 5.5 |
| Reaction steps | 1 isomerization | 2 oxidation (step 1), reduction (step 2) | 1 hydrolysis |
| Coenzyme necessary? | No | Yes, catalase for (step 1) to prevent P2Ox quick inactivation; NAD(P)H for step 2. NAD(P)H is continuously regenerated in situ. | No |
| Product purification | Difficult [d] | Simple (due to high selectivity) | Simple (due to high selectivity) |
| Product purity | 2–5% impurities [d] | High (99.9%) | High (99.9%) |
| Parameter | Nominal Initial Value | Remarks | |
|---|---|---|---|
| Data set # 1 (DS1) | [S]o = [kDG]o | 35 mM | Other species initial conc. [P]o = 0; [A(+)]o = [NADP(+)]o = 0; [EA]o = 0 |
| [A]o = [NADPH]o | 35 mM | ||
| [E]o = [ALR]o | 0.0048 U/mL | ||
| Data set # 2 (DS2) | [S]o = [kDG]o | 35 mM | |
| [A]o = [NADPH]o | 35 mM | ||
| [E]o = [ALR]o | 0.00257 U/mL | ||
| Data set # 3 (DS3) | [S]o = [kDG]o | 35 mM | |
| [A]o = [NADPH]o | 6 mM | ||
| [E]o = [ALR]o | 0.0055 U/mL | ||
| Data set # 4 (DS4) | [S]o = [kDG]o | 15 mM | |
| [A]o = [NADPH]o | 35 mM | ||
| [E]o = [ALR]o | 0.006 U/mL | ||
| Temperature, pH | 25 °C, 7 [47,51] (optimal) | pH buffer | |
| Optimization limits of initial loads | [S]o ∈ [5–100], mM [47,73] [NADPH]o ∈ [5–80], mM [74,75] | [E]o ∈ [0.003–0.1] U/mL [47,76] [FDH] ∈ [100–2000] (U/L) [12,51] | |
| NADPH regeneration | [HCOO]o = [kDG]o | Similar to Maria [55]; Slatner et al. [51] | |
| [CO2]o = 0; [FDH]o = 1000 U/L (adopted as an average) | [FDH]o should be determined using optimization | ||
| Reactor volume (L) | 1 | Up to 3 L capacity | |
| Batch time (tf) (h) | 24 | For DS1–DS4 | |
| Solubility in water | DG (kDG) | 5–7 M | (25–30 °C) [77] |
| DF | ca. 22.2 M | 25 °C, pH = 7 [https://en.wikipedia.org/wiki/Fructose, accessed on 14 August 2025] | |
| CO2 solubility [CO2] * | 31.3 (mM) at (25 °C) | [78,79] | |
| DG (kDG) water solution viscosity | 1–3 cps (for <0.3 M) 1000 cps (4.5 M, 30 °C) vs. 1094 cps (molasses, 38 °C) | [57,80] | |
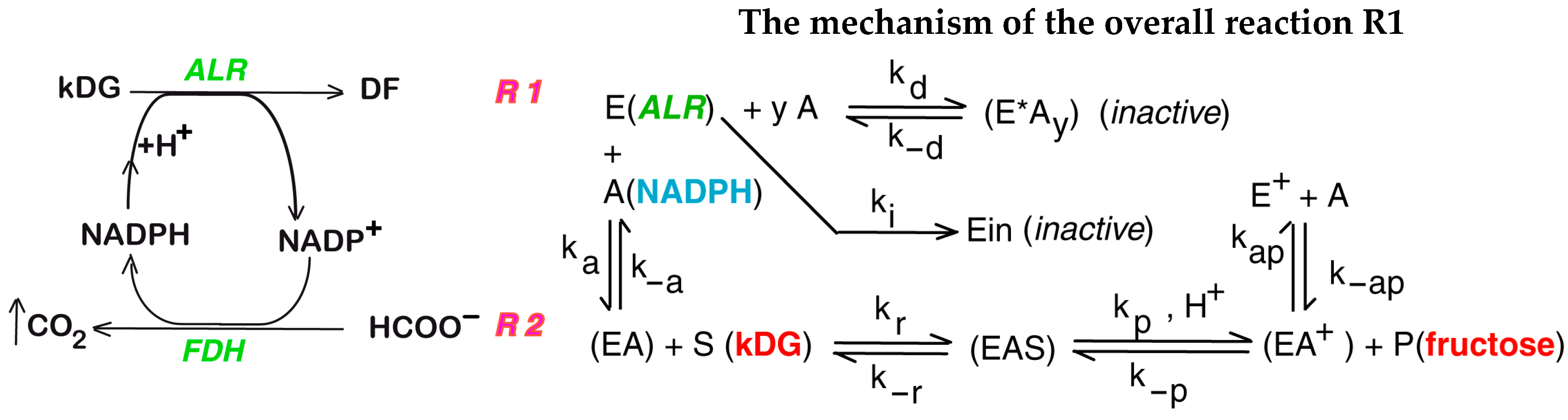
| The Overall Reaction R1 Shown in Figure 1 and Its Associated Side Reactions |
| Rate expressions of the reactions displayed in Figure 1—right, corresponding to the mechanism of the overall reaction R1 |
| , (successive Bi-Bi mechanism) ; ; ; ; ; |
| Rate Constant | Value | Rate Constant | Value |
|---|---|---|---|
| , mM/min/(U/mL) | 3.9 106 | , 1/(mM min) | 2.07·106 |
| , mM | 65.41 | , 1/min | 858.23 |
| , mM | 1.24 | , mM/(U/mL) | 1.48·104 |
| , mM | 1427 | , 1/min | 7.01·10−2 |
| , mM | 0.886 |
| , (mM/min) |
| kc2 = 0.1387, 1/min/(U/L); KM2 = 8.8047 × 10−2 mM; KHC = 5.0061 × 10−2; KNADP = 90.181 |
| Key Species Mass Balances in the BR (Corresponding to Equation (1)) | The Main Experimental Conditions in Table 2 |
|---|---|
| ; ; | Liquid volume = 1 L Phosphate buffer, pH = 7; 25 °C Initial concentrations are in the following ranges: [kDG] = 15–35 mM; [NADPH] = 6–35 mM; Initial [ALR] = 2.6–6 U/L; [HCOO]o = [kDG]o [56]; [FDH] = 100–2000 U/L. If [CO2] ≥ [CO2] *, then [CO2] ≈ [CO2] *, and the excess leaves the system. FDH inactivation is neglected. Notations: S = substrate (kDG); P = product (fructose); A = NADPH; A(+) = NADP(+); E = ALR. The units are in mM, min, and U/L. (*) denotes the saturation concentration of Table 2. |
| Bioreactor Operation | Raw Material Consumption (a,b,c) | DF Prod, mmol | |||||||
|---|---|---|---|---|---|---|---|---|---|
| kDG, mmol | NADPH, mmol | Final NADPH, mmol | ALR, (U) | FDH, (U) | |||||
| BR Non-optimal experiments [47] | Without NADPH regeneration, Figure 2 (d) (very poor) | DS1 | 35 | 35 | 0.18 | 4.8 | - | 11 | |
| DS2 | 35 | 35 | 0.18 | 2.57 | - | 11.1 | |||
| DS3 | 35 | 6 | 0.03 | 5.5 | - | 4.9 | |||
| DS4 | 15 | 35 | 0.29 | 6 | - | 7.8 | |||
| With NADPH regeneration, Figure 2 (d) (good) | DS1 | 35 | 35 | 1.25 | 4.8 | 1000 | 35 | ||
| DS2 | 35 | 35 | 1.06 | 2.57 | 1000 | 35 | |||
| DS3 | 35 | 6 | 0.5 | 5.5 | 1000 | 35 | |||
| DS4 | 15 | 35 | 1.19 | 6 | 1000 | 15 | |||
| BR optimal initial load, within limits in Table 2 | With NADPH regeneration Figure 3 (e,f) (best) | kDG | 100 | 100 | 26 | 1.17 | 3.38 | 440 | 100 |
| NADPH | 26 | ||||||||
| ALR | 3.38 | ||||||||
| FDH | 440 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maria, G.; Gheorghe, D.; Muscalu, C.; Scoban, A. The In Silico Optimization of a Batch Reactor for D-Fructose Production Using the Cetus Process with In Situ Cofactor Quick Regeneration. Dynamics 2025, 5, 35. https://doi.org/10.3390/dynamics5030035
Maria G, Gheorghe D, Muscalu C, Scoban A. The In Silico Optimization of a Batch Reactor for D-Fructose Production Using the Cetus Process with In Situ Cofactor Quick Regeneration. Dynamics. 2025; 5(3):35. https://doi.org/10.3390/dynamics5030035
Chicago/Turabian StyleMaria, Gheorghe, Daniela Gheorghe, Crina Muscalu, and Andreea Scoban. 2025. "The In Silico Optimization of a Batch Reactor for D-Fructose Production Using the Cetus Process with In Situ Cofactor Quick Regeneration" Dynamics 5, no. 3: 35. https://doi.org/10.3390/dynamics5030035
APA StyleMaria, G., Gheorghe, D., Muscalu, C., & Scoban, A. (2025). The In Silico Optimization of a Batch Reactor for D-Fructose Production Using the Cetus Process with In Situ Cofactor Quick Regeneration. Dynamics, 5(3), 35. https://doi.org/10.3390/dynamics5030035






