Geometrically Nonlinear Dynamic Analysis of an Imperfect, Stiffened, Functionally Graded, Doubly Curved Shell
Abstract
1. Introduction
2. Functionally Graded Double-Curved Shells
2.1. Modeling
2.2. Material Properties
3. Theoretical Formulation
3.1. Governing Equations
3.2. Constitutive Relations
3.3. Equation of Motion
4. Solution Procedures
4.1. Linear Vibration Analysis Solution
4.2. Solution of Nonlinear Static Equations
4.3. Solution of Nonlinear Dynamic Equations
4.4. Amplitude–Frequency Curve
4.4.1. Nonlinear Forced Vibration for Isotropic Shells
4.4.2. Nonlinear Free Vibration of Isotropic Shell
4.4.3. Nonlinear Free Vibration of FGM Shell
4.4.4. Nonlinear Forced Vibration of FGM Shell
5. Numerical Results Validation and Discussion
5.1. Natural Frequency Results
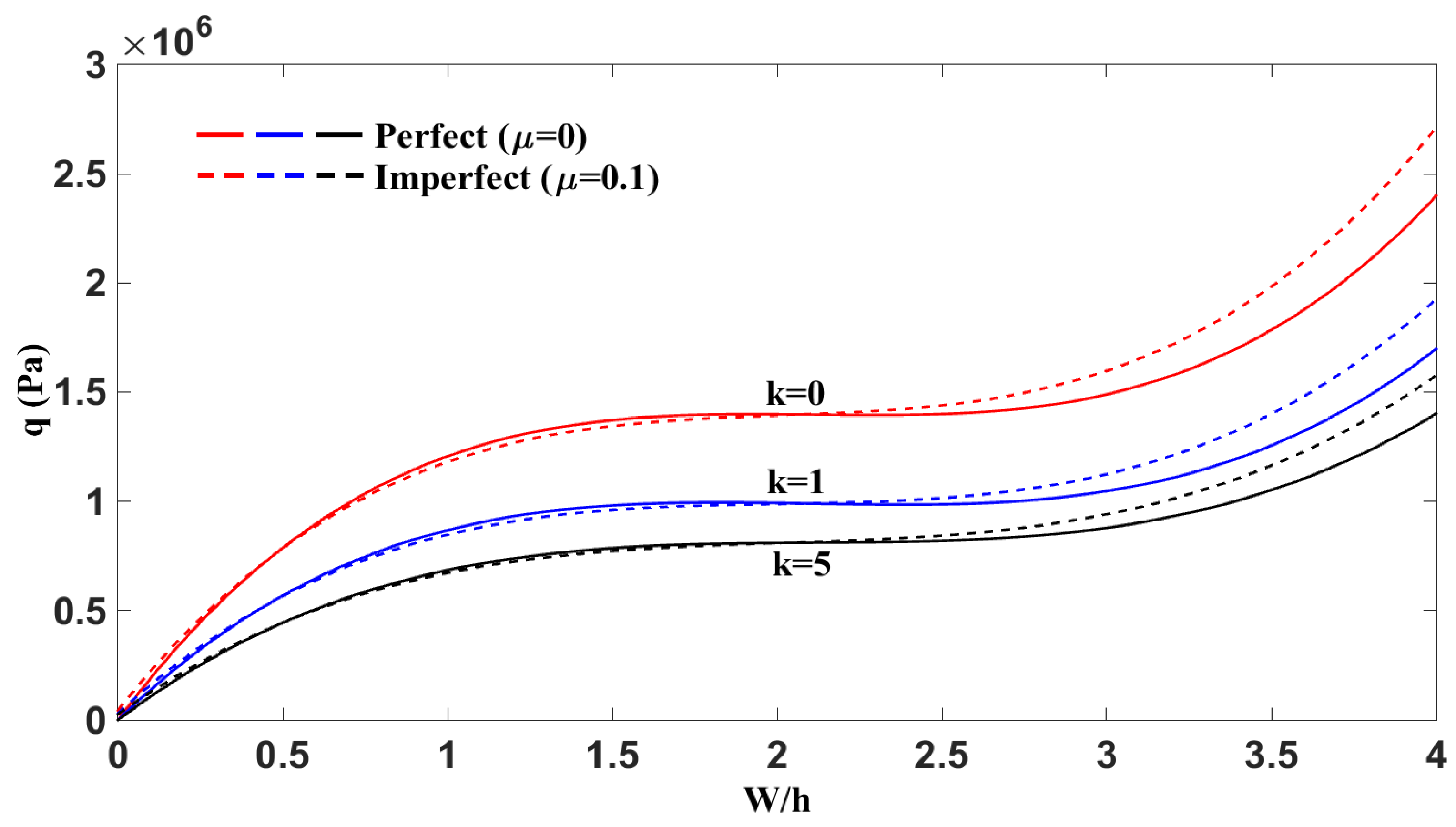
5.2. Nonlinear Static Analysis
5.3. Nonlinear Dynamic Analysis
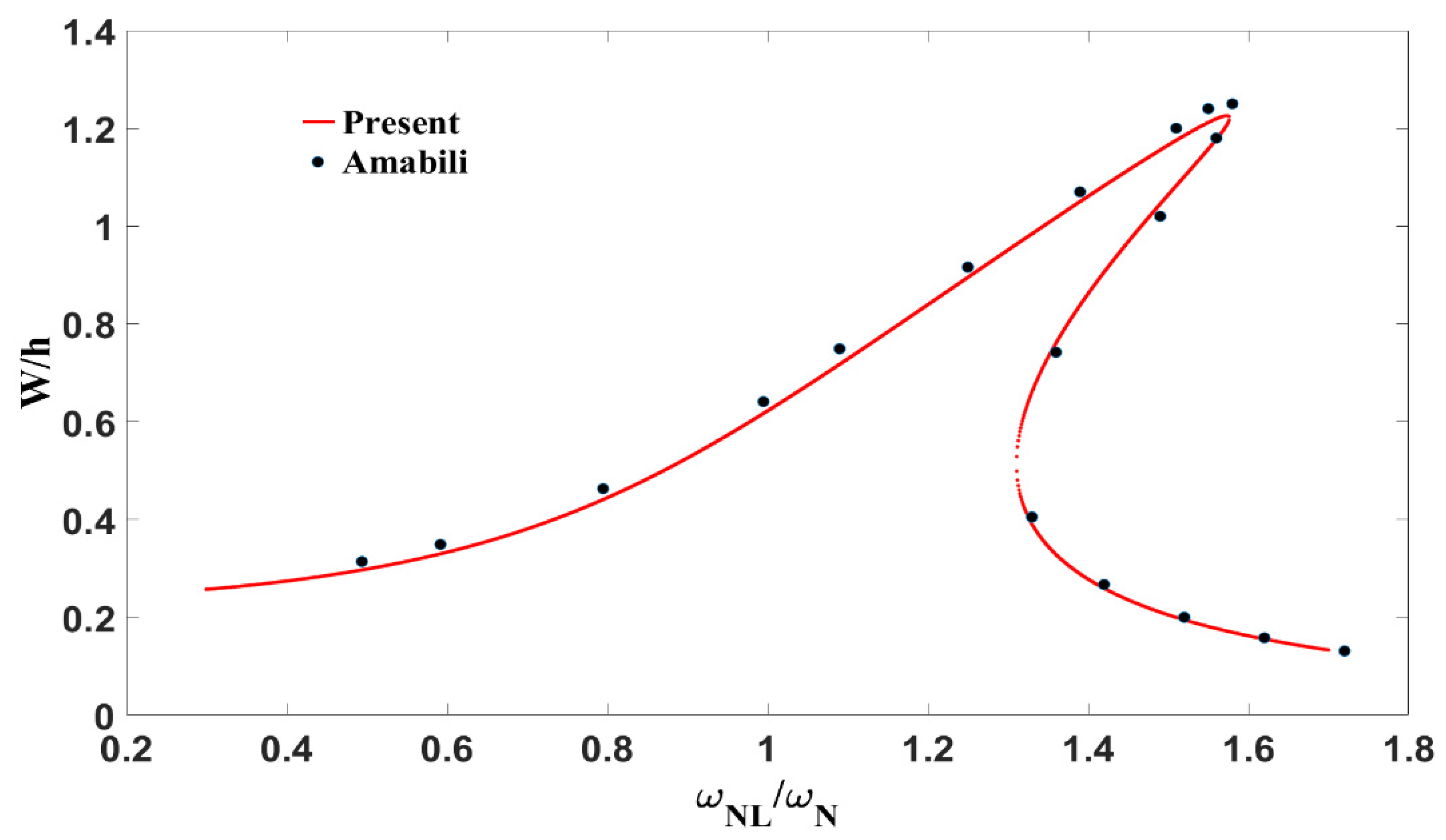
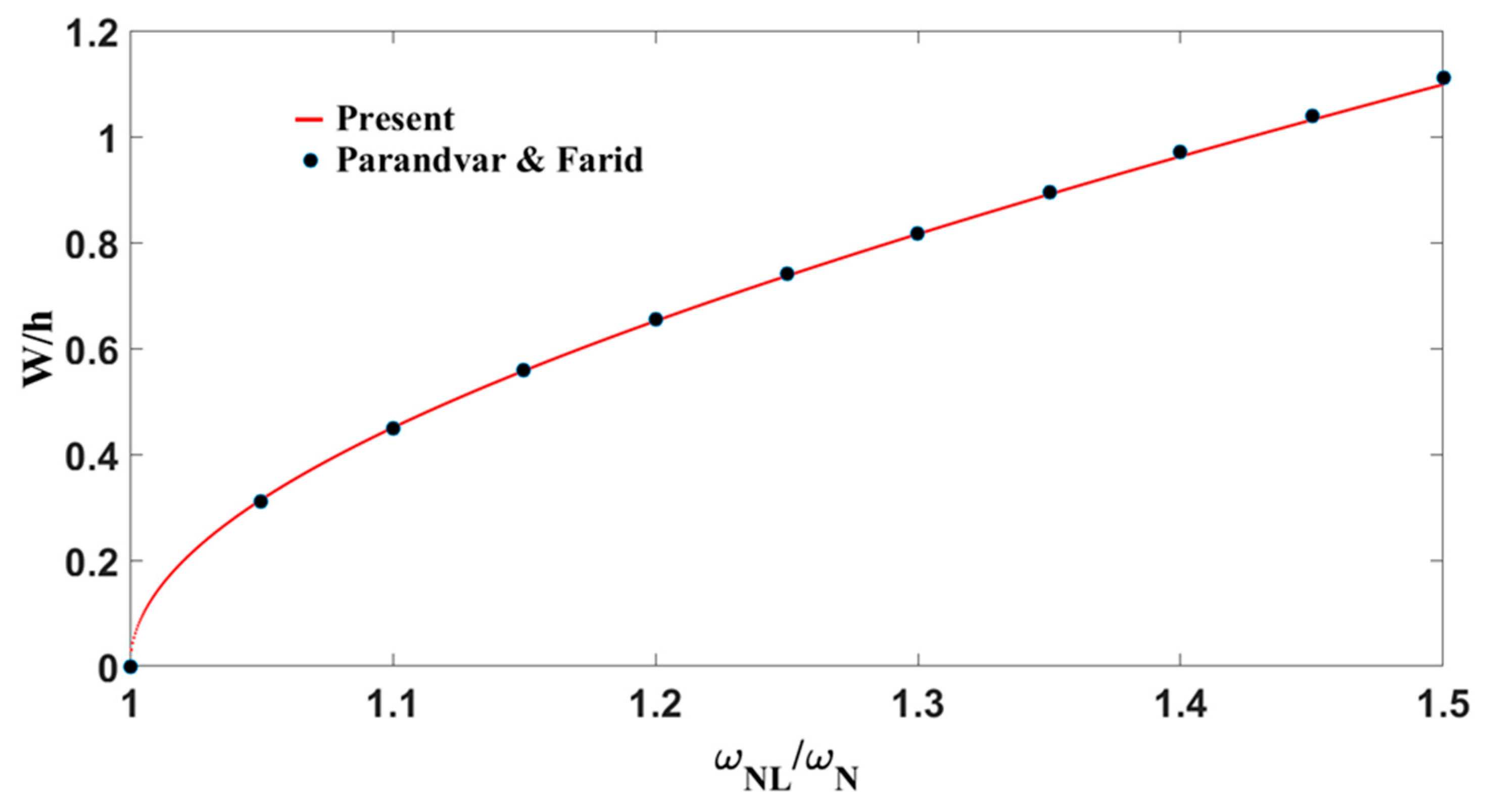
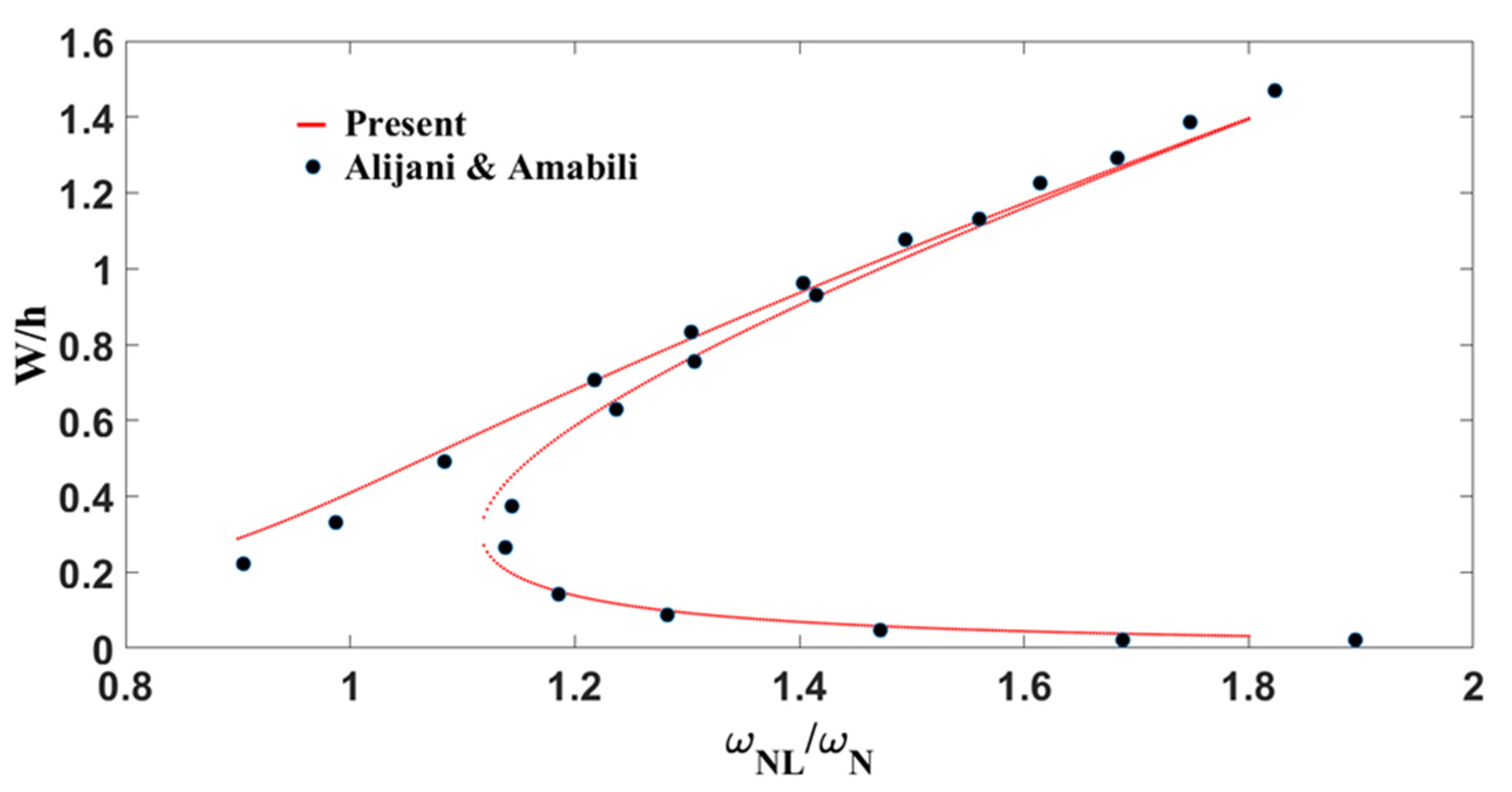
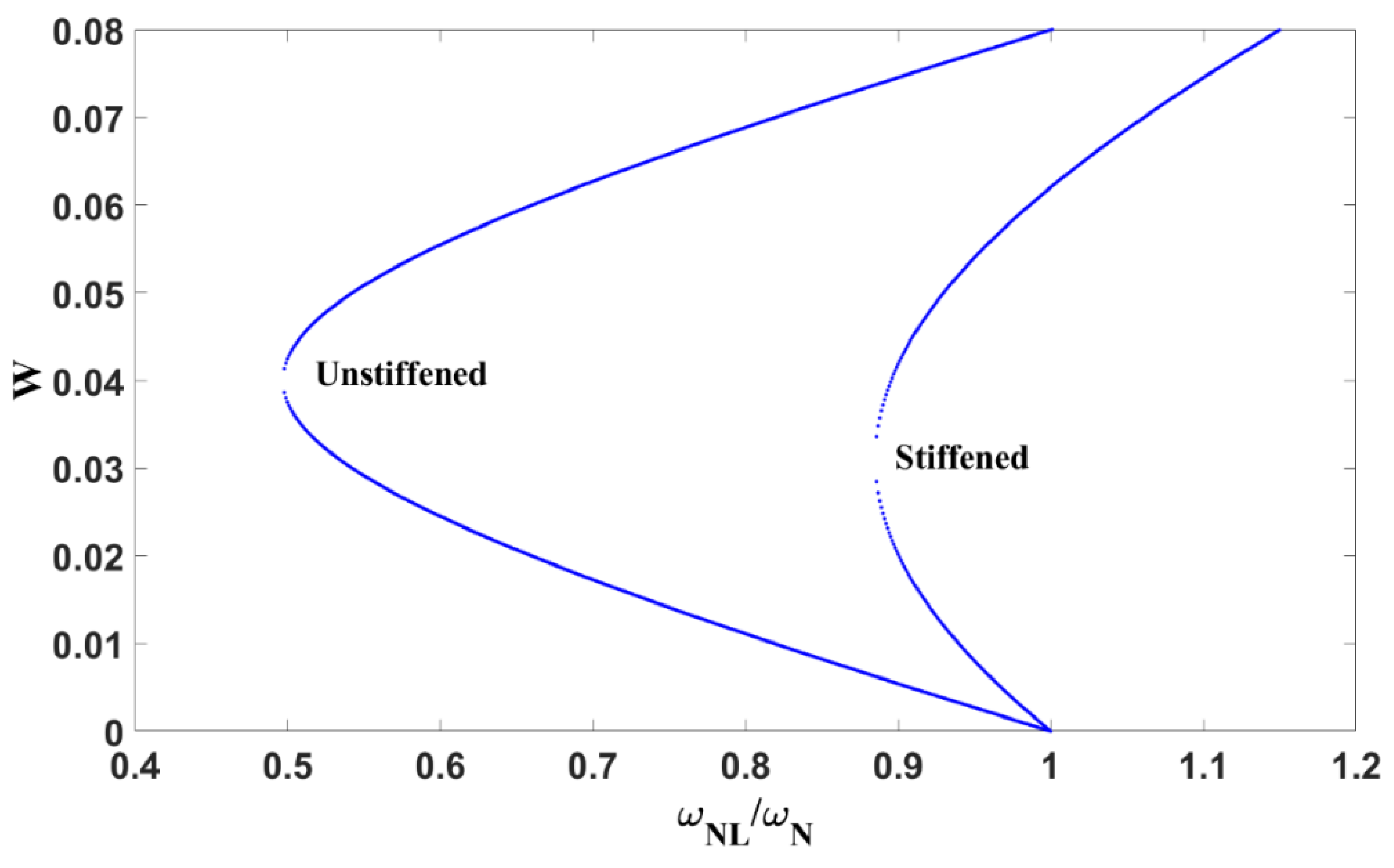
5.4. Nonlinear Frequency Response
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reddy, J.N. Analysis of Functionally Graded Plates. Int. J. Numer. Meth. Engng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Kawasaki, A.; Watanabe, R. Concept and P/M Fabrication of Functionally Gradient Materials. Ceram. Int. 1997, 23, 73–83. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Rokni Damavandi Taher, H.; Akhavan, H.; Omidi, M. Free Vibration of Functionally Graded Rectangular Plates Using First-Order Shear Deformation Plate Theory. Appl. Math. Model. 2010, 34, 1276–1291. [Google Scholar] [CrossRef]
- Xiang, S.; Kang, G.; Liu, Y. A Nth-Order Shear Deformation Theory for Natural Frequency of the Functionally Graded Plates on Elastic Foundations. Compos. Struct. 2014, 111, 224–231. [Google Scholar] [CrossRef]
- Strozzi, M.; Pellicano, F. Nonlinear Vibrations of Functionally Graded Cylindrical Shells. Thin-Walled Struct. 2013, 67, 63–77. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Loy, C.T.; Lam, K.Y.; Reddy, J.N. Vibration Characteristics of Functionally Graded Cylindrical Shells under Various Boundary Conditions. Appl. Acoust. 2000, 61, 111–129. [Google Scholar] [CrossRef]
- Shah, A.G.; Mahmood, T.; Naeem, M.N. Vibrations of FGM Thin Cylindrical Shells with Exponential Volume Fraction Law. Appl. Math. Mech. Engl. Ed. 2009, 30, 607–615. [Google Scholar] [CrossRef]
- Bich, D.H.; Xuan Nguyen, N. Nonlinear Vibration of Functionally Graded Circular Cylindrical Shells Based on Improved Donnell Equations. J. Sound Vib. 2012, 331, 5488–5501. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.-S. Free Vibration and Parametric Resonance of Shear Deformable Functionally Graded Cylindrical Panels. J. Sound Vib. 2003, 261, 871–893. [Google Scholar] [CrossRef]
- Patel, B.P.; Gupta, S.S.; Loknath, M.S.; Kadu, C.P. Free Vibration Analysis of Functionally Graded Elliptical Cylindrical Shells Using Higher-Order Theory. Compos. Struct. 2005, 69, 259–270. [Google Scholar] [CrossRef]
- Golpayegani, I.F.; Arani, E.M.; Foroughifar, A.A. Finite Element Vibration Analysis of Variable Thickness Thin Cylindrical FGM Shells under Various Boundary Conditions. Mater. Perform. Charact. 2019, 8, 491–502. [Google Scholar] [CrossRef]
- Alijani, F.; Amabili, M.; Karagiozis, K.; Bakhtiari-Nejad, F. Nonlinear Vibrations of Functionally Graded Doubly Curved Shallow Shells. J. Sound Vib. 2011, 330, 1432–1454. [Google Scholar] [CrossRef]
- Bich, D.H.; Long, V.D. Non-Linear Dynamical Analysis of Imperfect Functionally Graded Material Shallow Shells. Vietnam J. Mech. 2010, 32, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, H. Free Vibration and Stability of Functionally Graded Circular Cylindrical Shells According to a 2D Higher-Order Deformation Theory. Compos. Struct. 2009, 88, 519–531. [Google Scholar] [CrossRef]
- Zannon, M.; Abu-Rqayiq, A.; Al-bdour, A. Free Vibration Frequency of Thick FGM Spherical Shells Based on a Third-Order Shear Deformation Theory. Eur. J. Pure Appl. Math. 2020, 13, 766–778. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M.; Kant, T. Higher-Order Static and Free Vibration Analysis of Doubly-Curved FGM Sandwich Shallow Shells. Forces Mech. 2023, 11, 100194. [Google Scholar] [CrossRef]
- Benounas, S.; Belarbi, M.-O.; Van Vinh, P.; Daikh, A.A.; Fantuzzi, N. Finite Element Model for Free Vibration Analysis of Functionally Graded Doubly Curved Shallow Shells by Using an Improved First-Order Shear Deformation Theory. Structures 2024, 64, 106594. [Google Scholar] [CrossRef]
- Huy Bich, D.; Dinh Duc, N.; Quoc Quan, T. Nonlinear Vibration of Imperfect Eccentrically Stiffened Functionally Graded Double Curved Shallow Shells Resting on Elastic Foundation Using the First Order Shear Deformation Theory. Int. J. Mech. Sci. 2014, 80, 16–28. [Google Scholar] [CrossRef]
- Duc, N.D. Corrigendum to “Nonlinear Dynamic Response of Imperfect Eccentrically Stiffened FGM Double Curved Shallow Shells on Elastic Foundation” [Compos. Struct. 99 (2013) 88–96]. Compos. Struct. 2013, 102, 306–314. [Google Scholar] [CrossRef]
- Bich, D.H.; Dung, D.V.; Nam, V.H. Nonlinear Dynamical Analysis of Eccentrically Stiffened Functionally Graded Cylindrical Panels. Compos. Struct. 2012, 94, 2465–2473. [Google Scholar] [CrossRef]
- Rahimi, G.H.; Ansari, R.; Hemmatnezhad, M. Vibration of Functionally Graded Cylindrical Shells with Ring Support. Sci. Iran. 2011, 18, 1313–1320. [Google Scholar] [CrossRef]
- Duc, N.D.; Thiem, H.T. Dynamic Analysis of Imperfect FGM Circular Cylindrical Shells Reinforced by FGM Stiffener System Using Third Order Shear Deformation Theory in Term of Displacement Components. Lat. Am. J. Solids Struct. 2017, 14, 2534–2570. [Google Scholar] [CrossRef]
- Minh, T.Q.; Nam, V.H.; Duc, V.M.; Hung, V.T.; Ly, L.N.; Phuong, N.T. Nonlinear Vibration and Dynamic Buckling Responses of Stiffened Functionally Graded Graphene-reinforced Cylindrical, Parabolic, and Sinusoid Panels Using the Higher-order Shear Deformation Theory. Z. Angew. Math. Mech. 2024, 104, e202300580. [Google Scholar] [CrossRef]
- Bich, D.H.; Dung, D.V.; Nam, V.H. Nonlinear Dynamic Analysis of Eccentrically Stiffened Imperfect Functionally Graded Doubly Curved Thin Shallow Shells. Compos. Struct. 2013, 96, 384–395. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Chaikittiratana, A. An Analytical Investigation on Free Vibration of FGM Doubly Curved Shallow Shells with Stiffeners under Thermal Environment. Aerosp. Sci. Technol. 2015, 40, 181–190. [Google Scholar] [CrossRef]
- Singh, A.K.; Pal, A.; Sahu, A.; Roy, A. Non-Linear Strain Based FE Model for Free Vibration Analysis of Stiffened Functionally Graded Folded Plates in Hygrothermal Environment. Mech. Based Des. Struct. Mach. 2025, 53, 1–31. [Google Scholar] [CrossRef]
- Reddy, J.N.; Chin, C.D. Thermomechanical Analysis of Functionally Graded Cylinders and Plates. J. Therm. Stress. 1998, 21, 593–626. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Zhao, X.; Reddy, J.N. Postbuckling Analysis of Functionally Graded Plates Subject to Compressive and Thermal Loads. Comput. Methods Appl. Mech. Eng. 2010, 199, 1645–1653. [Google Scholar] [CrossRef]
- Brush, D.O.; Almroth, B.O. Buckling of Bars, Plates, and Shells; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Birman, V. Plate Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 178, ISBN 978-94-007-1714-5. [Google Scholar]
- Chia, C.-Y. Nonlinear Analysis of Plates; McGraw-Hill Inc.: New York, NY, USA, 1980; ISBN 0-07-010746-7. [Google Scholar]
- Kobayashi, Y.; Leissa, A.W. Large Amplitude Free Vibration of Thick Shallow Shells Supported by Shear Diaphragms. Int. J. Non-Linear Mech. 1995, 30, 57–66. [Google Scholar] [CrossRef]
- He, J.-H. Some Asymptotic Methods for Strongly Nonlinear Equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Quan, T.Q.; Duc, N.D. Nonlinear Vibration and Dynamic Response of Shear Deformable Imperfect Functionally Graded Double-Curved Shallow Shells Resting on Elastic Foundations in Thermal Environments. J. Therm. Stress. 2016, 39, 437–459. [Google Scholar] [CrossRef]
- Chorfi, S.M.; Houmat, A. Non-Linear Free Vibration of a Functionally Graded Doubly-Curved Shallow Shell of Elliptical Plan-Form. Compos. Struct. 2010, 92, 2573–2581. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Cinefra, M.; Soave, M. Effects of Thickness Stretching in Functionally Graded Plates and Shells. Compos. Part B Eng. 2011, 42, 123–133. [Google Scholar] [CrossRef]
- Parandvar, H.; Farid, M. Large Amplitude Vibration of FGM Plates in Thermal Environment Subjected to Simultaneously Static Pressure and Harmonic Force Using Multimodal FEM. Compos. Struct. 2016, 141, 163–171. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations of Rectangular Plates with Different Boundary Conditions: Theory and Experiments. Comput. Struct. 2004, 82, 2587–2605. [Google Scholar] [CrossRef]
- Alijani, F.; Amabili, M. Effect of Thickness Deformation on Large-Amplitude Vibrations of Functionally Graded Rectangular Plates. Compos. Struct. 2014, 113, 89–107. [Google Scholar] [CrossRef]







| Properties | Materials | ||||
|---|---|---|---|---|---|
| Metal | Ceramic | ||||
| SUS304 [9] | Al [35] | SI3N4 [9] | [35] | [35] | |
| 207.7 × 109 | 70 × 109 | 322.2 × 109 | 380 × 109 | 151 × 109 | |
| 8166 | 2707 | 2370 | 3800 | 3000 | |
| 0.28 | 0.3 | 0.28 | 0.3 | 0.3 | |
| Structures | a/Rx | b/Ry | Theory | k | |||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 4 | ||||
| Plate | 0 | 0 | CLPT | 0.0597 | 0.0506 | 0.0456 | 0.0396 |
| FSDT | 0.0581 | 0.0502 | 0.0446 | 0.0387 | |||
| HSDT | 0.0615 | 0.0519 | 0.0466 | 0.0404 | |||
| Present 1 | 0.0578 | 0.0495 | 0.0453 | 0.0397 | |||
| Cylindrical Shell | 0 | 0.5 | CLPT | 0.0648 | 0.0553 | 0.0501 | 0.0430 |
| FSDT | 0.0632 | 0.0543 | 0.0501 | 0.0422 | |||
| HSDT | 0.0662 | 0.0581 | 0.0525 | 0.0462 | |||
| Present 1 | 0.0623 | 0.0534 | 0.0491 | 0.0415 | |||
| Spherical Shell | 0.5 | 0.5 | CLPT | 0.0779 | 0.0676 | 0.0617 | 0.0520 |
| FSDT | 0.0767 | 0.0668 | 0.0611 | 0.0513 | |||
| HSDT | 0.0783 | 0.0691 | 0.0632 | 0.0529 | |||
| Present 1 | 0.0757 | 0.0658 | 0.0604 | 0.0507 | |||
| R1 = R2 | K | Unstiffened | Stiffened | ||
|---|---|---|---|---|---|
| CPT | Present 1 | CPT | Present 1 | ||
| 3 | 0.2 | 3291.88 | 3284.93 | 3446.03 | 3455.62 |
| 5 | 2250.15 | 2224.91 | 2687.97 | 2763.22 | |
| 10 | 2060.96 | 2035.04 | 2579.30 | 2626.50 | |
| 10 | 0.2 | 1287.67 | 1284.86 | 2412.76 | 2439.10 |
| 5 | 893.94 | 892.82 | 2294.78 | 2371.42 | |
| 10 | 839.28 | 838.11 | 2292.47 | 2366.81 | |
| ∞ (plate) | 0.2 | 866.22 | 865.69 | 2388.11 | 2417.22 |
| 5 | 614.33 | 613.55 | 2360.03 | 2399.45 | |
| 10 | 594.95 | 594.10 | 2359.30 | 2397.28 | |
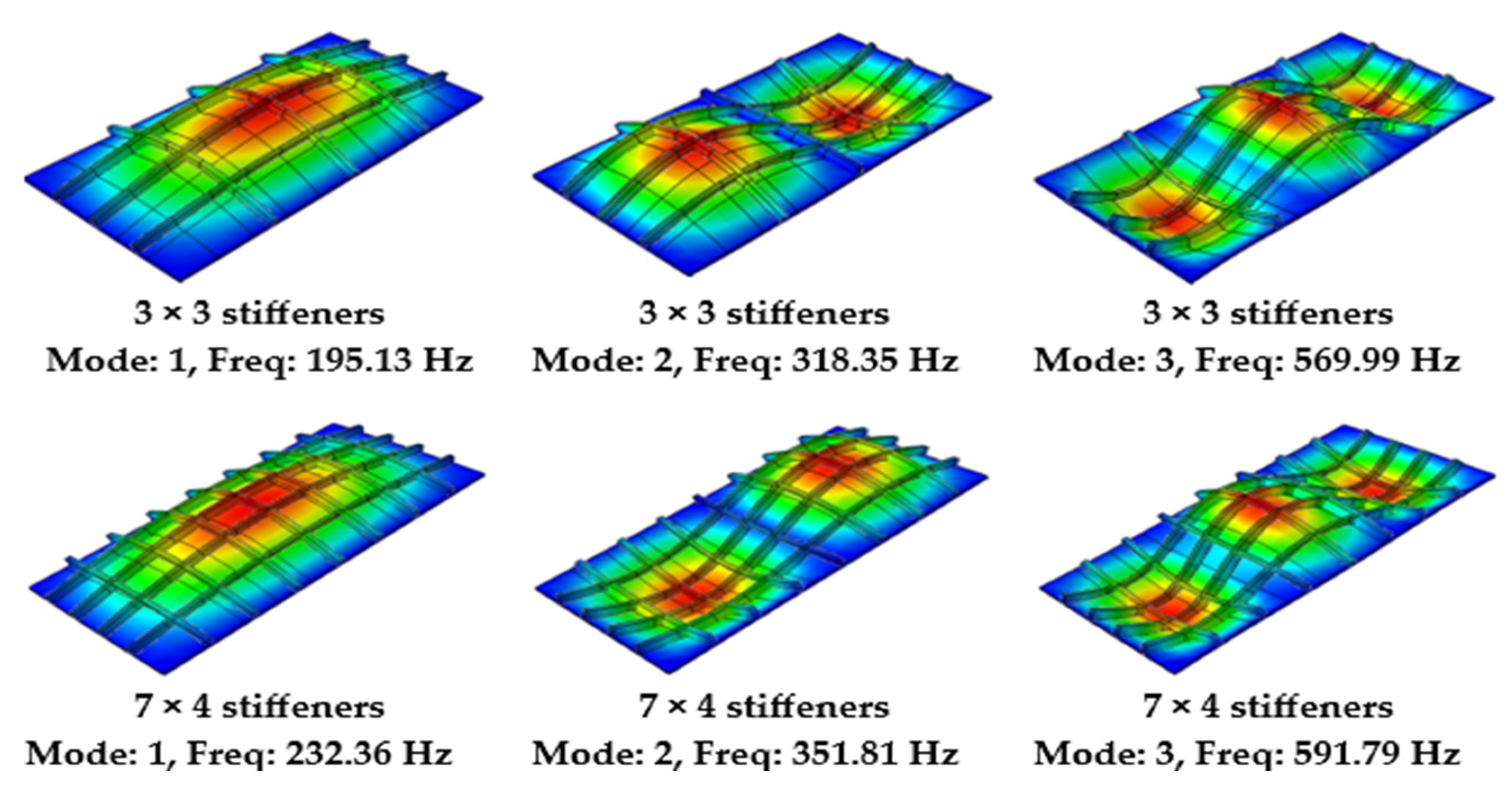
| Mode (m,n) | Arrangement | Unstiffened | X-Dir (7 Stiffs) | Y-Dir (7 Stiff) | X-Y Dir (7 × 7 Stiffs) | X-Y Dir (5 × 3 Stiffs) |
|---|---|---|---|---|---|---|
| 1 (1,1) | ABAQUS | 74.295 | 75.56 | 142.32 | 130.08 | 126.11 |
| Present | 74.46 | 74.83 | 142.8 | 129.432 | 126.74 | |
| %Diff | 0.22 | 0.97 | 0.33 | 0.5 | 0.5 | |
| 2 (1,2) | ABQAUS | 118.62 | 184 | 166.74 | 210.33 | 191.66 |
| Present | 119.035 | 182.07 | 166.199 | 208.17 | 191.968 | |
| %Diff | 0.35 | 1.05 | 0.32 | 1.03 | 0.16 | |
| 3 (1,3) | ABAQUS | 192.65 | 212.6 | 218.16 | 372.94 | 329.08 |
| Present | 193.16 | 212.97 | 216.52 | 370.191 | 331.674 | |
| %Diff | 0.26 | 0.17 | 0.75 | 0.74 | 0.78 |
| Mode (m,n) | 1 (1,1) | 2 (1,2) | 3 (1,3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Arrangement | ABAQUS | Present | %Diff | ABQAUS | Present | % Diff | ABAQUS | Present | % Diff |
| Unstiffened | 101.61 | 102.132 | 0.512 | 161.99 | 163.287 | 0.797 | 263.36 | 265 | 0.62 |
| X-Dir (3 stiffs) | 201.5 | 208.883 | 3.6 | 235.61 | 241.709 | 2.55 | 308.07 | 312.74 | 1.5 |
| Y-Dir (3 stiffs) | 111.44 | 109.477 | 1.77 | 274.91 | 273.233 | 0.61 | 314.66 | 311.902 | 0.88 |
| X-Y Dir (3 × 3 stiffs) | 195.13 | 195.316 | 0.09 | 318.35 | 320.646 | 0.71 | 565.99 | 570.705 | 0.82 |
| X-Y Dir (7 × 4 stiffs) | 232.36 | 231.151 | 0.52 | 351.81 | 348.359 | 0.98 | 591.79 | 591.79 | 0 |
| K | Theory | a/b | ||
|---|---|---|---|---|
| 4 | 10 | 100 | ||
| 1 | CPT | 0.5623 | 0.5623 | 0.5623 |
| FSDT | 0.7291 | 0.5889 | 0.5625 | |
| HSDT | 0.7251 | 0.5864 | 0.5539 | |
| Present 1 | 0.7291 | 0.5889 | 0.5625 | |
| 4 | CPT | 0.8281 | 0.8281 | 0.8281 |
| FSDT | 1.1125 | 0.8736 | 0.8286 | |
| HSDT | 1.1547 | 0.8777 | 0.8172 | |
| Present 1 | 1.1125 | 0.8736 | 0.8286 | |
| 10 | CPT | 0.9354 | 0.9354 | 0.9354 |
| FSDT | 1.3178 | 0.9966 | 0.9360 | |
| HSDT | 1.3846 | 1.0043 | 0.9247 | |
| Present 1 | 1.3178 | 0.9966 | 0.9396 | |
| Curves | Bifurcation (Saddle) Point | Motion | Behavior | ||
|---|---|---|---|---|---|
| Unstiffened | P0 | to | P1 | Stable | |
| P1 | to | P2 | Unstable | Softening | |
| P2 | to | P3 | Stable | Hardening | |
| P3 | to | P4 | Unstable | ||
| P4 | to | P5 | Stable | ||
| Stiffened | P0 | to | P6 | Stable | |
| P6 | to | P7 | Unstable | Softening | |
| P7 | to | P8 | Stable | Hardening | |
| P8 | to | P9 | Unstable | ||
| P9 | to | P5 | Stable | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azizi, B.; Eslami, H.; Jribi, K. Geometrically Nonlinear Dynamic Analysis of an Imperfect, Stiffened, Functionally Graded, Doubly Curved Shell. Dynamics 2025, 5, 18. https://doi.org/10.3390/dynamics5020018
Azizi B, Eslami H, Jribi K. Geometrically Nonlinear Dynamic Analysis of an Imperfect, Stiffened, Functionally Graded, Doubly Curved Shell. Dynamics. 2025; 5(2):18. https://doi.org/10.3390/dynamics5020018
Chicago/Turabian StyleAzizi, Boutros, Habib Eslami, and Kais Jribi. 2025. "Geometrically Nonlinear Dynamic Analysis of an Imperfect, Stiffened, Functionally Graded, Doubly Curved Shell" Dynamics 5, no. 2: 18. https://doi.org/10.3390/dynamics5020018
APA StyleAzizi, B., Eslami, H., & Jribi, K. (2025). Geometrically Nonlinear Dynamic Analysis of an Imperfect, Stiffened, Functionally Graded, Doubly Curved Shell. Dynamics, 5(2), 18. https://doi.org/10.3390/dynamics5020018






