Abstract
In chaos control, one usually seeks to stabilize the unstable periodic orbits (UPOs) that densely inhabit the attractors of many chaotic dynamical systems. These orbits collectively play a significant role in determining the dynamics and properties of chaotic systems and are said to form the skeleton of the associated attractors. While UPOs are insightful tools for analysis, they are naturally unstable and, as such, are difficult to find and computationally expensive to stabilize. An alternative to using UPOs is to approximate them using cupolets. Cupolets, a name derived from chaotic, unstable, periodic, orbit-lets, are a relatively new class of waveforms that represent highly accurate approximations to the UPOs of chaotic systems, but which are generated via a particular control scheme that applies tiny perturbations along Poincaré sections. Originally discovered in an application of secure chaotic communications, cupolets have since gone on to play pivotal roles in a number of theoretical and practical applications. These developments include using cupolets as wavelets for image compression, targeting in dynamical systems, a chaotic analog to quantum entanglement, an abstract reducibility classification, a basis for audio and video compression, and, most recently, their detection in a chaotic neuron model. This review will detail the historical development of cupolets, how they are generated, and their successful integration into theoretical and computational science and will also identify some unanswered questions and future directions for this work.
1. Background
The motivation that led to the discovery of cupolets came from the analysis of secure, chaotic communication schemes. The seminal work of Pecora and Carroll [1] showed that a chaotic transmitter-receiver pair could be created where the receiver could be driven into synchrony with the transmitter, and this was done simply by transmitting one of the dynamical variables from the chaotic transmitter circuit as the carrier for the message. The synchronization property was robust enough that the carrier signal could be modified by adding in a small message signal without breaking the synchrony. The receiver circuit could then remove the carrier, and the hidden message would be revealed.
Many further developments followed, with notable theoretical and practical improvements being developed by Oppenheim and Cuomo [2,3], He and Vaidya [4], and also by Wu and Chua [5], where the synchrony was shown to be guaranteed by Lyapunov functions. In the Wu and Chua work, the synchrony was established even in the presence of the hidden message signal.
In a related area, Hayes, Grebogi, and Ott (HGO) showed that one could analyze the dynamics of a chaotic system to learn about its symbolic dynamics [6], particularly if the system had a two-lobe structure like the double scroll system (also known as the Chua oscillator), shown in Equation (1).
where
If the lobes were labeled 0 and 1, then the symbolic dynamics were equivalent to the visitation sequence traced out by the dynamical system over time. This can be seen in Figure 1, where the control planes are seen edge-on, with the lobe labels indicated. The parameters used in the figure were the same as those used by Hayes et al.: and . The double scroll system is known to be chaotic for this parameter set, and its Poincaré maps, Lyapunov exponents, and bifurcation diagrams have all been extensively studied [7,8,9,10].
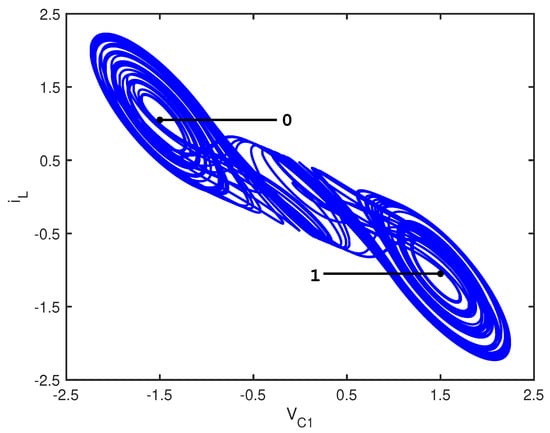
Figure 1.
Double scroll attractor projected into the plane, with control planes intersecting lobes 0 and 1 [11]. Reproduced from Kevin M. Short and Matthew A. Morena, “Signatures of quantum mechanics in chaotic systems”, Entropy 21(6), 618 (2019) https://doi.org/10.3390/e21060618 (accessed on 9 March 2024), with the permission of MDPI.
This work revealed that it was possible to learn the “grammar” of the chaotic system by studying the space of sequences generated by the symbolic dynamics, where the space could be defined as sequences of up to P visits to the lobes of the attractor for some chosen length P. The grammar is equivalent to the space of accessible (or possible) sequences generated by the chaos. To ascertain this information, HGO passed control planes through the two lobes of the attractor, where the intersections were essentially one-dimensional lines (hence, we will use “control planes” and “control lines” interchangeably). Then, the control planes were divided up into some large number of bins, call it N subdivisions, where in most investigations, so the control bins were very small. Then, the center of each bin was taken as an initial condition, and a simulation was run to allow the orbit starting at that initial condition to evolve around the attractor until it had visited P-many lobes. Each time the orbit visited a lobe, the binary value associated with that lobe was appended to the symbolic dynamic sequence associated with that bin. Thus, each bin was associated with a binary symbolic sequence . Then, one could look at neighboring bins and see if they had the same symbolic dynamics for length P sequences.
To make the analysis more tractable, the symbolic dynamic sequences were turned into a function based on binary fractions, , where x is a variable representing position along the control line. For a given position, , suppose that the future visitation sequence results in the binary sequence (where is either 0 or 1, representing a visit to lobe 0 or lobe 1, respectively), then the visitation sequence is mapped to the binary decimal given by
for tracking the trajectory forward in time for P trips around the attractor. When plotted as versus x, one sees plateaus where neighboring control bins all have the same visitation sequences for P trips around the attractor. The great insight of HGO was that by perturbing a trajectory when it passed through a bin, , so that it “falls off the plateau” and is shifted to nearby bin , one can change the future evolution of the chaos so that after P trips around the attractor, the trajectory will be on a different lobe of the attractor. Importantly, if one is willing to wait for a greater number of trips around the attractor (i.e., by setting P to a larger value), then the impact of a small perturbation would be amplified, and the function would have smaller plateaus and more fractal-like structure along the plateaus. An example of this is given in Figure 2, where we plot and for comparison. For most of the research done with cupolets and the developments described in the rest of this review, it turned out that was generally sufficient.
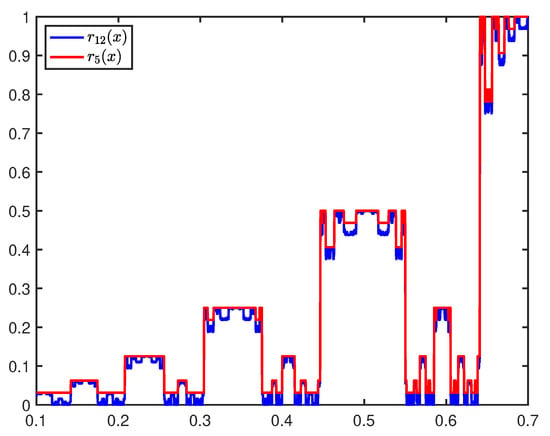
Figure 2.
Comparing the function for (red) future intersections with Poincaré surfaces and (blue) future intersections with the Poincaré surfaces.
The key point of the HGO approach was that any binary message bit string could be transmitted by steering the chaotic attractor to visit the different lobes of the attractor, so long as the first bits were discarded as initialization bits. Hence, one can take a text, such as a Shakespearean play encoded as ASCII bits, and induce the chaotic system to trace out the entire text simply by applying perturbations along the control planes. If the trajectory hits the control plane in position , the algorithm finds and looks at the last bit value. If that bit value is the same as the first bit that the text requires, then the trajectory is allowed to pass through the bin unhindered. However, if the text requires a different bit, then the trajectory is perturbed to the nearest bin on the control plane that has the correct final bit. In this way, the chaotic system can be directed to trace out any desired text, and since the perturbations are, in general, very small (and can always be made smaller by choosing P to be larger), the system would trace out a nice signal that creates the desired text.
There are a few technical details that are specific to the dynamical system chosen for the HGO approach. First, each dynamical system has a “grammar” that determines the possible sequences of visitations that may occur. In the double scroll system, it means that every time a trajectory visits one of the lobes, it loops around that lobe at least once before transitioning to the other lobe of the attractor. Hence, a binary visitation sequence like 010 will never occur, so it must not be allowed to occur in the text sequence. This conflict can be avoided by defining a protocol that would pre-process the text so that, for example, every block of identical bits would have a bit of the same type appended to the block. Thus, 010 would turn into 001100 and would then be consistent with the grammar of the attractor. Secondly, since the HGO scheme is not intended for secure communication, the presence of the kicks, while small, can still be detected in the chaotic trajectories, even if only one dimension is considered as the signal (for example, the first derivative reveals the timing of the perturbations). For secure communication, this would not be desirable. Nonetheless, the work of HGO showed that with subtle nudges to the chaotic system, a great deal of control over the future evolution of the chaos could be achieved.
2. Discovery of Cupolets and Applications to Secure Communication
In the late 1990s, A. Parker and Short (APS) began investigating secure communication techniques that used chaotic systems as the carrier signal. In most of the published approaches to chaotic secure communication, the transmitted signal was a combination of a chaotic carrier and a (hidden) message signal, and then the transmitted signal was used to drive an identical chaotic system into synchrony at the receiver end of the communication channel [1,2,3,4,5,12,13,14,15,16,17,18,19,20,21]. Using prior work developed for predicting chaotic dynamics in the presence of noise, e.g., to detect hidden simulated nuclear test explosions in seismic background noise [22], they began looking at whether the hidden message signals could be treated as noise, so that if a robust prediction of the chaotic carrier could be made, it would be possible to extract the hidden messages from chaotic communications. These efforts were successful, and in a series of papers, it was shown that the hidden messages in chaotic, secure communications could be detected and extracted by reconstruction and prediction [23,24,25,26,27,28], or other methods [29].
The main idea behind the approach to breaking secure chaotic communications was that since a diffeomorphic version of a chaotic attractor could be reconstructed from a one-dimensional time series [30], the chaotic carrier signal used in secure chaotic communications could be used to reconstruct a distorted version of the attractor, albeit perturbed by the presence of the message signal. The perturbations effectively acted as noise in the system, and the behavior of the message was inconsistent with the regular geometric structure of the attractor. Then, using local coordinate systems erected around every sample of the attractor, singular value decomposition techniques could be used to define local coordinates and then project down to the dominant subspace in the region. This transformation largely rejected the message signals, so a robust prediction of the carrier dynamics could be made and, when removed, revealed the hidden message signal.
Since the methods for breaking secure, chaotic communications exploited the fact that the chaotic carrier revealed the geometry of the original chaotic system (through reconstruction), APS looked for a way to build a chaotic communication scheme that never revealed the chaos in the communication channel. They realized that if an identical chaotic system were set up at both a transmitter and receiver, and if the HGO method was employed to steer the separate chaotic attractors from the same initial state, then a message could be transmitted if the required binary kicks could be transmitted. The only transmitted message that would be required would be the information about whether to perturb the chaotic system when it hits a Poincaré control plane, and this information is independent of the message being sent. Further, the control information was purely binary—e.g., “Kick” or “Don’t Kick”—so the communication link could be a typical modern digital data stream. The key challenge was finding a way to initialize the chaotic transmitter/receiver systems into the same state.
The digital communication aspect of the secure communication approach was dependent on the steering mechanism proposed by HGO, but the initialization required remotely defining a common initial state. Other researchers at this time were looking at ways to stabilize UPOs, and several approaches had been developed [6,31,32,33,34,35,36]. While it is a bit of an oversimplification, in most of these approaches, one needed to analyze the Jacobian of the system as it moved around the attractor and carefully access the stable and unstable manifolds to push the trajectory back toward the desired UPO. This was a successful strategy and had been used to stabilize a small number (order 10 or so) of UPOs in common chaotic systems. For the purposes of initialization, however, APS was looking for an approach that could be applied exclusively along the control planes.
Just prior to this period, there was some work published by Bainov, Lakshmanikantham, and Simeonov [37] on impulsive differential equations that looked at the behavior of chaotic systems after being perturbed in various ways. Other references looking at impulsive controls are in [38,39,40]. This work inspired APS to explore the behavior of the double scroll system under sequences of perturbations determined by kicks that corresponded to the kicks in the HGO control method. The investigation started with the control planes of the HGO method, divided into 2000 bins, and developed the appropriate function that tracked the future visitation sequence for all of the bin centers for P loops around the attractor. The method followed the protocol of HGO so that when a kick was applied, it pushed the dynamic system into the nearest bin center that had a single bit difference in the future visitation sequence, and this was called a macrocontrol. One slight alteration was that even when the algorithm called for no kick to be applied, a microcontrol was applied to shift the trajectory to the center of the current bin (of size on order ). This was done to simplify processing and avoid the need to ascertain bin edges with great precision.
With this setup, the investigation proceeded by sending in control bit strings that would determine whether the system applied kicks upon intersection with a control plane, and the bit strings were applied periodically until the system response was evident. Thus, a control bit string like 01011 meant that when a 1 was processed, the system applied a kick (i.e., a macrocontrol) at the next intersection with a control plane, and when a 0 was received, only a microcontrol was applied at the next intersection with a control plane. Since the controls were repeated periodically, the input was a bit string , and the system response was noted. It quickly became clear that the system would transition through a chaotic transient but then settle down into a periodic behavior, and that periodic behavior had a period that was some integer multiple of the length of the control string. Further investigation involved starting the application of the controls in every possible starting bin on the control plane and revealed a surprising and exciting result that held in all but one case—the resulting periodic orbits of the chaotic system were in one-to-one correspondence with the control strings, and this was independent of the initial conditions or starting bin. This is rarely the case with chaotic systems, given their high sensitivity to the choice of initial conditions. This meant that once the control scheme was set up, one could input a control string that would lead the chaotic system to stabilize on a periodic orbit that was uniquely tied to the control string, and it did not matter what was the initial state of the chaotic system. This solved the initialization problem for the chaotic communication scheme, since the transmitter and receiver did not need to be synchronized through communication of the chaotic system dynamics. All one needed to do was drive the transmitter-receiver pair of chaotic systems with the same initializing, periodically applied control string, and the transmitter and receiver would then be on the same periodic orbit—these periodic orbits that arise in the control scheme were dubbed cupolets, indicating that they are chaotic, unstable, periodic, orbit-lets. Explicitly, cupolets are periodic orbits that result from the specified control scheme when driven by a prescribed sequence of perturbations. Cupolets support a one-to-few connection between the given sequence of perturbations and the small number of resulting cupolets.
A side benefit of the cupolet stabilization approach was that thousands of cupolets were quickly found, and these were close approximations of true UPOs in most cases. Because the control scheme was driven by N-bit codes, it was fairly simple to write code that would exhaustively run through all possible control codes, and, in practice, codes of up to 16 bits in length were explored. For example, using the 16 bit codes and loops around the attractor to define the symbolic dynamics, more than 8000 cupolets were found for the double scroll system. This allowed for the creation of a large library of cupolets that could be examined and used for further applications.
With the introduction of cupolets as the initializing states of the communication scheme, it was thus possible to develop a communication protocol that was simple and effective [41]. A message transmission, involving a preamble that gave the initializing code, would be used to create the initial periodic cupolet in both the transmitter and receiver. The remaining bits of communication would then follow the HGO method to steer the receiver away from the cupolet so that it would visit the appropriate lobes of the attractor to trace out the text of the message. The communication channel only ever transmitted digital data corresponding to “control” or “no control,” and so the chaotic system used was never revealed. Further, so long as a new message uses a different cupolet as the initializing state, the transmitted bit stream would be different even if the same text was retransmitted. This work is described in greater detail in [42,43]. This approach was extended into a key generation scheme, whereby a session key could be produced by chaotic means at both transmitter and receiver, and then used in any standard communication protocol [44]. Finally, the presence of cupolets in other standard chaotic systems, as well as a cupolet analog in 2-D chaotic maps, is discussed in [42].
3. Cupolet Spectra Resemble Musical Instrument Spectra
After the discovery of cupolets in the double scroll system, APS created a digital library of all of the thousands of double scroll cupolets that had been found, up to cupolets with 16 bits in the control string. Each cupolet was stored in an ascii file with the name of the file incorporating the cupolet control code, so a file named C00101.txt indicated that the cupolet was created using the control string 00101 applied repeatedly to the double scroll system. Care was taken during the creation of this library to store each cupolet with 1024 samples taken from a single period of the cupolet with equal time steps. This had the benefit that multiple periods could be created simply by appending copies of the cupolet, and it simplified manipulation in the frequency domain since each oscillatory component of the cupolet would be perfectly periodic over the 1024 samples, so problems with spectral leakage would be avoided.
Two undergraduate students, Kimo Johnson and Dan Hussey, began an investigation of the properties of cupolets. Since cupolets evolve in 3-space, their x-, y-, and z-components each provide a time series representing nonlinear oscillatory behavior. The simplest cupolets, e.g., see Figure 3, are only slightly distorted sine waves, but more complicated cupolets have much more complex oscillatory patterns. Since each cupolet was produced with 16 bits of control information, it seemed that the production of complexity with just a few bits might be a way to compress information, so an examination of the spectra of the cupolets was conducted. Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show an original cupolet plotted in 3-D, labeled with the control code used in the production of the cupolet. In the center column, the x-, y-, and z-components are plotted for a single period, and in the rightmost column, the spectra of four periods of the signal are plotted (restricted to only 200 bins of the spectrum). In these figures, one can observe the vast diversity of behavior in cupolets, and these are just a small selection from over 8000 options.
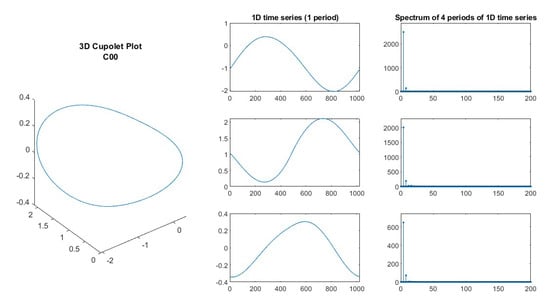
Figure 3.
Plot of the simplest cupolet, C00. Phase space plot in left column; time series plots for , , and coordinates in center column; Magnitude FFT spectrum of four periods of the corresponding , , and time series in right column.
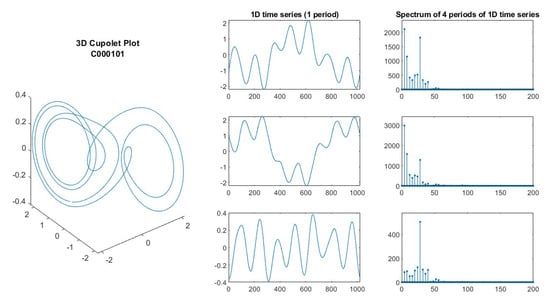
Figure 4.
Plot of cupolet C000101. Phase space plot in left column; time series plots for , , and coordinates in center column; Magnitude FFT spectrum of four periods of the corresponding , , and time series in right column.
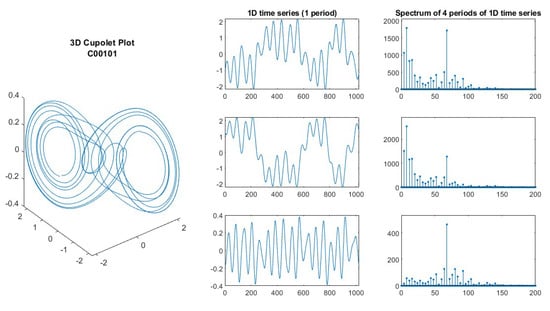
Figure 5.
Plot of cupolet C00101. Phase space plot in left column; time series plots for , , and coordinates in center column; Magnitude FFT spectrum of four periods of the corresponding , , and time series in right column.
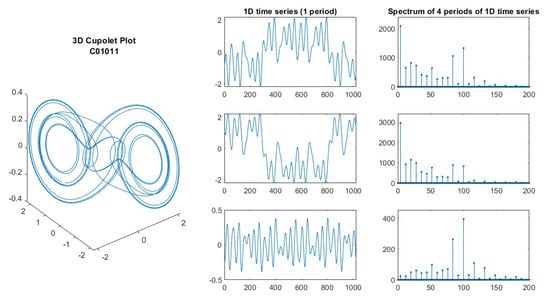
Figure 6.
Plot of cupolet C01011. Phase space plot in left column; time series plots for , , and coordinates in center column; Magnitude FFT spectrum of four periods of the corresponding , , and time series in right column.
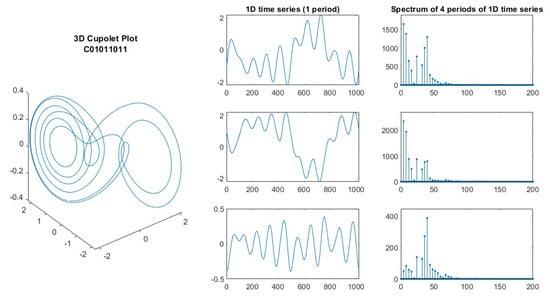
Figure 7.
Plot of cupolet C01011011. Phase space plot in left column; time series plots for x-, y-, and z-coordinates in center column; Magnitude FFT spectrum of 4 periods of the corresponding x-, y-, and z-time series in right column.
After observing many different cupolet spectra, Johnson and Hussey concluded that the spectra resembled those of musical instruments and subsequently wrote software to use the cupolets as digital instruments. Of further interest is the fact that a cupolet like C01011, seen in Figure 6, is perfectly symmetric and leads to spectra with only odd harmonics, whereas non-symmetric cupolets contribute all harmonics. These can be seen in the separation of the spectral lines in the figures; symmetric cupolets like C01011 have twice the spacing between the lines. This important feature is present in musical instruments as well, such as the differences in spectra between (approximately) closed-tube and open-tube woodwind instruments. Finally, some cupolets are very asymmetric, such as C01011011 seen in Figure 7. The net effect was that cupolets could be used like midi instruments to compose music and create a chaotic digital synthesizer, as described more fully in [45].
The creation of synthesized music using cupolets as midi instruments provided a wide range of options for the composer. The cupolets themselves played the role of the musical instruments (the , , and components would each be accessible separately), and with over 8000 cupolet options, only a subset has likely ever been examined, but among the options were cupolets that sounded like (synthesized) guitar, harpsichord, organ, chimes, and saxophone, with various versions of distortion effects on the instruments. Once the instrument was selected for a composition, one would then select the note to be played. The required pitch shifting was accomplished by taking the single period cupolet (or its spectrum) and resampling it to have the correct frequency and duration for the chosen musical note. In practice, this can be done most efficiently in the frequency domain, especially if the notes are cross-faded with a synthesis window like a Hanning window. In this case, the spectral elements of the single period spectrum are true delta functions, and to create an (almost) exact pitch, one can simply convolve the Fourier transform of the synthesis window (i.e., the Hanning window) with the pitch-shifted harmonics of the cupolet spectrum. The root frequency of the cupolet would be shifted by a factor of to the exact desired frequency, with all of the harmonics shifted to the appropriate multiples of , and then the delta-function spectrum would be convolved with the transform of the synthesis window and resampled onto the appropriate sampling grid. This process is simple and efficient and can produce cupolet-synthesized music at the exact desired frequencies.
Since each cupolet requires only 16 bits of information, the synthesized music exists naturally in a very compressed form. Along with the 16-bit control code defining the cupolet, the auxiliary metadata needed to produce the music would include the desired frequency and duration of the note, the loudness level, and any of the other common annotations in music (e.g., attack, decay, etc.). In fact, one side project that was never published involved simply composing on a graphic display using a standard musical staff and musical notation. Once the cupolet instruments were selected, all of the information needed for the transformations could be taken directly from the musical score.
4. Audio and Video Compression with Cupolets
Once it was demonstrated that cupolets could produce reasonably realistic synthesized instrument sounds, the natural next question was whether cupolets could be used to represent recorded audio, image, and video data. In order to address this question, the problems encountered in the music synthesis described in the previous section were somewhat reversed. In order to use cupolets to represent natural recordings, one had to first analyze and understand the content of the recordings and then consider whether there were cupolets that could efficiently and accurately represent the signals. More interesting was the question of whether the cupolets could represent the signals efficiently enough to provide a commercially valuable form of compressed audio, images, and video.
Thus, the problem of compressing audio, images, and video with cupolets was divided into two parts: front-end processing to identify the signal content in the source material, and then backend processing to identify which cupolets were most suitable to substitute in as replacements for the original signal. The subject of this paper is restricted to the history of cupolets, so the signal processing required for the front end analysis will not be included here. However, this work required much greater resolution than is normally provided by the fast Fourier transform (FFT), so a family of super-resolution frequency techniques was developed, called the complex spectral phase evolution (CSPE) family of algorithms [46,47,48,49,50]. In practice, when applied to modern recorded pop music, for instance, these techniques provided something like 200 times better frequency resolution than the FFT. Further details about these techniques can be found in [51].
As illustrated in the previous section, cupolets are very rich in structure and may be used to generate a variety of different waveforms, ranging from a simple sine-like wave with a single dominant spectral peak to more involved waveforms consisting of many harmonics. Figure 8a illustrates another example of the high diversity in spectral signatures found among cupolets. The data is taken from the FFT of a single period of oscillation for each cupolet. The corresponding cupolets in the time domain can be seen in Figure 8b. It is clear from comparing the figures that the simplest cupolet at the top of the figure is essentially sinusoidal, while a much richer structure is apparent in the other cupolets. Cupolets may thus be used to produce signals by using cupolet spectra to replace (part of) a signal’s spectrum. Each of these cupolets may be produced using very little information; typically, 16 bit control codes suffice. This makes cupolets especially suited for signal approximations and data compression, where efficiently representing real-world signals (e.g., audio and video) is important and can aid in achieving faster convergence rates.
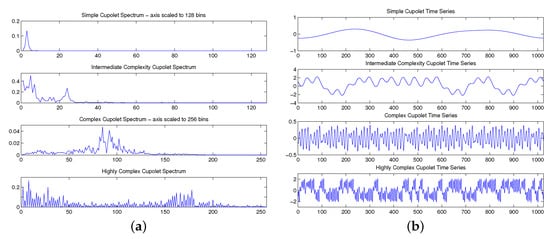
Figure 8.
Illustrating the diversity in cupolets with (a) their spectral variation among cupolets and (b) their time-domain variations [52].
A key step in using cupolets for compression of audio, image, and video signals is a front-end analysis of the signal to detect groupings of spectral elements that have a harmonic relationship, as well as components of the signal that are more broadband. This front-end analysis was done using the CSPE family of algorithms and allowed groupings of spectral elements to be extracted from the original signals. Each harmonic group is converted into a vector of harmonics so that it can be compared with the harmonics of the library of cupolets. This is accomplished by placing all of the single period spectra of the cupolets into a large matrix, suitably normalized, and then the selection of the best cupolet match can be done by multiplying the matrix with the vector of harmonics from the signal and selecting the maximal result. Specifically, if a matrix C holds the harmonics of each cupolet in a row of the matrix, with each row normalized to unit magnitude, then if contains a list of harmonics from a portion of a signal, then corresponds to the row with the best-fit cupolet to match the signal. In practice, this is usually done with just the magnitude of the spectral elements, with phase information derived from the original signal, and is similar to methods of matching pursuit or fitting with an overdetermined basis set. The broadband elements were matched in a similar way, but without the decomposition into harmonic groupings.
For example, in [52,53], Short et al. describe a high-quality, low-bitrate audio compression technology, one of the first practical applications of cupolets, which formed the basis for the launch of a company that pioneered downloading music to cellphones. As described in the previous paragraphs, cupolets with the spectral characteristics closest to a given signal component were chosen and adjusted in frequency, phase, and amplitude for the reconstruction. This allows cupolets to reproduce an audio sample since multiple bins in the sample’s FFT may be represented by a single cupolet. In practice, certain key signal elements were produced exactly, since the cupolet matches were less precise, but quite sufficient for the broader components of the signal. The original signal was thus rebuilt at a very low bitrate using this cupolet representation without significantly compromising signal quality and was the basis for the *.koz audio compression format that was used for music downloads to cellphones in one of the very first smartphone apps ever developed. The practical consequence of this technology was that it allowed efficient transfer of music over so-called 2.5G mobile networks, before 3G, 4G, and 5G networks were available, using the very first smart phones and even phones from previous generations. Numerous industry awards resulted from these efforts [54,55,56,57].
The use of cupolets as basis functions for approximations of many objects that have rich spectral content has been very successful. Several patents resulted from this work, including an audio compression method [51] that was the basis for the music download services and an image and video compression method [58] that was never commercially marketed.
5. Compact Cupolets for Compression
In a further application, the rich spectral content of cupolets allowed for manipulation of the phases of the cupolet components to create a compact form of a cupolet. This led to the development of an image compression method where the basis functions could span a continuum between a wavelet-like state and a sinusoidal-like state [59,60,61]. The key result here is that a phase transformation applied to cupolets can transform them from an oscillatory mode to a wavelet-like mode that can be used in a manner similar to wavelets for image compression. However, if we allow for phase fitting as well, we can generate an approach that is a hybrid of Fourier-like and wavelet-like representations.
A significant theoretical result is found in the investigation of Zarringhalam and Short, who demonstrate how to transform cupolets from their natural oscillatory state resembling the sinusoidal basis of Fourier analysis into a compact cupolet state [59]. Compact cupolets are wavelet-like since their energy is concentrated around a single maximum. From there, an adaptive basis for the space of real-valued functions of a discrete variable may be constructed from only a few compact cupolets. Fourier and wavelet transforms are two common techniques used in image compression, but compact cupolets combine the most useful features of both methods.
Zarringhalam and Short then extended this multiresolution analysis using compact cupolets to image compression [60]. The compression of a sample image using compact cupolets is illustrated in Figure 9. The size of the image is pixels, and the size of the data window is a single line scan, or 256 points. The number of basis elements per data window is and 120, respectively. At the third resolution level with 120 basis elements, the reconstructed image is essentially perfect. The convergence is extremely rapid when considering that such a low number of basis elements is needed.


Figure 9.
(a) Original image and incremental resolution levels. The number of basis elements in each resolution level is (b) 24 (c) 56 and (d) 120 per window [60]. Reproduced from Kourosh Zarringhalam and Kevin M. Short, “Generating an adaptive multiresolution image analysis with compact cupolets”, Nonlinear Dynamics, 52, 51-70 (2008) https://doi.org/10.1007/s11071-007-9257-7 (accessed on 9 March 2024), with the permission of Springer Publishing.
6. Theoretical Connections to Unstable Periodic Orbits (UPOs) and Shadowing
The connection of cupolets to true UPOs is advanced in the theoretical work included in the thesis by Zarringhalam [59]. Important shadowing theorems had previously been developed in [62,63], showing that computed orbits of chaotic systems can be considered reliable estimates of the true trajectories of the chaotic systems. Also, the method of containment developed by Grebogi, Hammel, Yorke, and Sauer [64], and later extended to higher dimensions by Hayes and Jackson [65,66], advanced the idea of looking at Poincaré sections erected along the trajectory of a dynamic system. Then, the development of Zarringhalam’s more flexible shadowing theorem was greatly aided by the work of Coomes, Koçak, and Palmer [67,68], where they developed the idea of a -pseudo orbit, whose deviations from a computed orbit to the true solution were bounded by some at each Poincaré section erected perpendicularly to the trajectory. This shadowing theorem combined the mappings from Poincaré section to Poincaré section and used the Brouwer fixed-point theorem to give conditions under which one can conclude that there is a true orbit shadowing the computed -pseudo orbit. Branching off from these approaches, Zarringhalam realized that since a cupolet’s orbit involves small kicks, the limits on implied by the Brouwer fixed-point theorem were impractical to prove the shadowing of cupolets. Further, it was necessary to build in a mechanism to control the twisting and rotation of the stable and unstable manifolds relative to the trajectory as a cupolet fulfills its orbit. The solution was to apply the Browder fixed-point theorem along cupolet trajectories, as well as continued establishment of flow-aligned local coordinates. In essence, at each sample along a (cupolet) orbit, the flow direction given by the dynamical equations provided one reference coordinate, with a hyperplane defined perpendicular to that direction. Singular value decomposition (SVD) was used to establish orthogonal coordinates on the hyperplane that was continually rotated to align with the stable and unstable directions. The combined mapping from the hyperplanes (e.g., Poincaré sections) could then be used with the Browder fixed-point theorem to establish conditions under which one can test whether a cupolet orbit is shadowed by a true solution of the dynamical system that would be one of the true UPOs of the system. It still remains to implement this proof in algorithmic form.
7. Targeting in Chaotic Systems Using Cupolets
The theory and application of cupolets was further advanced by the steering and targeting work developed by Morena, Short, and Cook (MSC) in 2014 [69]. This work relied on the propensity for cupolets to intersect at selected locations along the control planes. MSC developed an algorithm that would induce the underlying chaotic system to transition smoothly between the orbits of two intersecting cupolets, so long as the transition occurred precisely at their point of intersection. For non-intersecting cupolets, the technique would find a sequence of pairwise intersecting cupolets that would provide a path of smooth transitions between the original two cupolets. In this way, a chaotic system could be steered around its attractor by riding along the known orbits of its cupolets and jumping from one cupolet to another, as desired. This would allow the chaotic system to be made to acquire a specific orbit or to be steered to a specific region of phase space simply by using the cupolets as steps along a directed path to the desired target.
Steering and targeting the trajectories of nonlinear systems has long been the focus of several engineering applications. As an example, consider the scenario in which you are piloting a spacecraft in order to explore some moon, planet, or asteroid. Suddenly, one of the spacecraft’s engines malfunctions and its fuel supply begins to dwindle, jeopardizing your return mission home. After a brief moment of panic, you now need to know: Is there a path along which I can safely navigate the spacecraft home? If so, can I identify a safe return trajectory that is also the most fuel-efficient? These two questions largely drive research into applications of low-energy transfer, unstable ballistic capture, and spacecraft guidance [70].
Cupolet intersections are allowed by the control method described in Section 1 and Section 2 because whenever a chaotic trajectory is being directed onto a cupolet, a sequence of macrocontrols or microcontrols is applied whenever the trajectory passes through a control plane. These controls reset the trajectory to the center of a control bin, which permits some cupolets to intersect if they are steered through the same bin center. To initiate the transition between two intersecting cupolets, from an initial cupolet to a target cupolet, the controls of the initial cupolet must be replaced by a specific cyclic permutation of the controls of the target cupolet precisely when the initial cupolet passes through the cupolets’ intersection bin. This is because the bits of a cupolet’s control code are order-specific to the particular bins through which that cupolet passes. If the transition is not implemented precisely, then the incongruous control will steer the chaotic system away from the orbit of the original cupolet and along a transient path that will behave chaotically until a new cupolet is pursued. This means that the control code for the target cupolet must be cyclically rotated until its leading bit is precisely the control that defines the perturbation of the initial cupolet at this particular control bin. This is known as a controlled transition because, when it is implemented, the orbit of the initial cupolet is instantly redirected onto that of the target cupolet via the control scheme, eliminating the risk of incurring any wayward transients during the changeover. Intersecting cupolets are known more formally as switchable cupolets, given that it is possible to switch between them simply by switching control codes.
Figure 10 illustrates the difference between a transient-free transition and a lengthy transition between cupolets C00 (period-1) and C01 (period-4). Figure 10a shows the underlying chaotic system destabilizing from C00 and subsequently evolving along a transient. Figure 10b illustrates a transient-free transition from C00 to C01, which can be carried out provided that the appropriate permutation of controls that govern C01 are applied at the cupolets’ common bin of intersection. Otherwise, as Figure 10c,d show, the cupolets’ transition may involve a significant transient in order to be completed. The transition seen in Figure 10c,d requires 24 additional loops around the attractor before the target cupolet C01 is acquired.
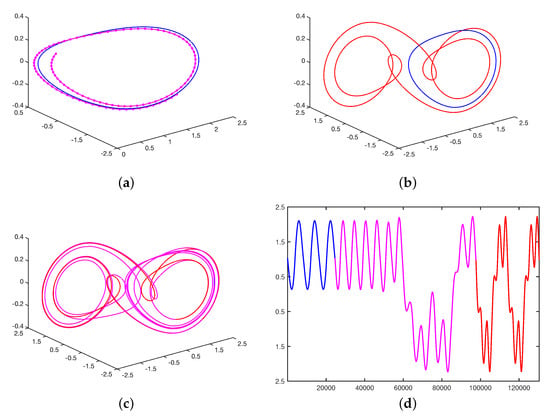
Figure 10.
(a) Cupolet C00 (blue orbit) destabilizes to a chaotic transient (purple orbit) when the implementation of its control sequence is disrupted, (b) a smooth, transient−free transition from C00 to C01 (red orbit), (c) a lengthy transition from C00 to C01 that involves multiple intermediary loops around the attractor, (d) time series showing the transition seen in (c). Reproduced from Matthew A. Morena, Kevin M. Short, and Erica E. Cooke, “Controlled transitions between cupolets of chaotic systems”, Chaos 24, 013111 (2014) https://doi.org/10.1063/1.4862668 (accessed on 9 March 2024), with the permission of AIP Publishing.
Transient-free transitions cannot be expected between non-intersecting cupolets. This is because the absence of an intersection means there is no way for the underlying system to simultaneously destabilize from the initial cupolet and stabilize onto the target cupolet. Instead, the system reverts to evolving chaotically around the attractor during an unpredictable transient phase that will eventually conclude with the target cupolet’s acquisition, assuming that the controls for the target cupolet are being repeatedly applied all the while. However, one may still transition smoothly between non-intersecting cupolets by identifying a chain of pairwise-switchable cupolets that link the initial and target cupolets together and by performing a series of controlled transitions along the chain until the system ultimately acquires the target cupolet. The entire transition is directed along known segments of other cupolets, thereby avoiding the unpredictable transients that can crop up otherwise.
Cupolets and UPOs are found densely embedded around the attractor of a chaotic system, which means there are bound to be numerous sequences of pairwise-switchable cupolets that collectively link two nonintersecting cupolets together. To determine the optimal transition sequence, MSC [69] devised a graph-theoretic approach that models the interconnectivity of cupolets around an attractor as a weighted directed graph, where control bins represent the graph’s vertices and cupolets represent its edges. Here, “optimal” refers to the particular transition sequence that collectively passes through the Poincaré section the least number of times, which determines the length of a transition sequence. For the double scroll system and its twin-lobed attractor, this is equivalent to the number of times the orbit of the transition sequence circumnavigates either of the attractor’s two lobes. As illustrated in Figure 11, two control bins are connected if there is a cupolet whose orbit passes from one of the bins to the other. The edges between two vertices are weighted according to the integer number of intermediary bins an associated cupolet visits when connecting the two associated bins. If multiple cupolets connect the same two control bins, the cupolet passing through the least number of intermediate bins is used, ensuring that at most one edge connects any two vertices.
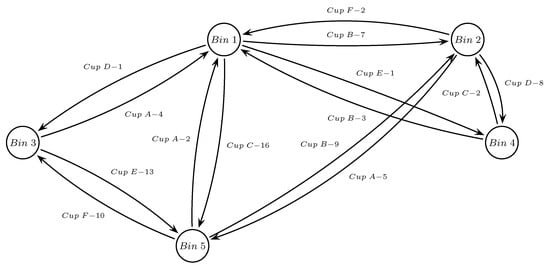
Figure 11.
A weighted digraph showing the interconnectivity of cupolets as edges and control bins as vertices. Reproduced from Matthew A. Morena, Kevin M. Short, and Erica E. Cooke, “Controlled transitions between cupolets of chaotic systems”, Chaos 24, 013111 (2014) https://doi.org/10.1063/1.4862668 (accessed on 9 March 2024), with the permission of AIP Publishing.
MSC deployed Dijkstra’s shortest path algorithm from algebraic graph theory to determine the path with the least cumulative weight between any two vertices. In terms of cupolet transitions, this represents the shortest path between the associated bin pair. To determine the shortest transition sequence from an initial cupolet to a target cupolet, the MSC algorithm compares all possible bin pairs between the two cupolets and selects the bin pair that can be connected by the least weighted sequence of intermediate cupolets, as determined by Dijkstra’s algorithm. The optimal transition sequence between the initial and target cupolets would begin and end at the bins of this bin pair.
In this way, the problem of targeting UPOs in chaotic systems reduces to the search for optimal paths through a graph. Path searching is a well-developed topic in computer science, and a number of algorithms exist that have remarkable efficiency. This is important because studies involving cupolets often rely on large libraries of pre-stabilized cupolets. This research also introduces certainty into the control and steering of chaotic systems. Although the prediction of chaotic systems is possible in the short term, the hypersensitivity of chaotic systems to perturbation makes accurate long-term predictions all but impossible. However, the technique for determining and implementing controlled transitions permits a chaotic orbit to be navigated purposely to multiple locations of an attractor simply by traversing along concatenated segments of known periodic orbits. This allows for the formulaic control of a chaotic trajectory beyond the standard predictability horizon.
It remains to be seen if the metric for describing the length of a transition sequence produces equivalent results if the length were computed differently. In MSC [69], the length of the transition sequence is determined by counting the number of times the underlying Poincaré section is pierced by a transition sequence. In this framework, a path that traverses back-and-forth across the attractor but that only intersects the Poincaré surface a handful of times would be weighted far less than a path that makes numerous Poincaré intersections in quick succession. There are other means to compare two transition sequences. The flow time and the path length, for instance, are two other metrics worth exploring. Both of these would assign more weight to paths that travel longer and farther and may produce results that relate better to the application at hand. Another approach would compute the local Lyapunov exponent along the path that connects two control bins, providing a sense of how chaotic the path is and the effort involved in directing the system along this path. It would be interesting to compare the results produced by all these different ways of defining a transition length.
8. Fundamental Cupolets
During the course of the targeting work, it became apparent that a transition sequence could be made to close up on itself and produce a closed loop around the attractor [71]. By interlacing the control sequences of the cupolets used in the transition sequence, the new orbit was seen to be a cupolet that had been created separately from the control method and was instead constructed by amalgamating the orbits of existing simpler cupolets. In some cases, the synthesized cupolet turned out to already exist in the working set of cupolets; in other cases, the new cupolet had been created beyond the working set of previously stabilized cupolets.
These observations inspired the development of a new irreducibility property that distinguishes the cupolets whose orbits can be decomposed by sequences of switchable cupolets from those cupolets whose orbits cannot be broken down in this manner [71]. Cupolets for which no decomposing set of cupolets can be found are said to be irreducible with respect to a working library of cupolets and are called fundamental cupolets. The cupolets that are amalgamations of fundamental cupolets are known as composite cupolets, and the set of fundamental cupolets that decompose a composite cupolet is known as its fundamental decomposition. Thus, the fundamental cupolets comprising the fundamental decomposition of a composite cupolet are all pair-wise switchable with each other, and, together, their entire orbits will exactly reconstruct the full orbit of the associated composite cupolet via a single sequence of controlled transitions. The sequence of controlled transitions is determined using the graph-theoretic technique described in Section 7. Since a fundamental cupolet can only be decomposed by itself, its fundamental decomposition is simply the set consisting only of itself.
Figure 12 illustrates the amalgamation of the period-16 cupolet C0001111101110111, by three, simpler “fundamental” cupolets, C000110111 (period-9), C01111 (period-5), and C11 (period-2). These three fundamental cupolets are pairwise switchable, and so their orbits can be spliced together at their intersections with transient-free controlled transitions that collectively assemble C0001111101110111. By doing so, the fundamental cupolets give the fundamental decomposition for this cupolet (see [71] for more details). The symbols shown along the cupolets’ orbits of Figure 12 serve simply to further distinguish the orbits of these cupolets.
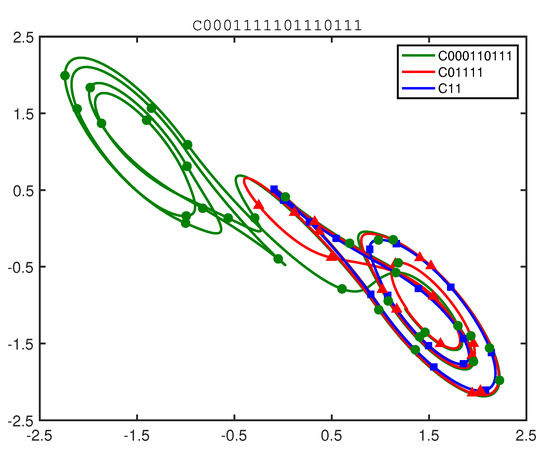
Figure 12.
Illustrating the amalgamation of composite cupolet C0001111101110111 (period-16) by simpler, fundamental cupolets C000110111 (period-9), C01111 (period-5), and C11 (period-2). Reproduced from Matthew A. Morena and Kevin M. Short, “Fundamental cupolets of chaotic systems”, Chaos, 30, 093114 (2020) https://doi.org/10.1063/5.0003443 (accessed on 9 March 2024), with the permission of AIP Publishing.
Identifying the fundamental cupolets from within a large, working library of cupolets allows a chaotic system to be analyzed from a completely new perspective. The fundamental cupolets effectively serve as basis-like building blocks for higher-order cupolets, which allows for a significant portion of a cupolet library to be completely collapsed onto its set of fundamental cupolets without incurring any information loss. For instance, the study described in [71] utilized a library of 13,896 cupolets, of which 2414 were composite cupolets whose fundamental decompositions were completely determined by the algorithm. This means that of the original cupolet library was superfluous and could be discarded without losing any dynamical information. Reducing the cardinality of a cupolet library offers several advantages. This greatly simplifies the process of obtaining higher-order cupolets, since these tend to be composite cupolets whose orbits may instead be acquired by splicing together sequences of simpler, fundamental cupolets via controlled transitions. Also, a cupolet library reduced to its smaller subset of fundamental cupolets will expedite many investigations involving large numbers of cupolets. This is because these investigations have involved iterating over each member of a cupolet library, so if the essential cupolets can be separated from the redundant cupolets, then these algorithms could be streamlined.
Future work will examine the suspicion that the fundamental cupolets will provide highly accurate approximations to several measures of chaotic systems, such as dimension, Lyapunov exponents, and natural measure. These measurements are typically formulated as orbit expansions over a specific set of irreducible UPOs, known as the prime UPOs. Prime UPOs are those that exhibit irreducible symbolic sequences and provide highly convergent approximations to these calculations. One could examine whether these dynamical measurements could be computed via orbit expansions over the fundamental cupolets. If the fundamental cupolets compare favorably to the results obtained via true UPOs, then subsequent work could be devoted to developing a new, cupolet-based framework for analyzing a chaotic system as an alternative to that which has been demonstrated with UPOs.
9. Chaotic Entanglement
Chaotic entanglement represents an emerging and interdisciplinary new area of cupolet research. In chaotic entanglement, two chaotic systems interact in such a way that the interaction is mutually stabilizing and each system stabilizes onto a cupolet so that the cupolets’ stabilities become deterministically linked; disturbing one cupolet from its periodic orbit subsequently affects the stability of the partner cupolet, and vice versa. In the related papers [11,72,73] the two chaotic systems interact via an interaction function that exchanges control information so that one system perturbs the other system. The interaction function takes in the symbolic dynamics information from one cupolet, e.g., its aforementioned visitation sequence, and outputs information as an emitted sequence that will be used as controls on the partner system. The perturbations in the partner system are made in accordance with the control technique that is used to stabilize cupolets.
The transition from chaotic behavior to stabilized cupolets has implications for the entropy in the systems. As it evolves, a free-running chaotic system generates information (e.g., Kolmogorov entropy) at a positive-finite rate. This information is typically encoded as symbolic dynamics for the system, which would simply be a list of the lobes of the attractor visited over time for the double scroll system. An example of this is a cupolet’s visitation sequence, which records the sequence of visits the cupolet makes to each control plane; of course, once stabilized onto a periodic cupolet, the visitation sequence becomes periodic, with entropy zero. A chaotic system thus naturally produces a binary information sequence that can be used as the argument to an interaction function that is meant to mimic the local environment, resulting in controls that impact the partner system, and vice versa, so that the two systems engage in a two-way exchange of information. The surprising discovery was that the two systems that would naturally exist in disordered, chaotic states often mutually stabilize each other onto the periodic orbits of their cupolets.
Figure 13, reprinted from [11], provides step-by-step illustrations of chaotic entanglement forming between two cupolets of the double scroll system. Table 1 provides the control, visitation, and emitted sequence of each cupolet. The cupolets’ entanglement process begins in Figure 13a with two chaotic systems, System I and System II, evolving without control and in close proximity to each other. A control sequence, e.g., 000011111, is applied from an external source to System I, causing the system to stabilize onto a particular cupolet, C000011111 in this case. Figure 13b shows this cupolet evolving about the attractor and generating its visitation sequence V000111111. The visitation sequence is then passed through an exchange function, where it is converted into an emitted sequence by way of a binary operation. In this example, V000111111 is converted to E011101111 by interpreting the bits of the visitation sequence as binary energy and imposing an energy threshold on the visitation sequence [72,73].
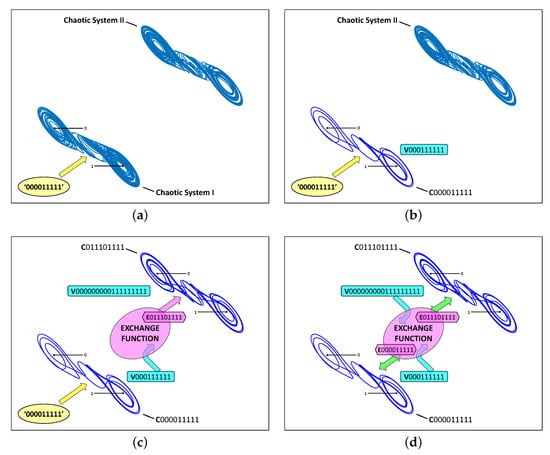
Figure 13.
Step-by-step formation of chaotic entanglement for the double scroll system [11]. (a) An external control is applied to System I. (b) This subsequently stabilizes System I onto cupolet C000011111, which then begins producing symbolic dynamics information in the form of its visitation sequence. (c) An interaction function converts the visitation sequence into the emitted sequence E011101111 and transmits this information as a control to System II. This induces System II to stabilize onto cupolet C011101111. (d) Cupolet C011101111’s visitation sequence is then converted to the emitted sequence E000011111 and transmitted as control information back to System I, replacing the external control. Each emitted sequence exactly matches the corresponding cupolet’s control sequence, which locks both systems onto the persistent, periodic orbits of their cupolets. The cupolets’ entanglement will perpetuate as long as the exchange function continues mediating the exchange of control information between the systems. Reproduced from Kevin M. Short and Matthew A. Morena, “Signatures of quantum mechanics in chaotic systems”, Entropy 21(6), 618 (2019) https://doi.org/10.3390/e21060618 (accessed on 9 March 2024), with the permission of MDPI.

Table 1.
(Color online) Summary of the entanglement seen transpiring in Figure 13. Cupolets C000011111 and C011101111 entangle because the control sequence for C000011111 is contributed by C011101111 via its emitted sequence, E000011111. Similarly, the stability of C011101111 is maintained by the emitted sequence, E011101111, which C000011111 generates. The interaction function mediates the entanglement functions by applying a ‘preponderance’ condition on the bits of each visitation sequence [11].
Figure 13c shows the interaction function transmitting the emitted sequence over to System II, where it is applied as a control sequence. This induces System II to stabilize onto the cupolet governed by the controls that make up the emitted sequence, which is cupolet C011101111 in this example. The cupolets’ interaction now reverses direction when System II transmits control information back to System I, as seen in Figure 13d. As C011101111 winds its way about the attractor, its visitation sequence V000000000111111111 is passed through the same interaction function, which outputs a second emitted sequence, E000011111. In a similar manner, this emitted sequence is fed back and applied as control instructions to cupolet C000011111 of System I. In some special cases, the emitted sequence produced by one cupolet exactly matches the control sequence of its partner cupolet, and vice versa. When this happens, the two cupolets are dynamically driving each other’s stability and generating the necessary control instructions themselves in a mutually self-stabilizing feedback loop. With this, the two chaotic systems are said to be chaotically-entangled. In fact, the original external control can be discontinued because a persistent feedback loop has been established between the two chaotic systems, whose stabilities are guaranteed as long as their two-way interaction is not disturbed.
All of this is mediated by the intermediary interaction function (also called the exchange function in [11,72,73]), which defines the interaction between the two chaotic systems. Interaction functions are described more thoroughly in [72,73], but essentially represent the environment or medium in which the interacting chaotic systems are found. A variety of interaction functions have been developed and tested, including integrate-and-fire models and several logic operations, demonstrating the interdisciplinary nature of chaotic entanglement. One interaction function used successfully in this work is based on Racicot’s empirical study of integrate-and-fire dynamics that are exhibited by firing neurons [74]. Some fifty pairs of entangled double scroll cupolets were found using this function, and its use inspired the subsequent study of mutual stabilization in neuronal systems described in Section 11 below. Another pair of chaotically-entangled cupolets, C000011 and C000111, is shown in Figure 14, and the visitation and emitted sequences of these cupolets are listed in Table 2. The interaction function that induces this entanglement is derived from the integrate-and-fire dynamics of firing neurons [72,73]. Overall, virtually every interaction function or class of interaction functions led to entangled cupolets, so it may be a robust property of certain chaotic systems.
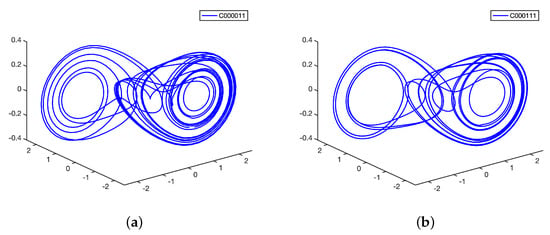
Figure 14.
Cupolets (a) C000011 (period 24) and (b) C000111 (period 18) can be induced into chaotic entanglement via an integrate−and−fire interaction function. The cupolets’ visitation and emitted sequences are listed in Table 2.

Table 2.
(Color online) Summary of the entanglement that forms between cupolets C000011 and C000111, seen in Figure 14. These cupolets entangle because the control sequence for C000011 is contributed by C000111 via its emitted sequence, E000011. Similarly, the stability of C000111 is maintained by the emitted sequence, E000111, which C000011 generates. The interaction function that mediates this entanglement derives from the integrate-and-fire dynamics of firing neurons.
Morena and Short then extended the original framework of chaotic entanglement so that it allows for the entanglement between more than two chaotic systems [75]. In the new framework, a given chaotic system can mutually stabilize with multiple other chaotic systems through localized interactions at specific locations of the attractors. For chaotic systems with multi-lobed attractors, such as the double scroll and Lorenz systems, each lobe is free to individually send and receive control information. This makes each lobe available to entangle with a lobe of another chaotic system. From here, networks of entangled chaotic systems have been assembled into various geometric structures with chaotic entanglement playing the role of a bonding agent between each pair of interacting systems. This is known as multi-system entanglement, and Morena and Short have developed a number of different topologies and arrangements that range in complexity from a simple tripartite lattice to loops and other types of networks.
10. Parallels with Quantum Mechanics
Chaotic entanglement is a relatively recently discovered phenomenon, but it has already played a pivotal role in several interdisciplinary applications. In [72,73,76], Morena and Short used chaotic entanglement to establish a new correspondence between classical and quantum mechanics. The notions of wave function collapse, entanglement, entropy readings, superposition of states, nonlocality, and the measurement problem are all fundamental to quantum mechanics, but have conventionally been considered incompatible with chaotic systems due to their inherent nonlinearities and sensitivity to perturbation. However, a similar framework of superposition and wave function collapse is supported in chaotic systems whose state vectors are provided by the cupolets (e.g., UPOs). This relates to the theoretical work of Grebogi, Yorke, and Ott, who characterized a chaotic system’s natural measure as being concentrated on its set of UPOs [34]. The dynamics of a chaotic system are thus locally dependent on these orbits, with each UPO or cupolet providing a nonzero contribution to the overall state dynamics, so that a UPO’s influence is strongest when the system is evolving in its near vicinity and weaker otherwise.
This framework allows a chaotic system’s state vector to be defined as the weighted contribution of each cupolet:
with each providing the contribution of the system’s kth cupolet at a particular time. Letting denote the state of the chaotic system, the associated wave function is:
where denotes the state space coordinates of the kth cupolet at time , where . If the system evolves on or extremely nearby its kth cupolet, then because at this moment and for all . If the state of the system is evolving in a region bounded by neighboring cupolets, then those nearby cupolets provide the greatest nonzero contribution to Equation (4), while cupolets located elsewhere contribute negligibly.
In this way, a freely-evolving chaotic system exists as a superposition of its cupolet states [76]. When the system is controlled by one of its cupolets, the controls that it repeatedly receives serve as the measurement process that leads to the collapse of its wave function. This occurs precisely when the chaotic system stabilizes onto a cupolet, , say, in which case and for all . This reduces Equation (4) to and Equation (3) to , whose only nonzero component is . Following the collapse, the chaotic system can be described uniquely by a single cupolet state.
As with quantum entanglement, chaotic entanglement is also highly sensitive to measurement. Disruptions to the interaction between two entangled cupolets will almost always destroy the entanglement unless a great deal is known about the control scheme. By measurement, we mean a perturbation that could be as subtle as the microcontrols or macrocontrols that are implemented by the aforementioned control scheme, or as general as an arbitrary perturbation applied to one of the two parent systems. As an example, consider the subtle effect of interchanging a ‘0’ bit for a ‘1’ bit in the control sequence of one of the two entangled cupolets. Control sequences are unique since they direct a chaotic system onto one specific cupolet. Disturbing the control sequence would perturb the cupolet into a different bin on the control plane and effectively destabilize it from its periodic orbit. This would result in the cupolet generating a different visitation sequence that would no longer guarantee the stability of the partner cupolet, likely destroying their entanglement. However, should the appropriate controls for the first cupolet be restored and continue to be periodically applied, then the two cupolets would eventually restabilize via the restarted entanglement process.
Finally, in the context of chaotic entanglement, the idea of “collapse of the wavefunction” is quite natural. Since interaction equals measurement, any measurement made on a chaotic system induces perturbations to the chaotic system and these might effectively act like controls applied to the system, directing it into a cupolet state. So, before the measurement, the system exists in a mixed state determined by local cupolets and chaotic dynamics, but after the measurement, a periodic cupolet state results.
Cupolets and chaotic entanglement also provide new perspectives for the measurement problem in quantum mechanics. The sensitivity of a quantum wave function to measurement makes it very difficult for researchers to prepare accurate experiments with quantum systems. This is problematic for studies in which multiple quantum systems must all be synchronized in advance. The systems must be prepared in the same state immediately prior to each measurement in order to ensure consistency and accuracy across the experiment. The new perspective on this problem comes from the cupolet-stabilizing control technique, which allows the user to determine the state of an evolving chaotic system by repeatedly applying controls since the resulting cupolet is independent of the initial condition. Or, provided one has access to measurement tools smaller than the scale of the control bins, a measurement could be designed whose effects would be subtle enough that they would not perturb an evolving cupolet to a new bin center on a control plane. The microcontrols would correct the deviation the next time the cupolet intersects a control plane. This technique can be extended to a pair of entangled cupolets, whereby a subtle measurement could be applied to one of the cupolets without jeopardizing their underlying entanglement. This would allow one to explicitly determine the state of the other cupolet, thus synchronizing the two systems and aiding in state preparation prior to an experiment.
It is perhaps not surprising that chaotic entanglement evokes so many connections to its quantum namesake, considering that a number of recent studies have detected signatures of chaos in quantum systems. Though seemingly incompatible, since chaos is considered nonlinear in classical physics while quantum physics is linear and supports superposition, one signature linking chaos and quantum is the sensitivity of some quantum systems to perturbation. This has been seen in experiments tracking quantum states that are evolving under slightly different Hamiltonians, whereby the differences in state evolution are associated with the positivity of a classically-derived Lyapunov exponent [77,78]. Chaudhury et al. experimentally observed that the differences could be related to whether the initial conditions correspond classically to chaotic versus regular regimes [79]. Another signature of chaos is present in the phenomenon of quantum scarring, where a quantum system’s associated wave function is concentrated on paths that correspond to periodic orbits in the classical limit [80,81,82,83]. This gives another area where periodic orbits and quantum effects are connected.
Quantum entanglement is also considered to be a reliable indicator of classical chaos [84,85]. Several kicked-top experiments of cesium (133Cs) atoms have produced phase plots revealing islands of regular motion surrounded by a sea of chaos [79]. If entropy measures are used to assess the strength of the entanglement, stronger entanglement develops between atoms whose initial states are prepared from a chaotic regime, whereas weaker entanglement develops between atoms that evolve from regular regions. It appears that the quantum regime reflects properties of the underlying classical system [86].
In addition to these similarities, Short and Morena also discussed several properties of quantum mechanics that are incompatible with classical, chaotic systems [11,75]. For starters, superposition in quantum mechanics pertains to the linear combinations of state vectors that separately satisfy Schrödinger’s equation and that collectively describe the state of an associated quantum system. This is not supported in chaotic systems due to their inherent nonlinearities, meaning that any linear combination of periodic orbits could not be expected to be a solution to their parent chaotic system. Superposition for chaotic systems instead refers to the state of a chaotic system existing as a mixture of its periodic orbits, even though, collectively, any linear combination of these orbits would not outright satisfy the governing equations. That said, the fundamental cupolets themselves effectively play the role of basis elements, albeit as an overdetermined basis. Further, if examined using spectral methods, it might appear that sinusoidal modes can be used to create “states” of a chaotic system. This would be wrong, since the states thus created would not lie on the chaotic attractor unless chosen to correspond to a cupolet or UPO. Thus, a Hilbert space like the Fourier basis can be misleading if an intimate knowledge of the nonlinear dynamics is not known.
Quantum entanglement also allows for spontaneous, nonlocal interactions, often referred to as instantaneous or “spooky” action at a distance. The communication between two quantum-entangled particles is both instantaneous and distance-independent. This is not supported in classical mechanics. For chaotic entanglement to occur, the two chaotic systems must be evolving in close proximity to each other in order to interact and exchange control information; for cupolets, we would say that interaction equals measurement, and any interaction could potentially trigger mutual stabilization. That stabilization would persist as long as a communication link remains between the systems, and if the communication is broken, the entanglement would decay on a time scale related to the local Lyapunov exponents of the cupolets. However, it would not be a truly instantaneous action at a distance, as supported in quantum mechanics. The chaotic entanglement does not materialize instantaneously nor decay instantaneously because a period of transition is required in order for a chaotic system to stabilize or destabilize fully from a cupolet, but on such a short time scale, this may not be easily accessible in experiments.
11. Cupolets in Neuron Systems
Over the past few decades, there has been increasing interest in developing mathematical models of neurons. The most comprehensive model is the Hodgkin-Huxley model [87], which is based on careful analysis of the biochemistry and biophysiology in the neuron, but the model is four-dimensional and has so many parameters that it is somewhat unwieldy. Simplified models have been developed that can reproduce the observed spiking behavior of neurons. A two-dimensional model called the Fitzhugh-Nagumo (FHN) model [88,89,90] can reproduce the spiking behavior of neurons, but since it is two-dimensional, it cannot reproduce the chaotic behavior sometimes exhibited by neurons (although coupled FHN neuron models can behave chaotically [91]). A popular three-dimensional model that has a closer connection to physical neurons and can display chaotic behavior is the Hindmarsh-Rose (HR) neuron model [92], given in Equation (5). The parameter values used are , , , , , and . Typically, the r and I parameters are varied and can be selected from a chaotic regime, if desired.
In this model, the x variable represents the neuron’s membrane voltage that produces the spiking behavior called the action potential, while the y and z variables govern the recovery or refractory period between the action potential spikes. The z variable has a slower characteristic timescale than the y recovery variable. As discussed in [92], the HR system can exhibit periodic firing, bursts, and random firing. The dynamics of the HR system are quite similar to those of biological neurons, and typically the x variable goes through a sequence of consecutive spikes (action potentials) before entering the refractory period. The system will produce chaotic dynamics when and , and that is the regime studied in [93,94] and the three-dimensional attractor of the HR neuron appears in Figure 15. The bursting behavior, particularly of the x variable time series, is illustrated in Figure 16.
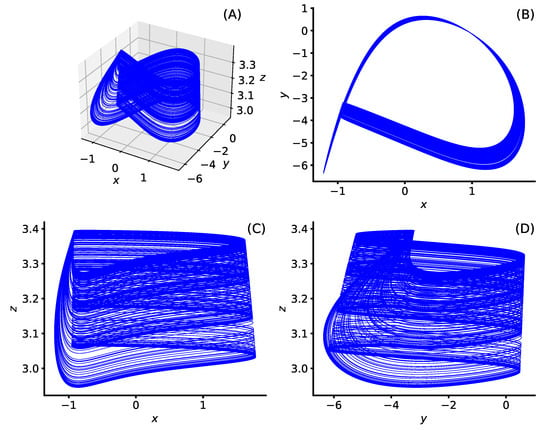
Figure 15.
Numerical integration of Equation (5) with and so that the model is in a chaotic region [93]. (A) 3-Dimensional phase space plot of the x, y, and z dynamics. Projection of (A) onto (B) the x-y plane, (C) the x-z plane, and (D) the y-z plane. Reproduced from John E. Parker and Kevin M. Short, “Cupolets in a chaotic neuron model”, Chaos 32, 113104 (2022) https://doi.org/10.1063/5.0101667 (accessed on 9 March 2024), with the permission of AIP Publishing.
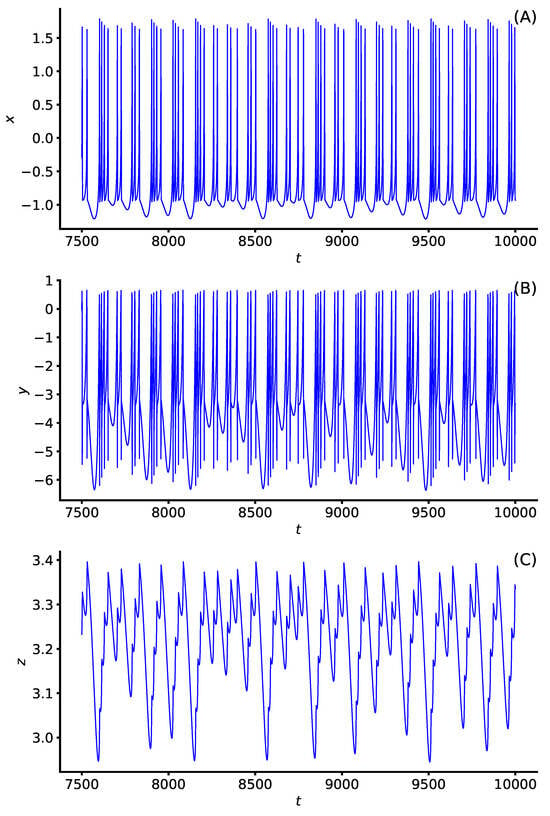
Figure 16.
One dimensional time series of each dynamical variable (A) x, (B) y, and (C) z in Figure 15 and Equation (5). Reproduced from John E. Parker and Kevin M. Short, “Cupolets in a chaotic neuron model”, Chaos 32, 113104 (2022) https://doi.org/10.1063/5.0101667 (accessed on 9 March 2024), with the permission of AIP Publishing.
Since the HR neuron model can behave chaotically, Parker and Short chose it for the first study of cupolets outside of the standard chaotic attractors found in the chaos/nonlinear dynamics literature. In this investigation, they found that cupolets exist in the HR neuron model [93], and further, there is evidence that mutual stabilization (e.g., chaotic entanglement) is possible within the HR model [94]. This recent development is potentially quite important since communication between biological neurons is via impulsive action potentials, and it is natural to equate the impulsive kicks applied along control planes in cupolet research with idealizations of the action potentials passed over the synapses of neurons.
The procedure for finding and stabilizing cupolets in the HR model followed the same approach as for other chaotic systems. The attractor was intersected by two planes, as indicated in Figure 17. This system was analyzed to find the symbolic dynamics of points along the control planes, and the appropriate function was created (it was similar but a bit simpler than that for the double scroll system), and the system was driven by sequences of repeating control codes. The result was a rich array of around 7000 cupolets; a selection is displayed in Figure 18.
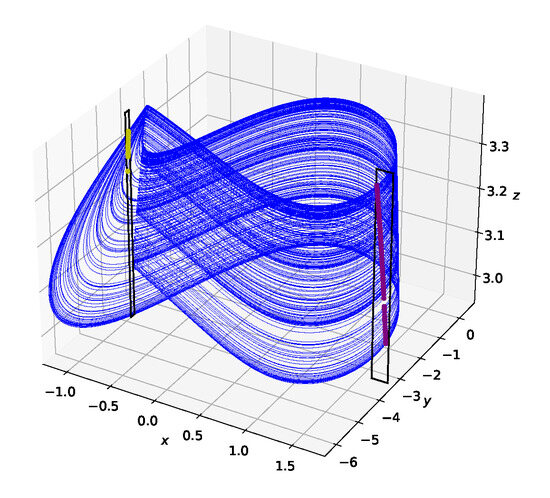
Figure 17.
Plot of the Hindmarsh-Rose dynamical system in chaotic regime with control planes [93]. Reproduced from John E. Parker and Kevin M. Short, “Cupolets in a chaotic neuron model”, Chaos 32, 113104 (2022) https://doi.org/10.1063/5.0101667 (accessed on 9 March 2024), with the permission of AIP Publishing.
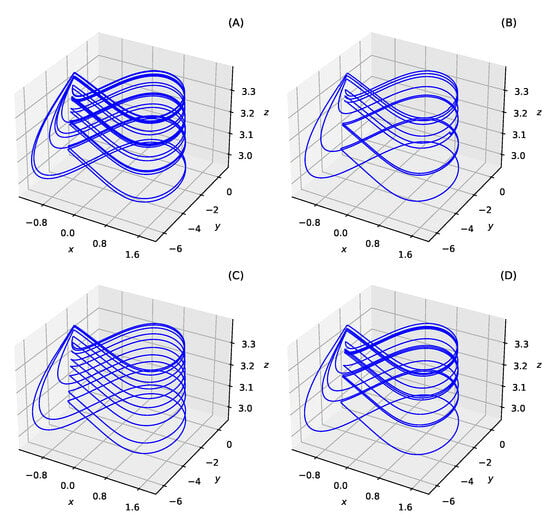
Figure 18.
Selection of Hindmarsh-Rose cupolets: (A) C11, (B) C0110, (C) C1010010, and (D) C01010010 [93]. Reproduced from John E. Parker and Kevin M. Short, “Cupolets in a chaotic neuron model”, Chaos 32, 113104 (2022) https://doi.org/10.1063/5.0101667 (accessed on 9 March 2024), with the permission of AIP Publishing.
One interesting discovery in the HR system was that not all cupolets were in one-to-one correspondence with the control codes. Instead, the development of the final cupolet was dependent on the initial condition, and such related cupolets were called homologous cupolets. The set of initial conditions that led to different homologs was similar to a fractal basin boundary. Cupolet C01000111 was found to support the greatest number of homologous cupolets, and Figure 19 shows four such multiplicities of this cupolet. One can see that some of the kicks along the control plane are large (e.g., Figure 19a, and this is related to the simpler structure of the HR attractor compared to the double scroll system and the fact that the associated function has several large flat plateaus [95].
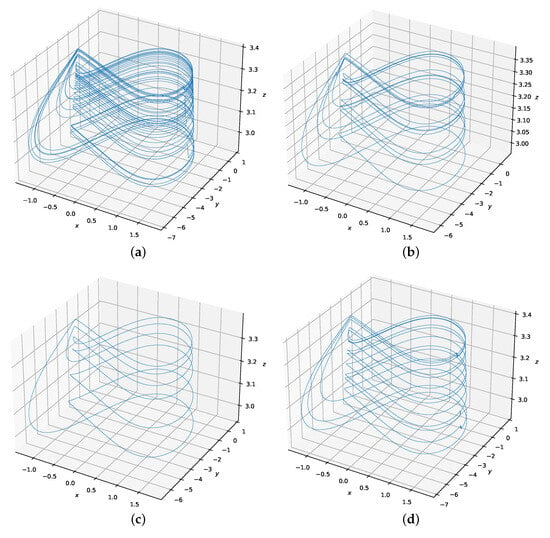
Figure 19.
(a–d) Homologous cupolets from the Hindmarsh-Rose system. All four cupolets derive from the control code 11100010, and the resulting cupolet is dependent on the initial condition.
In subsequent work, Short and Parker found that HR neurons could be made to mutually stabilize in a manner equivalent to that described previously in Section 9 on entangled cupolets. In this work, it was shown that when HR neurons communicate over a synapse, mediated by an interaction function, the interaction between HR neurons could be mutually stabilizing so that each separate neuron would converge onto a cupolet, and they would become locked into those cupolets by the interaction. This implies that the information passed into the HR neurons is trapped as long as the mutually stabilizing feedback loops continue—this may be an example of memory in a nonlinear system. This mutual stabilization was found in a variety of topologies and would be robust unless an interruption was injected into the system. The topologies considered include a bidirectional mutual stabilization between two HR neurons; stabilization that runs along a chain of HR neurons; and a chain feedback mutual stabilization where the output from the end of the chain of HR neurons feeds back to an earlier link in the chain, and stabilization ensues.
12. The Future of Cupolet Research
The research effort into cupolets has been very fruitful over the last 25 years. The simplicity of the control scheme and the abundance of stabilized cupolets have been surprising outcomes. In some sense, the discovery of cupolets amounts to allowing the chaotic system to tell us how it likes to behave, rather than going through an intensive control method that continually steers the trajectories back toward a desired outcome. The property that cupolets in the double scroll system are in (essentially) one-to-one correspondence with the control code and that the development of a given cupolet is independent of the initial conditions remains a remarkable and mysterious property of chaotic systems. It is true that some HR cupolets developed homologs that were not independent of initial conditions, but this work is still rather new and deserves further study. It may be that the function needed to be computed for greater values of P, or it could simply be that the attractor structure was simpler for the HR system. Further, while this paper focused on the double scroll system, with a brief mention of the HR system, cupolets have also been found in the Rössler and Lorenz systems, as well as in 2-D unimodal maps. These systems have not been studied as extensively, but it appears that the stabilization properties leading to cupolets may be common in chaotic systems. Certainly, it would be an interesting topic for further research.
The connections between chaotic entanglement and quantum entanglement remain interesting. The notion of a Hilbert space of states in quantum mechanics does not carry over to chaotic systems and may be misleading for chaotic systems since the chaotic systems are inherently nonlinear and the attractor geometry provides specific constraints. Future research may provide insight into how to use cupolets or UPOs to build up an appropriate mathematical formalism to replace Hilbert spaces for nonlinear problems.
The relationship between measurement, cupolet stabilization, and collapse of the wave function would be particularly intriguing if it could be tested in an experiment, but simply showing that interaction equals measurement in the context described here would be a conceptual advance. To explore the implications of spooky action at a distance, it would be useful to study the rates of decay of entanglement loss in quantum systems and compare it to what would occur in a chaotic entanglement scenario. Finally, in tests of quantum mechanics, the preparation of a consistent initial state is important to get clear results, but it is unclear how to do so from a classical perspective. It might be an interesting experiment to see if some sort of periodic pulsing of the initial state prior to an experiment can produce different results, with the assumption being that if the system exhibits some chaotic behavior, then the pulsing may cause the chaotic system to stabilize onto cupolets. In summary, since chaotic systems have the potential to entangle, future experiments in quantum entanglement should consider whether the results could have chaotic explanations.
One of the limitations of the cupolet research has been that the kicks along the control plane are effectively instantaneous. This information-theoretic approach allowed for much more extensive testing and the isolation of so many thousands of cupolets. However, to connect more closely with physical systems, these kicks should be converted to a distributed impulse over a small range, for example, in a thin region after the control plane. If this were implemented, then the perturbations would be fully continuous.
For the latest work on the HR neuron models, the use of kicks along the control planes is much more closely aligned with the expected behavior of neurons, since the signaling across a synapse is by impulses. Hence, it would not be surprising if these models were closer to a physical implementation. In fact, the initial use of integrate-and-fire interaction functions in the double scroll system was inspired by neuron behavior, so it has been rewarding to see that cupolets exist in HR neuron models as well. There remains a great deal of work that can be done in neuron models, including the incorporation of parameterized time delays in the feedback loops to examine more closely the impact on the development of mutual stabilization. Overall, it is intriguing to observe HR neurons locking into persistent states that might have some connection to memory. Perhaps the most exciting target for future work would be to examine the Hodgkin-Huxley model to see if it supports the development of cupolets and chaotic entanglement, since that model is more closely tied to the biophysiology and biochemistry of actual neurons.
There has been great interest in the development of quantum computers in the past decade. In particular, researchers have recently shown that the chaotic Belousov-Zhabotinsky reactions can be used in a manner similar to a quantum computer [96]. Another interesting avenue of future research would thus be to see if any quantum or chaotic computing frameworks could be designed around cupolets and their properties.
Author Contributions
All authors contributed equally. All authors have read and approved the final manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We would like to thank AIP and Springer Publishing for allowing us to reuse several figures. We would also like to thank the reviewers for their constructive feedback that further improved this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| APS | A. Parker and Short |
| CSPE | Complex Spectral Phase Evolution |
| FFT | Fast Fourier Transform |
| HGO | Hayes, Grebogi, and Ott |
| HR | Hindmarsh-Rose |
| MSC | Morena, Short, and Cooke |
| PS0 | Poincaré Surface 0 |
| PS1 | Poincaré Surface 1 |
References
- Carroll, T.; Pecora, L. Synchronizing chaotic circuits. IEEE Trans. Circuits Syst. 1991, 38, 453–456. [Google Scholar] [CrossRef]
- Cuomo, K.; Oppenheim, A. Chaotic signals and systems for communications. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Minneapolis, MN, USA, 27–30 April 1993. [Google Scholar] [CrossRef]
- Cuomo, K.; Oppenheim, A.; Strogatz, S. Synchronization of Lorenz-based chaotic circuits with applications to communications. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1993, 40, 626–633. [Google Scholar] [CrossRef]
- He, R.; Vaidya, P.G. Analysis and synthesis of synchronous periodic and chaotic systems. Phys. Rev. A 1992, 46, 7387–7392. [Google Scholar] [CrossRef]
- Wu, C.; Chua, L. A Simple Way to Synchronize Chaotic Systems with Applications to Secure Communication Systems. Int. J. Bifurc. Chaos 1993, 03, 1619–1627. [Google Scholar] [CrossRef]
- Hayes, S.; Grebogi, C.; Ott, E. Communicating with chaos. Phys. Rev. Lett. 1993, 70, 3031. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, T.; Chua, L.O.; Komuro, M. The double scroll. IEEE Trans. Circuits System 1985, 32, 797–818. [Google Scholar] [CrossRef]
- Chua, L.; Komuro, M.; Matsumoto, T. The double scroll family. IEEE Trans. Circuits Syst. 1986, 33, 1072–1118. [Google Scholar] [CrossRef]
- Chua, L.O.; Tichonicky, I. 1-D map for the double scroll family. IEEE Trans. Circuits Syst. 1991, 38, 233–243. [Google Scholar] [CrossRef]
- Komuro, M.; Tokunaga, R.; Matsumoto, T.; Chua, L.; Hotta, A. Global bifurcation analysis of the double scroll circuit. Int. J. Bifurc. Chaos 1991, 1, 139–182. [Google Scholar] [CrossRef]
- Short, K.M.; Morena, M.A. Signatures of quantum mechanics in chaotic systems. Entropy 2019, 21, 618. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Pecora, L.; Carroll, T. Synchronized chaotic signals and systems. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992. [Google Scholar] [CrossRef]
- Carroll, T.; Pecora, L. Synchronizing Chaotic Circuits. In Nonlinear Dynamics in Circuits; World Scientific: Singpore, 1991; Volume 38, pp. 215–248. [Google Scholar] [CrossRef]
- Cuomo, K.; Oppenheim, A.; Strogatz, S. Robustness and Signal Recovery in a Synchronized Chaotic System. Int. J. Bifurc. Chaos 1993, 03, 1629–1638. [Google Scholar] [CrossRef]
- Oppenheim, A.; Wornell, G.; Isabelle, S.; Cuomo, K. Signal processing in the context of chaotic signals. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992. [Google Scholar] [CrossRef]
- Halle, K.; Wu, C.; Itoh, M.; Chua, L. Spread Spectrum Communication through Modulation of Chaos. Int. J. Bifurc. Chaos 1993, 03, 469–477. [Google Scholar] [CrossRef]
- Kocarev, L.J.; Halle, K.S.; Eckert, K.; Chua, L.O.; Parlitz, U. Experimental Demonstration of Secure Communications via Chaotic Synchronization. Int. J. Bifurc. Chaos 1992, 02, 709–713. [Google Scholar] [CrossRef]
- Kocarev, L.J.; Parlitz, U. General approach for chaotic synchronization with applications to communication. Phys. Rev. Lett. 1995, 74, 5028. [Google Scholar] [CrossRef]
- Parlitz, U.; Chua, L.; Kocarev, L.J.; Halle, K.; Shang, A. Transmission of Digital Signals by Chaotic Synchronization. Int. J. Bifurc. Chaos 1992, 02, 973–977. [Google Scholar] [CrossRef]
- Rulkov, N.; Sushchik, M.; Tsimring, L.; Abarbanel, H. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980–994. [Google Scholar] [CrossRef]
- Short, K.M. Detection of Teleseismic Events in Seismic Sensor Data Using Nonlinear Dynamic Forecasting. Int. J. Bifurc. Chaos 1997, 7, 1833–1845. [Google Scholar] [CrossRef]
- Short, K. Computational issues in unmasking chaotic communications. In Proceedings of the Physics Computing ’95 Conference, Pittsburg, PA, USA, 5–7 June 1995. Invited Paper. [Google Scholar]
- Short, K.M. Steps Toward Unmasking Secure Communications. Int. J. Bifurc. Chaos 1994, 04, 959–977. [Google Scholar] [CrossRef]
- Short, K.M. Signal Extraction from Chaotic Communications. In. J. Bifurc. Chaos 1997, 07, 1579–1597. [Google Scholar] [CrossRef]
- Short, K.M. Unmasking a Modulated Chaotic Communications Scheme. In. J. Bifurc. Chaos 1996, 06, 367–375. [Google Scholar] [CrossRef]
- Short, K.M.; Parker, A.T. Unmasking a hyperchaotic communication scheme. Phys. Rev. E 1998, 58, 1159–1162. [Google Scholar] [CrossRef]
- Parker, A.T.; Short, K.M. Reconstructing the keystream from a chaotic encryption scheme. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 624–630. [Google Scholar] [CrossRef]
- Pérez, G.; Cerdeira, H. Extracting messages masked by chaos. Phys. Rev. Lett. 1995, 74, 1970–1973. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Proceedings of the Dynamical Systems and Turbulence, Warwick 1980: Proceedings of a Symposium Held at the University of Warwick 1979/80; Springer: Berlin, Germany, 2006; pp. 366–381. [Google Scholar]
- Pierson, D.; Moss, F. Detecting Periodic Unstable Points in Noisy Chaotic and Limit Cycle Attractors with Applications to Biology. Phys. Rev. Lett. 1995, 75, 2124–2127. [Google Scholar] [CrossRef] [PubMed]
- Auerbach, D.; Cvitanović, P.; Eckmann, J.; Gunaratne, G.; Procaccia, I. Exploring chaotic motion through periodic orbits. Phys. Rev. Lett. 1987, 58, 2387–2389. [Google Scholar] [CrossRef]
- So, P.; Ott, E.; Schiff, S.J.; Kaplan, D.T.; Sauer, T.; Grebogi, C. Detecting unstable periodic orbits in chaotic experimental data. Phys. Rev. Lett. 1996, 76, 4705. [Google Scholar] [CrossRef]
- Grebogi, C.; Ott, E.; Yorke, J.A. Unstable periodic orbits and the dimensions of multifractal chaotic attractors. Phys. Rev. A 1988, 37, 1711. [Google Scholar] [CrossRef]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling Chaos. Phys. Rev. Lett. 1990, 64, 1196–1199. [Google Scholar] [CrossRef]
- Hayes, S.; Grebogi, C.; Ott, E.; Mark, A. Experimental control of chaos for communication. Phys. Rev. Lett. 1994, 73, 1781–1784. [Google Scholar] [CrossRef]
- Bainov, D.; Lakshmikantham, V.; Simeonov, P. Theory of Impulsive Differential Equations; World Scientific Publishing Company: Singapore, 1989. [Google Scholar]
- Stojanovski, T.; Kocarev, L.; Parlitz, U. Driving and synchronizing by chaotic impulses. Phys. Rev. E 1996, 54, 2128–2131. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Yang, L.B.; Yang, C.M. Impulsive control of Lorenz system. Phys. D Nonlinear Phenom. 1997, 110, 18–24. [Google Scholar] [CrossRef]
- Yang, T.; Yang, C.M.; Yang, L.B. Control of Rössler system to periodic motions using impulsive control methods. Phys. Lett. A 1997, 232, 356–361. [Google Scholar] [CrossRef]
- Parker, A.T.; Short, K.M. An Impulsively initialized, digital chaotic communication scheme. Paper presented at the 1999 Joint Mathematics Meetings, San Antonio, TX, USA, 13–16 January 1999. [Google Scholar]
- Parker, A.T. Topics in Chaotic Secure Communication. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, 1999. [Google Scholar]
- Parker, A.T.; Short, K.M. Method and Apparatus for Secure Digital Chaotic Communication. U.S. Patent 6,363,153, 26 March 2002. [Google Scholar]
- Short, K.M. Method and Apparatus for Remote Digital Key Generation. U.S. Patent 7,440,570, 21 October 2008. [Google Scholar]
- Short, K.M.; Hussey, D.; Johnson, K. Method and Apparatus for Compressed Chaotic Music Synthesis. U.S. Patent 6,137,045, 24 October 2000. [Google Scholar]
- Nelson, D.J.; Short, K.M. A Channelized Cross Spectral Method for Improved Frequency Resolution. In Proceedings of the 1998 IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, Pittsburgh, PA, USA, 6–9 October 1998. [Google Scholar]
- Short, K.M.; Garcia, R.A. Signal Analysis Using the Complex Spectral Phase Evolution (CSPE) Method. In Proceedings of the AES 120th Convention, Paris, France, 20–23 May 2006; p. 6645. [Google Scholar]
- Short, K.M.; Garcia, R.A. Accurate Low-Frequency Magnitude and Phase Estimation in the Presence of DC and Near-DC Aliasing. In Proceedings of the AES 121st Convention, San Francisco, CA, USA, 5–8 October 2006; p. 6934. [Google Scholar]
- Short, K.M.; Garcia, R.A.; Daniels, M.L. Multichannel Audio Processing Using a Unified-Domain Representation. In Proceedings of the AES 119 Convention, New York, NY, USA, 7–10 October 2005; p. 6526. [Google Scholar]
- Short, K.M. Frequency Domain Phase Model of Transient Events. In Proceedings of the AES 121st Convention, San Francisco, CA, USA, 5–8 October 2006; p. 6935. [Google Scholar]
- Short, K.M. Method and Apparatus for the Compression and Decompression of Audio Files Using a Chaotic System. U.S. Patent 7,215,776, 2007. [Google Scholar]
- Short, K.M.; Garcia, R.A.; Daniels, M.L.; Curley, J.; Glover, M. An Introduction to the KOZ scalable audio compression technology. In Proceedings of the AES 118th Convention, Barcelona, Spain, 28–31 May 2005; p. 6446. [Google Scholar]
- Short, K.M.; Garcia, R.A.; Daniels, M.L. Scalability in KOZ audio compression technology. In Proceedings of the AES 119th Convention, New York, NY, USA, 7–10 October 2005; p. 6598. [Google Scholar]
- Chaoticom. Mobile Music Con 2003 Award. 2003; Chaoticom wins “Best Mobile Music Technology” and “Best Mobile Music Downloading Solution”. [Google Scholar]
- Chaoticom. Mobile Entertainment Forum Award. 2004. Chaoticom wins “Best Contribution to Mobile Music 2004” and “Best in Show”. Available online: https://www.etnow.com/news/2004/6/winners-announced-for-the-first-mef-mobile-entertainment-awards (accessed on 24 April 2024).
- Chaoticom. Cellular Telephone Industries Association (CTIA) Mobile Music Awards. 2004; Chaoticom wins “Most Innovative Mobile Music Application”. [Google Scholar]
- Groove Mobile. Fierce Mobile Top App Award. 2006. Groove Mobile wins Top App Award from Fierce Mobile for Sprint Music Store powered by Groove Mobile. Available online: https://www.globenewswire.com/Tr/news-release/2006/09/13/348207/6671/en/FierceMobileContent-Announces-Top-10-Applications-for-Wireless-Devices.html (accessed on 24 April 2024).
- Short, K.M. Method and Apparatus for the Compression and Decompression of Image Files Using a Chaotic System. U.S. Patent 7,110,547, 2006. [Google Scholar]
- Zarringhalam, K. CUPOLETS: Chaotic Unstable Periodic Orbits Theory and Applications. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, 2007. [Google Scholar]
- Zarringhalam, K.; Short, K.M. Generating an adaptive multiresolution image analysis with compact cupolets. Nonlinear Dyn. 2008, 52, 51–70. [Google Scholar] [CrossRef]
- Short, K.M.; Zarringhalam, K. Systems and Methods for Adaptive Multiresolution Signal Analysis with Compact Cupolets. US Patent 8,249,374, 2012. [Google Scholar]
- Hammel, S.M.; Yorke, J.A.; Grebogi, C. Do numerical orbits of chaotic dynamical processes represent true orbits? J. Complex. 1987, 3, 136–145. [Google Scholar] [CrossRef]
- Hammel, S.; Yorke, J.A.; Grebogi, C. Numerical orbits of chaotic processes represent true orbits. Bull. Am. Math. Soc. 1988, 19, 465–469. [Google Scholar] [CrossRef][Green Version]
- Grebogi, C.; Hammel, S.M.; Yorke, J.A.; Sauer, T. Shadowing of physical trajectories in chaotic dynamics: Containment and refinement. Phys. Rev. Lett. 1990, 65, 1527–1530. [Google Scholar] [CrossRef]
- Hayes, W.B.; Jackson, K.R. Rigorous Shadowing of Numerical Solutions of Ordinary Differential Equations by Containment. SIAM J. Numer. Anal. 2003, 41, 1948–1973. [Google Scholar] [CrossRef]
- Hayes, W.; Jackson, K.R. A survey of shadowing methods for numerical solutions of ordinary differential equations. Appl. Numer. Math. 2005, 53, 299–321. [Google Scholar] [CrossRef]
- Coomes, B.A.; Koçak, H.; Palmer, K.J. Shadowing orbits of ordinary differential equations. J. Comput. Appl. Math. 1994, 52, 35–43. [Google Scholar] [CrossRef]
- Coomes, B.; Koçak, H.; Palmer, K. Long periodic shadowing. Numer. Algorithms 1997, 14, 55–78. [Google Scholar] [CrossRef]
- Morena, M.A.; Short, K.M.; Cooke, E.E. Controlled transitions between cupolets of chaotic systems. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 013111. [Google Scholar] [CrossRef]
- Macau, E.E.; Grebogi, C. Control of chaos and its relevancy to spacecraft steering. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 2463–2481. [Google Scholar] [CrossRef]
- Morena, M.A.; Short, K.M. Fundamental cupolets of chaotic systems. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 093114. [Google Scholar] [CrossRef]
- Morena, M.A.; Short, K.M. On the Potential for Entangled States Between Chaotic Systems. In. J. Bifurc. Chaos 2014, 24, 1450077. [Google Scholar] [CrossRef]
- Morena, M.A. Mutual Stabilization of Chaotic Systems through Entangled Cupolets. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, 2014. [Google Scholar]
- Racicot, D.M.; Longtin, A. Interspike interval attractors from chaotically driven neuron models. Phys. D Nonlinear Phenom. 1997, 104, 184–204. [Google Scholar] [CrossRef]
- Morena, M.A.; Short, K.M. Chaotic Entanglement: Entropy and Geometry. Entropy 2021, 23, 1254. [Google Scholar] [CrossRef]
- Short, K.M.; Parker, A.T. Security Issues In Chaotic Communications. Paper presented at the SIAM Conference on Dynamical Systems, Snowbird, UT, USA, 23–27 May 1999. [Google Scholar]
- Habib, S.; Shizume, K.; Zurek, W.H. Decoherence, chaos, and the correspondence principle. Phys. Rev. Lett. 1998, 80, 4361. [Google Scholar] [CrossRef]
- Ghose, S.; Stock, R.; Jessen, P.; Lal, R.; Silberfarb, A. Chaos, entanglement, and decoherence in the quantum kicked top. Phys. Rev. A 2008, 78, 042318. [Google Scholar] [CrossRef]
- Chaudhury, S.; Smith, A.; Anderson, B.; Ghose, S.; Jessen, P. Quantum signatures of chaos in a kicked top. Nature 2009, 461, 768. [Google Scholar] [CrossRef]
- Heller, E.J. Bound-state eigenfunctions of classically chaotic Hamiltonian systems: Scars of periodic orbits. Phys. Rev. Lett. 1984, 53, 1515. [Google Scholar] [CrossRef]
- Berry, M. Quantum scars of classical closed orbits in phase space. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1989, 423, 219–231. [Google Scholar] [CrossRef]
- Doya, V.; Legrand, O.; Mortessagne, F.; Miniatura, C. Light scarring in an optical fiber. Phys. Rev. Lett. 2001, 88, 014102. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.; Doya, V.; Legrand, O.; Mortessagne, F. Selective amplification of scars in a chaotic optical fiber. Phys. Rev. Lett. 2007, 99, 224101. [Google Scholar] [CrossRef] [PubMed]
- Fujisaki, H.; Miyadera, T.; Tanaka, A. Dynamical aspects of quantum entanglement for weakly coupled kicked tops. Phys. Rev. E 2003, 67, 066201. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ghose, S.; Sanders, B.; Hu, B. Entanglement as a signature of quantum chaos. Phys. Rev. E 2004, 70, 016217. [Google Scholar] [CrossRef] [PubMed]
- McHarris, W. Chaos and the quantum: How nonlinear effects can explain certain quantum paradoxes. J. Phys. Conf. Ser. 2011, 306, 012050. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Fitzhugh, R. Thresholds and Plateaus in the Hodgkin-Huxley Nerve Equations. J. Gen. Physiol. 1960, 43, 867–896. [Google Scholar] [CrossRef]
- Fitzhugh, R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Parker, J.E.; Short, K.M. Sigmoidal synaptic learning produces mutual stabilization in chaotic FitzHugh–Nagumo model. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 063108. [Google Scholar] [CrossRef] [PubMed]
- Hindmarsh, J.L.; Rose, R.M. A Model of Neuronal Bursting Using Three Coupled First Order Differential Equations. PRoceedings R. Soc. Lond. B Ser. Biol. Sci. 1984, 221, 87–102. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.E.; Short, K.M. Cupolets in a chaotic neuron model. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 113104. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.E.; Short, K.M. Mutual Stabilization in Chaotic Hindmarsh–Rose Neurons. Dynamics 2023, 3, 282–298. [Google Scholar] [CrossRef]
- Parker, J. Existence of Mutual Stabilization in Chaotic Neural Models. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, 2021. [Google Scholar]
- Sharma, A.; Ng, M.T.K.; Parrilla Gutierrez, J.M.; Jiang, Y.; Cronin, L. A programmable hybrid digital chemical information processor based on the Belousov-Zhabotinsky reaction. Nat. Commun. 2024, 15, 1984. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).