Artificial Intelligence Modeling of the Heterogeneous Gas Quenching Process for Steel Batches Based on Numerical Simulations and Experiments
Abstract
1. Introduction
Outline of This Paper
2. Research Methodology
2.1. Materials
2.2. Sample Geometry
2.3. Experimental Setup with Measuring Techniques and Experimental Plan
3. Experimental Analysis
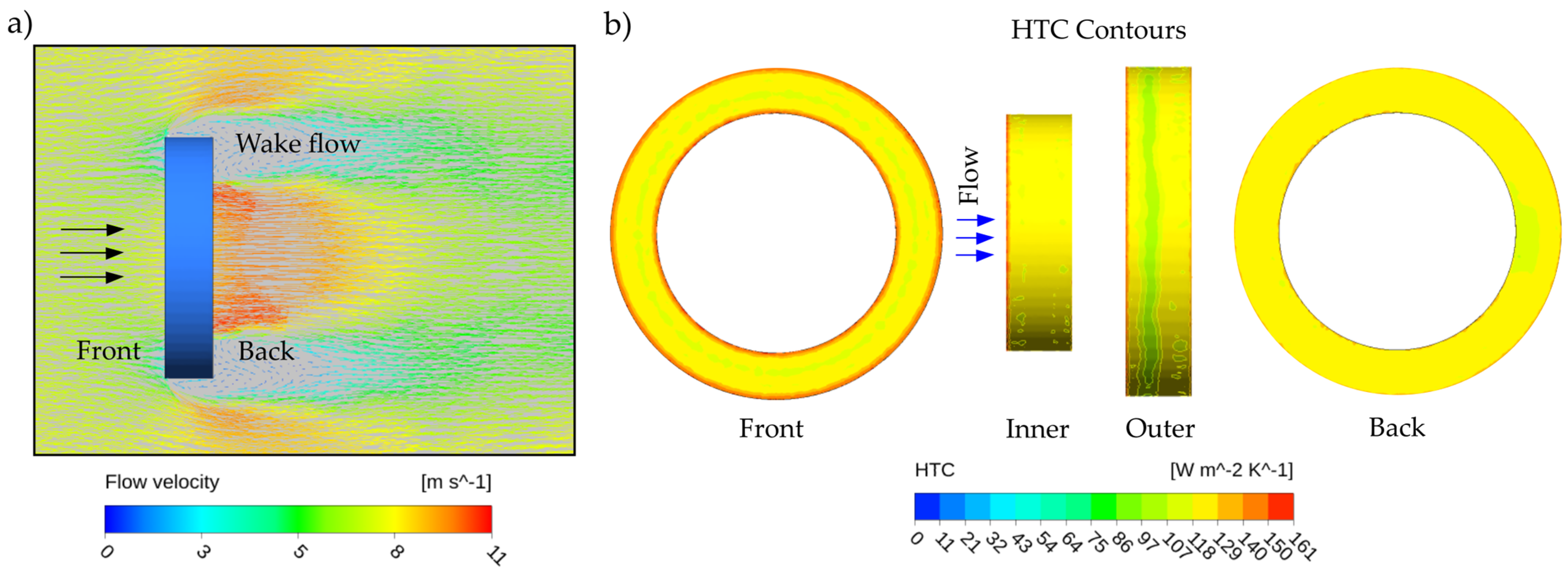
3.1. Determination of Flow Velocity and HTC in Wind Tunnel
3.2. Analysis of Flow Field within the Model Chamber
3.3. Quenching Trend within Batch and Probes
3.4. Influence of Gas Pressure, Probe Geometry, and Probe Material on Quenching
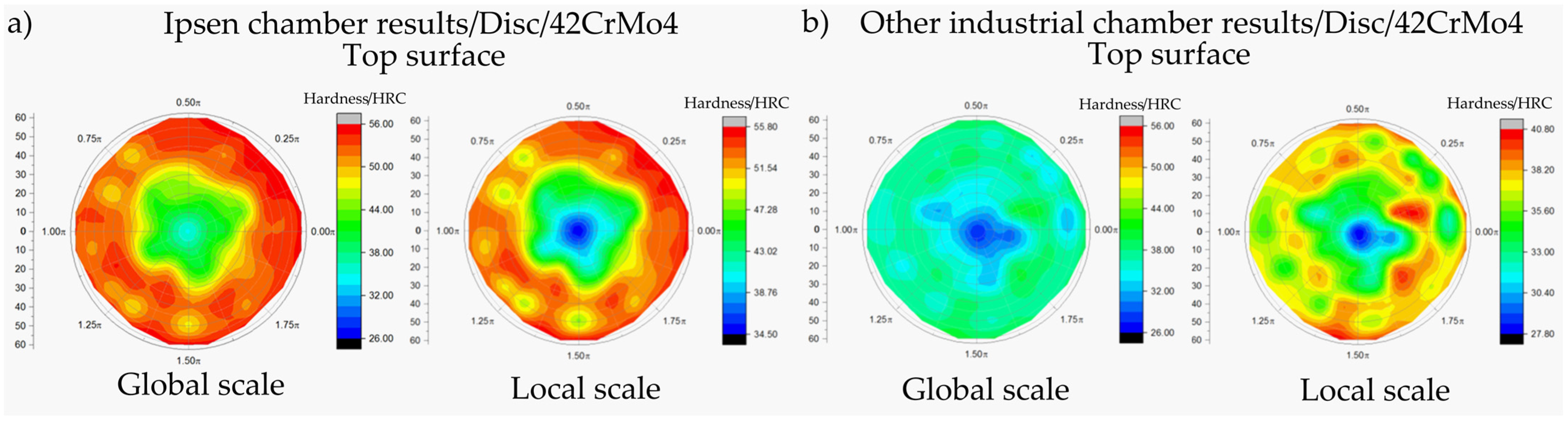
3.5. Influence of Quenching Parameters on Material Hardness
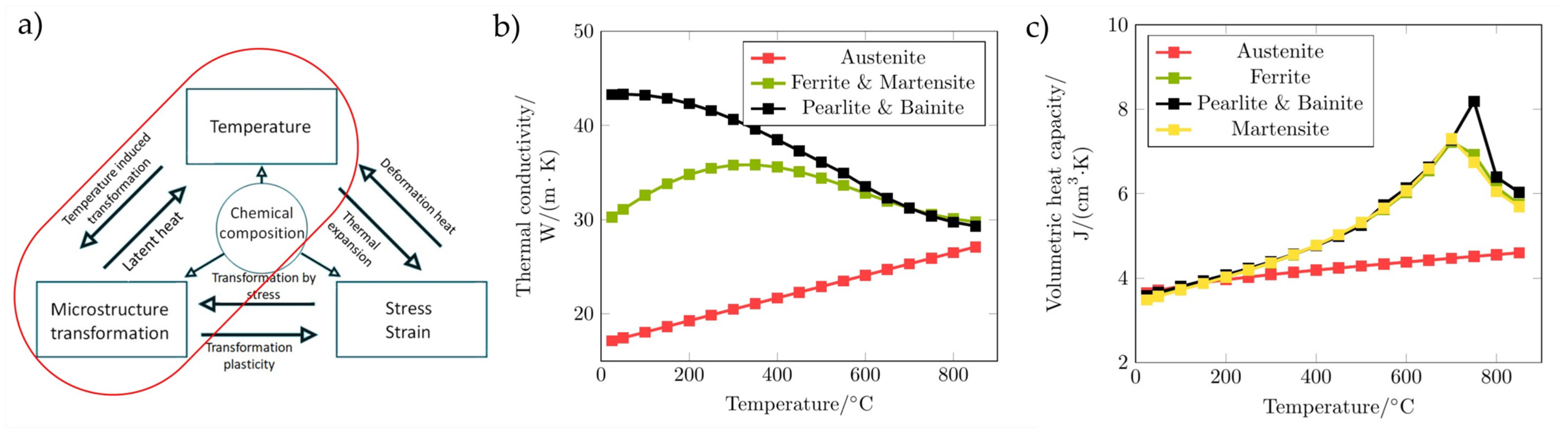
4. Numerical Modeling (CFD, FEM) and Artificial Neural Networking (ANN)
4.1. Computational Fluid Dynamics (CFD)
4.2. Finite Element Method (FEM)
4.3. Artificial Neural Network (ANN)
5. Discussion of Simulation Results
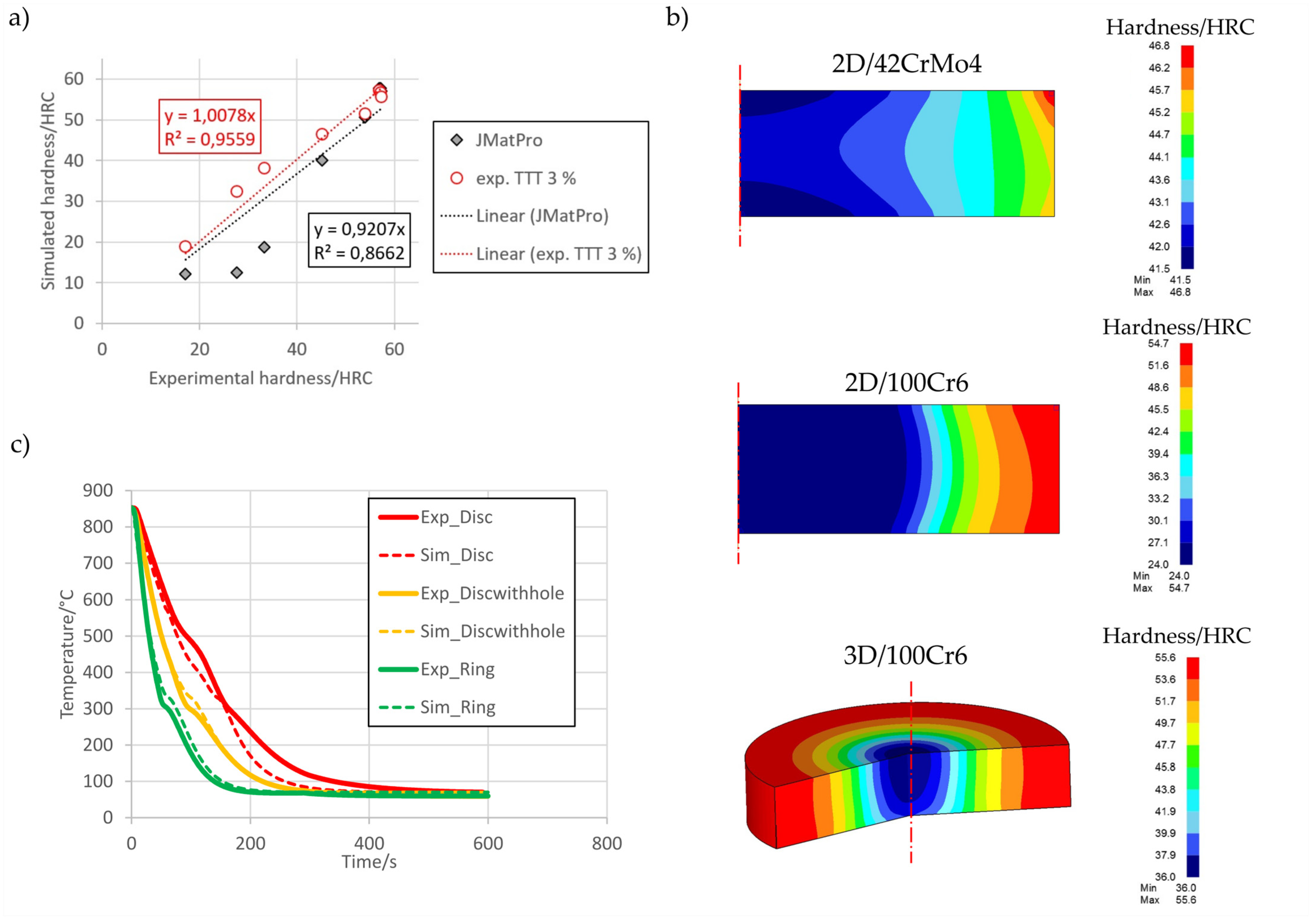
5.1. Validation of Numerical Model (CFD) and Numerical Results
5.2. Correlation for HTC
5.3. Results from FEM Modeling
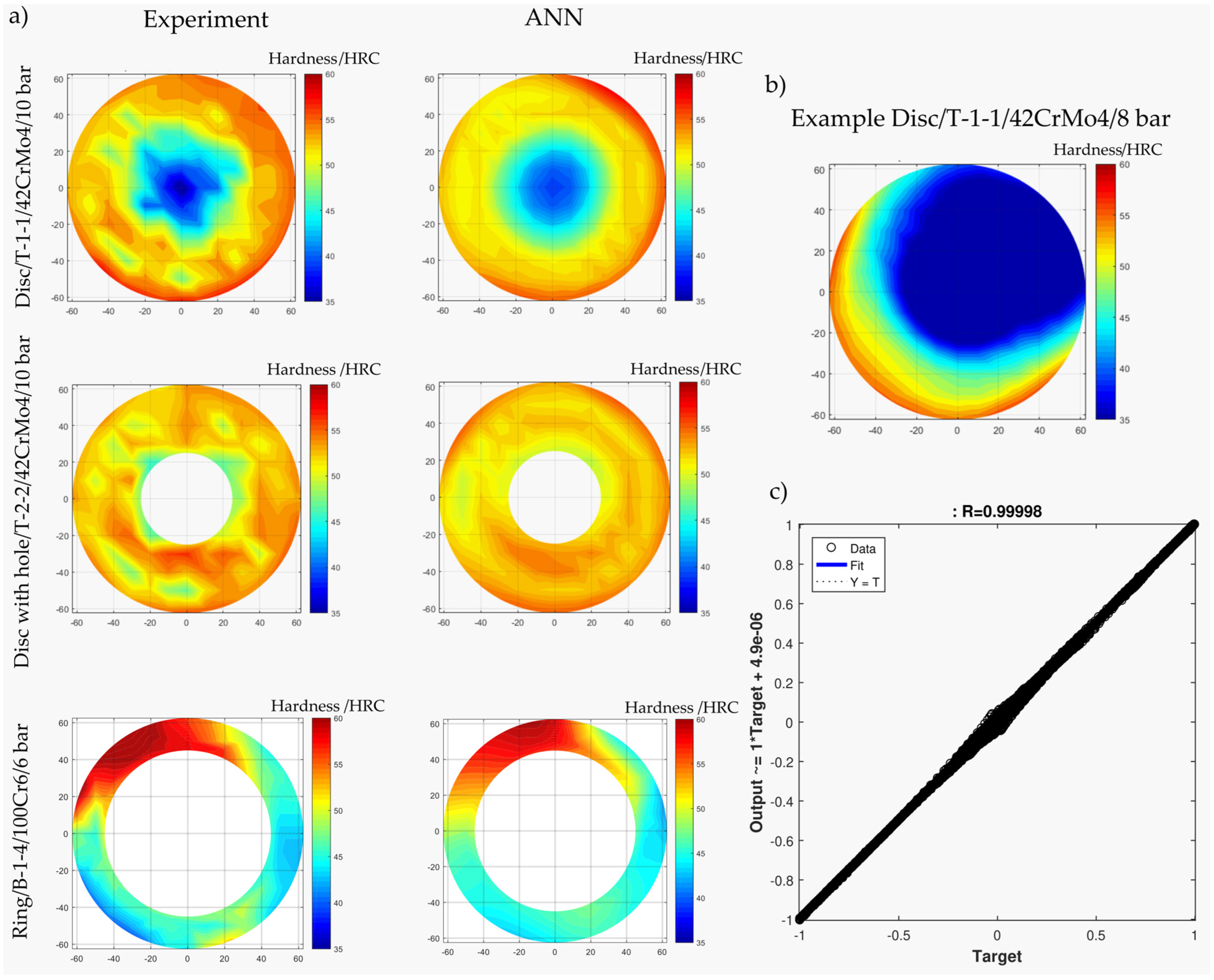
5.4. Results from ANN Modeling
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmidt, R.R. Zur Thermo-Fluid-Dynamik beim Hochdruckgasabschrecken: Experimentelle und Numerische Analyse der Hochdruckgasabschreckung Metallischer Bauteile zur Steigerung von Prozesshomogenität und-Intensität. Ph.D. Thesis, Fachbereich Produktionstechnik, Universität Bremen, Bremen, Germany, 2013. [Google Scholar]
- Bucquet, T.; Fritsching, U. Evaluating Heat Transfer Conditions in Gas Cooling for Complex Specimen Geometries. HTM J. Heat Treat. Mater. 2014, 69, 148–154. [Google Scholar] [CrossRef]
- Stephan, P.; Kabelac, S.; Kind, M.; Mewes, D.; Schaber, K.; Wetzel, T. VDI-Wärmeatlas (Fachlicher Träger VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen); Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Jung, M.; Lee, S.-J.; Lee, W.-B.; Moon, K.I. Finite Element Simulation and Optimization of Gas-Quenching Process for Tool Steels. J. Mater. Eng. Perform. 2018, 27, 4355–4363. [Google Scholar] [CrossRef]
- Bucquet, T. Flow Conditioning in Heat Treatment by Gas and Spray Quenching. Ph.D. Thesis, Produktionstechnik, Universität Bremen, Bremen, Germany, 2017. [Google Scholar]
- Narayan, N.M.; Moqadam, S.I.; Ellendt, N.; Fritsching, U. Multiphase numerical modeling and investigation of heat transfer for quenching of spherical particles in liquid pool. Int. J. Therm. Sci. 2023, 186, 108016. [Google Scholar] [CrossRef]
- Narayan, N.M.; Gopalkrishna, S.B.; Mehdi, B.; Ryll, S.; Specht, E.; Fritsching, U. Multiphase numerical modeling of boiling flow and heat transfer for liquid jet quenching of a moving metal plate. Int. J. Therm. Sci. 2023, 194, 108587. [Google Scholar] [CrossRef]
- Ferrari, J.; Lior, N.; Slycke, J. An evaluation of gas quenching of steel rings by multiple-jet impingement. J. Mater. Process. Technol. 2003, 136, 190–201. [Google Scholar] [CrossRef]
- Lior, N. The cooling process in gas quenching. J. Mater. Process. Technol. 2004, 155–156, 1881–1888. [Google Scholar] [CrossRef]
- Elkatatny, I.; Blicblau, A.S.; Das, S.; Doyle, E.D. Numerical analysis and experimental validation of high pressure gas quenching. Int. J. Therm. Sci. 2003, 42, 417–423. [Google Scholar] [CrossRef]
- Lior, N.; Papadopoulos, D. Gas-Cooling of Multiple Short Inline Disks in Flow along Their Axis. J. ASTM Int. 2008, 6, JAI101849. [Google Scholar] [CrossRef]
- Wang, J.; Gu, J.; Shan, X.; Hao, X.; Chen, N.; Zhang, W. Numerical simulation of high pressure gas quenching of H13 steel. J. Mater. Process. Technol. 2008, 202, 188–194. [Google Scholar] [CrossRef]
- Sugimoto, T.; Qin, M.; Watanabe, Y. Computational Study of Gas Quenching on Carburizing Hypoid Ring Gear. BHM Berg Hüttenmännische Monatshefte 2006, 151, 456–461. [Google Scholar] [CrossRef]
- Narayan, N.M.; Landgraf, P.; Lampke, T.; Fritsching, U. Experimental and numerical investigation of heterogenous gas quenching for determining optimal heat treatment parameters. In Proceedings of the 27th IFHTSE Congress and European Conference on Heat Treatment, Salzburg, Austria, 5–8 September 2022; pp. 81–87. [Google Scholar]
- Landgraf, P.M.; Narayan, N.M.; Fritsching, U.; Lampke, T. Development of a prognosis tool to predict heat treatment results for heterogeneous gas quenching of steels. In Proceedings of the 31st International Conference on Metallurgy and Materials, Brno, Czech Republic, 18–19 May 2022; pp. 395–401. [Google Scholar] [CrossRef]
- Wróbel, J.; Kulawik, A.; Bokota, A. Artificial Neural Network to the Control of the Parameters of the Heat Treatment Process of Casting. Arch. Foundry Eng. 2015, 15, 119–124. [Google Scholar] [CrossRef]
- Wróbel, J.; Kulawik, A. Calculations of the heat source parameters on the basis of temperature fields with the use of ANN. Neural Comput. Appl. 2018, 31, 7583–7593. [Google Scholar] [CrossRef]
- Muñoz-Rodenas, J.; García-Sevilla, F.; Coello-Sobrino, J.; Martínez-Martínez, A.; Miguel-Eguía, V. Effectiveness of Machine-Learning and Deep-Learning Strategies for the Classification of Heat Treatments Applied to Low-Carbon Steels Based on Microstructural Analysis. Appl. Sci. 2023, 13, 3479. [Google Scholar] [CrossRef]
- Chong, Z.S.; Wilcox, S.; Ward, J. The Use of Artificial Intelligence in the Modelling and Heat Treatment Parameters Identification for Alloy-Steel Re-Heating Process. In Proceedings of the Volume 1: 20th Biennial Conference on Mechanical Vibration and Noise, Parts A, B, and C, Long Beach, CA, USA, 24–28 September 2005. [Google Scholar]
- Opel, L. Kalibration einer Oberflächensonde; Studienarbeit; Universität Bremen: Bremen, Germany, 2008. [Google Scholar]
- Glue-on Filmprobe. Available online: https://www.dantecdynamics.com/components/hot-wire-and-hot-film-probes/miscellaneous-probes/ (accessed on 20 November 2023).
- XY Positioning Stage. Available online: https://www.optosigma.com/ (accessed on 20 November 2023).
- Datalogger. Available online: https://www.flukeprocessinstruments.com/ (accessed on 20 November 2023).
- Tell, J. Entwicklung eines Strömungs-Messystemes zur Qualifizierung von Gas Abschreckprozessen. Diploma Thesis, Productionstechnik, Universität Bremen, Bremen, Germany, 2012. [Google Scholar]
- ANSYS. ANSYS ICEM CFD User Manual; ANSYS: Canonsburg, PA, USA, 2012. [Google Scholar]
- ANSYS. ANSYS Fluent User’s Guide; ANSYS: Canonsburg, PA, USA, 2018. [Google Scholar]
- Kempf, A. Lecture Manuscript for Turbulence; University of Duisburg-Essen: Essen, Germany, 2015. [Google Scholar]
- Baehr, H.D.; Stephan, K. Wärme- und Stoffübertragung; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Schulze, P.; Schmidl, E.; Halle, T.; Lampke, T. Simulation der Wärmebehandlung von Stahl unter Berücksichtigung der Gefügeentwicklung. In Proceedings of the Energy-Efficient Technologies in Production ICMC 2014, Chemitz, Germany, 7–11 July 2014. [Google Scholar]
- DEFORM-3D v10.2, User’s manual, Columbus, Ohio. Available online: https://www.deform.com (accessed on 20 November 2023).
- JMatPro. Available online: https://www.sentesoftware.co.uk/site-media (accessed on 17 March 2024).
- Diemar, A. Simulation des Einsatzhärtens und Abschätzung der Dauerfestigkeit einsatzgehärteter Bauteile. Ph.D. Thesis, Bauhaus-Universität, Weimar, Germany, 2007. [Google Scholar]
- Macchion, O.; Zahrai, S.; Bouwman, J.W. Heat transfer from typical loads within gas quenching furnace. J. Mater. Process. Technol. 2006, 172, 356–362. [Google Scholar] [CrossRef]









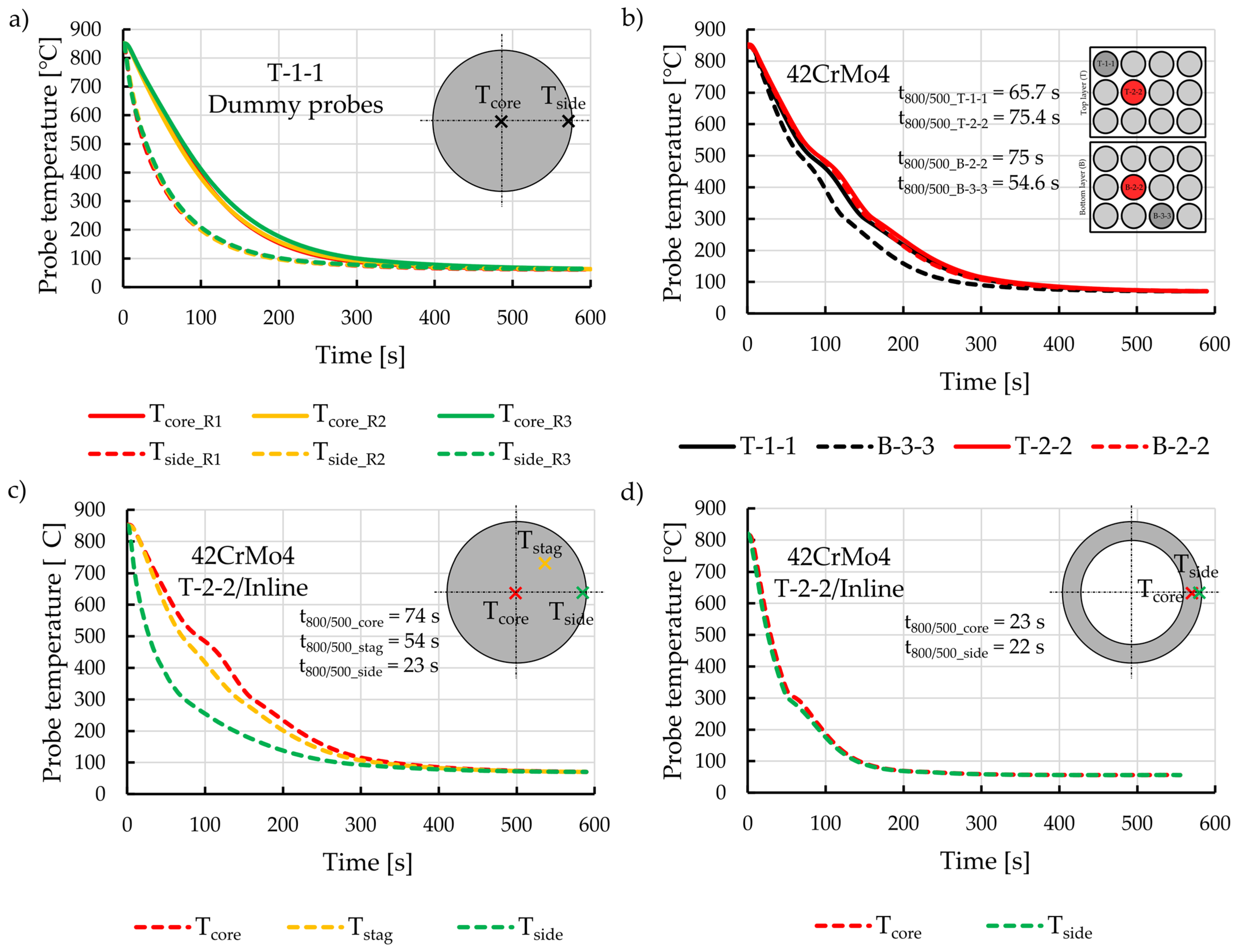











| Experimental Setup | Suction Wind Tunnel | Model Chamber |
|---|---|---|
| Probe | Disc | Disc, disc with hole, and ring |
| Material | Plastic (PVC) | Plastic (PVC) |
| Quenching fluid | Air at 1 atm | Air at 1 atm |
| Configuration | Single | Inline and staggered (Two layered) |
| Measurement | Flow velocity and HTC | Flow velocity/contour |
| Probe and measurement frequency | Film probe (100 Hz), 1D-CTA (500 Hz), pitot tube (1 Hz) | 1D-CTA (1000 Hz) |
| Wire temperature (Twire) | 100 °C | 150 °C |
| Mean flow velocity (Vavg) | 7.8, 9.8, and 12 m/s | 2.5, 5.1, and 6.2 m/s |
| Distance between probes | Not applicable | 5 mm |
| Distance between layers (supports) within the frame | Not applicable | 50 mm |
| Probes | Disc, disc with hole and ring |
| Material | 42CrMo4 and 100Cr6 |
| Quenching fluid | Nitrogen gas (N2) |
| Configuration | Inline/staggered—two layered |
| Measurement | Temperature |
| Furnace temperature (Tf) | 850 °C |
| Gas pressure (P) | 10 and 6 bar |
| Flow velocity (V) | 13.4 m/s (2970 1/Min) |
| Furnace hold time (tf) | 75 min |
| Measuring frequency | 3 Hz |
| Distance between probes | 5 mm |
| Distance between layers (supports) within the frame | 35 mm |
| Sl. No | Probe | Configuration | Pressure (bar) Vavg = 13.4 m/s | Minimum Cooling Rate from Batch (°C/s) | Maximum Cooling Rate from Batch (°C/s) | Average Cooling Rate from Batch (°C/s) |
|---|---|---|---|---|---|---|
| 1 | Disc | Inline | 10 | 4 | 5.49 | 4.52 |
| 2 | Disc | Staggered | 10 | 4.33 | 5.41 | 4.68 |
| 3 | Disc | Inline | 6 | 2.99 | 3.83 | 3.30 |
| 4 | Disc with hole | Inline | 10 | 7.32 | 9.09 | 8.05 |
| 5 | Disc with hole | Staggered | 10 | 8.47 | 9.52 | 8.96 |
| 6 | Disc with hole | Inline | 6 | 5.95 | 7.25 | 6.51 |
| 7 | Ring | Inline | 10 | 11.54 | 13.64 | 12.68 |
| 8 | Ring | Staggered | 10 | 11.76 | 14.49 | 12.89 |
| 9 | Ring | Inline | 6 | 7.94 | 10.99 | 9.55 |
| Probes | Disc, Ring |
| Material | 42CrMo4 |
| Quenching fluid | Air |
| Pressure (bar) | 1 |
| Flow velocity (m/s) | 7.8, 9.8, and 12 |
| Probe temperature (Tprobe) | 100 °C (373.15 K) |
| Air temperature (Tair) | 18 °C (291.15 K) |
| Probes | Disc, disc with hole, and ring |
| Configuration | Inline and staggered (two layered) |
| Material | 42CrMo4 |
| Quenching fluid | Nitrogen gas (N2) |
| Pressure (bar) | 6, 8 and 10 |
| Flow velocity (m/s) | 8, 10 and 13.4 |
| Probe temperature (Tprobe) | 850 °C (1123.15 K) |
| Gas temperature (TN2) | 70 °C (343.15 K) |
| 42CrMo4 (AISI4140) | Hardness/HRC |
| Austenite/Ferrite | 10 |
| Pearlite | 20 |
| Bainite | 42 |
| Martensite | 60 |
| Sl. No | Probe | Configuration | Gas Pressure (Bar) | Flow Velocity (m/s) | Minimum HTC from Batch (W/m2K) | Maximum HTC from Batch (W/m2K) |
|---|---|---|---|---|---|---|
| 1 | Disc | Inline | 10 | 13.4 | 357 | 2103 |
| 2 | Disc | Staggered | 10 | 13.4 | 393 | 2563 |
| 3 | Disc | Inline | 10 | 10 | 284 | 1670 |
| 4 | Disc | Inline | 10 | 8 | 240 | 1378 |
| 5 | Disc | Inline | 8 | 13.4 | 299 | 1749 |
| 6 | Disc | Inline | 6 | 13.4 | 210 | 1208 |
| 7 | Disc with hole | Inline | 10 | 13.4 | 279 | 1776 |
| 8 | Disc with hole | Staggered | 10 | 13.4 | 310 | 2016 |
| 9 | Disc with hole | Inline | 8 | 13.4 | 229 | 1481 |
| 10 | Disc with hole | Inline | 6 | 13.4 | 155 | 1037 |
| 11 | Ring | Inline | 10 | 13.4 | 318 | 1289 |
| 12 | Ring | Staggered | 10 | 13.4 | 307 | 1440 |
| 13 | Ring | Inline | 10 | 10 | 251 | 1013 |
| 14 | Ring | Inline | 10 | 8 | 210 | 910 |
| 15 | Ring | Inline | 8 | 13.4 | 264 | 1065 |
| 16 | Ring | Inline | 6 | 13.4 | 182 | 809 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narayan, N.M.; Landgraf, P.M.; Lampke, T.; Fritsching, U. Artificial Intelligence Modeling of the Heterogeneous Gas Quenching Process for Steel Batches Based on Numerical Simulations and Experiments. Dynamics 2024, 4, 425-456. https://doi.org/10.3390/dynamics4020023
Narayan NM, Landgraf PM, Lampke T, Fritsching U. Artificial Intelligence Modeling of the Heterogeneous Gas Quenching Process for Steel Batches Based on Numerical Simulations and Experiments. Dynamics. 2024; 4(2):425-456. https://doi.org/10.3390/dynamics4020023
Chicago/Turabian StyleNarayan, Nithin Mohan, Pierre Max Landgraf, Thomas Lampke, and Udo Fritsching. 2024. "Artificial Intelligence Modeling of the Heterogeneous Gas Quenching Process for Steel Batches Based on Numerical Simulations and Experiments" Dynamics 4, no. 2: 425-456. https://doi.org/10.3390/dynamics4020023
APA StyleNarayan, N. M., Landgraf, P. M., Lampke, T., & Fritsching, U. (2024). Artificial Intelligence Modeling of the Heterogeneous Gas Quenching Process for Steel Batches Based on Numerical Simulations and Experiments. Dynamics, 4(2), 425-456. https://doi.org/10.3390/dynamics4020023








