Abstract
Moving animal groups often spontaneously change their group structure and dynamics, but standard models used to explain collective motion in animal groups are typically unable to generate changes of this type. Recently, a model based on attraction, repulsion and asymmetric interactions designed for specific fish experiments was shown capable of producing such changes. However, the origin of the model’s ability to generate them, and the range of this capacity, remains unknown. Here we modify and extend this model to address these questions. We establish that its ability to generate groups exhibiting changes depends on the size of the blind zone parameter . Specifically, we show that for small swarms and mills are generated, for larger polarized groups forms, and for a region of intermediate values there is a bistability region where continuous switching between milling and polarized groups occurs. We also show that the location of the bistability region depends on group size and the relative strength of velocity alignment when this interaction is added to the model. These findings may contribute to advance the use of self-propelled particle models to explain a range of disruptive phenomena previously thought to be beyond the capabilities of such models.
1. Introduction
Animals that move together, e.g., flocks of birds, schools of fish and herds of sheep, can arrange themselves to form a variety of group shapes exhibiting different dynamics [1,2,3]; for example, swarms characterized by disorganized motion within the group, mills where the individuals rotate around a common center, and polarized groups where the individuals are all moving with the same heading [4]. A group’s structure or heading can also change as a result of external environmental factors such as predator attacks [5,6,7,8,9], or spontaneously without apparent cause as observed in starling flocks [10] and schools of fish [11,12,13].
To understand and explain collective motion in moving animal groups, so called self-propelled particle (spp) models have been used over the past decades [4,14,15,16,17,18,19,20,21,22,23,24,25]. In these models, particles represent the individual animals and the particles interact with other nearby particles via local interaction rules. Common choices for the interaction rules include combinations of attraction, repulsion and velocity alignment. Models incorporating these interaction rules successfully describe collective behavior across species [14,26,27,28]. In particular, these models explain how various group types may arise from the inter-individual interaction rules, and a large number of different models of this type can produce stable swarms, mills and polarized groups [14]. However, until recently it was thought that these types of models may be fundamentally unable to generate disruptive phenomena, such as spontaneous switches between two or more distinct group structures, that are ubiquitous in real flocks, schools and herds [10,11,12,13]. Specific arguments for the inability of these models to generate such changes in group structure included the inevitable dampening of perturbations proposed to result from the inclusion of velocity alignment [29] and “the averaging of interactions that takes place in most spp models” [30], suggesting, in particular, that the spp model would not be able to model the switching observed in the seminal golden shiner fish experiments [12]. In these experiments, groups of 30, 70, 150 and 300 gloden shiners (Notemigonus crysoleucas) were placed in an empty rectangular arena and left alone to school in the absence of external interference or disturbances. The main observation was that for all group sizes the system exhibited bistability, in the sense that the schools formed both mills and polarized groups without any apparent changes in conditions, and that the schools regularly switched between these two states, with switch rate decreasing with group size (See videos S1–S4 in [12]). Recently, it was shown that a standard model based on attraction, repulsion, and asymmetric interactions via blind zones designed to model this specific experiment is capable of generating continuous switching between two distinct states, specifically between milling and polarized groups, that is consistent with the experimental observations [31]. (See videos referred to in [31]). However, the mechanism behind the model’s ability to generate these switches using only standard components (attraction, repulsion, and blind zones) found in a large number of other models is not known and the range of its capacity to do so has not been quantified.
Asymmetric interactions implemented via a blind zone is a common component in spp models that is included to represent the limited perceptual fields of many animals [32]. While it has not been directly linked to spontaneous changes in group structure and dynamics within individual simulations, it is known to induce initial condition-dependent bistability in several models, and have a strong distruptive effect on group formation and resulting dynamics when varied [13,18,32,33,34]. For example, [13] found that large blind zones in models designed for fish contribute to the emergence of polarized groups and that reducing the blind zones led to an increase in group splits or disbandedness, and [33] included variation in the size of the blind zones (from 0 to only) and found that milling behavior degraded with increased blind zone ranges.
Given that asymmetric interactions are known to induce drastic changes in models when varied and lead to initial condition-dependent bistability, this component of the model in [31] is a natural starting point for seeking an explanation for the capacity in this model to generate groups that switch between group types within individual simulations. If it turns out that asymmetric interactions implemented via blind zones can be shown to drive robust bistability and switching in this model, this would suggest that there may be other published spp models that also have this capacity, but it has yet to be detected in them. Further investigations in this direction could potentially result in a new generation of spp model work capable of explaining disruptive collective motion just as well as previous, and current, spp models have been in explaining stable collective motion.
2. Materials and Methods
Here we extended the model presented in [31] to include an explicit alignment interaction from [17] that will be used for the second half of our study. In this model, particles move in a bounded planar region and update their headings depending on their neighbors positions. All particles that are located within a distance of R from a particular particle are neighbors of that particle. All neighbors contribute to the repulsive force on the particle, but only neighbors that are not located in a blind zone specified by a blind angle behind the particle contributes to the attractive and aligning forces on the particle. In each timestep t the new heading of particle i, denoted by , is given by the linear combination
where is particle i’s current heading, is the normalized direction towards the local center of mass of its neighbors except those in the blind zone, is the normalized average heading of its neighbors, is a local distance dependent repulsion term, is a heading noise term, and the parameters a, c, e and r specifies the relative strengths of the interaction terms. For a detailed description of all terms except the alignment term, see [29]. The alignment term is the standard Vicsek velocity alignment [17] and is defined by
where represents the set of neighbors and is the normalized current heading of neighbor j. The position in the next timestep of each particle is calculated through
where is the speed and is the timestep.
2.1. Measures
We rely on the same two measures that were used in [12,31] to quantify the group types produced in the simulations: the polarization and the rotation, or normalized angular momentum, . If we denote the number of particles by N, the current normalized heading of particle i by , and the normalized vector from the center of mass of all particles towards particle i by , then the polarization is defined by
and the rotation by
These measures can be used to distinguish polarized groups and mills, because polarized groups will have high polarization and low rotation, and mills will have low polarization and high rotation. More specifically, an ideal polarized group will have and , and an ideal milling group will have and .
2.2. Simulations
Following previous experimental [12] and modeling [31] work involving this system, we performed simulations for each of the group sizes 30, 70, 150 and 300. However, unlike previous models [29,31] that used a single fixed blind angle of , here we ran simulations for each value of the blind angle from 0 to 2 in increments of 0.1 to create density plots showing the recorded polarization and orientation values in simulations of timesteps for each value and for each groups size. This was then repeated for each group size for three different alignment parameter values , and to investigate how adding alignment influences the model behavior as a function of . In all simulations except those described in the next sentence, the particles move in a bounded rectangular area of size units of length, mimicking the setup in [12,31]. To determine if varying the size of the region critically affects the behavior under study here, we also ran simulations with 70 particles with the dimensions of the region being scaled by 1/3, 2/3, 4/3, 5/3, 2,5 and 10. The same slip boundary conditions used in [31] were used here, that is, if a particle’s preliminary positional update in a timestep would make it cross the boundary, it aligns its heading with the boundary in the direction that deviates the least from its approach angle. Each particle was assigned a random position and heading at the start of each simulation (random initial conditions) and all auxiliary parameters were kept as in [22], i.e., “, , , , ”. To determine whether the initial conditions affect the behavior under study here, we also ran 12 different timesteps in simulations with 70 particles to compare the outcome of one simulation and the average of the 12 simulations.
2.3. Analysis
To analyze the simulations, we adapted the approach in [31,35] and created density plots of all and values recorded for each value of for each group size, alignment condition, and region’s size condition when relevant. These density plots for each value, that can be thought of as relative frequency histograms of the measurement values for each , were then combined to create the final plots showing the polarization and rotation as a function of for each group size and alignment condition. From the data used to create the density plots, we also created corresponding plots showing the median polarization for each group size and alignment condition as a function of to illustrate the average behavior. To compare the variation in outcome over 12 different simulations, we present the density plots of one simulation, the average of 12 simulations, and the standard deviation over 12 simulations.
Estimating the Number of Switches and Lifetime of the Phases for Each Group Size as a Function of Blind Angle
To estimate the number of switches occurring in the timestep simulations, and the lifetimes of the mills and polarized groups produced, we used the time series of and values recorded for each value of and each group size. First a rolling average smoothing procedure was applied to remove sporadic large fluctuations and transitions in the timeseries. Then the number of switches and lifetimes of the groups present were calculated by creating two new vectors of length obtained by a thresholding procedure on the measures. One vector identifying when mills are present, and one vector when polarized groups are present defined as follows. Let and denote the smoothed measurement time series value at time t, then the t:th element of the polarized group vector if and , and otherwise. Similarly, the t:th element of the milling group vector if and , and otherwise. Once these vectors had been created, we go through the vector from to and count the number of consecutive timesteps that recorded a polarized group (i.e., consecutive 1s) and created a new vector recording the number of timesteps each polarized group survived before being interrupted by a switch. The same procedure was then performed on the mill vector M to create a vector recording the number of timesteps each mill survived before being interrupted by a switch. This procedure was performed for each near the bistability region (1.9–3.6) and each group size, and the number of switches, and average lifetimes of mills and polarized groups were calculated for each and plots were created to display the results.
3. Results
The size of the blind zone dictates the resulting group structure and we find stable versions of all three standard groups: swarm (Figure 1a), mill (Figure 1b), polarized group (Figure 1c) in different ranges. See Figure 2. For , we observe swarms characterized by low polarization and rotation for all group sizes. As increases milling groups form that exhibit an increasingly stable rotation up to a value when polarized groups start to form ( large, small), and the exact value for which the model stops reliably producing mills and start producing polarized groups increases with group size. Finally, once becomes large (close to 2), particles fail to aggregate and no group forms.
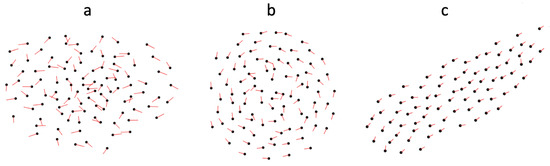
Figure 1.
The group types observed in the model. (a) Swarm ( and low). (b) Mill ( low and intermediate to high). (c) Polarized group ( high and low).
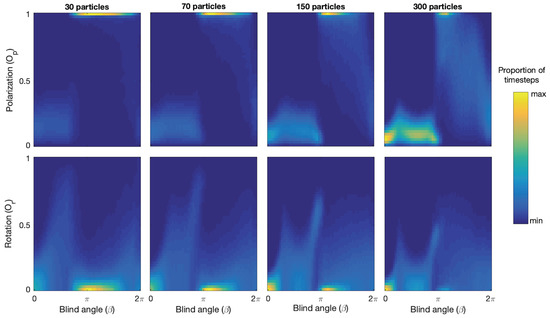
Figure 2.
Polarization and rotation densities for each from 0 to 2 for each group size 20, 70, 150 and 300. For each , the proportion of simulation timesteps that returned particular rotation () and polarization () values are shown in color code. Yellow means that a high proportion of the timesteps returned that value, whereas blue means that a low proportion of timesteps returned that value. Across all group sizes, we see the same general trend: For , both polarization and rotation is low, indicating that the model generates swarms there. As increases up towards , the polarization remains low but the rotation increases, indicating that milling groups are present. Then as approaches , we observe that the rotation drops and the polarization approaches 1, indicating that polarized groups are present. Finally, as increases towards both polarization and rotation approach values indicating that no group has formed.
There is a range of values over which the model generates bistability with continuous switching between polarized groups and mills. See red rectangles in Figure 3. We observe that bistability is present because both the polarization and rotation measure show two bands of returned values for each value in these ranges. For example, around for 150 particles we see a band near (polarized group) and another band near (mill), and in the corresponding rotation plot we see one band near (polarized group) and another one around (mill). We note that as increases in the bistability regions the proportion of timesteps where polarized groups were detected increases, and that as decreases the proportion of milling increases. We also note that the location of the bistability region is shifted towards higher values with increasing group size. More specifically, for 30 particles the region range is = 2.0–2.8, 70 particles = 2.6–3.2, 150 particles = 2.8–3.3, 300 particles = 2.9–3.4. Figure 4 shows the number of switches and the average lifetimes of polarized groups and mills as a function of near the bistability region for each group size and confirms that switching is taking place and provides quantitative estimates of the and group size-dependent switching rates, group type lifetimes, and location of the switching regions.
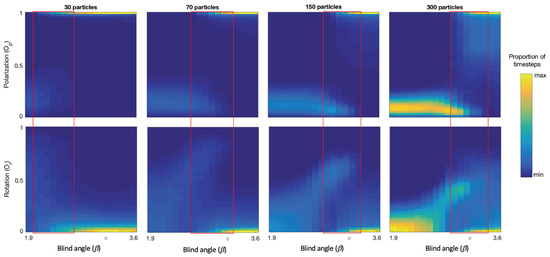
Figure 3.
Polarization and rotation near the bistability region. Zooming in on the region from 1.9 to 3.6 in Figure 2 shows that a region of bistability is present. In the red rectangles, we notice that the simulations are generating groups with distinct properties within individual simulation runs. In particular, we see that in some simulation timesteps the group exhibits very high polarization and in others very low polarization, and in the corresponding rotation plots we see that some timesteps yield very low rotation (polarized groups) and in other timesteps higher rotation (mills).
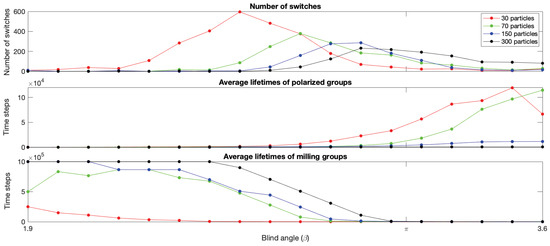
Figure 4.
Number of switches and lifetimes of the mills and polarized groups as a function of near the bistability region. The top plot shows that the maximum number of switches over the timesteps decreases, and the at which this maximum is reached, increases with group size. The average lifetime plots show that as increases over the bistability region the average lifetime of mills is decreasing and the average lifetime of polarized increases, and in the middle there are intervals for each group size where switching is taking place and the polarized and milling groups have moderate lifetimes.
The capacity of the model to generate bistability and switching is not inhibited by the addition of alignment. Figure 5 shows the polarization density plots for each group size and each alignment condition, and note that the region of bistability is shifted towards lower values for all group sizes as the relative strength of alignment increases. The presence of polarized groups increases for lower values and the presence of milling groups decreases for larger values as the alignment is increased. This is what we expect from adding alignment, promoting polarized groups at the expense of milling groups. We also note that increasing alignment leads to more intermediate polarization values being recorded, resulting in a progressively less clear separation of the phases in the bistability region. This is particularly striking for the largest 300 particle group, where at there is a distinct polarized group phase visible in the upper right corner, but as alignment is increased the polarization diffuses out towards lower polarization values. So, while the model produces polarized groups earlier as alignment is increased and promotes polarization in this sense, the polarization of the groups produced tends to be lower on average, especially for the large group sizes, as Figure 6 also shows.
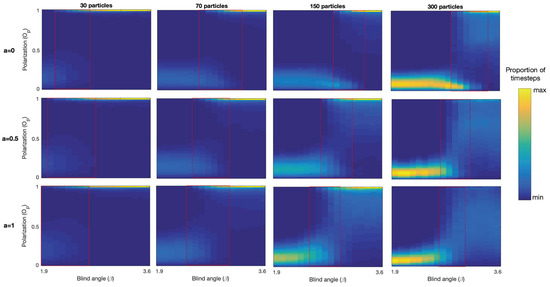
Figure 5.
Effects of including velocity alignment on the polarization in the bistability region. Here we see the polarization densities throughout simulations of timesteps for each from 1.9 to 3.6 for each group size 20, 70, 150 and 300 and each alignment condition , and . The red rectangle indicates the region of bistability and we note that for each group size the bistability region is shifted towards lower values with increasing alignment. We also note that the polarization of polarized groups decreases with increased alignment, especially for larger groups.
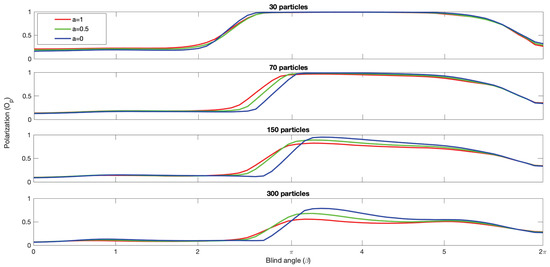
Figure 6.
Median polarization curves for each group size and each alignment condition. We note that as alignment increases the median polarization starts to increase for lower values for each group size, and that for the larger groups (150 and 300) the polarization of polarized groups generated with values above decreases significantly with increasing alignment. In each plot, the blue curve corresponds to the no alignment condition () and the red curve to the highest alignment condition (), showing that adding alignment decreases the average polarization of polarized groups, most prominent in the blue and red curves for the 300 particle plot.
4. Discussion
The finding that varying the size of the blind zone alone in this attraction repulsion model allows the three standard groups (swarms, mills, and polarized groups) produced by spp models to form (Figure 2) is important. While a large number of studies have included blind zones in spp models and observed their effect, e.g., [4,13,18,32,33,36], the main focus has typically been on other interactions and parameters; for example, size of the orientation zone [4], relative strength of attraction [18], alignment or attraction-repulsion [36], etc., including analysis of only one [18,36], or a few [13,32,33], fixed sizes of the blind zone. Systematic investigations of the full range of blind angles from 0 to for an otherwise fixed model are rare; the only exception we can find is [34], and to our knowledge no other spp model has been shown to generate all three standard groups by only varying the blind zone parameter. This indicates that the blind zone may be as important for group formation in these models as the interactions, e.g., attraction, repulsion and velocity alignment, that tend to be the focus in most studies.
The fact that the bistability and spontaneous switching between polarized and milling groups occur over a range of blind zone parameter values in combination with attraction and repulsion across all group sizes shows that the capacity of this model to generate these phenomena exceeds those presented in [31] and may provide a robust mechanism to induce them in a large number of classical spp models that include attraction, repulsion and asymmetric interactions. We now not only know that the suggestion that the averaging of interactions that takes place in spp models might preclude them from generating these phenomena [30] is incorrect, but also that they are more readily reproducible over a range of parameters and conditions than [31] has previously established. Furthermore, combining the results presented in [31] showing that the model exhibits bistability and switching in two free space situations, with the quantitative results here showing that varying the size of the available space from 2/3 to 10 times that available to the real fish in the experiments in [12] does not critically affect the group types produced or the characteristics near the transition region; this shows that this model’s capacity to induce bistability and switching is robust. See Figures S1 and S2.
The finding that adding velocity alignment does not prevent the model from generating bistability and switching provides further evidence that the argument made in [29], that the inclusion of alignment in models of this type may render them unable to produce disruptive phenomena such as switching between group types, is inaccurate. While this was previously known in special cases from the attraction, alignment and asymmetric interactions model work in [37], the systematic analysis presented here across group sizes and the full blind zone range solidifies the point that the inclusion of alignment does not appear to inhibit bistability and switching. However, our analysis does show that adding alignment affects the dynamics in partially unexpected ways. In particular, we found that adding alignment increases the range over which polarized groups form, but lowers the polarization of polarized groups for larger group sizes. The former observation is expected; the latter observation is not. Including velocity alignment in the spp model was a necessity in order to produce polarized groups before a range of other polarization-inducing mechanisms were recently discovered [20,31,35,38,39,40] and increasing the influence of alignment relative to other included interactions universally had the effect that polarization increased; see e.g., [4]. How can adding more alignment here lead to less polarized groups? In [22], eight different mechanisms for inducing polarized groups were compared and it was noted that the final polarization value of a polarized group depended on which mechanism had generated it (Figure 4 in [22]). In particular, polarized groups generated by velocity alignment alone ended up with a higher polarization than groups generated by explicit alignment and attraction, and both of these formed faster than polarized groups generated by attraction and blind zones. Perhaps the reason that we observe that the polarization of polarized groups is decreasing with increasing alignment is that the different mechanisms, all of which can induce polarization on their own, interfere with the polarization-inducing effects of each other, rather than reinforce them, when present at the same time. This may be useful to consider in analysis of spp models that include blind zones and where both attraction and velocity alignment are present, e.g., [4].
Combined, our findings suggest that detailed investigation of the effects of the blind zone across the full spectrum of values in any spp model that contains this component in combination with attraction, repulsion, and potentially velocity alignment, may reveal that it indeed has the capacity to generate bistability, switching and other types of disruptive phenomena, despite previous suggestions to the contrary [29,30]. In particular, we suspect that the standard attraction, repulsion, and alignment model in [4] that was originally used to model the bistability in [12] may also be capable of reproducing the spontaneous switching for blind angle values beyond those used in [12]. Similarly, if the analysis of the attraction and repulsion model in [33] was extended beyond blind angles from 0 to bistability and switching may present itself. Furthermore, from the results and materials presented in [34] we cannot conclude that this model is not already capable of producing bistability and switching. This is an alignment only model (Vicsek model [17]) with a blind zone added, and they establish that milling occurs over a range of blind zones, and mention that ’bands’ of particles also form. Therefore, in this minimal model, without attraction and repulsion, idealized versions of both key phases, mills and polarized groups, appear to be present. Unfortunately, they only quantify milling as a function of blind angle, not groups that they refer to as ’non-milling’ groups, so it is unclear whether milling and polarized groups are producible for the same blind angle (i.e., bistability). In addition, their analysis approach of only running short 2000 timestep simulations may not be long enough for switching to occur, and taking the average over the last 500 timesteps of the simulations for their measures would fail to detect any switching between the types. We expect that investigations in this direction may lead to new model-based explanations for a range of disruptive phenomena that were previously thought beyond the scope of spp models, and hope that ultimately spp models may become as successful in explaining these disruptive phenomena as they have been in explaining stable collective phenomena in the past.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/dynamics2040027/s1, Figure S1: Effects of varying the box size on the polarization and rotation measures for 70 particles. This figure was constructed in exactly the same way as Figure 2 for 70 particles but with different box sizes. The panels entitled ’Regular box size’ is the exact plots shown in Figure 2 for 70 particles. We note that as the box size decreases the blind angle range that produce polarized groups shrinks, and for the smallest box size (1/3) it is effectively non-existent. This is because the group effectively fill up the available space, so even if polarized groups could form they have no space to move to and will therefore, depending on the parameters, either assume a mill shape or swarm phase exhibiting disorganized motion. As the box size increases the range of values that produce polarized groups increases, but there are no drastic changes; Figure S2: Polarization and rotation near the bistability region in Figure S1 shows that a region of bistability is present. In the red rectangles we notice that the simulations are generating groups with distinct properties within individual simulation runs. In particular, we see that in some simulation time steps the group exhibits very high polarization and in other very low polarization, and in the corresponding rotation plots we see that some time steps yield very low rotation (polarized groups) and in other time steps higher rotation (mills); Figure S3: Effects of initial conditions on the polarization and rotation measures for 70 particles. Comparing the result of one time step simulation with the average of 12 different simulations shows that the difference between them is both qualitatively and quantitatively marginal, indicating that initial conditions do not critically affect our results.
Author Contributions
Conceptualization, D.S.; Data curation, D.S.; Formal analysis, D.S., G.T., R.G. and Z.C.; Investigation, D.S., G.T., R.G. and Z.C.; Methodology, D.S., G.T., R.G. and Z.C.; Software, D.S.; Supervision, D.S.; Validation, D.S.; Visualization, D.S.; Writing–original draft, D.S., G.T., R.G. and Z.C.; Writing—review & editing, D.S., G.T., R.G. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shaw, E. Schooling fishes: The school, a truly egalitarian form of organization in which all members of the group are alike in influence, offers substantial benefits to its participants. Am. Sci. 1978, 66, 166–175. [Google Scholar]
- Newlands, N.K. Shoaling Dynamics and Abundance Estimation: Atlantic Bluefin Tuna (Thunnus thynnus). Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2002. [Google Scholar]
- Heppner, F.H. Avian flight formations. Bird-Banding 1974, 45, 160–169. [Google Scholar] [CrossRef]
- Couzin, I.D.; Krause, J.; James, R.; Ruxton, G.D.; Franks, N.R. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 2002, 218, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Procaccini, A.; Orlandi, A.; Cavagna, A.; Giardina, I.; Zoratto, F.; Santucci, D.; Chiarotti, F.; Hemelrijk, C.K.; Alleva, E.; Parisi, G.; et al. Propagating waves in starling, Sturnus vulgaris, flocks under predation. Anim. Behav. 2011, 82, 759–765. [Google Scholar] [CrossRef]
- Herbert-Read, J.E.; Buhl, J.; Hu, F.; Ward, A.J.; Sumpter, D.J. Initiation and spread of escape waves within animal groups. R. Soc. Open Sci. 2015, 2, 140355. [Google Scholar] [CrossRef]
- Storms, R.; Carere, C.; Zoratto, F.; Hemelrijk, C. Complex patterns of collective escape in starling flocks under predation. Behav. Ecol. Sociobiol. 2019, 73, 1–10. [Google Scholar] [CrossRef]
- Romenskyy, M.; Herbert-Read, J.E.; Ioannou, C.C.; Szorkovszky, A.; Ward, A.J.; Sumpter, D.J. Quantifying the structure and dynamics of fish shoals under predation threat in three dimensions. Behav. Ecol. 2020, 31, 311–321. [Google Scholar] [CrossRef]
- Papadopoulou, M.; Hildenbrandt, H.; Sankey, D.W.; Portugal, S.J.; Hemelrijk, C.K. Self-organization of collective escape in pigeon flocks. PLoS Comput. Biol. 2022, 18, e1009772. [Google Scholar] [CrossRef]
- King, A.J.; Sumpter, D.J. Murmurations. Curr. Biol. 2012, 22, R112–R114. [Google Scholar] [CrossRef]
- Lecheval, V.; Jiang, L.; Tichit, P.; Sire, C.; Hemelrijk, C.K.; Theraulaz, G. Social conformity and propagation of information in collective U-turns of fish schools. Proc. R. Soc. B Biol. Sci. 2018, 285, 20180251. [Google Scholar] [CrossRef]
- Tunstrøm, K.; Katz, Y.; Ioannou, C.C.; Huepe, C.; Lutz, M.J.; Couzin, I.D. Collective states, multistability and transitional behavior in schooling fish. PLoS Comput. Biol. 2013, 9, e1002915. [Google Scholar] [CrossRef]
- Gautrais, J.; Jost, C.; Theraulaz, G. Key behavioural factors in a self-organised fish school model. Ann. Zool. Fenn. 2008, 45, 415–428. [Google Scholar] [CrossRef]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Hildenbrandt, H.; Carere, C.; Hemelrijk, C.K. Self-organized aerial displays of thousands of starlings: A model. Behav. Ecol. 2010, 21, 1349–1359. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef]
- Strömbom, D. Collective motion from local attraction. J. Theor. Biol. 2011, 283, 145–151. [Google Scholar] [CrossRef]
- Romanczuk, P.; Schimansky-Geier, L. Swarming and pattern formation due to selective attraction and repulsion. Interface Focus 2012, 2, 746–756. [Google Scholar] [CrossRef]
- Barberis, L.; Peruani, F. Large-scale patterns in a minimal cognitive flocking model: Incidental leaders, nematic patterns, and aggregates. Phys. Rev. Lett. 2016, 117, 248001. [Google Scholar] [CrossRef]
- Romenskyy, M.; Herbert-Read, J.E.; Ward, A.J.; Sumpter, D.J. Body size affects the strength of social interactions and spatial organization of a schooling fish (Pseudomugil signifer). Open Sci. 2017, 4, 161056. [Google Scholar] [CrossRef]
- Strömbom, D.; Tulevech, G. Attraction vs. Alignment as Drivers of Collective Motion. Front. Appl. Math. Stat. 2021, 7, 717523. [Google Scholar] [CrossRef]
- Zhao, Y.; Ihle, T.; Han, Z.; Huepe, C.; Romanczuk, P. Phases and homogeneous ordered states in alignment-based self-propelled particle models. Phys. Rev. E 2021, 104, 044605. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Huepe, C.; Romanczuk, P. Contagion dynamics in self-organized systems of self-propelled agents. Sci. Rep. 2022, 12, 2588. [Google Scholar] [CrossRef] [PubMed]
- Costanzo, A.; van Haeringen, E.; Hemelrijk, C. Effect of time-delayed interactions on milling: A minimal model. Europhys. Lett. 2022, 138, 22002. [Google Scholar] [CrossRef]
- Ward, A.; Webster, M. Sociality: The Behaviour of Group-Living Animals; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Sumpter, D.J. Collective animal behavior. In Collective Animal Behavior; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Herbert-Read, J.E. Understanding how animal groups achieve coordinated movement. J. Exp. Biol. 2016, 219, 2971–2983. [Google Scholar] [CrossRef] [PubMed]
- Strömbom, D.; Siljestam, M.; Park, J.; Sumpter, D.J. The shape and dynamics of local attraction. Eur. Phys. J. Spec. Top. 2015, 224, 3311–3323. [Google Scholar] [CrossRef]
- Katz, Y.; Tunstrøm, K.; Ioannou, C.C.; Huepe, C.; Couzin, I.D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. USA 2011, 108, 18720–18725. [Google Scholar] [CrossRef]
- Strömbom, D.; Nickerson, S.; Futterman, C.; DiFazio, A.; Costello, C.; Tunstrøm, K. Bistability and Switching Behavior in Moving Animal Groups. Northeast. J. Complex Syst. (NEJCS) 2022, 4, 1. [Google Scholar] [CrossRef]
- Romey, W.L.; Vidal, J.M. Sum of heterogeneous blind zones predict movements of simulated groups. Ecol. Model. 2013, 258, 9–15. [Google Scholar] [CrossRef]
- Newman, J.P.; Sayama, H. Effect of sensory blind zones on milling behavior in a dynamic self-propelled particle model. Phys. Rev. E 2008, 78, 011913. [Google Scholar] [CrossRef]
- Costanzo, A.; Hemelrijk, C. Spontaneous emergence of milling (vortex state) in a Vicsek-like model. J. Phys. D Appl. Phys. 2018, 51, 134004. [Google Scholar] [CrossRef]
- Strömbom, D.; Antia, A. Anticipation Induces Polarized Collective Motion in Attraction Based Models. Northeast. J. Complex Syst. (NEJCS) 2021, 3, 2. [Google Scholar] [CrossRef]
- Romanczuk, P.; Couzin, I.D.; Schimansky-Geier, L. Collective motion due to individual escape and pursuit response. Phys. Rev. Lett. 2009, 102, 010602. [Google Scholar] [CrossRef]
- Calovi, D.S.; Lopez, U.; Ngo, S.; Sire, C.; Chaté, H.; Theraulaz, G. Swarming, schooling, milling: Phase diagram of a data-driven fish school model. New J. Phys. 2014, 16, 015026. [Google Scholar] [CrossRef]
- Strömbom, D.; Hassan, T.; Hunter Greis, W.; Antia, A. Asynchrony induces polarization in attraction-based models of collective motion. R. Soc. Open Sci. 2019, 6, 190381. [Google Scholar] [CrossRef]
- Murakami, H.; Niizato, T.; Gunji, Y.P. Emergence of a coherent and cohesive swarm based on mutual anticipation. Sci. Rep. 2017, 7, 46447. [Google Scholar] [CrossRef]
- Peruani, F. Hydrodynamic equations for flocking models without velocity alignment. J. Phys. Soc. Jpn. 2017, 86, 101010. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).