On the Zero-Neutron Density in Stochastic Nuclear Dynamics
Abstract
:- b the neutron birth rate due to fission;
- d the neutron death rate due to fission;
- the total number of neutrons per fission: prompt and delayed;
- the constant of fission product ;
- the number of atoms of fission product produced per fission;
- q is the extraneous neutron sources.
- Case 1:
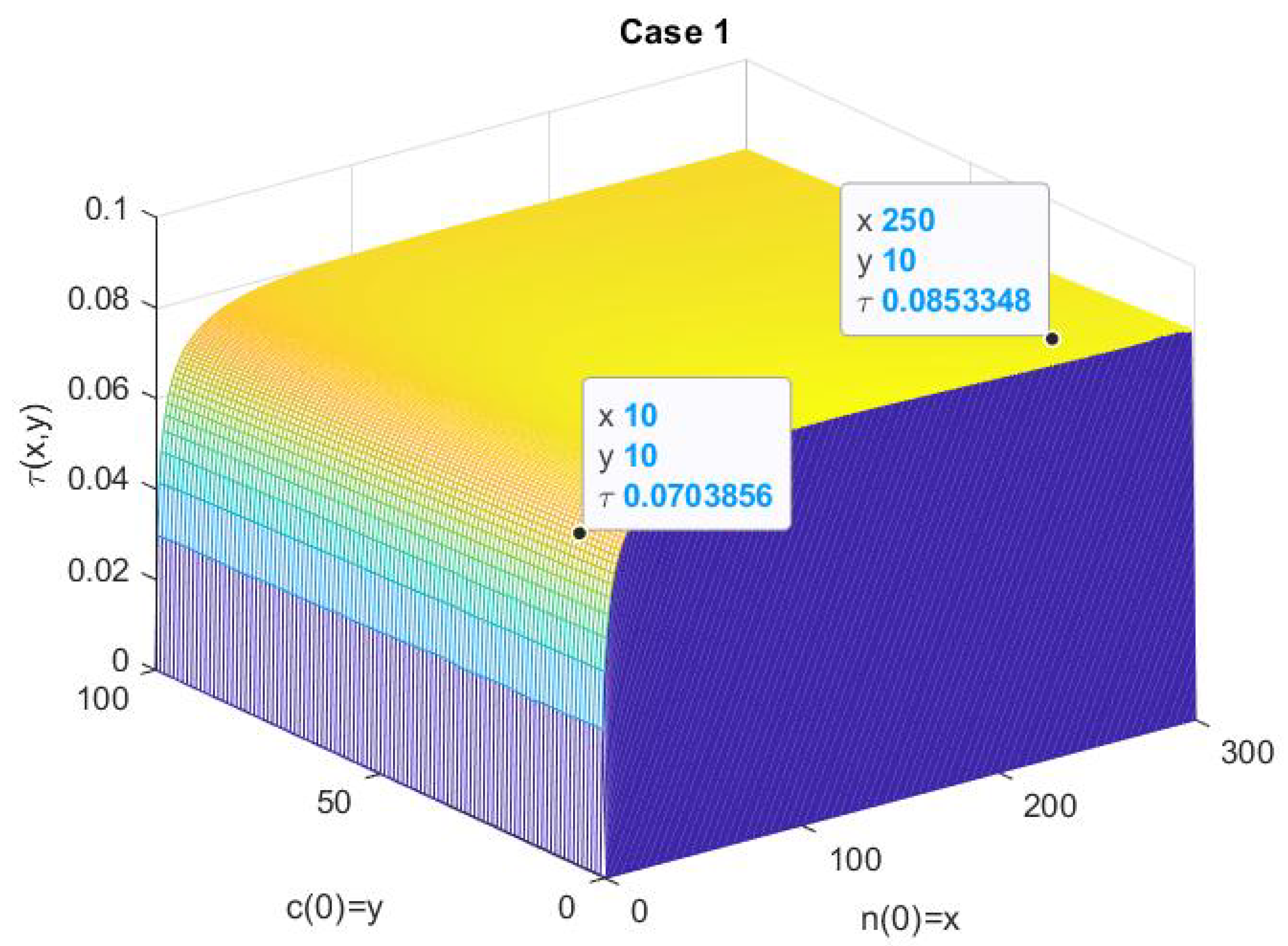
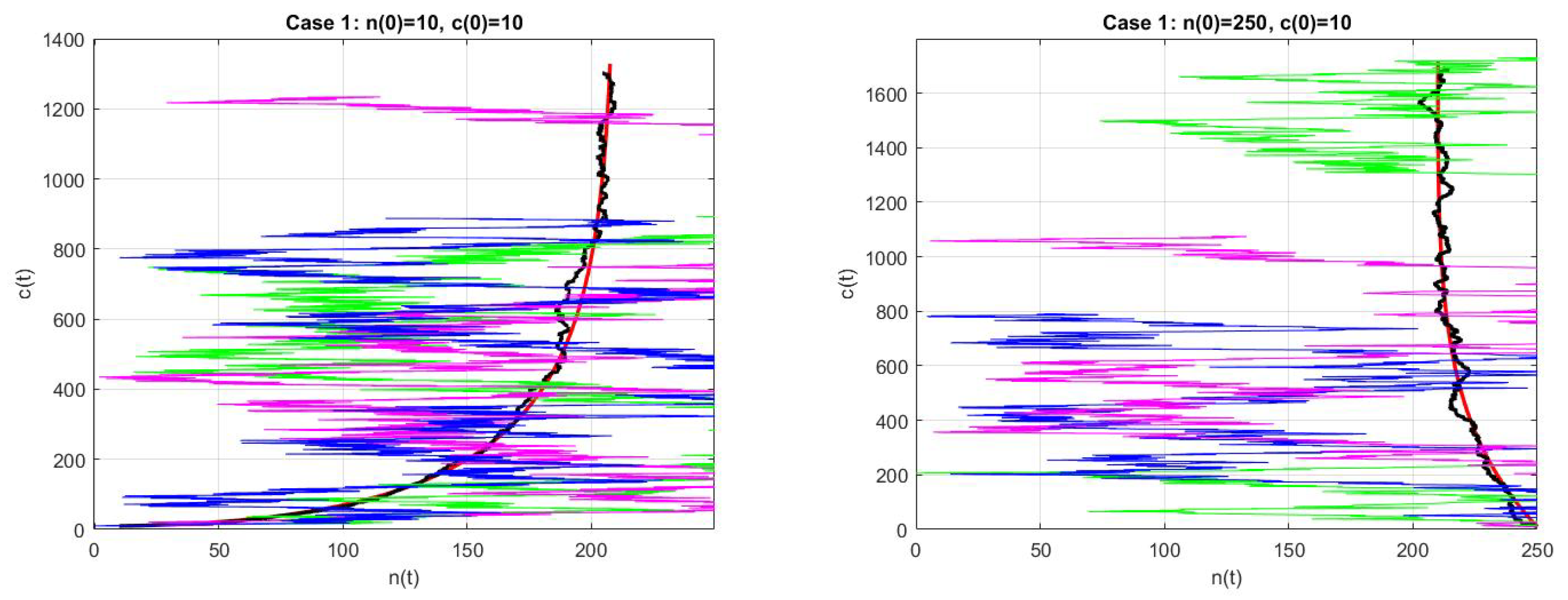
- As in the first numerical case, we consider the example in [6], p. 163, withwhich are values for a nuclear reactor involving the thermal fission of uranium-235 in [3]. For these values, the deterministic model (6) has a fixed point at and its Jacobian has eigenvalues of and , so the fixed point is unstable. In Figure 1, we plot the numerical solution with Matlab for and , . (We refer to [7,8,9,10] for a review of the numerical solutions of ODEs).
- Case 2:
Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hetrick, D. Dynamics of Nuclear Reactors; American Nuclear Sociaty: La Grange Park, IL, USA, 1993. [Google Scholar]
- Kinard, M.; Allen, E. Efficient numerical solution of the point kinetics equations in nuclear reactor dynamics. Ann. Nucl. Energy 2004, 31, 1039–1051. [Google Scholar] [CrossRef]
- Hetrick, D. Dynamics of Nuclear Reactors; University of Chicago: Chicago, IL, USA, 1971. [Google Scholar]
- Stacey, W. Nuclear reactor Physics, 2nd ed.; Completety Revised and Enlarged; WILEY-VCG Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007. [Google Scholar]
- Hayes, J.; Allen, E. Stochastic point-kinetics equations in nuclear reactor dynamics. Ann. Nucl. Energy 2005, 32, 572–587. [Google Scholar] [CrossRef] [Green Version]
- Allen, E. Modeling with Itô Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Higham, D.; Higham, N. MATLAB Guide; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Shampine, L.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Moler, C. Numerical Computing with MATLAB; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Sharin, M. Exploration of Mathematical Models in Biology with MATLAB; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kloeden, P.; Platen, E. Numerical Solution of Stochastic Differential Equations; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Higham, D. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Ray, S. Numerical simulation of stochastic point kinetic equation in the dynamical system of nuclear reactor. Ann. Nucl. Energy 2012, 49, 154–159. [Google Scholar]
- Suescún-Díaz, D.; Oviedo-Torres, Y.; Girón-Cruz, L. Solution of the stochastic point kinetics equations using the implicit Euler-Maruyama method. Ann. Nucl. Energy 2018, 117, 45–52. [Google Scholar] [CrossRef]
- Higham, D.; Kloeden, E. An Introduction to the Numerical Simulation of Stochastic Differential Equations; SIAM: Philadelphia, PA, USA, 2021. [Google Scholar]
- de la Hoz, F.; Vadillo, F. A mean extinction-time estimate for a stochastic Lotka-Volterra predator-prey model. Appl. Math. Comput. 2012, 219, 170–179. [Google Scholar] [CrossRef]
- Doubova, A.; Vadillo, F. Extinction-time for stochastic population models. J. Comput. Appl. Mathemtics 2016, 295, 159–169. [Google Scholar] [CrossRef]
- Vadillo, F. Comparing stochastic Lotka-Volterra predator-prey models. Appl. Math. Comput. 2019, 360, 181–189. [Google Scholar] [CrossRef]
- Gockenbach, M. Understanding and Implementing the Finite Element Method; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Ayyoubzadeh, S.M.; Vosoughi, N. An alternative stochastic formulation for the point reactor. Ann. Nucl. Energy 2014, 63, 691–695. [Google Scholar] [CrossRef]
- Elsayed, A.; El-Beltagy, M.; Al-Juhani, A.; Al-Qahtani, S. A New Model for the Stochastic Point Reactor: Development and Comparison with Available Models. Energies 2021, 14, 955. [Google Scholar] [CrossRef]
- Gillespie, D. Approximate accelerated stochastic simulation of chemically. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Gillespie, D. The Chemical Langevin and Fokker-Planck Equations for the Reversible Isomerization Reaction. J. Phys. Chem. 2002, 106, 5063–5071. [Google Scholar] [CrossRef]
- Gillespie, D.; Petzold, L. Numerical simulation for biochemical kinetics. In System Modeling in Cellular Biology From Concepts to Nuts and Bolts; Szallasi, Z., Stelling, J., Periwal, V., Eds.; MIT Press: Cambridge, MA, USA, 2006; pp. 331–353. [Google Scholar]
- Schilick, T. Molecular Modeling and Simulation. An Interdisciplinary Guide, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Vadillo, F. On Stochastic Models of Chemical Reactions. Chem. Phys. 2021, 549, 111259. [Google Scholar] [CrossRef]
- Hecht, F. New development in freefem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]


| Change | Probability |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vadillo, F. On the Zero-Neutron Density in Stochastic Nuclear Dynamics. Dynamics 2021, 1, 198-203. https://doi.org/10.3390/dynamics1020012
Vadillo F. On the Zero-Neutron Density in Stochastic Nuclear Dynamics. Dynamics. 2021; 1(2):198-203. https://doi.org/10.3390/dynamics1020012
Chicago/Turabian StyleVadillo, Fernando. 2021. "On the Zero-Neutron Density in Stochastic Nuclear Dynamics" Dynamics 1, no. 2: 198-203. https://doi.org/10.3390/dynamics1020012
APA StyleVadillo, F. (2021). On the Zero-Neutron Density in Stochastic Nuclear Dynamics. Dynamics, 1(2), 198-203. https://doi.org/10.3390/dynamics1020012