Abstract
Studies of many complex systems have revealed new collective behaviours that emerge through the mechanisms of self-organised critical fluctuations. Subject to the external and endogenous driving forces, these collective states with long-range spatial and temporal correlations often arise from the intrinsic dynamics with the threshold nonlinearity and geometry-conditioned interactions. The self-similarity of critical fluctuations enables us to describe the system using fewer parameters and universal functions that, on the other hand, can simplify the computational and information complexity. Currently, the cutting-edge research on self-organised critical systems across the scales strives to formulate a unifying mathematical framework, utilise the critical universal properties in information theory, and decipher the role of hidden geometry. As a prominent example, we study the field-driven spin dynamics on the hysteresis loop in a network with higher-order structures described by simplicial complexes, which provides a geometric-frustration environment. While providing motivational illustrations from physical, biological, and social systems, along with their networks, we also demonstrate how the self-organised criticality occurs at the interplay of the complex topology and driving mode. This study opens up new promising routes with powerful tools to address a long-standing challenge in the theory and applications of complexity science ingrained in the efficient analysis of self-organised critical states under the competing higher-order interactions embedded in complex geometries.
1. Introduction: Self-Organised Criticality and Complexity
The term self-organised criticality (SOC) [1,2] describes properties of out-of-equilibrium driven dynamical systems to reach a stationary state characterised by long-range correlations, resembling the once known near the equilibrium second-order phase transitions. Remarkably, in such cases, the system develops a multi-scale response involving many parts and gradually reaches a metastable state with the long-range spatial and temporal correlations without an obvious tuning parameter or a (dynamical) phase transition. Hence, the SOC states appear as an attractor of the nonlinear dynamics in an open system repeatedly driven by external (or endogenous) forces. A paradigmatic example of sandpiles describes the nature of the dynamics leading to SOC [3]. The system is driven by adding grains, which leads to grain accumulation and, consequently, disruption when the local stability is violated at a site. The unstable site relaxes by distributing grains to the neighbour site, which may induce more instabilities and a cascade of events (or an avalanche). The avalanche propagates until all sites are stable again. When an avalanche reaches the system’s open boundaries, some grains leave the system, thus maintaining stable fluctuations of the total mass. Typically, SOC occurs in systems with the threshold type nonlinearity. The driving time scale is much slower than the avalanche propagation, and the avalanche size is not linearly correlated with the driving force. The multi-scale response is characterised by self-similarity and scaling. Relevant quantities in the SOC state have power-law behaviour, fractal geometry, and scale invariance [2,4].
It is important to stress that SOC states emerge in many open driven systems [2] at different scales and types of interactions, as discussed below. These are the interacting nonlinear systems with many constitutive parts under the conditions with driving (external and internal forces), constraints (exerted by the substrate geometry allowing interactions and communication paths), and cooperation (interactions among the system’s elements at different scales). Thus, the evolution leads to structural complexity that, in turn, supports complex dynamical behaviours. The appropriate quantities that capture these features of the SOC behaviour can be defined and computed as the signature of SOC states; see an overview of quantities and numerical methods in Ref. [5], with our further highlight hereinafter. Recent surveys [2,6] reveal that, while the concept of SOC has evolved in different directions (see more discussion below), it remains a source of inspiring new research and surprising discoveries connecting the ideas of collective behaviours, the emergence and complexity, see Figure 1.
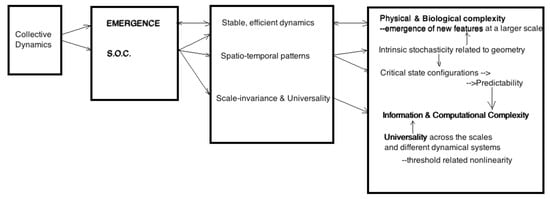
Figure 1.
Schematic view showing the role of SOC collective dynamics in relation to different aspects of complexity.
In this context, the sandpile automata (SPA) models serve as the paradigm of SOC, marked by the formulation of BTW sandpile automaton [3]. They have been a proper mathematical framework to define different quantities and characterise the threshold instability and the character of the emergent critical states [7]. In addition to the deterministic symmetrical BTW, other SPA models with probabilistic rules [8], directed deterministic [7] or stochastic [9] SPA all introduced new ways to SOC and different universal features (classes of criticality) [10].
Since the beginning, the idea of SOC was linked to complexity and contingency [11] in the sense of the emergent new feature through the collective dynamics. Hence, SOC provides an underlying mechanism for the physical complexity—the genesis of new collective properties from individual constituents, which is found in many complex systems across the scales (see more details below). It has been argued that the same physical principles lay the foundations for biological complexity [12]. Remarkably, the frustration caused by competing interactions at different levels could be identified as a “general driving force behind the emergence of complexity” [12].
Another link connects the information complexity [13] and SOC. In the context of data analysis, it concerns the relevance [14] of the information that can be stored in the critical state, as well as the related computational complexity [15,16], the problems of prediction of individual states [17], and mesoscopic avalanche prediction [18]. The idea that complex systems exhibit a hidden order, emerging through self-organised dynamics, links it to information that that ordering patterns may contain [19]. This idea becomes increasingly more interesting in the era of quantum information, which substantially extended the views of classical information theory introducing new concepts linked to complexity, see the main focus point in [20]. In this context, the occurrence of critical states with their self-similarity leads to the optimisation of information entropy [21], thus reducing the information complexity. Remarkably, considering the information relevance, it was shown [21] that the occurrence of a power-law frequency distribution (such as Zipf’s law) “arises at the optimal trade-off between resolution (i.e., compression) and relevance”. Such “maximally informative” samples, on the other hand, allow assessment of the number of parameters that can be inferred from a given dataset without prior knowledge about the underlying generative processes.
Furthermore, the information theory analysis also revealed a formal similarity of the SPA automata and several other systems with a threshold-like nonlinearity, in particular, the zero-temperature Ising spin dynamics [22]. Recent studies considered SPA dynamics on non-compact lattices and graphs [23], fractals and percolation clusters [24,25,26] and Penrose tailing [27], adapting the dynamical rules to the local connectivity of sites (nodes of the graph). It has been understood that the substrate structure may profoundly impact the dynamics yielding the stable critical states of different universality classes that can be reached. Moreover, the abelian nature of the dynamics (independence of the order of toppling) was one of the key features leading to the observed critical states [23]. Another line of research uses continuous models and connects SOC with tropical geometry in log-log scale (which can be understood as the zero-temperature limit of classical algebraic and geometrical operations; see [28] and references there). It was shown that the critical state and its evolution, where the toppling function satisfies the least action principle, can be described in terms of tropical geometry [28]. Other variants of the SPA models with disorder and finite driving rates that allow the study of “avalanche queues” lead to non-universal critical behaviours [29]. The models with the correlated disorder were studied by renormalization-group in [30,31,32].
The diversity of avalanches occurring in a SOC state and the role of open boundaries in maintaining the critical state is another relevant issue that receives renewed attention, e.g., in the context of the large avalanche prediction [18]. Again, SPA models appear as useful tools in this context too. Remarkably, in [33] the class of avalanches that spill the grains over the open boundaries are identified as responsible for the observed scaling behaviour of the SPA. The diversity of avalanches can be even higher in natural systems, and more realistic models of physical systems having multiscale structural patterns and entropy complexity are required [34]. They depend on the fractal energy landscape; for example, in the bistable spin systems under the slowly increasing external fields, the spanning avalanches in different dimensions obey different scaling properties [35]. Besides the physical geometry of the sample [36,37], the implicated portion of the phase space plays the role. Thus, the avalanches originating in the centre of the hysteresis loop, when the system is away from the two global minima, have different scaling properties compared to the ones observed at both ends of the loop [36]. In social systems, a different type of scale invariance is observed when the network that supports the dynamics grows during the avalanching dynamics [38], such that each avalanche touches the boundaries but without spill-over. Notably, in both cases, the sequence of avalanches represents a multifractal set with a non-random distribution of avalanche returns.
This feature article has two goals. Firstly, we give a brief survey of a diversity of current research trends of SOC systems across different scales and types of interactions. Secondly, we present new results on the field-driven spin dynamics in complex nanonetworks, an appearing prominent example of SOC behaviour induced by the substrate’s geometry. Using several representative examples of SOC systems of different nature and interaction patterns, we highlight some fundamental aspects of the dynamic complexity. The noisy output signal, representing a fingerprint of the system’s functioning, is often accessible from data, e.g., in biological, social and physical systems at different scales and often measured in the laboratory and produced by numerical simulations. We briefly define several quantities as signatures of SOC that can be determined from the output signal. Furthermore, focusing on the role of the complex-geometry substrate, we simulate the field-driven spin dynamics on nanonetworks with simplicial-complexes architecture. With the antiferromagnetic interactions among the neighbour spins, the triangle faces of the built-in simplexes provide the conditions for the spin frustration effects. By performing a detailed analysis of the simulated magnetisation noise signals, we demonstrate SOC behaviour occurring on the hysteresis loop in these complex assemblies at the interplay of geometric frustrations and external driving. Our study allows to identify and constructively describe the promising ways to investigate self-organised critical states under the competing higher-order interactions embedded in complex geometries.
2. Properties of the Self-Organised Critical States
In this section, we describe those fundamental properties of SOC states that are most important in our further discussion, and in doing so, we rely on some established results known from the literature. As stated above, the fingerprints of SOC are connected with the avalanching dynamics, exhibiting spatial and temporal correlations. Consequently, the corresponding quantities that characterize the occurrence of SOC states and the related universality class can be theoretically defined and numerically determined [5]. Specifically, some of the quantities that can be inferred from empirical time series data or model simulations are introduced in the following (see more in Section 4). For the continuous models, the renormalization group for non-equilibrium dynamical systems can be used; see, for example, references [30,31,32]. Recently, a new machine learning method was introduced to assess multi-scale structural complexity of emergent patterns [34].
The temporal activity correlations, -noise, and multifractal fluctuations. The system’s activity time series of data points, cf. an example in Figure 2, exhibits self-similarity with non-trivial temporal fluctuations. They are characterised by the temporal correlation function , algebraically decaying with the time lag . At the same time, the correlations of the signal’s profile increases, i.e., , where . These features are further manifested in the power-spectrum density exhibiting a power-law decay
valid for a range of frequencies f, where theoretically the scaling law holds.
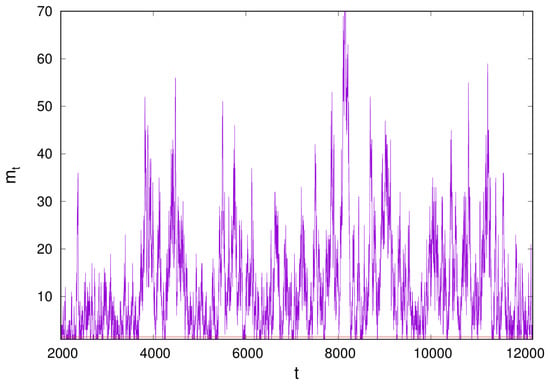
Figure 2.
The activity time series during the magnetisation reversal process in thin random-field ferromagnet [36].
These identified attributes of the system are closely related with the power-law singularity in time series, which manifests in the multi-fractal fluctuations [39] of the time series profile . It is suitably studied by the detrended multifractal analysis, see [40,41] and references therein. Specifically, dividing the signal into non-overlapping segments of the length n, the standard deviation around the local trend at each segment is determined as . The process is repeated starting from the end of the signal. Then, the r-th order fluctuation function is determined as [40,41]
Here, defines a generalised Hurst exponent, which can be determined from the slope of a straight line in the log-log plot of the fluctuation function for each r value. The parameter r takes a range of the negative and positive values, corresponding to the amplification of the small and large fluctuations, respectively. Note that for a mono-fractal time series for all values of r, where is the standard Hurst exponent.
Self-similarity, power-law avalanche distributions, and finite-size scaling. In the SOC systems, an avalanche of the activity may occur in response to the external perturbation (driving). The driving force can act at a single site, e.g., as in the SPA, which helps define mathematical limit known as the infinitely slow driving, or at several different sites, corresponding to a finite driving rate. Moreover, the SPA paradigm allows defining an adiabatic evolution, where the driving force is halted during the evolution of the avalanche, which is theoretically appealing, in contrast to the laboratory systems (see a more detailed discussion in [42]). The avalanche size s is then determined as the number of different sites where the activity occurred before the system is quiescent again. Similarly, the corresponding time since the avalanche is triggered until the activity ceases defines the duration T of the avalanche. Other related quantities, e.g., dissipated energy, can be defined depending on the physical system. Note that these quantities can be also determined from the activity time series, considering the avalanche as a segment of the time series between two consecutive drops to zero (or to a baseline, cf. Figure 2, discriminating random fluctuations [38].)
The most striking feature of SOC states is self-similarity or the absence of the characteristic length of avalanches within a given range determined by the finite system size. Ideally, their size and duration are described by a power-law function with the corresponding scaling exponent
Moreover, the exponential type of cut-off is induced by the finite system size. Given that different avalanche properties stem from the same nonlinear dynamics, their characteristics, e.g., the size and duration, are statistically related. Specifically, selecting all avalanches of a given duration, their average size scales with the duration T is given as , and the exponent is expressed as . We note that other properties in the dynamics, e.g., defects, can introduce a different scale, as discussed below. The scale-invariance of the avalanches has two immediate consequences. First, in the SOC state, a system-size event (catastrophic avalanche) has a finite probability. Moreover, the system size plays a vital role in determining the features of the events inside the system. Consequently, a thorough finite-size scaling (FSS) analysis is necessary, analogously to one known at the second-order phase transitions [43].
An additional relevant scale can appear along with the finite system size, leading to a two-parameter scaling function. As typical representative examples, we mention the system’s specific shape [36] and the intrinsic disorder, causing new types of critical behaviour [30,31]. The scale invariance, occurring when the linear system length L is rescaled by the factor ℓ, can be determined in the avalanche distribution , e.g., for the avalanche size or the duration in the presence of disorder p and the finite system of the linear size L. It is expressed by the generalised scaling function form , where is the generalised scaling factor of the distribution, meanwhile the corresponding variables scale with their respective factors and . Choosing the scaling factor, for example, such that , one can obtain the scaling form of the distribution of X. Specifically, we have , where we can identify is the scaling exponent measured in the power-law region of the distribution, and the two scaling variables can be identified, leading to the scaling form
where is the fractal dimension of the variable X. Meanwhile, is the characteristic length induced by the disorder variable p. The appropriate numerical values of the exponents , , and enable a successful scaling collapse. We note that describes how the cut-off length scales with the system size, , while depends on the type of defects. For example, if the random distribution of defect holes is considered, then we have [44] that defining the characteristic linear distance between the defects. In the absence of disorder , and the standard SPA scaling function of the variable is recovered.
The scaling collapse according to Equation (4) can be attempted in two limits. First, a weak disorder does not affect the scaling collapse for different system sizes as long as this length separation applies. In the opposite limit, when the disorder is strong, the length , and the scaling collapse can be attempted considering different p values and fixed large system size L, see, for example, Ref. [44] for the avalanche distributions in the case of the directed SPA with uncorrelated site defects. In between these two limits, however, a two-variable scaling function is needed. Such scaling collapse is challenging to achieve numerically, and it is rarely performed. Moreover, a disorder-induced dynamical phase transition may occur from SOC to a strong-disorder dynamical regime. The FSS with a two-variable function can then be used to determine the critical line, for example in [36,45].
The spatial propagation of avalanches strongly depends on the dynamical rules and the underlying substrate geometry. Often, the finite-size scaling form of the type (4) with a well-defined fractal dimension does not hold. Instead, a mutifractal scaling of avalanche distributions is obtained [29,46,47] according to
compatible with the spectrum of the fractal dimensions . Studies of SPA models have revealed that this type of scaling is related to multiple toppling of a site during the same avalanche, so-called toppling waves in BTW model [48]. Hence, the toppling numbers at neighbouring sites may differ considerably, exhibiting a power-law singularity, in analogy to the above mentioned time series. In the directed SPA, such conditions arise in temporally disordered flows [49], as well as in the case of dissipative sandpiles with finite driving rates [29]. It should be noted that the linear scale L in the above Expressions (4) and (5) is a good measure of the system size in the case of compact lattices and regular graphs. In the case of structured graphs, the graph’s diameter scales with the number of nodes N as ; meanwhile, the topological inhomogeneities at different scales may impact the avalanche propagation, depending on the stochastic process in question.
The power-law ranking (Zipf’s and Heaps’ laws) and inter-activity distributions. These properties of SOC states are closely related to the avalanche evolution. For example, in the earthquake data [50], knowledge-creation [51] and biological data [52], to mention only a few, they can be determined from the activity time series. In general, it has been shown [53] that in non-ergodic systems, the reduction of phase space due to self-adaptation of the system along an evolutionary path leads to Zipf’s law.
3. Self-Organised Critical Systems and Their Networks at Different Scales
Studies of a vast number of complex systems at different scales, natures and types of interactions have shown signatures of SOC; see the survey in the book [2]. The examples shown in Figure 3 are representative in complex systems and are along the significant research lines indicated below.

Figure 3.
Network representations of different complex systems: (a) core network of the human connectome, data from [54]; (b) network of the self-assembled nano-materials grown by the model rules [55]; (c) dialogue-based structure of the online social network, data from [56]; (d) bipartite-graph representation of the interacting agents and viruses in the model [57], indicating the infection transmission events. Different colours of nodes in (a–c) indicate the characteristic community structural features, which have a profound impact on the nature of collective behaviours.
The brain as an SOC system has been studied intensively as a prominent example of biological complexity. Both the brain imaging data and laboratory neural systems were considered; see reviews [58,59]. The main idea is that the SOC attractor maintains a stable response under ever-changing inputs, thus enabling robust brain function. It was demonstrated [60] that the self-organising dynamics of the brain waves reside on balanced excitatory–inhibitory interactions on the connectome. Another research line connects the hierarchical architecture of brain networks and SOC dynamics [61], also pointing out to the structural adaptation [62]. Recently, the occurrence of higher-order structures (simplicial complexes) in human connectomes were demonstrated [54,63]. The role of such complex topologies in brain dynamics was pointed out [64]. Even though the brain data increasingly confirm the evidence of SOC, understanding the precise role of brain criticality remains a challenging question [65,66]. The underlying dilemma, as pointed out in a recent perspective paper [65], is whether the primary cause for the brain criticality lies in the demand of its robustness or improved functionality, both of which are compatible with SOC states. Given the multiple brain functions that maintain human activity, psychology, and behaviour, there is almost no easy answer to these questions. In contrast to complex artificial systems designed to improve either robustness or functionality, for example, by using SOC as a guiding rule, the biological systems have developed through the evolutionary optimization processes. During these evolutionary developments, adapting both robustness and functional properties played their role. A deeper insight into the role of criticality in balancing the robustness and functionality can be achieved by studying empirical data regarding brain disorders [67]. For example, neurology studies confirm that several disorders, such as Parkison’s disease, are related to the appearance of specific protein aggregates and their subsequent diffusion among connected brain regions. In [68], where such proteinopathy inclusions in engineered human neural networks have been studied, it has been recognized that “self-organized criticality represents the critical point between resilience against perturbation and adaptational flexibility.”
Physical systems exhibiting well-pronounced signatures of SOC have been investigated in the laboratory experiments with liquid foams [69], criticality at the hysteresis loop in ferromagnets and ferroelectric switching [36,70,71], crackling noise in strained and porous materials [72], and shape-memory alloys [73]. On a larger scale, SOC was demonstrated in the data of natural systems from the forest fire [74], earthquakes [75] and ocean geophysical turbulence [76] to solar flares [77] and other astrophysical phenomena [2]. In these systems, the actual degrees of freedom, the nature of interactions, and driving forces are well known, enabling the description of the system’s evolution within the theoretical physics concepts. The Hamiltonian operator is readily constructed to describe the system’s energy at the microscopic scale, meanwhile taking into account all interaction properties and pertinent constraints, e.g., due to the system’s boundaries and geometry of the underlying grid. Furthermore, considering the global energy minimisation principle in physical systems, the frustration dynamics due to competing interactions at different scales can be formally described [78,79,80]. Continuum models of SOC are based on the stochastic PDEs describing, for example, the fluctuations of height (mass) [81], or energy correlations [82] of a SPA. Analysis of these evolution equations provides new insights into the nature and stability of the critical state and the scaling region of the implicated parameters. Moreover, continuum models enable the use of the dynamic renormalisation group to determine different classes of universal scaling behaviours and their stability depending on the identified relevant parameters [30,31,32].
Social systems with cooperative dynamics, studied using the dynamical data from online social sites [38,51,83,84,85], appear to possess the mechanisms of SOC that enable the genesis of collective values from the individual features (knowledge, emotions, and behaviours) of the communicating participants. The same active principle seems to underscore the emergence of languages [86,87], as well as the social protests [88], wars [89], and historical processes [90]. In contrast to the above mentioned physical systems, the interactions underlying social self-organisation have different attributes that are elusive to similar formal theories. However, these interactions are elucidated by the concepts of social psychology, and cognitive sciences [91]. For example, the participants’ cooperative behaviour during the collective knowledge creation manifests the meaningful interactions, more precisely, the interactions “designed to serve the needs of others” [92]. Such social endeavours, where individuals engage in sharing their abilities with the community [93] resulting in a collective value, often involve the mechanisms of SOC. A striking example is the dynamics of knowledge creation via “questions-and-answers” [38]. The growing knowledge shared by the active participants is an immediate common value quantified by different collective behaviour measures [51]. Furthermore, the network of knowledge contents used by the participants [84,94] remains as a permanent “explicit knowledge” outcome of the process.
Bio-social dynamics, such as epidemics spreading, is an example of collective phenomena that emerge from the features and behaviours of individuals. The genesis of the collective social behaviours connects the social interactions with factors related to the biology of the antigen (virus) [57,95]. It remains to be studied if the SOC signatures are present in the empirical data or if they can be incorporated to affect the evolution of the epidemic.
Designed systems utilise properties of the SOC critical state to improve their functional stability and efficiency. Examples include designed computer networks [96] and job scheduling [97], but also modelling the hospital management processes [98], empirical data of urban systems [99], and stock market dynamics [100]. New classes of functional materials, for example, frustrated spin systems [101,102,103], are being designed to improve their functional properties, for example, relevant to spintronics. We note that, in this inverse problem approach, the system’s elements, interactions and parameters of the dynamics are varied such that they eventually result in the desired SOC behaviour. In the following, our main exemplification of the analysis is given for a designed nano-structured system with simplicial complexes that support SOC dynamics of spin reversal. Here, we describe the key elements of the model for the self-assembly of pre-formatted groups on nanoparticles [55], which we use to grow the nano-network that underlies the spin interactions.
In the model, [55], the groups of particles that simultaneously join the growing structure are represented by cliques (complete graphs) of different sizes. The attachment of each clique is constrained by the geometric compatibility of its faces with the current structure (see also [104] for the case of defect edges), and the chemical affinity factors, controlled by the parameter . More precisely, a clique of the size is added by sharing one of its faces, of the size , with a clique present in the growing structure. Here, the faces define a single node, link, triangle, tetrahedron, and so on up to the largest sub-clique . The remaining new nodes are added simultaneously and mutually connected such that they form the clique with the nodes belonging to the shared face. The probability for attaching along the clique’s q-face is given by [55]
Here, the factor denoted by is the number of geometrically compatible locations for docking a simplex of the order q, found at the growth step on the entire network. In the most general case, the geometrical factor is weighted by the chemical affinity of the system towards the addition of new nodes. Notably, a more significant number of nodes can be added when , where the cliques share a single node, in contrast to the case with , where the probability to share progressively more significant face increases with the increasing . By varying the parameter , the sizes of cliques that appear in the process, and the number of steps , the model permits the growth of a variety of simplicial complexes (see the online demo on this link [105]). Some prominent examples of the emergent simplicial complexes and their structural analysis can be found in [55,104].
4. Hysteresis-Loop Criticality in Nanonetworks with Simplicial Complexes
The nano-network structure with simplicial complexes that enables complex interaction patterns is grown by the self-assembly algorithm described in [55,104]. It attaches cliques of different sizes , where their population decays algebraically with size as . Compared to the general model, we consider the case without the chemical affinity (); hence, the assembly rules are governed strictly by the geometric compatibility of the attaching clique with the growing structure. In addition, each clique has a potential defect bond that can affect the docking, as explained in [104]. The resulting assembly has an intrinsic simplicial complexes structure, which has been described in [104]. Consequently, its topological graph, i.e., 1-skeleton of the simplicial complex, is a Gromov hyperbolic graph with a small hyperbolicity parameter , as shown in [55].
For the present study, we show in Figure 4 several structural features of the network, consisting of N = 10,000 nodes and E = 29,483 edges, that are relevant to the spin dynamics. Particularly, the network’s heterogeneity (see Figure 3b) implies a fat-tail distribution of the node’s connectivity, k, the main part of which can be approximated by Tsallis -exponential distribution with . Its average degree is = 5.897, clustering coefficient = 0.712, and the path length is = 6.815; the graph’s diameter is . Moreover, it possesses assortative correlations among the node’s degrees, according to , where for . In the second inset of Figure 4, we show the distribution of the number of simplexes and faces of the size q, where indicates the nodes, edges, triangles, tetrahedrons, and so on, up to the largest clique of ten nodes. As described below, this structure can support complex interaction patterns of the dynamical variables associated with different geometrical faces.
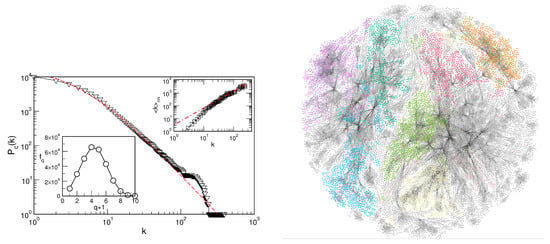
Figure 4.
(Left): The network’s cumulative degree distribution (main) and the assortative mixing (top right inset); the number of simplexes and faces of the order q, vs. q (lower left inset). (Right): The network view is shown with the community structure indicated by different colours of nodes.
To study the field-driven spin reversal dynamics on this network substrate, an Ising spin is attached to each network node and the interactions among spins are enabled by the simplex faces of different order. In the most general case, the Hamiltonian is given by
where h is the external field and the interaction differs from zero when the indexes belong to one of the simplexes faces in the set of the corresponding size ; the upper limit indicates the highest order of the considered interaction, which is determined by the order of the largest clique in the simplicial complex. Note that a precise identity of nodes that make each simplex and face of the order is necessary for determining the contribution of the interactions of that order in (7), see, for example, studies in [106,107] for the competing pairwise and triangle-based interactions. By growing the structure, we keep track of nodes that make each attached simplex. In general, such information is obtained by Q-analysis of a given simplicial complex [104,108]. It should also be noted that the leading (pairwise) interactions chiefly promote the long-range order; meanwhile, the higher-order terms determine the type of criticality and shape the hysteresis loop, in agreement with the renormalization-group theory [30,31,32] and also recent numerical studies of the dynamics on simplicial complexes [106,107,109].
In the present study, we introduce the antiferromagnetic interactions of the leading order, i.e., ; in conjunction with the triangle faces of simplexes, they induce the geometric frustration effects [101,102,110]. Specifically, attempting to minimize the energy, the orientations of all three spins on a triangle cannot be simultaneously satisfied. Consequently, a local interaction can have a large-scale impact. The system is driven by the external magnetic field h and applying the zero-temperature dynamics [36]. Specifically, starting from a state with all spins down, and a large negative field , the field is increased adiabatically in small steps. We note the absence of any magnetic disorder in the present system, and the natural driving rate is determined by the changing connectivity of nodes, cf. Figure 4. Hence, it is compatible with the integer steps , and corresponds to the largest connectivity node in the network.
A parallel update of all nodes is applied. For each time step t, the local field consisting of the current value of the external field and the contribution of the nearest-neighbour spins of each node is computed. Under the applied field, each spin attempts to align with its local field to minimize global energy. Alignment occurs with a probability , allowing frustrated spins to select one of the possible states. A reversed spin changes the local field at its neighbour nodes, which can trigger these spins to flip in the next time step, and so on, producing an avalanche. The avalanche stops when no more unstable spins are found. Then, the field is increased again. The process is repeated until , completing an ascending branch of the hysteresis loop, then the field is slowly decreased along the descending branch to complete the loop. A detailed program flow can be found in [110]. For the present analysis, the temporal variation of the field h, the magnetisation , and the magnetisation changes (Barkhausen noise) are sampled at each time step. The results are shown in Figure 5, Figure 6 and Figure 7.
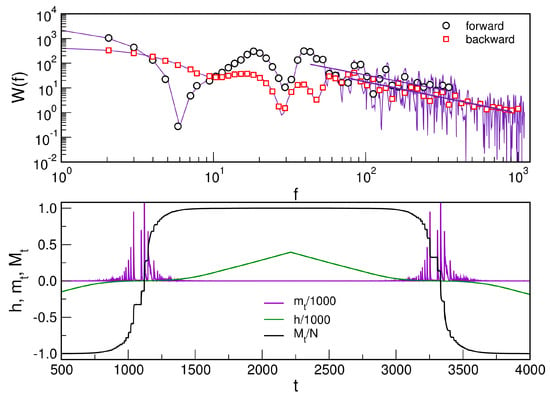
Figure 5.
(Bottom): Time dependence of the driving field h, the magnetisation , and the magnetisation fluctuations during the forward and then backward sweeps along the hysteresis loop. (Top): Power spectrum of the magnetisation fluctuations.
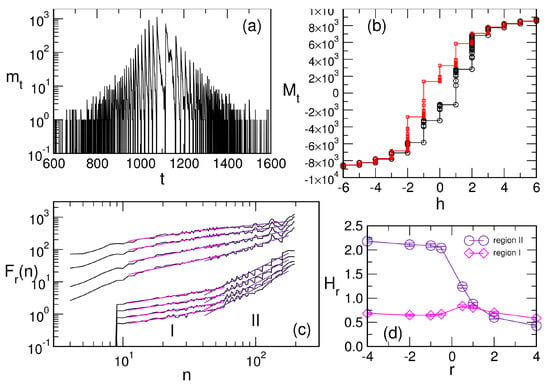
Figure 6.
The magnetisation fluctuations signal (a) during the forward sweep on the hysteresis loop shown on panel (b), and its multifractal function plotted against the interval n for different values of the amplification factor , panel (c). The generalised Hurst exponent as a function of r is shown on panel (d) for two scaling regions of , indicated as I and II in (c).
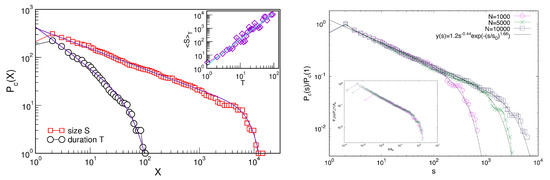
Figure 7.
Left: Cumulative distribution of the avalanches size s and duration T for the network size ; fits according to the Equation (3). Inset: The average size of the avalanches of a given duration T against T. The slope is the scaling exponent defined in the text. Right: Normalised distributions of the avalanche size s for different network sizes N indicated in the main figure, and their scaling collapse using the fitted values for cut-offs (inset).
The hysteresis loop shows plateaus of fractional magnetisation, cf. Figure 6b, resembling ones observed experimentally in frustrated antiferromagnetic materials [111]. Between these plateaus, the magnetisation increases in jumps of different sizes, see Figure 5 bottom panel. These magnetisation jumps comprise the Barkhausen noise signal , an example is shown in Figure 6a. A detailed analysis of the noise signal reveals several quantitative measures of SOC, as shown in Figure 5 and Figure 6. In particular, the power spectrum of the signals for both ascending and descending branches, shown Figure 5 top panel, obey the power-law decay in Equation (1) for a range of large frequencies with the exponent . Furthermore, by computing the fluctuation function defined in Equation (2) of the magnetisation jumps , we find multi-fractal features with large variations of the generalised Hurst exponent for a range of time-series segments ; meanwhile a monofractal fluctuations with the Hurst exponent occur at smaller segments, as shown in Figure 6c,d. Furthermore, we determine the avalanche size as and duration from the signal’s segments between two consecutive drops to zero at and points. The cumulative distributions of the avalanche size and duration, averaged over ten network samples, are shown in Figure 7. They are compatible with the expression in Equation (3), where we can extract the exponents and in the segment before the stretched exponential cut-offs; note that these values are close to the mean-field exponents. We further show that these cut-offs are due to the network size and no additional scale in the system. Consequently, the finite-size scaling form (4) with a single scaling variable applies, as shown in the inset to Figure 7 right panel. We note that we used the precise cut-off value to scale sizes in each distribution. Thus, we cannot determine the fractal dimension of these avalanches, given that the variations of the relevant linear scale are minimal for finite networks.
5. Discussion and Conclusions
The SOC occurs in many complex systems and networks at various scales, types of interactions, and intrinsic dynamics. They all obey some universal behaviours that can be captured by the properties of the emergent critical states. These are the long-range correlations, fractality, avalanching dynamics and scale invariance. It has been understood that these properties of the critical states can provide a deeper understanding of different aspects of complexity. In particular, recent research on various SPA models and real-world systems strives to underpin self-organised critical behaviour in the mechanisms underlying the emergence of new collective features, essential for the physical and biological complexity. They also provide a more transparent structure of information stored in the critical state and reduced computational complexity. In the context of complexity, understanding the role of various geometrical constraints in the critical dynamics and hidden geometry features that enable competing interactions at different scales are of paramount importance.
As a prominent example, we have studied the field-driven magnetisation reversal in antiferromagnetic nanonetworks with the simplicial complexes architecture. The underlying dynamics is related to the motion of domain walls separating the oppositely oriented Ising spins in this complex structure. With the state-of-the-art analysis, we have demonstrated the occurrence of SOC at the hysteresis loop in these assemblies. Remarkably, the simulated Barkhausen noise signal exhibits the multi-fractal features, the power-law decay of the power spectrum, and the scaling of avalanches. It should be stressed that the critical avalanches in our assembly appear without any magnetic disorder, in contrast to the case of random-field ferromagnets on a compact lattice where the criticality is associated with a critical disorder line [36]. The origin of SOC in our system can be attributed to the interplay between antiferromagnetic interactions and the network structure with triangle faces of simplexes providing the geometric frustrations, inducing non-local effects. Moreover, the finite driving rate (appropriate to this type of systems) may have its impact. In this context, we note that for a specific type of interaction, the driving mode can potentially change the criticality related to a dynamical phase transition to SOC [112]. The studied complex nano-assembly represents a rich laboratory to explore the geometry impact on the Ising spins dynamics, for example, by varying strength of the pairwise interactions [113] that can reduce the geometric frustration. Moreover, including the higher-order interactions of different order and sign according to Equation (7) and studying how they can modify the observed SOC behaviour remains one of the outstanding open questions. To this end, we have introduced the generalised Hamiltonian in Equation (7), indicating how these higher-order interactions can be implemented based on a concrete simplicial complex architecture. The renormalisation-group approaches complementing the numerical studies would be desired for determining the relevance of these geometrically constrained interactions of increasing orders.
Besides the popular SPA models, the motion of domain walls in complex substrates appear to be suitable physical models for the study of SOC. The domain walls are extended objects that can promote long-range impact based on local interactions. On the other hand, the substrate’s topology determines multiple walls and constraints their motion, potentially leading to the phenomenon of “domain-wall jamming”, for example, seen in ferroelectrics [72]. Our study has shown how the network substrates with the hierarchical architecture of simplicial complexes enable the competing interactions of different orders, potentially significant driving force of SOC [12] in these complex geometries. The presented analysis, obtained results, and motivating representative examples from physical, biological, and social systems, along with their networks, should stimulate further research in SOC dynamics, providing a deeper understanding of complexity.
Author Contributions
Conceptualization, B.T. and R.M.; methodology and software, B.T.; validation, B.T. and R.M.; formal analysis and visualization, B.T.; writing—original draft preparation, B.T.; writing—review and editing, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
B.T. research is funded by the program P1-0044 of The Slovenian Research Agency. R.M. thanks the NSERC and the CRC Program for their support and he is also acknowledging the support of the BERC 2018–2021 program and Spanish Ministry of Science, Innovation, and Universities through the Agencia Estatal de Investigacion (AEI) BCAM Severo Ochoa excellence accreditation SEV-2017-0718, and the Basque Government fund “AI in BCAM EXP. 2019/00432”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This is a theoretical study. Figure 3a,c is based on publicly available data first collected and used in references [54,56], respectively, cf. Figure caption.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jensen, H.J. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems; Cambridge Lecture Notes in Physics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Aschwanden, M.J. Self-Organized Criticality Systems; Open Academic Press: Berlin, Germany; Warsaw, Poland, 2013. [Google Scholar]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Marković, D.; Gros, C. Power laws and self-organized criticality in theory and nature. Phys. Rep. 2014, 536, 41–74. [Google Scholar] [CrossRef]
- McAteer, R.; Aschwanden, M.; Dimitropoulou, M.; Georgoulis, M.; Pruessner, G.; Morales, L.; Ireland, J.; Abramenko, V. 25 years of self-organized criticality: Numerical detection methods. Space Sci. Rev. 2016, 198, 217–266. [Google Scholar] [CrossRef]
- Watkins, N.W.; Pruessner, G.; Chapman, S.C.; Crosby, N.B.; Jensen, H.J. 25 years of self-organized criticality: Concepts and controversies. Space Sci. Rev. 2016, 198, 3–44. [Google Scholar] [CrossRef]
- Dhar, D. Self-organized critical state of sandpile automaton models. Phys. Rev. Lett. 1990, 64, 1613–1616. [Google Scholar] [CrossRef] [PubMed]
- Manna, S.S. Two-state model of self-organized criticality. J. Phys. Math. Gen. 1991, 24, L363–L369. [Google Scholar] [CrossRef]
- Tadić, B.; Dhar, D. Emergent spatial structures in critical sandpiles. Phys. Rev. Lett. 1997, 79, 1519. [Google Scholar] [CrossRef]
- Milshtein, E.; Buham, O.; Solomon, S. Universality classes in isotropic, Abelian, and non-Abelian sandpile models. Phys. Rev. E 1998, 58, 303. [Google Scholar] [CrossRef]
- Bak, P.; Paczuski, M. Complexity, contingency, and criticality. Proc. Natl. Acad. Sci. USA 1995, 92, 6689–6696. [Google Scholar] [CrossRef]
- Wolf, Y.I.; Katsnelson, M.K.; Koonin, E.V. Physical foundations of biological complexity. Proc. Natl. Acad. Sci. USA 2018, 115, E8678–E8687. [Google Scholar] [CrossRef]
- Braverman, M. Information complexity and applications. Jap. J. Math. 2019, 14, 27–65. [Google Scholar] [CrossRef]
- Song, J.; Marsili, M.; Jo, J. Resolution and relevance trade-offs in deep learning. J. Stat. Mech. Theory Exp. 2018, 2018, 123406. [Google Scholar] [CrossRef]
- Moore, C.; Nilsson, M. The computational complexity of sandpiles. J. Stat. Phys. 2020, 96, 205–224. [Google Scholar] [CrossRef]
- Goles, E.; Montealegre, P.; Perrot, K. Freezing sandpiles and Boolean threshold networks: Equivalence and complexity. Adv. Appl. Math. 2021, 125, 102161. [Google Scholar] [CrossRef]
- Formenti, E.; Perrot, K. How hard is it to predict sandpiles on lattices? Fundam. Inform. 2019, 171, 189–219. [Google Scholar] [CrossRef]
- Shapoval, A.; Savostianova, D.; Shnirman, M. Predictability and scaling in btw sandpile on a self-similar lattice. J. Stat. Phys. 2021, 183, 1–15. [Google Scholar] [CrossRef]
- Haken, H.; Portugali, J. Information and self-organization. Entropy 2017, 19, 18. [Google Scholar] [CrossRef]
- Mancini, S.; Marmo, G.; Pascazio, S. Quantum information and complexity. Eur. J. Phys. Plus 2014, 129, 269. [Google Scholar] [CrossRef][Green Version]
- Cubero, R.J.; Jo, J.; Marsili, M.; Roudi, Y.; Song, J. Statistical criticality arises in most informative representations. J. Stat. Mech. Theory Exp. 2019, 2019, 063402. [Google Scholar] [CrossRef]
- Moore, C. Majority-vote cellular automata, Ising dynamics, and p-completeness. J. Stat. Phys. 1997, 88, 795–805. [Google Scholar] [CrossRef]
- Zachariou, N.; Expert, P.; Takayashu, M.; Christensen, K. Generalized sandpile dynamics on artificial and real-world networks. PLoS ONE 2015, 10, e0142685. [Google Scholar] [CrossRef]
- Shapoval, A.; Shnirman, M. The BTW mechanism on a self-similar image of a square: A path to unexpected exponents. Phys. A 2020, 391, 15–20. [Google Scholar] [CrossRef]
- Bhaumik, H.; Santra, S.B. Critical properties of deterministic and stochastic sandpile models on two-dimensional percolation backbone. Phys. Stat. Mech. Its Appl. 2020, 548, 124318. [Google Scholar] [CrossRef]
- Najafi, M.N.; Cheraghalizadeh, J.; Luković, M.; Herrmann, H.J. Geometry-induced nonequilibrium phase transition in sandpiles. Phys. Rev. E 2020, 101, 032116. [Google Scholar] [CrossRef]
- Fersula, J.; Nous, C.; Perrot, K. Sandpile toppling on Penrose tilings: Identity and isotropic dynamics. arXiv 2020, arXiv:2006.06254v1. [Google Scholar]
- Kalinin, N.; Guzman-Saenz, A.; Prieto, Y.; Shkolnikov, M.; Kalinina, V.; Lupercio, E. Self-organized criticality and pattern emergence through the lens of tropical geometry. Proc. Natl. Acad. Sci. USA 2018, 115, E8135–E8142. [Google Scholar] [CrossRef] [PubMed]
- Tadić, B.; Priezzhev, V. Scaling of avalanche queues in directed dissipative sandpiles. Phys. Rev. E 2000, 62, 3266–3275. [Google Scholar] [CrossRef]
- Tadić, B. Disorder-induced critical behavior in driven diffusive systems. Phys. Rev. E 1998, 58, 168–173. [Google Scholar] [CrossRef]
- Antonov, N.V.; Gulitskiy, N.M.; Kakin, P.I.; Serov, V.D. Effects of turbulent environment and random noise on self-organized critical behavior: Universality versus nonuniversality. Phys. Rev. E 2021, 103, 042106. [Google Scholar] [CrossRef] [PubMed]
- Hwa, T.; Kardar, M. Avalanches, hydrodynamics, and discharge events in models of sandpiles. Phys. Rev. A 1992, 45, 7002. [Google Scholar] [CrossRef]
- Drossel, B. Scaling behavior of the Abelian sandpile model. Phys. Rev. E 2000, 61, R2168. [Google Scholar] [CrossRef]
- Bargov, A.A.; Iakovlev, I.A.; Iliasov, A.A.; Katsnelson, M.K.; Mazurenko, V.V. Multiscale structural complexity of natural patterns. Proc. Natl. Acad. Sci. USA 2020, 117, 30241–30251. [Google Scholar]
- Spasojević, D.; Janićević, S.; Knežević, M. Analysis of spanning avalanches in the two-dimensional nonequilibrium zero-temperature random-field Ising model. Phys. Rev. E 2014, 89, 012118. [Google Scholar] [CrossRef] [PubMed]
- Tadić, B.; Mijatović, S.; Janićević, S.; Spasojević, D.; Rodgers, G.J. The critical Barkhausen avalanches in thin random-field ferromagnets with an open boundary. Sci. Rep. 2019, 9, 6340. [Google Scholar] [CrossRef]
- Tadić, B. Dynamical implications of sample shape for avalanches in 2-dimensional random-field Ising model with saw-tooth domain wall. Phys. Stat. Mech. Its Appl. 2018, 493, 330–341. [Google Scholar] [CrossRef]
- Tadić, B.; Mitrović Dankulov, M.; Melnik, R. Mechanisms of self-organized criticality in social processes of knowledge creation. Phys. Rev. E 2017, 96, 032307. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, A.N.; Anishchenko, V.S. Multifractal analysis of complex signals. Phys. Uspekhi 2007, 50, 819–834. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Tadić, B. Multifractal analysis of Barkhausen noise reveals the dynamic nature of criticality at hysteresis loop. J. Stat. Mech. Theory Exp. 2016, 6, 063305. [Google Scholar] [CrossRef]
- Perez-Reche, F.J.; Tadić, B.; Manosa, L.; Planes, A.; Vives, E. Driving rate effects in avalanche-mediated first-order phase transitions. Phys. Rev. Lett. 2004, 93, 195701. [Google Scholar] [CrossRef]
- Privman, V. (Ed.) Finite Size Scaling and Numerical Simulation of Statistical Systems; World Scientific: Singapore, 1990. [Google Scholar]
- Tadić, B.; Nowak, U.; Usadel, K.D.; Ramaswamy, R.; Padlewski, S. Scaling behavior in disordered sandpile automata. Phys. Rev. A 1992, 45, 8536–8545. [Google Scholar] [CrossRef] [PubMed]
- Spasojević, D.; Mijatović, S.; Navas-Portella, V.; Vives, E. Crossover from three-dimensional to two-dimensional systems in the nonequilibrium zero-temperature random-field Ising model. Phys. Rev. E 2018, 97, 012109. [Google Scholar] [CrossRef]
- Tebaldi, C.; Menech, M.D.; Stella, A.L. Multifractal scaling in the Bak-Tang-Wiesenfeld sandpile and edge events. Phys. Rev. Lett. 1999, 83, 3952–3955. [Google Scholar] [CrossRef]
- Chang, T.; Wu, C.-C. Rank-ordered multifractal spectrum for intermittent fluctuations. Phys. Rev. E 2008, 77, 045401. [Google Scholar] [CrossRef]
- Ivashkevich, E.V.; Ktitarev, V.; Priezzhev, D.V.B. Waves of topplings in an Abelian sandpile. Phys. Stat. Mech. Its Appl. 1994, 209, 347–360. [Google Scholar] [CrossRef]
- Tadić, B. Temporally disordered granular flow: A model of landslides. Phys. Rev. E 1998, 57, 4375–4381. [Google Scholar] [CrossRef]
- Corral, Á. Local distributions and rate fluctuations in a unified scaling law for earthquakes. Phys. Rev. E 2003, 68, 035102. [Google Scholar] [CrossRef] [PubMed]
- Mitrović Dankulov, M.; Tadić, B.; Melnik, R. The dynamics of meaningful social interactions and the emergence of collective knowledge. Sci. Rep. 2015, 5, 12197. [Google Scholar] [CrossRef] [PubMed]
- Schwab, D.J.; Nemenman, I.; Mehta, P. Zipf’s law and criticality in multivariate data without fine tuning. Phys. Rev. Lett. 2014, 113, 068102. [Google Scholar] [CrossRef]
- Corominas-Murtra, B.; Hanel, R.; Thurner, S. Understanding scaling through history-dependent processes with collapsing sample space. Proc. Natl. Acad. Sci. USA 2015, 112, 5348–5353. [Google Scholar] [CrossRef]
- Andjelković, M.; Tadić, B.; Melnik, R. The topology of higher-order complexes associated with brain hubs in human connectomes. Sci. Rep. 2020, 10, 17320. [Google Scholar] [CrossRef]
- Šuvakov, M.; Andjelković, M.; Tadić, B. Hidden geometries in networks arising from cooperative self-assembly. Sci. Rep. 2018, 8, 1987. [Google Scholar] [CrossRef] [PubMed]
- Šuvakov, M.; Mitrović, M.; Gligorijević, V.; Tadić, B. How the online social networks are used: Dialogs-based structure of Myspace. J. Roy. Soc. Interface 2012, 10, 20120819. [Google Scholar] [CrossRef]
- Tadić, B.; Melnik, R. Modeling latent infection transmissions through biosocial stochastic dynamics. PLoS ONE 2020, 15, e0241163. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef]
- Plenz, D.; Niebur, E. (Eds.) Criticality in Neural Systems; Wiley-VCH Verlag GmbH & Co., KGaA: Weinheim, Germany, 2014. [Google Scholar]
- Atasoy, S.; Donelly, I.; Pearson, J. Human brain networks function in connectome-specific harmonic waves. Nat. Commun. 2015, 7, 10340. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O.; Thivierge, J.; Breakspear, M. Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput. Biol. 2011, 7, e1002038. [Google Scholar] [CrossRef] [PubMed]
- Maslenikov, O.V.; Shchapin, D.S.; Nekorkin, V.I. Transient sequences in a hypernetwork generated by an adaptive network of spiking neurons. Phylos. Trans. R. Soc. A 2016, 375, 20160288. [Google Scholar] [CrossRef] [PubMed]
- Tadić, B.; Andjelković, M.; Melnik, R. Functional geometry of human connectomes. Sci. Rep. 2019, 9, 12060. [Google Scholar] [CrossRef]
- Reimann, M.W.; Nolte, M.; Scolamiero, M.; Turner, K.; Perin, R.; Chindemi, G.; Markram, H. Cliques of neurons bound into cavities provide missing link between structure and function. Front. Comput. Neiurosci. 2017, 11, 48. [Google Scholar] [CrossRef]
- Gros, C. A devil’s advocate view on self-organized brain criticality. J. Phys. Complex. 2021, 2, 031001. [Google Scholar] [CrossRef]
- Plenz, D.; Ribeiro, T.L.; Miller, S.R.; Kells, P.A.; Vakili, A.; Capek, E.L. Self-Organized Criticality in the Brain. Front. Phys. 2021, 9, 639389. [Google Scholar] [CrossRef]
- Zimmern, V. Why Brain Criticality is Clinically Relevant: A Scoping Review. Front. Neural Circuits 2020, 14, 54. [Google Scholar] [CrossRef] [PubMed]
- Valderhaug, V.D.; Heiney, K.; Ramstad, O.H.; Brathen, G.; Kuan, W.-L.; Nichele, S.; Sandvig, A.; Sandvig, I. Early functional changes associated with alpha-synuclein proteinopathy in engineered neural networks. A J. Physiol. Cell Physiol. 2021, 320, C1141–C1152. [Google Scholar] [CrossRef]
- Ritacco, H.A. Complexity and self-organized criticality in liquid foams, a short review. Adv. Colloid Interface Sci. 2020, 285, 102282. [Google Scholar] [CrossRef]
- Shur, V.Y. Kinetics of ferroelectric domains: Application of general approach to LiNbO3 and LiTaO3. Front. Ferroelectr. 2006, 41, 199–210. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Xue, D.; Ding, X.; Dahmen, K.A.; Scott, J.F. Ferroelectric switching and scale invariant avalanches in BaTiO3. Phys. Rev. Mater. 2019, 3, 014415. [Google Scholar] [CrossRef]
- Nataf, G.F.; Salje, E.K.H. Avalanches in ferroelectric, ferroelastic and coelastic materials: Phase transition, domain switching and propagation. Ferroelectrics 2020, 569, 82–107. [Google Scholar] [CrossRef]
- Gallardo, M.C.; Manchado, J.; Romero, F.J.; del Cerro, J.; Salje, E.K.H.; Planes, A.; Vives, E.; Romero, R.; Stipcich, M. Avalanche criticality in the martensitic transition of Cu67.64Zn16.71Al15.65 shape-memory alloy: A calorimetric and acoustic emission study. Phys. Rev. B 2010, 81, 174102. [Google Scholar] [CrossRef]
- Malamud, B.; Morein, G.; Turcotte, D. Forest fires: An example of self-organized critical behavior. Science 1998, 281, 1840–1842. [Google Scholar] [CrossRef]
- Corral, Á. Long-term clustering, scaling, and universality in the temporal occurrence of earthquakes. Phys. Rev. Lett. 2004, 92, 108501. [Google Scholar] [CrossRef] [PubMed]
- Smyth, W.D.; Nash, J.D.; Moum, J.N. Self-organized criticality in geophysical turbulence. Sci. Rep. 2019, 9, 3743. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Dai, Z. Self-organized criticality in X-ray flares of gamma-ray-burst afterglows. Nat. Phys. 2013, 9, 465. [Google Scholar] [CrossRef]
- Diep, H.T. Frustrated Spin Systems; World Scientific: Singapore, 2005; Available online: https://www.worldscientific.com/doi/pdf (accessed on 20 October 2021).
- Petit, S.; Guitteny, S.; Robert, J.; Bonville, P.; Decorse, C.; Ollivier, J.; Mutka, H.; Mirebeau, I. Spin dynamics in highly frustrated pyrochlore magnets. Eur. Phys. J. Web Conf. 2015, 83, 03012. [Google Scholar] [CrossRef]
- Vanderstraeten, L.; Vanhecke, B.; Verstraete, F. Residual entropies for three-dimensional frustrated spin systems with tensor networks. Phys. Rev. E 2018, 98, 042145. [Google Scholar] [CrossRef]
- Banas, L.; Gess, B.; Neuss, M. Stochastic partial differential equations arising in self-organized criticality. arXiv 2021, arXiv:2104.13336v1. [Google Scholar]
- Zhang, Y.-C. Scaling theory of self-organized criticality. Phys. Rev. Lett. 1989, 63, 470. [Google Scholar] [CrossRef]
- Tadić, B.; Gligorijević, V.; Mitrović, M.; Šuvakov, M. Co-evolutionary mechanisms of emotional bursts in online social dynamics and networks. Entropy 2013, 12, 5084–5120. [Google Scholar] [CrossRef]
- Tadić, B. Self-organised criticality and emergent hyperbolic networks: Blueprint for complexity in social dynamics. Eur. J. Phys. 2019, 40, 024002. [Google Scholar] [CrossRef]
- Dmitriev, A.; Dmitriev, V. Identification of self-organized critical state on Twitter based on the retweets’ time series analysis. Complexity 2021, 6612785, 2021. [Google Scholar]
- Loretto, V.; Steels, L. Emergence of language. Nat. Phys. 2007, 3, 758. [Google Scholar] [CrossRef]
- Gromov, V.; Migrina, A. A language as a self-organized critical system. Complexity 2017, 2017, 9212538. [Google Scholar] [CrossRef]
- Zhukov, D.; Kunavin, K.; Lyamin, S. Online rebellion: Self-organized criticality of contemporary protest movements. SAGE Open 2020, 10, 2158244020923354. [Google Scholar] [CrossRef]
- Roberts, D.; Turcotte, D. Fractality and self-organized criticality of wars. Fractals 1998, 6, 351–357. [Google Scholar] [CrossRef]
- Zhukov, D.S.; Kanishchev, V.V.; Lyamin, S. Application of the theory of self-organized criticality to the investigation of historical processes. SAGE Open 2016, 6, 2158244016683216. [Google Scholar] [CrossRef]
- Sun, R. (Ed.) Grounding Social Sciences in Cognitive Sciences; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Kitchener, R.F. Piaget’s Social Epistemology. In Social Interactions and the Development of Knowledge; Carpendale, J.I.M., Müller, U., Eds.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2013; pp. 45–66. [Google Scholar]
- Seraj, M. We create, we connect, we respect, therefore we are: Intellectual, social, and cultural value in online communities. J. Interact. Mark. 2012, 26, 209–222. [Google Scholar] [CrossRef]
- Andjelković, M.; Tadić, B.; Mitrović Dankulov, M.; Rajković, M.; Melnik, R. Topology of innovation spaces in the knowledge networks emerging through questions-and-answers. PLoS ONE 2016, 11, e0154655. [Google Scholar] [CrossRef]
- Tadić, B.; Melnik, R. Microscopic dynamics modeling unravels the role of asymptomatic virus carriers in SARS-CoV-2 epidemics at the interplay between biological and social factors. Comput. Biol. Med. 2021, 133, 104422. [Google Scholar] [CrossRef]
- Laredo, J.L.J.; Guinand, F.; Oliver, D.; Bouvry, P. Load balancing at the edge of chaos: How self-organized criticality can lead to energy-efficient computing. HAL Arch. 2019, 01960412, 2019. [Google Scholar] [CrossRef]
- Gasior, J.; Seredynski, F. A sandpile cellular automata-based approach to dynamic job scheduling in cloud environment. Lect. Note Comput. Sci. Book Ser. Parallel Process. Appl. Math. 2016, 9574, 46. [Google Scholar]
- Martucci, R.; Mascia, C.; Simeoni, C.; Tassi, F. Hospital management in the COVID-19 emergency: Abelian sandpile paradigm and beyond. arXiv 2021, arXiv:2102.11974v1. [Google Scholar]
- Chen, Y.; Zhou, Y. Scaling laws and indicators of self-organized criticality in urban systems. Chais Solitons Fractals 2006, 35, 85–98. [Google Scholar] [CrossRef]
- Bartolozzi, M.; Leinweber, D.B.; Thomas, A.W. Self-organized criticality and stock market dynamics: An empirical study. Phys. A 2006, 350, 451–465. [Google Scholar] [CrossRef]
- Gilbert, I.; Nisoli, C.; Schiffer, P. Frustration by design. Phys. Today 2016, 69, 54. [Google Scholar] [CrossRef]
- Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231. [Google Scholar] [CrossRef]
- Sloetjes, S.D.; Urdahl, H.H.; Grepstad, J.K.; Folven, E. Tailoring the magnetic order in a supermagnetic metamaterial. AIP Adv. 2017, 7, 056325. [Google Scholar] [CrossRef]
- Tadić, B.; Šuvakov, M.; Andjelković, M.; Rodgers, G.J. Large-scale influence of defect bonds in geometrically constrained self-assembly. Phys. Rev. E 2020, 102, 032307. [Google Scholar] [CrossRef]
- Šuvakov, M.; Andjelković, M.; Tadić, B. Applet: Simplex Aggregated Growing Graph. 2017. Available online: http://suki.ipb.rs/ggraph/ (accessed on 20 October 2021).
- Tadić, B.; Gupte, N. Hidden geometry and dynamics of complex networks: Spin reversal in nanoassemblies with pairwise and triangle-based interactions. EPL (Europhys. Lett.) 2020, 132, 60008. [Google Scholar] [CrossRef]
- Chutani, M.; Tadić, B.; Gupte, N. Hysteresis and synchronization processes of kuramoto oscillators on high-dimensional simplicial complexes with the competing simplex-encoded couplings. Phys. Rev. E 2021, 104, 034206. [Google Scholar] [CrossRef]
- Beaumont, J.R.; Gatrell, A.C. An Introduction to Q-Analysis; Geo Abstracts; Norwich-Printed by Edmund Nome Press: Norwich, UK, 1982. [Google Scholar]
- Skardal, P.S.; Arenas, A. Abrupt desynchronization and extensive multistability in globally coupled oscillator simplexes. Phys. Rev. Lett. 2019, 122, 248301. [Google Scholar] [CrossRef]
- Tadić, B.; Andjelković, M.; Šuvakov, M.; Rodgers, G.J. Magnetisation processes in geometrically frustrated spin networks with self-assembled cliques. Entropy 2020, 22, 336. [Google Scholar] [CrossRef] [PubMed]
- Brunt, D.; Balakrishnan, G.; Mayoh, D.A.; Lees, M.R.; Gobrunov, D.; Qureshi, N.; Petrenko, O.A. Magnetisation process in the rare earth tetraborides, NdB4 and HoB4. Sci. Rep. 2018, 8, 232. [Google Scholar] [CrossRef]
- Pérez-Reche, F.-J.; Truskinovsky, L.; Zanzotto, G. Driving-induced crossover: From classical criticality to self-organized criticality. Phys. Rev. Lett. 2008, 101, 230601. [Google Scholar] [CrossRef] [PubMed]
- Krasnytska, M.; Berche, B.; Holovatch, Y.; Kenna, R. Ising model with variable spin/agent strengths. J. Phys. Complex. 2020, 1, 035008. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).