Geometry of an English Church Bell

Definition

The axisymmetric geometries of both internal and external profiles of church bells, along with the properties of the bell metal, are of vital importance to their acoustics. The role of “golden geometry” in determining the visual characteristics of the outer profile of a modern English church bell is presented. It is shown that a golden rectangle, a golden triangle, and a golden angle are all important factors. Three angular parameters are identified as measures of these attributes of the bell’s “goldenness”. Two of these features are shown to result from an underlying regular pentagon with one side defined by the bell’s mouth. The centre of this pentagon determines the location of the bell’s shoulders. Further minor features are also shown to be determined by golden geometry. The evolution of the three angular parameters over the previous millennium is included, showing a tendency to trend quickly towards the golden values in all the cases. Ultimately, the angular parameters for the English church bell of focus here are used for comparison with other modern European bells studied previously. The bells considered all displayed at least two of the three major golden features to an agreement of better than 1%.

1. Introduction

While also belonging to the musical instrument category, church bells are unique in their purpose and character to other bell types, such as handbells, orchestral bells or “chimes”, bells that are attached to animals (e.g., cows, elephants, and cats), other ornamental bells, and so on. Church bells are rung individually or sequentially in a small number of varying sizes—for example, for marking the hour or announcing a service. A carillon, alternatively, is a musical instrument consisting of a larger number of bells played from a console. While the larger of the bells in a carillon are similar to church bells, the smaller differ significantly. The focus of this contribution is on the large English church bell and, to a lesser extent but for context, several of its modern Western European counterparts.

Church bells and their vibroacoustics have been of interest to physicists at least since Lord Rayleigh’s time [1]. Reports have appeared concerning their acoustical spectra and normal modes, the phenomenon of “warble”, and the psycho-acoustical “strike note” [2,3]. Some success has been achieved in comparing predictions of finite-element models with experimental results for normal modes [4]. Modern founders tune the frequencies of at least the first five (musical) partials in the approximate ratios of 1:2:2.4:3:4. The second, known by founders as the “fundamental”, usually approximates to the “note” of the bell. The third, the “quint”, is a musical minor third above the fundamental and is responsible for the “ethereal” quality of the church bell’s sound. The vital importance of profiles to a bell’s acoustics is obvious but is also well demonstrated by the facts that (1) for a given outer profile, bells are tuned by removing metal from the inner profile in an axially symmetric way, and (2) modern Dutch founders have succeeded in producing bells with a major third, rather than a minor one, by drastically distorting their axisymmetric profiles in the waist region [5].

The geometry of church bells has, historically, mainly been of interest to antiquarians and founders. Much information on the subject has appeared in the relevant literature [6,7], but a large proportion is purely diagrammatic or qualitative in nature and restricted to outer profiles. An exception is the bell historian Elphick [8]. He attempted to parametrise outer profiles using trapezoids, but these are of limited use, as, in most cases, he did not include crowns in his analysis. There have been discussions on how the profiles evolved historically; how straight lines, circular arcs, and elliptical arcs can form parts of some profiles; and how these may influence important partials. However, little has been said about the mathematics underlying the complete profiles. An attempt at this was made by Perrin et al. [9], who produced an analytical formula giving reasonable fits to the outer profiles of modern Taylor church bells but which did not reproduce sharper regions, such as shoulders, sufficiently well.

The approximate axial symmetry of English church bells allows them to be described using cylindrical polar coordinates (r, $\theta$, z), with the z-direction lying on the axis of symmetry. Their geometry allows examination in a single plane for a fixed $\theta$, and any golden features located will be repeated at all the other values of $\theta$. The presence of axial symmetry in bells has important consequences for their normal modes and for the degeneracy structures of their vibration spectra, which have previously been studied for church bells [10] and for gamelan gongs [11]. For axially symmetric systems, it has been shown using group theoretical arguments that the modal functions must vary like either $sin\left(\mathrm{m}\theta \right)$ or $cos\left(\mathrm{m}\theta \right)$, where m = 0, 1, 2, … Those with m = 0 are singlets—either so-called breathing modes or twisting modes—while all the others are bending modes of some form in degenerate pairs [4].

A basic problem with seeking analytical formulae for axisymmetric bell profiles is that although overall forms are largely similar, details vary between founders, sometimes considerably, having evolved independently over centuries. What seems to be required is a more general approach, seeking to fix major features analytically while leaving room for minor variations. In this paper, we present evidence that “golden geometry” can fulfill this role for the outer profiles of many founders. Inner profiles, although important for acoustics, are not considered herein for reasons explained in Section 2. Research into various aspects of the geometry and its association with the acoustics of bells is still being undertaken, with a recent example being from Whyte et al. [12].

2. Golden Geometry in Bell Profiles

The idea that there is a connection between visual beauty and various aspects of “golden geometry” goes back to classical Greece [13]. Contemporary mathematical literature also makes many references to it [14,15,16]. Topics considered include paintings (especially Old Masters), architecture (including the Parthenon and the Great Pyramids), and natural history (including the human body). Of particular interest to musical acousticians has been its use to analyse violins of the Cremona school and other stringed musical instruments [17].

Hard scientific evidence for a connection between visual aesthetic satisfaction and golden geometry being “hard-wired” into the human brain came first from the 19th century physicist/psychologist Fechner [18]. He asked subjects to look at a series of rectangles with varying aspect ratios and select the one they found the most pleasing. The results were claimed to show a significant preference for golden and near-golden cases. Similar results were claimed for the ellipse. More recent works have taken various views but have broadly tended to confirm Fechner’s findings for rectangles [19].

While the modern Western bell cannot compete with the Stradivarius violin in visual beauty stakes, its form is certainly aesthetically pleasing. Since the bell had hitherto escaped the attention of golden geometers, it was decided to see if it contained any of the features usually associated with golden geometry. Since only the exterior of a bell is “on view”, investigations were restricted to the outer profile: Founders would have no reason to make their inner profiles look beautiful, leaving them available for tuning the bell’s acoustics. One preliminary study [20] involved a selection of church bells, large carillon bells, and handbells for which the profiles happened to be readily available and which were mainly of recent dates. All proved to display some golden features. The “major” features considered were a golden rectangle, a golden triangle, and a golden angle. Angular parameters were identified as measuring these three aspects of “goldenness”.

These earlier results were sufficiently encouraging for us to extend the study to look for further aspects of golden geometry in Western bells using more sophisticated CAD software to do so. In a previous article, we focused mainly on Mallmark C₅ handbells [21]. In the present paper, we concentrate mainly on Taylor church bells, review and extend the preliminary results for these, and point out several extra golden features. The most significant observation is that a regular pentagon underlies two of the three major golden features, while its centre determines the location of the bell’s shoulders. It is our hypothesis that many bells have major features determined by golden geometry, some also having minor features determined in this way, while others depend upon the unique traditions of the founder concerned.

Although founders are secretive about the geometrical constructions underlying the strickle boards from which their profiles are generated, quite a lot is known about them. Some information has been published [20,21], and the present writers have had the opportunity to study a few of the original geometrical drawings from which the strickle boards of Messrs. Taylor were first produced. These show a high degree of technical skill, including, for example, the use of mechanical ellipsographs to generate the region from the shoulder to the sound bow. However, there is no evidence for their having used the methods that would normally be employed by a golden geometer. The founders have used a complex method of their own devising to produce the “desired” result by other means. In other words, they have chosen profiles that look good but did not arise automatically from golden geometric types of construction. Precisely how founders contrived to produce profiles with golden characteristics without using standard golden methods is an open question.

3. Basic Mathematics of Golden Geometry

“Golden geometry”, sometimes known as “sacred geometry” (while there may be slightly different interpretations of these terminologies, they are used interchangeably herein), is a general term used to describe the golden ratio and various geometrical features based on it. The golden ratio is also sometimes referred to as the “extreme and mean ratio” or as the “divine proportion” and is normally given the symbol $\phi$. It is defined with reference to Figure 1, in which the straight line AB is divided at a point C, which is chosen such that

$${\displaystyle \frac{AB}{AC}}={\displaystyle \frac{AC}{CB}}\equiv \phi .$$

(1)

It is a simple matter to show [14] that $\phi$ is given by

$$\phi ={\displaystyle \frac{1+\sqrt{5}}{2}}=1.618\dots .$$

(2)

This is an irrational number and is, in fact, equal to the asymptotic limit of the ratio of successive terms in the Fibonacci series [14]. Of the many remarkable properties of $\phi$, the following two are especially “unusual” and can be proved by direct substitution:

$${\phi }^2=\phi +1\mathrm{and}{\phi }^{-1}=\phi -1.$$

(3)

Equation (2) is the positive root of a quadratic equation arising from Equation (1), but there is also a corresponding negative solution known as ${\phi }^{\prime }$, which can also be significant in some situations. This is given by

$${\phi }^{\prime }={\displaystyle \frac{1-\sqrt{5}}{2}}=-0.618...,$$

(4)

$$\mathrm{so}\mathrm{that}{\phi }^{\prime }+\phi =1$$

(5)

Some geometrical features with which the golden ratio is particularly associated are the golden rectangle (for which the ratio of the long to short sides are φ:1), the golden triangle (an isosceles triangle for which the ratio between either of the equal sides to the base is also φ:1), the regular pentagon, the pentagram, and the dodecahedron and icosahedron—the two highest Platonic solids. In the previous work, we were concerned with the the golden angle and the golden triangle plus the so-called “golden rectangle”. We now extend this to include some additional golden features, including a regular pentagon.

4. Modern D₅ Taylor Church Bell

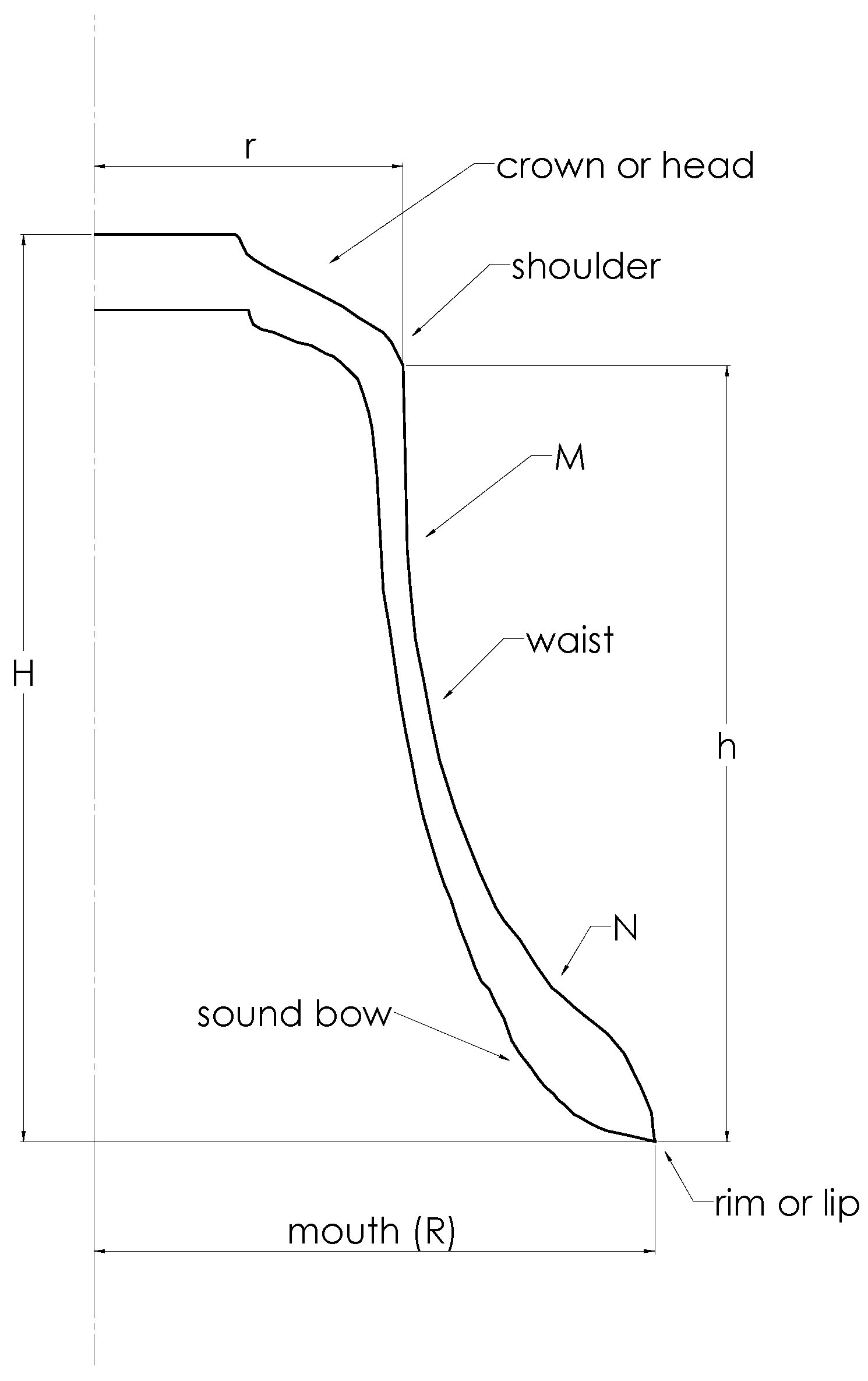
A modern (meaning post WWII) 214 kg Taylor church bell was placed on a horizontal surface. A vertical cross-section containing its symmetry axis was taken, and the left half was deleted (see Figure 2). Included is some terminology for readers unfamiliar with campanological jargon. The geometry of this bell had been measured previously, with considerable accuracy, for use in a finite-element model [4]. The profiles were measured by mechanical means, directly from the bell, in the laboratory decades ago. The measurement resolution was 0.1 mm. The profiles were subsequently (years later) compared with the “strickle boards”—giant stencils that are used to form the axisymmetric inner and outer moulds from which the bells are formed. The strickle boards themselves are the proprietary information of the bell founders and, as such, are difficult or impossible to obtain. The intellectual property of the bell founders extends, of course, to the means by which the profiles have been formed from (golden) geometrical characteristics. It is for this reason that in the work that has led to the results described herein, the aim is to recover these details from the “reverse engineering” of the profiles to discover the intrinsic golden parameters.

It should be noted that the inner and outer profiles are different, although in this paper, we are mainly concerned with the outer one. The depressions seen on the inner profile show where the founder has removed metal in an axisymmetric way to tune some partials. As with most modern bells, there are no “cannons” cast into the crown for hanging purposes. Parameters of importance in describing the outer profiles are the mouth radius (R), the shoulder radius (r), and the vertical heights above the mouth of the crown (H) and of the shoulder (h). The values of these parameters for the Taylor church bell in Figure 2 are R = 349 mm, r = 192 mm, H = 565 mm, and h = 484 mm (these values differ slightly from those in the preliminary study because we now have access to more sophisticated data-fitting software, namely SolidWorks 2022/3). Some small ambiguities arise over precisely where the shoulder and, to a lesser extent, the rim are considered to be located. These are discussed in Section 4.2 below. Such ambiguities do not occur in most handbells, where the shoulder and rim are both sharply defined in most cases [21].

Examining the Taylor church bell’s outer profile in detail shows that there is a linear region of the sidewall immediately below the shoulder. This morphs into an outwards bending elliptical arc at point M, followed by an inwards bending circular one at point N. These morphing points turn out to be connected to golden features, as will be described subsequently. According to the founder’s archives, the change from linear to elliptical occurs at “2½ brims” (a “brim” is usually defined as one-twelfth of the mouth’s diameter) below the shoulder. It should be emphasised that this geometrical arrangement is peculiar to modern Taylor church bells. Others have their own unique profiles, which, like the Taylor church bells, have evolved over centuries. In many cases, founders do not use elliptical arcs but rather various combinations of circular ones.

4.1. Some Golden Rectangles

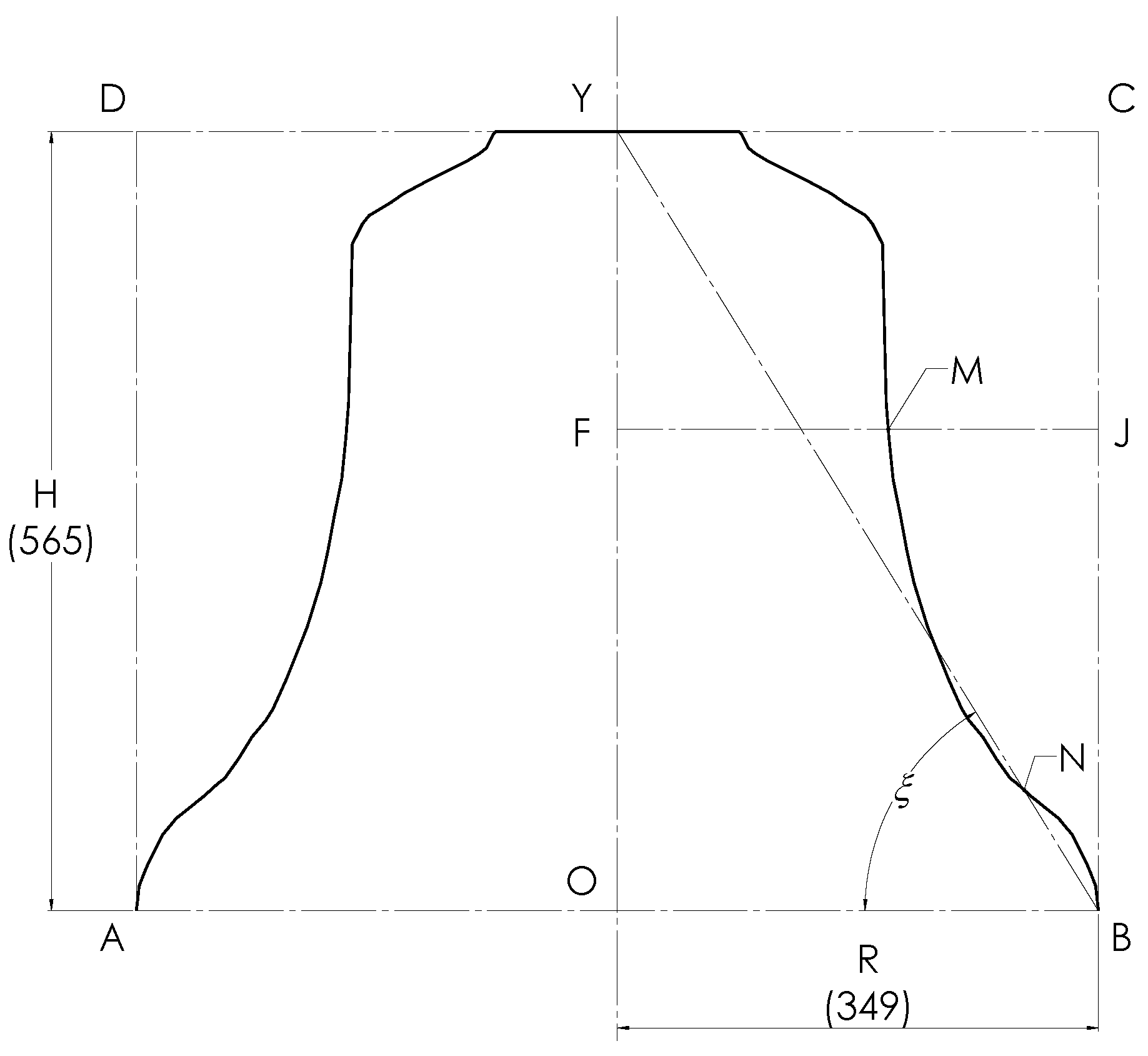
Figure 3 shows the complete outer profile of the Taylor church bell. Since it has R = 349 mm and H = 565 mm, it follows that H/R = 1.619, which is almost identical to the golden ratio of 1.618, so the rectangle OBCY is almost exactly golden. As a convenient alternative measure of its “goldenness”, we join the rim at B to the centre of the crown at Y and measure the angle $\xi$, which this makes with the mouth. Clearly $\xi$ = tan⁻¹(H/R), which gives $\xi$ = 58.30° in this case. As expected, this compares very favourably with the golden value of $\xi$_G = tan⁻¹ ($\phi$) = 58.28°. This angle ($\xi$) is the first of the “goldenness” parameters mentioned in the introduction. The larger rectangle (ABCD), containing the entire bell, is built up of two identical golden rectangles lying side by side. The diagonal (BY) of the right-hand rectangle cuts the outer profile in two places. The lower of these coincides with N, the morphing point from the elliptical-to-circular arcs.

A well-known property of the golden rectangle is that if one constructs an internal square based on a shorter side then the remaining portion is itself a (smaller) golden rectangle [21]. In our diagram, the square OBJF, based on the radius (R) of the mouth of the bell, leaves such a second golden rectangle (FJCY). The point where the square and the new golden rectangle intersect with the outer profile of the bell is where the upper morph point (M) occurs. Generating further, smaller, golden rectangles can be continued in this way ad infinitum but does not appear to yield any further significant results for this bell [21].

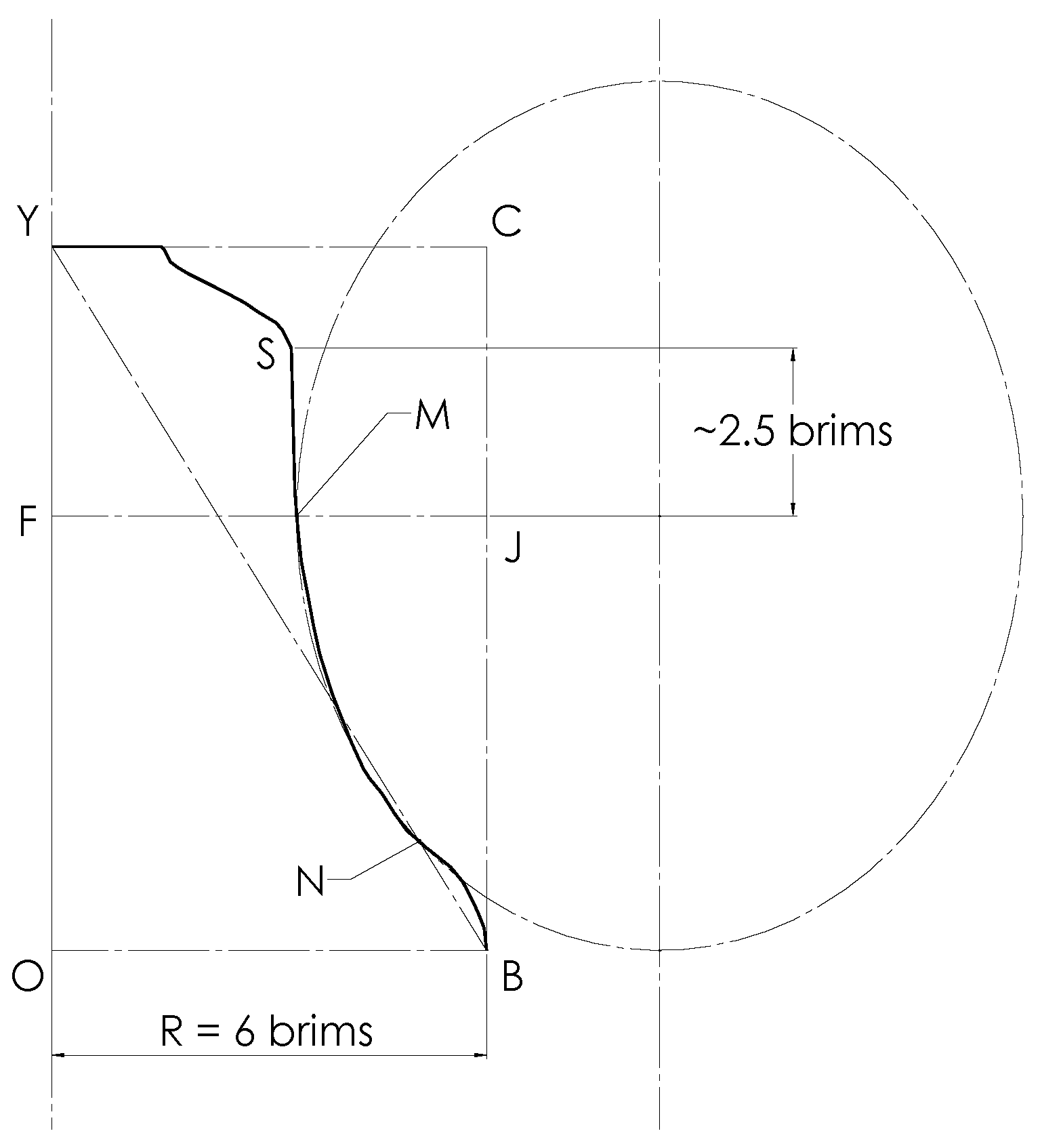
In Figure 4, for completeness, we again show the right-hand half of the Taylor church bell together with the enclosing golden rectangle, its diagonal, and the contained square, plus an ellipse which arc describes the bell’s profile between the two morphing points. The centre of the ellipse has been constrained to lie at the same height above rim as the first morph point. The bottom is lined up with the mouth. The resulting fit follows the central part of the profile well and passes through both morph points. It is not, however, a golden ellipse.

4.2. A Golden Triangle

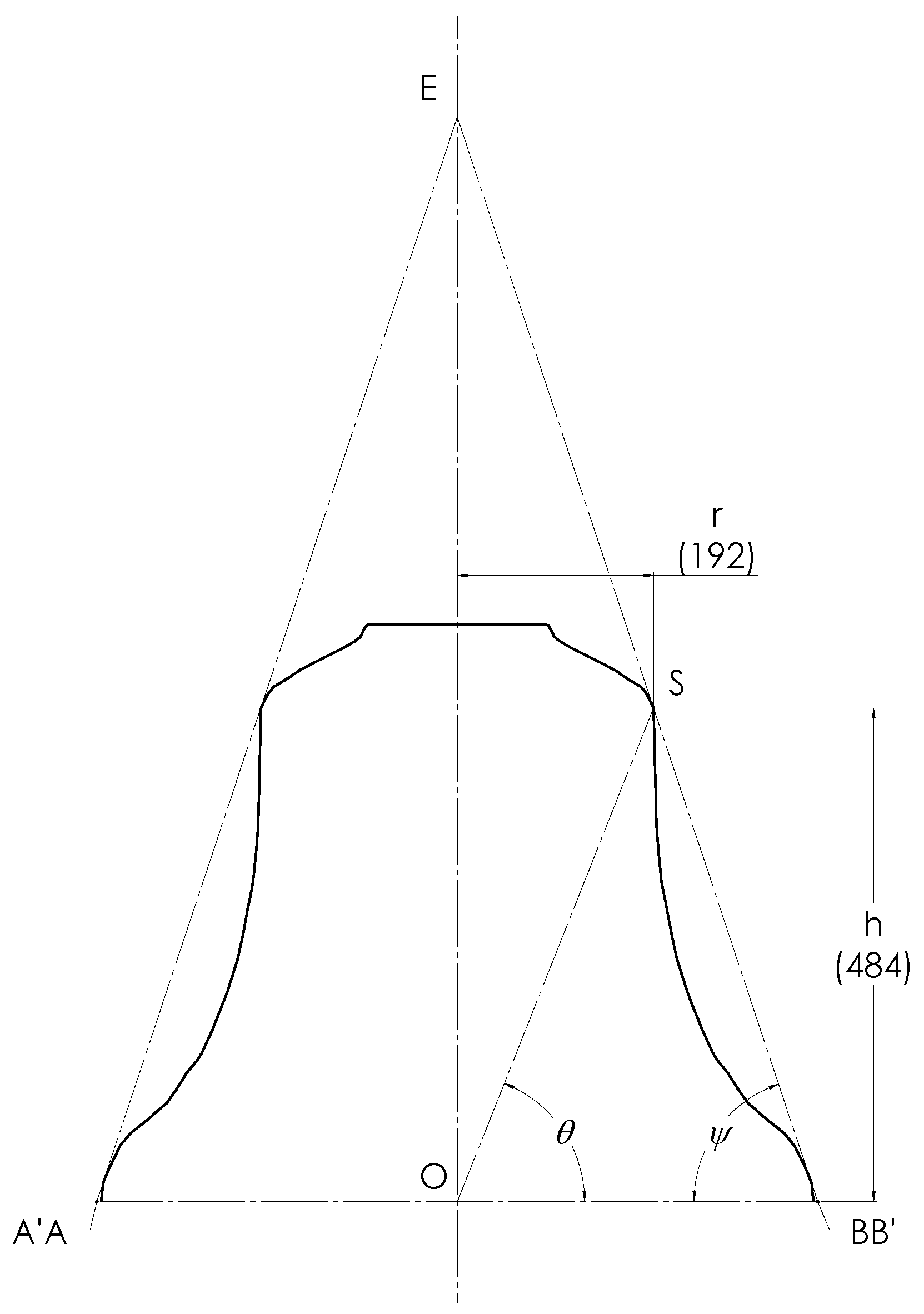
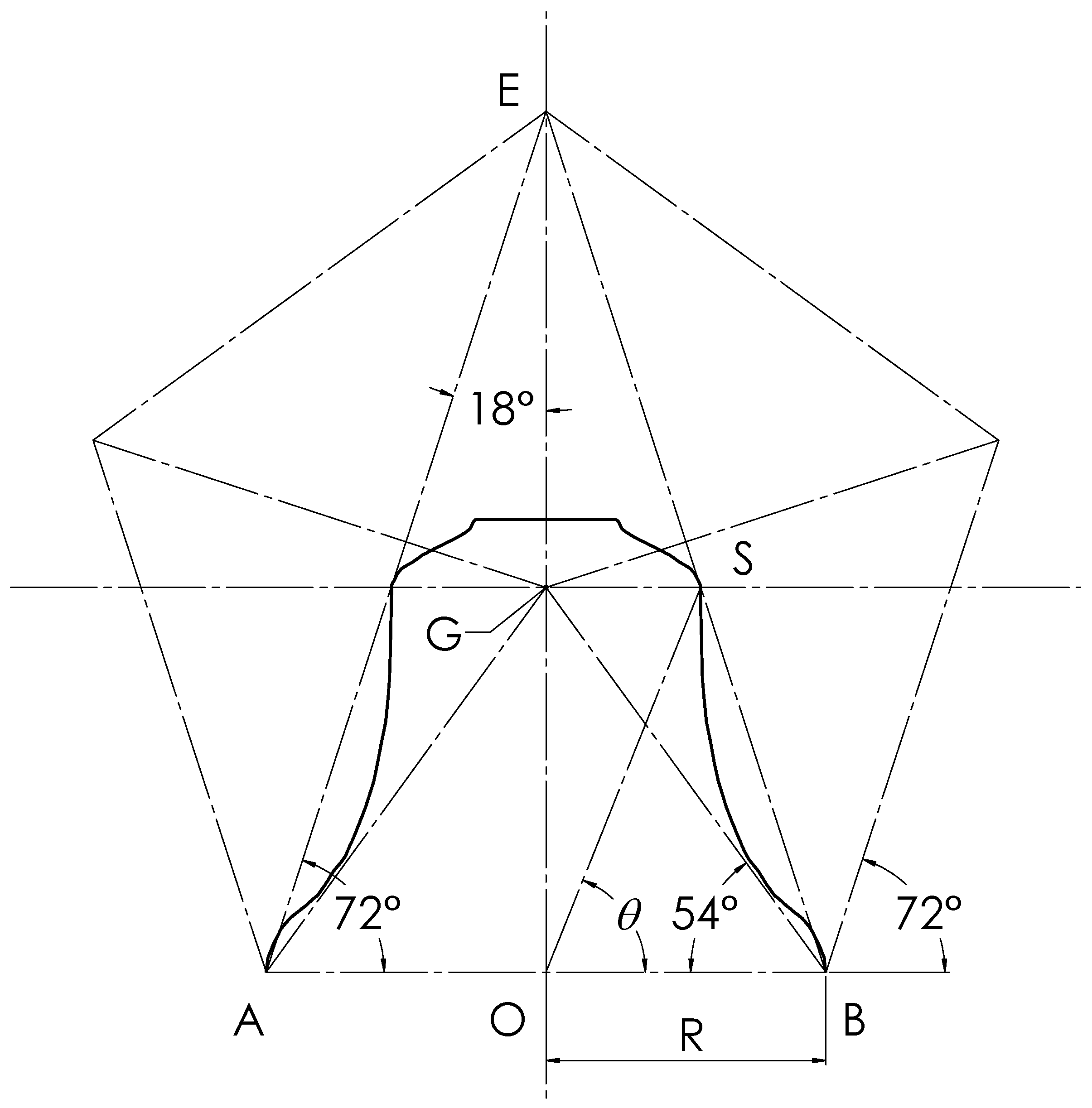
The question of where to take the shoulder location—as mentioned earlier in the context of small ambiguities surrounding the values of r and h—now needs to be addressed. There are several possibilities, but we find the most satisfactory one is to draw the common tangent to the shoulder and the sound bow regions and take the point S, where it touches the shoulder region, as its location. An alternative, which some founders seem to prefer, is to extrapolate the linear part of the wall upwards and take the point at which this intersects with an extrapolation of the approximately flat, downwards sloping part of the lower crown (not to be mistaken with the perfectly flat, horizontal part of the upper crown) outwards. A third possibility, which we have used in Figure 2 and Figure 4, is simply to take the upper end of the linear part of the profile. The numerical differences introduced by these approaches are so small that for simplicity, we shall treat them all as being identical. Nevertheless, we include some uncertainty analysis subsequently. In Figure 5, we again show the Taylor church bell but now with the common tangent on the right extrapolated to cut the symmetry axis at E and the plane of the mouth at B′. For this Taylor church bell, the difference between the lip (B) and the intercept (B′) is, again, so small that we shall treat them as identical. The tangent BE plus its mirror image in the symmetry axis (AE) and the baseline AOB form an isosceles triangle (ABE). We are interested in the angle OBE ≡ $\psi$ given by

$$tan\psi =h/(R-r).$$

(6)

Using the previously given values for R, h, and r gives

$$\psi =71.9°.$$

(7)

Should the selected shoulder position vary as previously described, it is conceivable that h may increase by 1%. In this case, it can be shown that $\psi$ will take a value of 72.2°.

A golden triangle is an isosceles triangle in which the length of the equal sides is $\phi$ times that of the base. This gives a golden value for $\psi$ of

$${\psi }_G={cos}^{-1}\left(1/2\phi \right)=72°\mathrm{exactly}.$$

(8)

The triangle defined by the common tangents and base is thus an almost perfect golden triangle. Clearly, if we add further lines parallel to AB, these will each form the base of a further golden triangle with E as its apex. None of these seems to be of particular significance. The angle $\psi$ is the second goldenness parameter referred to in the introduction.

4.3. A Golden Angle

What seems to be happening is that a golden rectangle fixes the overall height of this bell relative to its mouth radius. A golden triangle then constrains the shoulder to lie along a particular straight line as the locus. Fixing the absolute location of the shoulder along this line requires a further criterion. It is usual to define “the golden angle” as half a complete rotation divided by $\phi$. This is 111.25°. However, it is more convenient for our purpose to work with the complementary angle of 68.75°, which we designate as $\theta$_G.

In Figure 5, we also draw a straight line from the centre of the mouth (O) to the shoulder (S), as defined above. The angle ($\theta$) that OS makes with the mouth line (AB) fixes the location of the shoulder on the tangent line, giving

$$tan\theta =h/r.$$

(9)

Substituting the dimensions of the Taylor church bell gives $\theta$ = 68.30° (if h increases by 1%, $\theta$ = 68.56°), which agrees remarkably well with the value of $\theta$_G. The angle $\theta$ is the third goldenness parameter.

4.4. A Regular Pentagon

A textbook property of the regular pentagon, well known to the Pythagoreans, is that joining any corner to the ends of the opposite side produces an isosceles triangle with side angles of exactly 72° (i.e., a golden triangle). The two remaining (identical but rotated) portions of the pentagon are golden “gnomons”. Since the bell’s outer profile is partially defined by a golden triangle, it follows that there must be a regular pentagon underlying the design. Starting from the mouth of the bell as being one side of the pentagon (using A and B rather than A′ and B′) and using the known 72° angle, it is straightforward to construct the complete pentagon containing a very close approximation to our original golden triangle as a component. The result is shown in Figure 6, where we also include the lines joining G, the centre of the pentagon, to its vertices. Two interesting results arise from this as follows.

The first is that a horizontal line through the point G passes directly through the shoulder (S). The second is that the lines radiating out from G downwards towards the lips of the bell are tangential to the inner bulges of the external profile. If one joins the point O, the centre of the mouth, to the location of the shoulder (S), as defined by the position of G, then, for consistency with our empirical observations, the angle BOS (defined as $\theta$) must be, at least approximately, equal to the golden angle. This is not a textbook result for the geometry of the regular pentagon, but we show in a straightforward way in the Appendix A that $\theta$ = 68.11°, which is so close to the golden angle (68.75°) that for practical purposes, the two are identical. We therefore conclude that the values of $\psi$ and $\theta$ may both be determined by an underlying regular pentagon. There is no obvious connection between the pentagon and the golden rectangle and, hence, $\xi$.

5. Historical Evolution of the English Church Bell’s External Profile

The earliest known English church bells were essentially cylindrical with hemispherical crowns. The outer profiles tended to be linear with an outwards flare close to the rim. By the 11th century, there had been a shift to the profile being very slightly concave in form. These bells were much more conical than modern ones and were taller relative to their rim diameters. As time passed, the degree of concavity increased. This happened slowly at first but then continued to increase, while the aspect ratio of the height relative to the rim diameter decreased until, by about the 14th century, the outer profiles had become rather like the modern form. Further changes in the profiles did occur but were relatively minor in nature. Improvements in the bell sound, in more recent times, were partly due to further fine adjustments of the outer profile but mainly due to the introduction of the active tuning of musical partials. This involves adjusting the inner profile using a large lathe to turn metal off at selected locations in an axially symmetric way [22].

5.1. Bell Profile Data Origins

To investigate the variation in bell profiles over the centuries, a considerable amount of accurate data is required. Our own measurements, made previously for use in mathematical models, were known to be accurate but had been taken for only a small number of bells. It was therefore necessary to supplement them with published data from other sources. A literature search revealed several sources of technical information on church bells, but only a few had profile diagrams from which accurate data could be extracted. Some sources included photographs of bells, but their use is problematic unless they were taken at long range: In a bell tower, it is usually impossible to obtain a long-range view. The bulk of our data was, therefore, taken from diagrams.

The dates of the bells were sometimes known accurately from church records and/or inscriptions on the bell. In other cases, only ranges of dates were available if, for example, the founder had been identified and his working dates were known. In such cases, an average, indicative date was taken. Where there were multiple examples of bells by the same founder for the same date, we took representative cases.

Much useful data came from the publications of Elphick [7,8]. This was especially true of those examples that he presented as fully drawn profiles. Unfortunately, much of his published data is not in this form but rather is given in terms of trapezoids, which do not provide information about the height of the crown (H). These trapezoid data were, therefore, not useful in looking at the golden rectangle and, hence, the angle $\xi$. We therefore excluded these data from our analysis and concentrated on his diagrams.

5.2. Analysis of Results

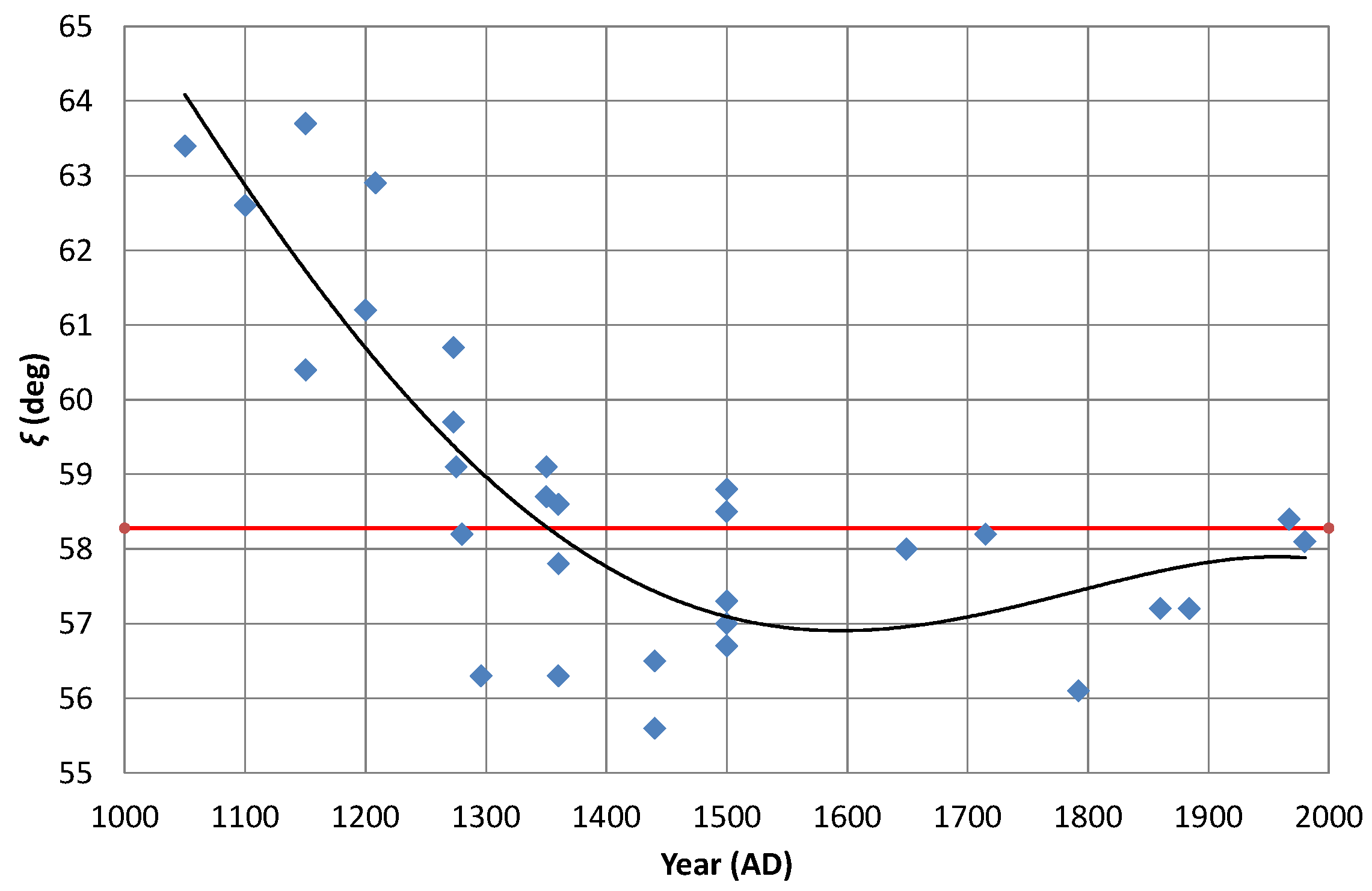
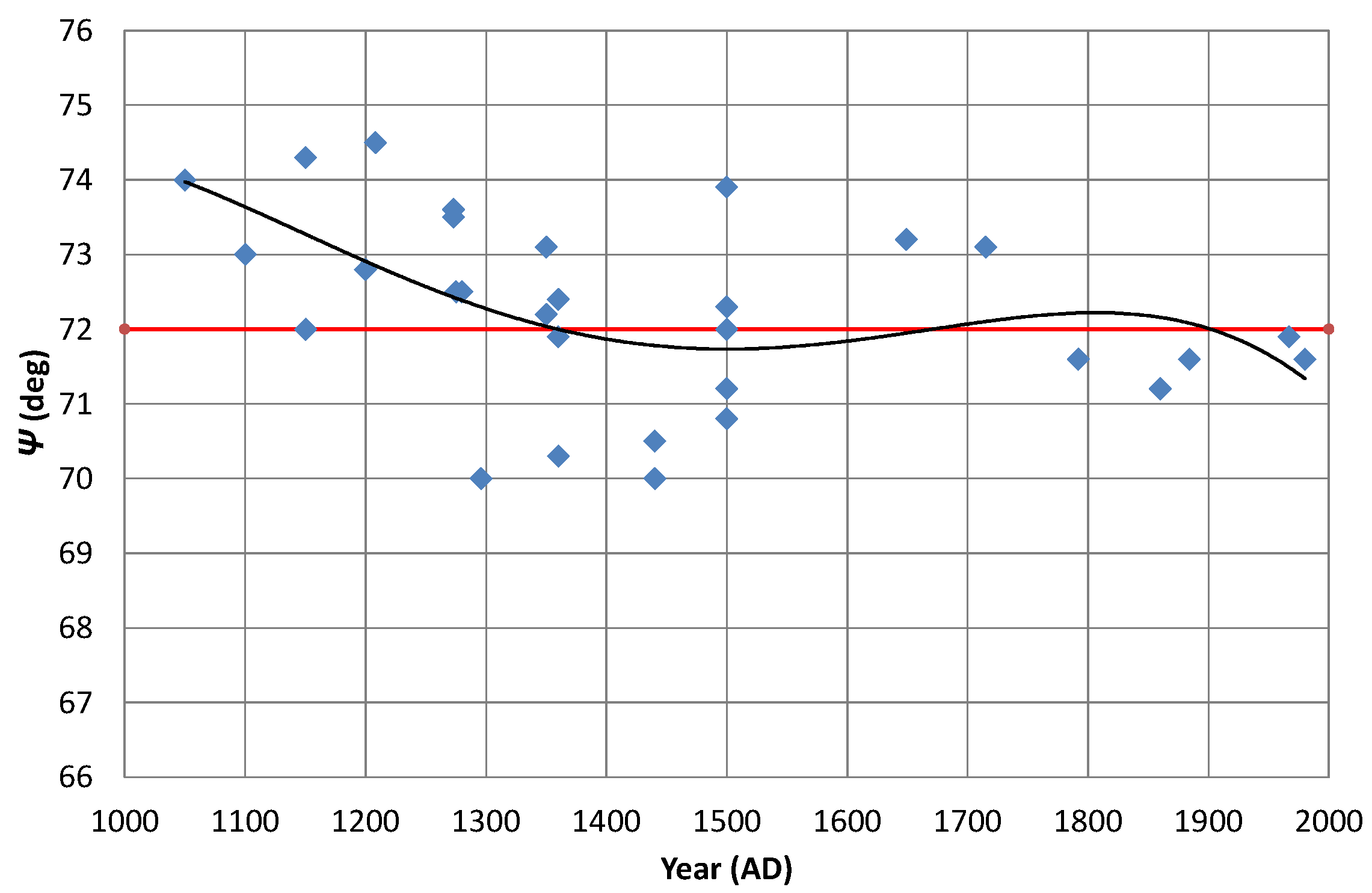
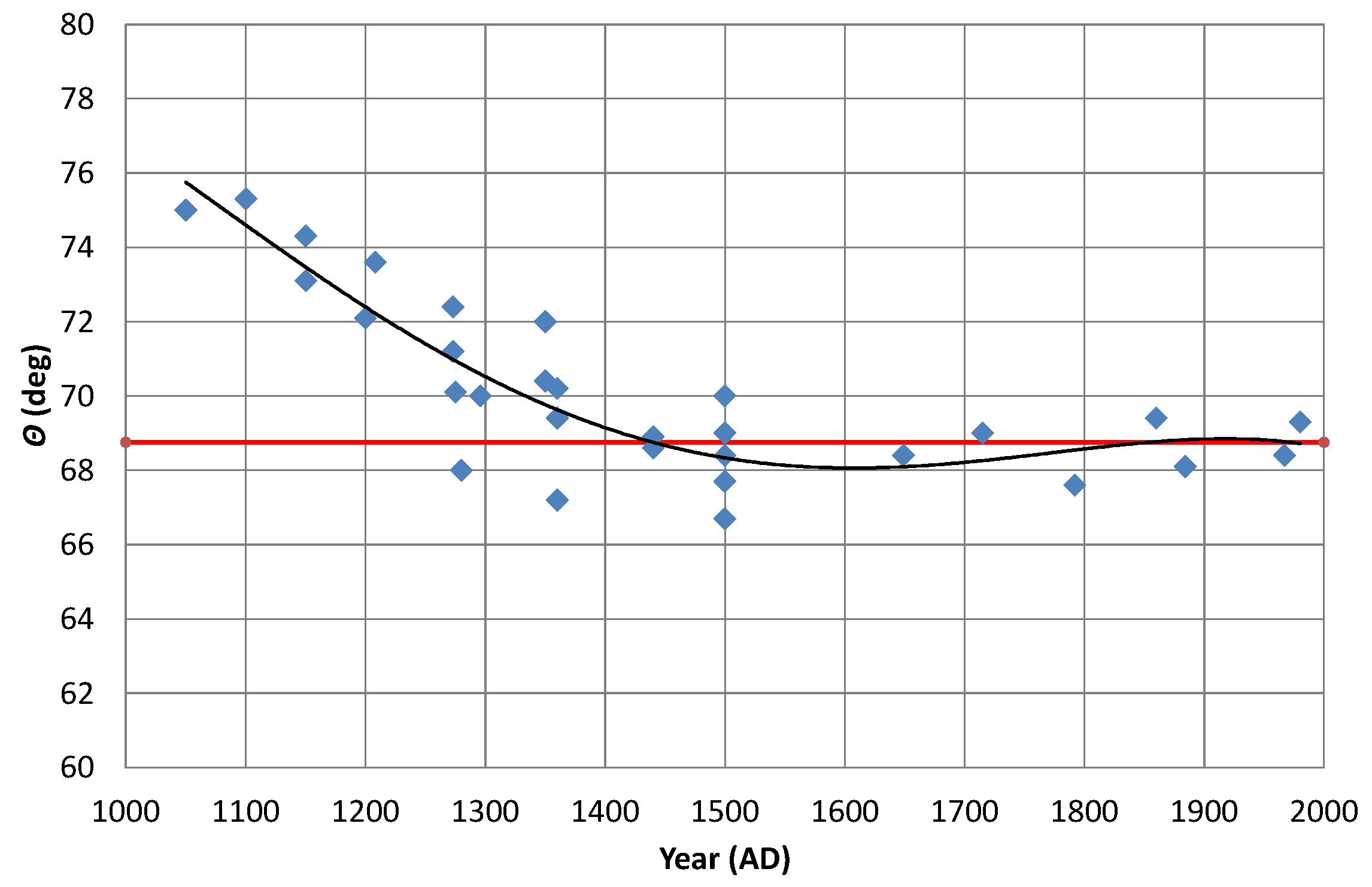
Here, we will consider the ways in which the golden parameters ($\xi$, $\psi$, and $\theta$)—introduced in Section 4 to characterise the outer profiles of English church bells—have varied over the last millennium. Their behaviours in this regard are shown graphically in Figure 7, Figure 8, and Figure 9, respectively. Trend lines (while polynomial order four is used, there is no basis for this choice other than that it seems to fit the argumentation quite well) have been added, as they seem to be helpful to track the changes over time together with indications of their golden values.

As might be expected, thanks to individual founders experimenting with the profiles, there is a lot of scatter in the data. However, some general trends seem to be present. The angle $\xi$ begins relatively high, at about 63°, at around 1100 AD (meaning that the crown height (H) was relatively large when compared with the mouth radius (R)), so the bell looks long and thin compared with a modern one, as previously discussed. By 1300 AD, $\xi$ had fallen to around the golden value of 58.28° and thereafter has fluctuated about this value, mostly within ±1°.

The angle $\psi$ has mostly never varied by more than ±2° from the golden value of 72°. It started at around 74° and then fell to around 72° and hovered about there. So, this golden aspect of the church bell profile can be seen to have been present from a very early date. In accordance with Equation (6), variations in $\psi$ correspond to the shoulder height (h) being greater or less than the difference between the mouth and shoulder radii (R and r, respectively).

Similarly to $\xi$, the golden angle ($\theta$) begins relatively high, at 75°, at around 1100 AD but then quickly falls to around its golden value of 68.75°. Subsequently, it varies about that value by only about ±2°. Again, the higher early values reflect the long and thin natures of the early bells. This time, with reference to Equation (9), driven by the shoulder height (h), being large compared to the shoulder radius (r).

6. Some Other Modern Western European Church Bells

The identification of three main aspects of golden geometry in the outer profile of a modern Taylor church bell is interesting but might be unique to this founder or even to this particular bell. Clearly, it needs to be checked in other bells. In the preliminary study [20], we looked at a selection of English and Dutch bells which profile details we happened to have readily available. They were all church bells or large carillon bells and reasonably modern, apart from a 17th century (Dutch) Hemmony case. The Hemmony bell is included to illustrate how advanced these Dutch founders had become at a relatively early date. We considered only the three major goldenness parameters. The identification of subsidiary features, such as the two morph points in the Taylor church bell, as having their origins in properties of golden rectangles cannot be expected to extend to all bells, as each one of them has a profile unique to its founder from shoulder to rim. They do not necessarily display identical morphing behaviours: Many do not contain elliptical arcs but rather one or more circular arcs in their profiles. The results are listed in

Table 1. Fits of angular features to outer profiles of church and large carillon bells (Adapted from [20]).

		$\mathit{\xi }$ (°)	$\mathit{\psi }$ (°)	$\mathit{\theta }$ (°)
		(±0.1°)	(±0.2°)	(±0.1°)
	Golden Geometry Theory	58.28	72.00	68.75
Founder	Taylor	58.30	72.05	68.30
	Whitechapel	58.1	71.6	69.3
	Royal Eijbouts	57.8	72.0	68.1
	Hemmony	58.0	72.8	68.5
	Gillet and Johnson	58.7	74.2	70.5
	Petit and Fritzen	57.9	74.8	70.1

.

The measured values of $\xi$ are all to within ±0.5° of the golden rectangle value, so all these bells have their aspect ratios fixed by the golden ratio. The values of $\psi$ are not quite as good, but three cases are to within ±0.5° and another to within ±1°. The last two in the list are different by between 2 and 3°. However, the (Dutch) bells of Petit and Fritzen are well known for being “different”, so their cases need not worry us too much. Overall, the involvement of the golden triangle seems to be confirmed. The results for $\theta$ are like those for $\psi$. The first four cases agree to within ±1°. The last two are out by between 1 and 2°, so the situation is slightly better than that for $\psi$. Overall, it seems we can say that the golden rectangle works well for all the bells, while the golden triangle and golden angle work well for some and approximately for the others. Measurements on modern handbells show that they too obey our three golden rules but rather better than do the church bells [20]. This may be because in the case of handbells, there is no ambiguity over the locations of either the shoulder or the rim: both are sharply defined.

7. Discussion and Conclusions

It is well known—as shown in some detail in Section 5—that the shapes of English church bells have changed over the centuries [7]. Twelfth century bells were far more conical than modern ones as well as being taller relative to their width. We have shown that even some of the early bells show evidence of underlying golden triangles, as demonstrated by $\varphi$ tending to the golden value of 72°. As the centuries passed, the outer profiles gradually developed into something like the modern form while additionally inserting golden rectangles and golden angles into the features, as demonstrated by $\xi$ and $\theta$ similarly tending to their golden values of 58.28° and 68.75°, respectively.

The other Western church and carillon bells described in Section 6 were all reasonably modern, apart from the 17th century Hemmony case. The evidence for golden rectangles in all their outer profiles is very strong. That for golden triangles and angles is less so but still good. All three golden angular features were present in the 17th century Hemmony bell, demonstrating that the Dutch founders had adopted golden geometry relatively early. Only English and Dutch bells were used, so it would be of interest to consider those from other Western countries in the future.

Although most founders are secretive about all the aspects of their craft, including the geometrical constructions underlying the strickle boards from which the profiles in the moulds are generated, quite a lot is known about it, and some has been published [23,24]. One of the authors (R.P.) has examined the original technical drawings from which the strickle boards were produced in the 19th century. These drawings showed a high level of technical skill and competency, including the ability to use bespoke mechanical ellipsographs. However, there is no evidence of them having used the methods of golden geometers. Rather, they seem to have used complex procedures of their own devising to generate the desired bell characteristics.

We have shown that a selection of modern Western church bells displayed evidence of golden geometry underlying several major features. This involved fixing the aspect ratios and relative locations of the crown, shoulders, and rim by means of golden rectangles, golden triangles, and golden angles. The last two of these are manifestations of an underlying regular pentagon. Other relatively minor features involving the shape of the wall are also fixed in this way for the Taylor church bell, but this is not necessarily the case for other founders or for older church bells. Future research into how golden or sacred geometry has influenced the profiles of church bells as they have evolved over the last millennium is suggested.