High-Power Lasers
Abstract
1. Introduction
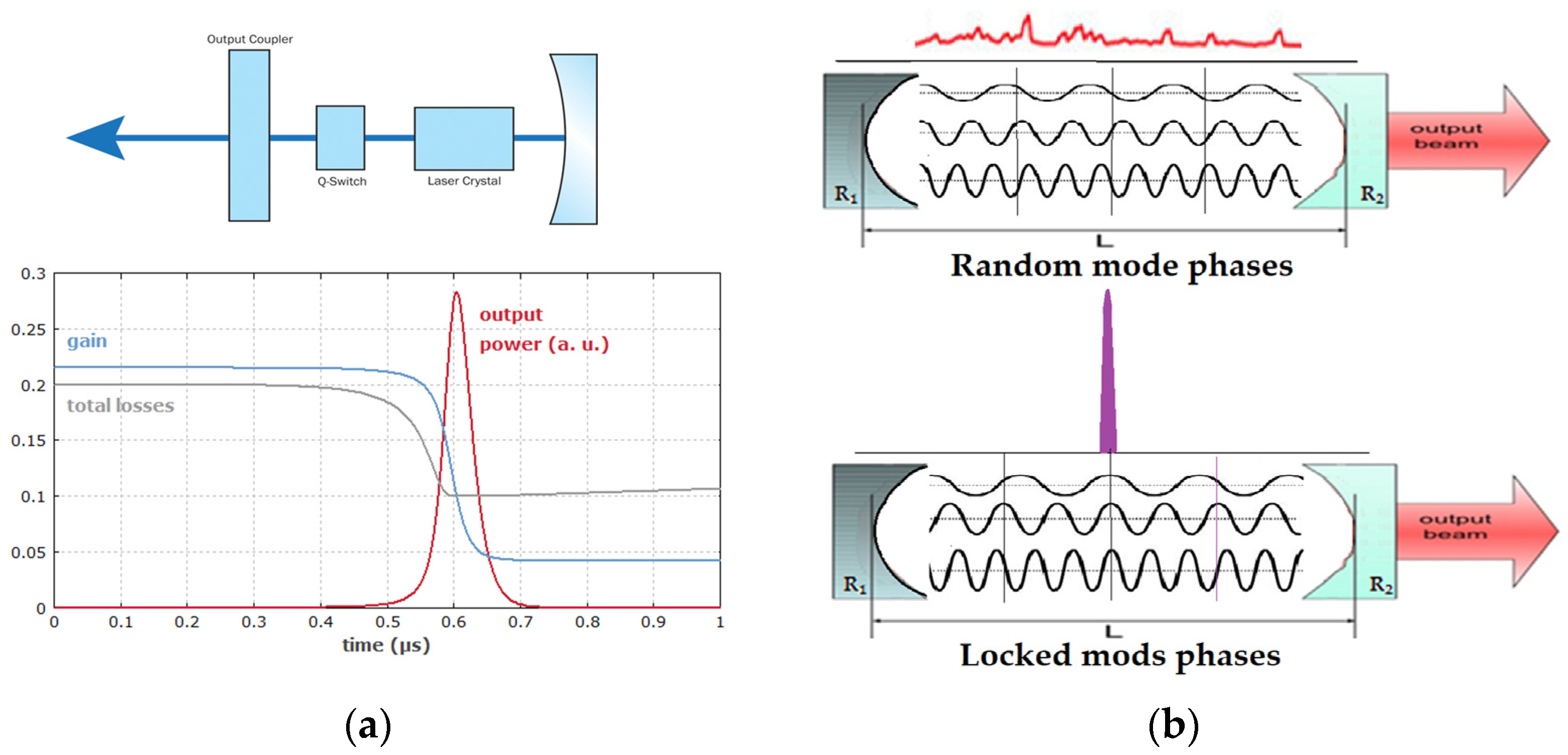
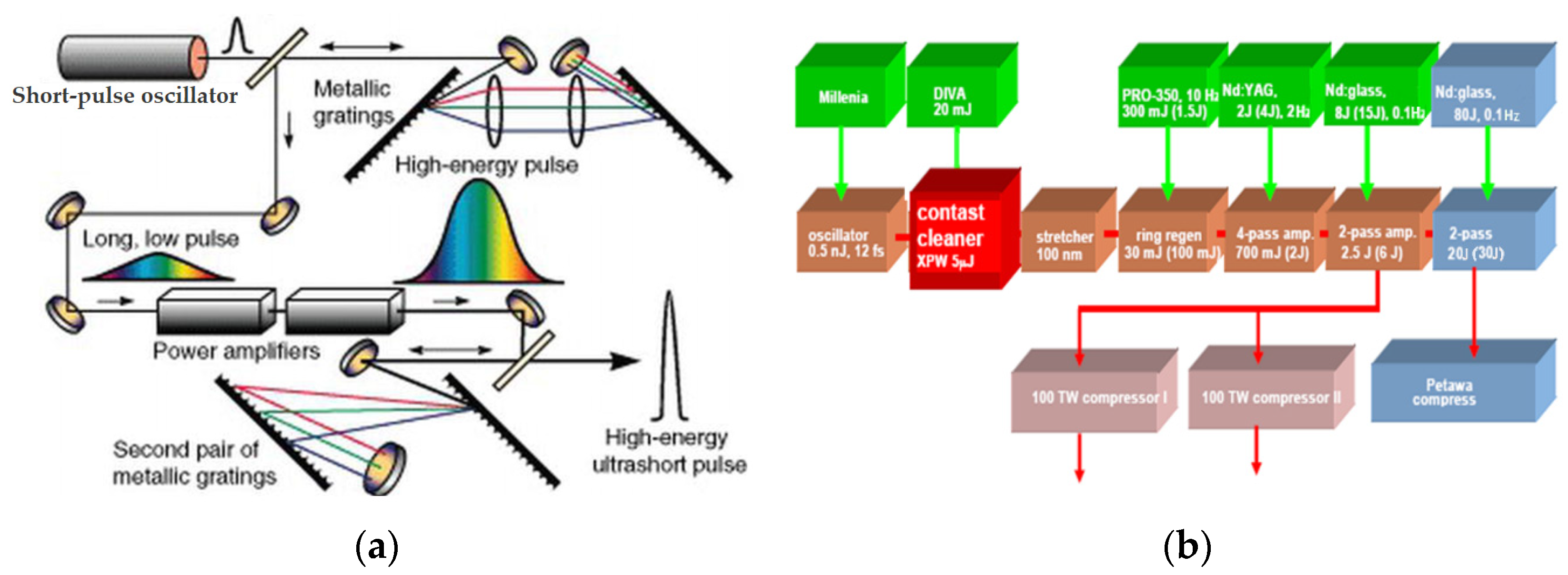
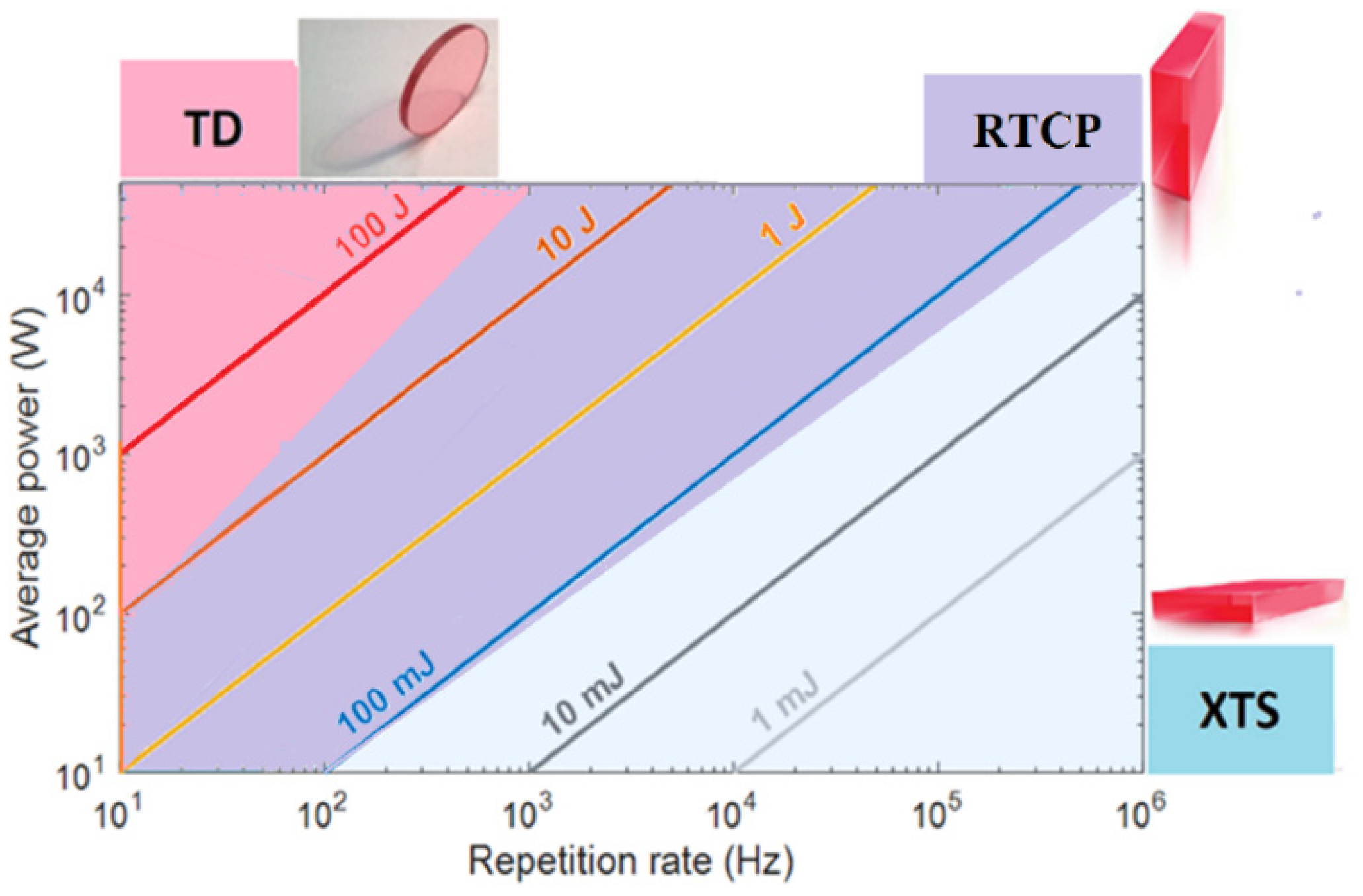
2. Ideas and Methods for Increasing Laser Power
3. Prospects and Conclusions
Funding
Conflicts of Interest
References
- Naresh; Khatak, P. Laser cutting technique: A literature review. Mater. Today Proc. 2021, 56, 2484–2489. [Google Scholar] [CrossRef]
- Dezaki, M.L.; Serjouei, A.; Zolfagharian, A.; Fotouhi, M.; Moradi, M.; Ariffin, M.K.; Bodaghi, M. A review on additive/subtractive hybrid manufacturing of directed energy deposition (DED) process. Adv. Powder Mater. 2022, 1, 100054. [Google Scholar] [CrossRef]
- Tajima, T.; Yan, X.Q.; Ebisuzaki, T. Wakefield acceleration. Rev. Mod. Plasma Phys. 2020, 4, 7. [Google Scholar] [CrossRef]
- Rockwood, A.; Wang, Y.; Wang, S.; Berrill, M.; Shlyaptsev, V.N.; Rocca, J.J. Compact gain-saturated X-ray lasers down to 6.85 nm and amplification down to 5.85 nm. Optica 2018, 5, 257–262. [Google Scholar] [CrossRef]
- Wurzel, S.E.; Hsu, S.C. Progress toward fusion energy breakeven and gain as measured against the Lawson criterion. Phys. Plasmas 2022, 29, 062103. [Google Scholar] [CrossRef]
- Fu, N.; Liu, Y.; Ma, X.; Chen, Z. EUV Lithography: State-of-the-Art Review. J. Microelectron. Manuf. 2019, 2, 19020202. [Google Scholar] [CrossRef]
- Sun, J.; Liu, L.; Han, L.; Zhu, Q.; Shen, X.; Yang, K. 100 kW ultra high power fiber laser. Opt. Contin. 2022, 1, 1932–1938. [Google Scholar] [CrossRef]
- Zhao, S.; Qi, A.; Wang, M.; Qu, H.; Lin, Y.; Dong, F.; Zheng, W. High-power high-brightness 980 nm lasers with >50% wall-plug efficiency based on asymmetric super large optical cavity. Opt. Express 2018, 26, 3518. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Killeen, T. Gas Lasers: CO2 lasers—Progressing from a varied past to an application-specific future. Laser Focus World 2016, 4, 3. [Google Scholar]
- Radier, C.; Chalus, O.; Charbonneau, M.; Thambirajah, S.; Deschamps, G.; David, S.; Barbe, J.; Etter, E.; Matras, G.; Ricaud, S.; et al. 10 PW peak power femtosecond laser pulses at ELI-NP. High Power Laser Sci. Eng. 2022, 10, e21. [Google Scholar] [CrossRef]
- Crane, J.; Martinez, M.; Moran, B.; Laumann, C.; Davin, J.; Rothenberg, J.; Beach, R.; Gollock, B.; Jones, R.; Wing, R.; et al. High-gain, Nd-doped-glass preamplifier for the National Ignition Facility (NIP) laser system. In Proceedings of the Conference Proceedings LEOS’96 9th Annual Meeting IEEE Lasers and Electro-Optics Society, Boston, MA, USA, 18–21 November 1996. [Google Scholar]
- Thoss, A. EUV lithography revisited. Laser Focus World 2019, 8, 29. [Google Scholar]
- Wolverton, M. A Solution for Almost Everything, 50 Years of the Laser. Invent. Technol. 2010, 25, 2. [Google Scholar]
- McClung, F.J.; Hellwarth, R.W. Giant Optical Pulsations from Ruby. J. Appl. Phys. 1962, 33, 828–829. [Google Scholar] [CrossRef]
- Lamb, W.E., Jr. Theory of an optical laser. Phys. Rev. 1964, 134, 1429. [Google Scholar] [CrossRef]
- Exploring Fundamental Physics at the Highest-Intensity-Laser Frontier (spie.org). Available online: https://spie.org/news/4221-exploring-fundamental-physics-at-the-highest-intensity-laser-frontier (accessed on 1 February 2024).
- Damm, T.; Kaschke, M.; Noack, F.; Wilhelmi, B. Compression of picosecond pulses from a solid-state laser using self-phase modulation in graded-index fibers. Opt. Lett. 1985, 10, 176–178. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Siegman, A.E. Fundamentals of Laser Oscillation. In Lasers; Kelly, A., Ed.; University Science Books: Sausalito, CA, USA, 1986; pp. 457–547. [Google Scholar]
- Laser Basics. Available online: https://www.slideshare.net/slideshow/part-i-laser-basics-lorenser-2009/1245640 (accessed on 5 August 2024).
- Khan, N.; Goldwasser, S.M.; Abas, N.; Kalair, A.; Haider, A. Experimental investigation of unidentified helium–neon lasers. Appl. Opt. 2017, 56, 10030. [Google Scholar] [CrossRef]
- Toesko, G.; Dehnert, C. Ultrafast Laser Optics: Femtosecond Laser Optics Combat Pulse Dispersion, Color Errors, and Reflections. Laser Focus World 2016. Available online: https://www.laserfocusworld.com/optics/article/16547107/ultrafast-laser-optics-femtosecond-laser-optics-combat-pulse-dispersion-color-errors-and-reflections (accessed on 1 March 2024).
- Moulton, P.F. Spectroscopic and laser characteristics of Ti:Al2O3. J. Opt. Soc. Am. B 1986, 3, 125–133. [Google Scholar] [CrossRef]
- Photonics Encyclopedia. Available online: https://www.rp-photonics.com/q_switching.html (accessed on 5 August 2024).
- Photonics Spectra. Available online: https://www.photonics.com/Articles/Understanding_Passively_Q-Switched_Solid-State/a56862 (accessed on 1 November 2014).
- Newport. Available online: https://www.newport.com/n/pulsed-laser-methods (accessed on 6 March 2024).
- Fork, R.L.; Martinez, O.E.; Gordon, J.P. Theory of passively mode-locked lasers including self-phase modulation and group-velocity dispersion. Opt. Lett. 1984, 9, 156. [Google Scholar]
- Hargrove, L.E.; Fork, R.L.; Pollack, M.A. Locking of He–Ne Laser Modes Induced by Synchronous Intracavity Modulation. Appl. Phys. Lett. 1964, 5, 4–5. [Google Scholar] [CrossRef]
- Ippen, E.; Shank, C.; Dienes, A. Passive mode locking of the cw dye laser. Appl. Phys. Lett. 1972, 21, 348–350. [Google Scholar] [CrossRef]
- Manes, K.R.; Ahlstrom, H.G.; Haas, R.A.; Holzrichter, J.F. Light–plasma interaction studies with high-power glass laser. J. Opt. Soc. Am. 1977, 67, 717–726. [Google Scholar] [CrossRef]
- Kelley, P.L. Self-focusing of optical beams. Phys. Rev. Lett. 1965, 15, 1005. [Google Scholar] [CrossRef]
- University of Michigan/Center for Ultrafast Optical Science (CUOS). Available online: https://cuos.engin.umich.edu/researchgroups/hfs/facilities/chirped-pulse-amplification/ (accessed on 6 April 2024).
- University of Michigan/Center for Ultrafast Optical Science (CUOS). Available online: https://cuos.engin.umich.edu/researchgroups/hfs/facilities/hercules-petawatt-laser/ (accessed on 6 April 2024).
- Martinez, O.E.; Gordon, J.P.; Fork, R.L. Negative group-velocity dispersion using refraction. J. Opt. Soc. Am. A 1984, 1, 1003–1006. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Y.; Sun, D.; Chai, L.; Sun, H.; Wang, C.-Y. Compact and material-dispersion-compatible Offner stretcher for chirped pulse amplifications. Opt. Commun. 2002, 206, 7–12. [Google Scholar] [CrossRef]
- Treacy, E. Optical pulse compression with diffraction gratings. IEEE J. Quantum Electron. 1969, 5, 454–458. [Google Scholar] [CrossRef]
- Cheriaux, G.; Walker, B.; Dimauro, L.F.; Rousseau, P.; Salin, F.; Chambaret, J.P. Aberration-free stretcher design for ultrashort-pulse amplification. Opt. Lett. 1996, 21, 414–416. [Google Scholar] [CrossRef]
- Bonod, N.; Neauport, J. Diffraction gratings: From principles to applications in high-intensity lasers. Adv. Opt. Photonics 2016, 8, 156–199. [Google Scholar] [CrossRef]
- Gonz, C.M.; Mart, O.E. Quartic phase compensation with a standard grating compressor. Opt. Lett. 1997, 22, 1186. [Google Scholar]
- Bagnoud, V.; Salin, F. Global optimization of pulse compression in chirped pulse amplification. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 445–448. [Google Scholar] [CrossRef]
- Chvykov, V.; Yanovsky, V. Precise Alignment of Large-aperture Compressor Gratings for High-power Lasers by Using Diffraction Interferometry. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 31 May–5 June 2009; p. JWB4. [Google Scholar]
- Campbell, J.H.; Hayden, J.S.; Marker, A. High-power solid-state lasers: A laser glass perspective. Int. J. Appl. Glass Sci. 2011, 2, 3–29. [Google Scholar] [CrossRef]
- Chi, H.; Wang, Y.; Davenport, A.; Menoni, C.S.; Rocca, J.J. Demonstration of a kilowatt average power, 1 J, green laser. Opt. Lett. 2020, 45, 6803–6806. [Google Scholar] [CrossRef] [PubMed]
- Joyce, D.; Ripley, B.; Schmid, K.; Cohen, S. High-Power Solid-State Lasers: Ti:sapphire laser crystals reach 200 mm diameter. Laser Focus World 2010, 2, 28. [Google Scholar]
- Chvykov, V. Ti:Sa Crystal Geometry Variation vs. Final Amplifiers of CPA Laser Systems Parameters. Crystals 2022, 12, 1127. [Google Scholar] [CrossRef]
- Patterson, F.G.; Bonlie, J.; Price, D.; White, B. Suppression of parasitic lasing in large-aperture Ti:sapphire laser amplifiers. Opt. Lett. 1999, 24, 963–965. [Google Scholar] [CrossRef] [PubMed]
- Chvykov, V.; Yanovsky, V.; Bahk, S.W.; Kalintchenko, G.; Mourou, G. Suppression of parasitic lasing in multi-pass Ti-sapphire amplifiers. In Proceedings of the Conference on Lasers and Electro-Optics, Munich, Germany, 22–27 June 2003. [Google Scholar]
- Chvykov, V.; Krushelnick, K. Large aperture multi-pass amplifiers for high peak power lasers. Opt. Commun. 2012, 285, 2134–2136. [Google Scholar] [CrossRef]
- Chvykov, V.; Krushelnik, K. Transverse amplified spontaneous emission: The limiting factor for output energy of ultra-high-power lasers. Opt. Commun. 2014, 312, 216. [Google Scholar] [CrossRef]
- Yanovsky, V.; Chvykov, V.; Kalinchenko, G.; Rousseau, P.; Planchon, T.; Matsuoka, T.; Maksimchuk, A.; Nees, J.; Cheriaux, G.; Mourou, G.; et al. Ultra-high intensity-300-TW laser at 0.1 Hz repetition rate. Opt. Express 2008, 16, 2109. [Google Scholar] [CrossRef] [PubMed]
- Butkus, R.; Danielius, R.; Dubietis, A.; Piskarskas, A.; Stabinis, A. Progress in chirped pulse optical parametric amplifiers. Appl. Phys. B Laser Opt. 2004, 79, 693–700. [Google Scholar] [CrossRef]
- Baumgartner, R.A.; Byer, R.L. Optical parametric amplification. IEEE J. Quantum Electron. 1979, 15, 432. [Google Scholar] [CrossRef]
- Kobayashi, T.; Baltuska, A. Sub-5 fs pulse generation from a noncollinear optical parametric amplifier. Meas. Sci. Technol. 2002, 13, 1671–1682. [Google Scholar] [CrossRef]
- Lozhkarev, V.V.; Freidman, G.I.; Ginzburg, V.N.; Katin, E.V.; Khazanov, E.A.; Kirsanov, A.V.; Luchinin, G.A.; Mal’Shakov, A.N.; Martyanov, M.A.; Palashov, O.V.; et al. 200 TW 45 fs laser based on optical parametric chirped pulse amplification. Opt. Express 2006, 14, 446–454. [Google Scholar] [CrossRef]
- Bromage, J.; Bahk, S.W.; Bedzyk, M.; Begishev, I.A.; Bucht, S.; Dorrer, C.; Feng, C.; Jeon, C.; Mileham, C.; Roides, R.G.; et al. MTW-OPAL: A technology development platform for ultra-intense optical parametric chirped-pulse amplification systems. High Power Laser Sci. Eng. 2021, 9, 63. [Google Scholar] [CrossRef]
- Li, Z.; Kawanaka, J. Possible method for a single-cycle 100 petawatt laser with wide-angle non-collinear optical parametric chirped pulse amplification. OSA Contin. 2019, 2, 1125–1137. [Google Scholar] [CrossRef]
- Photon Picture of Optical Parametric Amplification (OPA). Available online: https://upload.wikimedia.org/wikipedia/commons/9/98/Photon_picture_of_Optical_Parametric_Amplification_%28OPA%29.svg (accessed on 10 September 2017).
- Sistrunk, E.F.; Spinka, T.; Bayramian, A.; Betts, S.; Bopp, D.; Buck, S.; Charron, K.; Cupal, J.; Deri, R.; Drouin, M.; et al. All Diode-Pumped, High-repetition-rate Advanced Petawatt Laser System (HAPLS). In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 14–19 May 2017; p. STh1L.2. [Google Scholar]
- Giesen, A. Thin Disk Lasers—Power scalability and beam quality. PhotonicsViews 2005, 2, 42–45. [Google Scholar] [CrossRef]
- Tümmler, J.; Jung, R.; Stiel, H.; Nickles, P.V.; Sandner, W. High-repetition-rate chirped-pulse-amplification thin-disk laser system with joule-level pulse energy. Opt. Lett. 2009, 34, 1378–1380. [Google Scholar] [CrossRef]
- Photonics Encyclopedia. Available online: https://www.rp-photonics.com/thin_disk_lasers.html (accessed on 6 May 2024).
- Chvykov, V.; Nagymihaly, R.S.; Cao, H.; Kalashnikov, M.; Osvay, K. Design of a thin disk amplifier with extraction during pumping for high peak and average power Ti:Sa systems (EDP-TD). Opt. Express 2016, 24, 3721–3733. [Google Scholar] [CrossRef]
- Chvykov, V.; Cao, H.; Nagymihaly, R.; Kalashnikov, M.P.; Khodakovskiy, N.; Glassock, R.; Ehrentraut, L.; Schnuerer, M.; Osvay, K. High peak and average power Ti:sapphire thin disk amplifier with extraction during pumping. Opt. Lett. 2016, 41, 3017–3020. [Google Scholar] [CrossRef]
- Cao, H.; Nagymihaly, R.S.; Chvykov, V. Cross thin slab kW-class Ti: Sapphire amplifiers. Laser Phys. 2019, 29, 065802. [Google Scholar] [CrossRef]
- Chvykov, V.; Chi, H.; Wang, Y.; Dehne, K.; Berrill, M.; Rocca, J.J. Demonstration of a side-pumped cross-seeded thin-slab pre-amplifier for high-power Ti:Sa laser systems. Opt. Lett. 2022, 47, 3463–3466. [Google Scholar] [CrossRef]
- ELI BEAMLINES FACILITY. Available online: https://www.eli-beams.eu (accessed on 1 April 2024).
- ELI-ALPS Research Institute. Available online: https://www.eli-alps.hu (accessed on 1 April 2024).
- Nuclear Physics (ELI-NP). Available online: https://www.eli-np.ro (accessed on 1 April 2024).
- Li, W.; Gan, Z.; Yu, L.; Wang, C.; Liu, Y.; Guo, Z.; Xu, L.; Xu, M.; Hang, Y.; Xu, Y. 339 J high-energy Ti:sapphire chirped-pulse amplifier for 10 PW laser facility. Opt. Lett. 2018, 43, 5681–5684. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023 W/cm. Optica 2021, 8, 630–635. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Lu, X.; Chen, J.; Long, Y.; Li, W.; Chen, H.; Chen, X.; Bai, P.; Li, Y.; et al. 13.4 fs, 0.1 Hz OPCPA Front End for the 100 PW-Class Laser Facility. Ultrafast Sci. 2022, 2022, 9894358. [Google Scholar] [CrossRef]
- Mourou, G.; Mironov, S.; Khazanov, E.; Sergeev, A. Single cycle thin film compressor opening the door to Zeptosecond-Exawatt physics. Eur. Phys. J. Spec. Top. 2014, 223, 1181–1188. [Google Scholar] [CrossRef]
- Khazanov, E. Post-compression of femtosecond laser pulses using self-phase modulation: From kilowatts to petawatts in 40 years. Quantum Electron. 2022, 52, 208–226. [Google Scholar] [CrossRef]
- Chvykov, V.; Radier, C.; Chériaux, G.; Kalinchenko, G.; Yanovsky, V.; Mourou, G. Compression of Ultra-high Power Laser Pulses. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 16–21 May 2010; p. JThG4. [Google Scholar]
- Ginzburg, V.; Yakovlev, I.; Kochetkov, A.; Kuzmin, A.; Mironov, S.; Shaikin, I.; Shaykin, A.; Khazanov, E. 11 fs, 1.5 PW laser with nonlinear pulse compression. Opt. Express 2021, 29, 28297–28306. [Google Scholar] [CrossRef] [PubMed]
- Kaumanns, M.; Kormin, D.; Nubbemeyer, T.; Pervak, V.; Karsch, S. Spectral broadening of 112 mJ, 1.3 ps pulses at 5 kHz in a LG10 multipass cell with compressibility to 37 fs. Opt. Lett. 2021, 46, 929. [Google Scholar] [CrossRef] [PubMed]
- Savichev, V.; Tarkan, T.; Wang, Y.; Rocca, J.; Chvykov, V. Free Beam Propagation Multipass Cells for Post-Compression of High-Energy Laser Pulses. In Proceedings of the CLEO 2024, OSA/CLEO/IQEC, Charlotte, NC, USA, 5–10 May 2024; p. STh4I.2. [Google Scholar]
- Mourou, G.; Fisch, N.; Malkin, V.; Toroker, Z.; Khazanov, E.; Sergeev, A.; Tajima, T.; Le Garrec, B. Exawatt-Zettawatt pulse generation and applications. Opt. Commun. 2012, 285, 720–724. [Google Scholar] [CrossRef]
- Hur, M.S.; Ersfeld, B.; Lee, H.; Kim, H.; Roh, K.; Lee, Y.; Song, H.S.; Kumar, M.; Yoffe, S.; Jaroszynski, D.A.; et al. Laser pulse compression by a density gradient plasma for exawatt to zettawatt lasers. Nat. Photonics 2023, 17, 1074–1079. [Google Scholar] [CrossRef]
- Chesnut, K.D.; Barty, C. Ideal spatio-temporal pulse distribution for exawatt-scale lasers based on simultaneous chirped beam and chirped pulse amplification. Opt. Express 2023, 31, 5687–5698. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chvykov, V. High-Power Lasers. Encyclopedia 2024, 4, 1236-1249. https://doi.org/10.3390/encyclopedia4030080
Chvykov V. High-Power Lasers. Encyclopedia. 2024; 4(3):1236-1249. https://doi.org/10.3390/encyclopedia4030080
Chicago/Turabian StyleChvykov, Vladimir. 2024. "High-Power Lasers" Encyclopedia 4, no. 3: 1236-1249. https://doi.org/10.3390/encyclopedia4030080
APA StyleChvykov, V. (2024). High-Power Lasers. Encyclopedia, 4(3), 1236-1249. https://doi.org/10.3390/encyclopedia4030080







