Definition
This entry provides a review of economic models of professional sports leagues with and without revenue sharing. These include models that assume profit-maximizing and win-maximizing (sportsmen) club owners. Both approaches predict that revenue sharing will reduce the demand for player talent, depress player salaries, and transfer revenue from large-market to small-market clubs, but they differ on league parity effects. Empirical work has been sparse due to financial data limitations and has not yielded definitive results on the parity issue. Despite the growing awareness of sports economics in the sports industry, the lack of consensus from theoretical models has resulted in sports leagues searching for an optimal revenue sharing policy. The difficulty in providing consistent policy prescriptions in models that incorporate revenue sharing, salary caps, and other league policies has made economic modeling of sports leagues very difficult and complex. While revenue sharing remains an interesting theoretical modeling issue, it has not bridged the gap to real-world league policies.
1. Introduction
Revenue sharing is a business tool used by North American professional sports leagues to redistribute revenues from wealthy large-market clubs to less wealthy small-market clubs. The intention of revenue sharing is to ensure survival of the league by having enough clubs that are financially viable. The nature of professional team sports requires an opposing club at each match to produce an output, defined here as ticket sales from attendees. Neale [1] referred to this joint production as the “peculiar economics of professional sports”: while competition is encouraged on the field, clubs participate in a joint venture to maximize league revenue. Fan interest could dwindle if a league shrinks to only a few clubs. Revenue sharing is one of several tools a league can use to reach its optimal size, where it achieves its highest revenue and profitability. The purpose of this paper is to discuss the mechanics of different revenue sharing schemes, the development of theoretical models in sports economics that incorporate revenue sharing, and summarizing empirical work that test their predictions, particularly regarding league parity.
The sharing of league revenues that fall outside of the contests played is commonplace in professional sports leagues around the world. These revenues include national television, streaming, licensing, apparel, and other revenue sources that are negotiated and collected by the league offices. In most cases, these revenues are shared equally among the member clubs. Major League Baseball (MLB) clubs each received USD 60.1 million from the national revenue pool in 2023 [2]. The National Football League (NFL) clubs each received USD 372 million from the national revenue pool in 2022 [3]. One notable exception is the English Premier League (EPL), that shares 50% of these revenues equally among its member clubs, assigning 25% based progressively on order of finish in the 20-team league (higher finishing clubs earning a larger share), and the remaining 25% as a facilities fee for televised matches [4]. This could be a sensible policy to encourage greater competition in football leagues that feature promotion and relegation with lower leagues. However, North American leagues do not feature promotion and relegation systems, so an equal split of national revenues is sensible.
North American professional sports leagues have utilized two different types of systems to share local revenues that include gate revenue (not including suite revenue), some parking and concession revenue, and some local advertising revenue (signage and media). These revenues are commonly referred to as “baseball-related income” or “basketball-related income” depending upon the sport. The revenues included in these categories differ slightly among the four major leagues (MLB, NFL, National Basketball Association (NBA), and National Hockey League (NHL)). Gate revenue sharing requires that the home and visiting club split the revenue from each contest unequally. The NFL used a 60–40 split (home and visitor) for decades. MLB adopted a 50–50 split early in its history, moving to a roughly 95–5 split (the National League paid 50 cents to the visiting team for every ticket sold, which works out to a roughly 95–5 split over several decades) and 80–20 split (American League) until the mid-1990s. Gate revenue sharing resulted in disproportionate effects on club revenue since the system is sensitive to the playing schedule. A small-market club prefers being placed in a league division (or conference) that contains many large-market clubs to garner more revenue from the gate split. A large-market club would suffer a loss in potential revenue by being placed in a division with only small-market clubs. The result could be a “revenue reversal” [5], where a club changes position in the league revenue hierarchy due to the gate sharing system. Incentives for club owners to be competitive in matches and at the business table could become distorted. This premise relies on the property that clubs will move towards business decisions (player acquisitions, ticket pricing, etc.) that maximize league revenue in the absence of any restrictions (where marginal revenues are equated between clubs), which is a standard result of economic models of sports leagues [6].
Gate revenue sharing in North American sports leagues has been replaced with a pooled revenue sharing system in which each club contributes a common, fixed percentage of its local revenue to a central pool administered by the league office. Each club then receives an equal share of the revenue pool at the end of each playing season. These percentages are negotiated in the collective bargaining agreements of each league with the players since revenue sharing has the potential to depress player salaries if it is extensive (Fort and Quirk 1995). The 2023 contribution rates were 48% in MLB, 34% in the NFL, and 50% in the NBA. The NBA redistributes an amount to each club equal to the average club payroll. Small-market clubs must earn at least 70% of the average club local revenue to qualify to receive a share. The NHL revenue sharing system is more complex, with contributions to the league revenue pool made only by the top ten revenue teams (with some concessions to several U.S. teams) and an unequal split of pooled revenue based on local market size. NFL clubs equally shared a total revenue pool of approximately USD 12.3 billion in 2022 [7]; MLB clubs equally shared approximately USD 3.3 billion in 2022 [8]. A total of USD 404 million was redistributed among clubs in the NBA in 2022 [9]. Pool revenue sharing does not suffer from the potential of revenue reversals [5] and could be one of the reasons for its adoption by North American leagues.
In a pool revenue sharing system, clubs whose local revenue falls below the league average receive a net positive revenue transfer, while those clubs who fall above the league average are net payers. There is no change in the average club revenue; however, the distribution of club revenues becomes more compact, reflected in a smaller standard deviation. All clubs maintain their ranking in the local revenue hierarchy after revenue sharing. Figure 1 demonstrates this effect for the 2008 MLB season, when the contribution rate was 31%. Estimates of local club revenue after revenue sharing are produced each season by Forbes magazine and catalogued at a website [10]. The standard deviation of local club revenue fell from USD 67.1 million before revenue sharing to USD 46.3 million after revenue sharing, with a significant decrease in skewness.
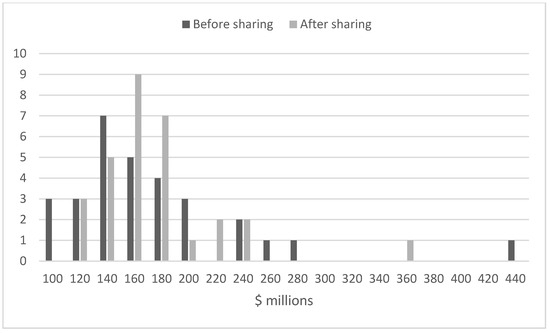
Figure 1.
Histogram of local club revenues before and after revenue sharing in MLB in 2008. Data from Forbes magazine estimates catalogued at [10].
The compression effect of revenue sharing on team revenues was more pronounced for the 2023 season in Figure 2 when the contribution was 48%. The standard deviation of local club revenue fell from USD 93.3 million before revenue sharing to USD 65.5 million after revenue sharing, again with a significant decrease in skewness.
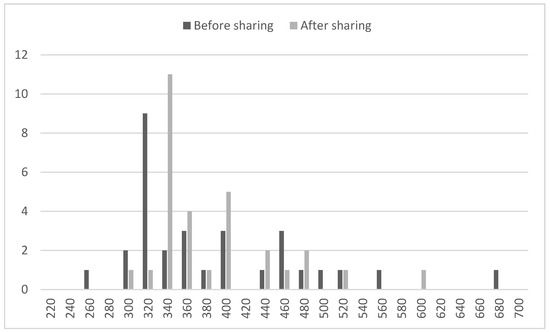
Figure 2.
Histogram of local club revenues before and after revenue sharing in MLB in 2023. Data from Forbes magazine estimates catalogued at [10].
There is no doubt that pool revenue sharing supports the survival of small-market clubs by transferring revenue to them from large-market clubs. Economists debate whether this is necessary or if it is better to simply let small-market clubs fail if they cannot survive without revenue sharing. The so-called invariance principle [11] states that the distribution of player talent among clubs will be the same over time whether club owners or players own the property rights to player talent. It is a precursor to the famous Coase theorem [12] that applied the invariance principle to problems of social cost, including pollution, crime, and other negative externalities. The invariance principle has been extended to consider whether league policies to affect parity do so. A lack of evidence that such policies affect parity is considered support for the invariance principle even though it was originally applied to only free agency and the reserve clause. If the invariance principle holds, clubs will pursue business behaviors that maximize total league revenue, even if that requires letting small-market clubs fail. This result requires very strict conditions that are not likely to hold and do not hold in the standard theoretical model of a sports league. It could be profit-maximizing to use revenue sharing to ensure the survival of small-market clubs if the resulting decrease in player salaries is large and the effects on league parity are small [13].
There are other motivations for a professional sports league to use revenue sharing in addition to supporting small-market clubs. The welfare of all the member clubs can be improved by reducing the volatility of club revenues after revenue sharing [14]. Leagues whose member clubs are in different countries can use revenue sharing to help mitigate the effects of exchange rate fluctuations [15] since revenues are garnered in local currency, but players are often paid in a single standard currency (such as U.S. dollars). Revenue sharing can increase social welfare and club profits under certain conditions [16] and it can facilitate collusion among club owners when bidding for new talent, resulting in lower player salaries [17].
Professional sports leagues employ other policies to promote parity in play and ensure the survival of small-market clubs. The EPL, NFL, NBA, and NHL use a salary cap system to limit the growth in player salaries to maintain profit stability. The North American leagues use similar systems, allocating a percentage of the anticipated sport-related league revenue to the players (48% in the NFL, 50% in the NBA, and 57% in the NHL) that is shared evenly among all clubs. Penalties for exceeding the club salary cap are severe in the NFL and NHL. The salary cap rules are negotiated in each league’s collective bargaining agreement. The EPL limits the amount of losses that clubs can accrue over a three-year period (profit sustainability rule or PSR), currently GBP 105 million, effectively tying the club payroll to its revenue over this period [18]. Unlike the North American system, the EPL allows clubs to increase their payrolls if revenue growth is sufficient. Violations can result in fines and points deductions. Restrictions on the abilities of clubs to generate revenue and subsequently afford higher payrolls make it difficult to predict the effects of revenue sharing alone in an economic model of a sports league. We restrict the analysis that follows to a league that uses revenue sharing only; however, we make note of research that has attempted to use revenue sharing and salary caps.
2. The Two-Team League Model
Economists provide policy recommendations by first developing an economic model of the problem that incorporates logical and simple economic assumptions about firm behavior. In comparison to the standard models of monopoly, oligopoly, and perfect competition utilized by economists, models of sports leagues were late in developing, perhaps due to their unusual business structure. Neale [1] noted the “peculiar economics” of sports leagues. A single club operating in a monopoly cannot survive since output and revenue requires a competing club, whereas competition encourages greater profitability. Sports leagues are perhaps best defined as joint ventures, but there is no consensus on how to define their structure. Economists have resorted to treating each club as a local monopoly in its geographic area with elements of a cartel.
2.1. The League Equilibrium without Revenue Sharing
The first economic model of a professional sports league [19] incorporated an N-team league and could not provide exact solutions for a revenue sharing league equilibrium due to its complexity. Simplifying the exposition to a two-team model has become standard practice as it allows for easier solutions for the league equilibrium without sacrificing generality. A commonly used model assumes two clubs, one large-market, the other small-market, that each choose a stock of talent to maximize profit. Talent is costly but is assumed to be available in any amount without poaching talent from the competing club. The stock of talent results in a club winning percentage through a contest success function. Clubs will equalize their marginal revenues from winning contests and their optimal winning percentages will be revealed at the league equilibrium. At this point, revenue sharing is introduced in the model and its effect on parity is revealed at the new solution for the league equilibrium. Assuming numerical values for the parameters in the league model allows for the solution of the revenue transfer from the large- to small-market club. A league model by Kesenne [20] is a simple example of league models in the literature.
The two-team league model derives a profit-maximization combination of winning percentages that add up to one. Team revenue is a positive function of the team winning percentage at a diminishing rate, reaching a maximum at a winning percentage of 1.0. The team market size acts as a scalar, shifting the revenue function upward with a larger market size. We assume that team A operates in a larger market size than team B, but it makes no difference to the exposition if this assumption is reversed. If both clubs have identical market sizes, the equilibrium will be identical winning percentages, . Each club produces outputs (hits, runs, goals, etc.) that translate into wins through an unspecified production function. Revenue is obtained through tickets sales via a demand curve that is also unspecified. This approach to the two-team league model ignores the deeper workings of production and demand, but it has become the standard approach. One can think of the market size as a scalar in the ticket demand function. Each club is assumed to be a local monopoly but together they act as a sort of joint venture since output cannot be produced by one club without the other.
Figure 3 provides a representation of the revenue functions, with the team A revenue function lying everywhere above team B’s revenue function due to its larger market size. The total revenue curve for team A is steeper than that for team B at any winning percentage, hence at any winning percentage.
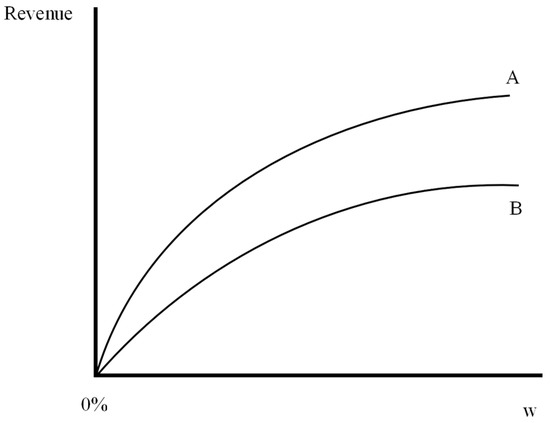
Figure 3.
Revenue functions for teams A and B for .
The league equilibrium can be found graphically by placing both marginal revenue lines in the same diagram, as depicted in Figure 4. Ties are not allowed and the winning percentage for each club, and , can be placed on the horizontal axis in opposite directions due to the adding up property.
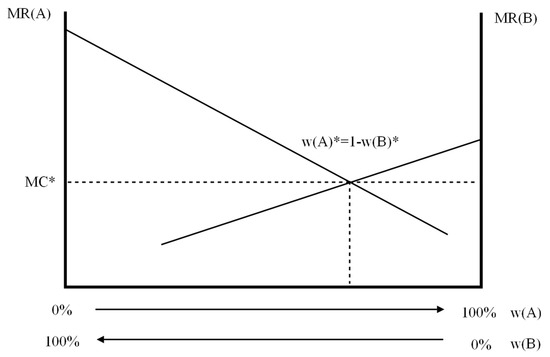
Figure 4.
The two-team league equilibrium winning percentages, and .
As a local monopolist, each will hire quality talent up to the point where . It is important to note that this is the marginal cost of winning, not the marginal cost of talent, although they are often treated the same way in the literature. Both clubs can maximize profit only where the marginal revenue lines intersect. We denote the equilibrium winning percentages for the two clubs as and . The marginal cost of winning will be for both teams. Here, we introduce the original statement of the invariance principle: the ultimate allocation of talent will be invariant to the initial allocation if player cash sales are allowed. Suppose initially that due to team A having a larger stock of talent than team B. It is profitable for team A to buy quality players from team B to improve its winning percentage since . Total revenue for team A will increase until is reached, at which point there is no further incentive to purchase talent from team B. If , then and the opposite will occur, team B will purchase talent from team A, increasing its revenue until the league equilibrium is reached. The league equilibrium is reached regardless of the initial allocation of talent. The total league revenue is the area under the two marginal revenue lines at the league equilibrium. Any other combination of winning percentages will fail to maximize the league revenue.
The upshot is that it is profit-maximizing for the two-team league to have the larger-market team A have a larger talent stock and win a majority of its games. The invariance principle requires that cash sales of players be allowed in the league so that talent can move to its most valued team. Cash sales have become infrequent in North American professional sports leagues since the 1970s, except for minor-league players or players of lesser talent. European football leagues maintain a transfer system that allows cash sales of players within and across borders.
Further results can be found by specifying an algebraic model of the two-team sports league. Team A’s revenue is a function of its market size, , and its winning percentage, .
An increase in shifts the revenue function upward, assumedly due to an upward shift in the demand curve for tickets, for a given winning percentage. The units for are left unspecified, but typically are the local metropolitan population in empirical studies. Revenue is a weighted average of the team A winning percentage, with the second term measuring the closeness of the winning percentages. This property of (1) is known as the uncertainty of outcome hypothesis or UOH. Since , the product of the two winning percentages reaches a maximum when and the contribution of the UOH to revenue is maximized. After collecting the terms, (1) can be rewritten as (2) below.
Each club acquires a stock of talent that generates a winning percentage specified by a logistic contest success function . At this point, it is necessary to distinguish between an open or closed talent market. For this, we consider the effect on when team A increases its stock of talent .
In the open talent market case, there is no need for team A to poach talent from team B as there is an infinite supply of talent in the market, hence and (3) reduces to . Team A can only increase its talent stock by poaching talent from team B in the closed market talent case, hence . The result is that (3) reduces to . It is easy to show that increases by more in the closed talent market case. Both are extreme cases, and the availability of talent is somewhere in between. Rockerbie and Easton [21] specify a club talent stock, , that is a function of the team payroll relative to the total league payroll that allows for a flexible talent market: open, closed, or in between. The approach is not directly applicable here as it addresses the complementarity between stadium investments and investments in club talent. One could also interpret the derivative as a talent conjecture, that is, the anticipated response of team B to an increase in , instead of a physical talent market constraint. Easton and Rockerbie [22] consider the cases of the Cournot competitive and cartel conjectures. Szymanski [23] argues that the Cournot conjecture is the only consistent conjecture to reach a league equilibrium in the open talent market case. The closed talent market case is more difficult to solve with Cournot conjectures [24].
The marginal revenue for team A is given by . The marginal revenue for team B is . Assume for simplicity that for both teams. If , then when or 100%. This is thought to be a desirable property. We have already shown that league revenue is maximized where . Simplifying, this gives the league equilibrium condition below.
Simplifying further gives the league equilibrium in (5) below.
The extent to which the winning percentage for team A rises above 0.5 is determined by the square root of the market size ratio, referred to as the competitive balance ratio. The relative talent stocks are found by inserting the logistic contest success function for the winning percentages in (5) and simplifying.
The ratio of the profit-maximizing talent stocks is the square root of the local market size ratio. This result assumes an open talent market where each team can acquire all the talent it desires without increasing the market wage rate for talent. The closed talent market result can be found in Vrooman [25], who showed that the league equilibrium is characterized by less parity than in the open talent market case above. This has come to be the standard algebraic model of the two-team professional sports league [26,27]. Its advantage is that it incorporates the UOH in the revenue functions for both clubs. Unfortunately, it is difficult algebraically to solve for the league equilibrium with revenue sharing, so we use a simpler model in the next section and follow that with the above model, solved using simulation.
2.2. The League Equilibrium with Revenue Sharing
We now consider revenue sharing without any other league policies to redistribute revenues or to restrict the behaviors of club owners. Marburger [28] considers revenue sharing and a luxury tax in a two-team sports league model. The luxury tax used in MLB, now known as the competitive balance tax, taxes the overage of club payroll above a threshold value, providing an incentive for clubs not to spend lavishly on players. The tax rate increases for repeat offenders. The luxury tax improves league parity if it is binding for the large-market club. The NBA adopted a payroll cap and individual salary cap in 1984, followed by the NFL in 1994 and the NHL in 2006. MLB does not feature a payroll or salary cap. Dietl et al. [29] construct a two-team league model of profit-maximizing club owners that use revenue sharing and a club payroll cap and find that the effect on league parity depends upon whether the payroll cap is binding for both clubs or only one club, and in each case is based on the difference in market sizes. The NFL, NBA, and NHL also feature a fixed sharing of anticipated league revenue to the players (48%, 57%, and 57%, respectively). This amount is divided evenly between the member clubs to establish a club salary cap. Spending above the club salary cap is punished with a variety of financial penalties. The club salary cap is determined by anticipated league revenue, which is determined by the profit-maximizing behavior of club owners. This endogeneity issue is addressed by Fujimoto [30] in an N-team sports league model that incorporates a time to accumulate talent and a fixed new flow of available talent each season (an amateur draft). The invariance principle is rejected.
In pool revenue sharing, a share of its local revenue is kept by each club, with the rest, (), contributed to a central pool managed by the league. Team A’s net revenue after sharing (a superscript S denotes after revenue sharing) depends upon its own local revenue as well as that of team B. The same is true for team B’s revenue after sharing. We assume that the central fund is split evenly between the two teams at the end of the playing season.
The marginal revenues are given below.
Why does appear in (9)? Team A increases its net revenue by when it increases its winning percentage, due to its share of the higher local revenue in the first term in (9), part of which is returned from the central pool. Team B’s winning percentage falls by the same amount as the increase for team A (, due to the adding up property) and its local revenue decreases, resulting in a smaller contribution to the central fund. Team A must absorb of the fall in team B’s local revenue from the central fund since The same effect holds for team B in (10). Figure 5 depicts the downward shifts in marginal revenues. The marginal cost of winning is also reduced at the profit-maximizing league equilibrium, much to the displeasure of the players.
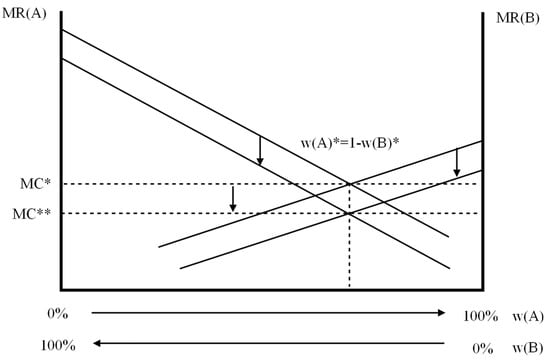
Figure 5.
Marginal revenues are decreased with pool revenue sharing. The marginal cost of winning is also decreased. The equilibrium winning percentages remain at and .
The profit-maximizing winning percentages at the new league equilibrium, and , cannot be determined without addressing the magnitudes of the shifts in the marginal revenue lines. A smaller shift in marginal revenue for one of the clubs will result in an improvement in the club’s winning percentage. Both marginal revenue lines shift down by the same amount in Figure 5, resulting in and being unchanged from the initial league equilibrium. This is not a general result but can occur if , an assumption used by Fort and Quirk [6]. Equations (9) and (10) then reduce to (11) and (12) below.
The league equilibrium is established when (11) is set equal to (12). The resulting expression after simplification is , the pre-revenue sharing marginal revenues, and Equations (4)–(6) result. League parity is left unaffected, and the invariance principle holds.
Pool revenue sharing worsens parity in the two-team league model, a now accepted theoretical result. Team A transfers revenue to team B equal to the area between its original and new marginal revenue lines up to . Using the same logic, team B transfers revenue to team A by a lesser amount resulting in a net gain in revenue for team B. Revenue sharing benefits the smaller-market team B much to the displeasure of the larger-market team A.
To ease the exposition, we respecify the revenue functions for team A and team B as and , where and . We still use (7) and (8) to express team revenues after revenue sharing. Profit is maximized after revenue sharing by choosing a club stock of talent. The marginal revenues in (9) and (10) after revenue sharing are given below.
Equating the marginal revenues in (13) and (14) gives (15) below (assuming an open talent supply).
Simplifying gives
or or or
Without revenue sharing, and (16) reduces to . One need only show that to find that league parity has worsened. It is easy to find the result holds if (or ), our assumption.
Competitive balance has worsened with revenue sharing. The logic is simple. With greater revenue sharing, both teams must absorb some of the other team’s losses in revenue when their opponent increases its stock of talent that also increases its winning percentage. Suppose that the small-market team B increases its stock of talent and winning percentage. Team B will earn more revenue from its own market but must absorb the loss in revenue from team A, a much larger-revenue team. The result is that team B loses net revenue and the line in Figure 3 shifts down by a lot (algebraically < if ). Team A’s marginal revenue shifts down as well with revenue sharing, but not by as much as team B since it absorbs a smaller loss in revenue from the small-market team B when team A increases its stock of talent. The net result of greater revenue sharing is a worsening of parity.
The marginal cost of talent does not appear in the first-order conditions in (4) and (13)–(14) due to the assumption that it is constant over whatever stock of talent is acquired. Cavagnac [31] builds a league model where the marginal cost of talent is an increasing function of the total league stock of talent, that is, . This function internalizes the negative externality team B places on team A when it bids up the price of talent with a limited talent supply. The first-order conditions for profit-maximization are more complex and the result is that invariance does not hold with revenue sharing. It is not clear if the use of revenue sharing increases league profits. The reduction in club payrolls increases profitability in the short-run but could reduce revenue and profitability in the long-run. Peeters [32] considers the issue in a profit-maximizing league model and finds that revenue sharing can increase profitability if the member clubs are heterogeneous in market sizes. Revenue sharing can reduce profitability if market sizes are homogeneous.
2.3. Revenue Sharing in the Sportsman League Model
Club owners in a “sportsman” professional sports league maximize wins subject to a break-even constraint. The PSR rule used in the EPL could be interpreted as a form of break-even constraint over three consecutive seasons. However, the tying of club expenses—mostly payroll—to club revenues is more complex than just breaking even. Club payroll is a function of club profit, which is a function of the club payroll and revenue. This is a tricky endogeneity problem that has yet to be modeled in the literature but is well worthy of study.
An exposition of the win-maximizing league model is Vrooman [25]. The break-even constraint forces each club to acquire talent up to the point where average revenue (AR) of winning equals the average cost of talent (AC). Using (2) and if , a constant, the break-even conditions are below (note that MC = AC of talent when c is a constant). Define total league talent as .
The league equilibrium is established where the average revenues are equal. This does not maximize total league revenue since each club will acquire a talent stock above its profit-maximizing stock. Using the adding-up property for the winning percentages yields the condition below.
Ignoring the cT term yields the solution for the league equilibrium.
In comparison to the profit-maximizing equilibrium in (5), parity is skewed more heavily to the large-market club—competitive balance is lower.
The win-maximizing conditions in (17) and (18) are now modified to incorporate pool revenue sharing below. Essentially, the two clubs are sharing average revenues.
The league equilibrium is established where the average revenues after revenue sharing are equal.
Simplifying (23) gives
The equilibrium winning percentages can be found through simulation, and then, compared to those from (20). We chose the parameter values , , and . The solution in the case with no revenue sharing is . With revenue sharing, . Parity is improved by using pool revenue sharing in a win-maximizing league. As , parity approaches its level without revenue sharing.
Empirically testing the effects of pool revenue sharing on league parity and player salaries is difficult since revenue sharing contribution rates do not change often. The NFL adopted the policy in 1994, with MLB following in 1997, the NHL in 2006, and the NBA in 2013. The NHL and NBA systems are too complex to be subjected to empirical testing, leaving changes in the contribution rates in the NFL and MLB to test for parity effects. A review of the difficulties in testing revenue sharing parity effects is given in Rockerbie [33]. A large hurdle is obtaining accurate financial data for club revenues, although Forbes magazine produces estimates for the four major North American leagues. In addition, the NFL, NBA, and NHL use salary caps that have parity effects, confounding the revenue sharing effect.
Attempts to estimate parity effects are scant in the literature. Fort et al. [34] provide a survey of early papers that mostly find a rejection of the invariance principle based on indirect evidence related to revenue sharing, such as player movements and talent investments. Solow and Krautmann [13] found that changes to the 1996 MLB revenue sharing agreement did not affect parity—a confirmation of the invariance principle—but did lower player salaries as the theoretical models predict. Rockerbie [33] found that the reduction in the contribution rate in the 2007 MLB revenue sharing agreement worsened parity, contrary to what the theoretical model developed earlier predicts. Both papers relied on estimating the shifts in the marginal revenue product lines in Figure 3. Hill and Jolly [34] found that player salaries increased following the lowered 2007 MLB contribution rate, more so for hitters than pitchers, confirming the prediction of the two-team league model, although they did not consider parity effects. Jolly [35] found that the dispersion of player salaries within clubs decreased following the 2007 MLB change, holding a set of variables constant, suggesting that clubs might be more equally balanced in play, although parity effects were not tested.
3. Conclusions
Pool revenue sharing is used by professional sports leagues in North America to redistribute local revenue from large-market clubs to small-market clubs to ensure financial stability. The nature of team sport is that it takes two clubs competing on the field to produce an output. Contrary to other industries, a league composed of only one club, a monopoly, cannot survive. Economists have analyzed the behavior of sports leagues using a simple two-team profit-maximizing model due to its ease of exposition and solving for its equilibrium. There is broad agreement that pool revenue sharing will decrease the marginal cost of talent, thereby lowering player salaries. Its effect on league parity relies on assumption about the availability of talent. Revenue sharing worsens parity with an open talent market (a completely elastic talent supply) while the invariance principle holds in the closed talent market case (a completely inelastic talent supply). Parity is also dependent, in either case, on the marginal cost of talent. If constant, the above parity results hold, but invariance does not hold in either if the marginal cost of talent is increasing. Finally, revenue sharing improves league profit if the decrease in player salaries is larger than the reduction in league revenue due to less parity (the UOH). Combining revenue sharing with a salary cap complicates the two-team model and, as expected, yields uncertain results regarding parity.
As Fort et al. [36] note, “revenue sharing wins the prize for neglect in the literature” when estimating its effects on league parity and profitability. The few papers that have made attempts have mixed results, largely due to difficulties in obtaining accurate financial data and the confounding effects of other league policies (salary caps, luxury taxes, etc.).
The theoretical literature has advanced to the stage where testable predictions under different assumptions have largely been exhausted. Extending the two-team league model to more teams could be useful, but its insights could be marginal, and its solutions could be intractable. That leaves future efforts to focus on empirical work. One must observe significant changes to the revenue sharing contribution rate to obtain reliable estimates, but since these are negotiated with many other policies in collective bargaining agreements, they are difficult to isolate with regression analysis. The recent changes in the MLB revenue sharing plan could offer a promising episode for empirical testing. Significant changes to the plan occurred in the 2017 and 2022 CBAs that increased the revenue sharing contribution rates. Alternatively, economists could focus on empirical testing using MLB and NFL financial data prior to the 1980s if it could be obtained. These earlier decades featured simple revenue sharing systems, albeit with a reserve clause that limited player movement. The literature is waiting for a paper that yields decisive results with quality financial data, but it may never appear.
Results from the sports economics literature has had a significant impact on the decisions made by sports executives and managers on the field. This is particularly evident in the use of analytics that had its origin in the sabermetrics literature beginning in the 1970s, with many more recent contributions in the economics literature (Berri and Schmidt provide a useful survey [37]). The successful use of analytics by Oakland Athletics was documented in the popular book Moneyball [38], resulting in a flood of sports executives hiring economists and statisticians to set up analytics systems. Analytics is so common today that its competitive benefits have largely been exhausted.
The same cannot be said for a bridge between policy prescriptions from economic models of sports leagues and actual league policies. Part of the reason is historical. The use of revenue sharing predates the economic models of sports leagues by over 100 years. The National League (NL) of baseball instituted revenue sharing at its inception in 1876. The NL was the first fully professional sports league in North America and wished to be the only one in baseball. Its eight teams operated in a concentrated area on the east coast of the United States. To maintain its monopoly on professional baseball, it needed to stave off the credible threats of rival leagues by achieving financial stability.
The NFL adopted revenue sharing in the 1950s in response to the threat posed by the All-American Football Conference (AAFC), a rival league operating in several major cities. Commissioner Pete Rozelle solidified the revenue sharing system and successfully lobbied congress to pass the Sports Broadcasting Act in 1961 allowing the NFL to negotiate television rights as a single league entity. The NBA and NHL adopted revenue sharing much later in their histories (2013 in the NBA and 2005 in the NHL), largely in response to financial difficulties faced by small-market clubs.
Do sports executives pay attention to results from economic publications regarding the use of revenue sharing? It is a question worthy of further study, perhaps by surveying sports executives, but as in most cases of testing economic models, we measure the observed behaviors of firms in comparison to predictions from theory. Revenue sharing is predicted to transfer revenue from large- to small-market clubs to maintain league stability. Since the late 1960s, the four North American leagues have been remarkably stable with few to no club failures, although relocations have occurred [39]. Revenue sharing has uncertain effects on league parity, worsening it in the most accepted sports league model. If profitability and fan utility is tied to better league parity [40], the premise of the UOH, it is in the interests of sports executives to adopt it. The empirical evidence for the UOH is very weak, suggesting that sports leagues must have other motives [41]. However, the implementation of revenue sharing requires the agreement of the player’s associations, who maximize their own interests in collective bargaining. Revenue sharing is predicted to depress player salaries but in a much less observable way than using a salary cap. Perhaps this is why NHL players preferred the adoption of extensive revenue sharing financed by a luxury tax over a salary cap in its 2004–2005 CBA negotiations [42]. The final agreement contained both.
MLB is still searching for its optimal revenue sharing plan that both the owners and players can agree to. The system has undergone many significant changes since 1996, perhaps in the players hope of avoiding a salary cap. The NBA and NHL revenue sharing plans are unnecessarily complex which, in combination with a league salary cap, makes them virtually impossible to model, resulting in few useful predictions from theory. The result is that revenue sharing remains an interesting problem in a theoretical model that abstracts from real-world CBAs, as is the case in our more general theories of monopoly, oligopolies, and joint ventures. It is useful to assume that sports executives move towards the predictions from theory, the feature of positive economics. Casting our theoretical models in the realm of normative economics has not advanced far enough. Definitive policy recommendations based on theoretical sports league models are still elusive.
Funding
This research received no external funding.
Data Availability Statement
The revenue data in Figure 1 and Figure 2 were obtained from https://sites.google.com/site/rodswebpages/codes (accessed on 18 June 2024) and are publicly available.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Neale, W. The peculiar economics of professional sports. Q. J. Econ. 1964, 78, 1–14. [Google Scholar] [CrossRef]
- Inside the Myth of Small-Market Suffering: A Look at the Pirates Revenue Sharing and Profits. Available online: https://pittsburghbaseballnow.com/inside-the-myth-of-small-market-suffering-a-look-at-the-pirates-revenue-sharing-and-profits/ (accessed on 6 May 2024).
- NFL National Revenue Was Almost $11.9 Billion in 2022. Available online: https://www.forbes.com/sites/mikeozanian/2023/07/11/nfl-national-revenue-was-almost-12-billion-in-2022/?sh=1258d95e2d74 (accessed on 6 May 2024).
- How Premier League TV Rights Work and How They Impact Your Costs and Subscriptions. Available online: https://www.nytimes.com/athletic/4240951/2023/08/25/premier-league-tv-rights-how-work-cost/ (accessed on 6 May 2024).
- Rockerbie, D. Free agent auctions and revenue sharing: A simple exposition. J. Sport Manag. 2009, 23, 87–98. [Google Scholar] [CrossRef]
- Fort, R.; Quirk, J. Cross-subsidization, incentives, and outcomes in professional team sports leagues. J. Econ. Lit. 1995, 33, 1265–1299. [Google Scholar]
- How Sports Teams, Leagues, and Owners Make Money. Available online: https://www.sportico.com/feature/how-sports-teams-leagues-make-money-1234766931/ (accessed on 6 April 2024).
- Major League Baseball Has a “Nutting” Problem. Available online: https://www.thetribune.ca/sports/mlb/ (accessed on 6 April 2024).
- Warriors, 9 Other Teams Paid $163.6 Million into Revenue Sharing Pool. Available online: https://www.espn.com/nba/story/_/id/35882999/warriors-9-other-teams-paid-163.6m-revenue-sharing-pool (accessed on 6 April 2024).
- Rodney Fort’s Sports Business Data. Available online: https://sites.google.com/site/rodswebpages/codes (accessed on 17 May 2024).
- Rottenberg, S. The baseball players’ labor market. J. Political Econ. 1956, 64, 242–258. [Google Scholar] [CrossRef]
- Coase, R. The problem of social cost. J. Law Econ. 1960, 3, 1–44. [Google Scholar] [CrossRef]
- Solow, J.; Krautmann, A. Leveling the playing field or just lowering salaries? The effects of redistribution in baseball. South. Econ. J. 2007, 73, 947–958. [Google Scholar] [CrossRef]
- Rockerbie, D. Revenue sharing in Major League Baseball: The moments that meant so much. Int. J. Financ. Stud. 2018, 6, 71. [Google Scholar] [CrossRef]
- Rockerbie, D.; Easton, S. Revenue sharing in professional sports leagues as a hedge for exchange rate risk. Int. J. Sport Financ. 2017, 12, 342–358. [Google Scholar]
- Dietl, H.; Lang, M. The effect of gate revenue sharing on social welfare. Contemp. Econ. Policy 2008, 26, 448–459. [Google Scholar] [CrossRef]
- Rockerbie, D. Revenue sharing and collusive behavior in the Major League Baseball posting system. Economies 2020, 8, 71. [Google Scholar] [CrossRef]
- What Are Premier League Profit and Sustainability Rules? Everton Handed Fresh Points Deduction for Financial Fair Play Breach. Available online: https://www.sportingnews.com/ca/soccer/news/premier-league-profit-sustainability-rules-financial-fair-play/42ef3c1a91043e191482250d (accessed on 15 July 2024).
- El-Hodiri, M.; Quirk, J. An economic model of a professional sports league. J. Political Econ. 1971, 79, 1302–1319. [Google Scholar] [CrossRef]
- Kesenne, S. Revenue sharing and absolute league quality; talent investment and talent allocation. Scott. J. Political Econ. 2015, 62, 51–58. [Google Scholar] [CrossRef]
- Rockerbie, D.; Easton, S. Of bricks and bats: New stadiums, talent supply and team performance in Major League Baseball. J. Sports Econ. 2019, 20, 3–24. [Google Scholar] [CrossRef]
- Easton, S.; Rockerbie, D. Revenue sharing, conjectures, and scarce talent in a model of a professional sports league. J. Sports Econ. 2005, 6, 359–378. [Google Scholar] [CrossRef]
- Szymanski, S. Professional team sports are only a game: The Walrasian fixed-supply conjecture model, Contest-Nash equilibrium and the invariance principle. J. Sports Econ. 2004, 5, 111–126. [Google Scholar] [CrossRef]
- Driskill, R.; Vrooman, J. It’s not over till the fat lady sings: Game-theoretic analyses of sports leagues. J. Sports Econ. 2016, 17, 354–376. [Google Scholar] [CrossRef]
- Vrooman, J. Theory of the perfect game: Competitive balance in monopoly sports leagues. Rev. Ind. Organ. 2009, 34, 5–44. [Google Scholar] [CrossRef]
- Szymanski, S.; Kesenne, S. Competitive balance and gate revenue sharing in team sports. J. Ind. Econ. 2003, 52, 165–177. [Google Scholar] [CrossRef]
- Kesenne, S. Revenue sharing and competitive balance: Does the invariance proposition hold? J. Sports Econ. 2005, 6, 98–106. [Google Scholar] [CrossRef]
- Marburger, D. Gate revenue sharing and luxury taxes in professional sports. Contemp. Econ. Policy 1997, 15, 114–123. [Google Scholar] [CrossRef]
- Dietl, H.; Lang, M.; Rathke, A. The combined effects of salary restrictions and revenue sharing in sports leagues. Econ. Inq. 2011, 49, 447–463. [Google Scholar] [CrossRef]
- Fujimoto, M. A dynamic analysis of equal revenue sharing and endogenous salary caps in the n-team leagues. J. Sports Econ. 2023, 24, 624–638. [Google Scholar] [CrossRef]
- Cavagnac, M. Revenue sharing and competitive balance when teams are not wage takers. Rev. Ind. Organ. 2009, 35, 299–313. [Google Scholar] [CrossRef]
- Peeters, T. Profit-maximizing gate revenue sharing in sports leagues. Econ. Inq. 2015, 53, 1275–1291. [Google Scholar] [CrossRef]
- Rockerbie, D. The invariance principle in baseball: New evidence. Appl. Econ. 2018, 50, 2613–2621. [Google Scholar] [CrossRef]
- Hill, J.; Jolly, N. Revenue sharing and player salaries in Major League Baseball. J. Sports Econ. 2017, 18, 831–849. [Google Scholar] [CrossRef]
- Jolly, N. Revenue sharing and within-team payroll inequality in Major League Baseball. Appl. Econ. Lett. 2015, 22, 80–85. [Google Scholar] [CrossRef]
- Fort, R.; Maxcy, J.; Diehl, M. Uncertainty by regulation: Rottenberg’s invariance principle. Res. Econ. 2016, 70, 454–467. [Google Scholar] [CrossRef]
- Berri, D.; Schmidt, M. Stumbling on Wins; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Lewis, M. Moneyball: The Art of Winning an Unfair Game; W. W. Norton Co.: New York, NY, USA, 2003. [Google Scholar]
- Quirk, J.; Fort, R. Pay Dirt: The Business of Professional Team Sports; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Micelli, T. A note on the preferences of sports fans: Partisanship versus uncertainty of outcome. J. Sports Econ. 2024, 25, 155–168. [Google Scholar] [CrossRef]
- Collins, C.; Humphreys, B. Contest outcome uncertainty and fan decisions: A meta-analysis. J. Sports Econ. 2022, 23, 789–807. [Google Scholar] [CrossRef]
- Staudohar, P. The Hockey Lockout of 2004-05, 2005. U.S. Bureau of Labor Statistics. Available online: https://www.bls.gov/opub/mlr/2005/12/art3full.pdf (accessed on 18 June 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).