Integrated Fabry–Perot Cavities: A Quantum Leap in Technology

Definition

Integrated Fabry–Perot cavities (IFPCs), often referred to as nanobeams due to their form factor and size, have profoundly modified the landscape of integrated photonics as a new building block for classical and quantum engineering. In this entry, the main properties of IFPCs will be summarized from the classical and quantum point of view. The classical will provide some of the main results obtained in the last decade, whereas the quantum point of view will explore cavity quantum electrodynamics (CQED), which promises to revolutionize the future “quantum internet”.

1. The Advent of Integrated Fabry–Perot Cavities

In the quest for faster optical communication, researchers have been motivated to explore innovative optoelectronic devices. In the meantime, electronics circuits are approaching their limits in terms of bandwidth and power efficiency. For these reasons, keeping signals in the optical domain is seen as a possible strategy to overcome these limitations and continue to improve the high-performance computing (HPC) throughput and power efficiency. To achieve this, optical micro-cavities, which confine light in small volumes at optical wavelength scales, have emerged as important components for signal processing functions. Fabry–Perot cavities, from their inception [1] to the present day, have found many applications in telecoms, spectroscopy and sensing technologies [2,3]. The development of integrated optics in the last few decades has brought renewed interest in integrated Fabry–Perot cavities (IFPCs). High-Q optical microcavities, in particular, characterized by their high quality factor (Q) and their ability to confine light in small modal volumes (V_M), have been at the heart of recent advancements in optical telecommunication. They play a pivotal role in various signal processing functions [4], including channel-drop filtering, on–off switching and light modulation. Moreover, the exaltation of optical non-linearity and spontaneous emission inhibition or exaltation is primarily governed by the Q/V_M ratio. Thus, the quest for ultra-small high-Q cavities [5] has been critical in optical telecommunications [6] and in quantum optics [7]. Several strategies have been proposed to obtain high-Q cavities, like photonic crystals [8], micro-rings, micro-disks [9,10], micro-toroids [11], micro-spheres [12], meta-materials [13], plasmonics [14] and other interesting schemes [15]. However, each of these strategies either produces very large Q factors in excess of 10⁶, but with rather large volumes, or, for the case of plasmonic resonators, a non-CMOS-compatible fabrication process. This entry will focus on arguably the most promising approach, Fabry–Perot cavities. It is believed that a Q factor as large as 10⁸ can be achieved with cavities offering mode volumes close to the theoretical limit of V_M $={(\lambda /2n)}^3$, where $\lambda$ is the resonant wavelength and n is the waveguide’s refractive index.

2. The Challenges with Current Cavities

While significant advancements have been made in developing high-Q cavities [16,17], challenges persist. Notably, while suspended membranes have proven viable at a research level, they present many drawbacks—namely, challenging electrical injection, deformation due to thermal dilatation and the related mechanical stability. As such, the development of IFPCs realized on a substrate, rather than on a membrane, has emerged as a critical issue in the field. In response to these challenges, researchers have turned their attention to integrated Fabry–Perot cavities. Specifically, researchers have demonstrated a practical and easy approach to cavity design consisting of two mirrors composed of a chain of periodic holes located on a ridge waveguide [18], with dedicated sections for the management of scattering losses. This design has proven to significantly enhance the Q factor, making it an attractive solution for the integration of high-Q cavities on a substrate.

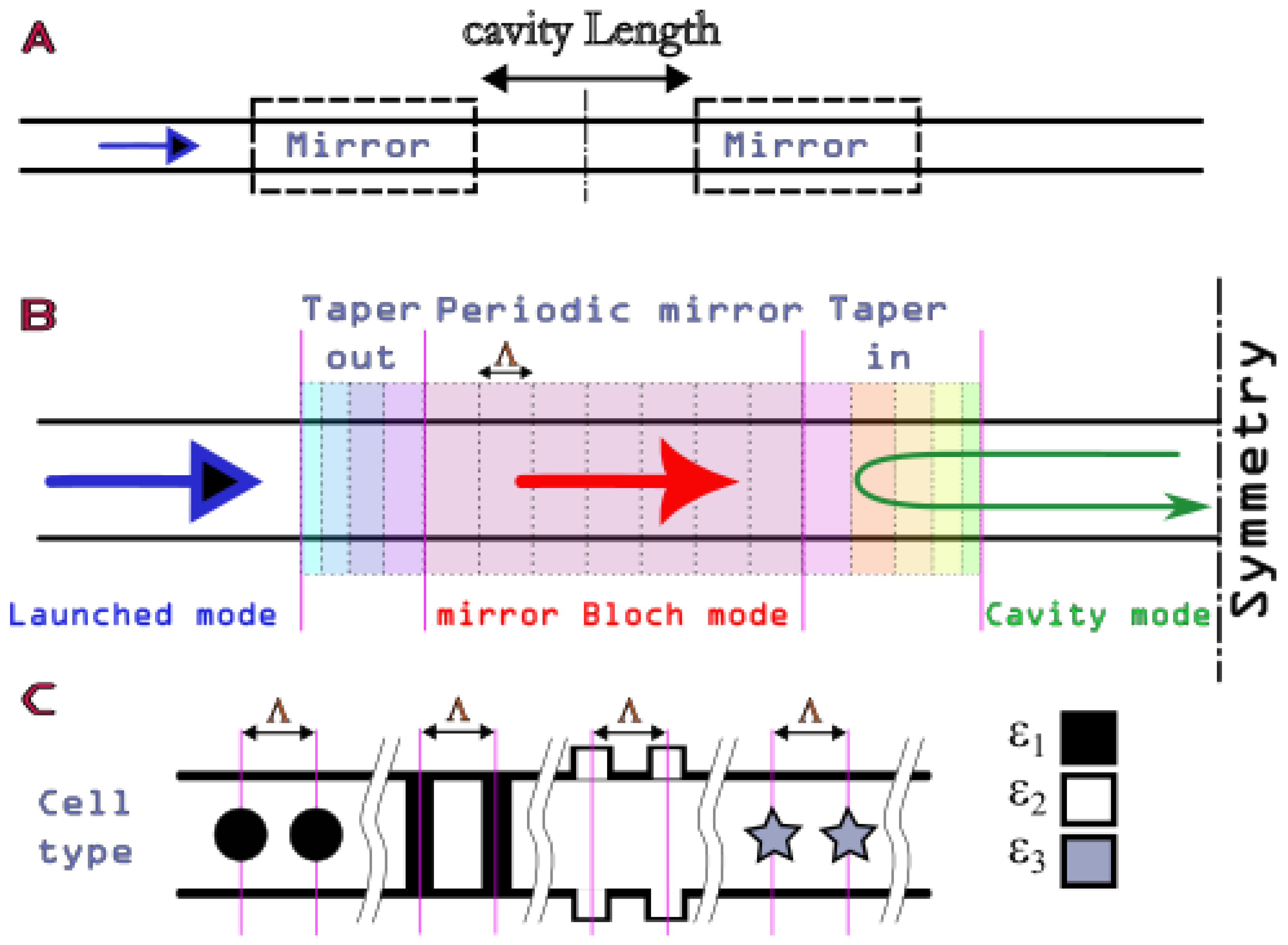
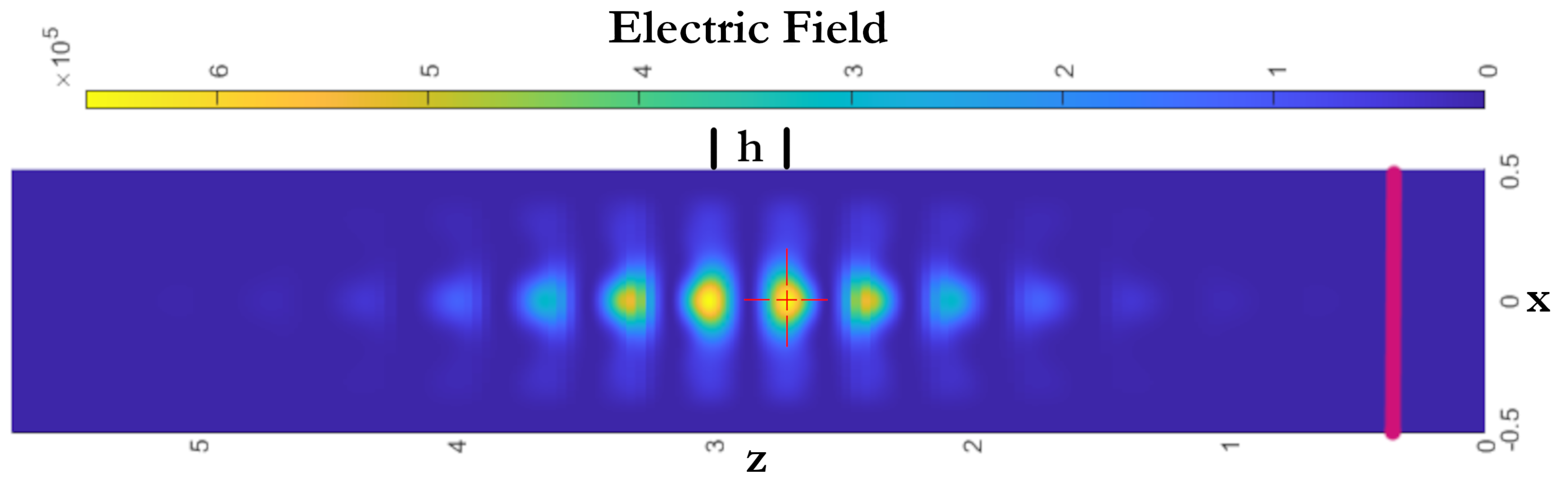
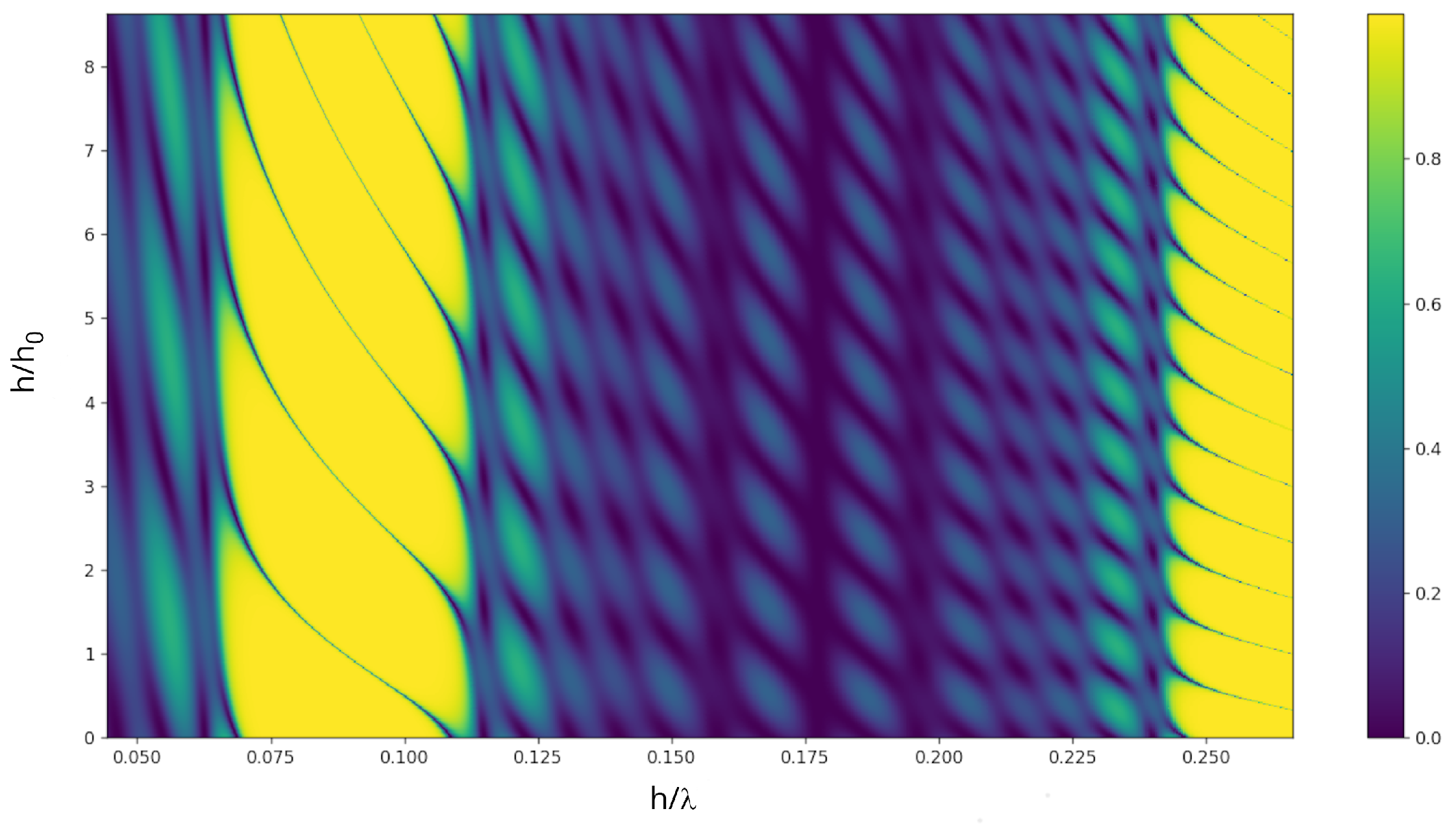
3. The Design of Integrated Fabry–Perot Cavities for Classical Light

The design of an IFPC involves a unique tapering process based on Bloch-mode engineering concepts. This procedure aims to adapt the mode profiles between the cavity fundamental mode, supported by the ridge waveguide, and the evanescent Bloch mode of the periodic mirror [19]. By doing so, it significantly reduces the radiation losses at the mirror–ridge interface, thereby enhancing the Q factor of the resonant peak. Demonstrations of this process have been given on a wide range of platforms, such as silicon-on-insulator, silicon nitride, diamond, GaN, III-V, etc.

The general structure is reported in Figure 1, where the basic scheme for a Fabry–Perot cavity is presented (A) and consists in a cavity delimited by two mirrors. Each mirror consists of three main zones(B), including an optional first taper where the launched mode, which can be a standard waveguide mode or Bloch mode itself, can be adapted to the mirror Bloch mode. Then, the mirror is obtained through the periodic variation in the refractive index. As shown in (C), the cell can be of multiple types and defines the properties of the Bloch mode but, in essence, it is always based on a periodic variation in the refractive index. Such variation is known to create a photonic bandgap [20] that excites contra-directional Bloch waves, resulting in very large reflection over a wide range of wavelengths. Finally, the inside taper (IN TAPER), which might be different from the external one (OUT TAPER), needs to be carefully crafted in order to minimize the losses experienced by the cycling cavity mode, which bounces back and forth due to the mode mismatch between the field profiles of both the cavity and mirror mode. Let’s note that other methodologies based on the framework of Fourier space analysis have been used [21] but bring little physical insight. The cavity length is defined by the physical separation of the mirror (A) however one needs to also consider the penetration depth inside the mirror. For example, in [22], the optical field has been measured on top of the cavity. The same can be obtained through a numerical simulation [23], as shown in Figure 2. As expected in a cavity, the field forms a standing wave due to the waveguide mode bouncing back and forth, which translates into a series of peaks (see red cross) and nodes. It can be seen that the field effectively spreads inside the optical mirror, requiring us to define the modal volume with an alternative definition to the simple physical length as $V_M=\frac{\int {ϵ\left|E\right|}^{2}dV}{max\left(ϵ\right|E{|}^2)}$, and it can be shown that the effective length is connected to the phase $\varphi$ of the reflected wave as $L_p=-\frac{{\lambda }_0^2}{4\pi n_g}\frac{\partial \varphi }{\partial \lambda }$, or the penetration length of the field, where n_g is the group velocity of the cavity mode and ${\lambda }_0$ the resonant wavelength.

The mirror is defined by three coefficients: the reflection R_m, the transmission T_m and the scattering losses L_m. R_m is determined by the length of the periodic mirror and by the loss management due to the tapering process. This is due to energy conservation, which imposes that $R_m+T_m+L_m=1$ or, in other words, all the energy is accounted for by the reflection, transmission and loss coefficients. Considering an infinite mirror allows us to derive an upper limit on the reflection: $R_m=1-L_m$. As for Bragg mirrors, $R_m$ is a function of the period number and the refractive index contrast. Therefore, the real upper limit is dictated by the losses. In order to obtain a very large Q factor, a simple condition, albeit difficult to achieve in integrated optics, is needed, namely $R_m>>T_m>>L_m$. Note that the losses L_m are mainly due to the scattering of light into the external radiation continuum of modes. Indeed, when light propagates in a waveguide mode, with a certain mode profile, the transition into another is characterized by a coupling coefficient and a loss, like the transition in microwaves between two regions of different impedance. The coupling and the loss coefficients are expressed as a function of an overlap integral ($\eta$) between the mode profiles of the two regions, as described in [24]. When the two modes are very much alike, the overlap is close to one and therefore the coupling is as well, whereas the losses can be obtained with a good approximation as L_m = 1−${\eta }^2$. The Bloch modes depend mainly on the geometry of the index modulation profile, and it can be shown that small holes at an appropriate period $\mathrm{\Lambda }/{\lambda }_0$, for a specific wavelength ${\lambda }_0$, exhibit lower losses. However, R_m drops drastically as well, implying a much longer mirror and larger cavity volume. The main idea of the tapering process is to bring gradually the mode profile of the cavity mode close to the one of the mirror. This transition cannot be obtained adiabatically; otherwise, L_p grows exponentially [25] and can be computed numerically [23] (even a simple linear transition is beneficial). Although the adaptation is done at a single wavelength, it is interesting to note that it is quite broadband as the roll-off is not excessively steep. This explains the relative robustness of the technique against fabrication variations. It is important to note that the transmission coefficient T_m could be made arbitrarily small by increasing the number of periods in the mirror. However, due to the loss channel available, the resonant behavior of the cavity also boosts the losses at resonance—see [6]—and any energy that is not transmitted is lost by the coupling to the radiation continuum. As a result, the maximum transmission at resonance is obtained and is equal to $T_{MAX}=\frac{1}{{(1+L_m/T_m)}^2}$. This simple relation indicates that the peak intensity at transmission vanishes to zero with T_m and therefore limits the practical value of the transmission coefficient. It is possible to derive the general expression for the Q factor based on the parameters defined previously:

$$Q=\frac{\pi \sqrt{R_m}}{1-R_m}\left[\frac{2h{n}_g}{{\lambda }_0}-\frac{{\lambda }_0}{\pi }\left(\frac{\partial \varphi }{\partial \lambda }\right)\right]$$

where h is the physical cavity length as defined in Figure 1. From this expression, it is possible to infer that several strategies can be used to boost the Q factor. It is possible to increase the group index n_g, as in [26]; to augment the mirror reflectivity using the method described previously; or finally to increment the cavity length. Thanks to this mode engineering, for the first time, in 2006, integrated Fabry–Perot cavities demonstrated impressive performance [17]. Experimental results have shown that these cavities can achieve a Q factor as high as 58,000, with a modal volume V_m of approximately 0.6($\lambda$/n)³. This led to a Q/V ratio as high as 1.0 10⁵ ($\lambda$/n)³, representing a significant milestone in the field and proving the viability of the approach.

A very simple model is illustrated in Figure 3, where the simplified computation of an IFPC is performed, as in [18]. The three coefficients of the mirror are calculated and then used in a simple transmission matrix algorithm. The cavity modes appear as dark thin lines, where the cavity is transmitting over a very narrow bandwidth (so R = 0)—in particular, at the center of the bandgap light strip. By increasing the cavity length, it is possible to observe a repeated cavity mode at a fixed wavelength. However, the increase in cavity length is detrimental for the mode volume. For filtering purposes [27], this strategy is a viable option, but, to harness the full potential of these cavities, the real metric of interest is the ratio Q/V_M. On the far right, another light vertical band appears, indicating another bandgap or reflection band due to the periodic nature of the structure. One can also notice some dark vertical bands that correspond to a range of wavelengths where the cavity is “transparent” and almost no reflection occurs.

4. Quantum Light in Cavity

As previously mentioned, a very large ratio Q/V_M is a direct reflection of the interaction between light and matter. As such, IFPCs have emerged as one of the most crucial tools for quantum information technologies. They can effectively isolate an atom–photon system from the external environment and significantly boost weak interactions between light and matter. The non-linear interactions, either through high-order susceptibility (${\chi }^{\left(2\right)},{\chi }^{\left(3\right)}$) or atomic interaction with the electronic dipole (quantum dots), are the key components to obtain quantum light. Hence, this capacity offers the perfect basis for cavity quantum electrodynamics (CQED), which has been confined to very complex cryogenic systems. CQED is expected to be a key facilitator of the future “quantum internet”. This technological breakthrough would be based on devices that mediate quantum entanglement between photons and atomic emitters. For instance, across a “quantum” network, specific nodes are defined, where quantum states (i.e., qubits) are stored and processed. Other nodes are enabled to broadcast through optical connections from entangled states to the whole network. It has been proposed that these networks might leverage arrays of tunable optical cavities, on a single chip or a series of interconnected chips, where atoms can be introduced in specific positions and trapped in order to create qubit memories [28]. However, the technological challenge is not only to create the cavity but to include an emitter inside the cavity [29]. It is not only the interplay between the atom and cavity that is at the center of quantum light generation, but also the ability to place the emitter at a strategic position, namely the maxima of the electric field, which is crucial. Some demonstrations [30,31] have shown the potential for this, but it remains elusive.

5. Fundamental Principles of CQED

Interactions between atoms and photons within a cavity are governed by three rate parameters [32]: the non-resonant atomic dipole lifetime ($\gamma =1/{\tau }_e$), the photon lifetime of the cavity ($\kappa =1/{\tau }_c$) and the atom–cavity coupling rate ($g_0$). As a consequence, the interaction between the atom electronic dipole and the cavity vacuum field controls the atom–cavity coupling rate. For a single two-level atom (for example, a quantum dot, a nanocrystal) placed conveniently at the maximum electric field of the cavity mode in an otherwise empty cavity, the atom–cavity coupling rate can be expressed as

$$g_0^2=\frac{{\mu }^2\omega }{2{ϵ}_0\hslash V_M}\approx {\mu }^2{E}_{cavity}^2\propto \frac{{\lambda }_0^2}{n_{cavity}}\frac{Q}{V_M}$$

where $\mu$ is the electric dipole moment for the transition and V_M is the fundamental cavity mode volume. In Figure 2, a red cross indicates the best location for a single quantum dot, as in [33]. This coupling rate is the main parameter that governs the system’s behavior and two main regimes can be identified. Again, it can be shown that this coupling is directly linked to the ratio Q/V_M.

5.1. Strong Coupling Regime

The first regime of interest is the “strong coupling regime”, which is achieved when the atom–cavity coupling rate ($g_0$) exceeds both the cavity and atomic decay rates ($\kappa$, $\gamma$), i.e., $g_0>>(\kappa ,\gamma )$. Under these conditions, the atomic system and the optical cavity mode can reversibly exchange energy back and forth faster than each system’s channel of loss. This energy is swapped through photon emission when the excited atomic system emits a photon and the same photon is absorbed back. This gives rise to an oscillation at the single-photon Rabi frequency ${\mathrm{\Omega }}_R=2g_0$. In the frequency domain, this mechanism is revealed by the splitting of the cavity resonance, which becomes a double-peaked cavity transmission (vacuum-Rabi splitting) with peaks centered at $\omega \pm g_0$ [34,35]. $g_0$ is of particular importance as it represents the interaction strength between the atomic system and the cavity without the effect of the losses. This regime results in a singular object called a polariton [36], which is a pseudo-particle constituted of the coupled system of excitons from the excited atomic system and photons of the cavity mode. Polariton devices are highly appealing for their narrow linewidth and polarized emission [37], and their profound quantum nature makes them interesting for quantum computation in general.

5.2. Weak Coupling Regime

Alternatively, the second regime, known as the “weak coupling regime”, occurs when $g_0<<(\kappa ,\gamma )$. In this regime, an important dimensionless factor known as the single-atom cooperativity C, defined as $C=g_0^2/2\kappa \gamma$, represents the effect that a single atom inserted appropriately, will have on the cavity mode. The single-atom cooperativity, often expressed as N₀ = 1/C, is termed the critical atom number and can be interpreted as the number of atoms required to significantly affect the cavity field. Therefore, large cooperativity indicates large coupling between the cavity mode and the atomic system, even with the addition of losses. In fact, the emitter placement greatly affects C and constitutes, in practice, the main parameter limiting it.

5.3. The Purcell Regime

An intermediate weak coupling condition that corresponds to $\kappa >>g_0>>\gamma$ and $C>>1$, where the coupled system can still interact quickly enough to exchange energy but the loss channel of the electronic system is faster, characterizes the so-called “Purcell regime” [38]. In this case, photon emission is scattered out of the cavity due to losses but significantly altered relative to the free-space situation due to the modification of the photonic density of the modes available to the emitting atom. The spontaneous emission from an atom is altered preferentially to a desired resonant mode of the cavity. This Purcell effect is a highly desirable property as it can be shown to be directly linked to the threshold of a lasing mode [26], since it forces the spontaneous emission to specific modes, as in the case of stimulated radiation.

5.4. Heralded Single Photon Emitters

Another application of weak coupling is non-linear atomic memory systems, or NLAMs, based on the non-linear interplay between atoms and light to establish entanglement among photons and atoms [39]. This interaction allows the electromagnetic field released by the atom to interfere with itself, thereby altering the rate at which the atom emits within the cavity. Under such conditions, the random emission into free space can be inhibited, paving the way for a highly directional emission and efficient interaction. Consequently, NLAM media can facilitate consistent entanglement between photons and atoms. A practical result [7] is the production of heralded single photons, where a non-linear interaction (four-wave mixing) has been harnessed to create entangled photons with the largest rate of emission yet.

6. Conclusions

IFPCs have emerged as a significant player in the field of CQED as well as in telecommunications due to their properties both in terms of filtering and electrodynamic light–matter interactions. These cavities can greatly enhance the inherently weak interactions between light and matter, thanks to the strong confinement in a very tight volume, offering a unique means of creating new quantum functions and paving the way towards a quantum internet.