Definition
In young Maxwell’s eyes, electricity, magnetism and fluid mechanics present analogies that let the first be mathematically grasped in a unitary way similarly to the latter. This entry sketches the first steps of James Clerk Maxwell’s unitary view of electromagnetism and fluid mechanics, with long-lasting effects on understanding the physical world. In his very first paper on the subject, Maxwell interpreted Faraday’s concept of lines of force of both electricity and magnetism as filaments of a flowing fluid. That is, Maxwell suggested to unify the previously distinct fields of electricity and magnetism, considering them as different aspects of the same entity, the ‘electromagnetic field’, which is mathematically described by four partial differential equations. In the literature there are several comprehensive works on Maxwell’s mature exposition of his theory; however, the aim of this entry contribution is rather more limited. Indeed, it is restricted to examining the contributions of Maxwell’s first paper towards developing the idea of electric current as the motion of an incompressible fluid. Thus, this entry highlights the strong connections of Maxwell’s epistemological view with the ‘mechanistic’ approach of the time to every aspect of physical phenomenology. For this purpose, this entry mentions some historical context surrounding the emergence of Maxwell’s innovative concepts.
1. Introduction
James Clerk Maxwell was born on 13 June 1831 in Edinburgh, Scotland, into a family of high intellectual and cultural standing [1]. He showed interest in natural sciences from an early age, studying the nature of his garden as a child and starting scientific studies at the University of Edinburgh in 1847. Aged only 14, he wrote his first paper “On the description of oval curves…”, which appeared in 1846 in the Proceedings of the Royal Society of Edinburgh [2] (pp. 1–3). In 1850, he moved to Cambridge (first Peterhouse, then Trinity College), but in the meanwhile, he continued preparing scientific works on geometry, algebra, and elasticity. One very interesting instance is “On the equilibrium of elastic solids” [2] (pp. 30–73), read in 1850 and published in 1853 in the Transactions of the Royal Society of Edinburgh. In this paper, he entered the much debated question on the exact number of constants for (isotropic linear elastic) solid bodies (see, e.g., [3,4] for some details) with astonishing maturity for a young man aged 18 or so.
While in Cambridge, Maxwell greatly improved his knowledge of calculus, algebra, geometry, and natural phenomena, merging them into what we now would label as mathematical physics, that is, strong mathematical models for interpreting and predicting physical phenomena. In addition to continuing publishing while still a student (one instance is [1] (pp. 115–118)), this led him to become second best at the Mathematical Tripos of 1854, to be appointed Professor of Natural Philosophy (this was the name given in 19th century to physics in British educational institutions) at Marischal College in Aberdeen and elected Fellow of the Royal Society of Edinburgh in 1856, aged just 24 [1].
Maxwell’s following astonishing career in research, plus its undoubtable legacy in many fields of modern and contemporary physics and technics, are well known. One can read details in the site of the foundation devoted to him [1], in the preface to his collected works [2] (pp. ix–xxix), and in some biographies [5,6,7,8,9,10,11,12,13], even though some of them were criticised by historians of science and epistemologists for being a bit naïve. In these documents (some of which are rather extended: for instance, ref. [5] counts about 600 pages!), we can also appreciate some descriptions of how Maxwell felt the influence of the Scottish culture of his time and the legacies of his families (his double surname actually comes from two influential Scottish families). Thus, this entry will not devote any space to these incredibly vast subjects, which would require a whole monograph to say the least, and will be limited to analysing in some detail the first paper where Maxwell dealt with electricity and magnetism.
In particular, it will focus on Maxwell’s unitary view of electrical and magnetic phenomena with those of another well-known branch of Natural Philosophy of his time, i.e., fluid motion. Indeed, in an entry work as the present one is, we believe that one should concentrate on a particular theme that can be of interest from both the epistemological and historical points of view. This entry then focuses on the apparent attempt by young Maxwell to reconcile ‘new’ branches of physics—i.e., electricity and magnetism—with the ‘mechanistic’ approach that was common in the epistemology of his time (see [3,4]), that is, the will to reduce all actions among bodies of whichever nature to those that could be seen as tractions or pressures.
Maxwell’s resorting to fluid mechanics came from his mastery in continuum mechanics; indeed, we should remember that he published several works in this field, e.g., [2] (pp. 80–114; pp. 246–247; pp. 248–262; pp. 377–409; pp. 514–525; pp. 598–604). In particular, the last two papers among the ones just quoted are known as original contributions in the theories of truss structures and of elasticity (a reciprocity theorem is formulated, which can serve as a means to solve redundant structures, see also [4]); to these, we should add [14] (pp. 102–104; pp. 161–207; pp. 492–497).
In the following, this entry will thus present Maxwell’s analogy between fluid flows and electric and magnetic flows, already highlighted in [15,16,17], on the basis of his first paper “On Faraday’s lines of force”, and thoroughly comment on its meaning and following developments. It will then also very briefly sketch some of the contents of the following papers, in order to highlight the above quoted developments. In technical publications it is not customary to quote original works massively; however, this entry will present a large number of excerpts from Maxwell’s “On Faraday’s lines of force”, sometimes in an extensive form. Indeed, far from being unwilling to provide our interpretation of Maxwell’s work, we firmly believe that any comment on the actual meaning and deep influence of scientific and technical contributions of the past cannot be thoroughly grasped if the original words of the author are filtered by the comments of the investigators. This is true not only for works on philology or philosophy, but it is well customary in history and philosophy of science and technology, in order to catch also the influence of culture, religion, and society of the time on the scientist’s thought and work. In this regard, it is worth recalling the second paragraph of [18], where we read that ‘science does not exist in a vacuum, and studies in the sociology, history, and philosophy of science often emphasize how scientists’ broader beliefs and practices influence their work, and thus the way that science develop’. Then, reporting Maxwell’s original words repeatedly and in full is not a mere action of bibliographic recovery, but a means of regaining the actual root of his thoughts. In addition, to the best of our knowledge, while in other monographs (e.g., [5,6]) attention is focussed on the most mature Maxwell’s treatise of 1873 (which will be only sketched below in this entry), little attention has been devoted to a detailed analysis of the origins of Maxwell’s investigations on electrical phenomena, basing on Faraday’s ideas of lines of force, apart from some hints in ref. [19] and a slightly more extensive discussion, completed by a French translation of the paper, in ref. [17]; thus, this will be the core of the entry’s contribution.
2. On Faraday’s Lines of Force
The electric and magnetic lines of force had been experimentally put into evidence by Michael Faraday (1791–1867) and disclosed to the public in his “Experimental researches in electricity” (Quaritch, London, 1839–1855). Having learnt to master both mathematics and physics, Maxwell apparently got in touch with Faraday’s work (see also [20,21]) and saw similarities between the trend of electric and magnetic lines of force and that of the flow of water or air. He thus came to believe that just as fluid flows of small particles could be modelled as continuous lines and represented by mathematical equations, so could the analogous flows of the lines of force of electricity and magnetism. This implied that the laws governing the behaviour of the motion of incompressible fluids and the laws governing electricity and magnetism could be ruled by similar sets of equations.
Maxwell’s first paper on the matter, “On Faraday’s lines of force”, was read at the Cambridge Philosophical Society between December 1855 and February 1856 and published in the relevant “Transactions” in 1864 [2] (pp. 155–229). Right from the start we read
No electrical theory can now be put forth, unless it shews the connexion not only between electricity at rest and current electricity, but between the attractions and inductive effects of electricity in both states [2] (p. 155).
That is, a robust and reliable theory of electricity and magnetism cannot consider the two physical aspects separately, but must take account of both, since Faraday’s experiments, among others, had shown the close connections between them. Maxwell continues,
The first process […] in the effectual study of the science, must be one of simplification and reduction of the results of previous investigation to a form in which the mind can grasp them. The results […] may take the form of a purely mathematical formula or of a physical hypothesis. In the first case we entirely lose sight of the phenomena to be explained; and though we may trace out the consequences of given laws, we can never obtain more extended views of the connexions of the subject. If, on the other hand, we adopt a physical hypothesis, we see the phenomena only through a medium, and are liable to that blindness to facts and rashness in assumption which a partial explanation encourages. We must therefore discover some method of investigation which allows the mind at every step to lay hold of a clear physical conception, without being committed to any theory founded on the physical science from which that conception is borrowed, so that it is neither drawn aside from the subject in pursuit of analytical subtleties, nor carried beyond the truth by a favourite hypothesis [2] (pp. 155–156).
It is then clear that, at this stage of his epistemological path, Maxwell did not rely on a purely mathematical representation of physical phenomena, which risks being so abstract that one loses any contact with actuality. At the same time, Maxwell did not want to rely on the consequences of a single phenomenological law (nowadays, we would call this a ‘constitutive law’). In the above quotation, Maxwell explicitly states that he thinks that both limit either the perception of reality or the range of possible applications; a new way of investigating the natural world, especially for electric and magnetic phenomena, shall be looked for. This is why Maxwell advances the proposal that
In order to obtain physical ideas without adopting a physical theory we must make ourselves familiar with the existence of physical analogies. By a physical analogy I mean that partial similarity between the laws of one science and those of another which makes each of them illustrate the other. [2] (p. 156).
Maxwell’s epistemology of this time (keep in mind he was aged 24 when he read this communication at Cambridge) apparently relies on something already known and used, for instance, by the French scholars that investigated elasticity via discrete models (for some details on that, see [3,4]). A physical analogy lets one use the powerful analytical means of a well-established theory (for instance, those of Lagrange’s analytical mechanics; see, for instance, ref. [22] for hints on Maxwell’s mastery in these tools) without the need to restrict oneself to particular phenomenological laws, thus overpassing the limits that Maxwell put forth in the first lines of this work. Maxwell presents some instances of fruitful physical analogies to corroborate his previous statement: refraction of light rays and path deviation of a moving particle subjected to a force; transmission of light and vibration of an elastic medium (the so-called ‘luminiferous aether’); and, most of all, some transmission of heat and attractions at a distance.
[…] the mathematical laws of the uniform motion of heat in homogeneous media are identical in form with those of attractions varying inversely as the square of the distance. We have only to substitute source of heat for centre of attraction, flow of heat for accelerating effect of attraction at any point, and temperature for potential, and the solution of a problem in attractions is transformed into that of a problem in heat [2] (p. 157).
Maxwell gives credit to William Thomson (1824–1907; at that time, Thomson was not yet entitled Lord Kelvin) for the last analogy. Maxwell’s stressing this point stems from epistemological facts: indeed, at that time the scientific community marked a strong difference between interactions at a distance (which Maxwell labels ‘attractions’ in the quotation above, and could not be visualised as hands pulling ropes, as it was traditional for forces since 1700) and mechanical actions exerted by contact, that is, by interposition of some physical medium that ‘transmits’ actions from one point to another in the physical space (these, contrarily to the former ones, could be visualised in the above quoted way):
[…] conduction of heat is supposed to proceed by an action between contiguous parts of a medium, while the force of attraction is a relation between distant bodies, and yet, if we knew nothing more than is expressed in the mathematical formulae, there would be nothing to distinguish between the one set of phenomena and the other [2] (p. 157).
We clearly see that ‘attractions’ are thought to be simply given by mathematical expressions that entail no epistemological explanation for their origin, while the scientists of the 18th and 19th centuries usually searched for causes of physical phenomena. Yet, even though Maxwell, on the wake of science of his time, sees the two phenomena as entirely different, he strongly believes that the analogy between them helps in opening one’s mind to describe physics:
It is by the use of analogies of this kind that I have attempted to bring before the mind, in a convenient and manageable form, those mathematical ideas which are necessary to the study of the phenomena of electricity [2] (p. 157).
Faraday’s experimental evidence of the lines of force are thus for Maxwell not only a way of visualising electricity and magnetism, they are also an explicit demonstration of the transmission paths of actions by contact, thus avoiding the purely mathematical, that is, abstract, notion of interaction at a distance—see also the comment in [23] (p. 173). Maxwell declares that his intention is not to establish a new physics, since he conducted no experiments nor discovered new phenomena; he only wants to use analogies to provide a unitary mathematical model of all phenomena related to electricity and magnetism:
[…] I hope to render it evident that I am not attempting to establish any physical theory of a science in which I have hardly made a single experiment, and that the limit of my design is to shew how, by a strict application of the ideas and methods of Faraday, the connexion of the very different orders of phenomena which he has discovered may be clearly placed before the mathematical mind [2] (pp. 157–158).
In Maxwell’s view, the lines of force represent the paths that a small test charge would follow if it were placed in an electric or magnetic field, as we would say nowadays. Maxwell’s own words are extremely clear and suggestive and could be easily used in basic teaching of physics also nowadays:
When a body is electrified in any manner, a small body charged with positive electricity, and placed in any given position, will experience a force urging it in a certain direction. If the small body be now negatively electrified, it will be urged by an equal force in a direction exactly opposite. The same relations hold between a magnetic body and the north or south poles of a small magnet. If the north pole is urged in one direction, the south pole is urged in the opposite direction. In this way we might find a line passing through any point of space, such that it represents the direction of the force acting on a positively electrified particle, or on an elementary north pole, and the reverse direction of the force on a negatively electrified particle or an elementary south pole. Since at every point of space such a direction may be found, if we commence at any point and draw a line so that, as we go along it, its direction at any point shall always coincide with that of the resultant force at that point, this curve will indicate the direction of that force for every point through which it passes, and might be called on that account a line of force. We might in the same way draw other lines of force, till we had filled all space with curves indicating by their direction that of the force at any assigned point [2] (p. 158).
While the direction of the lines of force indicates that of the force acting on the test charge, its intensity is still to be determined. Maxwell puts forth his original thought, stemming from physical analogies; in this case, as already remarked in the introduction to this entry, the analogy is borrowed from fluid mechanics:
[…] consider these curves not as mere lines, but as fine tubes of variable section carrying an incompressible fluid, then, since the velocity of the fluid is inversely as the section of the tube, we may make the velocity vary according to any given law, by regulating the section of the tube, and in this way we might represent the intensity of the force as well as its direction by the motion of the fluid in these tubes. […] In the case of a perfectly arbitrary system of forces, there will generally be interstices between the tubes; but in the case of electric and magnetic forces it is possible to arrange the tubes so as to leave no interstices. The tubes will then be mere surfaces, directing the motion of a fluid filling up the whole space [2] (pp. 158–159).
It is apparent how, driven by Faraday’s experimental results and bringing forward his own analogy, Maxwell admits that electric and magnetic lines of force behave like the well-known never intersecting flow lines of a perfect incompressible fluid. There remains the formulation of a proper law for the intensity of the force; Maxwell remarks that one could simply accept a law of ‘attraction’, that is, of an action at a distance, of which the causes are unknown and thus would remain simply a mathematical law, as we have pointed out above. On the other hand, Maxwell advances another strong position:
It has been usual to commence the investigation of the laws of these forces by at once assuming that the phenomena are due to attractive or repulsive forces acting between certain points. We may however obtain a different view of the subject, and one more suited to our more difficult inquiries, by adopting for the definition of the forces of which we treat, that they may be represented in magnitude and direction by the uniform motion of an incompressible fluid [2] (p. 159).
That is, the analogy with fluid mechanics may be brought further, accounting for a force that is transmitted by contact in an ideal, fictitious fluid medium: Maxwell imagines this ideal fluid as a medium that fills all space and is capable of flowing without inner viscosity, having a set of properties that allow it to model the behaviour of electric and magnetic fields (the idea of an elastic medium filling the whole space and transmitting electromagnetic actions is equivalent to that of the so-called ‘luminiferous aether’). Thus, Maxwell declares that the following of his paper is devoted, at a first step, to illustrating the mechanics of such a perfect, ideal fluid, in order to fully describe in a unitary way all known phenomena of electricity and magnetism:
I propose, then, first to describe a method by which the motion of such a fluid can be clearly conceived; secondly to trace the consequences of assuming certain conditions of motion, and to point out the application of the method to some of the less complicated phenomena of electricity, magnetism, and galvanism; and lastly to shew how by an extension of these methods, and the introduction of another idea due to Faraday, the laws of the attractions and inductive actions of magnets and currents may be clearly conceived, without making any assumptions as to the physical nature of electricity, or adding anything to that which has been already proved by experiment. By referring everything to the purely geometrical idea of the motion of an imaginary fluid, I hope to attain generality and precision, and to avoid the dangers arising from a premature theory professing to explain the cause of the phenomena [2] (p. 159).
Section I of “On Faraday’s lines of force” describes the motion of an ideal fictitious incompressible fluid: its only properties are freedom of motion and infinite resistance to compression. Because of incompressibility, each portion of fluid occupies the same volume at every time instant, thus a fluid is quantified in terms of volume. If the direction of the motion of the fluid is well established for each point in the space, a set of lines can be drawn, each of them following the direction of fluid motion; in such manner, lines of fluid motion are obtained, which are drawn at intervals of submultiples of a standard unit. If the direction and velocity of the motion at any fixed point are independent of time, we have a steady motion. Figure 1 and Figure 2 are drawn according to Maxwell’s words.
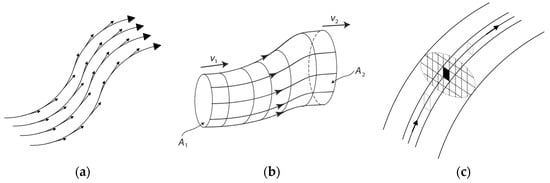
Figure 1.
Lines of force: the small arrows indicate the direction and intensity of the electric or magnetic force exerted onto a small test charge or magnet at that point, the big arrows indicate the direction of the imaginary fluid motion analogous to the lines of force (a); a tube of fluid motion: are the mean velocity of the imaginary fluid when crossing the imaginary surfaces of area (b); a unit tube of fluid motion, where the arrows have the same meaning as in the previous portions of the figure and the imaginary surfaces crossed are meshed in small portions (c).
Figure 2.
Flow through a closed surface (a); sink (in-flow with respect to the control volume) and source (out-flow with respect to the control volume) (b). As in Figure 1, big arrows denote the direction of the imaginary fluid motion analogous to the lines of force, but here small arrows indicate the outward unit normal to the considered closed surfaces.
Maxwell then presents very precisely the well-known concept of fluid flow rate through a surface of area of the tube of fluid motion, whatever its orientation with respect to the lines of flow, as well as the concepts of flow through a generic fixed closed surface, source (where a flow originates) and sink (where a flow extinguishes), as illustrated in Figure 2.
Section II deals with the contact force developed by the flow in a resisting medium, similarly to a fluid permeating a porous body (see also [17]). As it is usual in fluid mechanics, Maxwell assumes that this force depends on the nature of the medium, on the direction in which the fluid moves, and on its velocity. Then, the constitutive law has well-known nature, proportional to the velocity of the fluid front via a material constant , and resembles the resisting force of an isotropic elastic medium to an external cause of deformation. The pressure (that is, another contact force, for which the epistemological ambiguity related to ‘attractions’ is not present) that keeps the fluid flowing steadily must vary in order to maintain the velocity. Maxwell defines the surfaces of equal pressure to be orthogonal to the direction of the velocity (which is usual) and uses simple algebraic formulas to find the flow velocity and the pressure distribution originated by a point source at any generic place located at a distance from the source in an infinite medium. In this case, pressure vanishes at infinity, and Maxwell obtains the following known laws:
Then, he extends the result to several point sources by superposition of effects, and uses a refraction-like law to express the conditions given by a surface that separates two media with different coefficients of resistance. Maxwell continues by examining a non-isotropic medium and, by means of a suitable change of coordinates (which apparently resembles the search for a triad of principal axes) and of the well-established equation of continuity for fluid flows, he obtains the equation for the spatial distribution of pressure in the same Laplacian form of the equation of heat conduction, for which he gives credit to George Gabriel Stokes’ (1819–1903) “On the Conduction of Heat in Crystals” ([24], pp. 203–227) and part V of Lord Kelvin’s “On the Dynamical Theory of Heat” ([25]). Thus, Maxwell may affirm that
We may […], when the distribution of pressures is known, construct the surfaces of equal pressure, the tubes of fluid motion, and the sources and sink [2] (p. 173).
In addition, he is able to evaluate the work spent by a source or a sink (corresponding to a source with a minus sign) against a given pressure, and to formulate a kind of reciprocity theorem for sources and the relevant pressures [2] (p. 174). Maxwell is now able to apply his analogy to electric and magnetic phenomena:
[…] the velocity of our imaginary fluid due to a source S at a distance r varies inversely as . Let us see what will be the effect of substituting such a source for every particle of positive electricity. The velocity due to each source would be proportional to the attraction due to the corresponding particle, and the resultant velocity due to all the sources would be proportional to the resultant attraction of all the particles. Now we may find the resultant pressure at any point by adding the pressures due to the given sources, and therefore we may find the resultant velocity in a given direction from the rate of decrease of pressure in that direction, and this will be proportional to the resultant attraction of the particles resolved in that direction. Since the resultant attraction in the electrical problem is proportional to the decrease of pressure in the imaginary problem, and since we may select any values for the constants in the imaginary problem, we may assume that the resultant attraction in any direction is numerically equal to the decrease of pressure in that direction […] [2] (pp. 175–176).
A straightforward application of the definition of potential and of the above quoted reciprocity theorem lets Maxwell finally state that in an isotropic medium
[…] in the ordinary electrical problems the analogy in fluid motion is of this kind:
[and the] whole potential of a system , where is the work done by the fluid in overcoming resistance. The lines of forces are the unit tubes of fluid motion, and they may be estimated numerically by those tubes [2] (p. 177). (*)
Here, , the electric potential, is analogous (modulo an inessential sign) to the pressure on the ideal fluid. Going further, is the -component of the accelerating force, which we would nowadays call external force per unit volume, though here one deals with unit mass. This force equals the gradient of the potential-pressure, and is proportional via the material constant to the -component of the fluid velocity . To end with, is the unit electric particle, which we nowadays would call a test charge, and is the number of unit sources contained inside the surface surrounding the considered control volume. These equations are a simple exposition of the so-called “Gauss’ laws for electrostatics”. It is apparent how the electric-fluid analogy is powerful and suggestive, and one may adopt the strategies of fluid mechanics to investigate electricity and magnetism. That is, Maxwell at this stage of his scientific path is happy to show that it is possible to deal with ‘new’ physical phenomena by the well-known epistemological and analytical tools of the traditional, well-established ‘mechanistic’ approach.
Indeed, in the following sections of “On Faraday’s lines of force”, Maxwell presents his own view of all of the phenomenology concerning electricity of his time, explained by means of this analogy. As for the dielectrics, we read that
The electrical induction exercised on a body at a distance depends […] on the nature of the interposed medium, or dielectric. […] If we suppose that in our analogy of a fluid in a resisting medium the resistance is different in different media, then by making the resistance less we obtain the analogue to a dielectric which more easily conducts Faraday’s lines [2] (p. 177). (**)
Such a statement is precise, concise and illuminating, and is just but one example of the absolute power of Maxwell’s analogy; indeed, the above quotation defines what we call the electric field in a material with given dielectric properties, which thus results as simply proportional, via a material constant, to the electric field in the void. Another statement stemming from Maxwell’s analogy is about permanent magnets:
[…] it may be useful to examine the way in which the polarity of the elements of a magnet may be represented by the unit cells in fluid motion. In each unit cell unity of fluid enters by one face and flows out by the opposite face, so that the first face becomes a unit sink and the second a unit source with respect to the rest of the fluid. It may therefore be compared to an elementary magnet, having an equal quantity of north and south magnetic matter distributed over two of its faces [2] (p. 178).
Maxwell then presents the theories of paramagnetic and diamagnetic induction, of induction of crystals in a magnetic field, and of the electric current conduction. It is in this last respect that we read one of the most suggestive consequences of Maxwell’s analogy:
It is in the calculation of the laws of constant electric currents that the theory of fluid motion which we have laid down admits of the most direct application. […] we have here a current of fluid moving uniformly in conducting circuits, which oppose a resistance to the current which has to be overcome by the application of an electro-motive force at some part of the circuit. On account of this resistance to the motion of the fluid the pressure must be different at different points in the circuit. This pressure, which is commonly called electrical tension, is found to be physically identical with the potential in statical electricity, and thus we have the means of connecting the two sets of phenomena [2] (pp. 180–181).
Maxwell continues by characterising the electromotive force, which was well-known as a chemical action; since it keeps current flow in closed circuits against the resistance called for in the above quotation, by the electric/fluid analogy he re-writes what we now would name “Ohm’s law of resistance in electric conductors”. Analogously, he formulates a similar expression for magnetism.
In the following sections of the paper, Maxwell recalls the actions of electric currents at a distance, first put into evidence and translated into mathematics by André-Marie Ampère (1775–1836), then Faraday’s experimental evidence of electromotive forces due to magnetic induction in a moving conductor, and always interprets the phenomena in terms of lines of force transversed or cut. Then, he introduces the second part of his paper, in which he aims at establishing rigorous and general enough mathematical formulations for all of these phenomena by means of his usual analogy, and concludes as follows:
In the following investigation, therefore, the laws established by Faraday will be assumed as true, and it will be shewn that by following out his speculations other and more general laws can be deduced from them. If it should then appear that these laws, originally devised to include one set of phenomena, may be generalized so as to extend to phenomena of a different class, these mathematical connexions may suggest to physicists the means of establishing physical connexions; and thus mere speculation may be turned to account in experimental science [2] (p. 189).
We then read the definition of electric current in perfect analogy with the flow of a fluid in a tube across a surface, pushed by a difference in pressure, by means of what we still define as flux of a quantity and the application of the divergence theorem. Analogous definitions are provided for magnetic induction, with a simple change in the subscript for corresponding quantities (quantity of magnetic induction, resistance to it, magnetising forces, magnetic potential—analogous to pressure in the fluid: recall the previous remarks about this). Thus, the core of Maxwell’s work is to reconduct electricity and magnetism under the same unitary view, and the section title “Electro-magnetism” [2] (p. 193) is explicit in this respect. Maxwell recalls Ampère’s experimental laws, gives them a mechanical interpretation (for instance, ‘The first and second laws shew that currents are to be combined like velocities or forces’ [2] (p. 193)) and translates them into analytical language: in [2] (p. 194), we find the formulation in components of the well-known equation ( the magnetic induction, the intensity of electric current) for steady currents in closed circuits, which is now labelled as one of Maxwell’s equations for electromagnetism, and in the following pages, a series of theorems and differential tricks (credited to Carl Friedrich Gauss (1777–1855) and Lord Kelvin) that warrant the existence of a kind of potential describing the state of space and media, called electro-tonic state, in order to solve the equation above. Thus, Maxwell can state the following laws of electromagnetism:
Law I. The entire electro-tonic intensity round the boundary of an element of surface measures the quantity of magnetic induction which passes through that surface, or, in other words, the number of lines of magnetic force which pass through that surface. […]
Law II. The magnetic intensity at any point is connected with the quantity of magnetic induction by a set of linear equations, called the equations of conduction.
Law III. The entire magnetic intensity round the boundary of any surface measures the quantity of electric current which passes through that surface.
Law IV. The quantity and intensity of electric currents are connected by a system of equations of conduction. […]
Law V. The total electro-magnetic potential of a closed current is measured by the product of the quantity of the current multiplied by the entire electro-tonic intensity estimated in the same direction round the circuit. […]
Law VI. The electro-motive force on any element of a conductor is measured by the instantaneous rate of change of the electro-tonic intensity on that element, whether in magnitude or direction [2] (pp. 206–207).
Note that, at this point of his early scientific path, young Maxwell is happy with reducing electricity and magnetism to a limited set of laws that derive from his analogy. However, Maxwell was aware that this was not the last word on the subject; indeed, immediately after these, Maxwell states that, even though he has strongly relied on Faraday’s enormous experimental work and on his own formal analogy to formulate his laws, he must surely take account of Wilhelm Weber’s (1804–1891) ‘Elektrodynamische Maasbestimmungen…’ [26] (first memoir, pp. 25–214, 1846; second memoir, pp. 215–254, 1848), of which he says in a footnote that
The value of his [Weber’s] researches, both experimental and theoretical, renders the study of his theory necessary to every electrician [2] (p. 207).
After recalling Weber’s assumptions, and before presenting a series of examples that are meant simply as instances of proficuous applications of his results, Maxwell closes the theoretical part of his paper with a most interesting epistemological reflection on both Weber’s and his approach, which is worth reporting in full:
[Weber’s] is a really physical theory, satisfying the required conditions better perhaps than any yet invented, and put forth by a philosopher whose experimental researches form an ample foundation for his mathematical investigations. What is the use then of imagining an electro-tonic state of which we have no distinctly physical conception, instead of a formula of attraction which we can readily understand? I would answer, that it is a good thing to have two ways of looking at a subject, and to admit that there are two ways of looking at it. Besides, I do not think that we have any right at present to understand the action of electricity, and I hold that the chief merit of a temporary theory is, that it shall guide experiment, without impeding the progress of the true theory when it appears. There are also objections to making any ultimate forces in nature depend on the velocity of the bodies between which they act. If the forces in nature are to be reduced to forces acting between particles, the principle of the Conservation of Force requires that these forces should be in the line joining the particles and functions of the distance only. The experiments of M. Weber on the reverse polarity of diamagnetics, which have been recently repeated by Professor Tyndall [John Tyndall 1820–1893], establish a fact which is equally a consequence of M. Weber’s theory of electricity and of the theory of lines of force [2] (p. 208).
That is, Maxwell clearly realises that his contribution in this work is primitive and needs further refinements, on the sides of both the epistemological approach to the physical and mathematical models and the possibility of enriching the obtained equations in case of new discoveries in the phenomenology (which would actually lead him to adding a well-known term in Ampère’s law for the interactions of electric currents). This point has also been highlighted in previous publications in the literature [16,17,18,19,20,21,22,23]; a thorough and step-by-step presentation and analysis of Maxwell’s path in the model of what we now call the electromagnetic field, however, would be too vast and far beyond the scope of this entry contribution, which is intended only as an introduction to this most interesting and debated subject in the history of science and epistemology.
3. A Sketch on Some of the following Contributions by Maxwell
Maxwell’s following and broader contributions to electromagnetism are found in works such as “On Physical Lines of Force” (1861) [2] (pp. 451–513) and “A Dynamical Theory of the Electromagnetic Field” (1865) [2] (pp. 526–597). Anther paper that could be worth mentioning is “On Governors” (1867) [3] (pp. 105–120). Of course, the masterpiece in the field is the volume “A treatise on electricity and magnetism” (Oxford, Clarendon Press, 1873), which represents the sum and final word of Maxwell on the subject.
“On Physical Lines of Force” proposes a physical interpretation of the lines of force in electric and magnetic fields through vector analysis, differential equations and experimental evidence. Maxwell argues that these lines of force are not just a visual representation or a merely abstract mathematical construct but have a tangible existence in the physical world. Maxwell also suggests mechanical models in order to describe how the fluid can be thought of as having ‘vortices’, which correspond to the eddies and whirlpools that are observed in fluid dynamics, in accordance with the properties of lines of force.
In “A Dynamical Theory of the Electromagnetic Field”, Maxwell presents his famous set of equations that describe the behaviour of electromagnetic fields in terms of their sources. He also introduces the concept of displacement current, which completes the set of equations and provides a complete description of electromagnetic phenomena. In contemporary mathematical language, they can be written as
In Equation (2), is the electric field in materials, which is proportional to that in the void via a material constant (as highlighted in the quotation (**) above); its local flux depends on the density of electric charges , which is the local expression of the third equation in the quotation (*) above. In Equation (3), is the electric field in the void, to which that in materials is proportional via a material constant (as highlighted also above); its local flux vanishes since no singular magnetic charge exists. Equation (4) is a re-phrasing of Law VI of “On Faraday’s lines of force”; Equation (5) was already discussed and is only enriched by the term due to the instantaneous rate of change of the electric field .
In “On Governors”, Maxwell applies his unitary view of electromagnetism and fluid mechanics to the problem of governor design. He shows how the behaviour of a governor can be modelled using the same equations that describe the behaviour of a fluid flow, providing an elegant and unified explanation for the phenomenon.
“A treatise on electricity and magnetism”, as a unitary volume, is a complete treatise on electromagnetism, updated to Maxwell’s most recent researches and developments of his time, and was published when his view on the subject was mature (Maxwell died in 1879, and the treatise appeared in 1873). It is recognised worldwide as the basis for all following studies on electricity and magnetism, then leading also to the paradoxes for charges in motion and in some way also to the birth of contemporary physics (Lorentz force, invariance in space and time, Einstein’s view of the matter). For a more extensive outlook on this very last subject, the reader may refer to [27], where we explicitly read right from the start that ‘Maxwell’s theory of the electromagnetic field […] played a key role in the formulation and the development of Einstein’s special theory of relativity’, and where the matter is dealt with in some detail.
4. Conclusions and Perspectives
We read in every monograph on the history of science that Maxwell’s figure is of utmost relevance, without disturbing such rhetorical words as ‘genius’ or ‘giant’. His influence on both his contemporary colleagues in science and technology, and even decades after, is undoubtable, as we have already remarked and as it is reported in his biographies [5,6,7,8,9,10,11,12,13] (even though, as already remarked in the introduction, a couple of them were criticised as being a bit apologetic and not presented with an actual critical outlook). A more recent, though limited in length, epistemological outlook on Maxwell’s work is given in [28], especially with reference to the relationship between physical phenomenology and mathematical representation. As for Maxwell’s long-lasting and worldwide influence, beyond the already quoted [27], a most recent monograph [29] investigates how Maxwell affected Italian scientists and remarks how his legacy can be considered important in a very young nation at that time (Italy became a unitary state only in 1860), with a very active scientific community that looked for international cooperation (see some hints also in [4]).
While the mature exposition of Maxwell’s innovative, unitary view of electricity and magnetism is found in his world-famous treatise, the authors decided to examine in full detail the first ideas that he borrowed from Faraday’s experimental results and translated into a rigorous physical-mathematical treatment in the style of 19th century scientists. In order to do this, the authors ran through his very first paper on electricity and magnetism and tried to put into evidence that, in the way it was fashionable and scientifically justified at his time, Maxwell was pressed by the urge to find analogies between electricity and the most traditional branches of physics—that is, mechanics of continuous bodies (solids and fluids). This entry has shown, by letting his own words speak through several literal quotations from the above quoted “On Faraday’s lines of force”, that this analogy was well established at this early stage of Maxwell’s philosophical approach to science. We know that he changed his mind slightly somehow (see [15,16,17,18,19,20,21,22,23,27,28]), yet we think that our thorough analysis may serve as a good introduction for a better understanding of his later philosophical approach.
As we already remarked, a thorough exposition of Maxwell’s complete work in electricity and magnetism, plus the relevant comments and a deep epistemological collocation of his scientific thought and production, falls well beyond the scope of an entry. For all of the reasons mentioned above, the authors thought it sufficient to limit the focus to his first paper. Yet, it can be interesting to better investigate, and will be considered for future studies, a deeper analysis of the epistemological evolution leading Maxwell to pass from a simple view of physical analogy, contained in “On Faraday’s lines of force”, to a more complex vision of a new entity, which we now call the electromagnetic field, and which we find in its mature form in “A Treatise on electricity and magnetism”.
Author Contributions
Conceptualization, G.T.; methodology, G.R.; investigation, G.T. and G.R.; resources, G.R.; writing—G.T. and G.R.; supervision, G.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data are provided.
Acknowledgments
The authors both acknowledge the support of the institutional library facilities of the University “La Sapienza”, which permitted us to get in touch with the most interesting historical original papers that we have consulted.
Conflicts of Interest
The authors declare no conflict of interest.
References
- James Clerk Maxwell Foundation. Available online: https://clerkmaxwellfoundation.org (accessed on 7 August 2023).
- Clerk Maxwell, J. The Scientific Papers of James Clerk Maxwell; Niven, W.D., Ed.; University Press: Cambridge, UK, 1890; Volume 1. [Google Scholar]
- Capecchi, D.; Ruta, G.; Trovalusci, P. From classical to Voigt’s molecular models in elasticity. Arch. Hist. Exact Sci. 2010, 64, 525–559. [Google Scholar] [CrossRef]
- Capecchi, D.; Ruta, G. Strength of Materials and Theory of Elasticity in 19th Century Italy; Springer Int.: Cham, Switzerland, 2014. [Google Scholar]
- Campbell, L.; Garnett, W. The Life of James Clerk Maxwell…; MacMillan and Co.: London, UK, 1882. [Google Scholar]
- Tricker, R.A.R. The Contributions of Faraday & Maxwell to the Electrical Science; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Everitt, C.W.F. James Clerk Maxwell; Charles Scribner’s Sons: New York, NY, USA, 1975. [Google Scholar]
- Tolstoy, I. James Clerk Maxwell: A Biography; The University of Chicago Press: Chicago, IL, USA, 1982. [Google Scholar]
- Harman, P.G. The Natural Philosophy of James Clerk Maxwell; University Press: Cambridge, UK, 1998. [Google Scholar]
- Seitz, F. James Clerk Maxwell (1831–1879); Member APS 1875. Proc. Am. Phil. Soc. 2001, 145, 1–44. [Google Scholar]
- Mahon, B. The Man Who Changed Everything: The Life of James Clerk Maxwell; John Wiley: Chichester, UK, 2003. [Google Scholar]
- Flood, R.; McCartney, M.; Whitaker, A. (Eds.) James Clerk Maxwell: Perspectives on His Life and Work; University Press: Oxford, UK, 2014. [Google Scholar]
- Arthur, J.W. Brilliant Lives: The Clerk Maxwells and the Scottish Enlightenment; John Donald-Birlinn Publisher: Edinburgh, Scotland, 2014. [Google Scholar]
- The Scientific Papers of James Clerk Maxwell; Niven, W.D. (Ed.) University Press: Cambridge, UK, 1980; Volume 2. [Google Scholar]
- Siegel, D.M. Completeness as a goal in Maxwell’s electromagnetic theory. Isis 1975, 66, 361–368. [Google Scholar] [CrossRef]
- Turner, J. Maxwell on the method of physical analogy. British J. Phil. Sci. 1950, 6, 226–238. [Google Scholar] [CrossRef]
- Darrigol, O. Les équations de Maxwell: De MacCullagh à Lorentz; Belin: Paris, France, 2005. (In French) [Google Scholar]
- Hutchinson, I.H. The genius and faith of Faraday and Maxwell. New Atlantis 2014, 41, 81–99. [Google Scholar]
- Harman, P.M. Maxwell and Faraday. Eur. J. Phys. 1993, 14, 148–154. [Google Scholar] [CrossRef]
- O’Connell, J. Faraday, Maxwell and lines of force. J. Washington Acad. Sci. 2007, 93, 1–6. [Google Scholar]
- Israelsen, S.P. The scientific theories of Michael Faraday and James Clerk Maxwell. Purdue Hist. 2014, 7, 1. [Google Scholar]
- Marmottini, D.; Pisano, R. Nature-of-science teaching: Notes on the Lagrangian methods in Maxwell’s electromagnetic theory. In Proceedings of the 36th Annual Conference of the Italian Society for History of Physics and Astronomy, Bari, Italy, 26–29 September 2017; Esposito, S., Ed.; University Press: Pavia, Italy, 2017; pp. 263–268. [Google Scholar]
- Heimann, P.M. Maxwell and the modes of consistent representation. Arch. Hist. Exact Sci. 1970, 6, 171–213. [Google Scholar] [CrossRef]
- Stokes, G.G. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1901; Volume III. [Google Scholar]
- Thomson, W. (Lord Kelvin) On the Dynamical Theory of Heat. Trans. R. Soc. Edinb. 1853, 20, 261–288. [Google Scholar] [CrossRef]
- Weber, W.E.; Weber, H. Wilhelm Weber’s Werke, 3rd ed.; Springer: Berlin, Germany, 1893. [Google Scholar]
- Hall, G. Maxwell’s electromagnetic theory and special relativity. Philos. Trans. R. Soc. A 2008, 366, 1849–1860. [Google Scholar] [CrossRef]
- Pisano, R. Historical reflections on the physics mathematics relationship in electromagnetic theory. In The Dialectic Relation between Physics and Mathematics in the XIXth Century, History of Mechanism and Machine Science; Barbin, E., Pisano, R., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 16. [Google Scholar]
- Pelosi, G.; Selleri, S. The Roots of Maxwell’s A Dynamical Theory of the Electromagnetic Field—Scotland and Tuscany, ‘Twinned by Science’; University Press: Florence, Italy, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).