Definition
Within Lorenz models, the three major kinds of butterfly effects (BEs) are the sensitive dependence on initial conditions (SDIC), the ability of a tiny perturbation to create an organized circulation at large distances, and the hypothetical role of small-scale processes in contributing to finite predictability, referred to as the first, second, and third kinds of butterfly effects (BE1, BE2, and BE3), respectively. A well-accepted definition of the butterfly effect is the BE1 with SDIC, which was rediscovered by Lorenz in 1963. In fact, the use of the term “butterfly” appeared in a conference presentation by Lorenz in 1972, when Lorenz introduced the BE2 as the metaphorical butterfly effect. In 2014, the so-called “real butterfly effect”, which is based on the features of Lorenz’s study in 1969, was introduced as the BE3.
1. Introduction
Over a span of 50 years, the pioneering study of Lorenz in 1963 (Lorenz, 1963 [1], hereafter referred to as L63) and follow-up studies in 1969 and 1972 (Lorenz, 1969, 1972 [2,3], hereafter referred to as L69 and L72, respectively) have changed our view on the predictability of weather and climate [4] by revealing the so-called sensitive dependence on initial conditions (SDIC), also known as the butterfly effect. A literature review by Ghys in 2015 [5] indicated that the concept of the “butterfly effect” (i.e., SDIC) could be found in studies by Maxwell [6] and Poincare [7,8]. Such a butterfly effect is referred to as the first kind of BE (BE1). In [2], Lorenz applied a metaphor to discuss the possibility of whether a tiny perturbation could eventually create a tornado with a three-dimensional organized, coherent structure. The metaphorical butterfly effect is referred to as the second kind of BE (BE2). The scientific community accepts the idea that butterfly effects were “rediscovered” by Prof. Lorenz. However, one extraordinary contribution by Prof. Lorenz is that his models and methods have provided foundations that have inspired numerous studies and further advanced our understanding of chaotic nature and limited predictability.
Lorenz’s studies [1,2,9] laid a foundation for chaos theory, viewed as the third scientific achievement of the 20th century, after relativity and quantum mechanics. After the bestselling book entitled “Chaos: Making New Science” by Gleick, 1987 [10], two terms—chaos and the butterfly effect—have been used interchangeably. During the presentation for the 2021 Nobel prize in physics, the pioneering chaos study by Lorenz [1] was cited as a foundation for the awarded studies [11]. A long history exists regarding when and how the term butterfly effect was first introduced. As suggested in Lorenz’s book entitled “The Essence of Chaos” [9], the term became increasingly noticeable following Lorenz’s studies in 1963 and 1972 [1,2]. Over the past five decades, the aforementioned BEs have had direct or indirect impacts on our lives in numerous ways, including in routine numerical weather and climate predictions and even in Hollywood movies such as Jurassic Park. However, the meaning of the term “butterfly effect” in the L63 and L72 studies is not exactly the same. The exact relationship between the original butterfly effect (i.e., BE1 with SDIC) and the metaphorical butterfly effect (BE2) has become controversial. Inaccurate understandings and, thus, interpretations can easily be found. For clarification, this study documents the definitions and major features of the important kinds of butterfly effects.
Over a 10-year period between the L63 and L72 studies, the L69 model with multiscale modes was proposed for revealing the dependence of predictability on various scales (i.e., wavelengths) and suggested better predictability for larger-scale systems [3]. Furthermore, a predictability limit of two weeks has been suggested and highly cited (e.g., [4,12]). The findings regarding a predictability limit of two weeks for the atmosphere in [3] were partly supported (e.g., [13]) or not supported (Smagorinsky, 1969 [14]) by studies conducted near the time of Lorenz’s 1969 publication. For example, on pages 291 and 294, Smagorinsky, 1969 [14] documented that “In general even at 21 days, the perturbed map is still far from randomly related to the control—another way of saying that the deterministic limit has not yet been reached”. Additionally, Prof. Arakawa believed that the predictability limit is not necessarily a fixed number [12]. Recently, the idea of a predictability limit of two weeks has been challenged by new insights obtained using the L63 and L69 models, as well as generalized Lorenz models (e.g., [15,16,17]; and references therein), and promising simulations using advanced models (e.g., [18,19,20,21]).
As pointed out by Lorenz (e.g., Hillborn, 2004 [22]), the term “butterfly” appeared in Smagorinsky, 1969 [14] earlier than Lorenz, 1972 [2]. Fifty years since [1], Palmer et al., 2014 [4] reanalyzed major features of [3] in order to introduce the so-called “real butterfly effect”, terminology invented to emphasize the hypothetical role of small-scale processes in contributing to finite predictability. This butterfly effect is also different from BE1 and BE2 in [1,2]. Here, a comprehensive literature review is provided to illustrate that the meaning of the butterfly effect and its major characteristics within Lorenz’s studies have been inadequately interpreted and should be properly demonstrated. Outstanding questions and issues to be addressed include: (1) properly interpreting Lorenz’s findings, (2) providing clear definitions for butterfly effects, (3) gaining an understanding of the relationship amongst various BEs, and (4) revealing the influence of butterfly effects on the development of chaos theory, as well as numerical weather and climate models.
To achieve the above goals with the aim of promoting further investigations, below, this study provides definitions for the three major kinds of butterfly effects based on classical Lorenz studies [1,2,3], including the first, second, and third kinds of BE (e.g., BE1, BE2, and BE3), sometimes referred to as L63-, L72-, and L69 BE, respectively.
2. Definitions of Butterfly Effects
2.1. The First Kind of Butterfly Effect (BE1)
Based on the pioneering modeling study by Lorenz in 1963 [1], the original meaning (or definition) of the butterfly effect is the “sensitive dependence of solutions on initial conditions (SDIC)”. As briefly discussed here, such a feature is widely illustrated using the L63 model. The model, consisting of three first-order ordinary differential equations (ODEs) for three variables (X, Y, Z), describes the time evolution of the amplitudes for either stream functions (that yield flow velocity) or temperatures. Figure 1a compares the time evolution of solutions from the control and parallel runs. The only difference in the two runs is that a tiny perturbation with is added into the initial condition of the parallel run. Both runs initially produce very close results but very different results at a later time. Since such differences are associated with initial tiny perturbations, such a feature is referred to as the SDIC. The results may be interpreted as indicating that a tiny change in an initial condition (IC) may lead to a very different time evolution of a solution and, thus, finite predictability [17]. Supplementary materials of [17] provide detailed discussions for SDIC and finite predictability. Unfortunately, as later clarified, the SDIC has also been inaccurately interpreted as the capability of a tiny change in “creating” a different system.
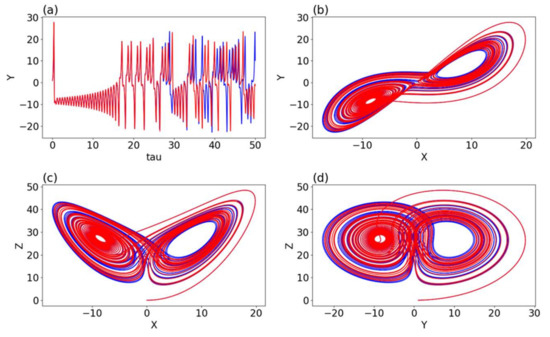
Figure 1.
The sensitive dependence on initial conditions (a) and diverged trajectories (b–d) using the Lorenz 1963 model with and . Each panel displays solutions from the control (in blue) and parallel (in red) runs, respectively. The control run has an initial condition of (X, Y, Z) = (0, 1, 0), and the parallel run additionally includes a small perturbation (1 × 10−10) in the initial value of Y. Chaotic solutions in the X-Y-Z phase space within the Lorenz model can be found in Figure 2 of [16].
A common method for analyzing the solutions of a system of ordinary differential equations (ODEs) is to apply state variables as coordinates in order to construct the so-called phase space and plot the time evolution of solutions as an orbit or trajectory within the phase space. Within the phase space, the dimension is equal to the number of variables. The term “dimension” is conventionally used within systems of ODEs (e.g., [23,24]). For example, three- and five-dimensional Lorenz models are used to indicate systems with three and five variables, respectively (e.g., [1,25]). Within the existing scientific literature, high-dimensional Lorenz models are also referred to as high-order Lorenz models (e.g., [26]).
While Figure 1a displays the time evolution of the single variable Y, Figure 1b–d displays the corresponding solutions for any two components, also called trajectories or orbits, within the two-dimensional phase space. The very different time evolution of solutions in panel (a) corresponds to the divergence of two initial, nearby trajectories in panel (b). In addition to the divergence of nearby trajectories, solution boundedness is clearly shown within the 1D and 2D phase spaces. As a result, while the term butterfly effect was initially used to indicate the phenomenon of SDIC (i.e., the BE1), its association with the geometric butterfly pattern of the solution within the phase space (e.g., Figure 1c,d of this study or Figure 2 of [9]) was also recognized by Lorenz (e.g., [9]).
In spite of “irregular” curves (that indicate variable trajectories) within the butterfly wing, a butterfly pattern illustrates the important features of solutions: boundedness associated with a finite size, time-varying curvatures, and solution recurrence. The latter is defined when a trajectory returns to the neighborhood of a previously visited state. Recurrence may be viewed as a generalization of “periodicity” that braces quasi-periodicity and chaos [24,27,28].
2.2. The Second Kind of Butterfly Effect (BE2)
The feature of SDIC that defines BE1 was indeed introduced in [1]. However, in Lorenz’s studies, the term “butterfly’’ did not appear until a conference presentation in 1972 (e.g., [2], available in the Appendix of [9]). The title of his conference presentation hypothesized the enabling role of tiny perturbations, at a butterfly scale, in producing an organized system remotely, at a tornado’s scale. In this study, such a feature is referred to as a butterfly effect of the second kind (BE2) or the L72 BE. The definition of BE2 requires interactions at various (physical) spatial scales and energy transfer across both spatial scales (e.g., intermediate scales between the scales of a butterfly and a tornado) and different physical regions (e.g., Brazil vs. Texas). More importantly, to illustrate the possibility of BE2, the causality between a butterfly’s flap and the formation of a tornado should be examined. Such a definition for BE2 is popular. However, it is challenging, if not impossible, to verify the appearance of BE2. Below, a review of Lorenz, 1972 [2] is provided in order to illustrate the most likely scenario under which BE2 was introduced and discussed.
In his 1972 conference presentation, Prof. Lorenz [2] raised the following three, and only three, questions:
- Predictability; Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?
- In more technical language, is the behavior of the atmosphere unstable (“on all spatial scales”) with respect to perturbations of small amplitude?
- How can we determine whether the atmosphere is unstable?
The above phrase “on all spatial scales” is added to facilitate discussions. In fact, the first question is the title of the 1972 presentation given by the conference session chair, Philip Merilees. Additionally, as reported by Hilborn, 2003 [22], the butterfly entered nonlinear dynamics as a result of the conversation between P. Merilees and Douglas Lilly. The three questions implicitly suggest that Lorenz addressed the first question (regarding the BE2) by answering the second and third questions. He specifically linked the BE2 with the release of instability by the atmosphere and the capability of transferring coherent energy by tiny perturbations. In recognition of the limited size of a butterfly and the limited performance of numerical methods in transferring a butterfly’s influence across different regions, Lorenz stated:
- One hypothesis, unconfirmed, is that the influence of a butterfly’s wings will spread in turbulent air, but not in calm air;
- We must therefore leave our original question (i.e., the first question) unanswered for a few more years, even while affirming our faith in the instability of the atmosphere (i.e., the second and third questions).
The above analysis indicates the necessary conditions for the appearance of BE2, which include: (1) the instability of the atmosphere and (2) the capability of transferring the energy of tiny perturbations. Here, it should be noted that the term “chaos” was introduced into nonlinear dynamics by the study of Li and Yorke (Li and Yorke, 1975 [29]). Detailed differences between instability and chaos have been discussed since that time. Additionally, as discussed above, the causality between a butterfly’s flap and the formation of a tornado should be examined. However, Prof. Lorenz did not directly answer the first question. Additionally, the presentation of Lorenz in 1972 [2] did not provide a mathematical model for addressing the source of instability and the mechanism of energy transfer across spatial scales and physical regions. A butterfly’s ability to create an organized weather system was also not addressed. As a result, the existence of BE2 has been heavily debated within the scientific and non-scientific literature. Even in 2008 (Lorenz, 2008 [30]), Lorenz still provided the following responses to a question regarding the possibility of BE2, “In the lecture, I did not answer the title question, and even today I am unsure of the proper answer, but I did consider the possibility that the answer might be ‘yes’”.
In order for a butterfly, or other small feature which generates kinetic energy to affect larger-scale features, however, part of this small-scale energy must not only be transferred to larger spatial scales through nonlinear interaction but must propagate vast distances while still retaining coherent information content. Given that motions will dissipate into heat, however, such a coherent transfer for BE2 cannot be verified using the L63 or L69 model. By comparison, as discussed earlier, BE1 with SDIC has been widely examined using the classical and generalized L63 models.
2.3. The Third Kind of Butterfly Effect (BE3)
Recent studies (e.g., [4,31,32]) have suggested that major features of the butterfly effect, including energy transfer across scales and the dependence of instability on scales, may have been shown in the L69 study. Palmer et al., 2014 [4] further introduced the term “the real butterfly effect” by applying major findings of [3]:
It is proposed that certain formally deterministic fluid systems which possess many scales of motion are observationally indistinguishable from indeterministic systems; specifically that two states of the system differing initially by a small observational error will evolve into two states differing as greatly as randomly chosen states of the system within a finite time interval, which cannot be lengthened by reducing the amplitude of the initial error.
Such a definition for the butterfly effect also suggests finite predictability. To reiterate the (collective) role of small-scale processes in contributing to finite predictability, Palmer et al. [4] additionally reanalyzed the convergent series constructed by Lorenz, 1969 [3]. Such a BE is referred to as the third kind of BE (BEs) or the L69 BE. Below, the study [3] is first reviewed, and comments on the real butterfly effect (i.e., BE3) are then provided.
The L69 model, consisting of a system of linear, second-order ODEs, was derived by applying a modified quasi-normal (QN) approximation into a simple partial differential equation (PDE) that conserves vorticity and contains no dissipative terms. Such a closure produces inconsistent properties and unphysical results (e.g., [33,34,35,36]). For example, it does not produce positive definite energy spectra. The issue was later resolved by the so-called “eddy damped” approximation, including the Eddy-Damped QN(EDQN) approximation and then the EDQN Markovian (EDQNM) approximation [33,35,36]. Recently, Shen et al., 2022 [17] pointed out that the L69 model is a closure-based, physically multiscale, mathematically linear, and numerically ill-conditioned system. Since the L69 model is ill-conditioned and can easily capture numerical instability, as suggested by [17], these features may, presumably, partially contribute to finite predictability. The L69 linear model is not a chaotic or turbulence model. Lorenz’s chaotic models and turbulence models were reported in separate publications (e.g., [1,37,38,39]). As a result, it is challenging to apply Lorenz’s 1969 linear model to address BE1 and BE2 (i.e., required to reveal the role of nonlinearity and to examine causality). As further illustrated below, the mechanisms for finite predictability within the L63 and L69 models are different.
Since Lilly, 1969 [40,41,42], efforts have been made to propose an empirical formula for illustrating finite predictability within the L69 model. The empirical formula that was well documented in [4,43] is reviewed here. To facilitate discussions, two time scales, that are functions of the wavenumber of the Fourier mode (denoted as ) for the background or the perturbation kinetic energy (KE), are defined as follows:
- 1.
- The turnover time ( is the time for a parcel with velocity to move a distance of , with being the velocity associated with wavenumber (e.g., Vallis, 2006 [44]).
- 2.
- The saturation time ( is defined as the time for the perturbation at wavenumber to become saturated (i.e., reaching the value of background kinetic energy). In [3], the saturation time () determines the predictability horizon at wavenumber
Simply speaking, the turnover time and saturation time represent how soon an initial perturbation could spread and amplify to reach an upper limit, respectively. It should be noted that the definitions of the above time scales do not explicitly consider the spatial distance that a small perturbation can generate a coherent feature, although it can be interpreted from the saturation time that there is a finite distance associated with the specific perturbation.To determine a predictability horizon, the following two major assumptions have been made: (1) eddy turnover time can provide an estimate for the differences between two successive saturation times, and (2) error transfers amongst a specific subset of wavenumbers (, 24, etc.; is the wavenumber associated with the largest scale). As a result, a predictability horizon can be determined as the sum of the eddy turnover time over the specific subset of wavenumbers, yielding the following empirical formula (e.g., Shen et al., 2022 [45]):
Here, represents an eddy turnover time for the background kinetic energy with a () energy spectrum. is the turnover time for the largest scale (i.e., ). Equation (1) is the same as Equation (5) of Lloveras et al., 2022 [43], with a () energy spectrum (i.e., For a finite number of , the difference between two truncated series with and ( + 1) terms, respectively, indicates the impact by the mode at the highest wavenumber (i.e., for the smallest scale). Major findings in the above equation include the following. (1) The equation with an infinite number of terms produces a convergent series and suggests a finite predictability horizon of 2.7 . (2) A higher wavenumber mode (associated with a larger value of always provides a positive contribution to the predictability horizon, although the contribution from (very) large wavenumbers may be negligible. If the effect of a butterfly’s flap can be emulated by a term at for a sufficiently large value of , a butterfly’s flap provides a negligible contribution to the predictability horizon. Additional comments on the validity of the aforementioned assumptions and the impact of different slopes within the kinetic energy spectra are provided in Section 3.
3. Discussion
Until this point, the BE1, BE2, and BE3 within Lorenz studies [1,2,3] have been identified and summarized in Table 1. Below, based on major features of the L63, L69, and generalized Lorenz models [46,47,48], additional comments are provided to clarify some inaccurate understandings of BE1 and BE3. A possibility for the appearance of BE2 will be addressed in a future study.

Table 1.
The Three Kinds of Butterfly Effects.
3.1. A Popular but Inaccurate Analogy for BE1 and Chaos
Shen, 2019 [20,46] discussed three types of solutions within the L63 model and revealed the ingredients for a sensitive dependence on ICs by comparing the L63 model with simplified systems. Chaotic solutions within the L63 model have been a focus for several decades. As previously discussed, three major features of chaotic orbits include the divergence of nearby trajectories, their boundedness, and their recurrence. These features are determined by the competitive or collective impact of three kinds of processes, including nonlinear processes and linear heating and dissipative processes. Although Lorenz, 1963 [1] emphasized nonlinear dynamics (i.e., chaotic dynamics), researchers often apply a “simple” analogy that contains monotonic growth, instead of time-varying growth and decay, in order to understand the characteristics of nonlinear solutions within the L63 model. Such a simplified analogy may have yielded inaccurate understandings.
Below, one popular but inaccurate analogy for chaos is provided. As discussed, the analogy only emphasizes divergence while neglecting recurrence and other features such as coexisting chaos and order (e.g., [15,17]). The sensitive dependence on initial conditions (i.e., the BE1) has been illustrated using the following folklore (e.g., [10,49]):
“For want of a nail, the shoe was lost.For want of a shoe, the horse was lost.For want of a horse, the rider was lost.For want of a rider, the battle was lost.For want of a battle, the kingdom was lost.And all for the want of a horseshoe nail”.
Based on the above, many people mistakenly believe that the impact of a tiny initial perturbation monotonically increases with time and that any tiny perturbation can eventually produce a large impact on numerical integrations. However, in 2008, Prof. Lorenz stated that he did not feel that this verse described true chaos but that it better illustrated the simpler phenomenon of instability and that the verse implicitly suggests that subsequent small events will not reverse the outcome (Lorenz, 2008 [30]). Based on the analysis, the verse only indicates divergence, not boundedness. Boundedness is important for the finite size of a butterfly pattern. As illustrated using high-dimensional Lorenz models (e.g., [46]), the verse also does not consider any (future) possibility for a (small-scale) process to cause negative feedback. Lastly, when a system possesses coexisting chaotic and non-chaotic processes, a tiny initial perturbation may or may not cause a large impact on predictability. (e.g., [15,17,46,47]).
3.2. A Positive Contribution by Small Scale Processes Within BE3
Physically and mathematically, the introduction of BE3 is important. However, how the L69 model may address BE1-BE3 should be carefully examined in order to understand the positive or negative contribution by a butterfly (small-scale processes). As discussed below, such a goal can be achieved by comparing two cases with different slopes for the kinetic energy (KE) spectra, one for the (−5/3) law and the other for the (−3) law.
In Section 2, Equation (1) was applied to define the BE3 with respect to the role of small-scale processes in contributing to the finite predictability of large-scale processes for the (−5/3) KE spectrum. As discussed, based on a truncated series with a finite number of terms in Equation (1), an additional term (e.g., ) always provides a positive contribution to the predictability horizon. By comparison, when the (−5/3) KE spectrum is replaced by a (−3) KE spectrum, the counterpart of Equation (1) becomes:
The above series with an infinite number of terms is divergent, suggesting an unlimited predictability when all wavenumbers are considered. A comparison between Equations (1) and (2) suggests that (a) small-scale processes at high wavenumbers provide a positive contribution to the predictability horizon in both equations, and (b) the collective contributions in Equations (1) and (2) yield a convergent and divergent series and, thus, limited and unlimited predictability, respectively. As a result, limited and unlimited predictability appear in different basic states for the (−5/3) and (−3) KE spectra, respectively.
As a conclusion for this section, an interesting question is how the above findings reveal the potential role of a butterfly’s flap. Within Lorenz models, a butterfly’s flap may represent a perturbation in “amplitude” (of the existing smallest scale mode) or “scale” (yielding the smallest scale). For the latter, in which a smaller scale is added, both Equations (1) and (2) suggest a positive contribution to the predictability horizon. Namely, it does not produce a negative contribution to the predictability horizon. This result is not consistent with the view that small perturbations may contaminate simulations of large-scale processes. Furthermore, it is required to examine the condition under which Equations (1) and (2) are valid and can, thus, be applied in order to address BE3 (i.e., yielding a finite time interval that cannot be lengthened by reducing the amplitude of the initial error). Unfortunately, the validity of assumptions that lead to a geometric series in Equation (1) is being challenged in Shen et al., 2022 [45]. More importantly, a common assumption within the L69 and turbulence models that views the atmosphere as an isotropic homogeneous turbulent fluid should be reexamined prior to applying the findings of the L69 study. Here, the Orszang definition is adopted as follows: the turbulence is homogeneous if all points in space are statistically equivalent; it is isotropic if all directions are statistically equivalent [35]. As a result, assumptions for these two features do not permit variations in climatological properties from one location to another location [3]. Additionally, it is impossible to apply the L69 model or the aforementioned turbulence models to examine the causality between a single butterfly flap and the formation of a tornado since all of the systems in these idealized models appear periodically in the entire physical domain.
4. Conclusions
Based on new insights on the features of classical Lorenz models, as well as a generalized Lorenz model, this study identified three major kinds of butterfly effects and provided their definitions as follows: (1) butterfly effects of the first kind (BE1) represent the sensitive dependence of solutions on initial conditions (SDIC) in [1]; (2) butterfly effects of the second kind (BE2) represent the hypothetical role of initial tiny perturbations in producing an organized large-scale system at large distances (e.g., a tornado) in [2]; and (3) butterfly effects of the third kind (BE3), or the so-called real butterfly effect, represent the role of small scale processes (within a highly turbulent region with a () KE spectrum) in contributing to the finite predictability of large scale processes in [3,4]. The three kinds of butterfly effects are not exactly the same. BE1 is known as chaos, BE2 is a metaphorical analogy, and BE3 has a very short history. Table 1 provides a brief summary.
The Lorenz 1963 model is nonlinear, but limited scale, while the Lorenz 1969 model is closure-based, physically multiscale, mathematically linear, and numerically ill-conditioned. No specific model was presented in [2]. Due to the simplicity of the Lorenz models, it is quantitatively challenging to address the need that BE2 requires energy transfer across spatial and spectral scales between a single butterfly flap and a three-dimensional tornado. A necessary requirement is that, when introducing more physics to the models, such as kinetic energy dissipation into heat (and thus loss of coherency), how the communication of kinetic energy forcing from small perturbations can remain coherent across the vast spatial scales needs to be explained. It is thus best to consider BE2 as a metaphor.
While both the 1963 and 1969 Lorenz models produce various types of solutions [15,16,17], only chaotic and linearly unstable solutions have been a focus. As a result, the concept of finite predictability associated with BE1 and BE3 within specific solutions should be generalized with caution. On the other hand, new insights regarding ill-conditioning and numerical instability within the Lorenz 1969 model may support L69′s view that a finite time interval cannot be lengthened by reducing the amplitude of the initial error.
Author Contributions
Conceptualization, B.-W.S., R.A.P.S., X.Z., and R.A.; methodology, B.-W.S.; software, B.-W.S., J.C., W.P., and S.F.-N.; writing—original draft preparation, B.-W.S., R.A.P.S., and X.Z.; writing—review and editing, B.-W.S., R.A.P.S., X.Z., J.C., S.F.-N., W.P., and R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank three anonymous reviewers, Geoffrey Vallis, Yongqiang Sun, Richard Rotunno, Hung-Chi Kuo, Daniel Lloveras, and Dale Durran for valuable comments and discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lorenz, E.N. Predictability: Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? In Proceedings of the 139th Meeting of AAAS Section on Environmental Sciences, New Approaches to Global Weather, GARP, AAAS, Cambridge, MA, USA, 29 December 1972. 5p. [Google Scholar]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Palmer, T.N.; Doring, A.; Seregin, G. The real butterfly effect. Nonlinearity 2014, 27, R123–R141. [Google Scholar] [CrossRef]
- Ghys, E. The Butterfly Effect. In Proceedings of the 12th International Congress on Mathematical Education, Seoul, Korea, 8–15 July 2012; Cho, S., Ed.; Springer: Cham, Switzerland, 2012. [Google Scholar]
- Maxwell, J.C. Matter and Motion; Dover Publications: Dover, UK, 1952. [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Poincaré, H. Science et Méthode, Flammarion. English Transl. 1908 ed.; Maitland, F., Ed.; Thomas Nelson and Sons: London, UK, 1914. [Google Scholar]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; 227p. [Google Scholar]
- Gleick, J. Chaos: Making a New Science; Penguin: New York, NY, USA, 1987; 360p. [Google Scholar]
- The Nobel Committee for Physics. Scientific Background on the Nobel Prize in Physics 2021 “for Groundbreaking Contributions to Our Understanding of Complex Physical Systems”. 2021. Available online: https://www.nobelprize.org/prizes/physics/2021/popular-information/ (accessed on 28 June 2022).
- Lewis, J. Roots of ensemble forecasting. Mon. Weather. Rev. 2005, 133, 1865–1885. [Google Scholar] [CrossRef]
- Leith, C.E.; Kraichnan, R.H. Predictability of turbulent flows. J. Atmos. Sci. 1972, 29, 1041–1058. [Google Scholar] [CrossRef]
- Smagorinsky, J. Problems and promises of deterministic extended range forecasting. Bull. Amer. Meteor. Soc. 1969, 50, 286–312. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is weather chaotic? Coexistence of chaos and order within a generalized Lorenz model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. Available online: https://journals.ametsoc.org/view/journals/bams/102/1/BAMS-D-19-0165.1.xml (accessed on 29 January 2021). [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R.; Reyes, T.A. Is Weather Chaotic? Coexisting Chaotic and Non-Chaotic Attractors within Lorenz Models. In Proceedings of the 13th Chaos International Conference CHAOS 2020, Florence, Italy, 9–12 June 2020; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. One Saddle Point and Two Types of Sensitivities Within the Lorenz 1963 and 1969 Models. Atmosphere 2022, 13, 753. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Wu, M.-L. African Easterly Waves in 30-day High-resolution Global Simulations: A Case Study during the 2006 NAMMA Period. Geophys. Res. Lett. 2010, 37, L18803. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Green, B. Coupling Advanced Modeling and Visualization to Improve High-Impact TropicalWeather Prediction (CAMVis). IEEE Comput. Sci. Eng. 2011, 13, 56–67. [Google Scholar] [CrossRef]
- Shen, B.-W. On the Predictability of 30-Day Global Mesoscale Simulations of African Easterly Waves during Summer 2006: A View with the Generalized Lorenz Model. Geosciences 2019, 9, 281. [Google Scholar] [CrossRef]
- Judt, F. Atmospheric Predictability of the Tropics, Middle Latitudes, and Polar Regions Explored through Global Storm-Resolving Simulations. J. Atmos. Sci. 2020, 77, 257–276. [Google Scholar] [CrossRef]
- Hilborn, R.C. Sea gulls, butterflies, and grasshoppers: A brief history of the butterfly effect in nonlinear dynamics. Am. J. Phys. 2004, 72, 425. [Google Scholar] [CrossRef]
- Hirsch, M.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos, 3rd ed.; Academic Press: Waltham, MA, USA, 2013; 432p. [Google Scholar]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; 437p. [Google Scholar]
- Shen, B.-W. Nonlinear feedback in a five-dimensional Lorenz model. J. Atmos. Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Moon, S.; Han, B.-S.; Park, J.; Seo, J.M.; Baik, J.-J. Periodicity and Chaos of High-Order Lorenz Systems. Int. J. Bifurc. Chaos 2017, 27, 1750176. [Google Scholar] [CrossRef]
- Faghih-Naini, S.; Shen, B.-W. Quasi-periodic orbits in the five-dimensional non-dissipative Lorenz model: The role of the extended nonlinear feedback loop. Int. J. Bifurc. Chaos 2018, 28, 1850072. [Google Scholar] [CrossRef]
- Reyes, T.; Shen, B.-W. A Recurrence Analysis of Chaotic and Non-Chaotic Solutions within a Generalized Nine-Dimensional Lorenz Model. Chaos Solitons Fractals 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Li, T.-Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Lorenz, E.N. The butterfly effect. In Premio Felice Pietro Chisesi E Caterina Tomassoni Award Lecture; University of Rome: Rome, Italy, 2008. [Google Scholar]
- Durran, D.R.; Gingrich, M. Atmospheric predictability: Why atmospheric butterflies are not of practical importance. J. Atmos. Sci. 2014, 71, 2476–2478. [Google Scholar] [CrossRef]
- Rotunno, R.; Snyder, C. A generalization of Lorenz’s model for the predictability of flows with many scales of motion. J. Atmos. Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Leith, C.E. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef]
- Orszag, S.A. Analytical theories of turbulence. J. Fluid Mech. 1970, 41, 363–386. [Google Scholar] [CrossRef]
- Orszag, S.A. Eluid Dynamics; Balian, R., Peuble, J.L., Eds.; Gordon and Breach: London, UK, 1977. [Google Scholar]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in Systems with Many Characteristic Times: The Case of Turbulence. Phys. Rev. E 1996, 53, 2337–2349. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, E.N. Predictability—A problem partly solved. Semin. Predict. 1996, I, ECMWF. [Google Scholar]
- Lorenz, E.N. Investigating the predictability of turbulent motion. Statistical Models and Turbulence. In Proceedings of the Symposium Held at the University of California, San Diego, CA, USA, 15–21 July 1971; Springer: Berlin/Heidelberg, Germany, 1972; pp. 195–204. [Google Scholar]
- Lorenz, E.N. Low-order models representing realizations of turbulence. J. Fluid Mech. 1972, 55, 545–563. [Google Scholar] [CrossRef]
- Lilly, D.K. Numerical simulation of two-dimensional turbulence. Phys. Fluid Suppl. 1969, 12, 240–249. [Google Scholar] [CrossRef]
- Lilly, D.K. Numerical simulation studies of two-dimensional turbulence: II. Stability and predictability studies. Geophys. Fluid Dyn. 1972, 4, 1–28. [Google Scholar] [CrossRef]
- Lilly, K.D. Lectures in Sub-Synoptic Scales of Motions and Two-Dimensional Turbulence Dynamic Meteorology; Morel, P., Ed.; Reidel: Boston, MA, USA, 1973; pp. 353–418. [Google Scholar]
- Lloveras, D.J.; Tierney, L.H.; Durran, D. Mesoscale Predictability in Moist Midlatitude Cyclones Is Not Sensitive to the Slope of the Background Kinetic Energy Spectrum. J. Atmos. Sci. 2022, 79, 119–139. [Google Scholar] [CrossRef]
- Vallis, G. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006; p. 745. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. Comments on “Mesoscale Predictability in Moist Midlatitude Cyclones Is Not Sensitive to the Slope of the Background Kinetic Energy Spectrum” by Lloveras, Tierney, and Durran. 2022. Available online: https://www.researchgate.net/publication/360919470_Comments_on_Mesoscale_Predictability_in_Moist_Midlatitude_Cyclones_Is_Not_Sensitive_to_the_Slope_of_the_Background_Kinetic_Energy_Spectrum_by_Lloveras_Tierney_and_Durran_2022?channel=doi&linkId=629272356886635d5caa6558&showFulltext=true (accessed on 28 June 2022).
- Shen, B.-W. Aggregated Negative Feedback in a Generalized Lorenz Model. Int. J. Bifurc. Chaos 2019, 2019, 1950037. [Google Scholar] [CrossRef]
- Shen, B.-W.; Reyes, T.; Faghih-Naini, S. Coexistence of Chaotic and Non-Chaotic Orbits in a New Nine-Dimensional Lorenz Model. In Proceedings of the 11th Chaotic Modeling and Simulation International Conference, CHAOS 2018, Rome, Italy, 5–8 June 2018; Springer Proceedings in Complexity; Skiadas, C., Lubashevsky, I., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Cui, J.; Shen, B.-W. A Kernel Principal Component Analysis of Coexisting Attractors within a Generalized Lorenz Model. Chaos Solitons Fractals 2021, 146, 110865. [Google Scholar] [CrossRef]
- Drazin, P.G. Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1992; p. 333. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).