Undecidability and Quantum Mechanics
Definition
1. Introduction
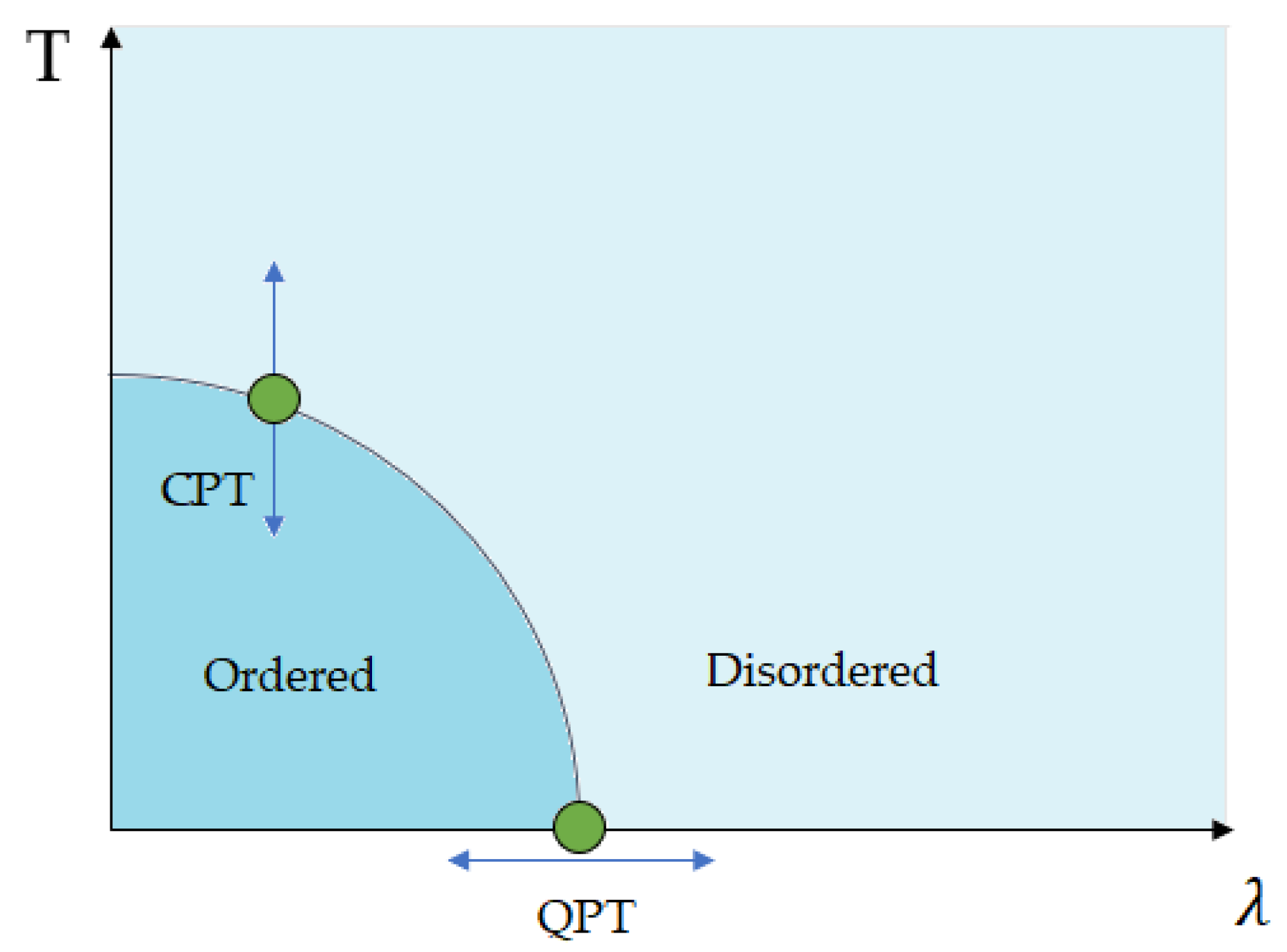
2. Undecidability and Quantum Phase Transitions
- (1)
- the ground state of H is q-fold (quasi)degenerate in the sense that there are q eigenvalues, E0,1,..., E0,q in the ground state sector at the bottom of the spectrum of H such thatΔE = max {μ,μ′} |E0,μ − E0,μ′| → 0 as |Λs| → ∞,|Λs| being the cardinality of the set Λs;
- (2)
- the separation between the ground-state energy and all the other energies within the spectrum is larger than a positive constant ΔE, which is independent of the dimension of |Λs|.
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Poonen, B. Undecidable problems: A sampler. In Interpreting Gödel; Kennedy, J., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 211–241. [Google Scholar]
- Lloyd, S. Quantum-mechanical computers and uncomputability. Phys. Rev. Lett. 1993, 71, 943–946. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S. Necessary and sufficient conditions for quantum computation. J. Modern Opt. 1994, 41, 2503–2520. [Google Scholar] [CrossRef]
- Van den Nest, M.; Briegel, H.J. Measurement-based quantum computation and undecidable logic. Found. Phys. 2008, 38, 448–457. [Google Scholar] [CrossRef]
- Wolf, M.M.; Cubitt, T.S.; Pérez-García, D. Are problems in quantum information theory (un)decidable? arXiv 2011, arXiv:1111.5425. [Google Scholar]
- Eisert, J.; Müller, M.P.; Gogolin, C. Quantum measurement occurrence is undecidable. Phys. Rev. Lett. 2012, 108, 260501. [Google Scholar] [CrossRef]
- Morton, J.; Biamonte, J. Undecidability in tensor network states. Phys. Rev. A 2012, 86, 030301. [Google Scholar] [CrossRef]
- Kliesch, M.; Gross, D.; Eisert, J. Matrix-product operators and states: NP-hardness and undecidability. Phys. Rev. Lett. 2014, 113, 160503. [Google Scholar] [CrossRef]
- De las Cuevas, G.; Cubitt, T.S.; Cirac, J.I.; Wolf, M.M.; Pérez-García, D. Fundamental limitations in the purifications of tensor networks. J. Math. Phys. 2016, 57, 071902. [Google Scholar] [CrossRef]
- Bendersky, A.; Senno, G.; de la Torre, G.; Figueira, S.; Acín, A. Nonsignaling deterministic models for nonlocal correlations have to be uncomputable. Phys. Rev. Lett. 2017, 118, 130401. [Google Scholar] [CrossRef]
- Elkouss, D.; Pérez-García, D. Memory effects can make the transmission capability of a communication channel uncomputable. Nat. Comm. 2018, 9, 11491–11495. [Google Scholar] [CrossRef]
- Komar, A. Undecidability of macroscopically distinguishable states in quantum field theory. Phys. Rev. 1964, 133, B542–B544. [Google Scholar] [CrossRef]
- Moore, C. Unpredictability and undecidability in dynamical systems. Phys. Rev. Lett. 1990, 64, 2354–2357. [Google Scholar] [CrossRef] [PubMed]
- Bausch, J.; Cubitt, T.S.; Watson, J.D. Uncomputability of phase diagrams. Nat. Comm. 2021, 12, 452. [Google Scholar] [CrossRef] [PubMed]
- Wolfram, S. Undecidability and intractability in theoretical physics. Phys. Rev. Lett. 1985, 54, 735–738. [Google Scholar] [CrossRef]
- Bondar, D.I.; Pechen, A.N. Uncomputability and complexity of quantum control. Sci. Rep. 2020, 10, 1195. [Google Scholar] [CrossRef]
- Watson, J.D.; Onorati, E.; Cubitt, T.S. Uncomputably complex renormalisation group flows. arXiv 2021, arXiv:2102.05145. [Google Scholar]
- Tachikawa, Y. Undecidable problems in quantum field theory. arXiv 2022, arXiv:2203.16689. [Google Scholar]
- Shiraishi, N.; Matsumoto, K. Undecidability in quantum thermalization. Nat. Commun. 2021, 12, 5084. [Google Scholar] [CrossRef]
- Richardson, D. Some undecidable problems involving elementary functions of a real variable. J. Symb. Log. 1968, 33, 514–520. [Google Scholar] [CrossRef]
- da Costa, N.C.A.; Doria, F.A. Undecidability and incompleteness in classical mechanics. Int. J. Theor. Phys. 1991, 30, 1041–1073. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the entscheidungsproblem. J. Math. 1936, 58, 345–363. [Google Scholar]
- Turing, A.M. On computable numbers, with an application to the entscheidungsproblem. A correction. Proc. London Math. Soc. 1938, 2, 544–546. [Google Scholar] [CrossRef]
- Cubitt, T.S.; Pérez-García, D.; Wolf, M.M. Undecidability of the spectral gap. Nature 2015, 528, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Cubitt, T.S.; Pérez-García, D.; Wolf, M.M. Undecidability of the spectral gap (full version). arXiv 2015, arXiv:1502.04573. [Google Scholar]
- Ando, Y.; Ono, S.; Sun, X.F.; Takeya, J.; Balakirev, F.F.; Betts, J.B.; Boebinger, G.S. Quantum phase transitions in the cuprate superconductor Bi2Sr2−xLaxCuO6+δ. Phys. Rev. Lett. 2004, 92, 247004. [Google Scholar] [CrossRef] [PubMed]
- Egetenmeyer, N.; Gavilano, J.L.; Maisuradze, A.; Gerber, S.; MacLaughlin, D.E.; Seyfarth, G.; Andreica, D.; Desilets-Benoit, A.; Bianchi, A.D.; Baines, C.; et al. Direct observation of the quantum critical point in heavy fermion CeRhSi3. Phys. Rev. Lett. 2012, 108, 177204. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, T.; Miyagawa, K.; Taniguchi, H.; Kato, R.; Kanoda, K. Quantum criticality of Mott transition in organic materials. Nature Phys. 2015, 11, 221–224. [Google Scholar] [CrossRef]
- Tian, G.-S.; Lin, H.-Q. Excited-state level crossing and quantum phase transition in one-dimensional correlated fermion models. Phys. Rev. B 2003, 67, 245105. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Brink, L.; Gunn, M.; José, J.V.; Kosterlitz, J.M.; Phua, K.K. (Eds.) Topological Phase Transitions and New Developments; World Scientific Publishing: Singapore, 2018. [Google Scholar]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. I. Classical systems. Sov. Phys. JETP 1971, 32, 493–500. [Google Scholar]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum systems. Sov. Phys. JETP 1972, 34, 610–616. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C: Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Domb, C. The Critical Point: A Historical Introduction to the Modern Theory of Critical Phenomena; Taylor & Francis Ltd: London, UK, 1996. [Google Scholar]
- Coleman, P.; Schofield, A.J. Quantum criticality. Nature 2005, 433, 226–229. [Google Scholar] [CrossRef] [PubMed]
- Bogoliubov, N.N. Quasimittelwerte in Problemen der statistichen Mechanik. Phys. Abhandl. Sowjetunion 1962, 6, 1–24. [Google Scholar]
- Bogoliubov, N.N. Quasimittelwerte in problemen der statistichen mechanik (1. Fortsetzung). Phys. Abhandl. Sowjetunion 1962, 6, 113–138. [Google Scholar]
- Bogoliubov, N.N. Quasimittelwerte in problemen der statistichen mechanik (2. Fortsetzung und schluß). Phys. Abhandl. Sowjetunion 1962, 6, 229–252. [Google Scholar]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133–1135. [Google Scholar] [CrossRef]
- Hohenberg, P.C. Existence of long-range order in one and two dimensions. Phys. Rev. 1967, 158, 383–386. [Google Scholar] [CrossRef]
- Auerbach, A. Interacting Electrons and Quantum Magnetism; Springer: New York, NY, USA, 1994. [Google Scholar]
- Su, G.; Schadschneider, A.; Zittartz, J. Absence of superconducting long-range order in low-dimensional Hubbard models. Phys. Lett. A 1997, 230, 99–104. [Google Scholar] [CrossRef]
- Noce, C. Quantum disorder in the periodic Anderson model. Phys. Rev. B 2005, 71, 092506. [Google Scholar] [CrossRef]
- Wojtkiewicz, J.; Pusz, W.; Stachura, P. Bogoliubov inequality for the ground state and its application to interacting rotor systems. Rep. Math. Phys. 2017, 80, 233–253. [Google Scholar] [CrossRef][Green Version]
- McBryan, O.A.; Spencer, T. On the decay of correlations in SO(n)-symmetric ferromagnets. Commun. Math. Phys. 1977, 53, 299–302. [Google Scholar] [CrossRef]
- Koma, T.; Tasaki, H. Decay of superconducting and magnetic correlations in one- and two-dimensional Hubbard models. Phys. Rev. Lett. 1992, 68, 3248–3251. [Google Scholar] [CrossRef] [PubMed]
- van Enter, A.C.D. Bounds on correlation decay for long-range vector spin glasses. J. Stat. Phys. 1985, 41, 315–321. [Google Scholar] [CrossRef]
- Naddaf, A. On the decay of correlations in non-analytic SO(n)-symmetric models. Commun. Math. Phys. 1997, 184, 387–395. [Google Scholar] [CrossRef]
- Gagnebin, M.; Velenik, Y. Upper bound on the decay of correlations in a general class of O(N)-symmetric model. Commun. Math. Phys. 2014, 332, 1235–1255. [Google Scholar] [CrossRef][Green Version]
- Benassi, C.; Fröhlich, J.; Ueltschi, D. Decay of correlations in 2D quantum systems with continuous symmetry. Ann. Henri Poincaré 2017, 18, 2831–2847. [Google Scholar] [CrossRef]
- Macris, M.; Ruiz, J. A remark on the decay of superconducting correlations in one- and two-dimensional Hubbard models. J. Stat. Phys. 1994, 75, 1179–1184. [Google Scholar] [CrossRef]
- Noce, C. Superconducting order in low-dimensional boson-fermion model: Absence of finite-temperature transition. Eur. Phys. J. B 2002, 30, 67–70. [Google Scholar] [CrossRef]
- Stachura, P.; Pusz, W.; Wojtkiewicz, J. Non-existence of Bose–Einstein condensation in Bose–Hubbard model in dimensions 1 and 2. J. Math. Phys. 2020, 61, 113303. [Google Scholar] [CrossRef]
- Koma, T. Spectral gap and decay of correlations in U(1)-symmetric lattice systems in dimensions D <2. J. Math. Phys. 2007, 48, 023303. [Google Scholar]
- Hastings, M.B.; Koma, T. Spectral gap and exponential decay of correlations. Commun. Math. Phys. 2006, 265, 781–804. [Google Scholar] [CrossRef]
- Nachtergaele, B.; Sims, R. Lieb-Robinson bounds and the exponential clustering theorem. Commun. Math. Phys. 2006, 265, 119–130. [Google Scholar] [CrossRef]
- Lieb, E.H.; Schultz, T.D.; Mattis, D.C. Two soluble models of an antiferromagnetic chain. Ann. Phys. 1961, 16, 407–466. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Phys. Lett. A 1983, 93, 464–468. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: Semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Valence bond ground states in isotropic quantum antiferromagnets. Commun. Math. Phys. 1988, 115, 477–528. [Google Scholar] [CrossRef]
- Pomata, N.; Wei, T.-C. AKLT models on decorated square lattices are gapped. Phys. Rev. B 2019, 100, 094429. [Google Scholar] [CrossRef]
- Pomata, N.; Wei, T.-C. Demonstrating the Affleck-Kennedy-Lieb-Tasaki spectral gap on 2D degree-3 lattices. Phys. Rev. Lett. 2020, 124, 177203. [Google Scholar] [CrossRef]
- Lemm, M.; Mozgunov, E. Spectral gaps of frustration-free spin systems with boundary. J. Math. Phys. 2019, 60, 051901. [Google Scholar] [CrossRef]
- Lemm, M. Finite-size criteria for spectral gaps in D-dimensional quantum spin systems. In Analytic Trends in Mathematical Physics; Abdul-Rahman, H., Sims, R., Young, A., Eds.; American Mathematical Society: Providence, RI, USA, 2020; pp. 121–132. [Google Scholar]
- Gödel, K. Über formal unentscheidbare sätze der Principia Mathematica und verwandter Systeme I (“On formally undecidable propositions of Principia Mathematica and related systems I”). Mon. Math. 1931, 38, 173–198. [Google Scholar] [CrossRef]
- Sipser, M. Introduction to the Theory of Computation; Chapter 4; PWS Publishing: Boston, MA, USA, 2006. [Google Scholar]
- Bausch, J.; Cubitt, T.; Lucia, A.; Pérez-García, D. Undecidability of the spectral gap in one dimension. Phys. Rev. X 2020, 10, 031038. [Google Scholar] [CrossRef]
- Noce, C. The periodic Anderson model: Symmetry-based results and some exact solutions. Phys. Rep. 2006, 431, 173–230. [Google Scholar] [CrossRef]
- Noce, C.; Romano, A. Thermodynamical properties of the Anderson model in the atomic limit. Physica B 1990, 160, 304–312. [Google Scholar] [CrossRef]
- Keiter, H.; Morandi, G. Thermodynamic perturbation theory for systems with strong local correlations. Phys. Rep. 1984, 109, 227–308. [Google Scholar] [CrossRef]
- Czycholl, G. Approximate treatments of intermediate valence and heavy fermion model systems. Phys. Rep. 1986, 143, 277–345. [Google Scholar] [CrossRef]
- Marinaro, M.; Noce, C.; Romano, A. Densities of states in the periodic Anderson model. J. Phys. Cond. Matter 1991, 3, 3719–3728. [Google Scholar] [CrossRef]
- Möller, B.; Wölfle, P. Magnetic order in the periodic Anderson model. Phys. Rev. B 1993, 48, 10320–10326. [Google Scholar] [CrossRef]
- Pruschke, T.; Bulla, R.; Jarrell, M. Low-energy scale of the periodic Anderson model. Phys. Rev. B 2000, 61, 12799–12809. [Google Scholar] [CrossRef]
- Sordi, G.; Amaricci, A.; Rozenberg, M.J. Metal-insulator transitions in the periodic Anderson model. Phys. Rev. Lett. 2007, 99, 196403. [Google Scholar] [CrossRef]
- Schäfer, T.; Katanin, A.A.; Kitatani, M.; Toschi, A.; Held, K. Quantum criticality in the two-dimensional periodic Anderson model. Phys. Rev. Lett. 2019, 122, 227201. [Google Scholar] [CrossRef]
- Ishizuka, J.; Yanase, Y. Periodic Anderson model for magnetism and superconductivity in UTe2. Phys. Rev. B 2021, 103, 094504. [Google Scholar] [CrossRef]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Ueda, K.; Tsunetsugu, H.; Sigrist, M. Singlet ground state of the periodic Anderson model at half filling: A rigorous result. Phys. Rev. Lett. 1992, 68, 1030–1033. [Google Scholar] [CrossRef] [PubMed]
- Tsunetsugu, H.; Sigrist, M.; Ueda, K. The ground-state phase diagram of the one-dimensional Kondo lattice model. Rev. Mod. Phys. 1997, 69, 809–863. [Google Scholar] [CrossRef]
- Schrieffer, J.R.; Wolff, P.A. Relation between the Anderson and Kondo Hamiltonians. Phys. Rev. 1966, 149, 491–492. [Google Scholar] [CrossRef]
- Bravyi, S.; Di Vincenzo, D.P.; Loss, D. Schrieffer–Wolff transformation for quantum many-body systems. Ann. Phys. 2011, 326, 2793–2826. [Google Scholar] [CrossRef]
- Tsunetsugu, H.; Hatsugai, Y.; Ueda, K.; Sigrist, M. Spin-liquid ground state of the half-filled Kondo lattice in one dimension. Phys. Rev. B 1992, 46, 3175–3178. [Google Scholar] [CrossRef]
- Nishino, T.; Ueda, K. Spin- and charge-excitation gaps in the one-dimensional periodic Anderson model. Phys. Rev. B 1993, 47, 12451–12458. [Google Scholar] [CrossRef]
- Guerrero, M.; Yu, C.C. Kondo insulators modeled by the one-dimensional Anderson lattice: A numerical-renormalization-group study. Phys. Rev. B 1995, 51, 10301–10312. [Google Scholar] [CrossRef]
- Ippoliti, E.; Caprara, S. Undecidability of the Spectral Gap: An Epistemological Look. J. Gen. Phil. Sc. 2021, 52, 157–170. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Roman, B.; Hansen, A.C. How to Compute Spectra with Error Control. Phys. Rev. Lett. 2019, 122, 250201. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Hawking, S. Gödel and the End of Physics. 2002. Available online: https://www.hawking.org.uk/in-words/lectures/godel-and-the-end-of-physics (accessed on 12 August 2022).
- Ben-Ya’acov, U. Gödel’s incompleteness theorem and universal physical theories. J. Phys. Conf. Ser. 2019, 1391, 012067. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noce, C.; Romano, A. Undecidability and Quantum Mechanics. Encyclopedia 2022, 2, 1517-1527. https://doi.org/10.3390/encyclopedia2030103
Noce C, Romano A. Undecidability and Quantum Mechanics. Encyclopedia. 2022; 2(3):1517-1527. https://doi.org/10.3390/encyclopedia2030103
Chicago/Turabian StyleNoce, Canio, and Alfonso Romano. 2022. "Undecidability and Quantum Mechanics" Encyclopedia 2, no. 3: 1517-1527. https://doi.org/10.3390/encyclopedia2030103
APA StyleNoce, C., & Romano, A. (2022). Undecidability and Quantum Mechanics. Encyclopedia, 2(3), 1517-1527. https://doi.org/10.3390/encyclopedia2030103





