Transit Time Determination Based on Similarity-Symmetry Method in Multipath Ultrasonic Gas Flowmeter
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental System Configuration
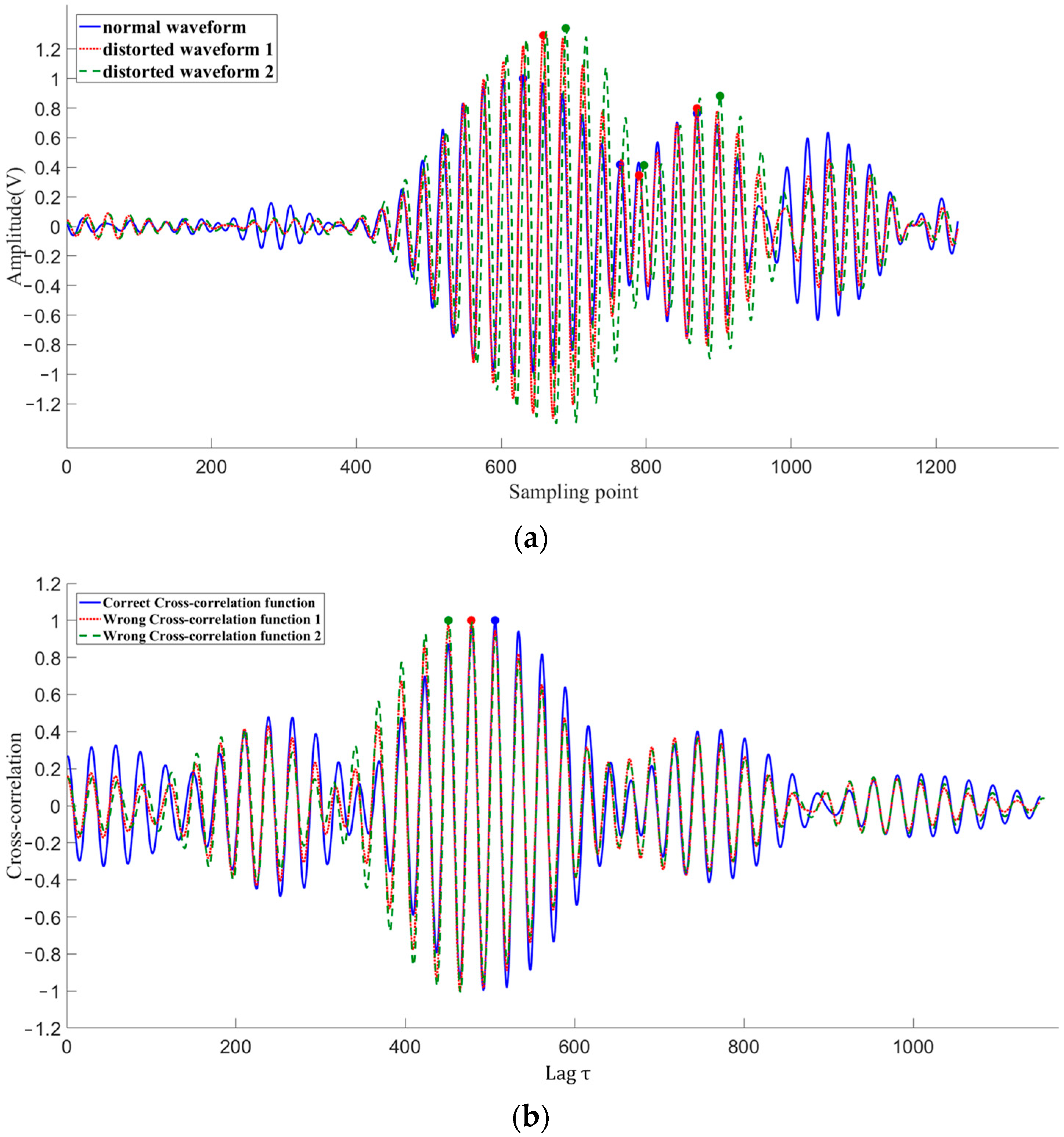
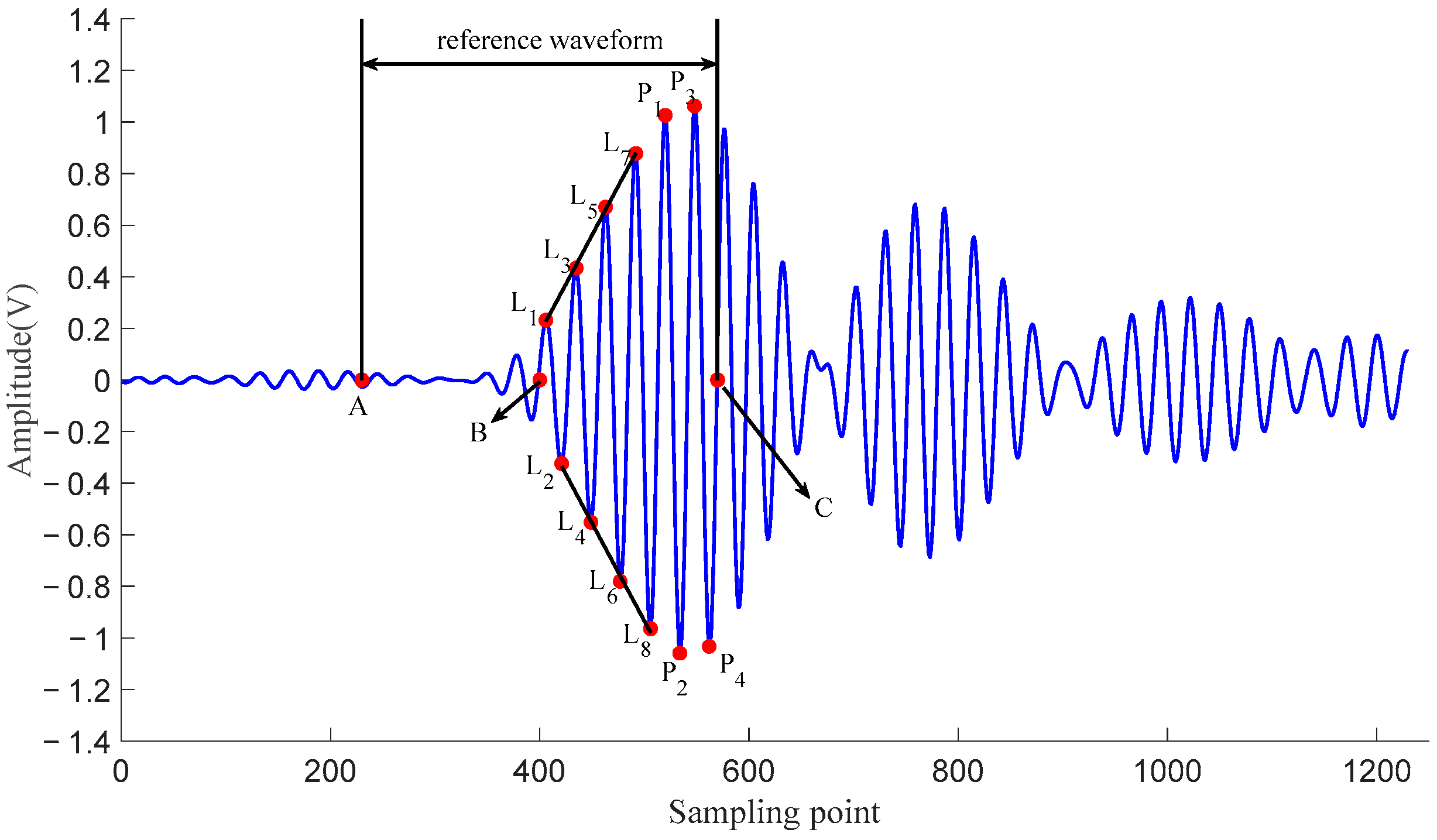
2.2. The Layer Feature of Transit Time by the Cross-Correlation Method
2.3. Transit Time Measurement Based on Similarity-Symmetry Method
2.3.1. Transit Time Measurement Based on Similarity Method
2.3.2. Symmetry of Transit Times
2.4. Symmetry-Based Transit Time Correction
- (1)
- Data Acquisition and Preprocessing: During flow measurement, a sequence of n ≥ 50 downstream and upstream echo signals is continuously acquired. The transit times in both directions are calculated using the similarity method. Outliers in the raw data are first removed according to the 3σ criterion to eliminate gross errors.
- (2)
- Cluster Analysis: The Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm is employed to cluster the remaining downstream and upstream transit times, identifying the dominant measurement modes and their respective cluster centers. For instance, under normal conditions, a path might yield one downstream cluster center, XD, and one upstream cluster center, XU. However, in the presence of cycle-skipping, an additional cluster may appear (e.g., XU2).
- (3)
- Cycle-Skip Detection: Let X0 be the static (zero-flow) transit time for the path. A cycle-skip is detected for a cluster with center XUi if the following symmetry condition is violated:
- (4)
- Deviation Period Calculation: For a cluster identified as erroneous, the number of deviated periods, n, is calculated as:
- (5)
- Data Correction: All transit time values, twrong, within the erroneous cluster are corrected using the formula:
3. Experimental Results
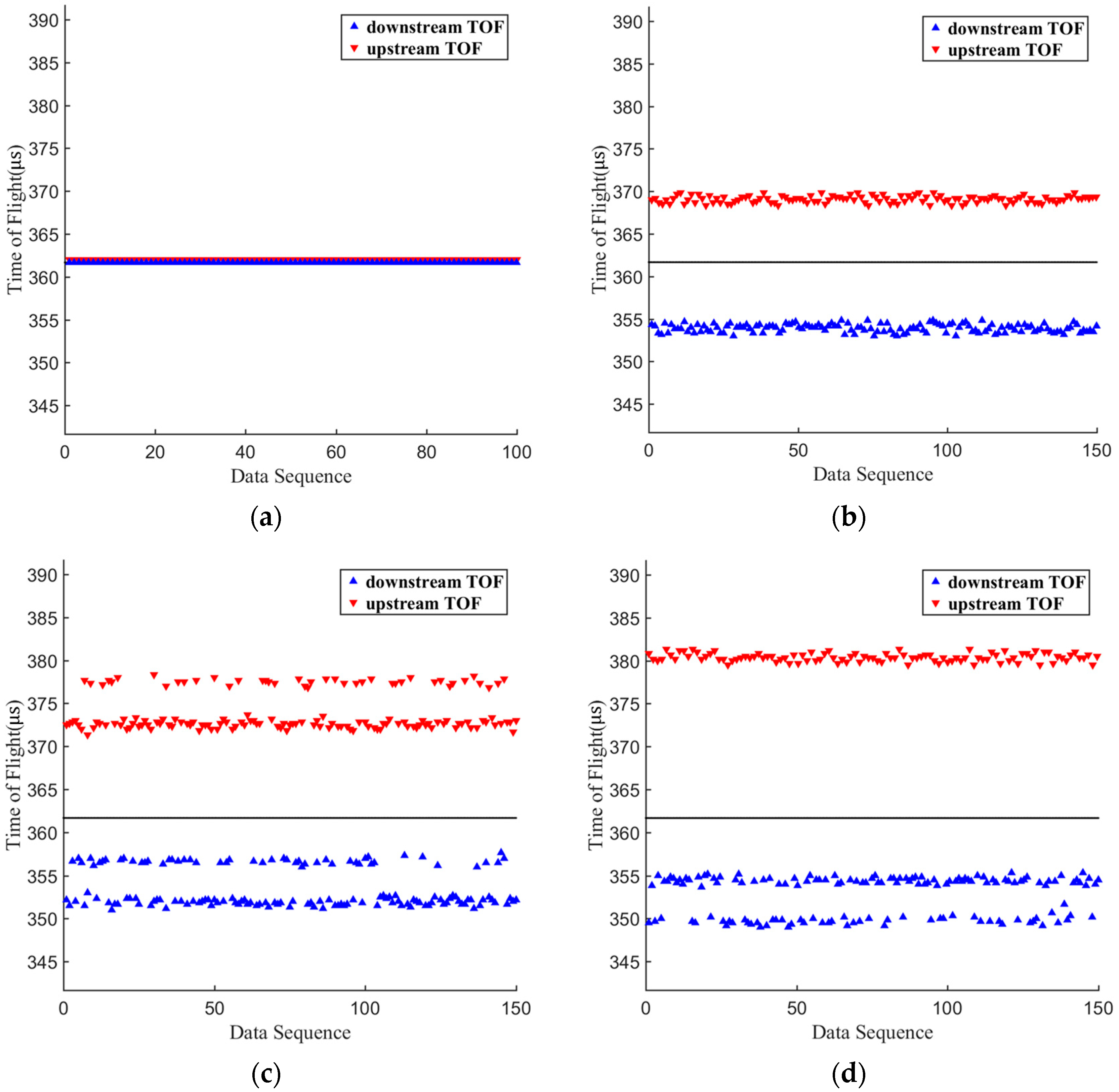
3.1. Measurements of Transit Time
3.2. Flow Rate Measurements Based on Similarity-Symmetry
4. Discussion
4.1. Effect of Waveform Distortion
- (1)
- Flow field effects. High-velocity flow conditions generate complex turbulent patterns that disrupt ultrasonic wave propagation. These disturbances become more pronounced at elevated flow rates, causing measurable waveform alterations.
- (2)
- Probe insertion variability. Installation inconsistencies lead to differential probe penetration depths across measurement paths. This variability creates non-uniform flow field disturbances that contribute to path-specific waveform distortion.
- (3)
- Multipath propagation. Three contributing factors merit consideration: natural beam divergence from finite probe aperture sizes, acoustic path deflection by fluid momentum transfer, and secondary signal reception from wall-reflected wavefronts. The superposition of these propagation modes produces composite waveform distortion.
- (4)
- Transducer performance characteristics. Manufacturing tolerances introduce inter-probe variability in frequency response characteristics, beam pattern consistency, and sensitivity thresholds. Pre-experimental probe pairing and calibration can mitigate these effects.
4.2. Measurement Accuracy at Low Flow Rate
4.3. Cycle-Skip in Both Downstream and Upstream
4.4. Applicability and Limitations
- (1)
- High-capacity gas pipelines where flow rates frequently approach the meter’s maximum capacity.
- (2)
- Applications requiring high accuracy across an extended dynamic range, minimizing the need for frequent calibration or redundancy.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UFM | Ultrasonic Flowmeter |
| UGFM | Ultrasonic Gas Flowmeter |
| TOF | Time-of-flight |
| PC | Personal Computer |
| DSP | Digital Signal Processor |
References
- Lynnworth, L.C.; Liu, Y. Ultrasonic flowmeters: Half-century progress report, 1955–2005. Ultrasonics 2006, 44, 1371–1378. [Google Scholar] [CrossRef] [PubMed]
- Dell’Isola, M.; Cannizzo, M.; Diritti, M. Measurement of high-pressure natural gas flow using ultrasonic flowmeters. Measurement 1997, 20, 75–89. [Google Scholar] [CrossRef]
- Takeda, Y. Ultrasonic Doppler Velocity Profiler for Fluid Flow; Springer: Tokyo, Japan, 2012; pp. 71–103. [Google Scholar]
- Tabin, J. Theoretical analysis of the ultrasonic Doppler flowmeter for measurements of high flow velocities. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 467–471. [Google Scholar] [CrossRef] [PubMed]
- Kupnik, M.; Schroder, A.; O’Leary, P.; Benes, E.; Groschl, M. Adaptive pulse repetition frequency technique for an ultrasonic transit-time gas flowmeter for hot pulsating gases. IEEE Sens. J. 2006, 6, 906–915. [Google Scholar] [CrossRef]
- Mahadeva, D.V.; Baker, R.C.; Woodhouse, J. Further studies of the accuracy of clamp-on transit-time ultrasonic flowmeters for liquids. IEEE Trans. Instrum. Meas. 2009, 58, 1602–1609. [Google Scholar] [CrossRef]
- Grzelak, S.; Kowalski, M.; Czoków, J.; Zielinski, M. High resolution time-interval measurement systems applied to flow measurement. Metrol. Meas. Syst. 2014, 21, 77–84. [Google Scholar] [CrossRef]
- Zhu, R.Z.; Wang, S.Q.; Tang, Z.; Lu, Z.H.; Lin, L.; Yu, X.P. A two-step time-to-digital converter with 5.6-ps resolution and 1-4255-μs measurement range. IEEE Trans. Circuits Syst. II-Express Briefs 2024, 71, 552–556. [Google Scholar] [CrossRef]
- Kobayashi, T.; Shigeta, K.; Fujii, T. Transit-Time Difference Type Ultrasonic Flowmeter. U.S. Patent 6,647,805, 18 November 2003. [Google Scholar]
- Li, W.; Chen, Q.; Wu, J. Double threshold ultrasonic distance measurement technique and its application. Rev. Sci. Instrum. 2014, 85, 044905. [Google Scholar] [CrossRef]
- Lang, T. Zero Crossing Detection of an Ultrasonic Signal with Variable Threshold Value. U.S. Patent 7,543,508 B2, 9 June 2009. [Google Scholar]
- Zhu, W.; Xu, K.; Fang, M.; Shen, Z.; Tian, L. Variable ratio threshold and zero-crossing detection based signal processing method for ultrasonic gas flow meter. Measurement 2017, 103, 343–352. [Google Scholar] [CrossRef]
- Sabatini, A.M. Correlation receivers using Laguerre filter banks for modelling narrowband ultrasonic echoes and estimating their time-of-flights. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 1253–1263. [Google Scholar] [CrossRef]
- Demirli, R.; Saniie, J. Model-based estimation of ultrasonic echoes part I: Analysis and algorithms. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 787–802. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, B.; Li, X.; Liu, D.; Wang, Y.; Huang, Z. A model-based hybrid ultrasonic gas flowmeter. IEEE Sens. J. 2018, 18, 4443–4452. [Google Scholar] [CrossRef]
- Zhou, H.; Ji, T.; Wang, R.; Ge, X.; Tang, X.; Tang, S. Multipath ultrasonic gas flowmeter based on multiple reference waves. Ultrasonics 2018, 82, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Oya, J.; Fort, E.H.; Miguel, D.N.; Rojas, A.S.; Carvajal, R.G.; Chavero, F.M. Cross correlation-based ultrasonic gas flow sensor with temperature compensation. IEEE Trans. Instrum. Meas. 2023, 72, 9509304. [Google Scholar] [CrossRef]
- Kong, L.C.; Zhang, L.; Zhao, N.; Xu, X.H. Time delay study of ultrasonic gas flowmeters based on VMD-Hilbert spectrum and cross-correlation. Sensors 2024, 24, 1462. [Google Scholar] [CrossRef]
- Fang, Z.; Hu, L.; Mao, K.; Chen, W.Y.; Fu, X. Similarity judgment-based double-threshold method for time-of-flight determination in an ultrasonic gas flowmeter. IEEE Trans. Instrum. Meas. 2018, 67, 24–32. [Google Scholar] [CrossRef]
- Liang, L.; Zheng, D.; Wang, M.S.; Liu, H.C.; Mei, J.Q. Research and implementation of automatic gain control method for time-difference ultrasonic gas meter. In Proceedings of the 2024 IEEE International Instrumentation and Measurement Technology Conference, Glasgow, UK, 20–23 May 2024. [Google Scholar]
- Liu, C.; Fang, Z.; Liu, W. A method to avoid the cycle-skip phenomenon in time-of-flight determination for ultrasonic flow measurement. J. Zhejiang Univ.-Sci. A 2021, 22, 695–706. [Google Scholar] [CrossRef]
- Bai, S.Z.; Zhang, J.Y.; Wang, X.; Li, T. A method to solve the periodic deviation in cross correlation measurement of ultrasonic echo signals. In Proceedings of the 2nd International Conference on Frontiers of Sensors Technologies, Shenzhen, China, 14–16 April 2017; pp. 358–362. [Google Scholar]
- Zhao, H.; Peng, L.; Takahashi, T.; Hayashi, T.; Shimizu, K.; Yomamoto, T. ANN based data integration for multi-path ultrasonic flowmeter. IEEE Sens. J. 2014, 14, 362–370. [Google Scholar] [CrossRef]
- Tang, X.; Xie, X.; Zhang, H.; Zhou, H. Data integration for multi-path ultrasonic flowmeter based on Levenberg–Marquardt algorithm. IET Sci. Meas. Technol. 2015, 9, 909–920. [Google Scholar] [CrossRef]
- de Aquino, G.S.; Martins, R.S.; Martins, M.F.; Ramos, R. An overview of computational fluid dynamics as a tool to support ultrasonic flow measurements. Metrology 2025, 5, 11. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Wu, J. Realization of a multipath ultrasonic gas flowmeter based on transit-time technique. Ultrasonics 2014, 54, 285–290. [Google Scholar] [CrossRef] [PubMed]
- AGA Report No. 9: Measurement of Gas by Multipath Ultrasonic Meters, 2nd ed.; American Gas Association: Washington, DC, USA, 2007.

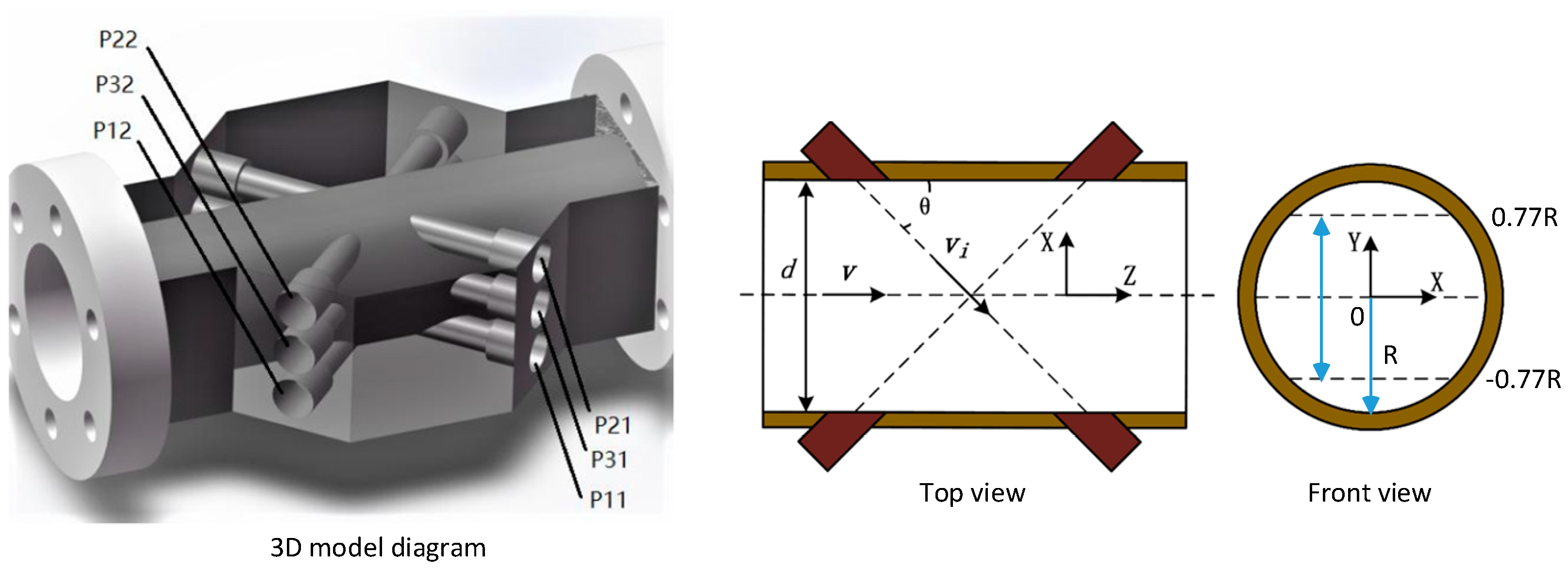


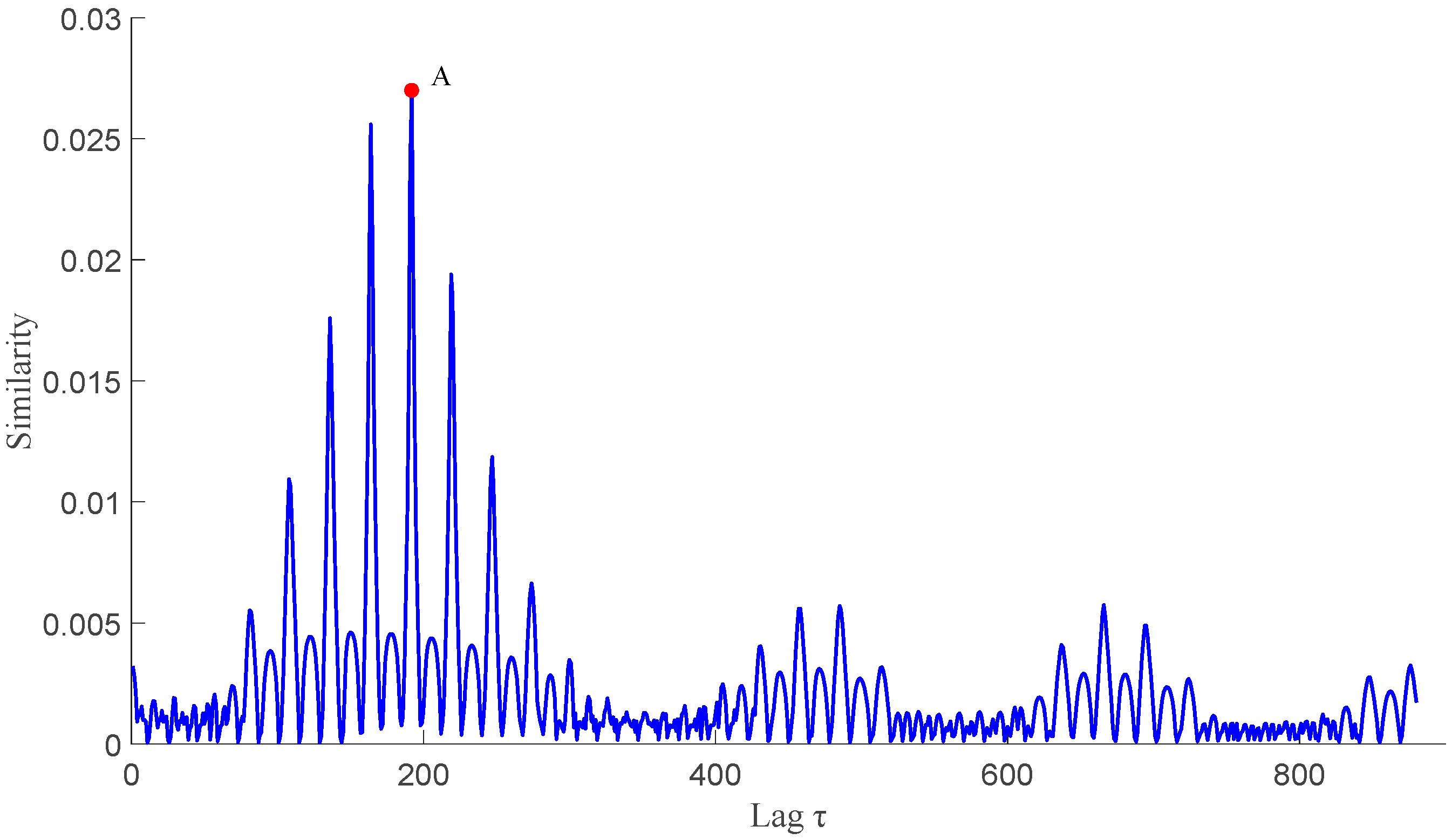

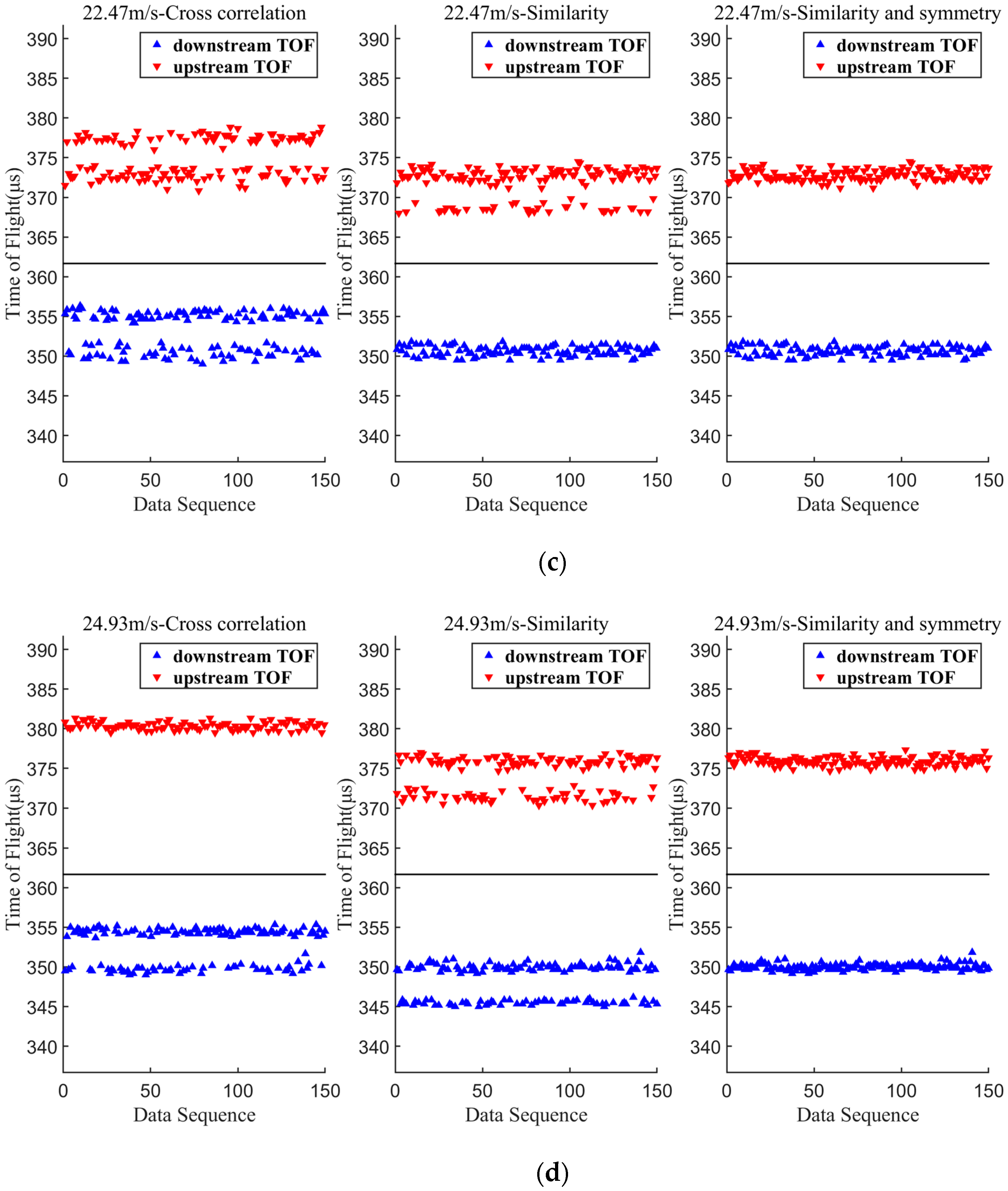
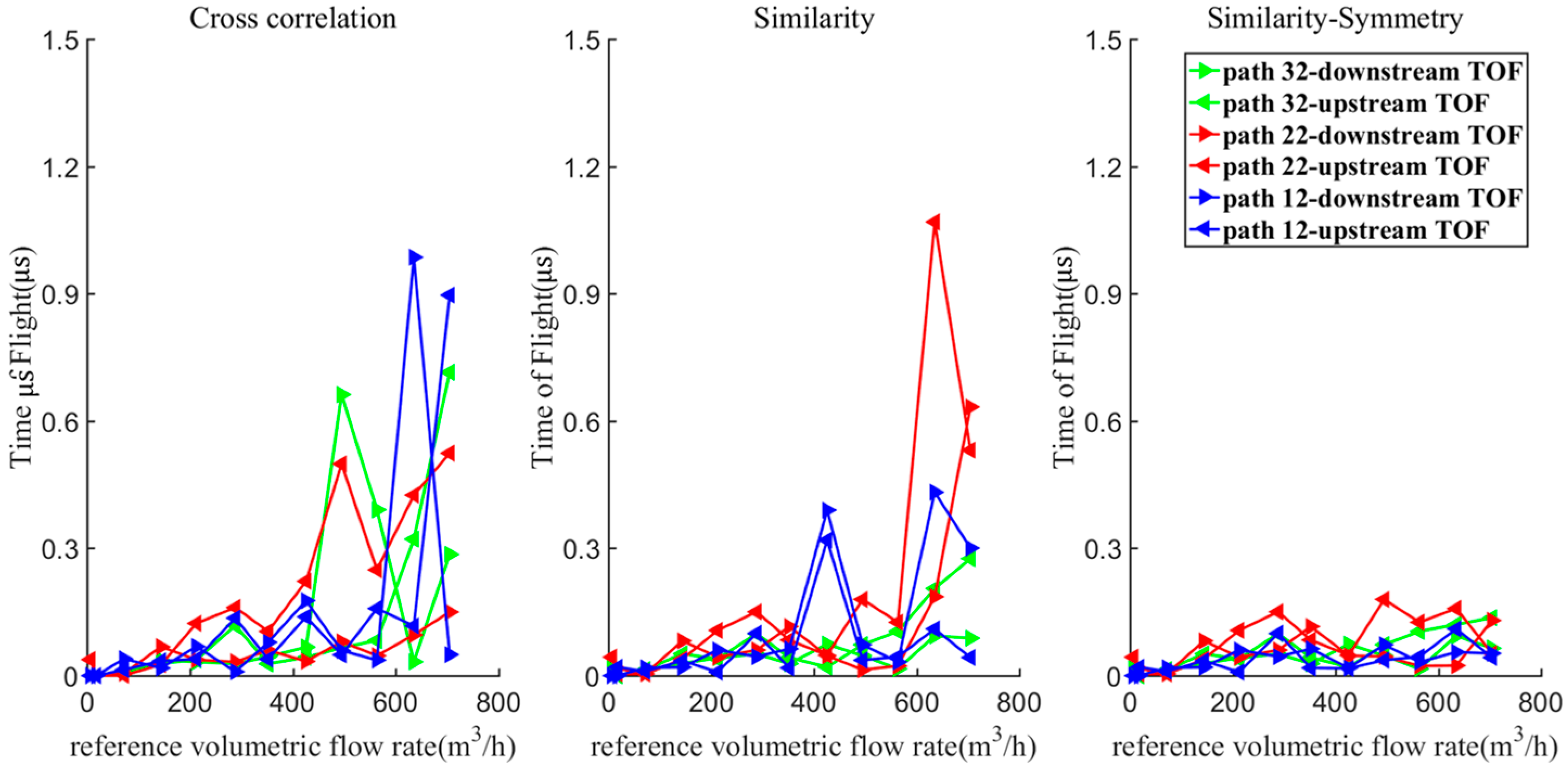
| Path No. | 32 | 31 | 22 | 21 | 12 | 11 |
| Position | 0 | 0 | 0.77R | 0.77R | −0.77R | −0.77R |
| Path Length/mm | 122.37 | 123.1 | 89.38 | 90.71 | 89.37 | 90.75 |
| V (m/s) | Peaks (6, 3) | Peaks (10, 5) | Peaks (8, 4) (Proposed) | |||
|---|---|---|---|---|---|---|
| Downstream | Upstream | Downstream | Upstream | Downstream | Upstream | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.6 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2.5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7.5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12.5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17.5 | 8.67% | 32.67% | 10% | 30% | 0 | 32.67% |
| 20 | 4.67% | 38.0% | 0 | 33.33% | 0 | 0 |
| 22.5 | 3.59% | 69.34% | 70% | 82.67% | 0 | 25.33% |
| 25 | 80% | 76.67% | 74.67% | 26.67% | 40.0% | 37.33% |
| Qr (m3/h) | Cross-Correlation | Similarity | Similarity-Symmetry | |||
|---|---|---|---|---|---|---|
| Qm (m3/h) | Er (%) | Qm (m3/h) | Er (%) | Qm (m3/h) | Er (%) | |
| 6.50 | 11.59 | 78.26 | 14.70 | 126.09 | 7.35 | 13.04 |
| 17.80 | 18.93 | 6.35 | 12.15 | −31.75 | 16.39 | −7.94 |
| 71.78 | 73.76 | 2.76 | 84.50 | 17.72 | 72.06 | 0.39 |
| 143.84 | 144.41 | 0.39 | 138.47 | −3.73 | 143.84 | 0.00 |
| 212.52 | 219.58 | 3.32 | 209.41 | −1.46 | 211.10 | −0.66 |
| 288.25 | 296.16 | 2.75 | 291.08 | 0.98 | 287.12 | −0.39 |
| 351.84 | 323.58 | −8.03 | 355.51 | 1.04 | 354.38 | 0.72 |
| 425.60 | 414.29 | −2.66 | 409.49 | −3.78 | 425.60 | 0.00 |
| 494.55 | 514.05 | 3.94 | 490.59 | −0.80 | 497.09 | 0.51 |
| 562.94 | 546.55 | −2.91 | 562.09 | −0.15 | 561.24 | −0.30 |
| 635.00 | 640.94 | 0.93 | 622.00 | −2.05 | 632.18 | −0.45 |
| 704.52 | 711.30 | 0.96 | 725.72 | 3.01 | 706.22 | 0.24 |
| Method | Maximum Error (%) | Average Error (%) | Computational Complexity | Robustness to Cycle-Skipping | Key Application Scenario |
|---|---|---|---|---|---|
| Proposed Similarity-Symmetry Method | <1.0 (>71.78 m3/h) <0.5 (f > 425 m3/h) | 0.37 (>71.78 m3/h) | Low | Excellent | High-precision, Wide-range, Noisy conditions |
| Standard Cross-Correlation [16] | 1.5 | 0.59 | Low | Poor | Stable, low-noise flow |
| VMD–Hilbert spectrum and cross-correlation [18] | <1.0 (<121 m3/h) <0.5 (>121 m3/h) | 0.40 (>90.91 m3/h) | High | Medium | High-precision, stable, Noisy conditions |
| Variable-ratio threshold Detection [12] | 0.35 | 0.28 | Very low | Poor | Low-cost, stable, low-noise flow |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Liu, Y.; Wu, Y. Transit Time Determination Based on Similarity-Symmetry Method in Multipath Ultrasonic Gas Flowmeter. Metrology 2025, 5, 71. https://doi.org/10.3390/metrology5040071
Zhou H, Liu Y, Wu Y. Transit Time Determination Based on Similarity-Symmetry Method in Multipath Ultrasonic Gas Flowmeter. Metrology. 2025; 5(4):71. https://doi.org/10.3390/metrology5040071
Chicago/Turabian StyleZhou, Hongliang, Yanchu Liu, and Yunxiao Wu. 2025. "Transit Time Determination Based on Similarity-Symmetry Method in Multipath Ultrasonic Gas Flowmeter" Metrology 5, no. 4: 71. https://doi.org/10.3390/metrology5040071
APA StyleZhou, H., Liu, Y., & Wu, Y. (2025). Transit Time Determination Based on Similarity-Symmetry Method in Multipath Ultrasonic Gas Flowmeter. Metrology, 5(4), 71. https://doi.org/10.3390/metrology5040071





