Metrologically Interpretable Soft-Sensing Technique for Non-Invasive Liquid Flow Estimation from Vibration Data
Abstract
1. Introduction
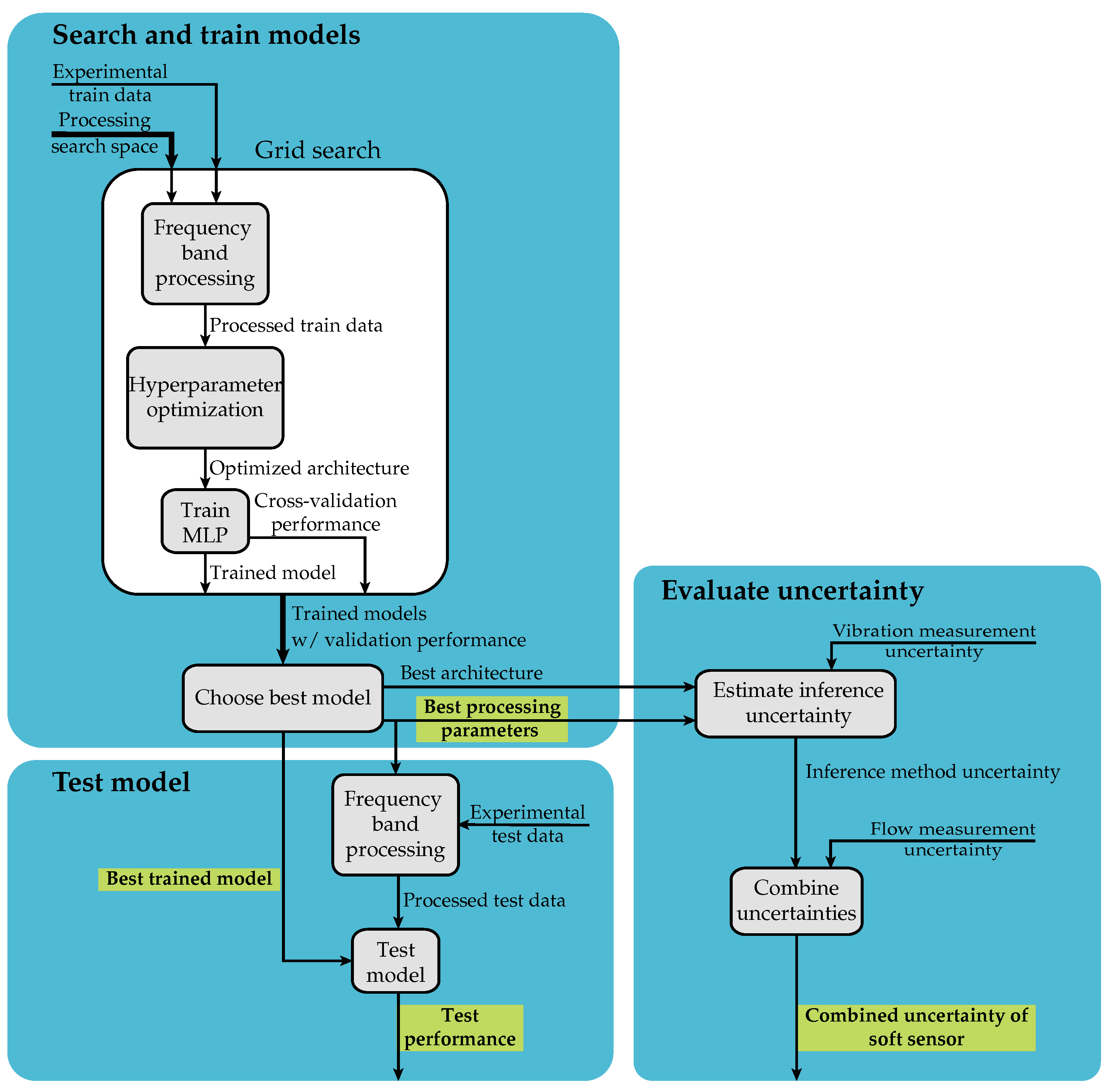
2. Materials and Methods
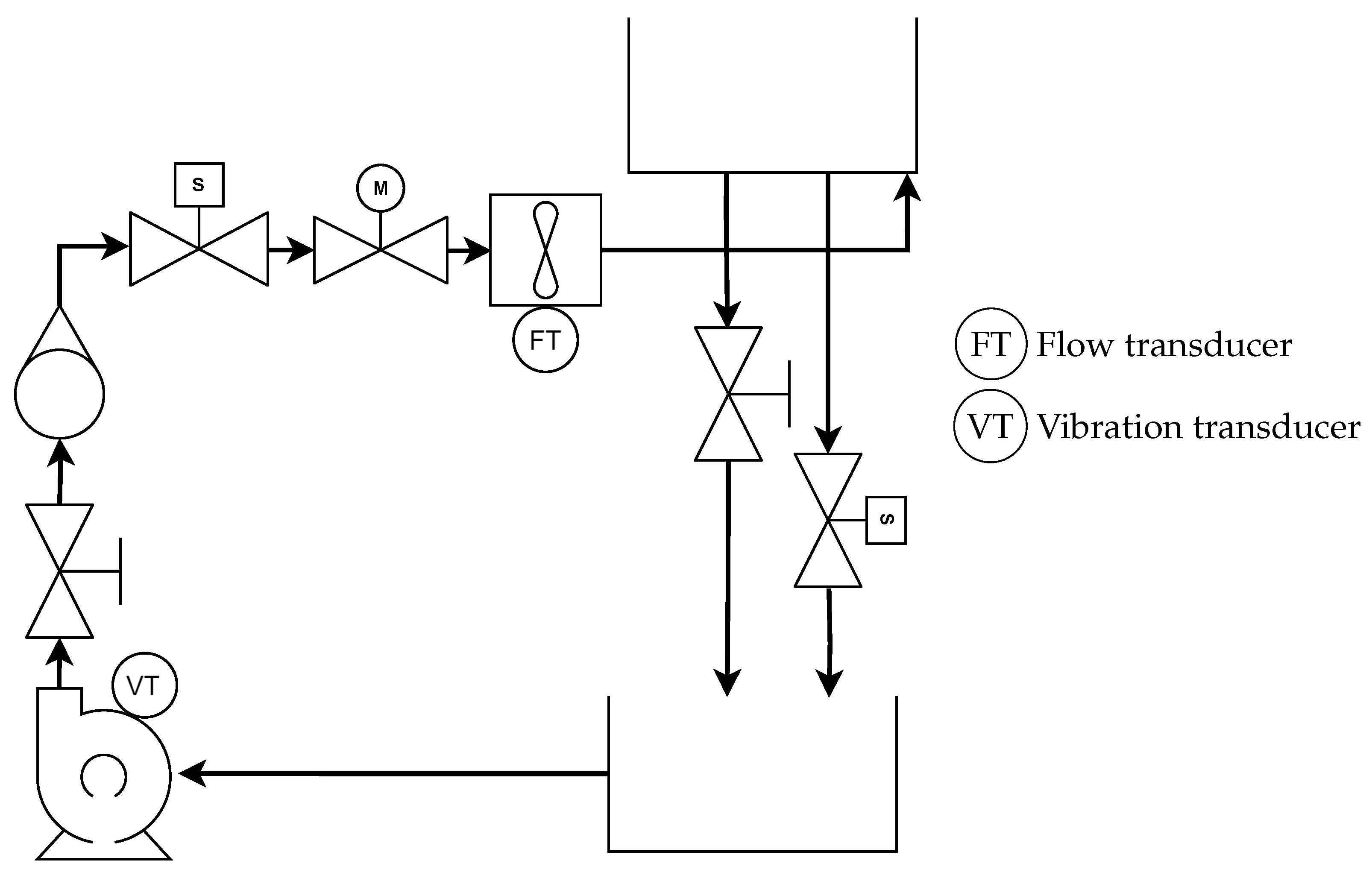
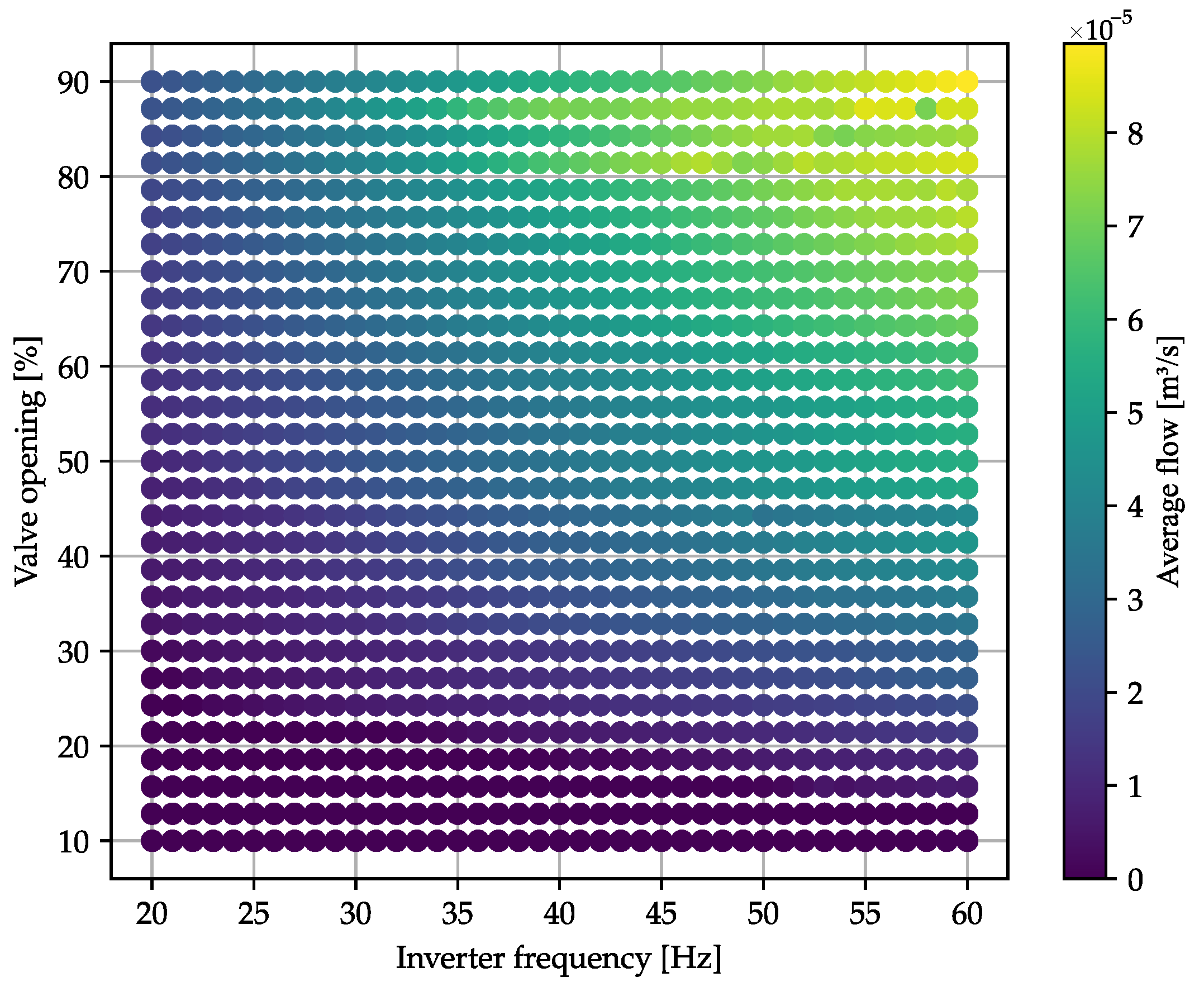
2.1. Experimental Setup
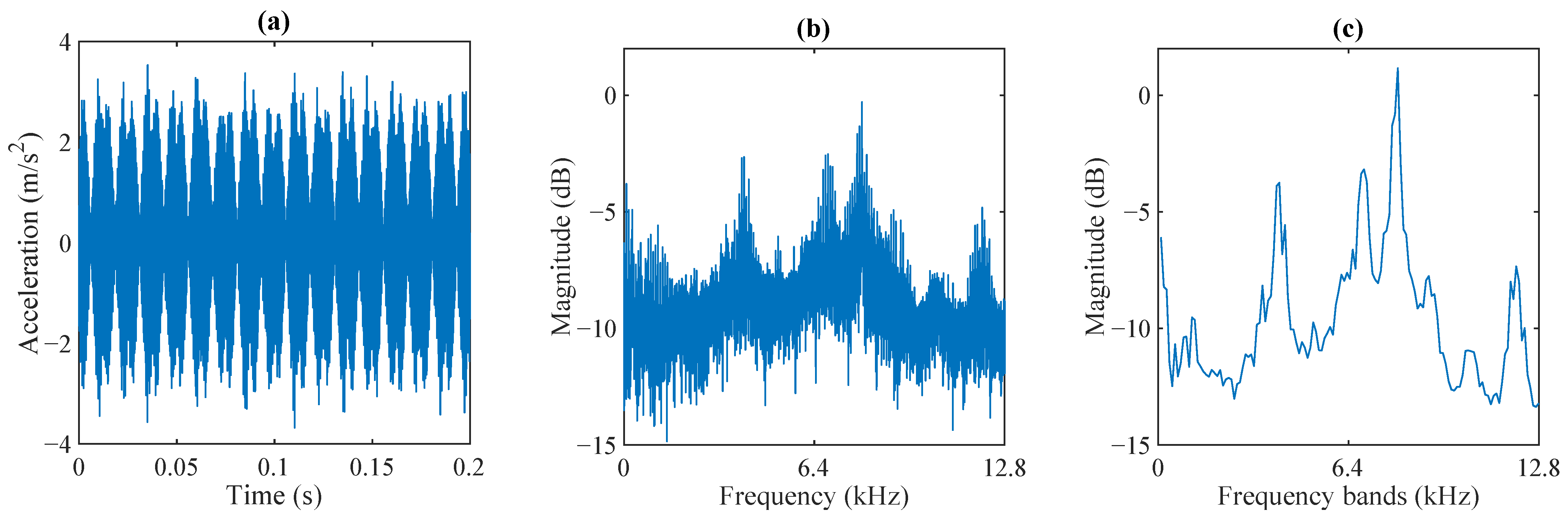
2.2. Vibration Signal Processing
2.3. Vibration Signal Uncertainty Modeling
2.4. Estimation of Regression Model Uncertainty
3. Uncertainty Contributions
3.1. Vibration Measurement Uncertainty
- The measurements for training and using the proposed soft sensor were taken using the same accelerometer. Thus, every vibration acquisition is subject to the same sensitivity, so and are negligible in this context;
- The accelerometer was not moved in between measurements. Also, the dataset was constructed using the same setup. For this reason, is considered to be negligible;
- The accelerometer was coupled using a magnetic base, so no considerable strain was expected for the measurement. Also, the measurements were subjected to the same strain, thus was considered negligible;
- Since the power-band processing method does not require phase information, was also not considered.
3.2. Flow Measurement Uncertainty
4. Results
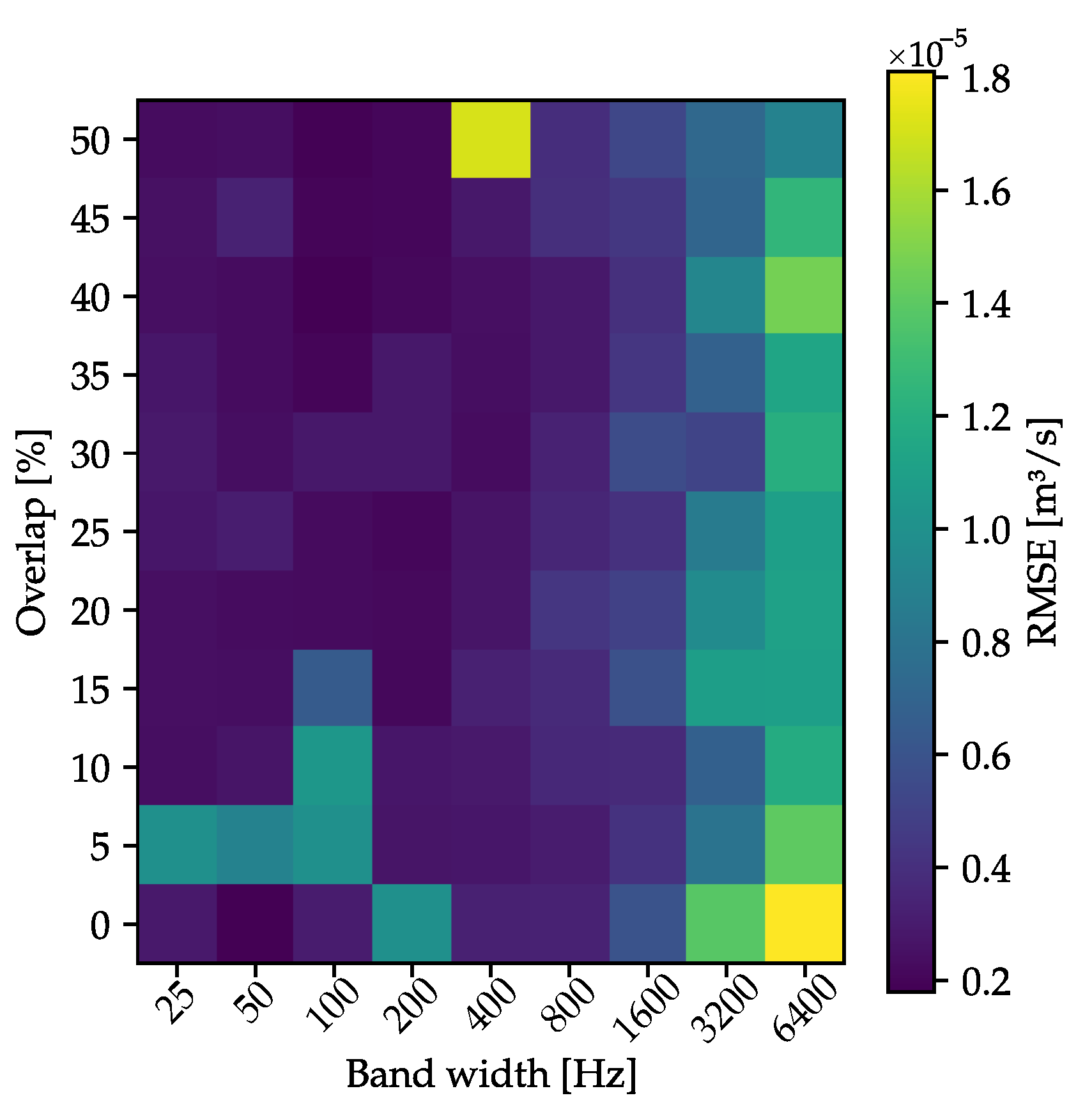
4.1. Grid Search and Hyperparameter Optimization
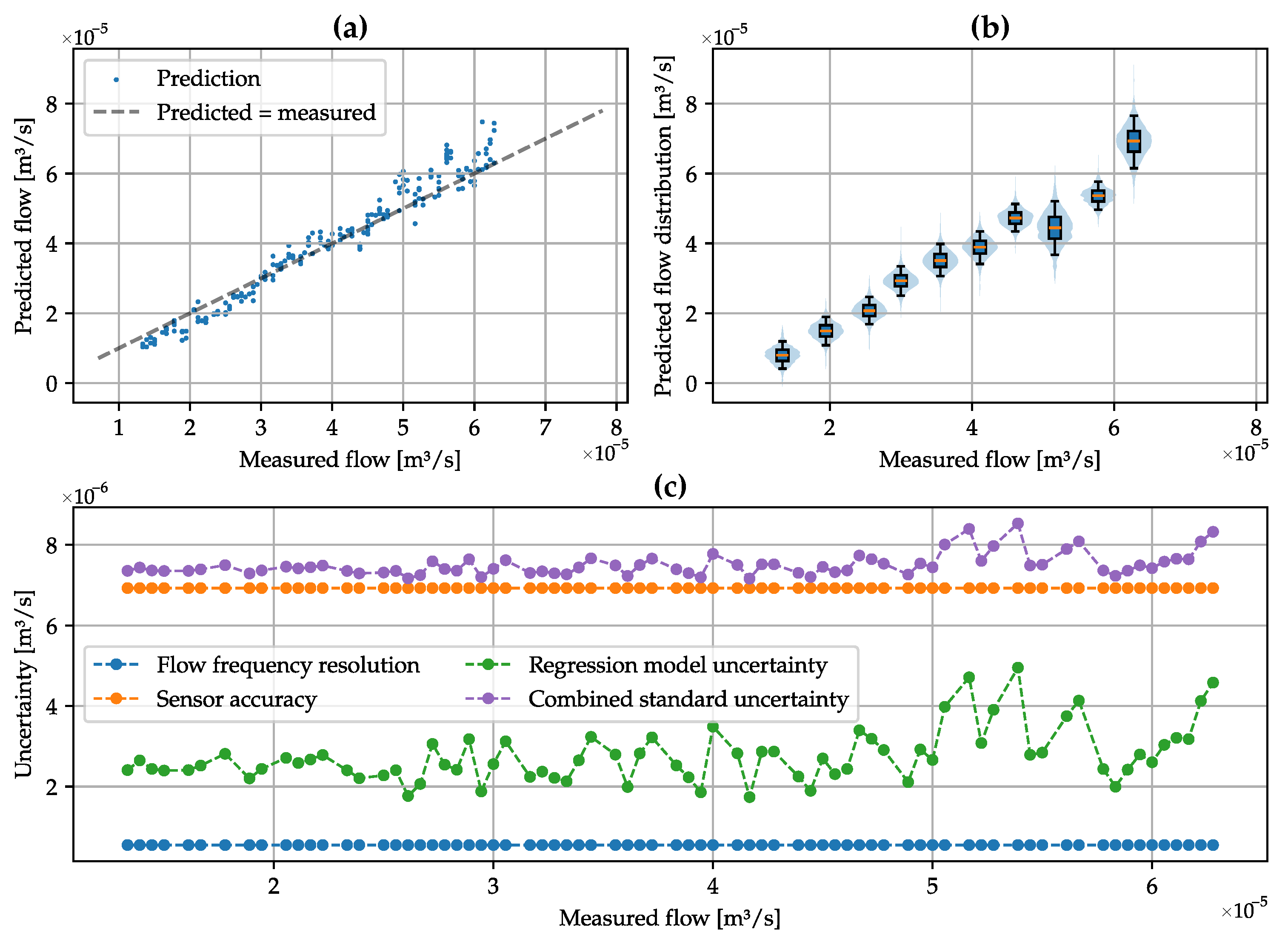
4.2. Uncertainty Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chowdhury, W.S.; Yan, Y.; Coster-Chevalier, M.A.; Liu, J. Mass flowrate measurement of slurry using coriolis flowmeters and data driven modeling. IEEE Trans. Instrum. Meas. 2024, 73, 1–12. [Google Scholar] [CrossRef]
- Baker, R.C. Positive Displacement Flowmeters. In Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications; Cambridge University Press: Cambridge, UK, 2000; pp. 182–214. [Google Scholar]
- Chen, B.; Zhou, Y.; Huang, T.; Ying, S.; Chen, T. Technical features and application of electromagnetic flow meter. In Proceedings of the 2020 International Conference on Communications, Information System and Computer Engineering (CISCE), Kuala Lumpur, Malaysia, 3–5 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Gu, X.; Cegla, F. The uncertainties induced by internal pipe wall roughness on the measurements of clamp-on ultrasonic flow meters. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 16–19 October 2019; pp. 1586–1589. [Google Scholar] [CrossRef]
- Li, Z.; Jin, H.; Dong, S.; Qian, B.; Yang, B.; Chen, X. Semi-supervised ensemble support vector regression based soft sensor for key quality variable estimation of nonlinear industrial processes with limited labeled data. Chem. Eng. Res. Des. 2022, 179, 510–526. [Google Scholar] [CrossRef]
- Mozharovskii, I.; Shevlyagina, S. A hybrid approach to soft sensor development for distillation-in-series plant under input data low variability. Meas. Sci. Technol. 2024, 35, 076211. [Google Scholar] [CrossRef]
- Sangiorgi, L.; Sberveglieri, V.; Carnevale, C.; De Nardi, S.; Nunez-Carmona, E.; Raccagni, S. Data-driven virtual sensing for electrochemical sensors. Sensors 2024, 24, 1396. [Google Scholar] [CrossRef]
- Vijayan, S.V.; Mohanta, H.K.; Rout, B.K.; Pani, A.K. Adaptive soft sensor design using a regression neural network and bias update strategy for non-linear industrial processes. Meas. Sci. Technol. 2023, 34, 085012. [Google Scholar] [CrossRef]
- Karatzas, S.; Merino, J.; Puchkova, A.; Mountzouris, C.; Protopsaltis, G.; Gialelis, J.; Parlikad, A.K. A virtual sensing approach to enhancing personalized strategies for indoor environmental quality and residential energy management. Build. Environ. 2024, 261, 111684. [Google Scholar] [CrossRef]
- Berrie, P. 3-Sensors for automated food process control: An introduction. In Robotics and Automation in the Food Industry; Caldwell, D.G., Ed.; Woodhead Publishing Series in Food Science, Technology and Nutrition; Woodhead Publishing: Cambridge, UK, 2013; pp. 36–74. [Google Scholar] [CrossRef]
- Wang, D.; Kang, Q.; Yang, J.; Gong, J.; Zhang, Q. Research on data-driven model for soft sensing of natural gas production system. Eng. Rep. 2022, 4, e12495. [Google Scholar] [CrossRef]
- Flores, T.K.S.; Villanueva, J.M.M.; Gomes, H.P.; Catunda, S.Y.C. Indirect feedback measurement of flow in a water pumping network employing artificial intelligence. Sensors 2021, 21, 75. [Google Scholar] [CrossRef]
- Chen, T.C.; Alizadeh, S.M.; Alanazi, A.K.; Grimaldo Guerrero, J.W.; Abo-Dief, H.M.; Eftekhari-Zadeh, E.; Fouladinia, F. Using ANN and combined capacitive sensors to predict the void fraction for a two-phase homogeneous fluid independent of the liquid phase type. Processes 2023, 11, 940. [Google Scholar] [CrossRef]
- Ling, T.; Qian, C.; Schiele, G. Towards auto-building of embedded FPGA-based soft sensors for wastewater flow estimation. In Proceedings of the 2024 IEEE Annual Congress on Artificial Intelligence of Things (AIoT), Melbourne, Australia, 24–26 July 2024; pp. 248–249. [Google Scholar] [CrossRef]
- Alencar, G.M.R.d.; Fernandes, F.M.L.; Moura Duarte, R.; Melo, P.F.d.; Cardoso, A.A.; Gomes, H.P.; Villanueva, J.M.M. A soft sensor for flow estimation and uncertainty analysis based on artificial intelligence: A case study of water supply systems. Automation 2024, 5, 106–127. [Google Scholar] [CrossRef]
- Lima, J.S.; Villanueva, J.M.M.; Catunda, S.Y.C. Modeling a virtual flow sensor in a sugar-energy plant using artificial neural network. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zheng, D.; Shao, S.; Liu, A.; Wang, M.; Li, T. Soft measurement model for wet gas flow rate based on ultrasonic and differential pressure sensing. Meas. Sci. Technol. 2024, 35, 055003. [Google Scholar] [CrossRef]
- Lima, R.P.G.; Mauricio Villanueva, J.M.; Gomes, H.P.; Flores, T.K.S. Development of a soft sensor for flow estimation in water supply systems using artificial neural networks. Sensors 2022, 22, 3084. [Google Scholar] [CrossRef]
- Manami, M.; Seddighi, S.; Örlü, R. Deep learning models for improved accuracy of a multiphase flowmeter. Measurement 2023, 206, 112254. [Google Scholar] [CrossRef]
- Andrade, G.M.; de Menezes, D.Q.; Soares, R.M.; Lemos, T.S.; Teixeira, A.F.; Ribeiro, L.D.; Vieira, B.F.; Pinto, J.C. Virtual flow metering of production flow rates of individual wells in oil and gas platforms through data reconciliation. J. Pet. Sci. Eng. 2022, 208, 109772. [Google Scholar] [CrossRef]
- Gilbert Chandra, D.; Vinoth, B.; Srinivasulu Reddy, U.; Uma, G.; Umapathy, M. Recurrent neural network based soft sensor for flow estimation in liquid rocket engine injector calibration. Flow Meas. Instrum. 2022, 83, 102105. [Google Scholar] [CrossRef]
- Chen, X.; Wei, Z.; Wei, C.; He, K. Machine learning approaches to estimate flow rate of drip irrigation emitter based on structure parameters and pressure. J. Phys. Conf. Ser. 2022, 2203, 012017. [Google Scholar] [CrossRef]
- Liu, Z.; Tan, H.; Li, Z.; Jiang, K. Water pump flow monitoring method for air conditioning system based on parameter model. Sustain. Cities Soc. 2020, 61, 102166. [Google Scholar] [CrossRef]
- Ren, W.; Su, W.; Sun, H.; Liu, C.; Lu, X.; Hua, Y. Soft sensing model of flow rate for independent metering valves based on LSTM. In Proceedings of the 2023 9th International Conference on Fluid Power and Mechatronics (FPM), Lanzhou, China, 18–21 August 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Deng, C.; Chen, G.; Liu, S.; Yao, Z.; Zhang, W.; lu, Z.; Wu, S. Operating flow rate prediction of H4 condition in NPP. J. Phys. Conf. Ser. 2023, 2520, 012044. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, H.; Liu, Y.; Peng, L.; Zhang, Y.; Chen, B.; Li, Y. A flow rate estimation method for gas–liquid two-phase flow based on transformer neural network. IEEE Sens. J. 2024, 24, 26902–26913. [Google Scholar] [CrossRef]
- Gandhi, M.; Mathew, A.; Chaudhari, S.; Shaik, R.; Vattem, A. IoT and ML-based water flow estimation using pressure sensor. In Proceedings of the 2023 IEEE 20th India Council International Conference (INDICON), Hyderabad, India, 14–17 December 2023; pp. 892–897. [Google Scholar] [CrossRef]
- Lu, D.; Su, L. A novel flow rate measurement method for fire hose based on vibration signal and neural network. Flow Meas. Instrum. 2024, 97, 102600. [Google Scholar] [CrossRef]
- Gawlikowski, J.; Tassi, C.R.N.; Ali, M.; Lee, J.; Humt, M.; Feng, J.; Kruspe, A.; Triebel, R.; Jung, P.; Roscher, R.; et al. A survey of uncertainty in deep neural networks. Artif. Intell. Rev. 2023, 56, 1513–1589. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wires Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Pacheco, A.L.S.; Flesch, R.C.C.; Flesch, C.A.; Iervolino, L.A.; Barros, V.T. Tool based on artificial neural networks to obtain cooling capacity of hermetic compressors through tests performed in production lines. Expert Syst. Appl. 2022, 194, 116494–116510. [Google Scholar] [CrossRef]
- Lathi, B.P. Linear Systems and Signals, 2nd ed.; Oxford University Press, Inc.: New York, NY, USA, 2009. [Google Scholar]
- ISO. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; Vol. JJCGM 100:2008; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- PCB Piezotronics Inc. Product Data: ICP Accelerometer Model 352C65. 2024. Available online: https://www.pcb.com/contentStore/docs/pcb_corporate/vibration/products/specsheets/m352c65_l.pdf (accessed on 10 November 2024).
- National Instruments Corp. NI-9234 Specifications. 2023. Available online: https://www.ni.com/docs/en-US/bundle/ni-9234-specs/page/specs.html (accessed on 10 November 2024).
- Sea Electronics Inc. YF-S201 Flow Sensor Specifications. 2020. Available online: https://abg.baidu.com/view/a7390ef3ba0d4a7302763adf (accessed on 10 November 2024).
- Machado, J.P.Z.; Thaler, G.; Pacheco, A.L.S.; Flesch, R.C.C. Impact of angular speed calculation methods from encoder measurements on the test uncertainty of electric motor efficiency. Metrology 2024, 4, 164–180. [Google Scholar] [CrossRef]
- Dinardo, G.; Fabbiano, L.; Vacca, G.; Lay-Ekuakille, A. Vibrational signal processing for characterization of fluid flows in pipes. Measurement 2018, 113, 196–204. [Google Scholar] [CrossRef]
- Campagna, M.M.; Dinardo, G.; Fabbiano, L.; Vacca, G. Fluid flow measurements by means of vibration monitoring. Meas. Sci. Technol. 2015, 26, 115306. [Google Scholar] [CrossRef]
- Evans, R.P.; Blotter, J.D.; Stephens, A.G. Flow rate measurements using flow-induced pipe vibration. J. Fluids Eng. Trans. ASME 2004, 126, 280–285. [Google Scholar] [CrossRef]
- Venkata, S.K.; Navada, B.R. Estimation of flow rate through analysis of pipe vibration. Acta Mech. Autom. 2018, 12, 294–300. [Google Scholar] [CrossRef]

| Year/Publication | Industry(ies) or Sector(s) | Application (Estimation of the) | Technology(ies) |
|---|---|---|---|
| 2023 [13] | Chemical, oil and gas, and petrochemical | Void fraction for a two-phase fluid | Multilayer perceptron (MLP) network |
| 2024 [14] | Wastewater treatment | Flow rates within the system | MLP network |
| 2024 [15] | Water service | Flow rates within the system | Long Short-Term Memory (LSTM) network |
| 2022 [16] | Sugar-energy plant | Flow of broth out of a decanter | MLP network |
| 2024 [17] | Chemical, oil and gas, and electric power | Wet gas flow rate | Support vector machine (SVM), decision tree, and MLP network |
| 2022 [18] | Water service | Flow rates within the system | MLP network |
| 2023 [19] | Chemical, oil and gas, pharmaceutical, food, mining, and biomedical | Oil and gas two-phase flow rate | Nonlinear autoregressive network |
| 2022 [20] | Oil and gas | Production flow of individual wells | Phenomenological models/data reconciliation |
| 2022 [21] | Aerospace | Injector propellants flow rate | Recurrent neural network |
| 2022 [22] | Smart agriculture | Flow rate of drip irrigation emitter | k-nearest neighbor, MLP, SVM, and radial base function |
| 2020 [23] | Air conditioning | Water pump flow rate | Parameter model |
| 2023 [24] | Hydraulic systems | Electro-hydraulic valve flow rate | LSTM network |
| 2023 [25] | Nuclear power plant | Volume flow rate of H4 condition | Mathematical model |
| 2024 [26] | Pharmaceutical, oil and gas, and petrochemical | Gas–liquid two-phase flow rate | Transformer neural network |
| 2023 [27] | Water service | Flow rates within the system | Convolutional neural network, support vector regression (SVR), and linear regression |
| 2024 [28] | Public safety | Flow rates within the system | Convolutional neural network |
| Symbol | Component | Uncertainty |
|---|---|---|
| Sensitivity deviation | ±10% | |
| Nonlinearity | ≤1% | |
| Transverse sensitivity | ≤5% | |
| Temperature sensitivity deviation | ||
| Broadband resolution | 0.0015 /s2 | |
| Base strain sensitivity | <0.05 (/s2)/με | |
| Frequency response | between 0.5 and 10,000 Hz between 0.3 and 12,000 Hz dB between 0.2 and 20,000 Hz | |
| Phase response | ||
| Spectral noise | 588 (μ/s2)/ at 1 Hz 157 (μ/s2)/ at 10 Hz 49 (μ/s2)/ at 100 Hz 14.7 (μ/s2)/ at 1000 Hz |
| Range [Hz] | p | k |
|---|---|---|
| 1 to 10 | 588.00 | |
| 10 to 100 | 503.04 | |
| >100 | 544.44 |
| Symbol | Component | Uncertainty |
|---|---|---|
| Reading accuracy | ||
| Temperature gain drift | 16 | |
| Analog converter resolution | 24 bits | |
| Master timebase accuracy | ppm maximum |
| Symbol | Component |
|---|---|
| Frequency estimation method uncertainty | |
| Sensor accuracy |
| Parameter | Search Space |
|---|---|
| Band width [] | {25,50,100,200,…,6400} |
| Band overlap [%] | {0,5,10,15,…,50} |
| Hyperparameter | Optimization Space |
|---|---|
| Number of hidden layers | {1,2,3,4,5} |
| Neurons per hidden layer | {1,2,3,…,500} |
| Activation function for hidden layers | {linear, sigmoid, tanh, ReLu} |
| Regularization factor | (0,] |
| Processing Method | Cross-Validation RMSE [m³/s] | Test RMSE [m³/s] |
|---|---|---|
| RMS [38] | 2.066 × 10−5 | 1.443 × 10−5 |
| Fundamental amplitude [39] | 2.184 × 10−5 | 1.278 × 10−5 |
| Fundamental amplitude and frequency [40] | 1.890 × 10−5 | 0.994 × 10−5 |
| RMS and fundamental amplitude and frequency | 1.974 × 10−5 | 1.128 × 10−5 |
| FFT (Full spectrum) | 0.738 × 10−5 | 0.802 × 10−5 |
| FFT (under 100 Hz) [41] | 1.636 × 10−5 | 1.419 × 10−5 |
| Power band | 0.182 × 10−5 | 0.389 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thaler, G.; Machado, J.P.Z.; Flesch, R.C.C.; Pacheco, A.L.S. Metrologically Interpretable Soft-Sensing Technique for Non-Invasive Liquid Flow Estimation from Vibration Data. Metrology 2025, 5, 6. https://doi.org/10.3390/metrology5010006
Thaler G, Machado JPZ, Flesch RCC, Pacheco ALS. Metrologically Interpretable Soft-Sensing Technique for Non-Invasive Liquid Flow Estimation from Vibration Data. Metrology. 2025; 5(1):6. https://doi.org/10.3390/metrology5010006
Chicago/Turabian StyleThaler, Gabriel, João P. Z. Machado, Rodolfo C. C. Flesch, and Antonio L. S. Pacheco. 2025. "Metrologically Interpretable Soft-Sensing Technique for Non-Invasive Liquid Flow Estimation from Vibration Data" Metrology 5, no. 1: 6. https://doi.org/10.3390/metrology5010006
APA StyleThaler, G., Machado, J. P. Z., Flesch, R. C. C., & Pacheco, A. L. S. (2025). Metrologically Interpretable Soft-Sensing Technique for Non-Invasive Liquid Flow Estimation from Vibration Data. Metrology, 5(1), 6. https://doi.org/10.3390/metrology5010006






