An Artificial Neural Network-Based Approach to Improve Non-Destructive Asphalt Pavement Density Measurement with an Electrical Density Gauge
Abstract
1. Introduction
2. Non-Destructive Devices
2.1. Nuclear Density Gauge (NDG)
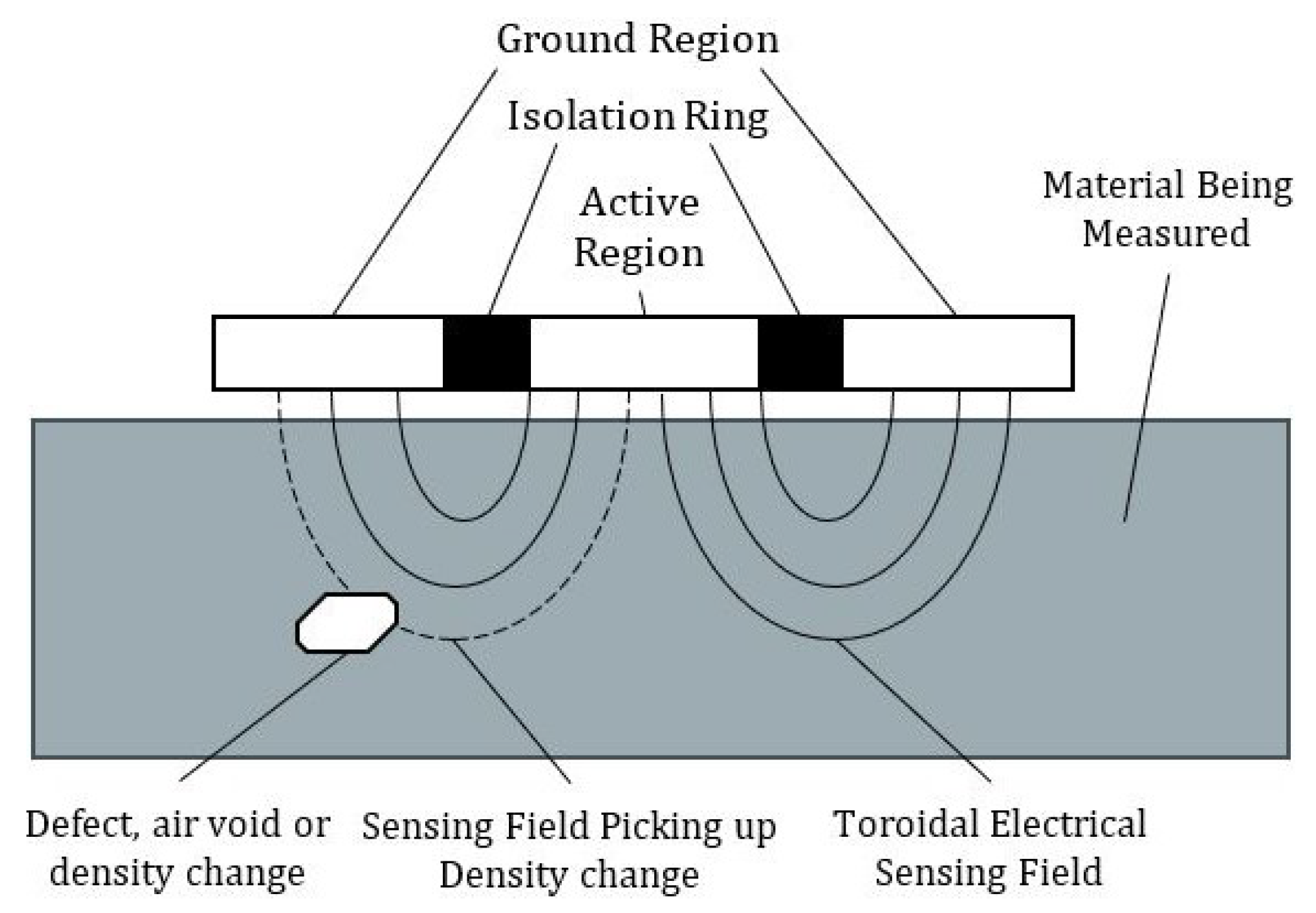
2.2. Electrical Density Gauge (EDG)
3. Artificial Neural Network (ANN)
3.1. Structure of the ANN Models
3.2. Training Process
3.3. Levenberg-Marquardt (LM) Algorithm
3.4. Bayesian Regularization (BR) Algorithm
3.5. Scaled Conjugate Gradient (SCG) Algorithm
3.6. Collected Data and Input Data
4. Methodology
5. Results and Discussion
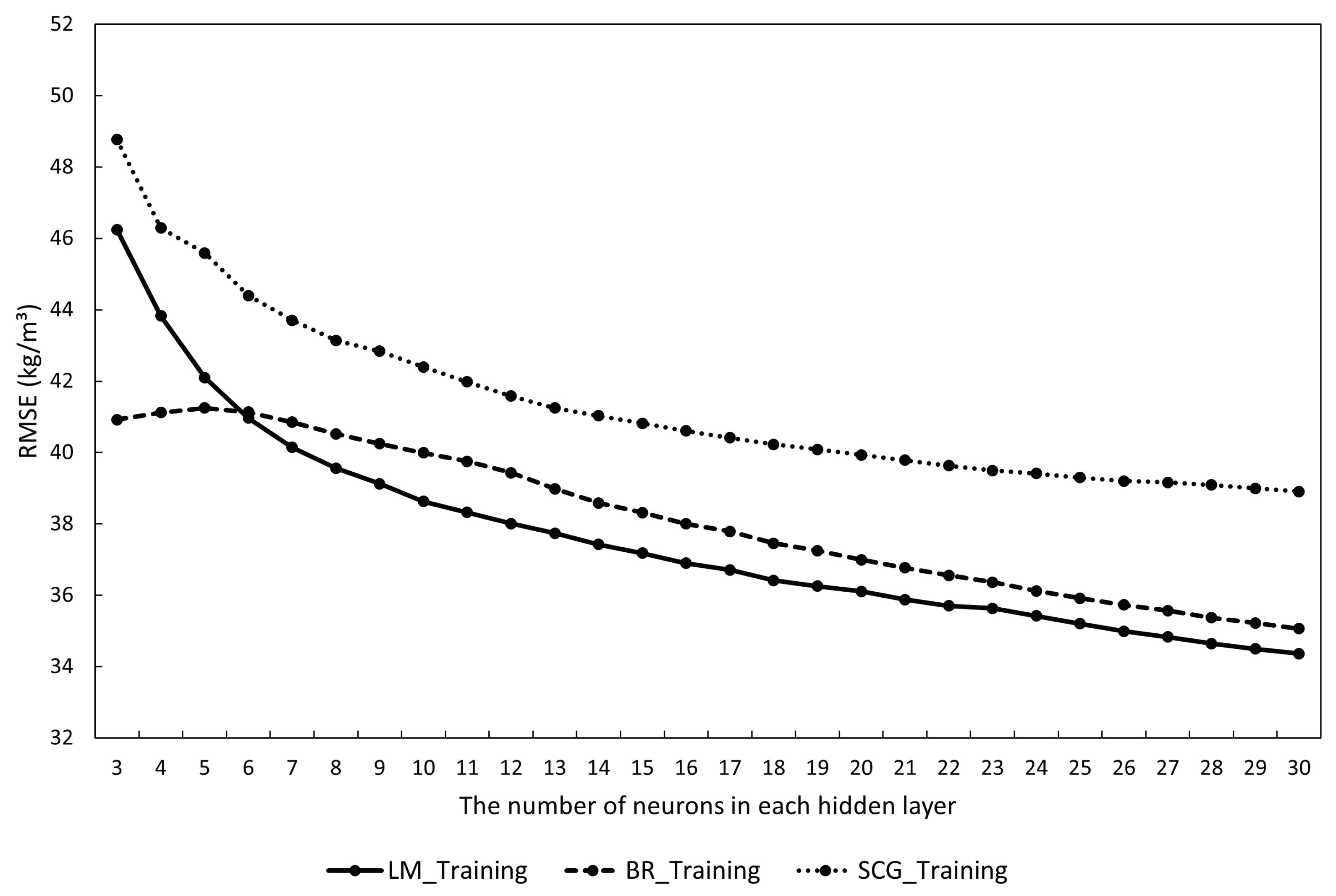
5.1. The Average Accuracy of the Three Models
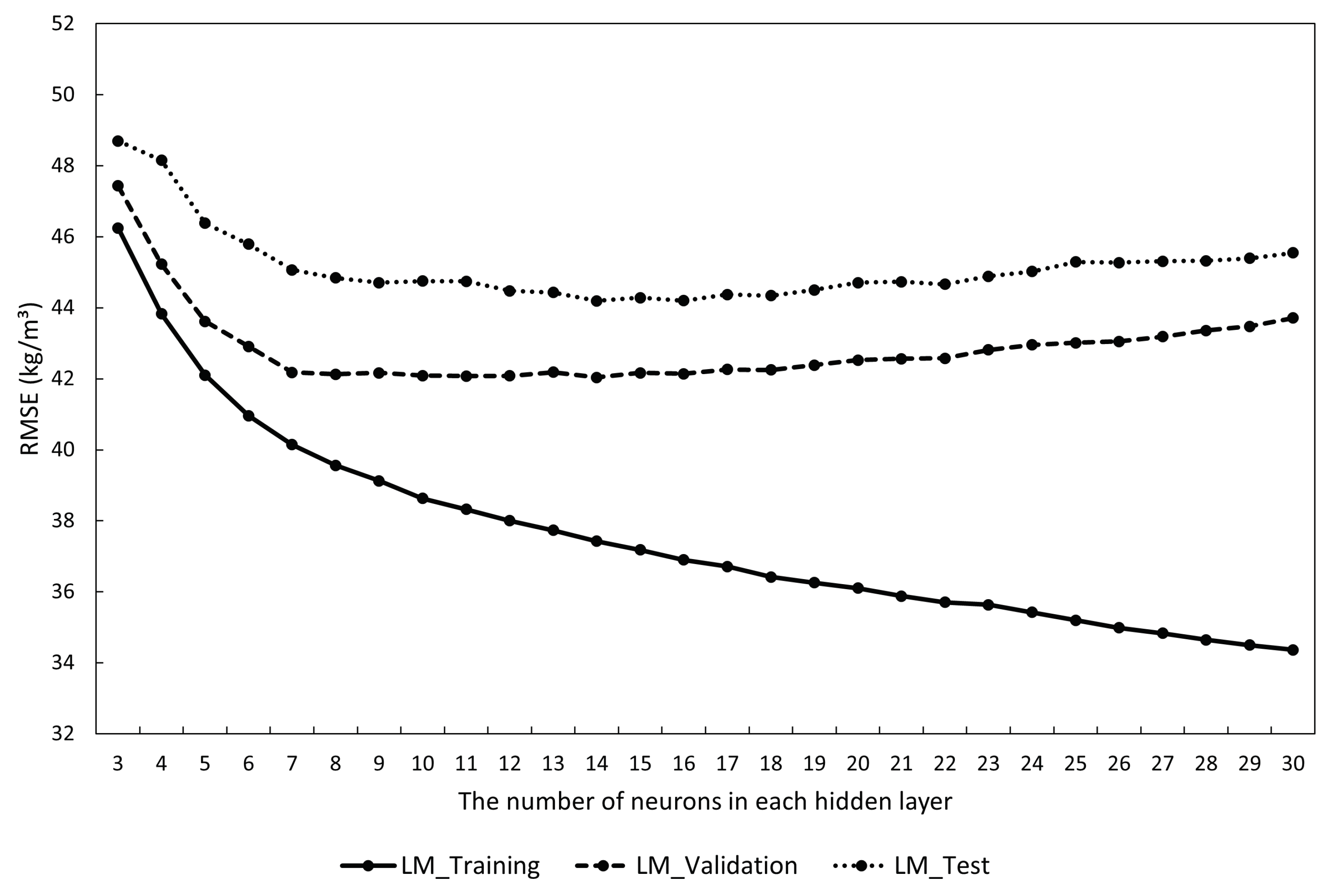
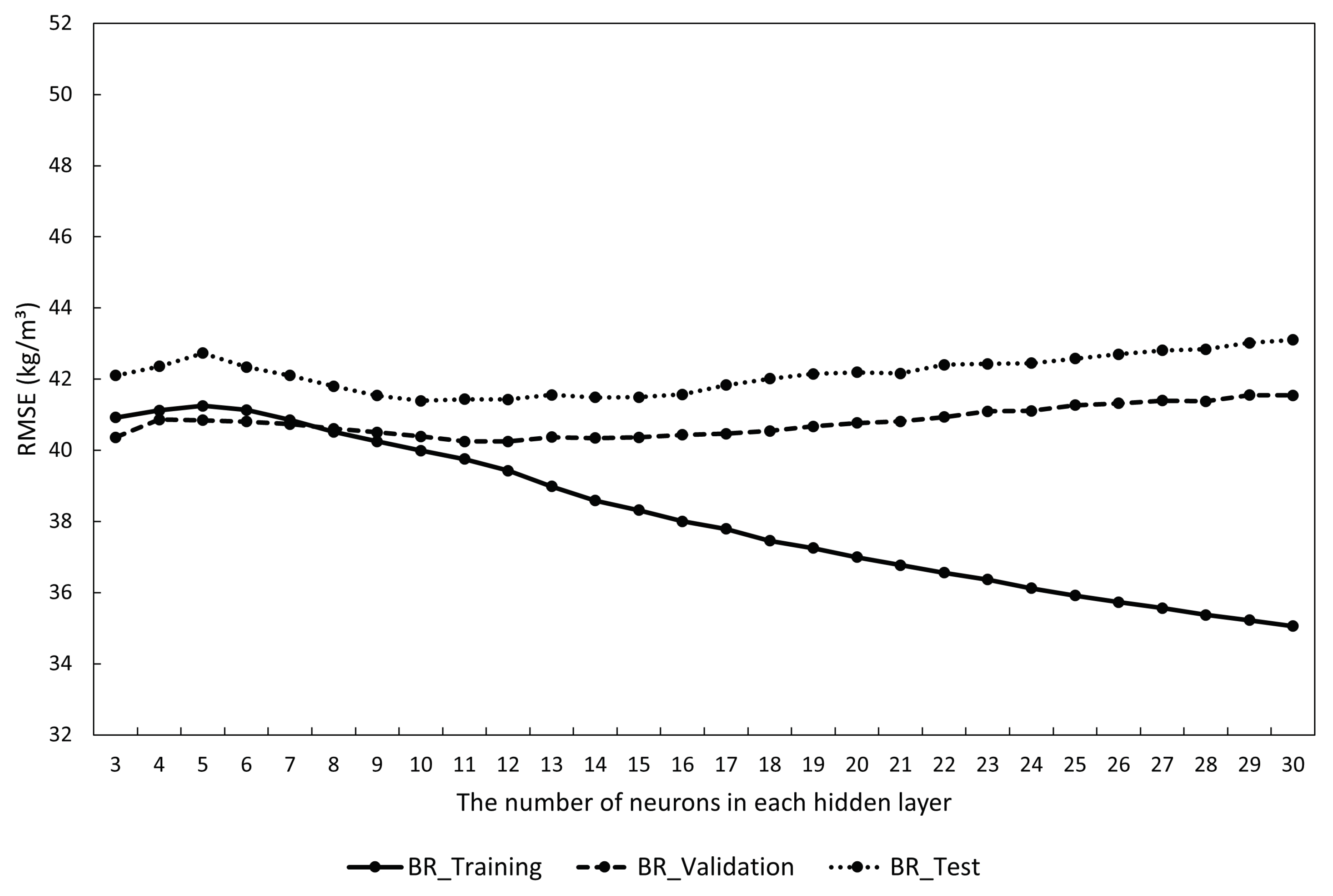
5.2. The Average Generalization Capability of the Three Models
5.3. The Average Training Time of the Three Models
5.4. The Performances of the Optimized Models
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, M.; Huang, L.; Al-Jumaily, A. Methods for Asphalt Road Density Measurement: A Review. In Proceedings of the 2021 27th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Shanghai, China, 26–28 November 2021; pp. 269–274. [Google Scholar] [CrossRef]
- AS/NZS 2891.1.2; Methods of Sampling and Testing Asphalt—Method 1.2: Sampling—Coring Method. Standards New Zealand: Wellington, New Zealand, 2020.
- AS/NZS 2891.9.1; Methods of Sampling and Testing Asphalt—Method 9.1: Determination of Bulk Density of Compacted Asphalt—Waxing Procedure. Standards New Zealand: Wellington, New Zealand, 2022.
- AS/NZS 2891.9.2; Methods of Sampling and Testing Asphalt—Part 9.2: Determination of Bulk Density of Compacted Asphalt—Presaturation Method. Standards New Zealand: Wellington, New Zealand, 2022.
- ASTM D2726/D2726M; Standard Test Method for Bulk Specific Gravity and Density of Non-Absorptive Compacted Asphalt Mixtures. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2019.
- ASTM D2950/D2950M; Standard Test Method for Density of Asphalt Mixtures in Place by Nuclear Methods. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2022.
- AASHTO T355; Standard Method of Test for In-Place Density of Asphalt Mixtures by Nuclear Methods. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2022.
- ASTM D7113/D7113M; Standard Test Method for Density of Bituminous Paving Mixtures in Place by the Electromagnetic Surface Contact Methods. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2020.
- AASHTO T343; Standard Method of Test for Density of In-Place Hot Mix Asphalt (HMA) Pavement by Electronic Surface Contact Devices. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2020.
- Helal, J.; Sofi, M.; Mendis, P. Non-Destructive Testing of Concrete: A Review of Methods. Electron. J. Struct. Eng. 2015, 14, 97–105. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2698. [Google Scholar] [CrossRef]
- Rubio, J.d.J. Stability Analysis of the Modified Levenberg–Marquardt Algorithm for the Artificial Neural Network Training. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3510–3524. [Google Scholar] [CrossRef] [PubMed]
- Sariev, E.; Germano, G. Bayesian regularized artificial neural networks for the estimation of the probability of default. Quant. Financ. 2020, 20, 311–328. [Google Scholar] [CrossRef]
- Yuan, G.; Li, T.; Hu, W. A conjugate gradient algorithm for large-scale nonlinear equations and image restoration problems. Appl. Numer. Math. 2020, 147, 129–141. [Google Scholar] [CrossRef]
- Yan, Z.; Zhong, S.; Lin, L.; Cui, Z. Adaptive Levenberg–Marquardt Algorithm: A New Optimization Strategy for Levenberg–Marquardt Neural Networks. Mathematics 2021, 9, 2176. [Google Scholar] [CrossRef]
- Wang, B.; Zhong, S.; Lee, T.L.; Fancey, K.S.; Mi, J. Non-destructive testing and evaluation of composite materials/structures: A state-of-the-art review. Adv. Mech. Eng. 2020, 12, 1687814020913761. [Google Scholar] [CrossRef]
- Gupta, M.; Khan, M.A.; Butola, R.; Singari, M. Advances in applications of Non-Destructive Testing (NDT): A review. Adv. Mater. Process. Technol. 2022, 8, 2286–2307. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Mumali, F. Artificial neural network-based decision support systems in manufacturing processes: A systematic literature review. Comput. Ind. Eng. 2022, 165, 107964. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Grum, M.; Gronau, N.; Heine, M.; Timm, I. Construction of a Concept of Neuronal Modeling; Springer Gabler: Wiesbaden, Germany, 2020. [Google Scholar]
- Kaloev, M.; Krastev, G. Comprehensive Review of Benefits from the Use of Neuron Connection Pruning Techniques During the Training Process of Artificial Neural Networks in Reinforcement Learning: Experimental Simulations in Atari Games. In Proceedings of the 2023 7th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkiye, 26–28 October 2023. [Google Scholar] [CrossRef]
- Kim, S. Improving ANN Training with Approximation Techniques for ROCOF Trajectory Estimation. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; pp. 1–6. [Google Scholar]
- Krajinski, P.; Sourkounis, C. Training of an ANN Feed-Forward Regression Model to Predict Wind Farm Power Production for the Purpose of Active Wake Control. In Proceedings of the 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; pp. 954–959. [Google Scholar]
- Tuan Hoang, A.; Nižetić, S.; Chyuan Ong, H.; Tarelko, W.; Viet Pham, V.; Hieu Le, T.; Quang Chau, M.; Phuong Nguyen, X. A review on application of artificial neural network (ANN) for performance and emission characteristics of diesel engine fueled with biodiesel-based fuels. Sustain. Energy Technol. Assess. 2021, 47, 101416. [Google Scholar] [CrossRef]
- Khakhar, P.; Dubey, R.K. Chapter 5—The integrity of machine learning algorithms against software defect prediction. In Artificial Intelligence and Machine Learning for EDGE Computing; Pandey, R., Khatri, S.K., Kumar Singh, N., Verma, P., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 65–74. [Google Scholar] [CrossRef]







| The Number of Neurons in Each Hidden Layer | LM-ANN Model | |||
|---|---|---|---|---|
| Training Time (s) | RMSE (kg/m3) | |||
| Training | Validation | Test | ||
| 3 | 0.086 | 46.25 | 47.44 | 48.70 |
| 4 | 0.078 | 43.83 | 45.23 | 48.16 |
| 5 | 0.078 | 42.10 | 43.62 | 46.38 |
| 6 | 0.075 | 40.96 | 42.91 | 45.79 |
| 7 | 0.075 | 40.14 | 42.18 | 45.06 |
| 8 | 0.076 | 39.56 | 42.13 | 44.84 |
| 9 | 0.077 | 39.12 | 42.17 | 44.71 |
| 10 | 0.077 | 38.63 | 42.09 | 44.75 |
| 11 | 0.079 | 38.32 | 42.07 | 44.75 |
| 12 | 0.080 | 38.00 | 42.09 | 44.48 |
| 13 | 0.081 | 37.73 | 42.19 | 44.43 |
| 14 | 0.082 | 37.42 | 42.04 | 44.19 |
| 15 | 0.085 | 37.18 | 42.17 | 44.29 |
| 16 | 0.087 | 36.90 | 42.14 | 44.20 |
| 17 | 0.092 | 36.71 | 42.26 | 44.37 |
| 18 | 0.098 | 36.42 | 42.25 | 44.34 |
| 19 | 0.104 | 36.26 | 42.39 | 44.50 |
| 20 | 0.111 | 36.10 | 42.53 | 44.71 |
| 21 | 0.123 | 35.88 | 42.57 | 44.73 |
| 22 | 0.130 | 35.71 | 42.58 | 44.66 |
| 23 | 0.141 | 35.63 | 42.81 | 44.89 |
| 24 | 0.152 | 35.42 | 42.96 | 45.02 |
| 25 | 0.169 | 35.20 | 43.01 | 45.29 |
| 26 | 0.184 | 34.99 | 43.05 | 45.27 |
| 27 | 0.204 | 34.83 | 43.19 | 45.31 |
| 28 | 0.224 | 34.65 | 43.36 | 45.32 |
| 29 | 0.250 | 34.50 | 43.48 | 45.39 |
| 30 | 0.279 | 34.36 | 43.71 | 45.55 |
| The Number of Neurons in Each Hidden Layer | BR-ANN Model | |||
|---|---|---|---|---|
| Training Time (s) | RMSE (kg/m3) | |||
| Training | Validation | Test | ||
| 3 | 0.095 | 40.92 | 40.36 | 42.10 |
| 4 | 0.092 | 41.12 | 40.87 | 42.36 |
| 5 | 0.093 | 41.25 | 40.84 | 42.73 |
| 6 | 0.093 | 41.13 | 40.80 | 42.34 |
| 7 | 0.094 | 40.85 | 40.73 | 42.10 |
| 8 | 0.097 | 40.52 | 40.61 | 41.80 |
| 9 | 0.098 | 40.25 | 40.50 | 41.54 |
| 10 | 0.100 | 39.99 | 40.39 | 41.39 |
| 11 | 0.102 | 39.75 | 40.25 | 41.43 |
| 12 | 0.103 | 39.43 | 40.25 | 41.43 |
| 13 | 0.105 | 38.98 | 40.37 | 41.56 |
| 14 | 0.108 | 38.59 | 40.34 | 41.49 |
| 15 | 0.113 | 38.32 | 40.36 | 41.49 |
| 16 | 0.116 | 38.00 | 40.43 | 41.57 |
| 17 | 0.123 | 37.79 | 40.47 | 41.84 |
| 18 | 0.132 | 37.46 | 40.54 | 42.01 |
| 19 | 0.143 | 37.25 | 40.67 | 42.15 |
| 20 | 0.154 | 37.00 | 40.77 | 42.19 |
| 21 | 0.170 | 36.77 | 40.81 | 42.16 |
| 22 | 0.183 | 36.56 | 40.94 | 42.41 |
| 23 | 0.200 | 36.37 | 41.09 | 42.43 |
| 24 | 0.223 | 36.12 | 41.11 | 42.45 |
| 25 | 0.248 | 35.92 | 41.27 | 42.58 |
| 26 | 0.277 | 35.73 | 41.32 | 42.70 |
| 27 | 0.310 | 35.57 | 41.40 | 42.81 |
| 28 | 0.346 | 35.37 | 41.37 | 42.84 |
| 29 | 0.388 | 35.22 | 41.55 | 43.02 |
| 30 | 0.447 | 35.06 | 41.54 | 43.10 |
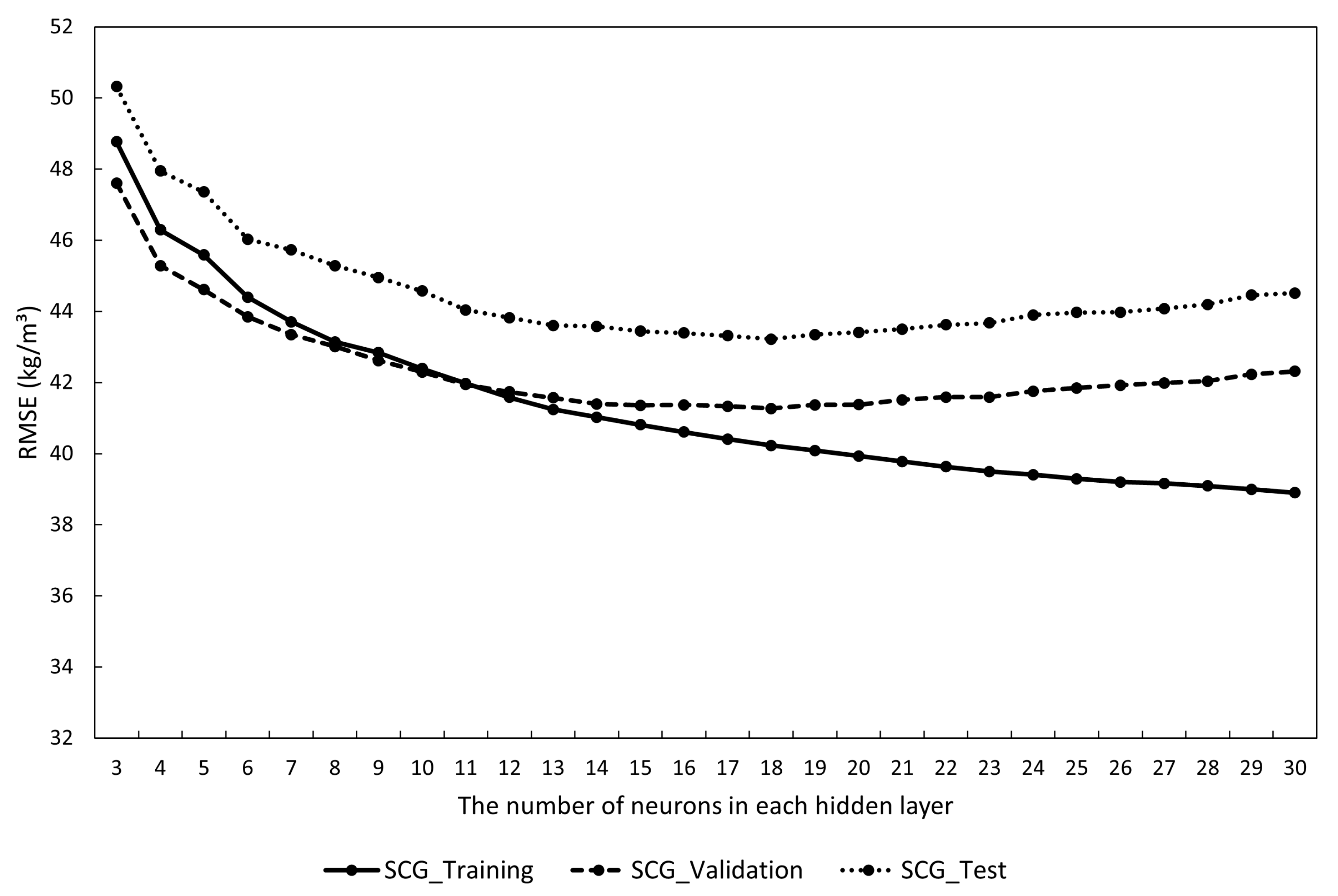
| The Number of Neurons in Each Hidden Layer | SCG-ANN Model | |||
|---|---|---|---|---|
| Training Time (s) | RMSE (kg/m3) | |||
| Training | Validation | Test | ||
| 3 | 0.070 | 48.77 | 47.61 | 50.32 |
| 4 | 0.068 | 46.29 | 45.28 | 47.95 |
| 5 | 0.067 | 45.59 | 44.61 | 47.36 |
| 6 | 0.067 | 44.40 | 43.85 | 46.03 |
| 7 | 0.066 | 43.70 | 43.35 | 45.73 |
| 8 | 0.066 | 43.14 | 43.01 | 45.28 |
| 9 | 0.066 | 42.84 | 42.61 | 44.96 |
| 10 | 0.066 | 42.39 | 42.30 | 44.58 |
| 11 | 0.066 | 41.98 | 41.94 | 44.04 |
| 12 | 0.066 | 41.58 | 41.74 | 43.82 |
| 13 | 0.066 | 41.25 | 41.57 | 43.61 |
| 14 | 0.067 | 41.03 | 41.39 | 43.58 |
| 15 | 0.067 | 40.81 | 41.36 | 43.45 |
| 16 | 0.067 | 40.61 | 41.38 | 43.39 |
| 17 | 0.067 | 40.41 | 41.34 | 43.32 |
| 18 | 0.067 | 40.23 | 41.27 | 43.22 |
| 19 | 0.068 | 40.09 | 41.37 | 43.35 |
| 20 | 0.068 | 39.93 | 41.38 | 43.41 |
| 21 | 0.068 | 39.78 | 41.52 | 43.51 |
| 22 | 0.068 | 39.63 | 41.59 | 43.62 |
| 23 | 0.069 | 39.50 | 41.59 | 43.68 |
| 24 | 0.069 | 39.41 | 41.75 | 43.90 |
| 25 | 0.070 | 39.30 | 41.85 | 43.97 |
| 26 | 0.070 | 39.20 | 41.92 | 43.98 |
| 27 | 0.070 | 39.16 | 41.98 | 44.08 |
| 28 | 0.070 | 39.09 | 42.04 | 44.20 |
| 29 | 0.071 | 39.00 | 42.23 | 44.46 |
| 30 | 0.071 | 38.90 | 42.32 | 44.52 |
| The Number of Neurons in Each Hidden Layer | LM-ANN Models | |||||
|---|---|---|---|---|---|---|
| R Value | RMSE (kg/m3) | |||||
| Training | Validation | Test | Training | Validation | Test | |
| 9 | 0.943 | 0.923 | 0.924 | 37.61 | 41.73 | 43.32 |
| 14 | 0.953 | 0.942 | 0.916 | 34.25 | 40.61 | 41.54 |
| The Number of Neurons in Each Hidden Layer | BR-ANN Models | |||||
|---|---|---|---|---|---|---|
| R Value | RMSE (kg/m3) | |||||
| Training | Validation | Test | Training | Validation | Test | |
| 5 | 0.938 | 0.930 | 0.945 | 38.26 | 36.06 | 39.42 |
| 10 | 0.937 | 0.912 | 0.954 | 38.52 | 37.95 | 37.82 |
| 16 | 0.947 | 0.945 | 0.919 | 36.41 | 38.55 | 37.52 |
| The Number of Neurons in Each Hidden Layer | SCG-ANN Models | |||||
|---|---|---|---|---|---|---|
| R Value | RMSE (kg/m3) | |||||
| Training | Validation | Test | Training | Validation | Test | |
| 8 | 0.928 | 0.930 | 0.951 | 41.44 | 39.86 | 37.08 |
| 14 | 0.948 | 0.947 | 0.931 | 36.81 | 35.33 | 34.97 |
| 18 | 0.947 | 0.940 | 0.952 | 35.17 | 36.86 | 38.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Huang, L. An Artificial Neural Network-Based Approach to Improve Non-Destructive Asphalt Pavement Density Measurement with an Electrical Density Gauge. Metrology 2024, 4, 304-322. https://doi.org/10.3390/metrology4020019
Li M, Huang L. An Artificial Neural Network-Based Approach to Improve Non-Destructive Asphalt Pavement Density Measurement with an Electrical Density Gauge. Metrology. 2024; 4(2):304-322. https://doi.org/10.3390/metrology4020019
Chicago/Turabian StyleLi, Muyang, and Loulin Huang. 2024. "An Artificial Neural Network-Based Approach to Improve Non-Destructive Asphalt Pavement Density Measurement with an Electrical Density Gauge" Metrology 4, no. 2: 304-322. https://doi.org/10.3390/metrology4020019
APA StyleLi, M., & Huang, L. (2024). An Artificial Neural Network-Based Approach to Improve Non-Destructive Asphalt Pavement Density Measurement with an Electrical Density Gauge. Metrology, 4(2), 304-322. https://doi.org/10.3390/metrology4020019






