Spectroscopic Reflectometry for Optimizing 3D Through-Silicon-Vias Process
Abstract
:1. Introduction
2. Spectroscopic Reflectometer System and Sample Details
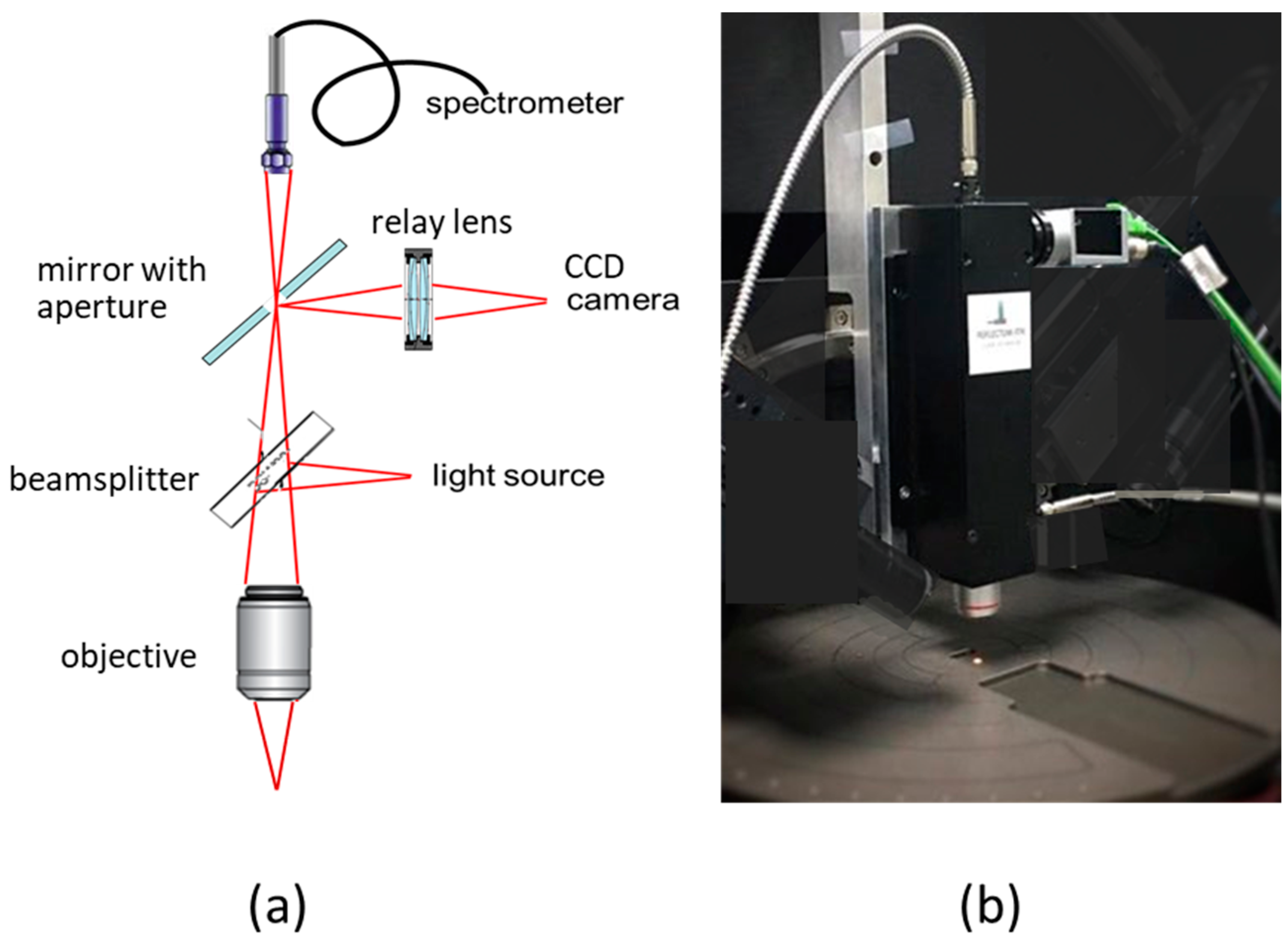
2.1. Reflectometer System Design
2.2. Sample Details
3. Theoretical Model
3.1. Basic Theoretical Model of Reflectance Spectrum
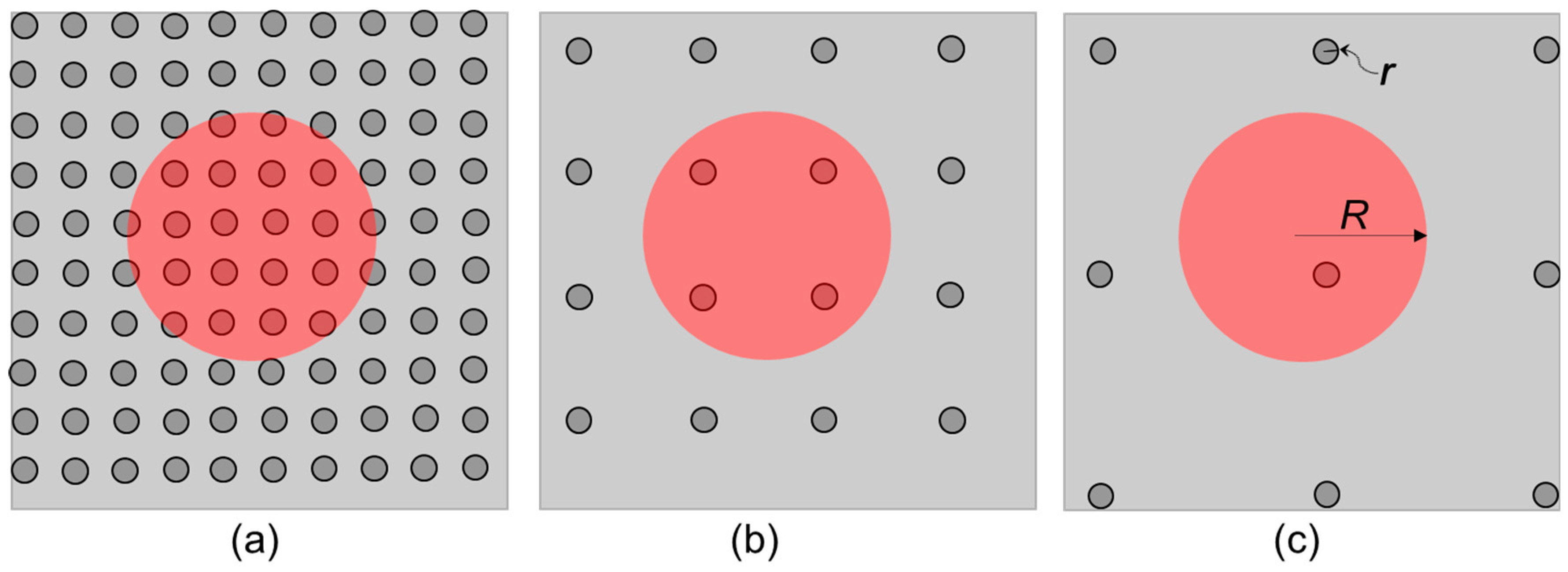
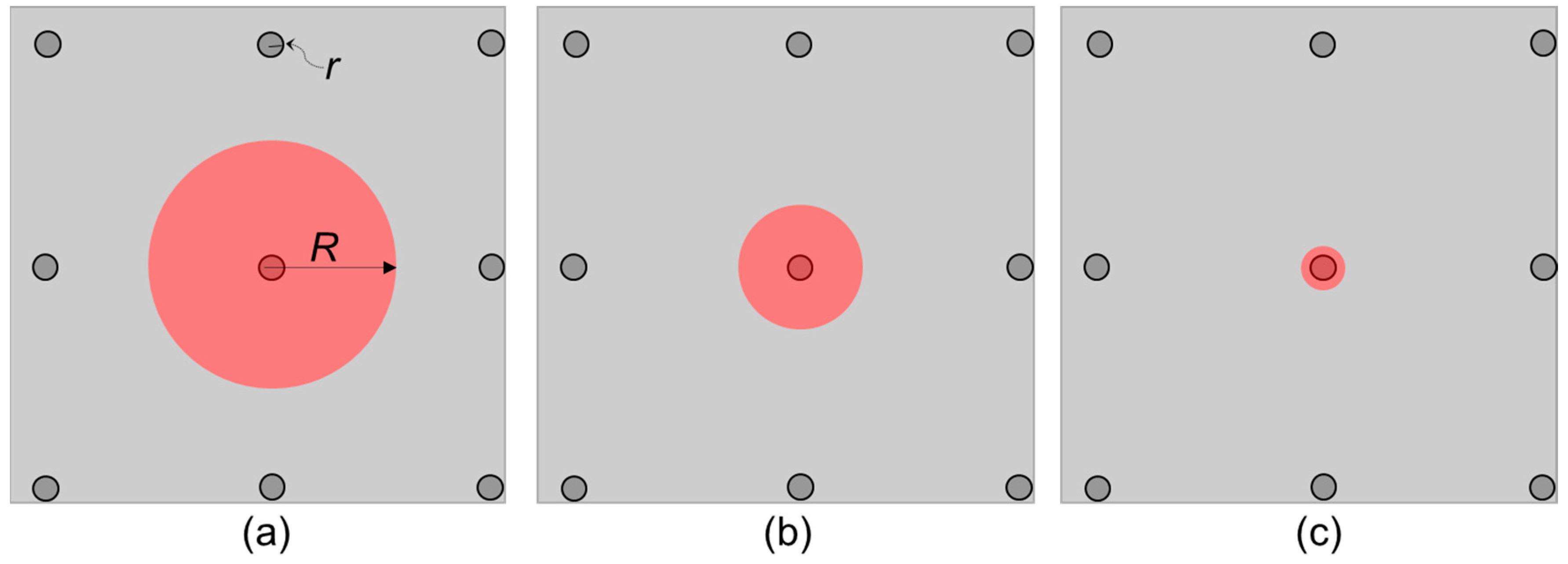
3.2. Modulation of Ratio of the Illuminated Areas
4. TSV Depth Measurement Algorithm
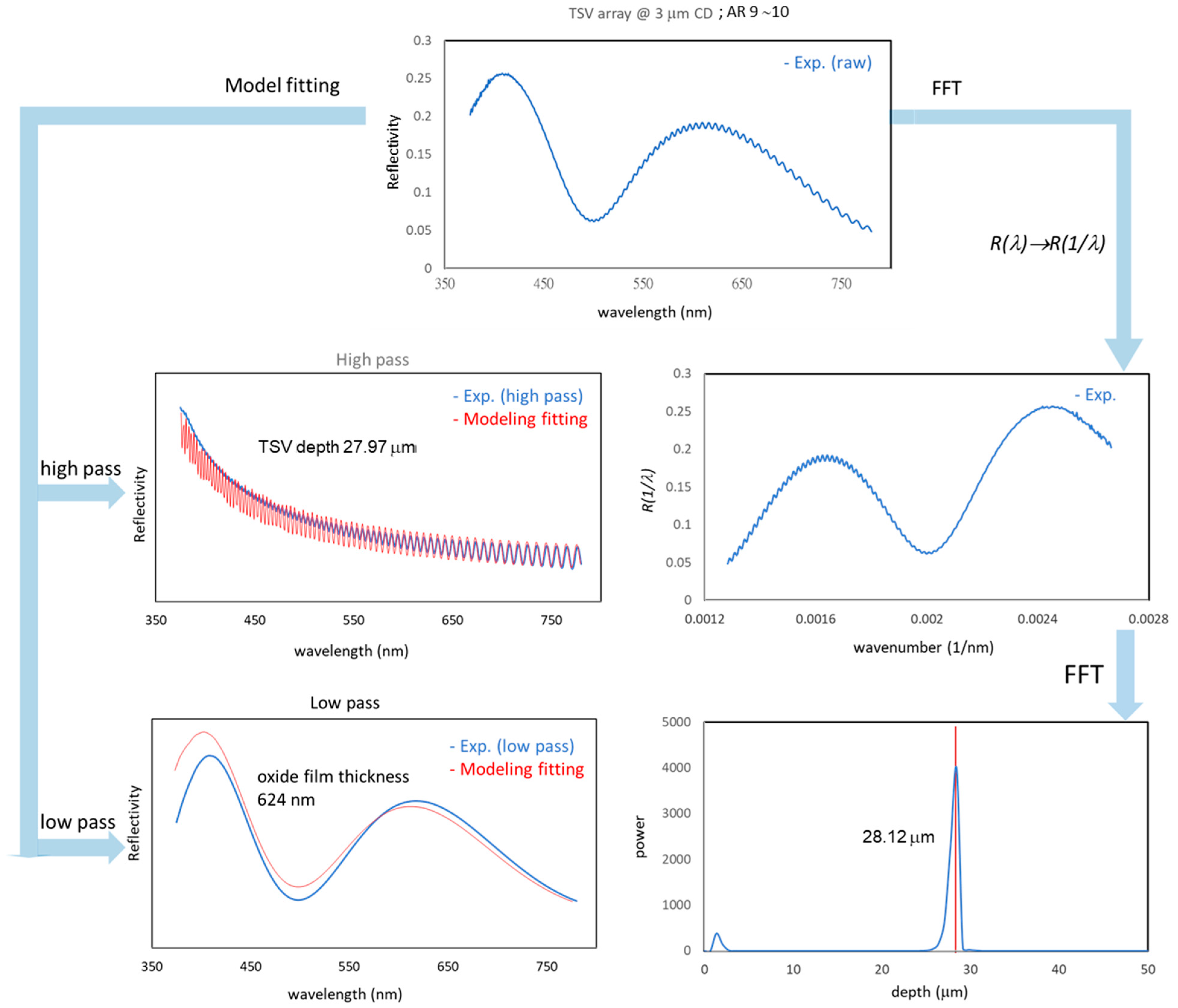
4.1. Fast Fourier Transformation (FFT)
4.2. Electromagnetic Model Fitting
5. Experimental Results and Discussion
5.1. TSV Measurement Results of Varying the Ratio of Illuminated Area
5.2. Aperture Technology Optimizing TSV Measurement
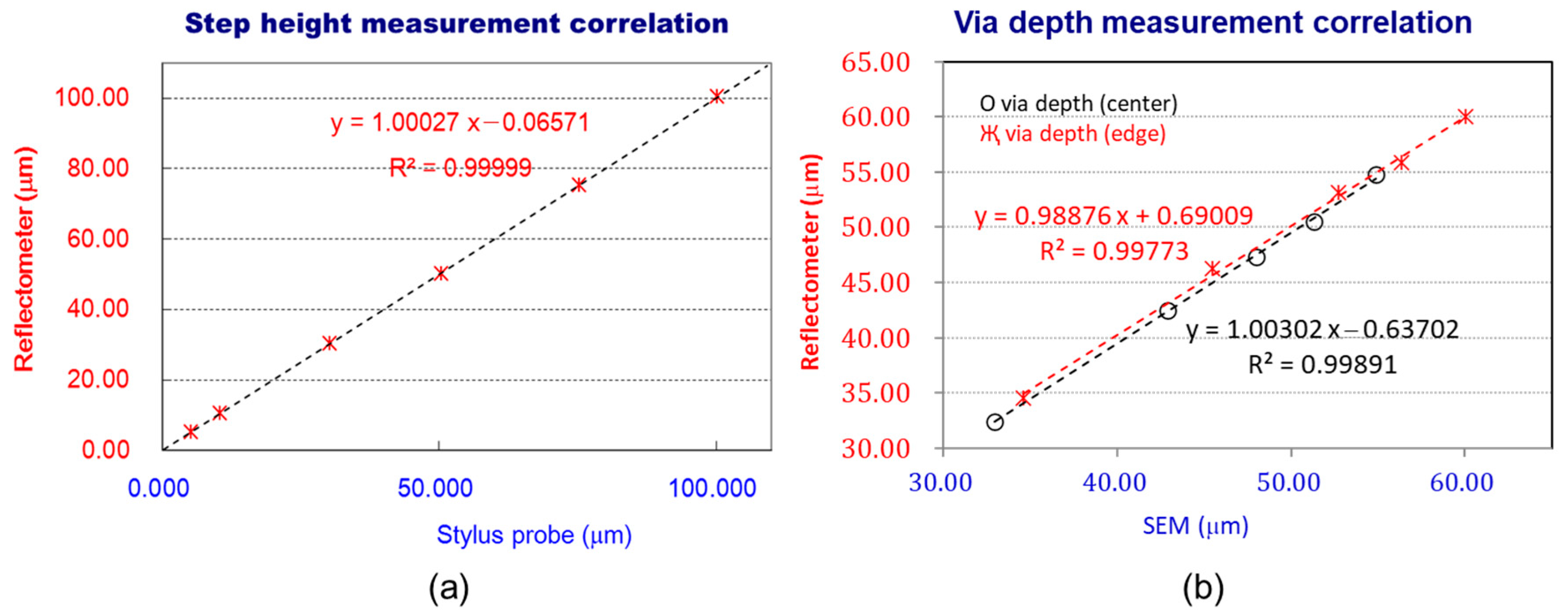
5.3. Accuracy and Resolution of Measuring TSV Depth
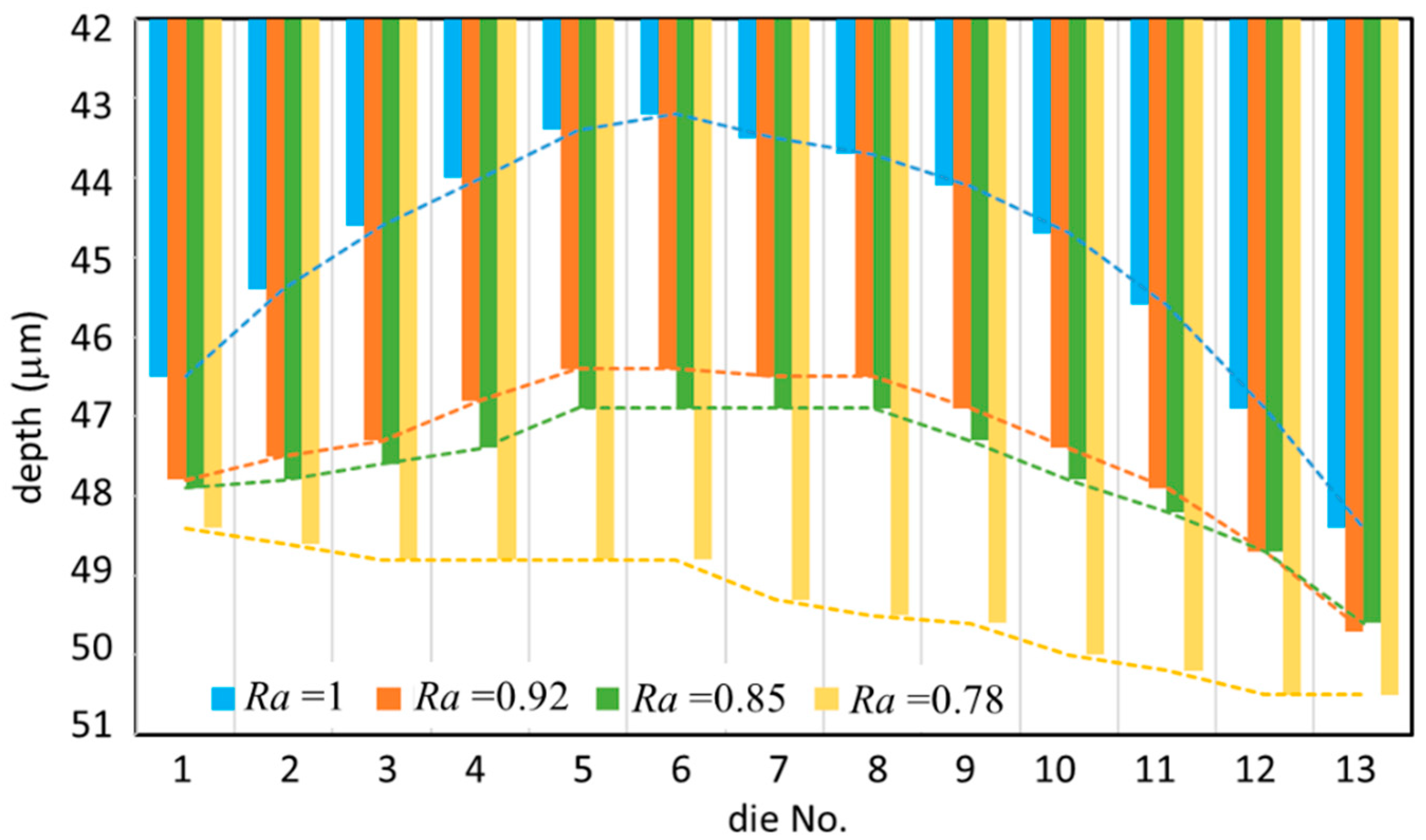
5.4. Uniformity of High Aspect Ratio TSV Etch
6. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IRDS Metrology 2023. Available online: https://irds.ieee.org/images/files/pdf/2023/2023IRDS_MET.pdf (accessed on 15 October 2023).
- Wang, J.; Duan, F.; Lv, Z.; Chen, S.; Yang, X.; Chen, H.; Liu, J. A Short Review of Through-Silicon via (TSV) Interconnects: Metrology and Analysis. Appl. Sci. 2023, 13, 8301. [Google Scholar] [CrossRef]
- Huang, P.K.; Lu, C.Y.; Wei, W.H.; Chiu, C.; Ting, K.C.; Hu, C.; Tsai, C.H.; Hou, S.Y.; Chiou, W.C.; Wang, C.T.; et al. Wafer Level System Integration of the Fifth Generation CoWoS®-S with High Performance Si Interposer at 2500 mm2. In Proceedings of the Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 1 June–4 July 2021; pp. 101–104. [Google Scholar] [CrossRef]
- Banijamali, B.; Lee, T.; Liu, H.; Ramalingam, S.; Barber, I.; Chang, J.; Kim, M.; Yip, L. Reliability evaluation of an extreme TSV interposer and interconnects for the 20 nm technology CoWoS IC package. In Proceedings of the Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; pp. 276–280. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, J.K.; Wickramanayaka, S.; Zhang, S.; Weerasekera, R.; Dutta, R.; Chang, K.; Chui, K.; Li, H.; Ho, D.; et al. Heterogeneous 2.5D integration on through silicon interposer. Appl. Phys. Rev. 2015, 2, 021308. [Google Scholar] [CrossRef]
- Semi Draft Document 5410. Guide for Metrology Techniques to be used in Measurement of Geometrical Parameters of Through-Silicon Vias (TSVs) in 3DS-IC Structures; Semiconductor Equipment and Materials International: San Jose, CA, USA, 2013. [Google Scholar]
- de Groot, P.; de Lega, X.C. Valve cone measurement using white light interference microscopy in a spherical measurement geometry. Opt. Eng. 2003, 42, 1232. [Google Scholar] [CrossRef]
- Belk, J.H.; Hulsey, D.E. Non-Contact Hole Depth Gage. U.S. Patent 2003/0107728 A1, 12 June 2003. [Google Scholar]
- Grimberg, H.; Bloomhill, M.; Koren, S. Depth Measurement of Narrow Holes. U.S. Patent 2011/0184694 A1, 28 July 2011. [Google Scholar]
- Teh, W.H.; Caramto, R.; Qureshi, J.; Arkalgud, S.; O’Brien, M.; Gilday, T.; Maekawa, K.; Saito, T.; Maruyama, K.; Chidambaram, T.; et al. A route towards production-worthy 5 μm × 25 μm and 1 μm × 20 μm non-Bosch through-silicon-via (TSV) etch, TSV metrology, and TSV integration. In Proceedings of the IEEE International Conference on 3D System Integration, San Francisco, CA, USA, 28–30 September 2009. [Google Scholar]
- Knowles, M. Optical metrology for TSV process control. In Proceedings of the 3D Interconnect Metrology at the SEMATECH Workshop during SEMICON West, San Francisco, CA, USA, 14–16 July 2009. [Google Scholar]
- Timoney, P.; Fisher, D.; Ko, Y.; Vaid, A.; Thangaraju, S.; Smith, D.; Kamineni, H.; Zhang, D.; Alapati, R.; Kim, W.; et al. New Interferometric Measurement Technique for Small Diameter TSV. In Proceedings of the 25th Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC 2014), Saratoga Springs, NY, USA, 19–21 May 2014; pp. 37–41. [Google Scholar] [CrossRef]
- Marx, D.; Grant, D.; Dudley, R.; Rudack, A.; Teh, W.H. Wafer Thickness Sensor (WTS) for Etched Depth Measurement of TSV. In Proceedings of the International Wafer-Level Packaging Conference (IWLPC), Santa Clara, CA, USA, 27–30 October 2009. [Google Scholar]
- Teh, W.H.; Marx, D.; Grant, D.; Dudley, R. Backside Infrared Interferometric Patterned Wafer Thickness Sensing for Through-Silicon-Via (TSV) Etch Metrology. IEEE Trans. Semicond. Manuf. 2010, 23, 419–422. [Google Scholar] [CrossRef]
- Ku, Y.S.; Yang, F.S. Reflectometer-based metrology for high-aspect ratio via measurement. Opt. Express 2010, 18, 7269–7280. [Google Scholar] [CrossRef] [PubMed]
- Ku, Y.S.; Huang, K.C.; Hsu, W. Characterization of high density through silicon vias with spectral reflectometry. Opt. Express 2011, 19, 5993–6006. [Google Scholar] [CrossRef] [PubMed]
- Fursenko, O.; Bauer, J.; Marschmeyer, S. In-line through silicon vias etching depths inspection by spectroscopic reflectometry. Microelectron. Eng. 2014, 122, 25–28. [Google Scholar] [CrossRef]
- Ku, Y.S. Spectral reflectometry for metrology of three-dimensional through-silicon vias. J. Micro/Nanolith. MEMS MOEMS 2014, 13, 011209. [Google Scholar] [CrossRef]
- Wu, B.; Kumar, A.; Pamarthy, S. High aspect ratio silicon etch: A review. J. Appl. Phys. 2010, 108, 051101. [Google Scholar] [CrossRef]
- Singh, H.; Rusu, C.; Vahedi, V. Etch challenges for 3-D integration. In Proceedings of the 3rd Workshop on Plasma Etch and Strip in Microelectronics, Grenoble, France, 4–5 March 2010. [Google Scholar]
- Puech, M.; Thevenoud, J.M.; Gruffat, J.M.; Launay, N.; Arnal, N.; Godinat, P. Fabrication of 3D packaging TSV using DRIE. In Proceedings of the Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS, Nice, France, 9–11 April 2008. [Google Scholar]
- Quinten, M. A Practical Guide to Optical Metrology for Thin Films; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012; ISBN 978-3-527-66434-4. [Google Scholar]
- Chen, L.; Wang, Q.; Griesmann, U. Plasma etching uniformity control for making large and thick dual-focus zone plates. Microelectron. Eng. 2011, 88, 2466–2469. [Google Scholar] [CrossRef]
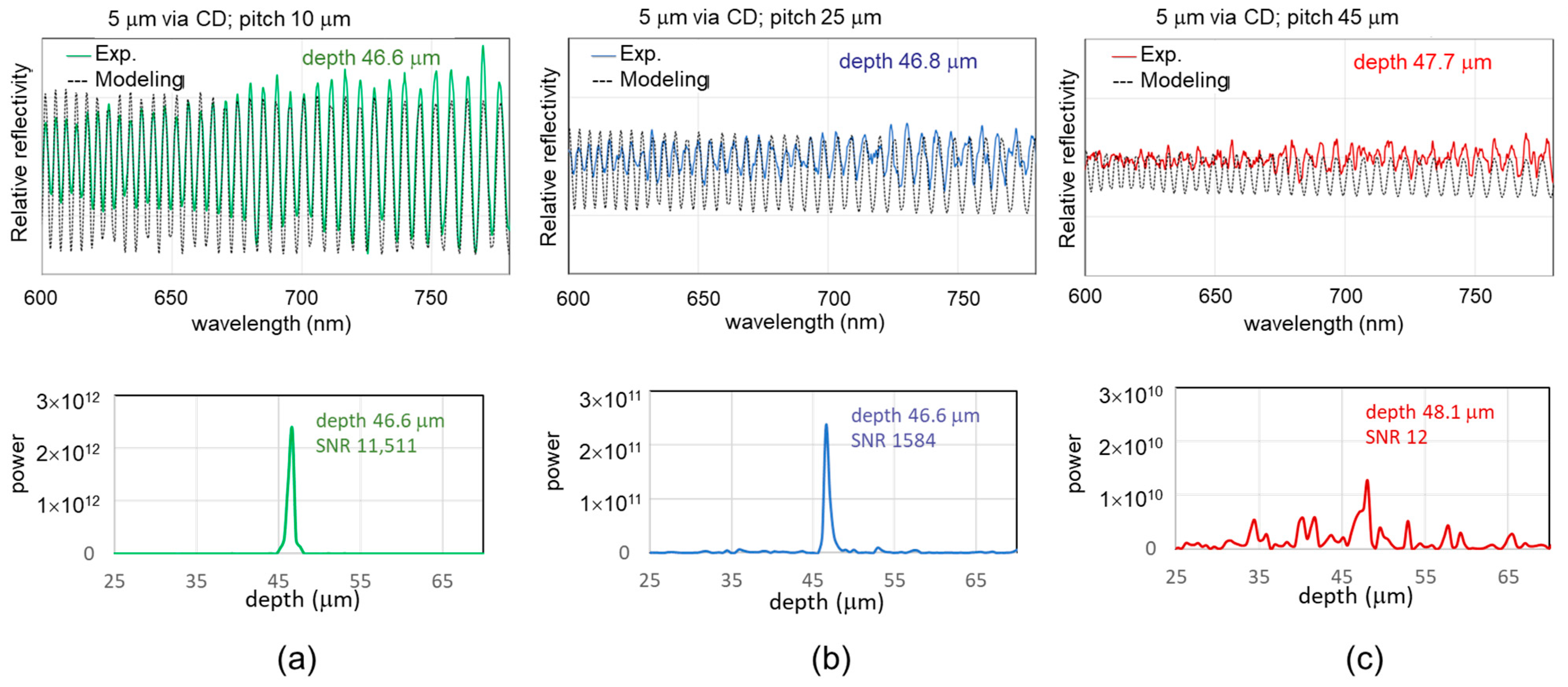


| Pitch (50 μm Spot; 5 μm Via Top CD) | 10 µm | 25 µm | 45 µm |
|---|---|---|---|
| 1 − α ratio of illuminated area (via) | 20% | 4% | 1% |
| α ratio of illuminated area (silicon surface) | 80% | 96% | 99% |
| Spot Size (5 μm Via Top CD) | 50 μm Pitch 45 µm | 25 μm Pitch 45 µm | 7.5 μm Pitch 45 µm |
|---|---|---|---|
| 1 − α: ratio of illuminated area (via) | 1% | 4% | 44% |
| α: ratio of illuminated area (silicon surface) | 99% | 96% | 56% |
| Ra\Die no. Depth (μm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | Ave. | Uniformity (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 46.5 | 45.4 | 44.6 | 44.0 | 43.4 | 43.2 | 43.7 | 43.7 | 44.1 | 44.7 | 45.6 | 46.9 | 48.4 | 44.92 | 5.79 |
| 0.92 | 48.6 | 47.5 | 47.3 | 46.8 | 46.4 | 46.4 | 46.5 | 46.5 | 46.9 | 47.4 | 47.9 | 48.7 | 49.7 | 47.32 | 3.48 |
| 0.85 | 47.9 | 47.8 | 47.4 | 47.4 | 46.9 | 46.9 | 46.9 | 46.9 | 47.3 | 47.8 | 48.2 | 48.7 | 49.6 | 47.68 | 2.83 |
| 0.78 | 48.4 | 48.6 | 48.8 | 48.8 | 48.8 | 48.8 | 49.3 | 49.5 | 49.6 | 50.0 | 50.2 | 50.5 | 50.5 | 49.37 | 2.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, Y.-S.; Lo, C.-W.; Lee, C.-K.; Cho, C.-H.; Cheah, W.-Q.; Chou, P.-W. Spectroscopic Reflectometry for Optimizing 3D Through-Silicon-Vias Process. Metrology 2023, 3, 365-376. https://doi.org/10.3390/metrology3040022
Ku Y-S, Lo C-W, Lee C-K, Cho C-H, Cheah W-Q, Chou P-W. Spectroscopic Reflectometry for Optimizing 3D Through-Silicon-Vias Process. Metrology. 2023; 3(4):365-376. https://doi.org/10.3390/metrology3040022
Chicago/Turabian StyleKu, Yi-Sha, Chun-Wei Lo, Cheng-Kang Lee, Chia-Hung Cho, Wen-Qii Cheah, and Po-Wen Chou. 2023. "Spectroscopic Reflectometry for Optimizing 3D Through-Silicon-Vias Process" Metrology 3, no. 4: 365-376. https://doi.org/10.3390/metrology3040022
APA StyleKu, Y.-S., Lo, C.-W., Lee, C.-K., Cho, C.-H., Cheah, W.-Q., & Chou, P.-W. (2023). Spectroscopic Reflectometry for Optimizing 3D Through-Silicon-Vias Process. Metrology, 3(4), 365-376. https://doi.org/10.3390/metrology3040022





