Abstract
Weather disturbances pose a significant challenge when estimating the energy production of photovoltaic panel systems. Energy production and forecasting models have recently been used to improve energy estimations and maintenance tasks. However, these models often rely on environmental measurements from meteorological units far from the photovoltaic systems. To enhance the accuracy of the developed model, a measurement Internet of Things (IoT) prototype was developed in this study, which collects on-site voltage and current measurements from the panel, as well as the environmental factors of lighting, temperature, and humidity in the system’s proximity. The measurements were then subjected to correlation analysis, and various artificial neural networks (ANNs) were implemented to develop energy estimations and forecasting models. The most effective model utilizes lighting, temperature, and humidity. The model achieves a root mean squared error (RMSE) of 0.255326464. The ANN models are compared to an MLR model using the same data. Using previous power measurements and actual weather data, a non-autoregressive neural network (Non-AR-NN) model forecasts future output power values. The best Non-AR-NN model produces an RMSE of 0.1160, resulting in accurate predictions based on the IoT device.
1. Introduction
Developing a country’s economy relies heavily on having access to sufficient energy resources [1,2]. In this sense, the energy demand has surged in recent decades due to population growth, rapid urbanization, and social needs [3]. According to a study by [2], the use of fossil fuels by energy companies to produce complementary energy contributes significantly to pollution. Therefore, it is crucial to halt this practice to minimize its negative consequences. As a solution, energy companies have taken measures by adopting alternative energy sources to not only lessen their environmental impact but also meet the growing energy demands [4].
One of the most significant sources is solar energy, which has received much attention in the last decade among all the other renewable energy systems [5,6]. The utilization of solar energy as a source of electricity has been a prevalent practice for years, with photovoltaic (PV) panels being the primary tool for this purpose. However, it is notable that the power generated by a PV panel is not solely determined by its design and construction. Several external factors, mainly the PV panels’ environmental variables, perform a crucial role in defining the panel’s power output. Additionally, intrinsic factors that are typical of semiconductors also limit the amount of power generated. Therefore, having a comprehensive grasp of the various environmental factors and the limitations of semiconductors is crucial for making the most efficient use of solar energy [7].
Multiple studies have shown that the efficiency of PV cells can be affected by interruptions and disruptions caused by fluctuating weather conditions [8,9,10,11,12]. The studies emphasize the importance of implementing reliable models in PV systems for energy production planning, maintenance, failure detection, and adjustments in large systems by decision making using the collected data.
The use of artificial intelligence (AI) has increased considerably in recent years due to its ability to model and solve complicated computational tasks [13], improve the measurement equipment’s profitability [14,15], predictive analytic tools [16], pattern recognition and classification [17], and coefficient estimator in heat transfer applications [18], and model a complex relationship without expert knowledge [19].
Considerable advances have been made in modeling and forecasting the energy output of solar panel systems. While regressor models can estimate current values based on specific inputs, they only provide predicted actual values. Forecasting, on the other hand, can predict future values based on past and current inputs. The length of the forecast can vary depending on the method used, ranging from short-term (a few seconds to a few minutes) to long-term (a few months to a year or more) methods [1,20].
In this context, several artificial intelligence (AI) and machine learning (ML) techniques have been employed to model energy generated by a photovoltaic (PV) system. These techniques enclose a variety of methodologies, including artificial neural networks (ANNs), k-nearest neighbors (KNNs), extreme learning machines (ELMs), and support vector machines (SVMs) [21,22,23]. These diverse approaches reflect the multidimensional nature of energy estimation in PV systems, each offering unique strengths and applicability depending on specific project requirements and objectives.
Artificial neural networks (ANNs) are highly effective for modeling energy estimations in photovoltaic (PV) panels due to several reasons. ANNs have the ability to perform nonlinear modeling [21], learn from available data without relying on explicit mathematical equations [22,23], extract features to determine the most influential factors in energy estimation [17], and can be scaled to handle large and complex datasets. Additionally, ANNs have the potential for high generalization on unseen data when properly trained and can continuously learn and integrate with IoT sensors to provide real-time monitoring and adaptive energy estimations [21,22,23].
While ANNs offer numerous advantages, it is important to note that their effectiveness depends on factors such as data quality, model architecture, and training methods. Researchers often choose ANNs for PV energy estimation due to their capacity to handle complex, dynamic, and nonlinear relationships inherent in photovoltaic systems, but the choice should always be guided by the specific goals and characteristics of the project.
Different models based on artificial neural networks (ANNs) have been developed to estimate or forecast the output energy of photovoltaic (PV) systems, each utilizing different sets of input data. Sangrody et al. (2017) employed ANNs to estimate PV output energy using weather data based on sky cover, humidity, and temperature [24]. Verma et al. (2016) utilized ANNs with input variables, including temperature, cloud cover, wind speed, humidity, rainfall, and panel elevation–azimuthal angle [25]. In this research, the authors develop linear regressor, logarithmic, and polynomial models to compare them against the ANN instance. The authors conclude that the ANN model gives the minimum error and is the most reliable technique. Similar works develop forecasting models using mainly solar radiation with variations in weather data [22,26,27].
These models demonstrate how ANNs can effectively adapt to different input data sources, highlighting their ability to capture the complex relationship between environmental variables that affect PV energy generation. However, it is worth noting that the models mentioned in this study mostly rely on meteorological data available online or a mix of local measurements with online data.
It is important to keep in mind that online or meteorological data come from a different location than the actual location of the PV system. In addition, some cited papers need more fundamental information, like sampling frequencies and the amount of data used for modeling. This missing information could result in insufficient continuity to track weather intermittency that affects the PV cells.
When utilizing online or meteorological data for a PV system, it is critical to keep in mind that the data originate from a separate location from the actual system. It is also significant that certain referenced papers should necessitate supplementary essential information, such as sampling frequencies and the quantity of data employed for the training process. In the absence of such details, deficient continuity in monitoring weather intermittency may occur, potentially impacting the model’s performance.
It was found that only a limited number of models are based on real-time and on-site measurements for PV applications [11,28,29]. Notably, these authors highlighted the significance of installing IoT systems close to PV systems to gather real-time data, especially in countries where micro-climates can differ drastically between PV and meteorological locations.
The present paper proposes a case study conducted in Michoacan, Mexico, where an Internet of Things (IoT) device is employed for real-time logging of on-site data related to electrical and weather aspects of a photovoltaic system. The designed IoT device gathers data about radiation levels, temperature, humidity, and electrical power parameters, specifically the panel’s voltage and current, with a consistent sampling frequency of 5 min. The data gathering is spanned over multiple months, allowing for the assembly of a more suitable dataset, which subsequently serves as the foundation for the modeling phase of the study.
This first approach uses a set of 1000 instances to train and compare different ANN topologies. As a result, a satisfactory topology has a root mean squared error (RMSE) of 0.255326464 for power-delivering estimations. Next, a non-autoregressive neural network (Non-AR-NN) model is developed to forecast the future power value. The model adopted has an RMSE of 0.1160.
Thus, the present paper is organized in the following way. Section 2 gives a general description of modeling using ANNs and the procedure followed in this research until the selection of the best model settings. Section 3 discusses the model’s performance in predicting power estimations using environmental variables. Also, the Non-AR-NN model is discussed to predict future estimations. Finally, Section 4 gives the final arguments about the finds in this paper.
2. Materials and Methods
The present section describes the basics of artificial neural networks (ANNs) and the general procedure for developing models based on ANN regressors. Then, details about the designed devices are given for collecting data. Next, preprocessing and correlation analysis are described to define the ANN model and its training process.
2.1. Artificial Neural Networks Basics
Artificial neural networks (ANNs) are computational models inspired by the structure and functioning of biological neural networks in the human brain [30]. The ANN consists of interconnected artificial neurons, also called processing units, organized in layers: an input layer, one or more hidden layers, and an output layer [31].
The perceptron is the fundamental processing unit; see Figure 1. It is a simple mathematical model that takes multiple input values (), each multiplied by a corresponding weight (), and then sums up these weighted inputs (X). The resulting sum is passed by an activation function to produce the output (). Different versions of this topology incorporate a bias input (b) in addition to the features.
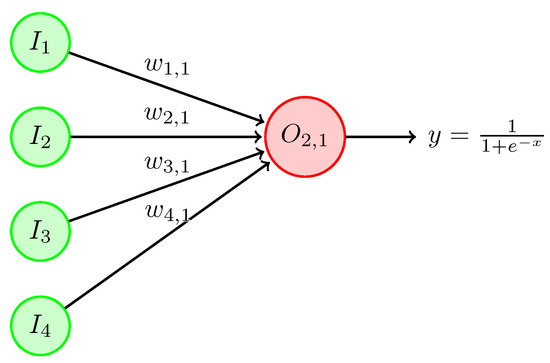
Figure 1.
Perceptron processing unit with four inputs and sigmoid activation function.
Thus, the perceptron operation can be described mathematically as follows:
where is the sigmoid activation function. However, this function can also be the hyperbolic tangent function, linear, RELU, among others.
The activation function introduces non-linearity, allowing perceptron and subsequent ANNs to model complex patterns and relationships in data. It is well known that a single perceptron can perform simpler linear classification problems [31,32]. On the other hand, multiple interconnected perceptron architectures, organized in layers, can handle more complex tasks.
The versatility of artificial neural networks (ANNs) is remarkable, as they can employ both linear and non-linear activation functions and different combinations of both. That is why they have proven to be useful in a wide range of scopes, including control, pattern recognition, classification, forecasting, and non-linear regressors [33].
The focus of this study is on universal function approximation or non-linear regression modeling. Thus, analytical models, which rely on the physical relationships within the modeled system, are a popular method for developing models in this context. These models are known as “White-box” and require extensive system knowledge. Alternatively, there is a second option known as “Black-box” models, which use statistical and machine learning methods to directly predict the system’s output. It is also important to consider a hybrid model, known as the “Grey-box”, which combines both techniques for more accurate results. However, most studies in non-linear applications tend to rely heavily on the “Black-box” model approach [28].
2.2. Implementation of an ANN Regressor
The typical process of creating a regressor or classifier ANN involves these steps: data preparation, network architecture selection, loss function definition, optimizer choice, training the ANN, hyper-parameter tuning, model evaluation, and prediction. In general terms, each step can be defined as follows:
- The process of data preparation involves collecting and preprocessing data from experiments or polls. A typical preprocessing step is scaling and normalizing input features and target values. These input features and targets are commonly known as instances; then, instances are commonly randomly grouped as training and testing datasets.
- The network architecture stage considers the architecture by determining the number of layers and neurons per layer, as well as the activation functions. For regression applications, the final layer should have a single neuron with a linear activation function.
- The choice of the loss (cost) function is crucial in creating accurate models. Metrics such as mean squared error (MSE) or mean absolute error (MAE) can lead to different outcomes.
- During the training stage, the neural network’s weights and bias can be updated using various numeral optimizers such as gradient descent, stochastic gradient descent, batch gradient descent, mini-batch gradient descent, and adaptive moment estimation (Adam).
- The model will be updated using the prepared dataset and the previously defined neural network architecture. The training process will be monitored by observing the loss decrease by the optimizer. Then, the model’s performance is evaluated over a validation dataset.
- Evaluating the model’s performance requires testing with various hyper-parameters, such as learning rate (), batch size (n), and number of epochs.
- After completing the training stage, the model’s performance is evaluated on a different test dataset. Metrics such as mean squared error, mean absolute error, and R-squared are used to determine the model’s prediction accuracy. Nevertheless, it is highly recommended to use the same previously defined loss function.
- Finally, if the initial results are not satisfactory, it is possible to try adjusting the network architecture, hyper-parameters, collecting more data, or even including additional inputs to improve the model’s performance.
2.3. Non-Autoregressive Neural Networks
Considering the previous description about the ANN and its implementations as a regressor model, the non-autoregressive neural network (Non-AR-NN) variant with sequential data input topology can be introduced. The Non-AR-NN is a type of ANN specifically designed for processing data sequences, also known as time series. Unlike traditional feed-forward neural networks, Non-AR-NNs can have a sequence of data as input, such as a time series of values or a sequence of tokens in natural language. Each element in the sequence is treated as an input feature at a specific time step emulating kind of sliding window lag. This non-recurrent structure allows for parallel prediction and faster computing without sequential constraints, making it capable of modeling temporal dependencies.
2.4. Data Preparation: IoT Device and Experimental Setup
Developing accurate models requires the collection and validation of representative data. To accomplish this, we have designed an IoT measurement prototype that gathers voltage and current measurements and environmental factors like radiation levels, temperature, and humidity on-site for the modeling PV system.
Figure 2 shows the general methodology for gathering and downloading data through the IoT device using a PC.
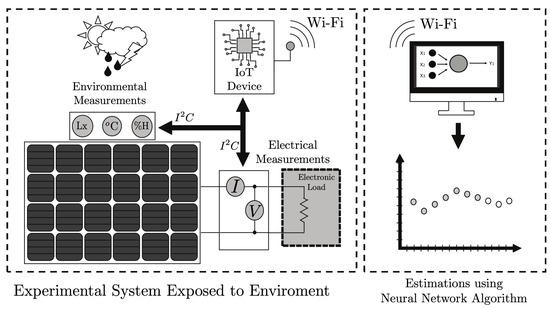
Figure 2.
Experimental setup for data gathering and analysis based on an IoT device attached to the PV system.
The designed IoT device is a small circuit based on the CC3200 microcontroller and embeds three sensors, an instrumentation amplifier, and a rechargeable battery as the power supply; see Figure 3. The sensors communicate via , a protocol that enables digital handshaking between microcontrollers and sensors. The microcontroller features a web server that facilitates storing and managing logged data for further processing. Then, the complete system uses the battery to enable all the circuitry and features of the IoT device supported by a small solar panel that charges it, making it efficient and self-powered.
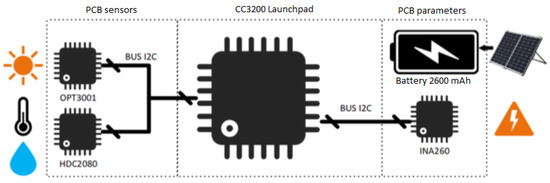
Figure 3.
Experimental setup system for measurements.
The symbols on the left in Figure 3 are the weather sensors and the OPT3001 and HDC2080 integrated circuits. The OPT3001 is a light sensor with a resolution, including an upper limit of 128 . However, an attenuating glass has been used to extend 55% of the device limit; a calibration procedure was conducted using the commercial digital luxometer MASTECH ms6612. Next, the HDC2080 sensor measures relative humidity (RH) and temperature. For temperature, the sensor has a ± 0.2 °C resolution with ranges of −40 °C to 85 °C, while the RH sensor gives measurements with a resolution.
Figure 4, shows a comprehensive view of the primary PV and IoT systems from both the front and rear. The front view highlights the lighting sensor fixture alongside humidity and temperature sensors. The rear view (Figure 4b) depicts the IoT circuitry implemented for measuring the PV’s current and voltage mounted over the CC33200 launchpad.

Figure 4.
Physical installation of the IoT device in a section of the PV system. (a) Front view of the small solar panel; (b) Rear view of the IoT system without its cover-box.
Before implementing the ANN model, the collected data are compared with readings from a commercial meteorological station that is installed in a close location as the IoT system. The data from both sources include information on solar radiation, humidity, and temperature. To ensure a correct comparison, data are normalized using Equation (2), since the measurements were obtained from different equipment:
where is the actual value to be normalized, is the minimum value of the entire data set, and is the maximum value of the entire data-set. The normalization process is utilized in subsequent stages, such as correlation analysis and training.
Figure 5 in this paper illustrates a comparison between the measurements gathered by the IoT system and those recorded by the meteorological station. The observed slight variations between the datasets can be attributed to the following installation factors: the lightning sensor angles, the temperature sensors’ location, and methods for humidity measurements.
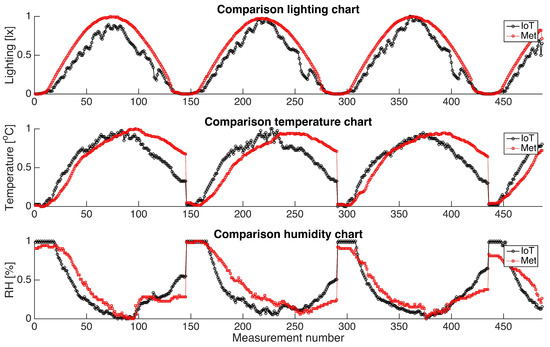
Figure 5.
Data comparison between the meteorological station and the IoT system.
After comparing the RMSE values, it was found that the error rates for lighting, temperature, and humidity are 0.096, 0.1796, and 0.1491, respectively. The temperature measurement error is primarily caused by the sensor location. The IoT system collects data on the panel’s temperature, which is crucial in identifying its impact on the panels’ efficiency. However, the meteorological station measures ambient temperature, leading to significant differences in the data.
Table 1 presents a selection of measurements acquired by the IoT system. Within the table, the initial column designates the timestamp for each measurement. Subsequently, the second column describes lighting data expressed in lux, followed by temperature in the third column, humidity in the fourth column, current in the fifth column, voltage in the sixth column, and, finally, the computed power values are listed in the seventh column.

Table 1.
Example measurements collected by the IoT device.
Within the context of data preparation for training the artificial neural network (ANN), an essential step involved the selection and preprocessing of data. Figure 6 provides an illustrative representation of measurements during nine consecutive days, containing all variables acquired by the IoT system. A particular data filtering process is implemented to enhance the dataset’s relevance and suitability for solar power estimation to exclude measurements recorded during night-time periods, as these measurements are non-contributory to the photovoltaic system’s power generation dynamics. This preprocessing step ensures that the dataset used for training the ANN encloses only the pertinent observations, thereby optimizing the model’s capacity for accurate power output predictions.
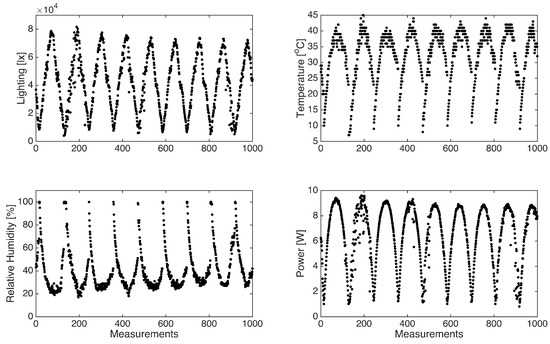
Figure 6.
IoT measurements for lighting, temperature, humidity, and the PV generated power.
Next, Figure 7 presents three correlation plots, each proposing distinct relationships: (a) examining the interaction between luxes, temperature, and power; (b) observing the associations among humidity, luxes, and power; and (c) exploring the correlations involving temperature, humidity, and power. It is important to highlight that the power variable is designated as the dependent or output variable under investigation in all three plots. Notably, the third plot, which accentuates the relationship between temperature, humidity, and power, exhibits a comparatively weaker correlation. This reduced correlation is attributed to an expanded data spread, suggesting that humidity may exert a less pronounced influence on the resultant model, thereby providing valuable insights into variable interactions within the dataset.
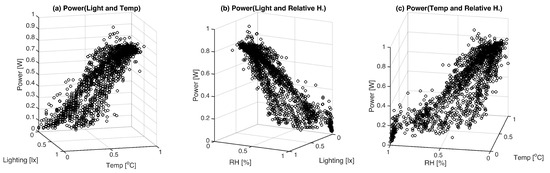
Figure 7.
Correlation variables plots for (a) luxes, temperature, and power; (b) humidity, luxes, and power; and (c) temperature, humidity, and power.
After collecting data, it is crucial to comprehend how the measured variables relate. One effective way to achieve this is by calculating the Spearman rank correlation coefficient matrix (). This tool is powerful as it shows the non-linear connection between pairs of variables.
Unlike the Pearson correlation coefficient, which measures linear relationships between continuous variables, the Spearman correlation operates on ranked data. This makes it a non-parametric measure.
Using the Spearman correlation matrix in this study has a significant advantage. It helps us to understand the relationship between variables at a glance, enabling us to identify pairs of variables that require further investigation due to their strong correlation. This efficient process saves time and allows us to focus on the most important variables.
The Spearman correlation matrix is computed using the complete data set, and the resulting coefficients are:
The dataset will undergo a systematic partitioning procedure, creating three distinct datasets: the training, validation, and testing datasets. Each dataset’s designated role in the modeling process corresponds to its nomenclature. To compose these datasets, instances will be randomly selected from the initial set of 1000 instances. Particularly, the training dataset will encompass 70% of the data, while the validation dataset will comprise 20%, and the remaining 10% will form the querying dataset. Subsequently, these datasets will be subjected to an array of neural network topologies as part of an extensive comparative analysis. Please refer to Figure 8 for a graphical representation clarifying the neural network’s training methodology.
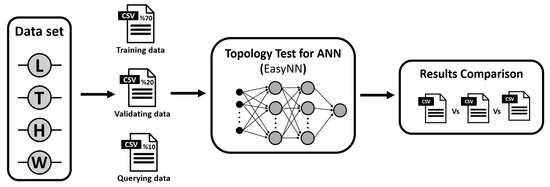
Figure 8.
Considered methodology for training, testing, and querying the proposed topologies.
During training, data are passed forward through the neural network in what is known as feed-forward. Each layer performs calculations based on the weights, biases, and activation functions defined in the topology. The resulting predictions are compared to the actual target power values, and an error (typically mean squared error for regression tasks) is calculated. The feed-forward process considers the dataset previously normalized and randomly organized. Then, any possible errors in estimations are improved by applying the backpropagation process.
This involves calculating the error gradient with respect to the network’s weights and biases. This gradient information is then used to update the weights and biases through optimization algorithms like stochastic gradient descent (SGD), Adam, or RMSprop. These updates are performed iteratively for multiple epochs until the model converges to a satisfactory performance level. For this research, the authors used the Adam algorithm.
The combination of feed-forward and backpropagation for each instance is the core of the training process. The aforementioned procedure is subsequently executed on the complete training dataset. It is repeated for the number of epochs specified for each topology with their respective hyper-parameters for the Adam algorithm [31].
3. Results
Two types of estimators based on ANNs are developed: an ANN for estimating the PV power generation and an RNN for forecasting the power delivery considering the previous power measurements. Thus, the following sections present the most relevant architecture models developed and trained for each case.
3.1. ANN for Estimating the PV’s Power
The ANN architectures have considered cases with two and three input variables: (i) lighting, temperature, and humidity (ii) lighting and temperature, (iii) lighting and humidity, and (iv) humidity and temperature; each option has been tested with different ANN topologies.
Table 2 presents only the neural network topologies with the lowest root mean square error (RMSE) for estimating the PV’s output power. The table’s initial column delineates the input variables (T: temperature, L: lighting, and H: humidity), while the second column signifies the adopted network topology, expressed as the number of input-nodes: hidden-nodes: output-nodes. The table’s third, fourth, and fifth columns indicate the hyper-parameters, which are the maximum training cycles, learning rate, and momentum, respectively. The last column shows the corresponding RMSE values. It is important to note that the hyper-parameters were selected based on the performance of the RMSE, determined through previous explorations with a small dataset.

Table 2.
Best ANN topologies tested for estimating PV systems.
The diagram in Figure 9 displays a sample of the 3:3:1 artificial neural network topology. It has one input, hidden, and output layer; there can be as many hidden layers as the problem requires. The input layer has three nodes to allocate each variable to the hidden layer. In this case, the hidden layer has three computation elements and links to the output layer, which only requires one computation element for regression tasks.
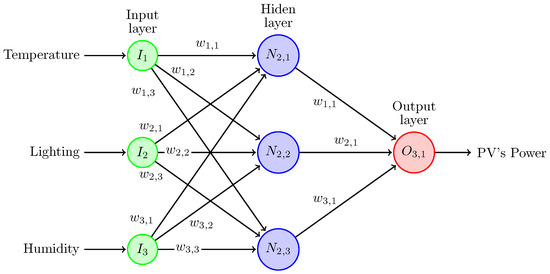
Figure 9.
The 3:3:1 ANN topology for estimating the PV’s power output.
To demonstrate the effectiveness of different topologies, Figure 10 displays their performance. The comparison focuses on one-day data, specifically in Figure 10a, where topology 3:3:1 estimations are compared to measured data. Notably, the lowest computed level error is achieved by this topology: 0.255326464.
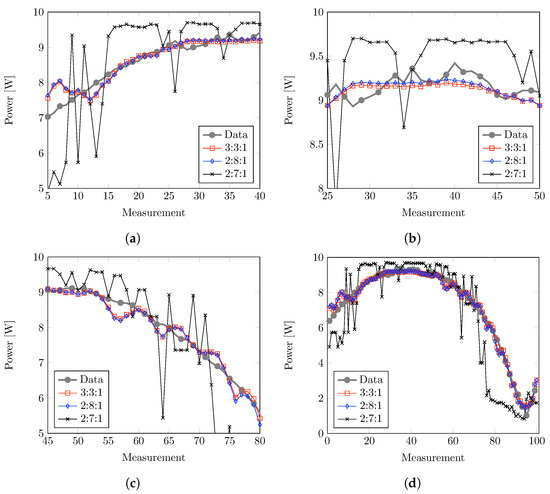
Figure 10.
Graphical comparison of estimations against measurements for topologies of two and three input variables: 3:3:1, 2:8:1, and 2:7:1. (a) Comparison during early morning; (b) comparison during noon; (c) comparison during afternoon; (d) overall day comparison.
Another good estimator has been implemented using only lighting and temperature, with a topology 2:8:1, resulting in an error level of 0.273086254; see Figure 10b.
In the case of the estimator based on the lighting and humidity, the best topology was 2:3:1, with an error level of 0.26061261; see Figure 10c. Finally, regarding the estimator based on temperature and humidity variables, the best-performing topology is 2:7:1, with an error level of 1.522621379; see Figure 10d.
Notice that the best network uses the three variables. However, the optional best-performance networks can be used when some data are missing or corrupted. For this research, the humidity sensor was the most problematic due to the warmth variability, specifically in Morelia city, resulting in saturated measurements during the early morning. Thus, the ANN can produce better estimations when all variables are pleasant.
The work also compares a multiple linear regression (MLR) using the three main variables from the same dataset. The proposed MLR model is defined by:
for observations and considering:
- is the PV’s power output;
- are the explanatory variables: lighting, temperature, and humidity;
- is the constant term;
- are the coefficients for each explanatory variable;
- is the model’s error term.
An ANOVA analysis was conducted on explanatory variables to determine their significance for the MLR model. The results are presented in Table 3, showing a regression model and its confident interval values. Based on the data shown in Figure 11, it is evident that the artificial neural network (ANN) model exhibits superior performance compared to the multiple linear regression (MLR) model.

Table 3.
ANOVA analysis of the x variables (independent variables) and the y variable (dependent variable).
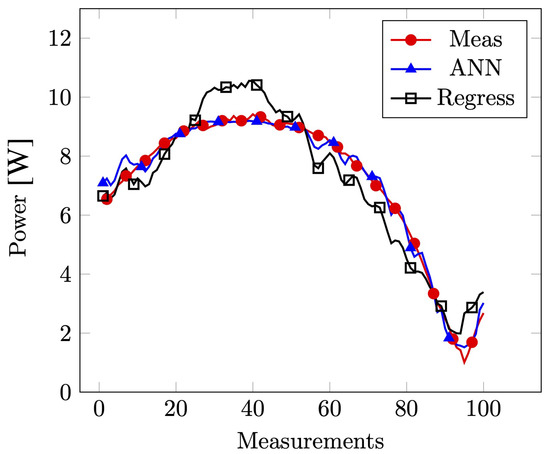
Figure 11.
Comparative figure of the performances between the estimations by ANN and MLR models.
3.2. Forecasting Model
A suggested approach for maximizing the potential of IoT devices and on-site measurements is to implement a non-autoregressive neural network (NARNN) topology. This neural network architecture is particularly suited for tasks that require the simultaneous generation of output elements without the constraints of sequential generation.
Thus, to forecast the next power output value, the topology proposes incorporating a set of historical power measurements, denoted as N previous measurements, alongside concurrent readings of illuminance, temperature, and humidity. This results in a total of input nodes. Figure 12 illustrates a schematic example of the NARNN topology.
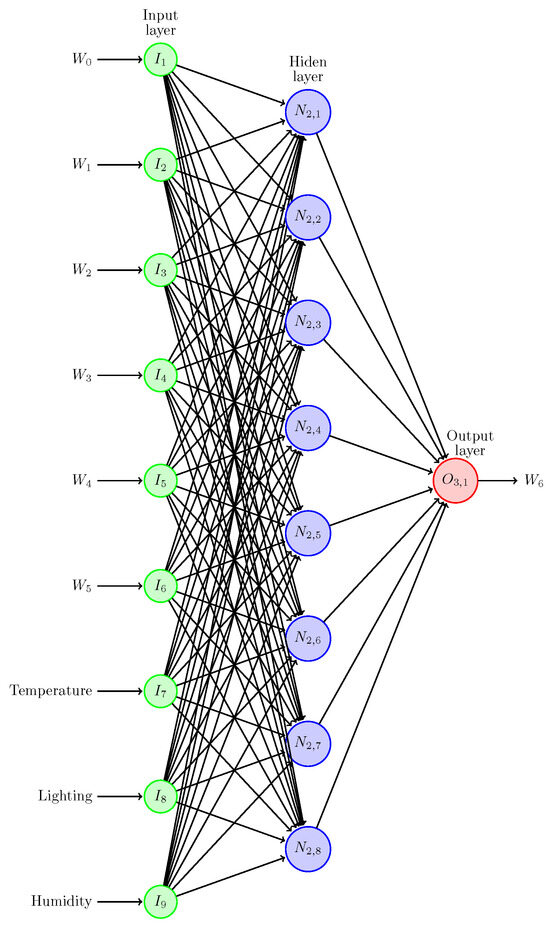
Figure 12.
Recurrent neural network model for topology 9:8:1.
Including past power measurements allows for the exploration of diverse model variations by adjusting the value of N, as well as the number of hidden nodes. The figure represents 9:8:1 topology, signifying nine input nodes, eight hidden nodes, and one output node. Notably, this configuration encompasses the utilization of six prior power measurements () as crucial input data.
Next, Table 4 shows the most relevant trained NARNN models and their respective performances. The Topology column indicates the topology used during the training process. The Input column indicates the variables used additionally with the N power measurements, L for lighting, T for temperature, and H for humidity. The Sampling column indicates the sampling frequencies. Epochs, Learning rate, and Momentums columns indicate the hyper-parameters used during the training stage. Finally, the RMSE indicates the error performance during the testing process.

Table 4.
Best Non-AR-NN models obtained for forecasting the PV system.
Two of the most relevant topologies for these models are 9:8:1 and 9:8:5:1. However, the difference in error between them is negligible. Therefore, the authors suggest the simplest topology to simplify the algorithm and reduce computational demands.
In Figure 13, we can see the results of forecasting 100 random points from the querying set using the 9:8:1 topology. As one can see, the model closely predicts the points. Finally, notice that the values close to zero most likely correspond to measurements taken during bad weather conditions.
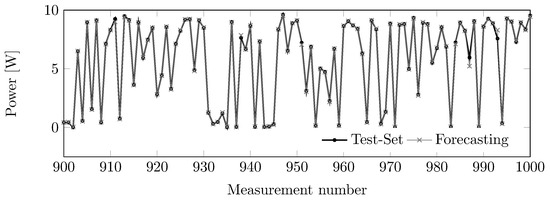
Figure 13.
Comparative figure of the performances between the forecasting by non-autoregressive neural network (Non-AR-NN) (9:8:1) and random measurements of the querying set.
4. Discussion and Conclusions
The significance of establishing the optimal neural network topology is highlighted by its dependence on input variables and their respective correlations. A series of models were trained, featuring a variety of input variable combinations, neuron quantities, and hidden layer configurations, with the overarching objective of identifying the most proficient model for the purposes of regression and forecasting. Nonetheless, certain limitations are inherent in the designed IoT prototype, encompassing aspects such as measurement resolution and ranges. Consequently, an evaluation was conducted to gauge the accuracy of the values derived from the IoT device. This evaluation involved a comparative analysis between the data generated by the prototype and those originating from a commercial meteorological station. After the computation of the root mean square error (RMSE) value, it was deduced that the data generated by our prototype exhibit reliability.
The presented methodology offers a comprehensive procedure for developing and utilizing artificial neural networks (ANNs) as regressors in conjunction with a measurement Internet of Things (IoT) device. This methodology can be applied further to larger photovoltaic (PV) systems or include more measurement variables. The data sets were prepared in Matlab®, and the model’s training process was implemented using EasyNN-plus software version V8, created by Neural Planner Software Ltd., from Cheadle, the United Kingdom.
Data have been partitioned into three key datasets: training (70% of the data), validation (20%), and querying or testing (10%). These sets were derived from an initial pool of 1000 instances. Then, training sets were processed through various neural network topologies for in-depth comparison. During the neural network training, data undergo a feed-forward process. Next, predictions made with the testing set are compared to target values to calculate errors.
The most suitable configuration allows for accurate power estimates of the modeling PV panel. After prudent analysis, it has been determined that the optimal topology for this regression task consists of three main variables as inputs, three computational elements in the hidden layers, and one element in the output layer (3:3:1). The ANNs’ weight and bias parameters were obtained after training diverse models that consider different input variables and ANN topologies. By utilizing the 3:3:1 topology, it is possible to accurately predict the behavior of the solar panel under normal conditions with an RMSE performance of 0.2553 or 2.8%. Even with the two-variable model (2:8:1), there is only a slight margin of error, with a reliability level of 0.2730 or 3.03%. However, this model must be used with caution because estimations are made without lighting information. It is important to note that two-variable models have a significant drawback when considering the humidity variable, consistently resulting in the highest root mean square error (RMSE) values compared to other models. The elevated RMSE values indicate a substantial difference between the predicted and observed values, suggesting that placing excessive focus on humidity may not be the most optimal approach for accurate predictions in this scenario. Several factors could contribute to this outcome. Although crucial in many environmental and climatic studies, humidity might interact with other unaccounted variables that influence the prediction accuracy in this study. High RMSE values highlight the importance of considering a more diverse set of predictors or re-evaluating the weight assigned to humidity in the models.
Additionally, note that the models are trained and validated using clear-sky data, which is one of the limitations of this study. Nonetheless, the IoT system is continuously collecting fresh data to enhance the current findings and refine the models. Although the present outcomes offer a comprehensive understanding of the model’s abilities in specific conditions, it is imperative to investigate and fine-tune the model under different sky conditions, particularly in cloudy and overcast settings. This is a critical avenue for future research that will ultimately enhance the models’ precision and dependability.
On the other hand, the forecasting model performs best with nine inputs: lighting, temperature, humidity, and six previous power values; the 9:9:1 topology. Next, eight nodes are in the hidden layer, and one node is in the output layer. The selected model is a non-autoregressive neural network (Non-AR-NN) that uses sequential data as input, together with actual environmental measurements.
The RMSE value forecasting predictions confirms that it is possible to make accurate estimates using the lighting, temperature, and humidity data next to the PV system. Forthcoming work will develop a more comprehensive multi-layer ANN model that considers larger datasets from on-site measurements. Also, more complex forecasting models can be developed using recurrent neural networks, autoregressive models, or medium-term models. Finally, the Internet of Things (IoT) accuracy can be improved and tested with larger systems.
Author Contributions
Conceptualization, G.M.C.-C., O.L.-N. and A.d.C.T.-A.; methodology, G.M.C.-C., R.L.-H., M.F.-A. and O.L.-N.; software and scripts, O.L.-N. and Y.M.C.-M.; validation, R.L.-H., O.L.-N. and Y.M.C.-M.; formal analysis, Y.M.C.-M., O.L.-N. and M.F.-A.; investigation, O.L.-N. and A.M.-C.; resources, A.d.C.T.-A., O.L.-N. and A.M.-C.; data curation, A.M.-C. and O.L.-N.; writing—original draft preparation, O.L.-N. and A.M.-C.; writing—review and editing, G.M.C.-C. and A.M.-C.; visualization, Y.M.C.-M. and G.M.C.-C.; supervision, Y.M.C.-M. and G.M.C.-C.; project administration, R.L.-H.; funding acquisition, R.L.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Tecnológico Nacional de México (TecNM) grant number 6127.17-P. Additionally, the student Lobato-Nostroza, O. received a scholarship from Consejo Nacional de Humanidades, Ciencia y Tecnología, with number 625015.
Data Availability Statement
The used data for the analysis and model development can be founded at https://osf.io/cu4r6/ (accessed on 20 August 2023).
Acknowledgments
The authors would like to acknowledge the National Laboratory SEDEAM for supporting the development of electronic prototypes used in this research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PV | Photovoltaic |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| ML | Machine Learning |
| KNNs | K-Nearest Neighbors |
| ELM | Extreme Learning Machine |
| SVM | Support Vector Machine |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| MLR | Multiple Linear Regressor |
| ANOVA | Analysis Of Variance |
| IoT | Internet of Things |
References
- Roungkvist, J.S.; Enevoldsen, P. Timescale classification in wind forecasting: A review of the state-of-the-art. J. Forecast. 2020, 39, 757–768. [Google Scholar] [CrossRef]
- El Kafazi, I.; Bannari, R.; Abouabdellah, A. Modeling and forecasting energy demand. In Proceedings of the Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 14–17 November 2016; pp. 746–750. [Google Scholar]
- Pham, A.D.; Ngo, N.T.; Ha Truong, T.T.; Huynh, N.T.; Truong, N.S. Predicting energy consumption in multiple buildings using machine learning for improving energy efficiency and sustainability. J. Clean. Prod. 2020, 260, 121082. [Google Scholar] [CrossRef]
- Enerdata. Global Energy Statistical Yearbook. 2023. Available online: https://www.energyinst.org/__data/assets/pdf_file/0004/1055542/EI_Stat_Review_PDF_single_3.pdf (accessed on 6 July 2023).
- Powell, K.M.; Rashid, K.; Ellingwood, K.; Tuttle, J.; Iverson, B.D. Hybrid concentrated solar thermal power systems: A review. Renew. Sustain. Energy Rev. 2017, 80, 215–237. [Google Scholar] [CrossRef]
- Rabaia, M.K.H.; Abdelkareem, M.A.; Sayed, E.T.; Elsaid, K.; Chae, K.J.; Wilberforce, T.; Olabi, A. Environmental impacts of solar energy systems: A review. Sci. Total Environ. 2021, 754, 141989. [Google Scholar] [CrossRef] [PubMed]
- Jayakumar, P. Solar Energy: Resource Assessment Handbook, Asian and Pacific Centre for Transfer of Technology, September 2009. Available online: https://repository.unescap.org/handle/20.500.12870/5255 (accessed on 20 August 2023).
- Cui, Y.; Su, Y.; Liu, Y.; Liu, Y.; Smith, D. Study of variability metrics for solar irradiance and photovoltaic output. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Niemi, A.; Lehtonen, M.; AbdelHadi, H.A.R. Analysis of solar irradiance variations as a source of flicker associated with PV systems. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Turin, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Tan, W.C.; Saw, L.H.; San Thiam, H.; Xuan, J.; Cai, Z.; Yew, M.C. Overview of porous media/metal foam application in fuel cells and solar power systems. Renew. Sustain. Energy Rev. 2018, 96, 181–197. [Google Scholar] [CrossRef]
- Ruz-Hernandez, J.A.; Matsumoto, Y.; Arellano-Valmaña, F.; Pitalúa-Díaz, N.; Cabanillas-López, R.E.; Abril-García, J.H.; Herrera-López, E.J.; Velázquez-Contreras, E.F. Meteorological Variables’ Influence on Electric Power Generation for Photovoltaic Systems Located at Different Geographical Zones in Mexico. Appl. Sci. 2019, 9, 1649. [Google Scholar] [CrossRef]
- Hassan, M.A.; Al-Ghussain, L.; Khalil, A.; Kaseb, S.A. Self-calibrated hybrid weather forecasters for solar thermal and photovoltaic power plants. Renew. Energy 2022, 188, 1120–1140. [Google Scholar] [CrossRef]
- Mohammed, S.A.; Shirmohammadi, S. A multimodal deep learning-based distributed network latency measurement system. IEEE Trans. Instrum. Meas. 2020, 69, 2487–2494. [Google Scholar] [CrossRef]
- Alippi, C.; Ferrero, A.; Piuri, V. Artificial intelligence for instruments and measurement applications. IEEE Instrum. Meas. Mag. 1998, 1, 9–17. [Google Scholar] [CrossRef]
- Fogel, D.B. Machine intelligence. IEEE Instrum. Meas. Mag. 2006, 9, 12–16. [Google Scholar] [CrossRef]
- Chhajer, P.; Shah, M.; Kshirsagar, A. The applications of artificial neural networks, support vector machines, and long–short term memory for stock market prediction. Decis. Anal. J. 2022, 2, 100015. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Umar, A.M.; Linus, O.U.; Arshad, H.; Kazaure, A.A.; Gana, U.; Kiru, M.U. Comprehensive Review of Artificial Neural Network Applications to Pattern Recognition. IEEE Access 2019, 7, 158820–158846. [Google Scholar] [CrossRef]
- Skrypnik, A.N.; Shchelchkov, A.V.; Gortyshov, Y.F.; Popov, I.A. Artificial neural networks application on friction factor and heat transfer coefficients prediction in tubes with inner helical-finning. Appl. Therm. Eng. 2022, 206, 118049. [Google Scholar] [CrossRef]
- Lu, C.; Li, S.; Lu, Z. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2022, 262, 111718. [Google Scholar] [CrossRef]
- Mir, A.A.; Alghassab, M.; Ullah, K.; Khan, Z.A.; Lu, Y.; Imran, M. A Review of Electricity Demand Forecasting in Low and Middle Income Countries: The Demand Determinants and Horizons. Sustainability 2020, 12, 5931. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education Limited: London, UK, 2016. [Google Scholar]
- Fu, X. Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control. Mod. Power Syst. 2022, 7, 5. [Google Scholar] [CrossRef]
- Abubakar Mas’ud, A. Comparison of three machine learning models for the prediction of hourly PV output power in Saudi Arabia. Ain Shams Eng. J. 2022, 13, 101648. [Google Scholar] [CrossRef]
- Sangrody, H.; Sarailoo, M.; Zhou, N.; Tran, N.; Motalleb, M.; Foruzan, E. Weather Forecasting Error in Solar Energy Forecasting. IET Renew. Power Gener. 2017, 11, 1274–1280. [Google Scholar] [CrossRef]
- Verma, T.; Tiwana, A.; Reddy, C.; Arora, V.; Devanand, P. Data Analysis to Generate Models Based on Neural Network and Regression for Solar Power Generation Forecasting. In Proceedings of the Intelligent Systems, Modelling and Simulation (ISMS), Bangkok, Thailand, 25–27 January 2016; pp. 97–100. [Google Scholar]
- Tao, Y.; Chen, Y. Distributed PV power forecasting using genetic algorithm based neural network approach. In Proceedings of the 2014 International Conference on Advanced Mechatronic Systems, Kumamoto, Japan, 10–12 August 2014; pp. 557–560. [Google Scholar]
- Brenna, M.; Foiadelli, F.; Longo, M.; Zaninelli, D. Solar radiation and load power consumption forecasting using neural network. In Proceedings of the Clean Electrical Power (ICCEP), Santa Margherita Ligure, Italy, 27–29 June 2017; pp. 726–731. [Google Scholar]
- Talayero, A.P.; Melero, J.J.; Llombart, A.; Yürüşen, N.Y. Machine Learning models for the estimation of the production of large utility-scale photovoltaic plants. Sol. Energy 2023, 254, 88–101. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Lai, Y.-H.; Huang, C.-L.; Phuong, N.T.B.; Tan, W.-S. Artificial Intelligence Applications in Estimating Invisible Solar Power Generation. Energies 2022, 15, 1312. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Rashid, T. Make Your Own Neural Network; CreateSpace Independent Publishing Platform: North Charleston, SC, USA, 2016; Volume 29. [Google Scholar]
- Nrgaard, M.; Ravn, O.; Poulsen, N.K.; Hansen, L.K. Neural Networks for Modelling and Control of Dynamic Systems: A Practitioner’s Handbook; Springer: London, UK, 2000. [Google Scholar]
- Silva, I.N.d.; Spatti, D.H.; Flauzino, R.A. Redes Neurais Artificiais para Engenharia e Ciências Aplicadas; Artliber Editora: São Paulo, Brazil, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).