Abstract
Non-destructive measurements of high aspect ratio microscale features, especially those with internal geometries such as micro-holes, remain a challenging metrology problem that is increasing in difficulty due to the increasing requirement for more complexity and higher tolerances in such structures. Additionally, there is a growing use of functional surface texturing for improving characteristics such as heat transfer and wettability. As a result, measurement techniques capable of providing dimensional form and surface finish for these features are of intense interest. This review explores the state-of-the-art inspection methodologies compatible with high-aspect-ratio structures and their suitability for extracting three-dimensional surface data based on identified high-aspect ratio structure types. Here, the abilities, limitations, challenges, and future requirements for the practical implementation and acceptance of these measurement techniques are presented.
1. Introduction
Component miniaturisation is an essential part of the technological development driven by the evolution of microfabrication techniques such as micro-electro discharge machining [1,2], ultrasonic micro-cutting [3]/drilling [4], micro- and nano-lithography [5,6], nanoimprint [7], and micro-moulding and forming [8]. This allows the creation of structures tens of micrometres in diameter and greater than 1 mm in depth, such as micro-holes, -nozzles, and -channels.
There is also increasing interest in the application of functional surface texture for improving performance characteristics of parts, especially within areas of heat transfer [9,10,11,12,13,14], lubrication [15,16,17], and wettability [18,19,20,21,22,23,24]. The development and increasing use of additive manufacturing for functional parts also allows for the construction of parts which are impossible to manufacture through conventional methods of machining. This includes complex internal cavities for weight reduction, performance enhancement, and compactness of design.
Internal features, especially those of small blind holes and internal micro-structures, present significant metrological challenges and are typically more difficult to measure than external features. The main difficulty in performing precise and accurate measurements of micro-holes using contact probe-type approaches is the contact force, which can damage the sample. Additionally, the limited probing space often requires a long and thin probe, which can lead to stylus deformation and measurement error. Measurement speed is also limited in order to reduce the probe’s impulse leading to slow scanning speeds. Traditional optical measurement techniques are inhibited by the line of sight, where the radiation beam is obstructed or reflected by the sidewall of the micro-hole. These challenges have led to the development of a wide range of sensors for probing hard-to-reach regions.
Despite measurement difficulties, it is necessary to inspect the fabricated products to verify and improve their quality, which requires accurate and repeatable measurements of component geometry and surface texture. This leads to implications on the required measurement range, speed, and resolution in both axial and radial dimensions. As these high-aspect-ratio (HAR) structures increase in complexity, the chosen metrology tools used to characterise these features must have an appropriate level of performance.
This review covers the state-of-the-art technologies suited for providing a three-dimensional measurement of HAR features, focusing on internal geometries along with a critical analysis of their performance. Here, an overview of noted current limitations and the capabilities of each method are presented, summarised, and contrasted with another.
1.1. Exemplar Features
The areas considered in this review are measurement techniques for form and surface texture metrology in HAR structures for internal structures with a diameter of 0.1 mm to 10 mm and depths greater than 1 mm. These structures can be separated into four categories: (1) straight; (2) tapered; (3) with internal geometry; and (4) non-straight. For micro-hole structures, there are five geometric features which are of primary interest: (1) cylindricity; (2) diameter; (3) straightness; (4) taper; and (5) surface roughness. Each measurement technique’s ability to measure the above structures and geometric features is highlighted within this review.
Some exemplar micro parts with HARs are shown with applications and typical dimensions in Figure 1. It can be seen that, for all of these parts, both dimensional and surface roughness parameters are of critical importance to their intended operating characteristics, and further that the feature scales are very challenging.
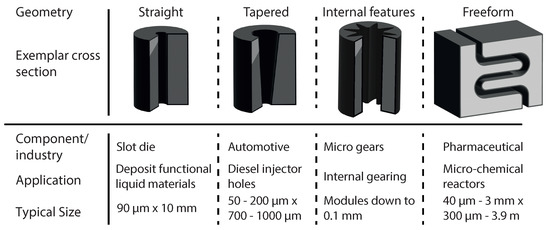
Figure 1.
Geometry types with exemplar cross-sections, associated components and dimensions from industrial applications [25,26,27,28,29,30,31].
1.2. Measurement System Requirements
The following considerations should be applied when selecting a probing system for dimensional analysis of HAR structures: (1) minimising system cost—the implemented sensing principle should be as simple as possible with a minimal number of sensors; (2) ease of integration with scanning technologies such as a CMM/CMM/motorised stages and required measurement mechanism—scanning or point base; (3) ability to measure in workshop environments or on-machine–environment impact; (4) measurement speed; (5) traceability and calibration; (6) probe dimensions; (7) operating range; and (8) measurement characteristics: resolution, accuracy, precision and, uncertainty. For features such as holes, the ability to measure the sidewalls may only be required due to manufacturing philosophy dictating extending the hole deeper beyond required removing the requirement for a measurement operation.
The measurement techniques presented as part of this review are separated into contact and non-contact methods and then sub-categorised based on the measurement principle employed; this separation can be seen in Figure 2 in addition to the section in which each measurement technique is discussed.

Figure 2.
Contact and non-contact measurement techniques and their corresponding location in the paper.
2. Contact Measurement Techniques
The main issues associated with tactile microprobes include surface force effects, probe stiffness, probing force, pre-travel speed, constant contact–stylus flight (trackability), sensitivity to operating conditions, fabrication difficulty, cost, and probe contamination. These elements are expanded upon below.
At the micro-scale, surface interactions can become the dominant force over gravity. These forces include capillary, van der Waals, and electrostatic forces and each is affected by the material, surface properties, environment, and probe size [32]. Surface forces attract the probe tip to the sample surface and can result in a stick-slip effect during scanning measurements [33], potentially contaminating the probe tip or surface and reducing measurement repeatability and accuracy. These effects can be reduced by increasing the probe stiffness or introducing probe vibration.
To measure HAR microstructures, probes need to have a long thin stylus. Due to this, stylus bending and contact deformation of the probing head limit the measurable depth. Increasing probe stiffness can produce large measurement forces, which may result in plastic deformation of the measured surface [34] and probe tip wear during scanning measurements. Work in micro-CMMS has been aimed at reducing the probing force to several mN [35]; however, by reducing the triggering force, false positives become increasingly likely, and due to the inertia of the probes, slow scanning speeds may be required.
Due to the long slender probing shaft required for HAR measurements, a significant amount of shaft bending (elastic deformation) can occur during measurement, which needs to be accounted for when determining the instance of contact. This can be described by Equation (1) [36] for a symmetrical cylindrical shaft of diameter d and length l, under a probing force F with Young’s modulus E.
According to Hertz theory, the maximum probing force F before plastic deformation occurs can be described by Equations (2) and (3) and varies depending on the probing sphere radius R [37]:
where is the yield strength of the workpiece, v is the Poisson’s ratio, and is the equivalent Young’s modulus of the corresponding contacting probe p and sample s surface.
Noting that some probes have an operating range of just a few micrometres, if the approach speed of the probe to the surface is too high, then over-travel after contact with the sample surface may occur, leading to damage to the sample or probe. The maximum operating speed u for a probe of a set mass m can be calculated by Equation (4) [38].
During scanning profilometry, the stylus tip cannot always follow the surface variation of the sample; this separation of the stylus tip from the measured surface is referred to as stylus flight (also known as trackability) and produces errors in the measured profile. Methods for compensating for these errors through hardware modification (spring stiffness, stylus mass) have been demonstrated along with enhanced control using kinematic modelling to predict the influence of the measurement setup [39]. Error compensation for triangular microstructures has also been demonstrated, correcting errors caused by the specimen inclination and the probe radius [40].
When measuring microscale components, the measurement uncertainty is required to be very low, often less than 100 nm; this means that environmental effects such as temperature variation and vibrations from the floor or acoustic excitation become a crucial impacting factor on measurement quality [41]. This limits many techniques’ ability to be transferred out of the laboratory environment towards the shop floor.
The manufacture and assembly of microprobe systems with a HAR and high sphericity probe tip are difficult to achieve at the required size and within the required tolerances [42]. Ball tips with a diameter of less than 100 m and a sphericity and eccentricity of far less than 1 m are specified for the measurement of micro features [43], and the production of probe sizes down to diameters of 50 m have been demonstrated [44]. Current manufacturing approaches can be grouped into the two following categories: either the spherical probe tip is attached to a shaft, or the end of a probe shaft is melted to produce a probe tip [45]. Suitable microspheres are commercially available, and at a laboratory scale, production can be effectively attached to the probe tip via adhesive bonding [45]. However, this process does not currently scale well to commercial production volumes. Melting or fabricating the probe tip [32,46] produces characteristics (diameter, sphericity, and surface texture) which are strongly dependent on the processing conditions, requiring post-process dimensional verification. This adds time and cost due to the current lack of on-machine measurement approaches appropriate for manufacturing line implementation [47].
Probe surface contamination arising from the physical contact between the probe and measured surface gradually builds up on the surface of the stylus tip and affects the dimensional accuracy of the measurement [48]. Additional inspection should also accompany the cleaning procedure to verify the effectiveness, determine an appropriate cleaning interval, and identify contamination or probe damage. Inspection in situ is challenging with the use of microscopy demonstrated in literature [49], which increases system cost, complexity, operation downtime, and applicable implementation environments.
Many types of microprobe systems have been proposed [36,50,51] and can be broadly classified by their detection mechanism. This work distinguishes contact probes into three groups: (1) flexure-based probes with an elastic mechanism, (2) vibrating probes, and (3) fibre-based probes using optical detection methods, though some hybrid systems exist.
Some techniques are not covered within this work due to their inability to measure HAR features on the scales identified, long scanning times, and/or high sensitivities to environmental disturbances; these include optical trapping probes [52], 3D atomic force microscopy probes [53], and tunnelling effect probes.
2.1. Elastic Mechanism-Based Flexure Probes
Elastic mechanism-based flexure probes consist of three major components, as shown in Figure 3a: (1) a stylus; (2) an elastic mechanism; and (3) sensors to detect the deflection. Typically, the stylus is attached to a floating plate with a probing sphere at its free end. This floating plate is suspended with an elastic mechanism. At the point of contact, the elastic mechanism’s deformation is detected by a series of sensors. These sensors can be broadly categorised as either electrical (capacitive, piezoresistive, and inductive) or optical methods (interferometric, laser beam deflection, and fibre Bragg gratings (FBGs)). The profile of the part is constructed by determining the location of the probe once contact with the part has been detected at discrete locations.
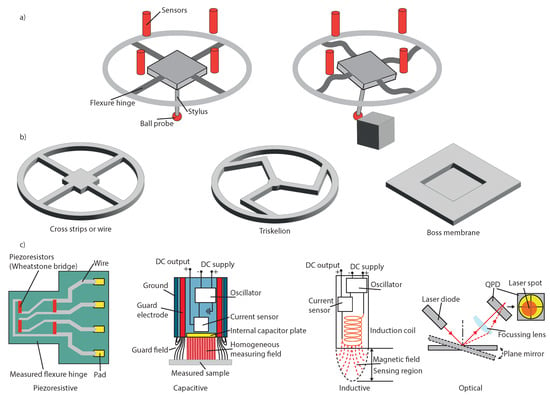
Figure 3.
(a) Schematic showing the principle of operation for flexure hinge-based tactile probes and an overview of the components and sensors commonly applied in the creation of these probes, (b) Common flexure hinge designs, and (c) Common sensing principles used to detect distortion of the flexure hinges.
The elastic mechanism is typically constructed from Beryllium–copper flexure strips, microwaves, patterned leaf springs, slender rods, flexure hinges, or membranes [54,55,56] example hinging mechanisms are shown in Figure 3b. The use of variable stiffness probing systems has been shown to reduce the contact force whilst maintaining measurement speed [57,58]. Additional approaches include the use of a mechanical-magnetic coupled structure to ensure a constant force of the scanning probe [59].
Isotropic probing stiffness for constant deflection is important because it directly relates to the contact force. Highly anisotropic (materials/structures) may cause the slipping of the probe tip, resulting in component damage and decreased measurement quality. Additionally, coupling between the 3-axis deflection is prevalent in many of the presented implementations, potentially leading to measurement errors.
The following sections provide an overview of flexure hinge probes with approaches separated according to the sensing principle used.
2.1.1. Piezoresistive
Piezoresistive sensing techniques measure the change in electrical resistivity due to the deformation of piezoresistive strips either bonded onto the elastic suspension or which make up the suspension, allowing for determination of the probe tip deflection. Microprobes can be made from monocrystalline silicon, which exhibits a strong piezoresistive effect; this allows for integrated sensitive sensors in thin mechanical constructions. Silicon also benefits from the use of advanced fabrication processes at the wafer level, offering low cost and high manufacturing accuracy and reproducibility. However, these sensors are affected by temperature variation, exhibit self-heating, and typically have a small deflection range of <10 m.
The emergence of these probes began in the late 1990s [60,61]. One of the early designs used a three-element diaphragm with integrated strain gauges similar to the three-element configuration is shown in Figure 3b. This probe can achieve an uncertainty below 10 nm when probing in the z-axis. However, due to the hinge design, when this system is displaced in the z direction, it exhibits parasitic translations in the length direction of the rods producing a rotation around the z-axis [60,62]. It was found that a reduction in drift and hysteresis effects could be achieved through the removal of globtop from the MEMS electrical connections; this was due to the material’s visco-elastic effects [63]. Compensation for the probe’s anisotropic behaviour through mechanical design was demonstrated, resulting in an approximately fourfold increase in measurement range and reduction in uncertainty over this range [64]. This probe was further developed and shown to exhibit an XYZ repeatability (k = 1) is 2 nm over its measurement range and an uncertainty (k = 2) of 17.4 nm [65]. This probe is now commercially available from Xpress Precision Engineering B.V. as the ‘Gannen XP.’ The Gannen XP is typically used with a stylus of 6.8 mm exhibiting an isotropic stiffness of 480 N/m with similar sensitivity in each probing direction.
The Physikalisch-Technische Bundesanstalt (PTB) probe was based on a boss membrane with four piezoresistive sensors located at each branch of the elastic mechanism [61]. This gave a repeatability (k = 1) of 4.4 nm in the XY, and 1.3 nm in the z-axis [66]. However, in this configuration, the membrane suspension is overdetermined, resulting in a non-linear stiffness, and the length of the membrane must increase when the probe tip is moved; this prevents the use of this probe in a scanning machine with standard controllers. The stiffness of this microprobe was later modified by inserting apertures into the membrane producing higher mechanical strains and sensitivity and increasing the operating deflection range of the probe from 30 m to 50 m in the vertical axis. This system demonstrated high accuracy in the measurement of micro-gears with a measurement standard deviation (STD) (k = 2) of <100 nm.
In 2019 the Institute of Microtechnology (IMT), in collaboration with PTB, re-designed the silicon-piezoresistive microprobe. Here, three orthogonally stacked silicon-based measurement cells are able to isolate displacement per cell along a transverse axis with three identical measuring cells allowing for XYZ displacement detection. This probe has a low stiffness in the XY plane of approximately 320 N/m with an anisotropy of 1.1:1. This produces contact forces of approximately 15 mN when using a stylus with a probe tip diameter of 300 m, and a 2 mm shaft, this configuration is able to operate over a much larger measurement range of ±400 m but has a lower resolution of 200 nm to 500 nm [67].
A compliant cantilever implementation using piezoresistive elements in a Wheatstone bridge configuration for the determination of deformation of the cantilever beam was shown in 2008. A stylus of length 1.5 mm to 5 mm, width 30 m to 200 m, and thickness 25 m to 50 m with an operating range of a 200 m, nanometre resolution, and several tens of N probing force have been produced [68]. A low probe wear (few nm/m) was observed whilst performing scanning measurements of a roughness artefact with a probing force of 30 N and scanning velocity of 0.5 mm/s, with features less than 1 m in width being resolvable [69].
In 2014, a closed-loop system where the cantilever readout signal served as the control signal to the moving stage was shown. The contact force between the cantilever and the artefact surface could be set before measurements. An uncertainty of (k = 2) ±10 nm during a measurement speed of 20 m/s and probing force of 7 N was demonstrated [70].
2.1.2. Capacitive
Capacitive distance sensors can achieve nanometric resolution with a measuring range of hundreds of micrometres and low mass. However, they exhibit a non-linear response across their measuring range, and the measured response is a function of the air permittivity, which depends on the temperature, barometric pressure, and the CO content of the ambient air.
In 1999, the National Physical Laboratory (NPL) demonstrated a miniature probe with a three-element diaphragm using beryllium–copper flexure strips and capacitance sensors placed above each strip. The probe exhibited equal stiffness in XYZ axes with a low probing force of 0.1 mN at 10 m displacement and a working range of ±20 m and a confirmed resolution of 3 nm and a theoretical uncertainty (k = 1) of 11 nm [71].
In 2012, the Institute of Machine Tools and Manufacturing (IWF) presented a probing system using a three-element elastic mechanism similar to NPL but with a replaceable probing stylus which also operates as a mechanical fuse and can be manufactured with standard metal cutting machine tools [72]. Here, the uncertainty (k = 2) is increased to ±220 nm in the XY axes and reduced to ±30 nm in the z-axis.
In 2013, a new approach to capacitive sensing was developed using a differential capacitor to detect probe deflection, using the flexure itself as a capacitive element as opposed to external capacitive sensors. This system reduces the total probe mass and tackles the issue of expense by using low-cost and highly accurate MEMS manufacturing techniques. Experimental results indicate this probing system could be used for the sub-micrometre measurement of small structures. A stiffness of 22.62 N/m in the x and y axes, and 337.84 N/m in the z-axis were demonstrated with a displacement resolution better than 10 nm along the axial direction and 25 nm along the radial direction [73]. However, the system only has a scanning range of 1 m. A similar approach was taken in 2014, demonstrating a sensor resolution of better than 5 nm, with a measurement range of 11.6 m [74].
2.1.3. Inductive
Inductive sensors generate a high-frequency electromagnetic field; if a metallic object enters this field, the field will be altered depending on the object’s distance, material, and size. This detected change can be used to determine object distance. Such probes offer a high dynamic range and are less sensitive to environmental influences than capacitive sensors. However, typically inductive probes are larger and bulkier than the alternatives mentioned in this section because they require a larger coil of wire to generate the electromagnetic field needed for induction. Due to the use of an electromagnetic field, these sensors are also sensitive to electromagnetic influences, such as nearby electromagnetic fields or currents, which can affect the accuracy of the measurement and may require special precautions such as shielding the probe or using it in a shielded environment, to prevent interference.
The Federal Institute of Metrology (METAS) developed a tactile probing system which utilises inductive sensors to determine probe deflection after contact with the measured surface. The METAS probing system uses three perpendicular transversal axes formed with a monolithic spring box mechanism with aluminium flexure hinges. The displacement in each axis is measured via three inductive sensors mounted on the probe housing. The probe has an isotropic stiffness of 20 N/m, giving a repeatability (k = 1) of 5 nm across a measurement range of ±200 m [35,38,75].
2.1.4. Optical
The use of optical techniques to determine the deflection of the probing system is an area of very active research. Three approaches dominate: detecting flexure detection using the position of a reflected laser beam on quadrant photodetectors (QPDs), position-sensitive detectors (PSDs), and interferometric approaches.
QPD and PSD
QPDs and PSDs are two types of photodetectors that share a similar functionality: detecting the position of an incoming light spot. They are commonly used as low-cost, miniature optical displacement sensors in various applications, such as DVD pick-up heads. QPDs are equipped with four individual detector elements, whereas PSDs feature a single detector element divided into multiple pixels. PSDs can be manufactured in various sizes and shapes and are generally more affordable than QPDs. However, using PSDs instead of QPDs comes with some trade-offs in terms of sensitivity and accuracy. The response of PSDs/QPDs is sensitive to the shape and size of the detected light spot. These parameters require careful adjustment to ensure that the initial signals of these sensors are set to approximately “zero” before measurements.
These probes determine the displacement/rotation of a surface by detecting a laser beam reflected from the surface and measuring the displacement from the ‘zeroed’ position, as shown in Figure 3c. Other analysis methods have also been used, such as determining the astigmatic focus error by placing cylindrical lenses before the detector and observing the incident spot shape. Probes typically require multiple PSDs/QPDs or cooperation with other sensing methods to achieve part detection in 3D due to signal coupling between horizontal and vertical displacements [55].
In 1998, a tactical probe capable of XYZ deflection detection was created using three PSD-based sensors operating on the principle shown in Figure 3c. The probe was supported by a three-element elastic flexure hinge and consisted of a stylus of length 40 mm and diameter 2 mm and a 4 mm diameter probing head. The evaluated measurement uncertainty (k = 2) of the probe was 0.5 m and was able to achieve an accuracy of 1.5 m at a 70 mm/s high probing speed [76].
In 2007, the use of two commercial DVD optical pickup heads (QPD-based) to reduce system cost was shown. The first sensor measures stylus motion in the Z-axis using the mentioned focus error method, and the second measures rotations about the XY axes using the approach shown in Figure 3c. The probe was suspended by a cross-form structure made of thin steel strips to limit the degrees of freedom (DoF) to 3, preventing rotational motion about the z-axis and limiting translation of the probe in XY. However, this system only operated as a touch trigger probe, so scanning was not possible. With a trigger threshold set to a pre-travel distance of 0.5 m and corresponding trigger force of >0.1 mN, this system gave a pretravel error of less than 96 nm and a unidirectional repeatability (k = 2) of 46 nm. A sensitivity to variation in temperature was found with a 52 nm change in readout over 20 min with a ±0.5 K fluctuation [77].
To further reduce system cost, size, and complexity, an investigation into using a single QPD as a 2D angle sensor for a touch trigger probe was developed in 2015 and characterised in 2016. A four v-shaped ‘leaf’ flexure configuration was used, demonstrating a near isotropic stiffness of less than 1000 N/m and linear trigger range of 1 m and maximum operating range of ±8 m. A stylus 10 mm long with a 0.5-mm diameter probe tip was used and demonstrated to have a unidirectional repeatability (k = 2) of less than 4 nm in XYZ and a resolution below 5 nm when measuring a 2 mm × 2 mm square hole. The thermal drift whilst operating was at a temperature of 20 ± 0.05 C 3 nm over 2 h [78,79]. This design was later simplified, and the maximum operating range was extended to ±14 m.
In 2022, a touch trigger probe based on a modified optical lever method with a resolution of up to 1 nm was achieved in 3D, with a measurement uncertainty (k = 1) of 18.45 nm and an operating range of ±20 m with mN level contact force. This work used a single QPD. To improve the sensitivity of the probe in the vertical direction, an asymmetric elastic suspension design was implemented [55]. A 5.2 nm thermal drift over 30 min was determined with a temperature variation of less than 0.04 C.
In 2015, another implementation used five commercial DVD optical pickup heads (QPD-based) with astigmatic focus error processing to determine offset distance from the QPD for surface scanning. A new vertical orthogonal sensor configuration was implemented; this allows for opposing sensors for the xy axes and differential detection improving the sensor resolution by 2 to 0.5 nm in xy and 1 nm in z due to there being a singular sensor. The probe consisted of two sections, a 100-mm-long carbon fibre bar and a 2.5-mm-diameter, 50-mm-long ceramic rod, and a 3-mm probing ball. The maximum deflection was 6.7 m with a probing force of 5.15 mN (1470 N/m × 3.5 m) with a measurement uncertainty (k = 2) of ±0.28 m. A thermal drift of 8 nm over 30 min when operating in temperature controlled environment of 20 ± 0.2 C was determined [80].
A double elastic mechanism with two QPD angle sensors was implemented in 2018 for scanning measurements whilst decoupling horizontal and vertical displacement signals of the probe to improve system sensitivity and accuracy. Here, each layer of the elastic mechanism was detected using a QPD [81]. The system was able to achieve a resolution better than 5 nm and repeatability (k = 1) of 18.2 nm over an operating range of less than ±10 m, and a thermal drift of 23 nm over 30 min within a temperature-controlled environment within 0.13 C.
QPD + Interferometric
Hybrid implementations using both a QPD-based 2D angle sensor and a Michelson interferometer have been shown in the literature. In 2010, a system using a singular laser beam focused onto the backside of the flexure element, the reflected beam was then split by a beam-splitter with one part directed to a QPD detecting tilt about the xy axes, and the other part was directed to the interferometer to determine z-axis deflection. A theoretical resolution of 0.3 nm for the interferometer and 0.93 nm for the tilt measurement system with a repeatability (k = 2) in all directions of 3.4 nm was noted. However, this probe was limited to a maximum scanning speed of 5 m/s due to surface interactions and anisotropic stiffness [56,82].
To avoid sensing coupling between XYZ displacement on the QPD 2D angle sensor, a new optical layout was developed [83]. A resolution of 1 nm was indicated from experimental results, and a measurement uncertainty (k = 1) of 30 nm with an isotropic probing stiffness of 1000 N/m. However, it also reduced the operating range to ±10 m because the reflected beam separated from the interferometer reference beam during horizontal probing. The probe stylus was 10 mm in length and 0.5 mm in diameter with a 1 mm diameter probing ball. The thermal drift was less than 50 nm over three hours in an environment with temperature fluctuations less than 0.05 C. To expand the measurement range to ±20 m, a parallel optical path using two separate laser diodes was established [84], the leaf spring design was altered to provide a stiffness of 500 N/m with an average contact force of 11 mN.
Interferometric
In 2010, the use of a Fizeau interferometer to detect the deflection of a probe’s floating element was demonstrated. A theoretical resolution of 100 nm in the xy plane and 40 nm in the z-axis was stated with a measured repeatability (k = 2) and uncertainty (k = 2) of 190 nm and 240 mm, respectively. A 160 nm thermal drift over 4 hours was determined under 20 ± 0.05 C operating conditions [85].
2.2. Vibrating Probes
The use of vibrating probes has been shown to have benefits in terms of low measurement force and reduction of the influence of sticking [86]. However, these systems typically have small operating ranges requiring slower scan speeds and increased sensitivity to changes in the environment. There have been many types of vibrating probes reported in the literature relying on different detection mechanisms, including the use of vibroscanning–electrical contact, resonant probes using vibration analysis, and acoustic emission.
2.2.1. Vibroscanning—Electrical Contact
The vibroscanning technique was first presented in 1993 [87], operating on the principle of sensing electrical contact between a vibrating probe and the measured sample. The location of the sample is determined by the duration of contact per vibration period of the probe; thus, scanning-based profile measurements are possible. An on–off voltage signal of several volts is achieved. Hence little amplification is required giving a high signal to noise (SNR). The probes vibration also prevents dispersion of electrical contact, improving result reliability. However, the application of this method is restricted to electrically conductive materials. This also influences the measurement reproducibility because the process parameters depend on the sample material. The principle of operation is shown in the schematic in Figure 4a. Scanning measurement speeds of up to 50 m/s have been demonstrated [88].
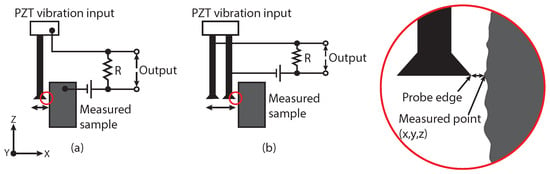
Figure 4.
Schematic of vibroscanning probe in (a) single-probe conductive contact and (b) double-probe non-conductive contact implementations.
Extension of this technique to non-electro-conductive materials using a twin probe approach has been demonstrated [89]. The principle of operation is shown in Figure 4b. Here, the electrical contact condition is between two probes with a narrow gap between them of approximately 5 m. Investigation into fabrication methods and materials allowed for probes up to 3 mm in length and 20 m in thickness to be produced [90]. Demonstration of this technique for the measurement of micrometre scale HAR structures has also been presented with measurement speeds of up to 2 mm/s and an estimated precision of 0.5 m [91].
2.2.2. Resonant Vibration Probe
The detection of a vibrating probe’s change in resonance frequency due to contact or interaction with the measured component’s surface has been largely discussed in the literature with several designs presented, including the use of piezoresistive elements, MEMs systems, tuning forks for creating a standing wave, and shear force detection. Here a probe with a HAR shaft is typically attached to a tuning fork oscillator or bulk lead zirconate titanate (PZT) element such that when the oscillator vibrates the shaft, the free end creates a free-standing wave with an amplitude greater than the probe shaft diameter. Interactions between this vibrating end and the measured surface lead to a change in the vibration response, which can be used to determine distance from the object. It has been identified that for a multi-axis vibrating probe, the maximum and isotropic sensitivity throughout the sensor’s measurement range is achieved when a probe has repeated natural frequencies [92].
These probes can achieve high resolution with very low probing force, and are not as affected by sticking surface forces. However, they typically operate as touch trigger probes without the capability to perform scanning measurements, have a limited measuring range, are fragile, are not suitable for in situ measurements with sensitivity to vibrations which can affect measurement accuracy, and can be more complex to design and operate requiring specialised knowledge and equipment.
Piezoresistive Vibrating Probe
The use of PZT elements was shown in 2000 with the creation of a cantilever-type probe constructed from a thin silicon cantilever with an integrated sharp tip. Here, a drive PZT causes the probe to resonate, and a detection PZT film is used for vibration sensing, as shown in Figure 5a. This technique is based on the detection of a resonance frequency shift, which is produced by the strain caused by the mechanical contact between the probe and the sidewalls. This system is able to perform sidewall scanning measurements of HAR features by vibrating in the axis of probing (tapping). The cantilever probes vary from 20 m to 500 m in diameter and 10 m to 2000 m in length. Operating with an accuracy of 0.1 m and a contact force predicted to be less than 50 N [93]. This probe was demonstrated by measuring 200 m diameter holes to a depth of 1 mm. However, the measurement performance varies with approach and bending direction. Alternative approaches using axial vibration of a stylus allow for equal vibration restraint independent of the approach direction [94]—however, the application of this technique to HAR 3D measurement, especially for side walls, is difficult.
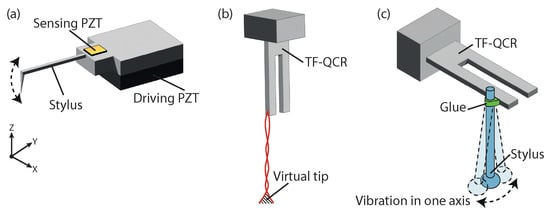
Figure 5.
Operating principle of vibrating resonance probe-based tactile measurement techniques. (a) Cantilever probe, (b) standing wave probe using a tuning fork quartz crystal resonator (TF-QCR), and (c) shear force probe using a TF-QCR.
In 2010 NPL developed a vibrating probe with a three-element suspension and two built-in PZT actuators per flexure, allowing for vibration in the direction of probing [95]. Subsequently, in 2013, they presented the characterisation of the sensor [96]. The probe was demonstrated vibrating with an amplitude of 0.3 to 1.5 m, and through analysis of the signal phase, the surface could be detected approximately 100 nm from the object; hence a zero-force measurement could be achieved. However, accurate determination of this distance is difficult to achieve.
MEMS
The development of a MEMS-based microprobe system utilising three electrostatic actuators for precise control of stylus probe vibration in xyz axes, and differential capacitive sensing for measuring the shift in oscillation amplitude and phase has been demonstrated. The use of electrostatic actuators provides an attractive alternative to PZT transducers, as they can be easily integrated into MEMS devices, allowing for low-cost batch production, reduction in crosstalk, and high force output. However, these actuators are sensitive to environmental conditions such as humidity and particle density and require operation in a controlled measurement chamber.
The probe oscillation amplitudes are set at x = 0.5 m, y = 1 m, and z = 2 m, with a predicted contact force of less than 20 N. The sensor has demonstrated a high contact resolution of 45 nm in the Z direction and 30 nm in xy. However, the triaxial microprobe only provides binary information in the xy directions, indicating only whether there is contact or not [97].
Standing Wave
The use of a standing wave probe has been demonstrated for very low contact force measurements (estimated as less than 50 nN). Here, a slender probe is bonded along the length of a tuning fork. When the tuning fork is excited, it causes the probe to oscillate and create a standing wave at its free end, as shown in Figure 5b. The free end has a length of 5 mm and a diameter of 7 m, which produces a virtual tip ranging from a few micrometres to several tens of micrometres. This virtual tip creates a region greater than the diameter of the shaft, removing the need for a probing element and reducing system complexity and cost while enabling the measurement of very small diameter features. The tuning fork provides both actuation to the probe and detects changes in the signal, allowing for the determination of the probe’s contact with a surface [98].
The probe oscillates in a single horizontal direction, making it sensitive in 1D, and it should be positioned normal to the measured surface through positioning stages. This probe was shown to achieve repeatability (k = 1) between 56 nm and 229 nm when measuring step heights in contact and non-contact modes, respectively [99,100].
Another approach using a quartz tuning fork as the input was shown in 2017. Here, the microsphere tip of the probe interacts with the sample surface in tapping mode in the z-axis, whereas it interacts in friction mode in the xy plane though it cannot distinguish the contact direction. The unidirectional repeatability of the probe was approximately 40 nm with a sub-nanometre resolution of 0.38 to 0.45 nm in all directions [101].
Shear Force
Generally, there is a thin liquid layer on the surface of an object measuring in the tens of nanometres in thickness. In 2014, the damping effect this layer has on a vibrating probe was used to detect the distance from a measured sample’s surface [25,102]. The probe consists of a glass micro-stylus shaft with a micro-glass sphere attached to one end; the stylus is attached to a tuning fork quartz crystal resonator (TF-QCR) which is driven by a PZT at the TF-QCR’s resonant frequency, as shown in Figure 5c. Here, the positioning stage control is very important because the gap between the probe tip and the surface is a few tens of nanometres when the probe signal changes. Probes with tip diameters between 9 m to 100 m have been demonstrated operating with measurement uncertainty (k = 2) of 78.3 nm [103] and resolution of less than 3 nm [104]. As the measurable detection is limited to one direction, the application of this technique for the measurement of features such as micro-holes or free-form surfaces is difficult.
2.2.3. Acoustic Emission
The use of a rotating wire probe determining contact based on acoustic emission (AE) as a cost-effective and sensitive probing system was presented in 2012 [105]. The probe is created from a stainless steel tube with a wire with a diameter of 177 m bonded onto the tube, as shown in Figure 6. The wire section is bent at an angle of 45 for better repeatability with various probe diameters achievable by cutting the wire to the desired length. When the rotating wire contacts the part surface, a burst of generated AE signal is detected. The AE signal is generated due to the rubbing or impact between the rotating wire and the part surface.
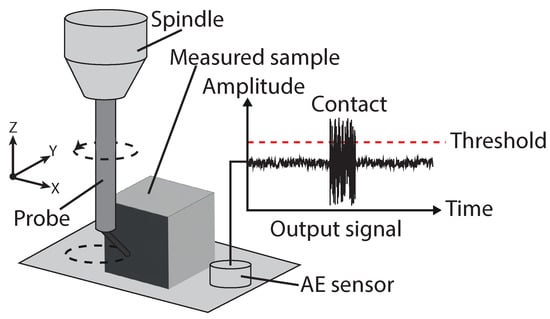
Figure 6.
Operating principle of acoustic emission probes.
Due to the use of acoustic emission to trigger a contact event, surface damage on measured parts is evident though damage may be limited through the selection of wire material [106]; only point-based trigger measurements are possible, surface geometry such as roughness and form can impact on the repeatability of the measurement. This also raises the question of limited traceability to the metre measurement and the requirement for regular calibration with tool wear.
This system has demonstrated the ability to measure micro holes down to a diameter of 500 m at depths of up to 1 mm and triggering repeatability (k = 1) of 126 nm [107].
2.3. Fibre-Probe Deflection
Optical fibre probes take optical measurements of the stylus tip or stem to determine contact with the sample. These probes have high flexibility, low cost, low probing force, and are simple to manufacture. The contact state of the probe tip is measured by detecting the deflection of the fibre using the following techniques: deflection of a guided laser on a pixel array, deviation of the fibre probe’s shadow, and probes with built in FBGs.
2.3.1. Laser Guidance/Back Reflection
PTB and Werth developed a fibre opto-tactile probe in 1998 able to perform 2D measurements, with a 3D implementation being developed in 2001 [108]. Here, an optical fibre serves as the probing stylus and waveguide for a laser diode with a glass probing ball at its tip, which is illuminated by the light exiting the fibre. The light backscattered from the tip is imaged on a CCD sensor as a bright spot, which can be seen in Figure 7a. When the tip makes contact, it is displaced in relation to the camera and the position of the light spot on the sensor changes by a distance , as shown in Figure 7b. A lateral contact resolution of the measuring system of less than 50 nm is predicted, though this is strongly dependent on the quality of the imaged light spot.
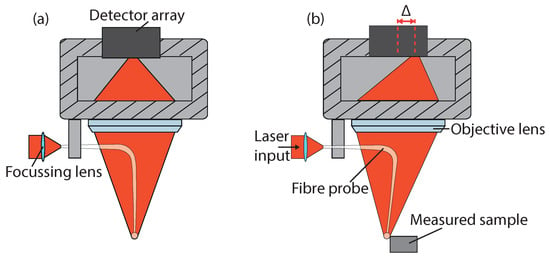
Figure 7.
Operating principle of fibre-probe-based tactile measurement techniques using laser guidance/back reflection. (a) shows the probe in a stationary position, (b) shows the deflected probe due to contact with a measured sample, this results in a shift of the imaged reflected light from the probe tip on the detector array by .
Fibre diameters of 15 m and probing ball diameters of 25 m have been realised [108] allowing for analysis of micro-parts such as micro-gears with probe vibration to overcome stick-slip friction effects [109]. Larger scale probes with a probe diameter of 74 m and a 1.5 mm long, 25 m diameter glass stylus have also been demonstrated for the characterisation of the micro-holes in fuel injectors (160 m diameter × 0.9 mm length) [28].
The Werth probe style design was expanded on in 2011 by coupling the light directed down the fibre probe into a secondary probe attached to the primary probe, allowing for the light to be redirected back towards the detecting camera pixel array. This removed the issue of shadowing for HAR measurements with a reported spatial resolution of 40 nm and measurement repeatability (k = 1) of 60 nm, and probing force of <1 N [110,111,112]. An axicon lens was added to the end of the probe to increase reflection with an improved accuracy of 30 nm in xy plane and maximum deformation of 40 m [113]. This was extended in 2018, using a specifically designed spherical coupler to reduce loss of emergent light in the coupling, improving both the resolution to 10 nm and SNR of output spot and its stability [114].
2.3.2. Probe Deflection Detection
This type of sensor configuration illuminates the cross-section of the fibre probe and detects its shadow on a CCD camera; once contact with a sample occurs, the fibre probe is deflected, and correspondingly its shadow moves across the CCD. This was first described in 2004 [115] and expanded in 2006 [116] with an achievable uncertainty (k = 2) of 70 nm when measuring a fibre ferrule hole (129 m diameter over 0.5 mm depth). Probes with lengths between 20 mm to 30 mm, diameters of 50 m to 125 m, and ball tip diameters 75 m to 155 m have been shown with a contact force of 0.2 N during a 20 m deflection.
Later work in 2010 illuminated the fibre-probe stem from the side with a laser source, as shown in Figure 8a When the stem is deflected, the light is diverted across the receiving camera pixel array, as shown in Figure 8b [117] or in other implementations a dual-element photodiode [32,118]. This approach only measures x and y deflection and exhibits x and y coupling. The vibration of the probe was added in 2012 to prevent stick-slip friction behaviour due to surface forces, requiring characterisation of the vibration path to compensate for elliptical motion [119,120,121].
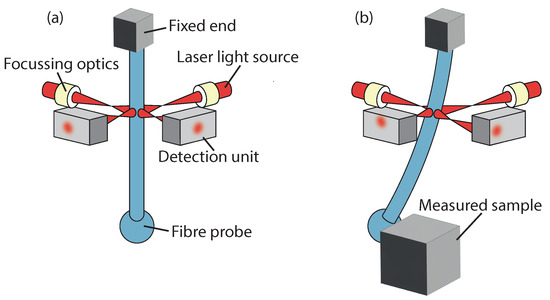
Figure 8.
Operating principle of fibre-probe deflection based tactile measurement techniques. (a) Shows the fibre probe in a stationary position, (b) shows the deflected probe due to contact with a measured sample, which results in a shift of the measured laser spot.
This type of probe can be used in deflection and buckling [122]. However, coupling between buckling and deflection means they need to be operated independently and may impact each other’s results. In 2016, an FBG was used in the fibre-stem probe to both improve axial resolution and decouple the axes [123]. This enabled a radial and axial resolution of 5 nm and 8 nm, respectively, with a repeatability (k = 1) between 39 nm to 50 nm when measuring a 900 m and 800 m diameter ring gauge respectively.
Due to the fibre illumination, there is a limitation to the allowable component width before shadowing. An optical slit can be used to reduce the beam width, but this also reduces the illumination intensity and measurement sensitivity; installing a prism near the stylus shaft has been shown to remove this limitation [124]. Fibre illumination angle using oblique irradiation showed an improvement in measurement sensitivity [125]. The use of contact triggering via displacement threshold detection potentially gives large errors due to the surface geometry resulting in a time lag between real contact and detected contact. A method for detecting the starting point of contact using a Long Short Term Memory (LSTM), a type of deep learning, was shown to reduce this effect to within 0.04 m [126].
Another approach to detecting probe deflection consisting of a fixed block, an optical fibre cantilever with a shaft connected perpendicular to the cantilever with a probing sphere on the end was shown in 2017. Here, a laser beam is coupled into one end of the fibre and emitted from the free end of the fibre cantilever and is focused onto a camera pixel array allowing for the determination of the probe’s deflection [127]. This probe is easy to fabricate, inexpensive, has a high SNR, resolutions of 10 nm, 30 nm, and 5 nm in xyz, respectively, and measurement uncertainly (k = 1) of 45 nm.
2.3.3. Fibre Bragg Gratings
As an FBG is subjected to stress, the reflected Bragg frequency will shift due to a change in the periodic spacing of the grating. Direct integration of an FBG into the core of a fibre probe stem has been demonstrated in 2009 [128], as the probe is deflected due to contact with a sample, the Bragg frequency will shift according to this principle, as shown in Figure 9a,b and thus a correlation with displacement can be determined. This probe is sensitive to axial loading with a measurement resolution of 60 nm but is insensitive along the radial direction due to the fibre core being located in the neutral plane during radial bending. In 2012, the use of a double FBG sensing structure was shown; here, both FBGs are housed in a stainless steel tube, with one FBG acting as a reference and the other extending beyond the end of the tube housing for probing and sensing displacement. This configuration reduces the effect of noise, especially due to temperature changes, with the resulting sensor having an improved axial resolution of 10 nm [129].
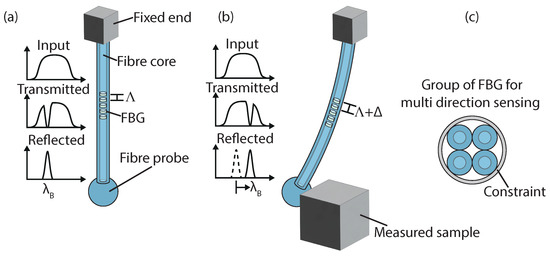
Figure 9.
Operating principle of FBG-based tactile measurement. (a) shows the probe in a stationary position, the input signal into the FBG sensor along with the result reflected value is shown, (b) shows the probe after deflection due to contact with a measured sample, which results in a shift of the reflected wavelength, as shown. (c) shows a top view of a 4-core FBG sensor for multi-direction sensing, the cores are constrained within a rigid tube.
In 2013, the use of a single-core and the simulation of a four-core FBG in a configuration, as shown in Figure 9c, for a touch trigger with a probe of length 5 mm and end ball diameter of 105 m, with an axial resolution of 100 nm was shown. The FBG probe with four cores was determined to have a theoretical axial resolution as high as that of a single-core FBG probe with the capability to decouple 2D radial displacement with a resolution of 13 nm [130]. In 2014, a double fibre probe with a single FBG was shown to be able to measure in both axial and radial directions with an axial resolution of 8 nm and radial resolution of 30 nm [131]. This probe was demonstrated measuring nozzles in the injection plate of a rocket engine with hole diameters from 218 m to 536 m at a depth of 3 mm. This works given that the FBG core is no longer located in the neutral plane with low stress from radial contact displacement. 3D measurements have also been demonstrated using a two and four-core FBG in 2016 [132,133].
From 2016 to 2018, an FBG-based dynamic nano CMM probe was developed. The probe stylus and FBG sensors were fixed onto the support, which was suspended with a three-arm cantilever fabricated via chemical etching. A resolution of 13 nm was achieved with a measurement force of less than 1.5 mN and an xyz repeatability (k = 1) of less than 50 nm [134,135].
2.4. Summary of Contact Measurements
Contact measurement techniques suitable for high-aspect-ratio structure measurements have been presented in this section and are separated by their operating mechanism (flexure hinge, vibration, fibre probe) and summarised in Table 1, Table 2 and Table 3. Although many methods have been presented in the literature, very few have made it through to commercial production with the possibility of being purchased off the shelf. Some commercially available tactile probes are available, including Xpress—Ganenn series and Heimen series probes, IBSPE—Triskelion probe, Mitutoyo vibrating UMAP probe, Werth’s 2D and 3D fibre probes, Zeiss – F25 SSP, and Renishaw TP200.

Table 1.
List of some typical characteristics for flexure hinge based measurement techniques.

Table 2.
List of some typical characteristics for vibration analysis based measurement techniques.

Table 3.
List of some typical characteristics for fibre probe based measurement techniques.
From the tabulated information and previous sections, it can be seen that flexure hinge approaches typically have a higher probing speed than vibration and fibre probes and a higher resolution whilst maintaining a low measurement uncertainty. However, these probes can be difficult to fabricate and require multiple sensing elements increasing probe cost; additionally, they are typically larger than fibre or vibrating probes and hence have a worse lateral resolution.
Vibrating probes offer the lowest probing force with the smallest scale probing heads at a very high resolution. However, they typically can only measure in one direction and can be difficult to use due to their vibration axis. Vibrating probes can also be highly sensitive to their operating environment, especially temperature and vibrations; they also typically have a probing depth which is less than the fibre- and hinge-based methods.
Fibre probes are simple in design and do not require complex electronics or mechanical components, which can lead to a lower cost. These probes have a HAR with shaft lengths into the tens of millimetres. These probes also exhibit low probing forces whilst maintaining a high resolution and low measurement uncertainty/repeatability.
3. Non-Contact Measurement Techniques
Non-contact measurement is of significant interest because it generally allows for fast data-point capture rates allowing for the creation of dense 3D point clouds which more closely represent the sample’s topography without deforming the measured surface. The basic principle of an active non-contact range-finding system is to project an electromagnetic wave onto an object and process the reflected signal to determine its distance. There are many developed techniques for dimensional measurement that fall into this category; however, not all are suitable for the measurement of HAR due to factors such as deployment configuration leading to shadowing effects, material dependence on the measurement result, and the required measurement scale applicable in this review. Approaches covered in this review include low coherence interferometry (LCI), laser triangulation, X-ray computed tomography (XCT), and capacitive.
Optical methods are promising non-contact measurement techniques, able to obtain high resolution and precision [136,137] in the axial dimension. However, contact-type measurements can provide a higher lateral resolution than optical methods; this is due to optical measurement techniques being impacted by the sample’s surface parameters and by the quality of the optics implemented for focusing, with the lateral resolution being ultimately constrained by the diffraction limit.
One of the main issues associated with optical measurement techniques is the effect of the measured component’s properties (geometry, surface, material, etc.) on the measurement result. For instance, some surfaces can introduce spurious phase changes into the light due to material properties. Thus, the relationship between the object properties and the measurement uncertainty must be known for each optical sensor [138].
The reliability of optical profilers is strongly linked to light reflection with diffuse scattering surfaces causing the incident light to scatter in many directions and a marginal fraction back to the observation system. Although well known, this dependence on the surface roughness and texture has not yet been quantified due to the difficulty in understanding the relationship between surface geometry and Maxwell’s equation, with the additional dependency on optical configuration/technique and the surface—change any of these and the relationship changes. This is in contrast to mechanical probing systems, which can be easily modelled and their behaviour simulated to various surface topographies.
As the back-reflected signal from the sample is detected, there is a maximum measurable surface slope angle; this corresponds to half the aperture angle of the optical system. This is given by the Numerical Aperture (NA) equation (Equation (5)), noting that the refractive index n of air is approximately 1. Thus, a smooth surface with an inclination angle greater than reflects no light back to the observation system and cannot be measured. Nevertheless, an optical sensor’s ability to measure steep surfaces can be improved by varying the sample alignment to the sensor’s optical axis [139].
3.1. Low Coherence Interferometry
LCI is based on the principle of coherence gating, allowing for absolute distance measurements to be achieved through analysis of the interference region between the sample and reference signal supplied using a low temporal coherence (broadband) light source or a tuneable laser. There are many configurations that can be used to implement an LCI system, as shown in Figure 10a–c. Here, the use of time-domain, reference scanning Figure 10a, single-shot stepped reference Figure 10b, and Fourier/spectral-domain Figure 10c implementations are shown. These systems can provide absolute depth-resolved measurements, simple sensor multiplexing, and fibre-optic coupling with high axial and lateral resolutions. However, these probes only have the capability to measure in one dimension, making them subject to drift within the measured hole about the axis of rotation and unable to perform measurements of overhangs or the bottom of holes/features.
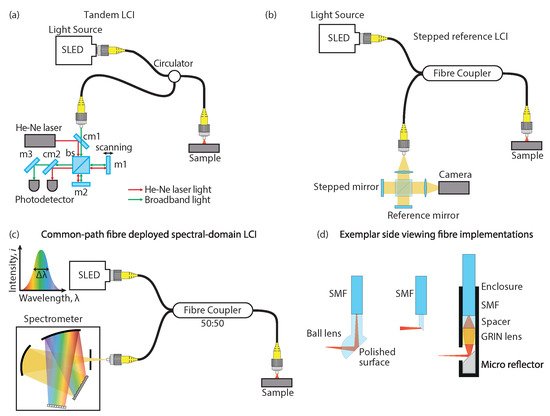
Figure 10.
Schematics of exemplar LCI probe layouts for HAR measurement. (a) scanning reference mirror, cm = cold mirror, m = mirror, bs = beam splitter, (b) single-shot tilted/stepped reference mirror, (c) single-shot spectral-domain, and (d) exemplar side-angled probes for measuring HAR sidewalls.
The use of optical fibres has been investigated across various sensor areas demonstrating their ability to greatly improve the performance of interferometric systems. This is mainly attributed to their small size, low weight, multiplexing, remote sensing, high flexibility, low propagating loss, high sensitivity, low fabrication cost, small form factor, high accuracy, immunity to electromagnetic interference, and robustness to high temperature and irradiation, which make them attractive for many applications [140]. There have been many instances of fibre-deployed LCI profilometers, most notably in the field of biomedical science, where it is termed optical coherence tomography due to its use in tomographic measurement of the human body [141]. Some implementations for dimensional metrology of industrial components and in-hole measurements have also been demonstrated, as detailed in this section.
A fibre-based LCI sensor in a common-path Fizeau donor/Michelson receiver configuration using a tilted reference mirror to remove the requirement for reference stepping and provide single-shot measurement is shown in the literature. However, this limits the operating range due to the fringe’s visibility relationship with the tilt angle. This system has a variable working distance of 100 m, measuring range of 160 m, accuracy in the nanometre range, and depth dependent uncertainty between 16.9 nm to 67.6 nm (linear increase with distance from measurement object). A 80 m diameter fibre with a focusing probe made from a GRIN prism ground with an angle of 45 producing a spot size of approximately 7 m was implemented. The measurement of automotive injection nozzles was demonstrated with a measurement uncertainty (k = 1) of less than 100 nm [142].
In 2012, a tandem LCI sensor was developed with a common-path Fizeau sensing probe using a 30 m diameter fibre probe with a 45° angle polished onto it to measure the side walls of small diameter holes with a measurement uncertainty (k = 2) of 89 nm [143]. Here, a measurement- and reference-interferometers connected by single-mode optical fibre produce an interference fringe if the optical path lengths are the same in both interferometers. This setup is shown in Figure 10a. Hence, by scanning the reference mirror and tracking its position using the interference fringes generated using the He-Ne laser, the surface distance can be determined.
A fully-deployed LCI sensor using a common-path spectral domain configuration and bare single-mode fibre sensing head (as depicted in Figure 10c) has proven to be an effective method for measuring surface topography [144]. This system is highly robust in diverse operating environments due to its common-path and single-shot measurement capabilities. The system has been tested in air, water, paraffin, and metalworking fluid with minimal effects on linearity ((k = 2) 135 nm to 159 nm), measurement accuracy, and precision ((k = 2) of 56 nm to 76 nm in air and water, respectively) [145]. Moreover, the sensor can operate with the sensing head coupled within a high-speed liquid jet to flush surface contaminants while maintaining a homogeneous operating environment [146]. The sensor’s measurement range is limited by the spectral sampling frequency of the spectrometer, with the current configuration yielding a measurement range of 2.1 mm.
The development of a low-cost, compact, monocrystalline silicon interferometer for performing the profilometry measurement, which was 390 m × 550 m, and 4 mm long [147], took place in 2012, which demonstrated the potential affordability and scalability of low-coherence interferometry for microprobe implementations. Additionally, a traceable, low cost, and fast axial calibration scheme has also been presented [148], which takes advantage of LCI’s ability to perform tomographic measurements, and this is suitable for on-machine or embedded application.
3.2. Laser Triangulation
Laser triangulation for dimensional surface measurement is well established within the industry, being a cost-effective solution to provide micrometre-level measurement accuracy with fast scan speeds. However, due to the operating principle, it is difficult to miniaturise to a sub-millimetre scale and can exhibit long warm-up times (approximately 20 min) for stable operation [149]. The technique works, as shown in Figure 11a, as the measured object moves through the measurement plane, the location of the beam reflected from the sample surface on the detector will change. The distance of the object from the scanner can then be determined through triangulation.
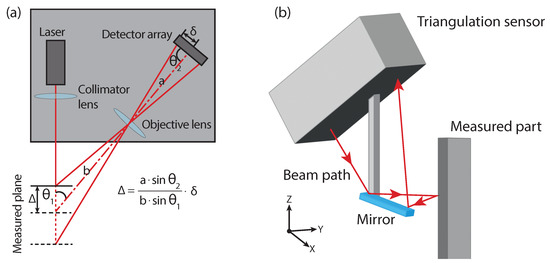
Figure 11.
(a) Schematic showing the principle of triangulation sensors for calculating the distance of a part. describes the distance from the zeroed region and the corresponding shift of the laser spot on the detector array. is calculated from the known distances a and b and the known angles and . (b) an application example of how an existing triangulation sensor can be adapted for in-hole measurement.
In 2014, the measurement of internal screw threads (<M4) took place using a commercial laser displacement sensor and redesigning the optical path using a 45° inclined mirror to allow sidewall measurement, as shown in Figure 11b. The sensor was specified with an accuracy of 1.5 m, an axial resolution of 30 nm, a measurement range of 30 mm ± 5 mm, and with an effective laser spot size of 20 m to 100 m [150]. This approach was also used in 2021 to measure the sidewalls of slots and bores [151]. Due to the mirror size employed and minimal offset, the smallest measurable hole diameter was 1.44 mm. Due to the shadowing of the holes, the measurement depth was strongly linked to the hole diameter with 6 mm, 8 mm, and 10 mm diameter holes giving measurable depths of 3.9 mm, 5.35 mm, and 6.9 mm, respectively, with an axial resolution of 1.3 m.
In 2016, a custom hardware solution was shown for the measurement of shaft holes inside car engine blocks (92 mm diameter × 550 mm length), using four laser triangulation sensors installed at different positions. The measuring error was less than 4 m and standard deviation less than 2 m with a measuring time of 3 min per engine block [152].
3.3. X-ray Computed Tomography
XCT is an imaging technique that provides a non-destructive volumetric reconstruction of a component by placing a sample within a conical beam of X-rays, which pass through the object and are detected by a flat panel detector. By rotating the object and taking successive 2D images, 3D reconstruction of the object can be achieved, as shown in Figure 12a. However, these systems are often expensive, have a slow measurement speed, have a low resolution which reduces with offset from the X-ray source, are large, use a radioactive source, require expert operators, and produce image artefacts dependent on multiple parameters from misalignment of the source, rotation axis, sample, or detector, scattering, beam hardening due to polychromatic X-ray source, ring artefacts from defective or uncalibrated detector elements, etc., which result in generates distortions in the reconstructed CT volume that induce errors [153].
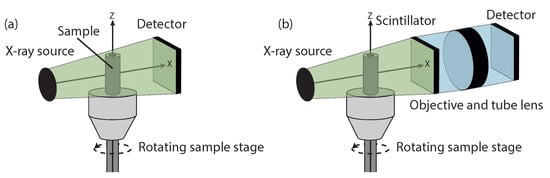
Figure 12.
Schematic showing how X-ray CT systems work in both (a) traditional XCT formats and in a (b) XCT microscopy format.
The spatial resolution of XCT systems for dimensional measurement is typically limited around 4 m to 10 m for objects with dimensions in the 0.5 mm to 25 mm range [154], for larger samples, the achievable resolution is several tens of micrometres [155]. To improve voxel resolution, the incorporation of a scintillator mask followed by optical lenses to optically magnify the image before reaching the CCD detector, as shown in Figure 12b, has been demonstrated. This technique is known as X-ray microscopy (XRM) and enables images down to 500 nm. Additionally, X-ray focusing elements have been demonstrated in literature for improving XRM resolution using Fresnel zone plates or Kirkpatrick-Baez mirrors [156]; these approaches are known as nano-XRM, with commercial systems (Sigray TriLambda-30 NanoXRM) claiming resolutions down to 35 nm. However, these additions limit the operating range of the system; XRM systems can perform dimensional measurements on volumes of 5 mm or less [155], and Nano-XRM systems have a limited field of view with sample sizes typically below 100 m in diameter.
Examples of using XCT techniques for the dimensional measurement of parts have also been shown in the literature. In 2012, the use of a Synchrotron (XRM) for distinguishing between EDM and CNC drilled diesel injectors (designed diameters: of the CNC nozzle 320 m and EDM nozzle 180 m) was demonstrated, the spatial resolution of this system was 9 m with a 15-min measurement time [157]. In 2018, hard-to-measure compliant structures ranging from 0.6 mm to 65 mm were also shown, with <2 m difference between XCT and extrapolated CMM results [158]. In 2022, the use of an XRM system for performing accurate 3D dimensional metrology of multi-sphere phantoms was shown to give a repeatability (k = 1) of 100 nm and a reproducibility of 350 nm [155].
3.4. Capacitive Probes
As mentioned in Section 2.1.2, capacitive probing techniques measure the change in capacitance between a probe tip and measured surface to detect the surface’s position. This section looks at using this principle to directly determine the distance of the probe to the sample surface using two approaches demonstrated in the literature and shown schematically in Figure 13. The measurement quality is strongly affected by the environmental conditions, material type, and topography, noting that only metallic surfaces are measurable. Typically, these sensors tend to have a low lateral resolution due to the extended electric field but a very high axial sensitivity with 3D isotropic detection and low cost.
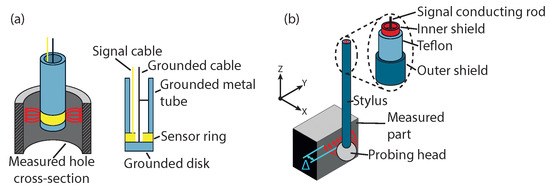
Figure 13.
Schematic showing how capacitive probes work in both (a) capacitive rod and (b) spherical coupling implementations.
In 2009, an approach to fast hole diameter measurement in less than 8 s was presented using a capacitive rod probe, as shown in Figure 13a, a comparative measurement with a CMM took at least 1 min depending on a number of points taken with an accuracy of within 3 m when measuring holes with diameters of approximately 2.45 mm to 2.75 mm. However, factors such as circularity and profile are not captured [159].
A capacitive probing sensor with a 3 mm diameter spherical probing head was developed in 2010, demonstrating a resolution better than 5 nm and less than 10 nm non-linearity over its operating range of 1 m [160]. A wide range of probe geometries are possible for hole diameter measurement, for general probing operations (3 mm × 100 mm) [160], and the use of novel flake shaped probes of thickness 30 m for measurement of micro-moulds (100 m × 1500 m) [161].
In 2019, a spherical scattering electrical-field probe was developed, as shown in Figure 13b to achieve 1 nm resolution with 6 nm nonlinearity within a sensing range of 1.2 m, after correction. This was achieved using probes with diameters from 1.5 mm to 3 mm and a 150 mm long stylus [162], with a measurement uncertainty (k = 2) of 200 nm [163]. In 2020, modelling of this sensor allowed for the determination of point probing capabilities with 31% of total surface charge on a 1 mm diameter ball, which was concentrated in 1% of the total probing ball surface when operating with a 0.3 m probing gap and remained unchanged with varying surface geometry or probing gap within the sensing range allowing approximate point probing capability [164].
3.5. Summary of Non-Contact Measurements
Various types of non-contact measurement sensors suited to the measurement of high-aspect-ratio features have been covered in this section. Table 4 presents a summary of these systems operating characteristics. Some of the methods presented are currently commercially available; these include Werth—Interferometer probe WIP, Sempre group—Novacam Tubeinspect and Bore also inspect LCI based, Bruker Alicona—vertical focus probing, Taylor Hobson—TALYscan 280, and Nikon—X-ray CT.

Table 4.
List of some typical characteristics for covered non-contact measurement techniques.
LCI can provide high-aspect ratio probes whilst maintaining high resolution and measurement speeds with an adequate operating range and low measurement uncertainty. However, due to the fibres being highly flexible, there may be issues in maintaining a stable position during measurement with either the sample of the sensor requiring translation and rotation for in-hole measurement.
From Table 4 and the previous sections, it can be seen that commercial laser triangulation systems can be readily converted for hole sidewall measurements; alternatively, custom-configured systems can be made. These systems offer fast measurement speed and large operating ranges; however, they are difficult to miniaturise, have a lower resolution and limited operating depth.
X-ray CT can measure internal features not accessible to other techniques, but is more expensive, time-consuming, limited resolution, and utilises ionising radiation which can potentially harm human operators if not properly controlled.
Capacitive probes can achieve high axial precision but typically have a small linear operating range and lower lateral resolution and cannot operate as a profilometer.
4. Challenges
Measurement of the HAR feature poses a difficult metrology challenge with expected increased complexities in future applications. Some of the issues encountered during the measurement of HAR features have been highlighted in the technology review portion of this paper. The following topics are considered in this section, covering surface topography complexity, in-process metrology, measurement range, and translation mechanisms.
The increasing use of internal structures due to techniques such as additive manufacturing poses a particularly difficult metrology problem with current solutions and research often limited to XCT. Current contact techniques for HAR measurements have a limited operating range; angling the probe provides some expansion of capabilities though it is still very constrained [165]. However, optical probes with specially designed probing heads are available for measuring undercuts in holes or with MEMS mirrors for steerable beam delivery within a hole.
To perform a measurement, the sensor needs to be positioned within the vicinity of the sample (or vice-versa). Thus, the translation mechanism has a large impact on measurement accuracy, volume, speed, and repeatability, and limits what geometries can be measured. XYZ scanning stages and rotary stages are commonly used. To allow further flexibility, sensors may in the future be coupled with flexible ‘snake’ probes commonly used within biomedical endoscopic procedures. Current ‘snake-probes’ with 2 degrees of freedom (DoF) and a diameter of 2.6 mm have been demonstrated [166] or 5 DoF with a 3 mm diameter have also been shown [167]. However, to be deployed successfully, these translational tools require a more precise determination of the probe orientation and position within the sample. Additionally, only certain techniques may be applicable to this approach, such as fibre-based non-contact or capacitive methods. This is becoming a common occurrence within the biomedical field, and some of the sensors presented in this review have a footprint which could be integrated with current technologies.
Due to the increasing interest in the application of functional surface texture design for improving performance characteristics of parts, the need to measure geometry and surface texture simultaneously and accurately is rapidly increasing. This requires techniques which can function over a large measurement range and provide high data-point density; thus, measurement speed becomes increasingly important, as well as adequate lateral and axial resolutions to capture the features of the part.
The need for in-process measurement is becoming increasingly desirable. In situ measurement requires high-speed, robust sensors, resilient to the manufacturing environment, with efficient algorithms to allow appropriate machine adaptation without slowing down the manufacturing process. As mentioned, the requirement for form and roughness measurement is challenging, for in-line measurements, this requires sensors and algorithms able to handle the high-acquisition and processing speeds required for an in-line inspection regime. Most of the reviewed techniques have been developed within environmentally controlled laboratories and have yet to demonstrate robustness within industrial measurement settings, with many showing high sensitivity to thermal changes.
5. Summary and Outlook
There is a growing requirement for measurement systems able to provide dimensional information on HAR structures. There is also an increase in the incorporation of surface texturing for performance enhancement to improve characteristics such as heat transfer, lubrication, and wettability. These factors have resulted in the need for measurement systems which can reach these difficult regions and acquire dimensional information across multiple orders of magnitude from surface roughness to form. Increased richness in datasets is also becoming an apparent need in terms of data-point density and data types offering a better understanding of the object.
This paper reviews and provides a summary of state-of-the-art techniques for 3D surface measurement in relation to HAR structures. It has shown that although many techniques have been developed, the majority remain within the prototype to in-laboratory operation stage with high sensitivity to environmental disturbances and relatively slow data-point capture or scanning speeds. There are also few studies focusing on their use for surface profile measurements of complex internal microstructures. Additionally, the studies focus on simple geometries, such as straight holes without expansion to the more complex structures, which are of increasing interest. Currently, only XCT approaches are readily able to provide insight into these structures. However, these systems are large, slow, difficult to qualify for traceability, require highly skilled users and utilise hazardous radiation with no clear path to an application for mass inspection regimes. Hence, the expansion of methods with flexible probes, such as optical fibre-based or capacitive-based systems, may allow for better measurement traceability, resolution, accuracy, and convenience.
To meet the speed, resolution, flexibility, operating range, and robustness requirements, in-line measurement of the highlighted structure types probing a surface with an intentionally manipulated light beam such as LCI appears currently to be a cost and time-effective approach to perform 3D surface and form reconstruction measurements currently. However, the selection of measurement hardware is case dependent, and it has been noted that there are still many persisting challenges; the requirement to consolidate best practices and progress the integration of metrology with modern manufacturing systems is clear. Careful evaluation of the original works referenced within this paper is required before spending effort adopting any for practical applications.
Author Contributions
Conceptualization, T.H., J.P., N.L. and P.K.; methodology, T.H.; investigation, T.H.; resources, J.P., P.K. and N.L; data curation, T.H.; writing-original draft preparation, T.H.; writing-review and editing, T.H., J.P., W.G., C.G., L.J. and N.L; supervision, J.P., P.K. and N.L; funding acquisition, P.K., J.P. and N.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors wish to acknowledge the support of the Research England Development (RED) for funding this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tong, H.; Li, Y.; Zhang, L.; Li, B. Mechanism design and process control of micro EDM for drilling spray holes of diesel injector nozzles. Precis. Eng. 2013, 37, 213–221. [Google Scholar] [CrossRef]
- Yu, P.; Xu, J.; Hou, Y.; Yu, H. Mechanism design and process control of micro-EDM for drilling deep hole of bellows. J. Adv. Manuf. Technol 2021, 115, 2423–2432. [Google Scholar] [CrossRef]
- Aziz, M.; Ohnishi, O.; Onikura, H. Novel micro deep drilling using micro long flat drill with ultrasonic vibration. Precis. Eng. 2012, 36, 168–174. [Google Scholar] [CrossRef]
- Sun, X.Q.; Masuzawa, T.; Fujino, M. Micro ultrasonic machining and its applications in MEMS. Sens. Actuator A Phys. 1996, 57, 159–164. [Google Scholar] [CrossRef]
- Vala, M.; Homola, J. Flexible method based on four-beam interference lithography for fabrication of large areas of perfectly periodic plasmonic arrays. Opt. Express 2014, 22, 18778–18789. [Google Scholar] [CrossRef]
- Meijer, T.; Beardmore, J.; Fabrie, C.; van Lieshout, J.; Notermans, R.; Sang, R.; Vredenbregt, E.; Van Leeuwen, K. Structure formation in atom lithography using geometric collimation. Appl. Phys. B 2011, 105, 703–713. [Google Scholar] [CrossRef]
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Nanoimprint lithography. J. Vac. Sci. 1996, 14, 4129–4133. [Google Scholar] [CrossRef]
- Heckele, M.; Schomburg, W. Review on micro molding of thermoplastic polymers. J. Micromech. Microeng. 2003, 14, R1. [Google Scholar] [CrossRef]
- Pais, M.; Chow, L.; Mahefkey, E. Surface roughness and its effects on the heat transfer mechanism in spray cooling. J. Heat Transfer 1992, 114, 211–219. [Google Scholar] [CrossRef]
- Attinger, D.; Frankiewicz, C.; Betz, A.R.; Schutzius, T.M.; Ganguly, R.; Das, A.; Kim, C.J.; Megaridis, C.M. Surface engineering for phase change heat transfer: A review. MRS Energy Sustain. 2014, 1, E4. [Google Scholar] [CrossRef]
- Grabas, B. Vibration-assisted laser surface texturing of metals as a passive method for heat transfer enhancement. Exp. Therm. Fluid Sci. 2015, 68, 499–508. [Google Scholar] [CrossRef]
- Piasecka, M.; Strąk, K.; Grabas, B. Vibration-assisted laser surface texturing and electromachining for the intensification of boiling heat transfer in a minichannel. Arch. Metall. Mater. 2017, 62, 1983–1990. [Google Scholar] [CrossRef]
- Kumar, G.U.; Suresh, S.; Kumar, C.S.; Back, S.; Kang, B.; Lee, H.J. A review on the role of laser textured surfaces on boiling heat transfer. Appl. Therm. Eng. 2020, 174, 115274. [Google Scholar] [CrossRef]
- Dhadda, G.; Hamed, M.; Koshy, P. Electrical discharge surface texturing for enhanced pool boiling heat transfer. J. Mater. Process. Technol. 2021, 293, 117083. [Google Scholar] [CrossRef]
- Pettersson, U.; Jacobson, S. Influence of surface texture on boundary lubricated sliding contacts. Tribol. Int. 2003, 36, 857–864. [Google Scholar] [CrossRef]
- Hsu, S.M.; Jing, Y.; Zhao, F. Self-adaptive surface texture design for friction reduction across the lubrication regimes. Surf. Topogr. Metrol. Prop. 2015, 4, 014004. [Google Scholar] [CrossRef]
- Uddin, M.; Ibatan, T.; Shankar, S. Influence of surface texture shape, geometry and orientation on hydrodynamic lubrication performance of plane-to-plane slider surfaces. Lubr. Sci. 2017, 29, 153–181. [Google Scholar] [CrossRef]
- Edachery, V.; Shashank, R.; Kailas, S.V. Influence of surface texture directionality and roughness on wettability, sliding angle, contact angle hysteresis, and lubricant entrapment capability. Tribol. Int. 2021, 158, 106932. [Google Scholar] [CrossRef]
- Kubiak, K.; Wilson, M.; Mathia, T.; Carval, P. Wettability versus roughness of engineering surfaces. Wear 2011, 271, 523–528. [Google Scholar] [CrossRef]
- Misyura, S.; Kuznetsov, G.; Feoktistov, D.; Volkov, R.; Morozov, V.; Orlova, E. The influence of the surface microtexture on wettability properties and drop evaporation. Surf. Coat. Technol. 2019, 375, 458–467. [Google Scholar] [CrossRef]
- Hitchcock, S.; Carroll, N.; Nicholas, M. Some effects of substrate roughness on wettability. JMST 1981, 16, 714–732. [Google Scholar] [CrossRef]
- Ijaola, A.O.; Bamidele, E.A.; Akisin, C.J.; Bello, I.T.; Oyatobo, A.T.; Abdulkareem, A.; Farayibi, P.K.; Asmatulu, E. Wettability transition for laser textured surfaces: A comprehensive review. Surf. Interfaces 2020, 21, 100802. [Google Scholar] [CrossRef]
- Wassmann, T.; Kreis, S.; Behr, M.; Buergers, R. The influence of surface texture and wettability on initial bacterial adhesion on titanium and zirconium oxide dental implants. Int. J. Implant Dent 2017, 3, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bico, J.; Thiele, U.; Quéré, D. Wetting of textured surfaces. Colloids Surf. A 2002, 206, 41–46. [Google Scholar] [CrossRef]
- Ito, S.; Kikuchi, H.; Chen, Y.; Shimizu, Y.; Gao, W.; Takahashi, K.; Kanayama, T.; Arakawa, K.; Hayashi, A. A micro-coordinate measurement machine (CMM) for large-scale dimensional measurement of micro-slits. Appl. Sci. 2016, 6, 156. [Google Scholar] [CrossRef]
- Nam, J.; Carvalho, M.S. Flow in tensioned-web-over-slot die coating: Effect of die lip design. Chem. Eng. Sci. 2010, 65, 3957–3971. [Google Scholar] [CrossRef]
- Pickett, L.M.; Siebers, D.L. An investigation of diesel soot formation processes using micro-orifices. Proc. Combust. Inst. 2002, 29, 655–662. [Google Scholar] [CrossRef]
- Kao, C.C.; Shih, A.J. Form measurements of micro-holes. Meas. Sci. Technol. 2007, 18, 3603. [Google Scholar] [CrossRef]
- Jantzen, S.; Neugebauer, M.; Meeß, R.; Wolpert, C.; Dietzel, A.; Stein, M.; Kniel, K. Novel measurement standard for internal involute microgears with modules down to 0.1 mm. Meas. Sci. Technol. 2018, 29, 125012. [Google Scholar] [CrossRef]
- Santos, R.J.; Sultan, M.A. State of the art of mini/micro jet reactors. Chem. Eng. Technol. 2013, 36, 937–949. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, Y.; Du, L.; Liu, J.; Yao, J. Review of the applications of microreactors. Renew. Sustain. Energy Rev. 2015, 47, 519–539. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Onikura, H.; Sajima, T.; Kawagoishi, N.; Kondo, E. Development of a system for measuring micro hole accuracy using an optical fiber probe. J. Adv. Mech. 2010, 4, 995–1004. [Google Scholar] [CrossRef]
- Bos, E.; Delbressine, F.; Haitjema, H. High-accuracy CMM metrology for micro systems. Vdi Berichte 2004, 1860, 511–522. [Google Scholar]
- Meli, F.; Küng, A. AFM investigation on surface damage caused by mechanical probing with small ruby spheres. Meas. Sci. Technol. 2007, 18, 496. [Google Scholar] [CrossRef]
- Meli, F.; Küng, A.; Thalmann, R. Ultra precision micro-CMM using a low force 3D touch probe. In Proceedings of the Optics and Photonics, San Diego, CA, USA, 24 August 2005; pp. 265–272. [Google Scholar]
- Weckenmann, A.; Estler, T.; Peggs, G.; McMurtry, D. Probing systems in dimensional metrology. CIRP Ann. 2004, 53, 657–684. [Google Scholar] [CrossRef]
- Van Vliet, W.; Schellekens, P. Accuracy limitations of fast mechanical probing. CIRP Ann. 1996, 45, 483–487. [Google Scholar] [CrossRef]
- Küng, A.; Meli, F.; Thalmann, R. Ultraprecision micro-CMM using a low force 3D touch probe. Meas. Sci. Technol. 2007, 18, 319. [Google Scholar] [CrossRef]
- Fang, H.; Xu, B.; Yin, D.; Zhao, S. A method to control dynamic errors of the stylus-based probing system for the surface form measurement of microstructures. J. Nanomater. 2016, 2016, 3727514. [Google Scholar] [CrossRef]
- Yin, Q.; Xu, B.; Yin, G.; Gui, P.; Xu, W.; Tang, B. Surface profile measurement and error compensation of triangular microstructures employing a stylus scanning system. J. Nanomater. 2018, 2018, 6396871. [Google Scholar] [CrossRef]
- Bos, E.J. Aspects of tactile probing on the micro scale. Precis. Eng. 2011, 35, 228–240. [Google Scholar] [CrossRef]
- Claverley, J.D.; Burisch, A.; Leach, R.K.; Raatz, A. Semi-automated assembly of a MEMS-based micro-scale CMM probe and future optimization of the process chain with a view to desktop factory automation. In Proceedings of the Precision Assembly Technologies and Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–16. [Google Scholar]
- Li, R.; Chen, C.; Li, D.; Fan, K.C.; Cheng, Z.; Huang, Q.; Dang, X. Ball tips of micro/nano probing systems: A review. Chin. J. Mech. 2017, 30, 222–230. [Google Scholar] [CrossRef]
- Ferreira, N.; Brennecke, A.; Dietzel, A.; Büttgenbach, S.; Krah, T.; Metz, D.; Kniel, K.; Härtig, F. Reducing the probe ball diameters of 3D silicon-based microprobes for dimensional metrology. In Proceedings of the 7th International Conference on Sensing Technology, Wellington, New Zealand, 3–5 December 2013; pp. 301–306. [Google Scholar]
- Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K. Fabrication of ultra-small-diameter optical-fiber probe using acid-etch technique and CO2 laser for 3D-micro metrology. Int. J. Autom. 2017, 11, 699–706. [Google Scholar] [CrossRef]
- Sheu, D.Y. Multi-spherical probe machining by EDM: Combining WEDG technology with one-pulse electro-discharge. J. Mater. Process. Technol. 2004, 149, 597–603. [Google Scholar]
- Michihata, M. Surface-Sensing Principle of Microprobe System for Micro-Scale Coordinate Metrology: A Review. Metrology 2022, 2, 46–72. [Google Scholar] [CrossRef]
- Kinnell, P.; Habeb, R. An evaluation of cleaning methods for micro-CMM probes. Meas. Sci. Technol. 2013, 24, 085603. [Google Scholar] [CrossRef]
- Feng, X.; Pascal, J.; Lawes, S. A microscopy approach for in situ inspection of micro-coordinate measurement machine styli for contamination. Meas. Sci. Technol. 2017, 28, 095010. [Google Scholar] [CrossRef]
- Weckenmann, A.; Peggs, G.; Hoffmann, J. Probing systems for dimensional micro-and nano-metrology. Meas. Sci. Technol. 2006, 17, 504. [Google Scholar] [CrossRef]
- Fan, K.C.; Li, R.J.; Xu, P. Design and verification of micro/nano-probes for coordinate measuring machines. Nanomanuf. Metrol. 2019, 2, 1–15. [Google Scholar] [CrossRef]
- Kobayashi, M.; Michihata, M.; Hayashi, T.; Takaya, Y. Coordinate measurement of micro groove on MEMS device by optically controlled microprobe. In Proceedings of the International Symposium on Optomechatronic Technologies, Toronto, ON, Canada, 25–27 October 2010; pp. 1–5. [Google Scholar]
- Yacoot, A.; Koenders, L. Recent developments in dimensional nanometrology using AFMs. Meas. Sci. Technol. 2011, 22, 122001. [Google Scholar] [CrossRef]
- Nouira, H.; Bergmans, R.H.; Küng, A.; Piree, H.; Henselmans, R.; Spaan, H.A. Ultra-high precision CMMs and their associated tactile or/and optical scanning probes. Int. J. Metrol. Qual. Eng. 2014, 5, 204. [Google Scholar] [CrossRef]
- Feng, X.Y.; Xu, P.; Li, R.J.; Lei, Y.J.; Zhang, L.S.; Wang, B.; Huang, Q.X. Development of a High-Resolution Touch Trigger Probe Based on an Optical Lever for Measuring Micro Components. IEEE Sens. J. 2022, 22, 6466–6475. [Google Scholar] [CrossRef]
- Balzer, F.G.; Hausotte, T.; Dorozhovets, N.; Manske, E.; Jäger, G. Tactile 3D microprobe system with exchangeable styli. Meas. Sci. Technol. 2011, 22, 094018. [Google Scholar] [CrossRef]
- Alblalaihid, K.; Lawes, S.; Kinnell, P. Variable stiffness probing systems for micro-coordinate measuring machines. Precis. Eng. 2016, 43, 262–269. [Google Scholar] [CrossRef]
- Alblalaihid, K.; Kinnell, P.; Lawes, S.; Desgaches, D.; Leach, R. Performance assessment of a new variable stiffness probing system for micro-CMMs. Sensors 2016, 16, 492. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, J.; Gao, R.; Yang, Y. A novel constant-force scanning probe incorporating mechanical-magnetic coupled structures. Rev. Sci. Instrum. 2011, 82, 075101. [Google Scholar] [CrossRef]
- Pril, W.; Struik, K.; Schellekens, P. Development of a 2D probing system with nanometer resolution. In Proceedings of the 2th Annual Meeting of the American Society for Precision Engineering, Monterey, CA, USA, 9–14 November 1996; pp. 438–442. [Google Scholar]
- Kleine-Besten, T.; Loheide, S.; Brand, U.; Bütefisch, S.; Büttgenbach, S. Development and characterisation of new probes for dimensional metrology on microsystem components. In Proceedings of the 1st Euspen International Conference; European Society for Precision Engineering and Nanotechnology: Cranfield, UK, 1999; Volume 2, pp. 387–390. [Google Scholar]
- Haitjema, H.; Pril, W.; Schellekens, P. Development of a silicon-based nanoprobe system for 3-D measurements. CIRP Ann. 2001, 50, 365–368. [Google Scholar] [CrossRef]
- Bos, E.; Delbressine, F.; Dietzel, A. Characterization of measurement effects in an MST based nano probe. In Proceedings of the 5th Euspen International Conference; European Society for Precision Engineering and Nanotechnology: Cranfield, UK, 2005; pp. 349–352. [Google Scholar]
- Bos, E.; Heldens, R.; Delbressine, F.; Schellekens, P.; Dietzel, A. Compensation of the anisotropic behavior of single crystalline silicon in a 3D tactile sensor. Sens. Actuator A Phys. 2007, 134, 374–381. [Google Scholar] [CrossRef]
- Bos, E. Tactile 3D Probing System for Measuring MEMS with Nanometer Uncertainty: Aspects of Probing, Design, Manufacturing and Assembly. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2008. [Google Scholar]
- Dai, G.; Bütefisch, S.; Pohlenz, F.; Danzebrink, H.U. A high precision micro/nano CMM using piezoresistive tactile probes. Meas. Sci. Technol. 2009, 20, 084001. [Google Scholar] [CrossRef]
- Metz, D.; Jantzen, S.; Wessel, D.; Mies, G.; Lüdenbach, J.; Stein, M.; Kniel, K.; Dietzel, A. Integration of an isotropic microprobe and a microenvironment into a conventional CMM. Meas. Sci. Technol. 2019, 30, 115007. [Google Scholar] [CrossRef]
- Peiner, E.; Balke, M.; Doering, L. Slender tactile sensor for contour and roughness measurements within deep and narrow holes. IEEE Sens. J. 2008, 8, 1960–1967. [Google Scholar] [CrossRef]
- Peiner, E.; Balke, M.; Doering, L.; Brand, U. Tactile probes for dimensional metrology with microcomponents at nanometre resolution. Meas. Sci. Technol. 2008, 19, 064001. [Google Scholar] [CrossRef]
- Xu, M.; Kirchhoff, J.; Brand, U. Development of a traceable profilometer for high-aspect-ratio microstructures metrology. Surf. Topogr. Metrol. Prop. 2014, 2, 024002. [Google Scholar] [CrossRef]
- Peggs, G.; Lewis, A.; Oldfield, S. Design for a compact high-accuracy CMM. CIRP Ann. 1999, 48, 417–420. [Google Scholar] [CrossRef]
- Liebrich, T.; Knapp, W. Improvements and experimental validation of a 3D-probing system for micro-components. CIRP Ann. 2012, 61, 475–478. [Google Scholar] [CrossRef]
- He, M.; Liu, R.; Li, Y.; Wang, H.; Lu, X.; Ding, G.; Wu, J.; Zhang, T.; Zhao, X. Tactile probing system based on micro-fabricated capacitive sensor. Sens. Actuators Phys. 2013, 194, 128–134. [Google Scholar] [CrossRef]
- Lei, L.H.; Li, Y.; Fan, G.F.; Wu, J.J.; Jian, L.; Cai, X.Y.; Li, T.B. Development of MEMS-based micro capacitive tactile probe. Chin. Phys. B 2014, 23, 118703. [Google Scholar] [CrossRef]
- Thalmann, R.; Meli, F.; Küng, A. State of the art of tactile micro coordinate metrology. Appl. Sci. 2016, 6, 150. [Google Scholar] [CrossRef]
- van Vliet, W.P.; Schellekens, P.H. Development of a fast mechanical probe for coordinate measuring machines. Precis. Eng. 1998, 22, 141–152. [Google Scholar] [CrossRef]
- Chu, C.L.; Chiu, C.Y. Development of a low-cost nanoscale touch trigger probe based on two commercial DVD pick-up heads. Meas. Sci. Technol. 2007, 18, 1831. [Google Scholar] [CrossRef]
- Li, R.J.; Xiang, M.; Fan, K.C.; Zhou, H.; Feng, J. Optimal design of a touch trigger probe. In Proceedings of the 9th International Symposium on Precision Engineering Measurement and Instrumentation, Changsha, China, 8–10 August 2014; pp. 462–468. [Google Scholar]
- Li, R.J.; Xiang, M.; He, Y.X.; Fan, K.C.; Cheng, Z.Y.; Huang, Q.X.; Zhou, B. Development of a high-precision touch-trigger probe using a single sensor. Appl. Sci. 2016, 6, 86. [Google Scholar] [CrossRef]
- Cui, J.; Bian, X.; He, Z.; Li, L.; Sun, T. A 3D nano-resolution scanning probe for measurement of small structures with high aspect ratio. Sens. Actuator A Phys. 2015, 235, 187–193. [Google Scholar] [CrossRef]
- Li, R.J.; Xu, P.; Wang, P.Y.; Fan, K.C.; Cheng, R.J.; Huang, Q.X. Development of a micro/nano probing system using double elastic mechanisms. Sensors 2018, 18, 4229. [Google Scholar] [CrossRef]
- Balzer, F.; Hofmann, N.; Dorozhovets, N.; Hausotte, T.; Manske, E.; Jäger, G. Investigation of the metrological properties of a 3-D microprobe with optical detection system. In Proceedings of the Instrumentation, Metrology, and Standards for Nanomanufacturing IV; SPIE: Paris, France, 2010; Volume 7767, pp. 168–177. [Google Scholar]
- Li, R.J.; Fan, K.C.; Miao, J.W.; Huang, Q.X.; Tao, S.; Gong, E.m. An analogue contact probe using a compact 3D optical sensor for micro/nano coordinate measuring machines. Meas. Sci. Technol. 2014, 25, 094008. [Google Scholar] [CrossRef]
- Li, R.J.; Fan, K.C.; Huang, Q.X.; Zhou, H.; Gong, E.M.; Xiang, M. A long-stroke 3D contact scanning probe for micro/nano coordinate measuring machine. Precis. Eng. 2016, 43, 220–229. [Google Scholar] [CrossRef]
- Liebrich, T.; Knapp, W. New concept of a 3D-probing system for micro-components. CIRP Ann. 2010, 59, 513–516. [Google Scholar] [CrossRef]
- Hidaka, K.; Saito, A.; Koga, S. Study of a micro-roughness probe with ultrasonic sensor. CIRP Ann. 2008, 57, 489–492. [Google Scholar] [CrossRef]
- Masuzawa, T.; Hamasaki, Y.; Fujino, M. Vibroscanning method for nondestructive measurement of small holes. CIRP Ann. 1993, 42, 589–592. [Google Scholar] [CrossRef]
- Kim, B.J.; Sawamoto, Y.; Masuzawa, T.; Fujino, M. Advanced vibroscanning method for micro-hole measurement, High speed and stability improvement of measurement technique. Int. J. Electr. Mach. 1996, 1, 41–44. [Google Scholar]
- Masuzawa, T.; Kim, B.; Bergaud, C.; Fujino, M. Twin-probe vibroscanning method for dimensional measurement of microholes. CIRP Ann. 1997, 46, 437–440. [Google Scholar] [CrossRef]
- Kim, B.; Masuzawa, T.; Fujita, H.; Tominaga, A. Dimensional measurement of microholes with silicon-based micro twin probes. In Proceedings of the 11th Annual International Workshop on Micro Electro Mechanical Systems: An Investigation of Micro Structures, Sensors, Actuators, Machines and Systems, Heidelberg, Germany, 25–29 January 1998; pp. 334–339. [Google Scholar]
- Kim, B.; Masuzawa, T.; Bourouina, T. The vibroscanning method for the measurement of micro-hole profiles. Meas. Sci. Technol. 1999, 10, 687. [Google Scholar] [CrossRef]
- Van Riel, M.; Bos, E.; Homburg, F. Analysis of the measurement sensitivity of multidimensional vibrating microprobes. Meas. Sci. Technol. 2014, 25, 075008. [Google Scholar] [CrossRef]
- Yamamoto, M.; Takeuchi, H.; Aoki, S. Dimensional measurement of high aspect ratio micro structures with a resonating micro cantilever probe. Microsyst. Technol. 2000, 6, 179–183. [Google Scholar] [CrossRef]
- Hidaka, K.; Schellekens, P. Study of a small-sized ultrasonic probe. CIRP Ann. 2006, 55, 567–570. [Google Scholar] [CrossRef]
- Claverley, J.D.; Leach, R.K. A vibrating micro-scale CMM probe for measuring high aspect ratio structures. Microsyst. Technol. 2010, 16, 1507–1512. [Google Scholar] [CrossRef]
- Claverley, J.D.; Leach, R.K. Development of a three-dimensional vibrating tactile probe for miniature CMMs. Precis. Eng. 2013, 37, 491–499. [Google Scholar] [CrossRef]
- Goj, B.; Dressler, L.; Hoffmann, M. Design and characterization of a resonant triaxial microprobe. J. Micromech. Microeng. 2015, 25, 125011. [Google Scholar] [CrossRef]
- Bauza, M.B.; Hocken, R.J.; Smith, S.T.; Woody, S.C. Development of a virtual probe tip with an application to high aspect ratio microscale features. Rev. Sci. Instrum. 2005, 76, 095112. [Google Scholar] [CrossRef]
- Bauza, M.B.; Woody, S.C.; Seugling, R.M.; Smith, S.T. Dimensional Measurements of Ultra Delicate Materials Using Micrometrology Tactile Sensing; Technical Report; Lawrence Livermore National Lab: Livermore, CA, USA, 2010.
- Bauza, M.; Woody, S.; Woody, B.; Smith, S. Surface profilometry of high aspect ratio features. Wear 2011, 271, 519–522. [Google Scholar] [CrossRef]
- Huang, Q.; Chen, C.; Wu, K.; Zhang, L.; Li, R.; Fan, K.C. A three-dimensional resonant triggering probe for micro-CMM. Appl. Sci. 2017, 7, 403. [Google Scholar] [CrossRef]
- Ito, S.; Kodama, I.; Gao, W. Development of a probing system for a micro-coordinate measuring machine by utilizing shear-force detection. Meas. Sci. Technol. 2014, 25, 064011. [Google Scholar] [CrossRef]
- Ito, S.; Chen, Y.L.; Shimizu, Y.; Kikuchi, H.; Gao, W.; Takahashi, K.; Kanayama, T.; Arakawa, K.; Hayashi, A. Uncertainty analysis of slot die coater gap width measurement by using a shear mode micro-probing system. Precis. Eng. 2016, 43, 525–529. [Google Scholar] [CrossRef]
- Ito, S.; Shima, Y.; Kato, D.; Matsumoto, K.; Kamiya, K. Development of a Microprobing System for Side Wall Detection Based on Local Surface Interaction Force Detection. Int. J. Autom. 2020, 14, 91–98. [Google Scholar] [CrossRef]
- Goo, C.S.; Jun, M.B.; Saito, A. Probing system for measurement of micro-scale components. J. Manuf. Process 2012, 14, 174–180. [Google Scholar] [CrossRef]
- Elfurjani, S.; Bayesteh, A.; Park, S.; Jun, M. Dimensional measurement based on rotating wire probe and acoustic emission. Measurement 2015, 59, 329–336. [Google Scholar] [CrossRef]
- Elfurjani, S.; Ko, J.; Jun, M.B. Micro-scale hole profile measurement using rotating wire probe and acoustic emission contact detection. Measurement 2016, 89, 215–222. [Google Scholar] [CrossRef]
- Schwenke, H.; Wäldele, F.; Weiskirch, C.; Kunzmann, H. Opto-tactile sensor for 2D and 3D measurement of small structures on coordinate measuring machines. CIRP Ann. 2001, 50, 361–364. [Google Scholar] [CrossRef]
- Tutsch, R.; Andras, M.; Neuschaefer-Rube, U.; Petz, M.; Wiedenhofer, T.; Wissmann, M. Three dimensional tactile-optical probing for the measurement of microparts. In Proceedings of the SENSOR + TEST; AMA: Seattle, WA, USA, 2009; pp. 139–144. [Google Scholar]
- Cui, J.; Li, L.; Tan, J. Optical fiber probe based on spherical coupling of light energy for inner-dimension measurement of microstructures with high aspect ratios. Opt. Lett. 2011, 36, 4689–4691. [Google Scholar] [CrossRef]
- Cui, J.; Li, L.; Tan, J. Opto-tactile probe based on spherical coupling for inner dimension measurement. Meas. Sci. Technol. 2012, 23, 085105. [Google Scholar] [CrossRef]
- Cui, J.; Li, L.; Li, J.; Tan, J.B. Fiber probe for micro-hole measurement based on detection of returning light energy. Sens. Actuators A Phys. 2013, 190, 13–18. [Google Scholar] [CrossRef]
- Cui, J.; Chen, Y.; Tan, J. Improvement of dimensional measurement accuracy of microstructures with high aspect ratio with a spherical coupling fiber probe. Meas. Sci. Technol. 2014, 25, 075902. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, J.; Tan, J. Spherical coupling probe for measuring inner dimensions of microstructures. Opt. Express 2018, 26, 33523–33533. [Google Scholar] [CrossRef] [PubMed]
- Muralikrishnan, B.; Stone, J.; Vemuri, S.; Sahay, C.; Potluri, A.; Stoup, J. Fiber deflection probe for small hole measurements. In Proceedings of the ASPE Annual Meeting, New Orleans, LA, USA, 19–22 September 2004; pp. 24–27. [Google Scholar]
- Muralikrishnan, B.; Stone, J.; Stoup, J.R. Fiber deflection probe for small hole metrology. Precis. Eng. 2006, 30, 154–164. [Google Scholar] [CrossRef]
- Tan, J.; Wang, F.; Cui, J. Fiber deflection probing method based on micro focal-length collimation. Opt. Express 2010, 18, 2925–2933. [Google Scholar] [CrossRef] [PubMed]
- Murakami, H.; Katsuki, A.; Onikura, H.; Sajima, T.; Kawagoishi, N.; Kondo, E.; Honda, T. An Optical Fiber Probe for 3-D Micro Metrology. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2010; Volume 447, pp. 524–528. [Google Scholar]
- Sajima, T.; Murakami, H.; Katsuki, A.; Tabuchi, D.; Ohnishi, O.; Kurokawa, S.; Onikura, H.; Doi, T.K. Precision profile measurement system for microholes using vibrating optical fiber. Sens. Mater. 2012, 24, 387–396. [Google Scholar]
- Murakami, H.; Katsuki, A.; Sajima, T. Analysis and evaluation of surface force effects in vibrating fiber probing system for 3-D micro structure measurements. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2012; Volume 523, pp. 907–912. [Google Scholar]
- Murakami, H.; Katsuki, A.; Sajima, T.; Suematsu, T. Study of a vibrating fiber probing system for 3-D micro-structures: Performance improvement. Meas. Sci. Technol. 2014, 25, 094010. [Google Scholar] [CrossRef]
- Cui, J.; Li, J.; Feng, K.; Tan, J. Three-dimensional fiber probe based on orthogonal micro focal-length collimation for the measurement of micro parts. Opt. Express 2015, 23, 26386–26398. [Google Scholar] [CrossRef]
- Cui, J.; Li, J.; Feng, K.; Tan, J.; Zhang, J. A 3D fiber probe based on orthogonal micro focal-length collimation and fiber Bragg grating. Meas. Sci. Technol. 2016, 27, 074005. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K.; Yoshida, I.; Hamano, Y.; Honda, H. Development of measurement system for microstructures using an optical fiber probe: Improvement of measurable region and depth. Meas. Sci. Technol. 2020, 31, 075902. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K.; Yoshida, I.; Hamano, Y.; Honda, H. Investigation of factors affecting sensitivity enhancement of an optical fiber probe for microstructure measurement using oblique incident light. Appl. Sci. 2020, 10, 3191. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K.; Sata, Y. Development of the contact detection method in free-form surface of the optical fiber probe for microstructure measurement using long short term memory. Meas. Sens. 2021, 18, 100170. [Google Scholar] [CrossRef]
- Zou, L.; Ni, H.; Zhang, P.; Ding, X. Assembled Cantilever Fiber Touch Trigger Probe for Three-Dimensional Measurement of Microstructures. Sensors 2017, 17, 2652. [Google Scholar] [CrossRef]
- Ji, H.; Hsu, H.; Kong, L.; Wedding, A. Development of a contact probe incorporating a Bragg grating strain sensor for nano coordinate measuring machines. Meas. Sci. Technol. 2009, 20, 095304. [Google Scholar] [CrossRef]
- Liu, F.; Fei, Y.; Xia, H.; Chen, L. A new micro/nano displacement measurement method based on a double-fiber Bragg grating (FBG) sensing structure. Meas. Sci. Technol. 2012, 23, 054002. [Google Scholar] [CrossRef]
- Cui, J.; Feng, K.; Zhu, S.; Zhang, Y.; Hu, Y.; Tan, J. Development of FBG probes for dimensional metrology with micro parts of high aspect ratio. J. Mod. Opt. 2013, 60, 2001–2011. [Google Scholar] [CrossRef]
- Cui, J.; Feng, K.; Li, J.; Tan, J. Development of a double fiber probe with a single fiber Bragg grating for dimensional measurement of microholes with high aspect ratios. Opt. Lett. 2014, 39, 2868–2871. [Google Scholar] [CrossRef]
- Feng, K.; Cui, J.; Zhao, S.; Li, J.; Tan, J. A twin FBG probe and integration with a microhole-measuring machine for the measurement of microholes of high aspect ratios. IEEE-ASME Trans. Mechatron. 2016, 21, 1242–1251. [Google Scholar] [CrossRef]
- Feng, K.; Cui, J.; Dang, H.; Zhang, H.; Zhao, S.; Tan, J. Four-cores FBG probe based on capillary self-assembly fabrication technique for 3D measurement. IEEE Photon. Technol. Lett. 2016, 28, 2339–2342. [Google Scholar] [CrossRef]
- Liu, F.; Chen, L.; Wang, J.; Xia, H.; Li, R.; Yu, L.; Fei, Y. Modeling and prototyping of a fiber Bragg grating-based dynamic micro-coordinate measuring machine probe. Meas. Sci. Technol. 2016, 27, 025016. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Chen, L.; Li, R.; Xia, H.; Yu, L. Development and characterization of a high-sensitivity fiber Bragg grating-based vibrating nano-probe for 3D measurement. Sens. Rev. 2018, 39, 199–207. [Google Scholar] [CrossRef]
- Schmitt, R.; Pfeifer, T.; Depiereux, F.; König, N. Novel fiber-optical interferometer with miniaturized probe for in-hole measurements. Optoelectron Lett. 2008, 4, 140–142. [Google Scholar] [CrossRef]
- Zhao, W.; Tan, J.; Qiu, L.; Zou, L. A new laser heterodyne confocal probe for ultraprecision measurement of discontinuous contours. Meas. Sci. Technol. 2005, 16, 497. [Google Scholar] [CrossRef]
- Ehrig, W.; Neuschaefer-Rube, U.; Neugebauer, M.; Meeß, R. Traceable optical coordinate metrology applications for the micro range. In Proceedings of the Three-Dimensional Imaging Metrology; SPIE: Paris, France, 2009; Volume 7239, pp. 134–143. [Google Scholar]
- Fang, H.; Xu, B.; Chen, W.; Tang, H.; Zhao, S. A slope-adapted sample-tilting method for profile measurement of microstructures with steep surfaces. Nanomaterials 2015, 2015, 2. [Google Scholar] [CrossRef]
- Miliou, A. In-fiber interferometric-based sensors: Overview and recent advances. Photonics 2021, 8, 265. [Google Scholar] [CrossRef]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, T.; Schmitt, R.; Konig, N.; Mallmann, G.F. Interferometric measurement of injection nozzles using ultra-small fiber-optical probes. Chin. Opt. Lett. 2011, 9, 071202. [Google Scholar] [CrossRef]
- Matsui, K.; Matsumoto, H.; Takahashi, S.; Takamasu, K. New non-contact measurement of small inside-diameter using tandem low-coherence interferometer and optical fiber devices. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2012; Volume 523, pp. 871–876. [Google Scholar]
- Hovell, T.; Petzing, J.; Justham, L.; Kinnell, P. From light to displacement: A design framework for Optimising spectral-domain low-coherence interferometric sensors for in situ measurement. Appl. Sci. 2020, 10, 8590. [Google Scholar] [CrossRef]
- Hovell, T.; Matharu, R.S.; Petzing, J.; Justham, L.; Kinnell, P. Lensless fiber-deployed low-coherence interferometer for in-situ measurements in nonideal environments. Opt. Eng. 2020, 59, 014113. [Google Scholar] [CrossRef]
- Hovell, T.; Petzing, J.; Justham, L.; Kinnell, P. In-situ measurement of electrochemical jet machining using low coherence interferometry. In Proceedings of the Euspen’s 20th International Conference & Exhibition; Euspen: Bedford, UK, 2020. [Google Scholar]
- Malak, M.; Marty, F.; Nouira, H.; Salgado, J.; Bourouina, T. All-silicon interferometric optical probe for non-contact dimensional measurements in confined environments. In Proceedings of the 25th International Conference on Micro Electro Mechanical Systems (MEMS), Paris, France, 29 January–2 February 2012; pp. 628–631. [Google Scholar]
- Hovell, T.; Petzing, J.; Justham, L.; Kinnell, P. Pragmatic micrometre to millimetre calibration using multiple methods for low-coherence interferometer in embedded metrology applications. Sensors 2021, 21, 5101. [Google Scholar] [CrossRef]
- Zhang, F.; Qu, X.; Ouyang, J. An automated inner dimensional measurement system based on a laser displacement sensor for long-stepped pipes. Sensors 2012, 12, 5824–5834. [Google Scholar] [CrossRef]
- Tong, Q.b.; Jiao, C.q.; Huang, H.; Li, G.b.; Ding, Z.l.; Yuan, F. An automatic measuring method and system using laser triangulation scanning for the parameters of a screw thread. Meas. Sci. Technol. 2014, 25, 035202. [Google Scholar] [CrossRef]
- Hošek, J.; Linduška, P. Simple Modification of a Commercial Laser Triangulation Sensor for Distance Measurement of Slot and Bore Side Surfaces. Sensors 2021, 21, 6911. [Google Scholar] [CrossRef]
- Li, X.Q.; Wang, Z.; Fu, L.H. A laser-based measuring system for online quality control of car engine block. Sensors 2016, 16, 1877. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Herazo, E.L.; Smith, S.T. X-ray computed tomography: From medical imaging to dimensional metrology. Precis. Eng. 2019, 60, 544–569. [Google Scholar] [CrossRef]
- Wang, S. Investigation of X-ray computed tomography for dimensional measurement. In Proceedings of the Euspen SIG: Advancing Precision in Additive Manufacturing; Euspen: Bedford, UK, 2019. [Google Scholar]
- Villarraga-Gómez, H.; Kotwal, N.; Parwani, R.; Weiß, D.; Krenkel, M.; Kimmig, W.; Vom Hagen, C.G. Improving the dimensional accuracy of 3D X-ray microscopy data. Meas. Sci. Technol. 2022, 33, 074002. [Google Scholar] [CrossRef]
- Ice, G.E.; Budai, J.D.; Pang, J.W. The race to x-ray microbeam and nanobeam science. Science 2011, 334, 1234–1239. [Google Scholar] [CrossRef]
- Wu, Z.j.; Li, Z.l.; Huang, W.d.; Gong, H.f.; Gao, Y.; Deng, J.; Hu, Z.j. Comparisons of nozzle orifice processing methods using synchrotron X-ray micro-tomography. J. Zhejiang Univ. Sci. A 2012, 13, 182–188. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Lee, C.; Smith, S.T. Dimensional metrology with X-ray CT: A comparison with CMM measurements on internal features and compliant structures. Precis. Eng. 2018, 51, 291–307. [Google Scholar] [CrossRef]
- Lee, N.K.; Chow, J.K.; Chan, A.C. Design of precision measurement system for metallic hole. J. Adv. Manuf. Technol 2009, 44, 539–547. [Google Scholar] [CrossRef]
- Tan, J.; Cui, J. Ultraprecision 3D probing system based on spherical capacitive plate. Sens. Actuator A Phys. 2010, 159, 1–6. [Google Scholar] [CrossRef]
- Chen, S.T.; Lin, S.m. Development of a capacitive sensing technology for the measurement of perpendicularity in the narrow, deep slot-walls of micromolds. Microelectron. Reliab. 2018, 83, 216–222. [Google Scholar] [CrossRef]
- Xingyuan, B.; Yesheng, L.; Yamin, Z.; Jiubin, T.; Junning, C. Processing circuits of weak capacitance signal for spherical scattering electrical-field probing sensor. In Proceedings of the 14th International Conference on Electronic Measurement & Instruments (ICEMI); IEEE: Piscataway, NJ, USA, 2019; pp. 692–697. [Google Scholar]
- Bian, X.; Cui, J.; Lu, Y.; Tan, J. Ultraprecision diameter measurement of small holes with large depth-to-diameter ratios based on spherical scattering electrical-field probing. Appl. Sci. 2019, 9, 242. [Google Scholar] [CrossRef]
- Bian, X.; Cui, J.; Lu, Y.; Zhao, Y.; Cheng, Z.; Tan, J. Quantitative investigation of surface charge distribution and point probing characteristics of spherical scattering electrical field probe for precision measurement of miniature internal structures with high aspect ratios. Appl. Sci. 2020, 10, 5268. [Google Scholar] [CrossRef]
- Pourciel, J.B.; Jalabert, L.; Masuzawa, T. Profile and surface measurement tool for high aspect-ratio microstructures. JSME Int. J. Ser. C 2003, 46, 916–922. [Google Scholar] [CrossRef]
- Kim, J.; de Mathelin, M.; Ikuta, K.; Kwon, D.S. Advancement of flexible robot technologies for endoluminal surgeries. Proc. IEEE 2022, 110, 909–931. [Google Scholar] [CrossRef]
- Hong, W.; Schmitz, A.; Bai, W.; Berthet-Rayne, P.; Xie, L.; Yang, G.Z. Design and compensation control of a flexible instrument for endoscopic surgery. In Proceedings of the International Conference on Robotics and Automation (ICRA), Paris, France, 31 May 2020–31 August 2020; pp. 1860–1866. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).