Enhancing Feature Selection Optimization for COVID-19 Microarray Data

Abstract

The utilization of gene selection techniques is crucial when dealing with extensive datasets containing limited cases and numerous genes, as they enhance the learning processes and improve overall outcomes. In this research, we introduce a hybrid method that combines the binary reptile search algorithm (BRSA) with the LASSO regression method to effectively filter and reduce the dimensionality of a gene expression dataset. Our primary objective was to pinpoint genes associated with COVID-19 by examining the GSE149273 dataset, which focuses on respiratory viral (RV) infections in individuals with asthma. This dataset suggested a potential increase in ACE2 expression, a critical receptor for the SARS-CoV-2 virus, along with the activation of cytokine pathways linked to COVID-19. Our proposed BRSA method successfully identified six significant genes, including ACE2, IFIT5, and TRIM14, that are closely related to COVID-19, achieving an impressive maximum classification accuracy of 87.22%. By conducting a comparative analysis against four existing binary feature selection algorithms, we demonstrated the effectiveness of our hybrid approach in reducing the dimensionality of features, while maintaining a high classification accuracy. As a result, our hybrid approach shows great promise for identifying COVID-19-related genes and could be an invaluable tool for other studies dealing with very large gene expression datasets.

1. Introduction

The utilization of DNA microarray technology provides a useful means of measuring gene expression levels simultaneously, making it a valuable tool for various applications, such as SNP and mutation detection, tumor classification, target gene and biomarker identification, chemo-resistance gene identification, and drug discovery [1]. Both microarrays and RNA-seq are valuable technologies for gene expression analysis, but they have their respective strengths and limitations. Here are some scenarios where microarrays might have advantages over RNA-seq: (1) Microarrays are generally less expensive than RNA-seq, making them a more budget-friendly option, especially when dealing with a large number of samples. (2) Microarray data generate smaller datasets compared to RNA-seq, which can be advantageous when dealing with limited storage or computational resources. (3) Microarrays have been in use for a longer time, and the experimental protocols are well-established. The process is relatively straightforward, while RNA-seq requires more complex sample preparation and data analysis workflows [2].

Despite its usefulness, the high cost of these experiments often results in a limited availability of experiments for classification. In combination with a large number of genes being present in each experiment, this creates the “curse of dimensionality”, which presents a challenge for both classification and data processing in general. The majority of genes present are housekeeping genes that provide little information for the classification task, while only a small proportion of genes are discriminatory [3,4]. Therefore, gene selection (GS) is an essential step in achieving effective classification. GS aims to identify discriminatory genes and reduce the number of genes used for classification, which is required in many applications. It should be noted that the number of irrelevant genes is typically much higher than the number of discriminatory genes.

The process of GS involves identifying the most consistent, non-redundant, and relevant features for use in constructing a model, as outlined by Lai et al. [5]. When increasing the size and diversity of datasets, it is crucial to systematically reduce their size. The primary objective of feature selection is to enhance the performance of predictive models while minimizing the computational costs associated with modeling.

There are four types of feature selection methods, namely filter methods [6], wrapper methods [7], hybrid methods [8], and embedded methods [9]. Filter methods select a subset of appropriate features that are independent of any learning algorithm and use the intrinsic and statistical characteristics of the features. To weight features, these methods assign a weight to each feature based on its relevance to class labels, often using correlation criteria and information-theory-based criteria. Examples of gene selection filter methods include minimum redundancy maximum relevance (MRMR) [10], information gain (IG) [11], and chi-square [12]. Wrapper methods employ heuristic search algorithms to find a subset of features. These methods begin with a randomly generated solution and progress toward the best subset of the solution with each iteration. The genetic algorithm [13], whale optimization algorithm [14], ant colony optimization algorithm [15], binary particle swarm optimization algorithm [16], binary grey wolf search algorithm [17], binary dragonfly algorithm [18], and other evolutionary algorithms are used in wrapper methods.

In the field of microarray data analysis, researchers have proposed hybrid approaches to enhance the identification of disease biomarkers. These methods aimed to overcome the limitations of the filter and wrapper methods. Filter methods are useful for datasets with a high number of features since they involve fewer computations, but their accuracy may be compromised. Conversely, wrapper methods yield superior classification accuracy but demand significantly more computational resources. Due to the complementary strengths and weaknesses of the two methods, the hybrid approach was developed. This involves first selecting a subset of features based on their importance using a filter method, followed by applying the wrapper method to the selected features, to determine the most effective ones [19,20].

Although numerous non-iterative optimization algorithms (NIOAs) have been employed in microarray data, there is no assurance that these techniques will discover the best subset of genes for classification problems, because of their stochastic nature [21]. In addition, gene selection remains a challenging task, due to the large search space of genes and intricate gene interactions [22,23]. Therefore, further research is necessary to develop an efficient gene selection approach.

Among the different optimization algorithms, the gray wolf optimization (GWO) algorithm is a bio-inspired optimization technique introduced by Mirjalili et al. [24] for feature selection in classification problems and imitates the hunting behavior of gray wolves in nature. Later, the binary version of gray wolf optimization (BGWO) [17] was proposed, to maximize the classification accuracy, while minimizing the number of selected features. BGWO provided significant results when compared to two well-known feature selection methods and using KNN as a classifier.

Abualigah et al. [25] introduced the reptile swarm algorithm (RSA), which mimics the hunting behavior of crocodiles, specifically their encircling and hunting coordination and cooperation. However, the RSA currently only works for single-objective optimization problems with conflicting variables, but it could be extended to handle binary and multi-objective variants to address a wide range of discrete and multi-objective real-world optimization problems.

The RSA algorithm has gained popularity due to its attractive features, such as requiring minimal initialization parameters and not needing derivative information in basic search. It is also a scalable, easy-to-use, and sound algorithm, making it suitable for various real-world problems. However, like other metaheuristic algorithms, RSA’s performance may also be affected by the problem’s size and complexity, leading to premature convergence, due to a lack of balance between exploration and exploitation capabilities [26]. To overcome these limitations, the problem-specific knowledge embedded in the search space should be considered, and the optimization structure of RSA should be appropriately adjusted. Moreover, there is evidence in the literature to show that continuous nature-inspired algorithms can be converted into a binary version using appropriate transfer functions to enhance classification accuracy. As a binary version of RSA has not yet been developed, in this study a novel binary version of the RSA algorithm is proposed and evaluated using COVID-19 data analysis.

In this study, a two-stage hybrid feature selection approach is utilized to improve classification performance. Initially, the best transfer function was selected among the common support vector machine (SVM) [27], random forest (RF) [28], and k-nearest neighbor (KNN) [29] classifiers. It is worth noting that most binary versions of nature-inspired algorithms in the literature employ average classification accuracy as the fitness function. Therefore, in the second stage, an alternative fitness function was explored, to yield better results in terms of feature selection and classification accuracy.

Indeed, a novel optimized feature selection method is proposed, combining the LASSO regression method with the binary reptile search algorithm (BRSA). This hybrid approach guides the search for a more robust and useful subset of genes while considering feature selection accuracy and stability. The performance of the proposed BRSA was evaluated with the identified best classifier and appropriate sigmoid transfer function, and the results indicated its superior classification accuracy compared to other existing gene selection techniques. Finally, the proposed method was used to identify the optimal subset of genes associated with COVID-19 from the RNA-seq dataset.

2. The Preliminaries

This section begins by introducing the LASSO filtering method and proceeds to describe the standard RSA and its basic steps. Additionally, the SVM classification algorithm is introduced.

2.1. The Penalized Logistic Regression—LASSO Method

LASSO, which stands for least absolute shrinkage and selection operator, is a method used for feature selection and regression analysis [30]. Its primary objective is to reduce certain coefficients while setting others to zero. The LASSO method employs an $l_1$ penalty, which results in some of the estimated coefficients becoming equal to zero.

Given a linear regression with standardized predictors $x_{ij}$ and centered response values $y_i$ for $i=1,2,\cdots ,N$ and $j=1,2,\cdots ,p$, LASSO solves the $l_1$-penalized regression problem as

$${\arg \min }_{{\beta }_1,\dots ,{\beta }_p}\sum _{i=1}^N{(y_i-{\beta }_0-\sum _{j=1}^p{x}_{ij}{\beta }_j)}^2+\lambda \sum _{j=1}^p\parallel {\beta }_j\parallel ,$$

(1)

where $\lambda$ is a tuning parameter that controls the amount of shrinkage applied to the coefficients. The optimal value of $\lambda$ is typically determined through techniques such as cross-validation.

Cross-validation [31] is a statistical technique employed to assess a model’s performance and its ability to generalize to unseen data. It involves dividing the dataset into subsets, training the model on some of them, and validating it on the remaining data. Cross-validation helps to evaluate a model’s robustness and prevent overfitting. Optimal lambda cross-validation [32] is a specific application of cross-validation used to find the optimal value of lambda in LASSO regression, balancing the trade-off between model complexity and data fitting. By performing optimal lambda cross-validation, the most suitable lambda value is determined, resulting in an effectively tuned LASSO model with improved predictive performance and meaningful variable selection [33].

2.2. The Reptile Search Algorithm (RSA)

Nature-inspired optimization algorithms often take inspiration from various natural processes and organisms to develop efficient algorithms. Abualigah et al. [25] introduced the RSA, a metaheuristic optimization algorithm inspired by the hunting behavior of crocodiles. The algorithm mimics the natural habitat of crocodiles, which prefer areas with abundant food and water and are able to hunt both in and out of the water. The RSA algorithm incorporates essential features of modern optimization algorithms to compute its main formula. The procedure of RSA can be summarized as below:

Stage 1: RSA parameter initialization

Before running the RSA algorithm, it is necessary to initialize the control and algorithmic parameters. The control parameters consist of N, the number of candidate solutions (i.e., the number of crocodiles); T, the maximum number of iterations, $\alpha$, which controls the exploitation ability; and $\beta$, which controls the exploration ability. These parameters are used throughout the search process to balance exploration and exploitation.

Stage 2: Population initialization of RSA

In this stage, a random set of solutions is initialized using the following equation, as proposed by Abualigah et al. [25]:

$$\begin{array}{c}\hfill x_{ij}=rand\ast (UB-LB)+LB,i=1,2\cdots ,N,\mathrm{and}j=1,2,\cdots ,n.\end{array}$$

(2)

Here, $x_{i,j}$ refers to the jth position of the ith solution, n is the dimension size of the problem, rand is a random value between 0 and 1, $LB$ is the lower bound value, and $UB$ is the upper bound value. Thus, a set of N solutions is generated and stored in a matrix:

$$X=\left[\begin{array}{ccccc}{x}_{1,1}& \cdots & x_{1,j}& x_{1,n-1}& x_{1,n}\\ x_{2,1}& \cdots & x_{2,j}& x_{2,n-1}& x_{2,n}\\ .& \cdots & .& .& .\\ .& \cdots & .& .& .\\ x_{N-1,1}& \cdots & x_{N-1,j}& x_{N-1,n-1}& x_{N-1,n}\\ x_{N,1}& \cdots & x_{N,j}& x_{N,n-1}& x_{N,n}\end{array}\right].$$

(3)

Stage 3: Fitness function estimation

The fitness value of each solution $x_{ij}$ in the population, denoted by X, is computed as $f\left(x_{ij}\right)$.

Stage 4: Exploration phase

The RSA algorithm utilizes two strategies, known as high walking and belly walking, during the exploration phase to discover better solutions by exploring new regions in the problem’s search space. The following equation is used to update the position of each solution in the population during the exploration phase:

$$\begin{array}{c}\hfill x_{i,j}(t+1)=Bes{t}_j\left(t\right)\ast -{\eta }_{i,j}\left(t\right)\ast \beta -R_{i,j}\left(t\right)\ast rand\mathrm{if}(t\le T/4),\end{array}$$

(4)

and

$$\begin{array}{c}\hfill x_{i,j}(t+1)=Bes{t}_j\left(t\right)\ast x_{r_1,j}\ast ES\left(t\right)\ast rand\mathrm{if}(T/4<t\le 2T/4)\end{array}$$

(5)

with $x_{i,j}$ representing the decision variable of the ith solution at the jth position. The value of $Bes{t}_j\left(t\right)$ corresponds to the jth position in the best solution obtained at iteration t, while $t+1$ represents the new iteration, and t represents the previous iteration. The hunting operator of the jth position in the ith solution, ${\eta }_{i,j}\left(t\right)$, can be calculated using Equation (6). $x_{r_1,j}$ refers to the decision variable at the jth position in the ith solution, where $r_1$ is a value between 1 and N. The high walking strategy is controlled by $t\le T/4$, whereas the belly walking strategy is controlled by $T/4<t\le 2T/4$ [25]. The values of ${\eta }_{i,j}$, $M\left(x_i\right)$, $P_{i,j}$, $R_{i,j}$ and $ES\left(t\right)$ are calculated using

$${\eta }_{i,j}=Bes{t}_j\left(t\right)\ast P_{i,j},$$

(6)

$$M\left(x_i\right)=\frac{1}{n}\sum _{i=1}^n{x}_{(i,j)},$$

(7)

$$P_{i,j}=\alpha +\frac{x_{i,j}-M\left(x_i\right)}{Bes{t}_j\left(t\right)\ast (U{B}_j-L{B}_j)+ϵ},$$

(8)

$$ES\left(t\right)=2\ast r_3\ast (1-1/T),$$

(9)

and

$$R_{i,j}=\frac{Bes{t}_j\left(t\right)-x_{r_2,j}}{Bes{t}_j\left(t\right)+ϵ}.$$

(10)

Here, the percentage difference between the decision variable at the jth position of the best solution ($Bes{t}_j\left(t\right)$) and the decision variable at the position of the current solution ($x_i$) is denoted by $P_{i,j}$, while $\alpha$ is used to control the exploration capability of the RSA during the hunting phase, with a value of $\alpha =0.1$. Additionally, $ϵ$ is a random value between 0 and 2, and $M\left(x_i\right)$ is the average value of all decision variables of the current solution. The variable $R_{i,j}$ is used to reduce the search area of the jth position in the ith solution. The evolutionary sense probability, $ES\left(t\right)$, is randomly assigned a value decreasing from 2 to $-2$, and is calculated using Equation (9). The parameter $r_2$ is a random value between 1 and N, and $r_3$ is a random integer value of $-1$, 0, and 1 [25].

Stage 5: Exploitation phase

This phase of RSA is designed to exploit current search areas, to find optimal solutions using two strategies: hunting coordination and hunting cooperation, as shown in

$$\begin{array}{c}\hfill x_{i,j}(t+1)=Bes{t}_j\left(t\right)\ast P_{i,j}\ast rand\mathrm{if}(2T/4\le t\le 3T/4),\end{array}$$

(11)

and

$$\begin{array}{c}\hfill x_{i,j}(t+1)=Bes{t}_j\left(t\right)-{\eta }_{i,j}\ast ϵ-R_{i,j}\ast rand\mathrm{if}(3T/4\le t\le T).\end{array}$$

(12)

During the time interval $2T/4\le t\le 3T/4$, the hunting coordination strategy is employed, while during the time interval $3T/4\le t\le T$, the hunting cooperation strategy is used.

Stage 6: Stop criterion

The process of Steps 3–5 needs to be repeated iteratively, until the maximum number of iterations T is achieved.

Finally, a flow chart of the continuous RSA is shown in Figure 1, and Algorithm 1 presents the pseudo-code of the RSA.

2.3. Support Vector Machine

SVMs are known to perform exceptionally well in microarray data analysis, which can be attributed to several theoretical factors [34]. First, SVMs are resilient to high ratios of variables to samples, as well as large numbers of variables. Additionally, they can effectively learn complex classification functions in a computationally efficient manner and employ robust regularization principles to prevent overfitting.

The fundamental principle underlying SVM classifiers is to identify a hyperplane with a maximum margin that can effectively separate two classes of data [35]. However, in situations where the data are not linearly separable, kernel functions are utilized to implicitly map the data to a higher-dimensional space and identify a suitable hyperplane. In this study, the linear kernel implementation of the SVM classifier was adopted, utilizing the “libSVM” software library [36].

Algorithm 1: Pseudocode of the Reptile Search Algorithm (RSA)

1: Initialization phase 2: Initialize RSA parameters 3: Initialize the solution’s positions randomly; $X:i=1,\cdots ,N$ 4: while$t<T$do 5:     Calculate the Fitness value for the candidate solutions $\left(X\right)$ 6:     Find the best solution 7:     Update the ES using Equation (9) 8:     The beginning of the RSA 9:     for ($i=1$ to N) do 10:         for ($j=1$ to n) do 11:            Update the ${\eta }_{i,j}$, $P_{i,j}$, $R_{i,j}$ and values using Equations (6), (8) and (10), respectively 12:            if $(t\le T/4)$ then 13:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)\ast -{\eta }_{(i,j)}\left(t\right)\ast \beta -R_{(i,j)}\left(t\right)\ast rand$ 14:            else if $(t\le 2T/4$ and $t>T/4)$ then 15:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)\ast x_{(r_1,j)}\ast ES\left(t\right)\ast rand$ 16:            else if $(t\le 3T/4$ and $t>2T/4)$ then 17:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)\ast P_{(i,j)}\ast rand$ 18:            else 19:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)-{\eta }_{(i,j)}\ast ϵ-R_{(i,j)}\ast rand$ 20:            end if 21:         end for 22:     end for 23:     $t=t+1$ 24: end while 25: Return the best solution $\left(Best\right(X\left)\right)$

3. The Proposed Method

This section provides a detailed account of the methodology and techniques utilized in the proposed BRSA approach, which is divided into two primary modules:

• LASSO-based filter approach: This stage involves identifying a set of relevant features through the application of a LASSO-based filter approach;
• BRSA-based wrapper approach: In this stage, the final subset of features is determined utilizing a BRSA-based wrapper approach.

The following subsections provide a complete description of these two phases.

3.1. The First Stage: Filter Approach

The LASSO approach involves utilizing the LASSO method to choose an initial subset of features based on gene significance and redundancy, rather than exhaustively studying all extracted features. By reducing the high dimensionality of the original dataset, the LASSO method generates more discriminative genes for the wrapper method, resulting in improved classification accuracy and reduced computational burden. The LASSO method achieves parameter regularization by shrinking and eliminating some regression coefficients, resulting in a feature selection phase that includes only non-zero values in the final model.

3.2. The Second Stage: Wrapper Approach

In this phase, the wrapper method is utilized to choose a subset of the most significant genes from the list of top genes identified by the LASSO filtering technique. BRSA was specifically designed to serve as a rapid search strategy for the wrapper model. RSA is a gradient-free, population-based method that can tackle both simple and complex optimization problems, subject to certain constraints. Although the RSA is susceptible to local optimization, it is more stable than other algorithms and can be applied to a binary algorithm. The recommended BRSA evaluates the quality of feature subsets using the F-measure as the fitness function, with the ultimate goal of improving classification performance by minimizing the number of selected genes.

3.2.1. Solution Representation

The process of feature selection involves identifying the most important features from the original dataset, in order to perform classification. This is achieved using the BRSA algorithm, where features are assigned a value of either ‘0’ to denote non-selected features or ‘1’ to indicate selected features.

3.2.2. The Fitness Function

In general, feature selection aims to identify a small set of features that exhibit high classification performance. The quality of the chosen subset is determined by the combination of high classification accuracy and a low number of selected features. With this in mind, the fitness function for the proposed feature selection technique was carefully designed. The F-measure was selected as the fitness function, with higher scores indicating better performance, ranging from 0 (worst) to 1 (best). Therefore, the optimization problem focused on maximizing the fitness function.The formula for the F-measure is expressed as

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{F-measure}=\frac{2\ast \mathrm{True}\mathrm{Positive}}{2\ast \mathrm{True}\mathrm{Positive}+\mathrm{True}\mathrm{Negative}+\mathrm{False}\mathrm{Negative}}.\end{array}\end{array}$$

(13)

It should be noted that reducing the number of selected genes can enhance classification accuracy. Therefore, when two subsets exhibit a similar classification accuracy, the subset containing fewer genes is preferred.

3.2.3. Binary Reptile Search Algorithm (BRSA)

The first stage of the proposed approach involves the selection of the top n genes using the LASSO filter approach, which is then passed on to the new BRSA algorithm in the second stage. In this phase, the BRSA algorithm is utilized to design an effective gene selection strategy that offers improved exploration and exploitation capabilities, with rapid convergence. While the BRSA algorithm is conceptually similar to the original RSA algorithm, the main difference lies in the search space. The original RSA operates in a continuous search space, whereas the binary version operates in a discrete search space. Since the search space for the BRSA is restricted to binary values (0 and 1), it is not possible to alter the position of the search space. To overcome this, the sigmoid transfer function is employed to transform the new reptile’s position from continuous to binary values. The sigmoid transfer function is chosen to ensure that the selected transfer function lies within the range of $[0,1]$.

3.2.4. Sigmoid Transfer Functions

The transfer function plays a crucial role in determining the probability of changing binary solution values from 0 to 1. The S-shaped transfer function is mathematically defined as

$$S=\frac{1}{1+exp(-x)}.$$

(14)

The positions in the S-shaped function are updated using

$$Bstep=\left\{\begin{array}{cc}1\hfill & \mathrm{if}(s\ge randn)\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.,$$

(15)

and

$$X_{i,j}(t+1)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}(x_{i,j}+Bstep\ge 1)\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.,$$

(16)

where $randn$ means a random number between 0 and 1.

In this study, the impact of four different sigmoid transfer functions on the performance of BRSA was examined [37]. The mathematical formulas for each of these functions are provided in

Table 1. Description of the four sigmoid transfer functions [37].

Function	Formula
$S_1$	$1/(1+exp(-x\left)\right)$
$S_2$	$1/(1+exp(-x/2\left)\right)$
$S_3$	$1/(1+exp(x/2\left)\right)$
$S_4$	$1/(1+exp(x/3\left)\right)$

, and their corresponding graphs are shown in Figure 2.

To sum up, the proposed BRSA is presented in Algorithm 2, and its corresponding flow chart is provided in Figure 3.

Algorithm 2: Pseudo-code of the Binary Reptile Search Algorithm (BRSA)

1: Initialization phase 2: Initialize BRSA parameters $\alpha$, $\beta$, etc. 3: Initialize the solution’s positions randomly. $X:i=1,\cdots ,N$ 4: while$t<T$do 5:     Calculate the Fitness Function for the candidate solutions $\left(X\right)$. 6:     Find the Best solution so far. 7:     Update the ES using Equation (9) 8:     The beginning of the BRSA 9:     for ($i=1$ to N) do 10:         for ($j=1$ to n) do 11:            Update the $\eta ,R,P$ and values using Equations (6), (8) and (10), respectively 12:            if $(t\le T/4)$ then 13:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)\ast -{\eta }_{(i,j)}\left(t\right)\ast \beta -R_{(i,j)}\left(t\right)\ast rand$ 14:            else if $(t\le 2T/4$ and $t>T/4)$ then 15:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)\ast x_{(r_1,j)}\ast ES\left(t\right)\ast rand$ 16:            else if $(t\le 3T/4$ and $t>2T/4)$ then 17:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)\ast P_{(i,j)}\ast rand$ 18:            else 19:                $x_{(i,j)}(t+1)=Bes{t}_j\left(t\right)-{\eta }_{(i,j)}\ast ϵ-R_{(i,j)}\ast rand$ 20:            end if 21:            Update the position using Equations (15) and (16) 22:         end for 23:     end for 24:     $t=t+1$ 25: end while 26: Return the best solution $\left(Best\right(X\left)\right)$

4. Case Study

4.1. GSE149273 (COVID19) Dataset

The GSE149273 dataset is an SRA dataset downloaded from the GEO that contains 25343 genes, 90 samples, and three categories (RVA, RVC, Control). A description of the dataset is given below:

• Status—Public on 25 April 2020
• Title—RV infections in asthmatics increase ACE2 expression and stimulate cytokine pathways implicated in COVID-19
• Organism—Homo sapiens
• Experiment type—Expression profiling using high throughput sequencing
• Summary—We present evidence that (1) viral respiratory infections are potential mechanisms of ACE2 overexpression in patients with asthma and that (2) ACE activation regulates multiple cytokine anti-viral responses, which could explain a mechanism of cytokine surge and associated tissue damage.

These results suggest that the recent finding of severe COVID-19 in asthma patients with recent exacerbations may be attributable to synergistic biomolecular interactions with viral co-infections.

Overall design—In paired design experiments across discovery and validation cohorts of asthmatic patients, biological replicates treated with RVA and RVC were compared to non-treated ones [38].

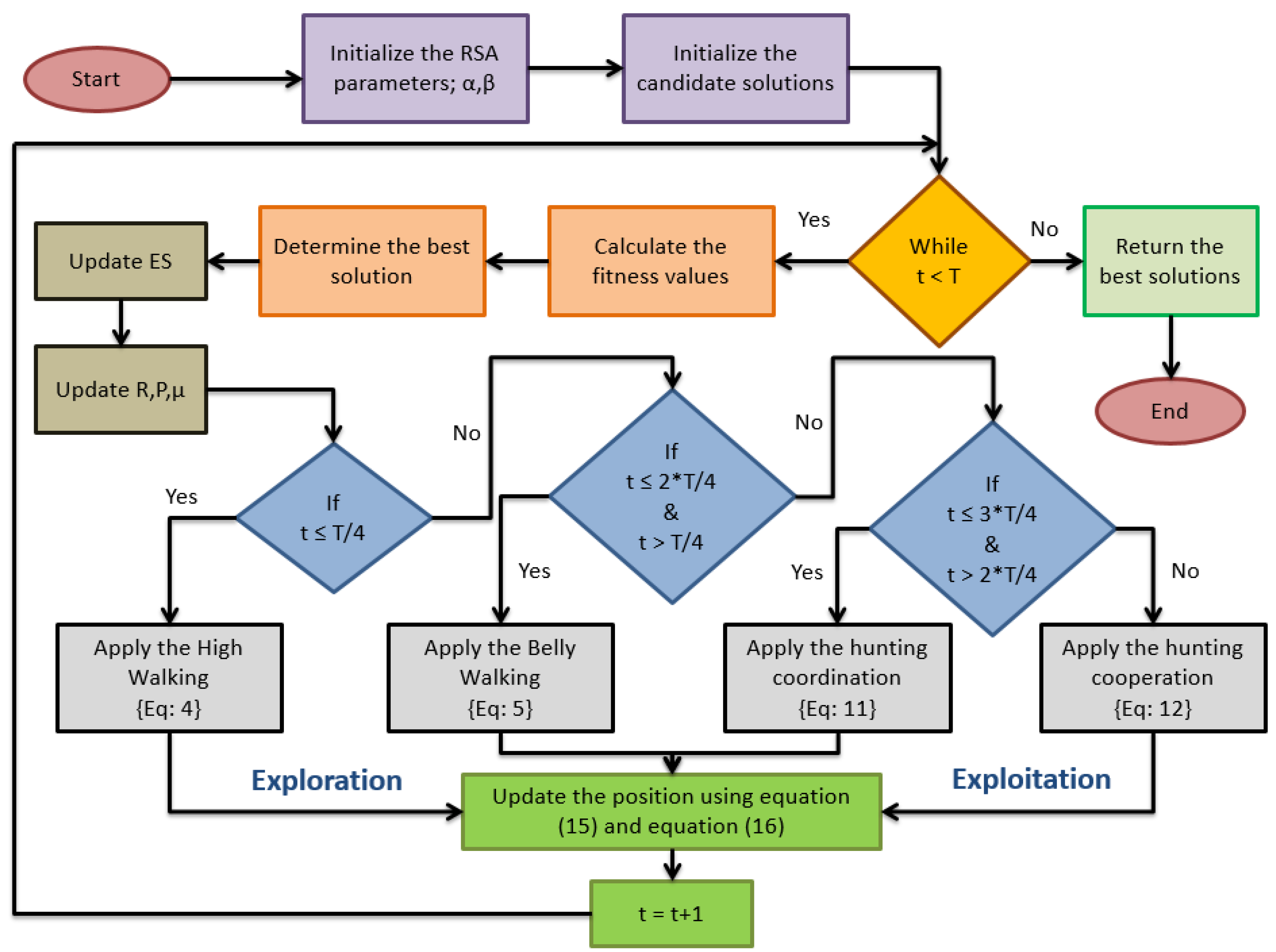
4.2. Experimental Results

This study utilized a binary metaheuristic algorithm to decrease the number of features in the common gene dataset obtained through differential expression analysis, resulting in an optimized dataset that includes only crucial features pertinent to the research. The LASSO regression method was used to analyze data from a maximum of 14 genes.

The implementation of the method was carried out using R software. In LASSO regression, the lambda ($\lambda$) value needs to be kept constant, to adjust the amount of coefficient shrinkage. The optimal lambda cross-validation for the dataset minimizes the prediction error rate. Figure 4 shows that the left dashed vertical line corresponds to the logarithmic value of the optimal lambda that minimizes the prediction error, which is approximately $-5$ and provides the most accurate results.

In general, regularization aims to balance accuracy and simplicity by finding a model with the highest accuracy and the minimum number of predictors. The optimal value of lambda is usually chosen by considering two values: $lambda.1se$ and $lambd{a}_{min}$. The former produces a simpler model but may be less accurate, while the latter is more accurate but less parsimonious. In this study, the accuracy of LASSO regression was compared with the accuracy of the full logistic regression model, as shown in

Table 2. Accuracy comparison.

Parameter Name	Accuracy
$lambd{a}_{min}$	0.988764
$lambda.1se$	0.9775281
Original logistic model	0.9325843

. The results showed that $lambd{a}_{min}$ produced the highest accuracy, and the obvious choice of the optimal value was 0.001. Finally, the most significant genes were selected based on this optimal value.

The LASSO method applies $l_1$ or absolute value penalties in penalized regression and is particularly effective for variable selection in the presence of many predictors. The resulting solution is often sparse, containing estimated regression coefficients with only a few non-zero values.

Table 3. Extracted genes from the LASSO model.

No	Gene	No	Gene
1	ANKRD33	8	RAB34
2	BEX2	9	SLC7A6
3	CHST13	10	SNHG9
4	DNAJC30	11	TMEM229A
5	DUSP21	12	TRIM14
6	IFIT5	13	VPS35
7	X4.Mar	14	ZNF354A

presents the list of selected genes obtained using the LASSO method.

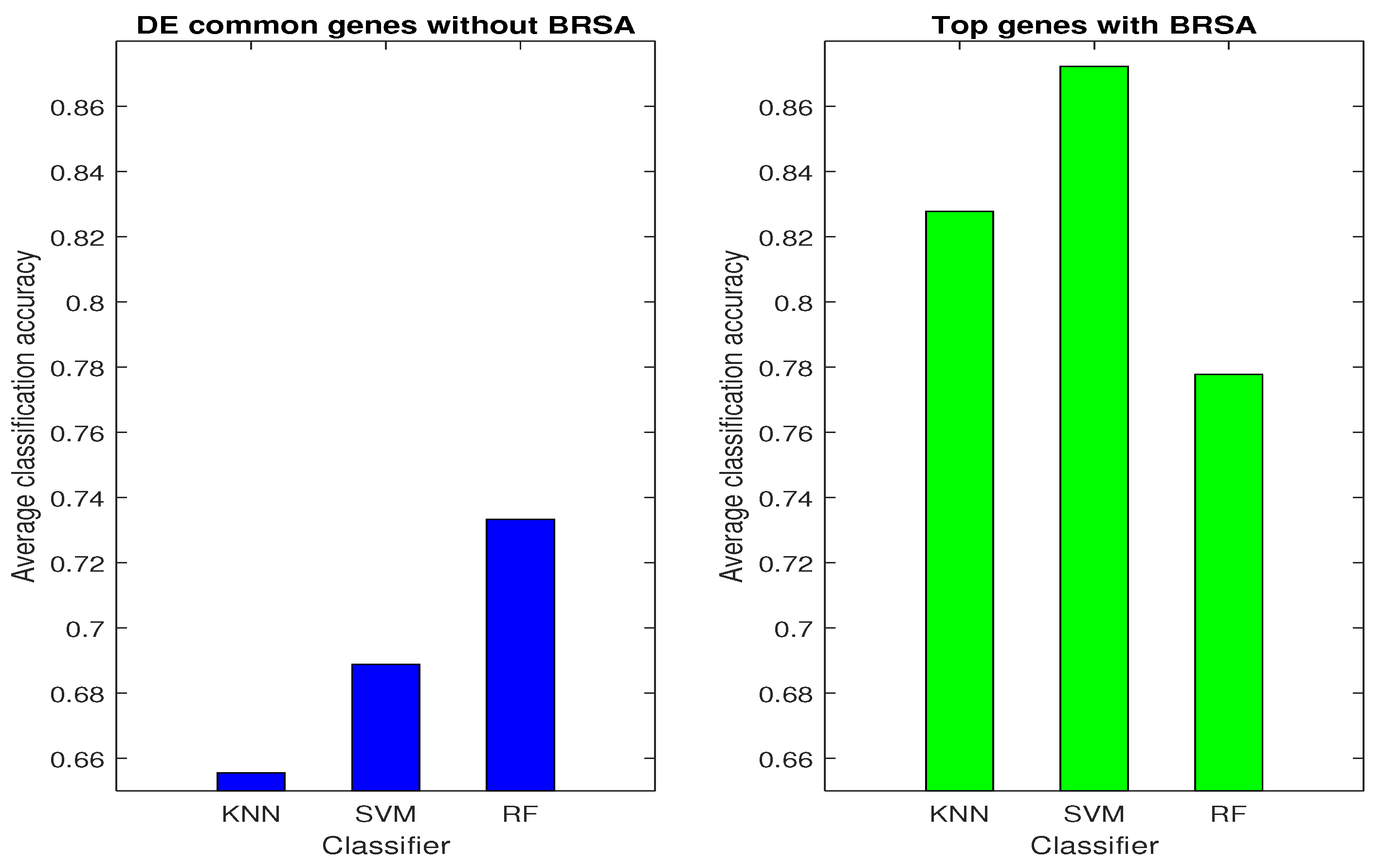
Next, the best classification algorithm was selected among SVM, RF, and KNN, by applying each algorithm to the full dataset and the filtered dataset separately. As shown in

Table 4. Mean and standard deviation of the classification accuracy of the three classifiers.

	All Genes without BRSA			Top Genes with BRSA
	KNN	SVM	RF	KNN	SVM	RF
Mean	0.65557	0.6889	0.73332	0.82777	0.87222	0.77776
STD	0.11653	0.09515	0.12505	0.04098	0.04573	0.08282

and Figure 5, the RF algorithm achieved the highest average accuracy of 73.32% on the full dataset. On the other hand, the filtered dataset performed very well with the SVM classifier, achieving a high average classification accuracy and low variance. The performance of SVM with the BRSA algorithm was found to be the highest (87.22%) when compared to the KNN and RF classifiers. Therefore, the SVM was selected as the best classifier to be adopted in this study.

To convert the continuous search area into a binary version in BRSA, a sigmoid function was used.

Table 5. Performance of the evaluation matrices.

		${\mathit{S}}_1$	${\mathit{S}}_2$	${\mathit{S}}_3$	${\mathit{S}}_4$
Accuracy	AVG	0.8611	0.8583	0.8667	0.8722
	STD	0.0494	0.0525	0.0522	0.0480
	Best	0.9444	0.9444	0.9444	0.9444
	Worst	0.7778	0.7778	0.7778	0.7778
F-measure	AVG	0.8696	0.8696	0.8757	0.8789
	STD	0.0472	0.0466	0.0504	0.0475
	Best	0.9474	0.9474	0.9474	0.9474
	Worst	0.7778	0.8000	0.7778	0.7778
Precision	AVG	0.8238	0.8154	0.8253	0.8444
	STD	0.0731	0.0739	0.0735	0.0773
	Best	0.9000	0.9000	0.9000	0.9000
	Worst	0.7273	0.7273	0.7273	0.7500
Sensitivity	AVG	0.9278	0.9264	0.9320	0.9208
	STD	0.0903	0.0777	0.1005	0.0984
	Best	1.0000	1.0000	1.0000	1.0000
	Worst	0.7778	0.7500	0.7500	0.7500
Specificity	AVG	0.8000	0.7945	0.8056	0.8278
	STD	0.1117	0.1098	0.1074	0.0986
	Best	1.0000	1.0000	1.0000	1.0000
	Worst	0.6667	0.6667	0.6667	0.6667
No. of selected features	AVG	6.6500	6.1500	6.2500	6.0500
	STD	1.7252	1.6944	1.7733	1.3169
	Best	3.0000	4.0000	4.0000	4.0000
	Worst	10.0000	11.0000	9.0000	9.0000

shows the statistical outcomes obtained for each of the evaluation matrices used in each sigmoid transfer function. The best statistical results of the sigmoid transfer functions are highlighted in bold.

The fourth sigmoid transfer function ($S_4$) showed significantly higher averages for classification accuracy, fitness value, precision, and specificity compared to the other three transfer functions. Specificity refers to the percentage of true negatives, and $S_4$ exhibited a specificity of 82.78%, indicating that 82.78% of those without the target disease will test negative. The best and worst values for the evaluated matrices of the four transfer functions were almost equal. Figure 6 provides a clearer representation of the average number of selected features, where $S_4$ has the fewest significant features (6.05). Furthermore, Figure 7, shows that $S_1$ and $S_2$ had similar average fitness values, but different accuracy and sensitivity values. A higher sensitivity in $S_2$ indicates that the model correctly identifies most positive results, whereas a low sensitivity means the model misses a significant number of positive results.

Furthermore, the convergence of four distinct sigmoid functions is compared in Figure 8 and illustrates the efficiency of the algorithms.

Figure 8 depicts that the $S_4$ sigmoid transfer function not only attained a superior convergence speed but also acquired the best fitness scores. It typically achieved its optimal solution in around 70 iterations, whereas $S_1$ began with a low fitness value and converged to a high fitness value after approximately 220 iterations. As a result, the $S_4$ sigmoid transfer function was deemed the most appropriate for the proposed BRSA.

Next, the proposed BRSA was compared with four alternative algorithms: the binary dragonfly algorithm (BDA), binary particle swarm optimization (BPSO), and two variants of the binary gray wolf optimization algorithm (BGWO1 and BGWO2). To initiate the analysis, we applied various statistical metrics, and the results are presented in

Table 6. Comparison of BRSA with the other algorithms based on evaluation matrices.

		BRSA	BDA	BPSO	BGWO1	BGWO2
Accuracy	AVG	0.8472	0.8278	0.8250	0.7806	0.8194
	STD	0.0472	0.0595	0.0924	0.0459	0.0740
	Best	0.8889	0.9444	0.9444	0.8889	0.9444
	Worst	0.7778	0.7222	0.5556	0.7222	0.7222
F-measure	AVG	0.8624	0.8261	0.8255	0.7576	0.8091
	STD	0.0381	0.0599	0.0864	0.0622	0.0902
	Best	0.9474	0.9412	0.9474	0.8750	0.9474
	Worst	0.8000	0.7143	0.7000	0.7059	0.6154
Precision	AVG	0.7970	0.8556	0.8355	0.8459	0.8443
	STD	0.0772	0.1196	0.1126	0.0795	0.0909
	Best	1.0000	1.0000	1.0000	1.0000	1.0000
	Worst	0.6923	0.6923	0.5385	0.7273	0.7273
Sensitivity	AVG	0.9500	0.8222	0.8389	0.7000	0.7945
	STD	0.0672	0.1162	0.1418	0.1146	0.1498
	Best	1.0000	1.0000	1.0000	1.0000	1.0000
	Worst	0.7778	0.5556	0.5556	0.5556	0.5556
Specificity	AVG	0.7444	0.8334	0.8111	0.8556	0.8445
	STD	0.1146	0.1464	0.1575	0.0960	0.1045
	Best	1.0000	1.0000	1.0000	1.0000	1.0000
	Worst	0.5556	0.5556	0.6667	0.6667	0.6667
No. of selected features	AVG	6.2000	5.4000	6.9500	7.1500	6.8500
	STD	1.5079	1.5694	1.6694	1.5985	1.5985
	Best	4.0000	2	4	4	4
	Worst	9	8	10	9	10

. Indeed, Table 6 indicates that the average accuracy, average F-measure, and average sensitivity of BRSA were higher than those of the other algorithms, except for the average precision value.

Additionally, BDA was found to be the most competitive algorithm, with BRSA following closely behind. Based on these findings, we can infer that BRSA outperformed BPSO, BDA, BGWO1, and BGWO2 in selecting the most relevant features from the tested datasets to optimize classification performance, while minimizing the number of selected features.

Furthermore, according to the conclusion by Demšar [39] and Benavoli et al. [40] that “the non-parametric tests should be preferred over the parametric ones”, we employed the Friedman test [41] to validate the obtained results and determined that the differences between the competing methods were significant.

Table 7. Ranks of accuracy using the Friedman test.

Algorithm	Final Rank
BRSA	1
BDA	3
BPSO	2
BGWO1	5
BGWO2	4

,

Table 8. Ranks of fitness value using the Friedman test.

Algorithm	Final Rank
BRSA	1
BDA	3
BPSO	2
BGWO1	5
BGWO2	4

and

Table 9. Ranks of number of selected features using the Friedman test.

Algorithm	Final Rank
BRSA	2
BDA	1
BPSO	4
BGWO1	3
BGWO2	5

display the final rank of each algorithm as determined by the Friedman test. The test was conducted using IBM SPSS Statistics version 22. Based on the ranks, it is evident that BRSA achieved the first rank in terms of performance measures for both classification accuracy and fitness value, thereby taking first place among all algorithms. However, in terms of the number of selected features, BRSA ranked second, with BDA obtaining first place in the Friedman test.

After implementing the proposed BRSA approach on 4055 common DE genes, the top subset of six genes was identified as the optimal subset with 87.22% accuracy for the SVM classifier.

Table 10. Proposed prediction model for COVID-19 identification.

	Gene Index	Gene Name
Covid-19 GSE149273	1637	BEX2
	3527	CHST13
	5239	DUSP21
	8554	IFIT5
	20839	SNHG9
	23214	TRIM14

presents the selected genes obtained using this approach.

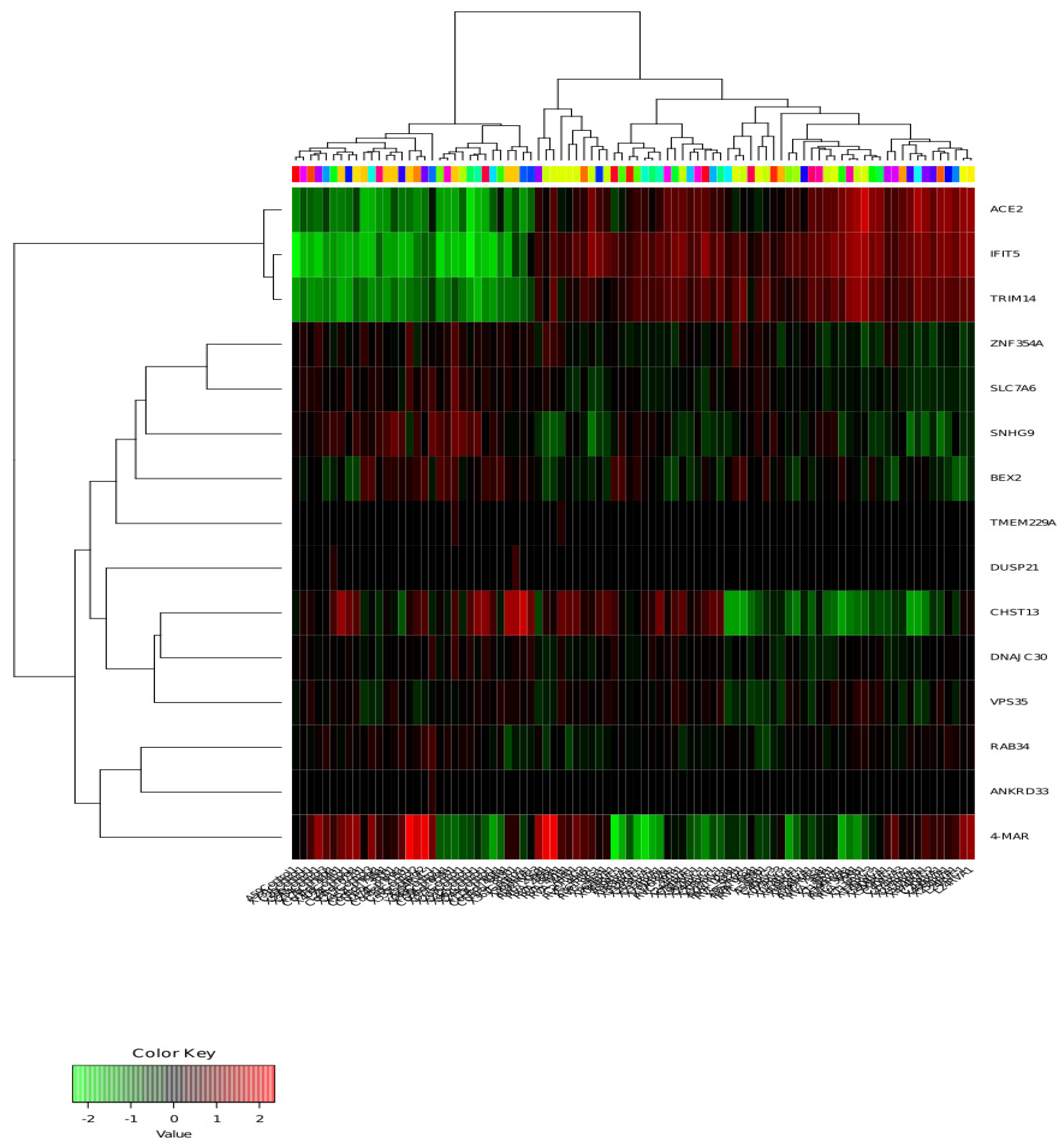
In order to enhance the predictive accuracy of ACE2 in COVID-19 diagnosis, the selected genes obtained using the proposed method were compared with the ACE2 gene, and genes were identified through LASSO regression. Figure 9 illustrates a heatmap presenting the ACE2 gene and the genes selected through LASSO regression. Displaying gene expression data as a heatmap is a popular way to visualize it. A heatmap can also be used in conjunction with clustering techniques, which pair together genes and/or datasets based on how similarly their genes are expressed. This can be helpful for determining the biological signatures linked to a specific situation (such as disease or an environmental condition) or genes that are frequently regulated.

The heatmap displayed in Figure 9 indicates that the expressions of ACE2, IFIT5, and TRIM14 were almost identical, and the proposed algorithm selected them. This implies that IFIT5 and TRIM14 share the characteristics of ACE2, which is a COVID-19-related gene. ACE2, also known as ACEH, may play opposing roles in health and disease. The COVID-19 virus uses the ACE2 receptor to enter human cells, and this receptor is found in almost all organs of the body [42,43]. In addition, BEX2 and SNHG9 show similarities in their up and downregulated genes, but they are not related to COVID-19 symptoms. According to “the National Library of Medicine” website, BEX2, and SNHG9 genes have no connection with COVID-19 symptoms.

5. Conclusions

This paper introduced the binary reptile search algorithm (BRSA), an extension of the reptile search algorithm (RSA), which is critical for enhancing the performance of machine learning algorithms and delivering superior results in gene selection problems. The proposed method is divided into two stages. First, the LASSO regression method is utilized to select 14 genes (as shown in Table 3). Next, the identified gene subset is passed through the BRSA to extract the most significant genes. The SVM was selected as the best classifier among KNN and RF as classification models, with an average classification accuracy of $87.22\%$. Out of the four sigmoid transfer functions, $S_4$ proved the optimal choice, with a high average classification accuracy; moreover, the F-measure was introduced as a fitness function in BRSA. Finally, the performance of the proposed method was evaluated using COVID-19 gene expression data.

The effectiveness of the BRSA was compared with existing binary metaheuristic algorithms, which identified that the BRSA outperformed the others, with a higher accuracy. Evaluating the proposed method with a COVID-19 dataset yielded even better results, with a higher average classification accuracy, a higher average fitness value, and fewer features than the existing methods. Using BRSA, six significant genes were selected (BEX2, CHST13, DUSP21, IFIT5, SNHG9, and TRIM14), and the heatmap revealed that there were similarities between ACE2, IFIT5, and TRIM14. As ACE2 is a COVID-19-related gene, we could conclude that IFIT5 and TRIM14 are likely to be classified as COVID-19-related genes. However, the performance of the proposed method was limited when working with an unbalanced dataset.

As the importance of feature selection in machine learning continues to grow, there is a need for further research to improve its efficiency. This study lays a foundation for future research to enhance feature selection. Other supervised learning algorithms, such as logistic regression [44], naive Bayes [45], and decision trees [46], could be incorporated to improve performance. Additionally, combining the BRSA with various continuous metaheuristic algorithms and their binary counterparts could create a new hybrid algorithm to solve feature selection problems. The proposed method has potential applications in various real-world domains. To further improve the classification accuracy, state-of-the-art filter feature selection methods such as MRMR [47] and Relief [48] could be integrated with the current method. In addition, our study’s main contribution was identifying genes associated with COVID-19 through an analysis of the GSE149273 dataset with a modified binary optimization algorithm, and this work did not extensively delve into the generalizability aspect using various benchmark datasets. Hence, we will further validate and refine our new algorithm through comparisons with additional datasets in future work. Moreover, since most modern analyses are in fact performed using RNA seq [49], for data modeling, we may further modify our method to handle new challenges, e.g., discrete count-based expression, overdispersion, normalization, batch effects, and reference integration.