Efficiency of Energy Exchange Strategies in Model Bacteriabot Populations

Abstract

Micro/nanorobotics is becoming part of the future of medicine. One of the most efficient approaches to the construction of small medical robots is to base them on unicellular organisms. This approach inherently allows for obtaining complex capabilities, such as motility or environmental resistance. Single-celled organisms usually live in groups and are known to interact in many ways (matter, energy, and information), paving the way for potentially beneficial emergent effects. One such naturally expected effect is an increase in the sustainability of a population as a result of a more even redistribution of energy within the population. Our in silico experiments show that under harsh conditions, such as resource scarcity and a rapidly changing environment, altruistic energy exchange (supplying energy to weaker agents) can indeed markedly increase the sustainability of model bacteriabot groups, potentially increasing the efficiency of treatment. Although our work is limited exclusively to the development and use of a phenomenological computer model, we consider our results to be an important argument in favor of practical efforts aimed at implementing altruistic energy exchange strategies in real swarms of single-cell medical robots.

1. Introduction

The term nanorobot was coined in 1987 by Eric Drexler, one of the pioneers in nanotechnology [1]. As is often the case, earlier references to nanotechnology (although not yet at the nanoscale) can be found in science fiction (e.g., The Next Tenants by A. C. Clarke, 1956) and futuristics (e.g., There’s Plenty of Room at the Bottom by R. Feynman, 1959). Today, the technologies for creating extremely small particles (both passive and active) and methods for controlling them are turning from fiction into a promising area of engineering sciences [2,3]. One of the most promising applications is in micro/nanomedicine [4,5]. It can be predicted that affordable analysis of individual health characteristics (such as genotype, microbiome, or organic acids in body fluids), together with the rapid development of micro/nanomedicine operational methods, will pave the way for a breakthrough to full-fledged personalized medicine [6,7,8].

In this paper, medical micro/nanorobots (MRs/NRs) refer to autonomous or semi-autonomous small agents carrying out intentional diagnostic and treatment procedures within an organism (microrobots (MRs) are sized below 1 mm, and nanorobots (NRs) are sized below 10 $\mathsf{\mu }$m) [9,10]. Due to its size, an individual MR/NR can do little alone; MRs/NRs have to work in groups to provide the necessary diagnostic and/or treatment capabilities. However, often, brute mass effect is not the only result of teamwork. There are numerous examples of systems (see, e.g., [11]) in which a group, as an entity, demonstrates properties and capabilities far beyond what could be expected from the mere sum of its members. One of the key conditions for these emergent effects to appear is the ability of the group’s members to interact with each other. Unicellular organisms, e.g., bacteria, are known to exchange matter, information, and energy (see the references in Section 2.2 below), which means that groups of bacteria-based MRs/NRs may be suitable candidates for emergent effects to appear naturally or be induced artificially. In some organ systems, such as the intestinal tract, where the immune response is naturally lower, bacteriabots can be built based on the bacteria that make up the normal microflora. In other systems, bacteriabots may face a strong immune response, so additional engineering may be required to prevent bacteriabots from being destroyed before the treatment is complete (see, e.g., [12]) and to destroy them once their mission is over (see [13]).

In our research, we study whether such systemic effects can emerge as a result of the introduction of particular strategies of energy exchange between model MRs/NRs. Specifically, we hypothesize that altruistic energy exchange (where, in all pairwise interactions, energy flows from the stronger organism to the weaker one) may enhance a group’s chances of survival in changing, harsh environments. Our goal is to detect and measure the potential magnitude of this effect.

Although our work is entirely about designing and running a computer model, we consider it an important proof of concept to show whether it is worth the effort to engineer altruistic energy exchange strategies in real bacteria-based MR/NR populations.

2. Literature Review: Teamwork in the World of Small-Scale Systems

Most of the modern problems that MRs/NRs are designed to solve require the involvement of a large number of agents. Working as a dense group, MRs/NRs have better speed and resistance to flow, as well as better directional movement, carrying capacity, and sensitivity [10,14,15,16]. Some other important practical advantages of using swarms instead of single agents in medical micro/nanorobotics are (1) the possibility of solving complex problems with simple agents (simple means cheap and reliable); (2) fault tolerance due to decentralization and self-organization inherent to swarms, which allows them to reach the goal even if some individuals of the swarm malfunction or fail [15]; and (3) higher contrast in medical imaging due to the aggregation effect and synchronized motion [10].

Some bacteria even behave differently in groups. For example, many bacteria species, including E. coli, exhibit a collective movement pattern—swarming. Bacterial cells involved in this pattern move in direct contact with each other, forming structures known as rafts. A cell that falls out of the raft stops moving after a short time. However, this cell may resume movement and join another passing raft if the raft comes into contact with it [17].

2.1. Interaction Between Artificial MRs/NRs

In [15],

Table 1. Amounts of variance explained by the linear model after the exclusion of each variable.

Excluded Variable	Remained ${\mathit{R}}^2$
$\mathbb{A}$	0.20
$\mathbb{B}$	0.54
$\mathbb{D}$	0.59
$\mathbb{G}$	0.49
$\mathbb{K}$	0.54

, swarm communication activities are divided into two types: direct and environment-mediated. The most natural way of interaction for both cells and MRs/NRs is chemical signaling. For example, silver ions are already used as a means of communication among MRs/NRs, leading to changes in the acceleration of the communicating agents [18]. Another example is the effect of self-assembly in the swarms of Janus micromachines exchanging ${\mathrm{SiO}}_2$ molecules [19] (note that self-assembly is often a desirable feature; for example, it allows for flexible programming and control if the NPs incorporate DNA [20]).

For charged nanoparticles (NPs), an electrostatic field can be used as a means of communication. NPs with unevenly distributed charges (e.g., dipoles) may show self-assembly effects [21,22] as well. For asymmetric photocatalytic NPs (e.g., ${\mathrm{TiO}}_2/\mathrm{Pt}$ Janus submicrospheres), the binding electrostatic forces can be externally controlled by light [23]. A magnetic field is another means of interaction among NPs containing magnetic components. This type of interaction allows NPs to assemble into more complex mechanisms, e.g., helicopter-like machines [24], or to form swarms of desirable shapes, e.g., chain, vortex, and ribbon-like shapes [25].

The interactions between MRs/NRs can be transmitted in several other ways: hydrodynamic disturbance in viscous fluid, local change in Reynolds number by the MRs/NRs, acoustic field (which can direct swarming), van der Waals forces, optical binding, or hydrophobic forces. Most of these forces not only connect the MRs/NRs with each other but also provide the means for connection with the environment, which opens possibilities to explicitly control and direct the collective behavior and self-organization in the swarms of MRs/NRs [15].

2.2. Interaction Between Living MRs/NRs

The future challenges of personalized medicine, such as continuous DNA repair and vascular cleansing, as well as artificial blood or immune systems, will require more sophisticated MR/NR communities. Retrofitted free-living single-cell organisms may prove to be good candidates for solving such challenging problems. Indeed, compared to simpler fully artificial agents, single-cell organisms may bring collective behavior to a whole new level of population, where the individuals can reproduce, adapt to the environment, and exchange chemical compounds, genetic material, and energy [26,27,28,29].

Information exchange among bacteria (quorum sensing) can occur in both single-species and heterogeneous populations [30,31]. Note that although the intermediaries in such an exchange are physical entities that carry energy, the essence of this exchange is information, and the purpose is to coordinate behavior and/or population density.

Works that emphasize the exchange of some form of energy tend to focus on interspecies interactions. Indeed, the exchange of benefits between different species is more natural, as different species may have complementary resources and talents, helping each other to survive and flourish. However, from a practical point of view, it seems easier to implement groups of living MRs/NRs consisting of unicellular organisms of the same species (at least it is likely that this is what engineers will start with). With this in mind, we focus on the less studied area of intraspecies energy and resource exchange in microbial collectives.

Populations of E. coli have provided two examples of intraspecies exchange of resources among bacteria. The first example demonstrates one-way “unintentional” exchange: glucose-utilizing cells released acetate (as a metabolic byproduct) into the environment and thus supplied acetate-utilizing mutant cells with carbon [32]. The second example demonstrates bidirectional cooperative cross-feeding. In this experiment, an E. coli population was artificially divided into two types: the producers of a specific amino acid and the consumers of this acid. Monocultures of each type could not grow well; the producers suffered from high concentrations of amino acid, while the consumers lacked the amino acid they needed. When combined, the two E. coli types outperformed the fitness of the original population from which they were engineered [33]. Similar results, where the complementary traits evolved in E. coli strains, were reported in [34]. These results have also been observed in unicellular fungi [35] and have even been supported by theoretical computational experiments [36]. Although all organisms in the populations in these examples were of the same species, meaning that technically, they are examples of intraspecific exchange, the difference between the strains is large, so the examples are rather artificial.

To migrate from one single-cell organism to another, metabolites do not necessarily have to pass through the intercellular environment. The exchange may also be facilitated through some kind of connection, such as direct surface contact [37], vesicle chains [38], or intercellular nanotubes [39].

One very special type of metabolite that microorganisms can exchange is ATP. Several bacterial species are known to both release ATP into the extracellular space and consume the extracellular ATP [29,40]. This process can potentially become a keystone in the design of mutual energy support in groups of living MRs/NRs and open further opportunities for the engineering of complex controlled altruistic behavior. Indeed, in [40], the authors reported that the presence of extracellular ATP increases the survival rate of E. coli and Salmonella. Based on the obtained results, they suggested that the release of ATP by individual bacteria could be beneficial for the whole group of bacteria. The control of the process of ATP exchange in bacterial collectives could potentially be achieved through the mechanism of quorum sensing [31]. A possible scheme might be as follows: lower bacteriabot fitness results in lower energy. An agent whose energy falls below a certain threshold may begin signaling via quorum sensing. The agents that are not “in need” can respond to such signals by excreting ATP (we already know that such an excretion of “excess ATP” is possible [40]).

So far, we have reached two conclusions: (1) energy exchange in bacterial communities could potentially be beneficial, and (2) although implementing such an exchange poses significant challenges, it is not insurmountable. The question is: Do the potential advantages outweigh the potential costs and engineering challenges?

2.3. Efficiency of Exchange Strategies

Exchange between microorganisms can take different forms, from cooperation to competition, including mutualism and parasitism [41,42,43,44,45]. The ubiquity of cooperative behavior in the world of natural selection demonstrates that cooperation can be quite a competitive strategy. One of the most illustrative examples of the efficiency of cooperation in nature is the flourishing of multicellularity [46]. Artificial multi-agent and robotic systems are also known to benefit from cooperation, trophallaxis, and energy exchange [47,48,49,50].

Although the genesis of altruism has been relatively well studied both in nature [41,51,52,53,54,55] and in models  [47,48,56,57], the quantitative estimation of the influence of altruistic behavior on the success of adaptation has received much less scholarly attention.

The authors are aware of only one paper [58] where groups of selfish, neutral, and altruistic agents are directly compared in terms of survival efficiency. Moreover, although the results in [58] apply to swarms of artificial MRs/NRs (e.g., DNA-based), it remains unclear how much energy exchange strategies contribute to the survival of living agents that can adapt to the environment through reproduction, mutation, and selection (e.g., bacteria-based). We started to answer this question in [59], where E.E. Ivanko studied the effect of energy exchange strategies on the survival of evolving agents in an intentionally simplified situation: (1) only two opposing energy exchange strategies were considered (strong altruism versus strong selfishness), and (2) the environment changed catastrophically. The results in [59] show that altruistic energy exchange among organisms radically changes the survival rate of populations. In [60], we continued this research, conducting more detailed experiments: (1) the number of considered energy exchange strategies was increased from two to seven, uniformly covering the cooperation–competition continuum; (2) we refined the model of the organism by adding growth, aging, and “death from old age”; and (3) a catastrophic pattern of environmental changes was replaced with a temperate one. The computational experiments conducted in the new settings confirmed the strong preference for altruistic energy exchange in populations in unfavorable environments. In [60], we also found that the proportion of energy taken away from an ancestor by its descendants does not affect the results of the experiments (which suggests that the results may apply to the full spectrum of r-/K-selection strategies).

2.4. Previous Works

In the present paper, we place our research in the context of medical nanorobotics, summarize the results obtained in our previous works [59,60], further develop our model, and significantly extend the computational experiments and data analysis. In particular, the following aspects of the present work set it apart from our previous works:

–

We introduce a parameter that regulates the extent to which the fitness of the organisms to the environment affects their ability to grow and reproduce (parameter $\mathbb{G}$) and study the influence of this parameter on the survival rate of populations;

–

We introduce a mechanism that regulates the frequency of energy exchange events between organisms in a model population (parameter $\mathbb{D}$) and study how this frequency affects the survival rate of this population under different energy exchange strategies;

–

The volume of computational experiments is increased significantly to obtain more detailed and reliable results;

–

Enhanced data visualization and additional statistical analysis are used to demonstrate the influence of the energy exchange factor on the survival rate of the populations.

3. Materials and Methods

The computational model consists of a population of artificial organisms and an environment. The organisms can receive energy from the environment, exchange energy with each other, and reproduce. The environment is homogeneous; it is characterized by a single parameter—temperature—which changes at a moderate rate during the experiment. The success of energy accumulation depends on the organism’s fitness to the temperature of the current environment. This fitness is determined by the difference between two scalar numbers: the environmental temperature and the organism’s genotype (see Figure 1). While the former number changes over the course of the experiment, the latter remains constant throughout the organism’s life.

An organism that has managed to accumulate enough energy (i.e., has reached a certain pubertal level) can produce offspring whose genotypes differ slightly (and stochastically) from those of the ancestor. Through this inheritance with mutations, new generations in the population adapt to the changing environment. The organisms that are poorly adapted to the current environmental temperature receive less energy support and grow more slowly, which means they will produce fewer offspring, and their genotype will gradually be eliminated from the population.

The central feature of our model is the exchange of accumulated energy between accidentally contacting organisms. We study different grades of such exchange, from “egoistic” (where the organism with more energy—the “stronger” one—strips most of the accumulated energy of the organism with less energy—the “weaker” one) to neutral (without energy exchange) and “altruistic” (where the organism with more energy gives most of the accumulated energy to the organism with less energy). The energy exchange strategy is set the same for all organisms in the population and remains constant during each individual experiment. Such uniformity and constancy allow us to distill the effect that the strategy of energy exchange has on the survival of the population.

Unfavorable energy exchange events can lower the energy of a participating organism below a survival threshold. In addition to an unfavorable energy exchange, organisms can die from accidents or old age.

The model time is discrete: at each iteration, the environmental temperature changes, while the organisms can consume energy, reproduce, exchange energy with each other, and cease.

In general, during each experiment, the population attempts to adjust to its ever-changing environment, and we study how the adopted energy exchange strategy affects the efficiency of this adjustment. Let us consider each component of the model in more detail.

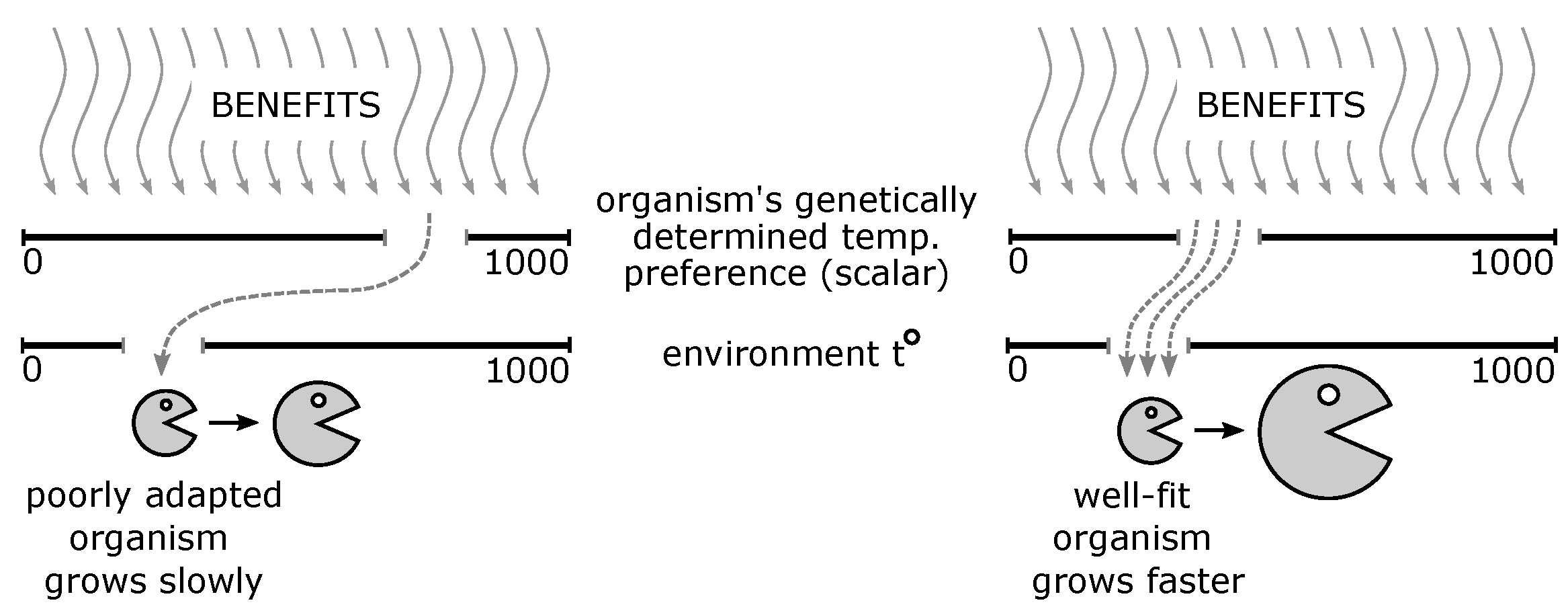
3.1. Environment

The environment is deliberately kept minimal so that the effect of the energy exchange strategy is not mistakenly attributed to the effects of other complex aspects of the model. One such omitted aspect is geometry. In our model, we assume that the environment is homogeneous and allow organisms to interact freely. There are no properties such as “boundaries” or “regions”, “close” or “far” (note that in our previous paper, we studied a model with agents moving and interacting in space and obtained similar results). As a prototype of such a model, one can imagine bacteria in an intensely agitated environment.

The environment in our model is characterized by a single parameter—“temperature”. In our model, it plays the role of a composite factor expressing the favorability of the environment in all its multiplicity, as if all the environmental factors were approximated by one principal component.

The fluctuations of the environmental temperature in our model have their prototype in the changes in the Earth’s surface temperature recorded over 172 years (1850–2021) [61] (see Figure 2).

In our previous work, we studied the behavior of a similar model in a catastrophically changing environment [59]. Here, we were looking for a gradual natural process that combined both regular and stochastic parts. The global temperature plot gave us exactly what we were looking for: it combines a global warming trend and the annual “noise” of a complex “real” nature.

We believe that in the first proof-of-concept stage of research, these two models of change (catastrophic and gradual natural) are sufficient to determine whether the altruistic energy exchange is significantly beneficial and if it is worth further attention. Specialized models of changes close to medical practice will become more important in the next stages of research, where efforts will move from proving the existence of the effect to studying its properties and parameters in real medical environments.

Let $T=(t_1-t_1,t_2-t_1,\dots ,t_{172}-t_1)$ denote the sequence of the 172 values shown in Figure 2, shifted for convenience so that the sequence starts at 0. Using the notation $T\left[i\right]$ for the i-th value of T, let $T^{\prime }=(T^{\prime }\left[1\right],\dots ,T^{\prime }\left[172\right])$ be the “opposite” (horizontally symmetric) sequence, so that $T^{\prime }\left[i\right]:=-T\left[i\right]$. These two short 172-value pieces—T and $T^{\prime }$—are used as building blocks, randomly selected, sequentially combined, and normalized to form a long, 10000-value series (see Figure 3) through which each population must survive. This long series is constructed in advance and remains fixed so that all experiments run within the same environmental temperature dynamics.

Formally, let $T_1:=T$. For all $j\in \overline{2, 60}$, let $T_j$ be such that $T_j\left[i\right]=\tilde{T}\left[i\right]+T_{j-1}\left[172\right]$, where $\tilde{T}$ is randomly selected from $\{T,T^{\prime }\}$. Let $\mathbf{T}=T_1{T}_2\dots T_{60}$. Normalize $\mathbf{T}$ into the range $[0, 1000]$:

$$\mathbf{t}\left[i\right]={\displaystyle \frac{1000·\left(\mathbf{T}\right[i]-min(\mathbf{T}\left)\right)}{(max(\mathbf{T})-min(\mathbf{T}\left)\right)}},$$

(1)

such that $\mathbf{t}:\overline{1, 172·60}\to [0, 1000]$.

Note that the environmental temperature sequence (1) serves as a mere example of a nature-inspired gradual process that fluctuates around some mean value (as the number of glued blocks tends to infinity, this mean value converges to the initial value $\mathbf{t}\left[0\right]$, which due to normalization, lies in the middle of the range: $\left(\right(1000-0)/2=500$) (see Figure 3).

3.2. Organisms

In order to study the behavior of the populations under different conditions, we limit the computational resources spent on exploring each particular population. Since the number of interacting agents in the model strongly affects the duration of each experiment (quadratically), to keep the time per experiment low, we assume that the environment cannot support a population larger than 100 organisms.

At the beginning of each experiment, the population contains exactly 10 organisms.

The model of the organism is minimalistic. We intentionally exclude most of the features of real organisms that are not necessary to study how the energy exchange strategy affects the survival of MR/NR populations.

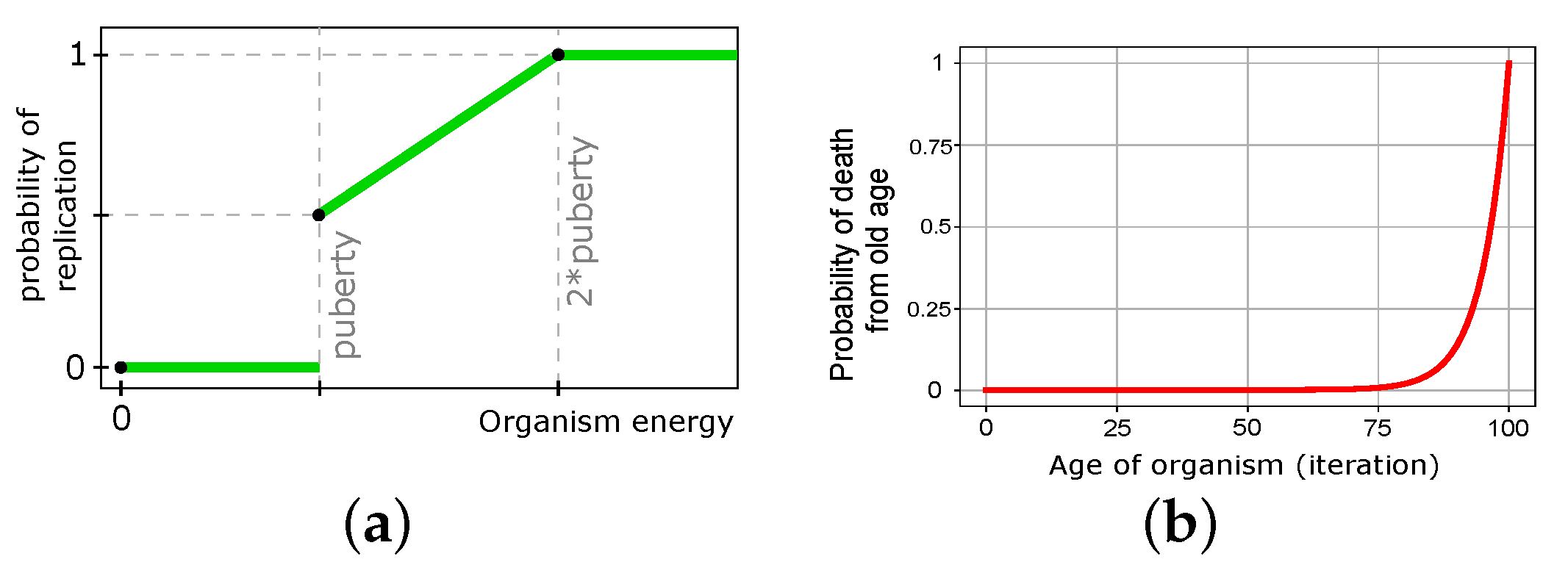
3.2.1. Organism’s Structure

Each organism has three parameters:

(1) Temperature preference (TP), $tp\left(org\right)$, a scalar number (e.g., 3.1376), the only “genetically hard-coded” feature of the organism $org$ that remains constant during the organism’s lifetime and is inherited (with possible mutation) from the organism’s ancestor. The TPs of the initial 10 organisms are chosen uniformly from the temperature range specified in (1): $tp\left(org\right)\sim \mathcal{U}[0, 1000]$.

(2) Energy, $e\left(org\right)$, a scalar number that indicates how much energy the organism $org$ has already accumulated (or, in other words, how thriving the organism is). For illustration purposes, we sometimes use organism characteristics such as size or strength, both of which refer to energy. Furthermore, “energy” in our model is any beneficial entity that has the following two properties: (i) it is important for an agent to survive and grow, and (ii) it can be exchanged between agents. Following this definition, for example, important metabolites can also be considered a form of energy, and the degree of satisfaction of the need for certain metabolites can act as $e\left(org\right)$.

In the model mechanics, energy plays several roles:

(a) Energy defines the probability that the organism will reproduce. There is a pubertal energy threshold $ppb=1000$ below which reproduction is considered impossible (the organism is too “small” or too “weak”). Once the threshold is crossed, the probability of reproduction grows linearly with energy volume until it reaches 1 (see Figure 4a). The particular value of $ppb$ can be chosen arbitrarily, since all other energy constants, as well as the energy dynamics law (3), are expressed through it.

(b) There is a minimal amount of energy needed to survive. In our model, if $e\left(org\right)<10$, which is 1% of $ppb$, the organism $org$ dies.

(c) Energy is transferred between two organisms in energy exchange events, where either the rich can get richer or the poor can improve their condition, depending on the adopted energy exchange strategy (the main feature of the present work).

At the beginning of each experiment, the energies of the 10 initial organisms are chosen uniformly from the interval $[10, 1000]$ (from minimum survival energy to puberty level).

(3) Age, $a\left(org\right)$, a scalar number indicating how many iterations the organism has survived. The probability of death by decay increases with age according to a variant of the Gompertz law (see Figure 4b), growing up to 1 as the age approaches 100 iterations.

The age limit of 100 iterations was chosen to be consistent with the duration of each experiment (${100}^2$ = 10,000). This value is small enough to allow fast switching between generations but large enough to allow an organism to leave its mark on the experiments.

3.2.2. Organism’s Actions

During its life, each organism can perform the following actions:

(1) Accumulate energy (grow). The efficiency of energy accumulation depends on the fitness coefficient Δ, which shows the relative closeness between the current temperature of the environment and the organism’s TP (see Figure 1 for an illustration):

$$▵(i,org)=1-\sqrt[\mathbb{G}]{{\displaystyle \frac{|{\mathbf{t}}^{\mathbb{G}}\left[i\right]-t{p}^{\mathbb{G}}\left(org\right)|}{max\{\underset{o\in Pop}{max}\{t{p}^{\mathbb{G}}\left(o\right)\}, {\mathbf{t}}^{\mathbb{G}}\left[i\right]\}-min\{\underset{o\in Pop}{min}\{t{p}^{\mathbb{G}}\left(o\right)\}, {\mathbf{t}}^{\mathbb{G}}\left[i\right]\}}}},$$

(2)

where i is the current iteration; $org$ is the organism we are considering; $tp\left(org\right)$ is the temperature preference (TP) of $org$; $Pop$ is the population of organisms alive at the current iteration; and $\mathbb{G}$ is the amplification index (independent experimental parameter) that controls how sensitive the organisms’ growth is to changes in their fitness to the environment.

Despite its seeming unwieldiness, the expression (2) is straightforward. For simplicity, let us first consider the case $\mathbb{G}=1$: the powers and the square root disappear, and the nominator in the fraction shows how far the organism’s temperature preference is from the current environmental temperature (i.e., how well the organism has adapted). The denominator normalizes this value to [0, 1]; for example, if $\mathbf{t}\left[i\right]\ge tp\left(org\right)$, then

$$\begin{array}{c}|\mathbf{t}\left[i\right]-tp\left(org\right)|=\mathbf{t}\left[i\right]-tp\left(org\right)\le max\{\underset{o\in Pop}{max}\{tp\left(o\right)\},\mathbf{t}\left[i\right]\}-tp\left(org\right)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \le max\{\underset{o\in Pop}{max}\{tp\left(o\right)\}, \mathbf{t}\left[i\right]\}-min\{\underset{o\in Pop}{min}\{tp\left(o\right)\}, \mathbf{t}\left[i\right]\}.\end{array}$$

The case $\mathbf{t}\left[i\right]<tp\left(org\right)$ can be treated similarly. Raising to the power of $\mathbb{G}$ does not change the chain of inequalities. Note that the normalization denominator in (2) is specific to each iteration i. Although such relativity is not natural, it allows us to intensify the influence of the environment on each organism depending on its fitness. If the max and min in the denominator were taken globally over all iterations, a large denominator would suppress the difference in fitness coefficients between the organisms. With a subtle difference in the fitness coefficients, it would take many more iterations to reveal the effect that the energy exchange strategy has on the flourishing of the populations.

Returning to $\mathbb{G}$, it regulates the sensitivity of the fitness coefficient Δ to the deviation of $tp\left(org\right)$ from the actual temperature $\mathbf{t}\left[i\right]$: for larger values of $\mathbb{G}$, the same difference between $\mathbf{t}\left[i\right]$ and $tp\left(org\right)$ will lead to a larger decrease in fitness. To demonstrate this, consider a simplified population with two organisms: $tp\left(or{g}_1\right)=1$, $tp\left(or{g}_2\right)=2$, and $\mathbf{t}\left[i\right]=3$ for all i. For $\mathbb{G}=1$, the value of $▵(i, or{g}_2)$ is $1-(3-2)/(3-1)=0.5$; for $\mathbb{G}=2$, the fitness is much smaller, $▵(i, or{g}_2)=1-{[(3^2-2^2)/(3^2-1^2)]}^{0.5}\approx 0.21$.

Using the fitness coefficient, the change in energy at each iteration is expressed as follows:

$$\forall org\in Pope\left(org\right)\leftarrow e\left(org\right)+\mathbb{K}·▵(i, org)·ppb,$$

(3)

where $e\left(org\right)$ is the energy accumulated by $org$; $\mathbb{K}$ is one of the independent parameters of the experiments—the intensity of energy input in the system; $ppb$ (puberty threshold) is used here for scaling since both $\mathbb{K}$ and Δ lie in [0, 1].

(2) Reproduce. Starting at the puberty energy threshold $ppb=1000$, the organisms are able to reproduce, spawning one descendant per replication. At each iteration, a reproduction event may occur with a probability that depends on the energy level of the organism (see Figure 4a). During the process of replication, part of the ancestor’s energy is withdrawn to become the initial energy of the descendant. In our previous study [60], we found that the size of this part does not affect the results of the experiments, so here we choose it uniformly from 0.5% to 50%.

The temperature preference (TP) of the descendant (its “genotype”) is inherited from the ancestor with mutation. The maximum allowed deviation of the descendant’s TP from that of the ancestor is one of the independent experiment parameters—$\mathbb{B}$—taking values from 1.5% to 50.5% in steps of 0.5%. The TP of a particular descendant $or{g}^{\prime }$ is chosen uniformly based on the TP of its ancestor $org$ and the maximum allowed deviation $\mathbb{B}$

$$tp\left(or{g}^{\prime }\right)\sim \mathcal{U}(max\{0, tp\left(org\right)(1-\mathbb{B})\}, min\{tp\left(org\right)(1+\mathbb{B}), 1000\}).$$

(4)

Reproduction is prohibited once the population has reached 100 organisms.

(3) Interact with the other organisms. A pair of organisms may exchange energy. The way this exchange takes place in each particular population is determined by the parameter $\mathbb{A}$, which is the most important independent parameter in our study. Positive values of $\mathbb{A}$ (we consider 25, 50, and 75%) correspond to the “egoistic” spectrum of energy exchange strategies. Here, $\mathbb{A}$ shows the proportion of energy of the “weaker” organism (with less energy) that goes to the “stronger” one in each energy exchange event that occurs during the experiment. Negative values of $\mathbb{A}$ (−25, −50, and −75%) correspond to the “altruistic” situation, where the “stronger” organism (with more energy) shares $\mathbb{A}$ percent of its energy with the “weaker” one. Suppose without loss of generality that $e\left(or{g}_1\right)\ge e\left(or{g}_2\right)$, then

$$\mathrm{if}\mathbb{A}\ge 0\left\{\begin{array}{c}e\left(or{g}_1\right)\leftarrow e\left(or{g}_1\right)+\mathbb{A}·e\left(or{g}_2\right),\hfill \\ e\left(or{g}_2\right)\leftarrow e\left(or{g}_2\right)-\mathbb{A}·e\left(or{g}_2\right),\hfill \end{array}\right.$$

(5)

$$\mathrm{if}\mathbb{A}<0\left\{\begin{array}{c}e\left(or{g}_1\right)\leftarrow e\left(or{g}_1\right)-\mathbb{A}·e\left(or{g}_1\right),\hfill \\ e\left(or{g}_2\right)\leftarrow e\left(or{g}_2\right)+\mathbb{A}·e\left(or{g}_1\right).\hfill \end{array}\right.$$

(6)

Note that $\mathbb{A}$ is fixed for each particular population and remains constant for all energy exchange events occurring during the experiment with this population. Such constancy allows us to clearly reflect the influence of a particular energy exchange strategy on the survival and adaptive potential of the population.

(4) Cease. There are three possible causes that can trigger the death of an organism in the model: (1) Old age. The probability of death increases with each iteration (see Figure 4b) and reaches 1 at the age of 100 iterations. (2) Accident. At each iteration, the probability of accidental death is 0.1%. (3) An unfavorable energy exchange event, where an organism gives away too much energy, so that the remaining energy is not enough to survive (see (5) and (6)). Death due to the first two factors can be formalized as follows:

$$P_{death}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}e\left(org\right)<10,\hfill \\ min\left\{1;0.001+e^{{\displaystyle \frac{a\left(org\right)-100}{5}}}\right\},\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(7)

3.3. Computational Experiments

Our experimental setting is parameterized by the following five values (independent parameters):

-

$\mathbb{A}$: The direction and intensity of the energy exchange between the weaker and the stronger organisms in an interacting pair (see (5) and (6));

-

$\mathbb{B}$: The maximum allowed deviation of the temperature preference (TP) of descendants from the TP of their ancestor (see (4));

-

$\mathbb{D}$: The frequency of interactions among organisms. The regulation of this parameter allows us to study the behavior of the system for different ratios between the speed of growth and the intensity of energy exchange;

-

$\mathbb{G}$: The extent to which the organisms’ fitness to the environment affects their growth (see (2));

-

$\mathbb{K}$: The abundance of energy supply to the system (see (2) and (3)).

In our experiments, we study how successfully the populations manage to survive under different conditions specified by different values of the above independent variables. The general mechanics of each single population survival experiment is represented by the following Algorithm 1.

Algorithm 1 Pop_Survive

Input: $\mathbb{A},\mathbb{B},\mathbb{D},\mathbb{G},\mathbb{K}$ Output: True (1) or False (0) 1. Create an initial population consisting of 10 organisms. The parameters of each organism in the initial partition are chosen uniformly from their corresponding intervals: a. Energy—from 10 (minimal survival value) to 1000 (the level of puberty); b. Temperature preference (TP)—from 0 to 1000 (the range of environmental temperatures; see (1)); c. Age—from 0 to the maximum possible age (100); 2. While$172·60$ = 10,320 iterations are not over and the population contains at least 2 organisms: a. Change the “weather”, i.e., take the next value from the sequence $\mathbf{t}$ as the current “temperature”. b. Let each organism grow according to its fitness to the current temperature (apply (2) and (3)). c. Let each organism with enough energy (“adult”) reproduce with the probability shown in Figure 4a, spawning a descendant with a temperature preference similar to that of its ancestor (see (4)). Reproduction is only allowed until the population reaches the “carrying capacity of the environment” (100 organisms). d. Perform $\mathbb{D}\times {\displaystyle \frac{\left|Pop\right|\left(\right|Pop|-1)}{2}}$ interaction events accompanied by energy exchange governed by $\mathbb{A}$ (see (5) and (6)). The pair of organisms for each interaction is chosen at random. e. Apply (7) to withdraw from the population those organisms that have an energy level below the minimum survival threshold and have been selected for accidental or old age death. 3. Return$True\left(1\right)$ if the population contains more than two organisms; otherwise, return $False\left(0\right)$

3.3.1. Variation Ranges of Independent Parameters

In order to make the model as general as possible, we need to maximize the considered parameter ranges. Since we cannot study all possible parameter values, we focus on the parameter ranges where “something interesting happens”, specifically where the dependent parameter (survival rate) varies substantially. Based on the observed trends within the considered ranges (see, e.g., Figure 5), and with additional support from experiments using starting parameters outside these ranges, we can make assumptions about the asymptotic behavior of the survival rate beyond the considered ranges. As a result, we have a model that covers all possible parameter values. This model can be used to speculate about the behavior of the survival rate, even though the actual biological values of the parameters are unknown.

The input (independent) parameters of the algorithm Pop_Survive were varied over the following grids in the parameter space:

• The parameter $\mathbb{K}$ controls the energy supply to the system. In our experiments, it takes values from the set $R_{\mathbb{K}}$, which consists of the following three ranges:

  –

  From 0.01 to 0.5 in increments of 0.01;

  –

  From 0.55 to 1 in increments of 0.05;

  –

  From 1.1 to 2 in increments of 0.1.

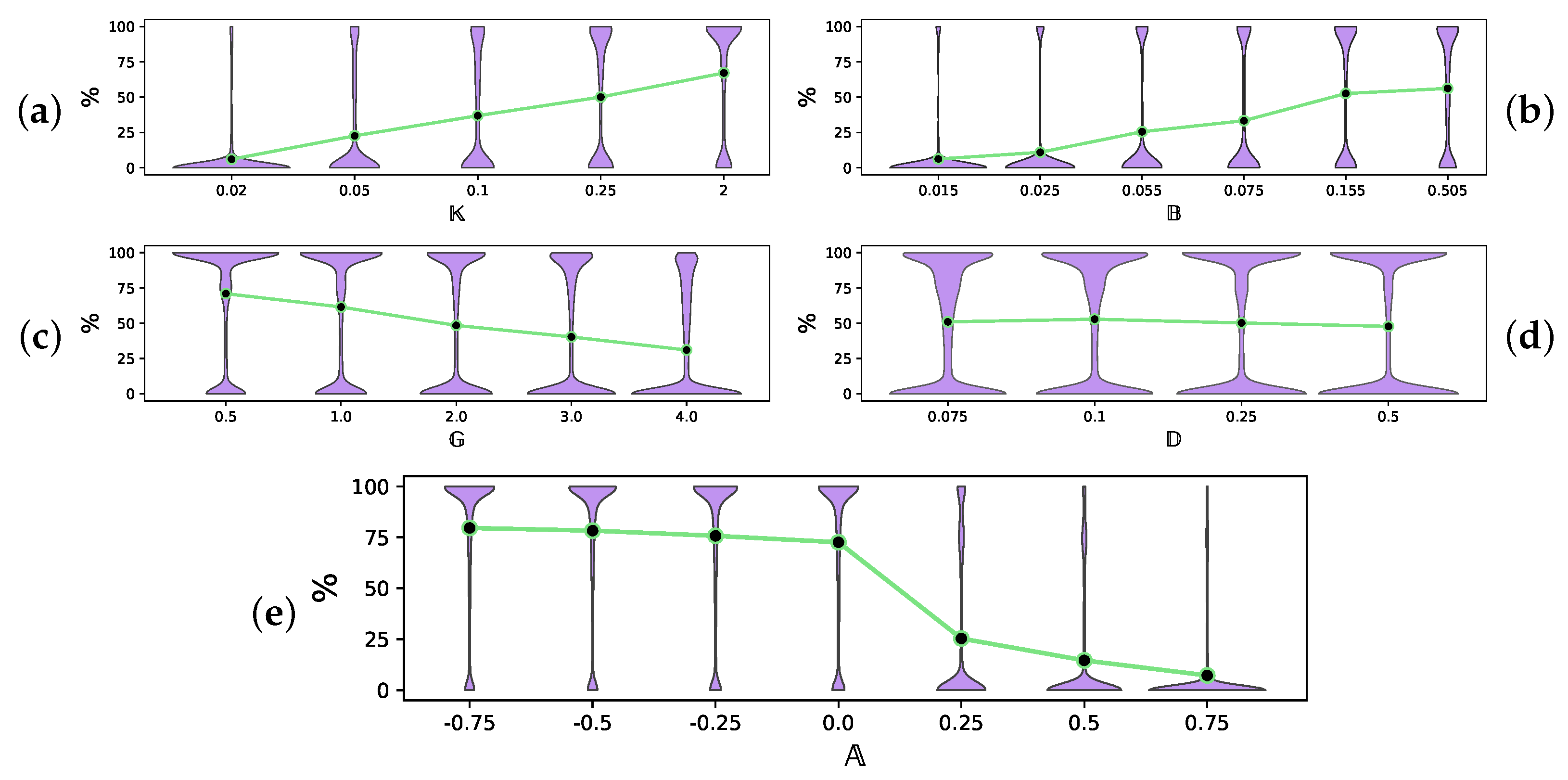
  Values below 0.01 do not allow the system to provide enough energy for the populations to survive. Preliminary experiments showed that with $\mathbb{K}\le 0.005$, the death mechanics withdrew more energy from the population than the growth mechanics provided, so the populations died out regardless of the values of the other independent parameters. On the other hand, values of $\mathbb{K}\ge 2$ make the energy flow into the system excessively abundant, so that all other independent parameters have almost no effect on the survival of the populations. Note that we use a denser grid for small values of $\mathbb{K}$ to study the situation of scarce energy in more detail, which seems to be of most interest in practical applications.
• The parameter $\mathbb{B}$ controls the mutation rate. In our model, it regulates how far the temperature preference of the descendant can deviate from that of the ancestor. In the experiments, $\mathbb{B}$ takes values from

  $$R_{\mathbb{B}}=\{0.015, 0.020, 0.025, ..., 0.500, 0.505\}.$$
  Although values of $\mathbb{B}$ below 0.015 are more realistic, we have to consider higher mutation rates for the system to be able to evolve observably in a relatively short time (≈10,000 iterations). Values above 0.5 hardly fit the concept of evolution as a gradual process.
• The parameter $\mathbb{D}$ regulates the number of interactions among organisms per iteration. It takes values from

  $$R_{\mathbb{D}}=\{0.07, 0.1, 0.25, 0.5\}.$$
  Values of $\mathbb{D}$ below 0.07 make the interactions so rare that the model fails to provide enough data to serve its main purpose—assessing the efficiency of different energy exchange strategies. Values above 0.5 involve more than 50% of all possible pairs in the system in interaction (see step 2(d) in the algorithm Pop_Survive). Such a high rate is hardly consistent with the idea of an algorithm iteration as a relatively small discrete unit of time, which is desirable to follow the development of the system gradually.
• The parameter $\mathbb{G}$ controls how sensitive the growth of the organism is to the fitness of this organism to the environment (the higher $\mathbb{G}$, the stronger the response). In our experiments, $\mathbb{G}$ takes values from

  $$R_{\mathbb{G}}=\{0.5, 1, 2, 3, 4\}.$$
  It has been experimentally shown that the values $\mathbb{G}>3$ change the behavior of Δ (see (2)) only slightly compared to $\mathbb{G}=3$.
• The parameter $\mathbb{A}$, the central parameter for this study, controls the “selfishness” of the agents. In our model, $\mathbb{A}$ takes values from

  $$R_{\mathbb{A}}=\{-0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75\},$$

  covering the entire spectrum of energy exchange behavior, from the explicit robbery of weaker agents to indifference and the explicit sharing of energy with weaker agents.

For each possible combination of input experiment parameters $(\mathbb{A},\mathbb{B},\mathbb{D},\mathbb{G},\mathbb{K})\in R_{\mathbb{A}}\times R_{\mathbb{B}}\times R_{\mathbb{D}}\times R_{\mathbb{G}}\times R_{\mathbb{K}}$, we repeat the algorithm Pop_Survive 100 times. Depending on N—the number of “true” outcomes (those where the population survived)—the tuple of initial parameters is assigned one of three labels:

• Favorable if $N\ge 95$;
• Ambiguous if $5<N<95$;
• Unfavorable if $N\le 5$.

The results of these experiments are presented and discussed in Section 4.

3.3.2. Scientific Constants

Some constants in the model serve as controlled variables or scientific constants in the sense of the theory of experimental design ([62], Chapter 4)). In the following, we briefly discuss the constants that have not previously been discussed in the course of the presentation of the model.

Temperature ranges. The ranges within which both $\mathbf{t}$ (“environmental temperature”) and $tp\left(org\right)$ (“organism temperature preferences”) vary have been chosen only for ease of reading. Following normalization to [0, 1], as described in (2), the particular sizes of the ranges no longer matter.

Experiment duration. With limited computational time, the experiment duration of 10,000 iterations allows us to balance two opposing requirements: maximizing the length of each experiment to study the long-term effect of energy exchange, and maximizing the studied area in the parameter space (i.e., maximizing the number of experiments).

Puberty. The specific value of $ppb$ can be chosen arbitrarily since the other energy aspects of the model are expressed through it: (1) the lowest possible energy of a living agent is 1% of $ppb$ (this value is also a scientific constant); and (2) the energy dynamics in (3) are expressed in multiples of $ppb$.

Death. The constants in (7) are chosen so that the organism significantly increases its chances of dying as it approaches 100 iterations. The maximum age of 100 iterations is a scientific constant, which should be small enough compared to the duration of each experiment (10,000 iterations) to allow fast switching between generations but large enough to allow an organism to leave its mark in the experiment. The value $100=\sqrt{10,000}$ was found to be appropriate.

4. Results and Discussion

4.1. Dependence of Survival on Starting Conditions

First, we study how the survival rate depends on the starting parameters of the experiments.

The PDFs (probability density functions) of the survival rate in Figure 5 are both bimodal and truncated, which is not surprising given that this is a count random variable inspired by biological processes. Based on the shape of the distributions, we assume that the observed PDFs could be efficiently approximated by a mixture of two Poisson distributions (one per mode); however, such results may be difficult to interpret in relation to the experimental starting parameters.

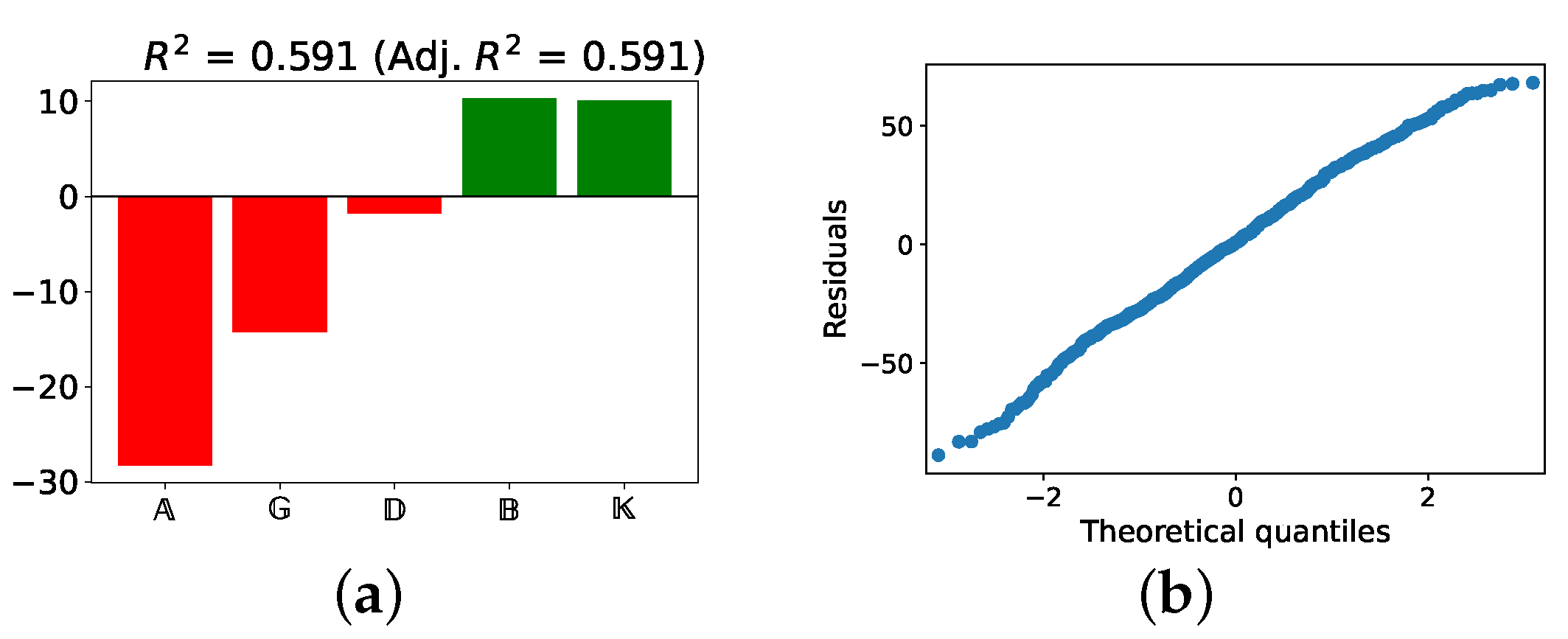
4.1.1. Linear Model

As a first straightforward step toward understanding the influence of the experimental starting conditions on the survival rate of the populations, we construct a linear regression with $\mathbb{A},\mathbb{B},\mathbb{D},\mathbb{G},$ and $\mathbb{K}$ as independent variables, and the proportion of surviving populations (equal to $N/100$) as the dependent variable (recall that we repeat the experiment 100 times for each specific tuple of values of the independent variables). The resulting standardized regression coefficients are visualized in Figure 6a. Although the $R^2$ is moderate (about 60%), the model and coefficient p-values are close to 0, and the QQ plot in Figure 6b shows that the distribution of the residuals is close to normal.

The influence of $\mathbb{A}$ is predictably negative: altruistic behavior, expressed through mutual replenishment of energy, helps the populations to survive. Interestingly, the influence of this parameter on the survival rate is the strongest among all the independent parameters (the largest absolute value among the standardized regression coefficients).

The parameter $\mathbb{G}$ indicates how much the misalignment between the organism’s TP and the environmental temperature affects the organism’s growth efficiency. The negative coefficient may be explained as follows: smaller values of $\mathbb{G}$ allow the organism to be less demanding about the accuracy of the match between its TP and the environmental temperature, allowing the organism to thrive in a wider range of environmental conditions. For the population, this means a higher chance of survival.

Compared to the other parameters, the number of interactions, $\mathbb{D}$, has only a marginal effect on the survival rate, so we do not discuss it.

The parameter $\mathbb{B}$ controls the mutation range. Its coefficient is expected to be positive. The larger the mutation range, the more likely the population will keep up with the changing environment. Indeed, with a larger mutation range, the population has a greater chance of producing organisms that are well adapted to new environmental temperatures, which increases the chances of survival for that population.

The last parameter, $\mathbb{K}$, controls the efficiency of the organisms’ energy consumption. Not surprisingly, it is also positive because increasing the energy input increases the survival rate.

Note the almost equal influence of $\mathbb{B}$ and $\mathbb{K}$. In other words, the efficiency of energy consumption is almost as important for the survival of the population as the speed of change. We see this as a sign of a “balanced model”.

4.1.2. Importance of Variables

We have already seen that the standardized coefficient of $\mathbb{A}$ has the largest absolute value (Figure 6a). The next approach to estimating the “importance” of the five independent variables is to exclude one variable at a time and compare the amount of variance that can still be explained by the linear model with the four remaining variables. The results shown in Table 1 confirm the superior importance of the energy exchange factor: the explained variance suffers most from the exclusion of $\mathbb{A}$.

Because the shape of the survival distribution is quite complex (truncated bimodal; see Figure 5), a linear regression model has limited explanatory power. To study the influence of model parameters in a more general setting, we use a more universal (but still interpretable) regression model—decision trees of different heights from 1 to 5 (equal to the number of independent variables). The results in

Table 2. Coefficients of determination ($R^2$) for decision tree regression models with different tree heights. The independent variables are $\mathbb{A}$, $\mathbb{B}$, $\mathbb{D}$, $\mathbb{G}$, and $\mathbb{K}$, and the dependent variable is the survival rate. The second row shows the $R^2$ values for models with all 5 independent variables included. The subsequent rows show the $R^2$ values for models with one variable excluded.

Tree Height		1	2	3	4	5
$R^2$ of full model		0.44	0.57	0.65	0.70	0.73
$R^2$ without	$\mathbb{A}$	0.08	0.16	0.23	0.26	0.29
	$\mathbb{B}$	0.44	0.56	0.63	0.68	0.71
	$\mathbb{D}$	0.44	0.57	0.69	0.76	0.81
	$\mathbb{G}$	0.44	0.54	0.63	0.67	0.70
	$\mathbb{K}$	0.44	0.57	0.65	0.70	0.73

support the previous conclusion: excluding $\mathbb{A}$ reduces the explanatory power of the decision tree model much more significantly than excluding any other parameter. Furthermore, in trees built with all five regressors, the first decision rule (root) is always $\alpha \ge 0.25$ (which separates selfish energy exchange from altruistic and neutral).

It is interesting to note that excluding $\mathbb{D}$ even improves the quality of the model. Based on this observation and the results in Table 1 (which shows that excluding $\mathbb{D}$ hardly changes the explained variance in the linear regression), we assume that the frequency of interactions does not affect the survival rate.

4.2. The Effect of Altruism in Different Experimental Settings

To reveal the effect of the energy exchange direction on the populations’ survival rate, we use one-way ANOVA to pairwise compare the survival rate in three groups: $E^{-}$—experiments with altruistic energy exchange ($\mathbb{A}\in \{-0.75,-0.5,-0.25\}$); $E^{+}$—experiments with selfish energy exchange ($\mathbb{A}\in \{0.75, 0.5, 0.25\}$); and $E^0$—experiments with neutral energy exchange ($\mathbb{A}=0$). The third group serves as a natural reference for the first two groups, so we are mostly interested in the comparisons of $E^{+}$ with $E^0$ and $E^{-}$ with $E^0$, but for completeness, we also compare $E^{+}$ with $E^{-}$.

To gain a more complete understanding, we perform separate ANOVA tests for experiments conducted under different initial conditions. First, we combine the experiments into subsets (possibly overlapping sets), where each subset consists of the experiments in which one of the starting parameters ($\mathbb{B}$, $\mathbb{D}$, $\mathbb{G}$, or $\mathbb{K}$) is fixed to one of its values (see Section 3.3.1). For example, one such subset consists of experiments where $\mathbb{G}=0.5$. Hereafter, we call them fixed-parameter subsets. Second, we divide the experiments within each subset into three groups according to their direction of energy exchange ($E^{+}$, $E^{-}$, and $E^0$) and perform a one-way ANOVA test on each of the three possible pairs of groups. For instance, for the subset from the previous example, we run ANOVA tests on the following groupings: $(E_{\mathbb{G}=0.5}^{-}, E_{\mathbb{G}=0.5}^0)$, $(E_{\mathbb{G}=0.5}^{+}, E_{\mathbb{G}=0.5}^0)$, and $(E_{\mathbb{G}=0.5}^{+}, E_{\mathbb{G}=0.5}^{-})$.

In all ANOVA tests, except for the comparison of survival means between groups $E_{\mathbb{K}=2}^{-}$ and $E_{\mathbb{K}=2}^0$, the p-value was less than 0.5% and the F-statistic was greater than 8 (typically $p\approx 0$ and $F>100$). In the grouping $(E_{\mathbb{K}=2}^{-}, E_{\mathbb{K}=2}^0)$, the p-value was 0.0183 and the F-statistic was 5.57.

In Figure 7, the dependency of the shape of the distribution of the survival rate on the value of $\mathbb{A}$ is visualized for each fixed-parameter subset separately. Each plot in Figure 7 is constructed based only on those experiments for which the corresponding parameter was fixed at the corresponding value (see the plot heading). Each violin in the plot shows the distribution of the survival rate in the experiments with $\mathbb{A}$ set to the value shown under the violin. For example, the first violin in the plot for $\mathbb{B}=0.015$ shows the distribution of the survival rate in the experiments conducted with $\mathbb{A}=-0.75$ and $\mathbb{B}=0.015$.

Figure 7 carries several messages:

(1) In almost all experimental settings, egoistic energy exchange reduces population survival.

(2) In most experimental settings, zero energy exchange (no exchange) yields survival rates only slightly worse than those of altruistic energy exchange. This is good news for nanorobotics engineering because, in a wide range of conditions, energy exchange may not be a concern at all.

(3) In the case of low energy input (or low energy assimilation ability; see Figure 7 ($\mathbb{K}=0.01$)) and in the case of a low mutation rate (see Figure 7 ($\mathbb{B}=0.015$)), the difference between altruistic and neutral energy exchange populations becomes significant. We believe that both conditions can occur in practice.

For bacteriabots inside a patient’s body, low energy input (low values of $\mathbb{K}$ in the model) may be associated with entering unfavorable conditions. These unfavorable conditions can vary in several ways. For example, some bacteriabots may be engineered to operate in aerobic environments, while others are designed for anaerobic environments (e.g., within solid tumors). As bacteriabots travel to the target area, they may encounter unfavorable oxygen conditions, which can suppress their metabolic processes and reduce their survival and therapeutic capabilities [63]. Another environmental factor that may become unfavorable for bacteriabots is temperature. Although the body generally maintains a relatively stable temperature, localized infections or inflammation can cause fluctuations. Just like natural bacteria, bacteriabots rely on enzymes for cellular functions, which are highly sensitive to temperature changes. If the temperature rises excessively, enzymes may denature, diminishing the bacteriabots’ metabolism and functionality [64]. Other factors include the presence of antibiotics, varying concentrations of certain ions, and the influence of other bacterial populations (e.g., through toxin excretion or depletion of essential metabolites). We believe that in all these cases, a well-designed energy exchange mechanism could significantly increase the survival rate of real MR/NR populations.

As for the mutation rate, due to technical constraints, we considered $\mathbb{B}\ge 0.015$, as described in (4), whereas real mutation rates are much lower [65]. In the plot for $\mathbb{B}=0.015$ in Figure 7, we can see the clear difference between the violins for negative $\mathbb{A}$ and the violin for zero $\mathbb{A}$. We expect this advantage of altruistic energy exchange to be even more pronounced for extra-small values of $\mathbb{B}$.

4.3. Visualization of Raw Results

The raw results of the experiments are visualized in

Table A1. $\mathbb{A}=-0.75$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

,

Table A2. $\mathbb{A}=-0.5$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

,

Table A3. $\mathbb{A}=-0.25$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

,

Table A4. $\mathbb{A}=0.00$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

,

Table A5. $\mathbb{A}=0.25$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

,

Table A6. $\mathbb{A}=0.5$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

and

Table A7. $\mathbb{A}=0.75$.

$\mathbb{G}$∖$\mathbb{D}$	0.07	0.1	0.25	0.5
0.5
1
2
3
4

in Appendix A. There is a separate table for each value of $\mathbb{A}$ (energy exchange parameter). The columns of each table correspond to the values of $\mathbb{D}$ (frequency of interactions), and the rows correspond to the values of $\mathbb{G}$ (the extent to which the fitness to the environment affects growth). In each plot, the horizontal axis shows the values of $\mathbb{B}$ (mutation rate), and the vertical axis shows the values of $\mathbb{K}$ (energy input). Each small rectangle in the plots corresponds to a specific tuple ($\mathbb{B}$, $\mathbb{K}$) and is one of three colors: (a) red if the number of surviving populations in the series of 100 repetitions is less than or equal to 5; (b) gray if the number of survivors is between 5 and 95; or (c) white (no color) if the number is greater than or equal to 95.

5. Conclusions

Nanorobotic technologies have the potential to become an important part of future personalized medicine. Due to their size, nanorobots almost always work in groups. One promising way to engineer such groups is by employing populations of unicellular organisms. This approach has many advantages: right off the bat, such agents can resist immune attacks, move, replenish energy, reproduce, and even adapt to the changing environment.

Relatively recent discoveries show that some single-celled organisms exchange information, matter, or energy within populations. In this paper, we use an in silico model to analyze whether energy exchange between agents in populations is important for their survival under different conditions. In practical terms, we study whether it is worth the effort to simulate energy exchange in real-world medical nanorobot populations.

We explored a wide range of energy exchange strategies, which can be divided into three broad types: altruistic (supports the weaker), neutral (no exchange), and selfish (takes from the weaker). Our experiments demonstrated the following in terms of the survival rate:

(1) Under all experimental conditions considered, selfish energy exchange is inferior to the other two types;

(2) Although, in a wide range of experimental conditions, there was almost no difference between altruistic and neutral energy exchange, under harsh conditions, the altruistic strategy is preferable.

In our model, harsh conditions include two cases: low energy input (or low energy absorption capacity) and a low mutation rate (the environment changes so quickly that populations struggle to adapt).

Both of these conditions are likely to occur in real-world medical bacteriabot populations, so our results suggest that engineering the altruistic energy exchange strategy into future unicellular micro/nanorobot populations may noticeably increase the survival rate of these populations, making treatment more efficient.