Implementation of Numerical Model for Prediction of Temperature Distribution for Metallic-Coated Firefighter Protective Clothing
Abstract
1. Introduction
2. Materials and Methods
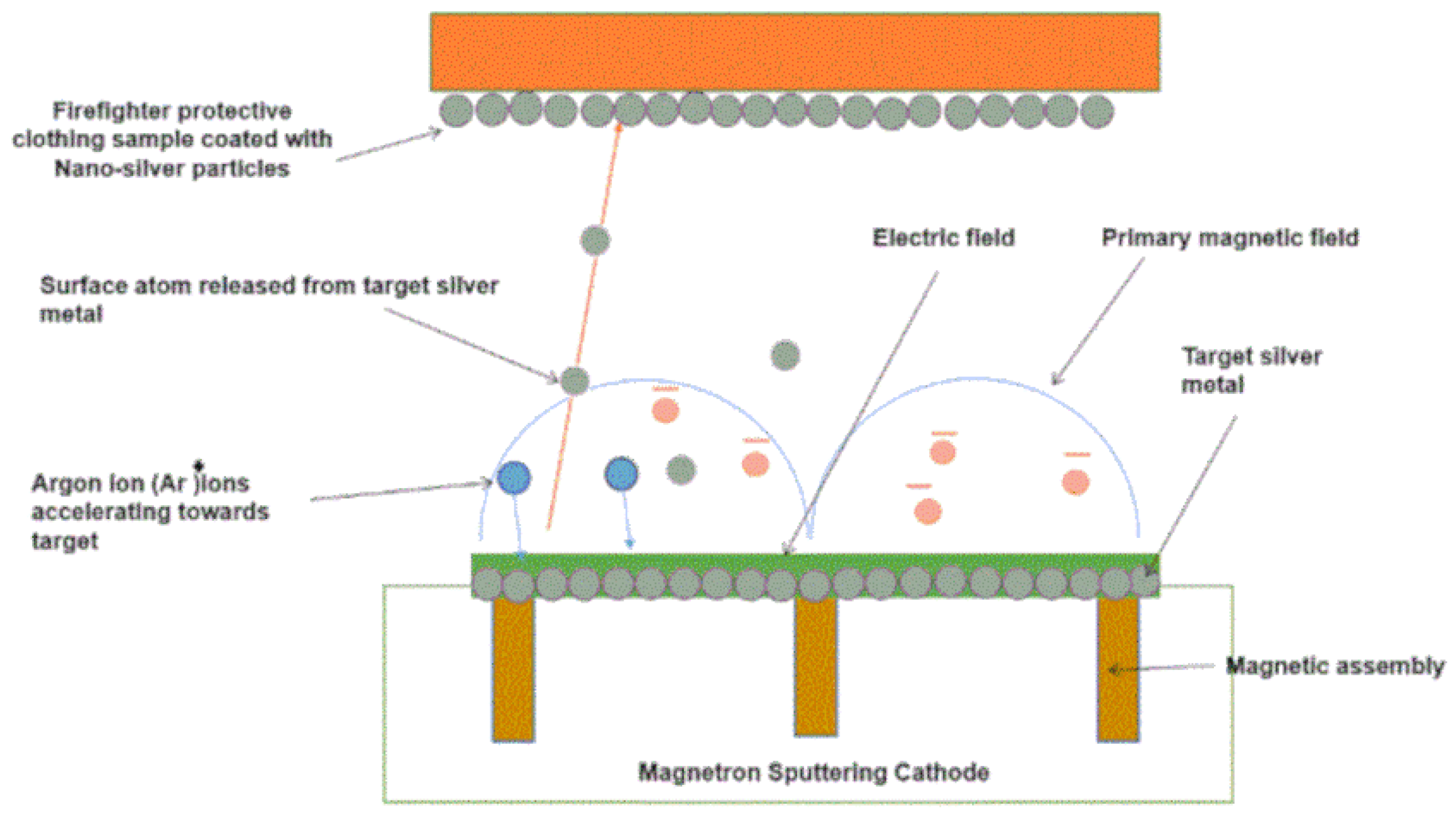
2.1. Coating of Samples through Magnetron Sputtering
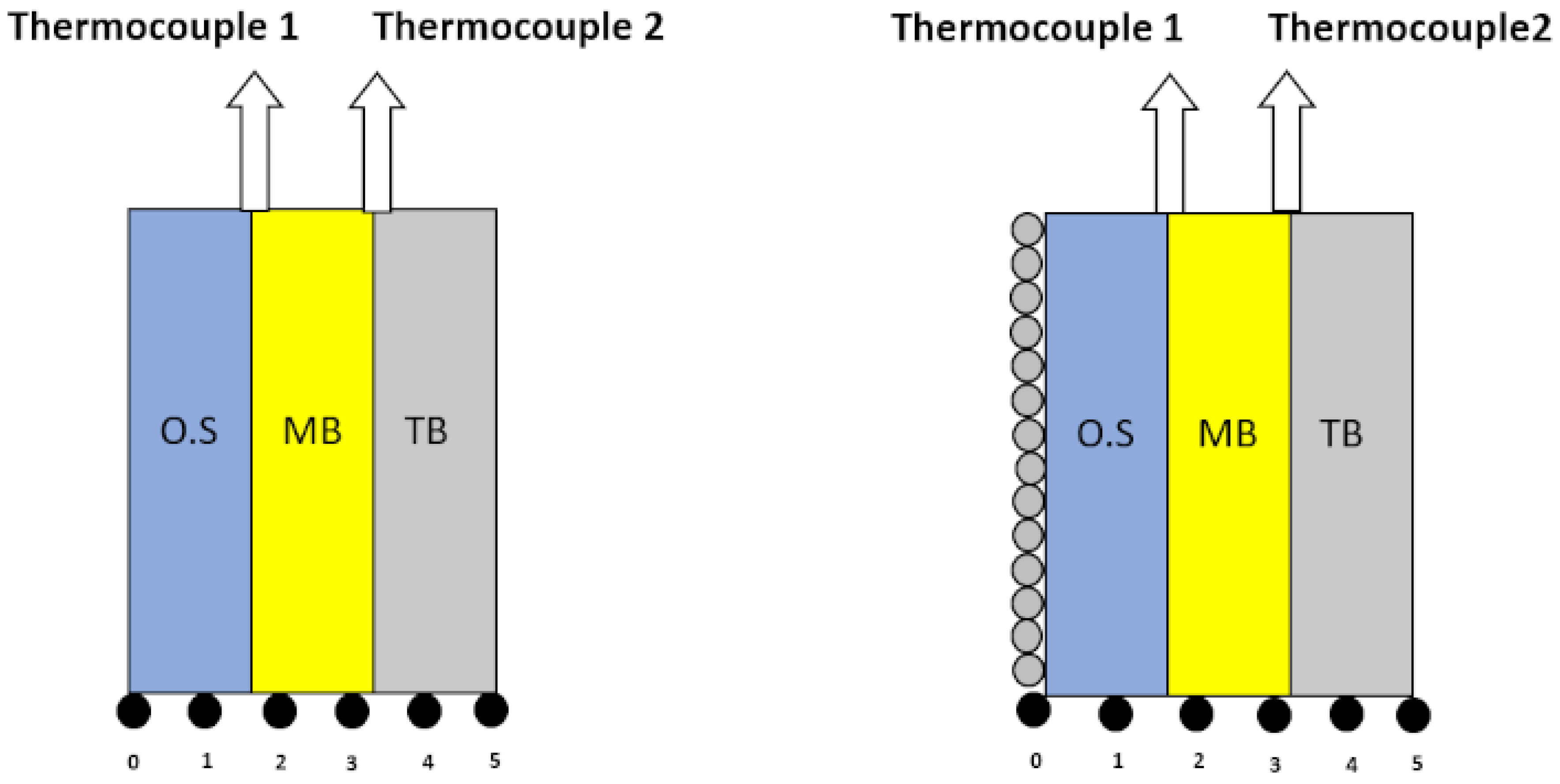
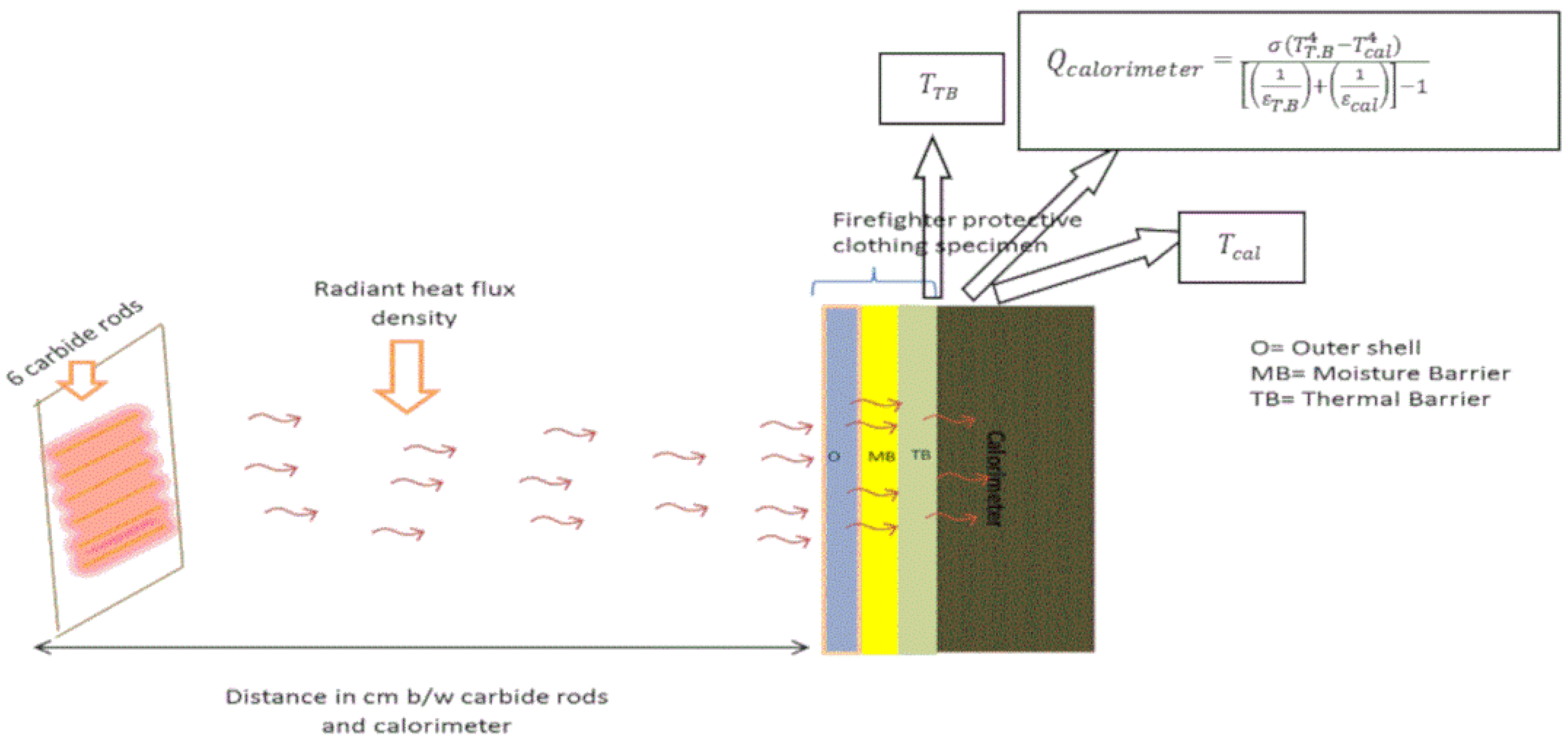
2.2. Radiant Heat Transmission Equipment and Measurement Protocol
- Transmission of heat takes place in one dimension only.
- The transfer of mass is negligible.
- Radiation only penetrates through the exterior shell of the multilayer assembly as almost 95% of incident energy is in the form of radiation that is absorbed after covering a distance equivalent to the outer shell thickness.
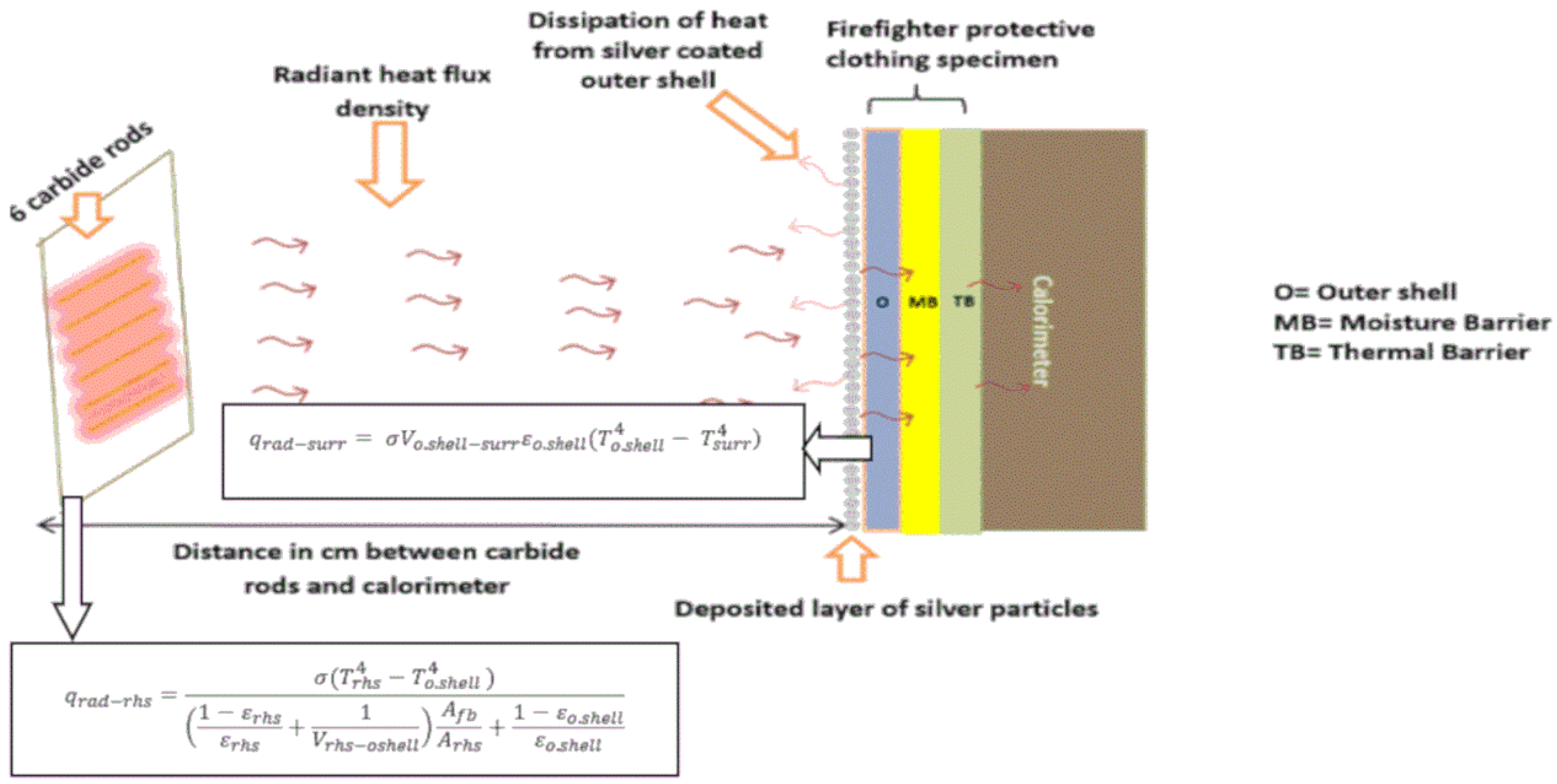
3. Transmission of Heat from Heating Source to Firefighter Clothing Assembly
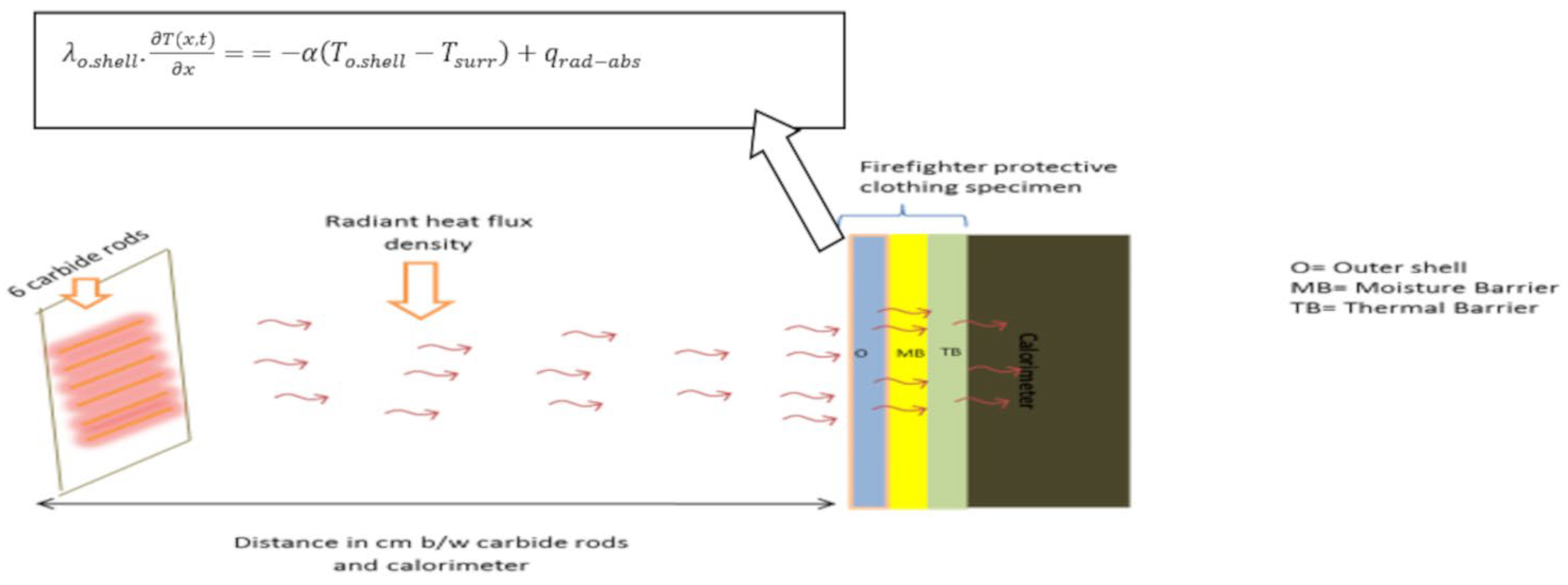
3.1. Numerical Solution
Boundary Conditions
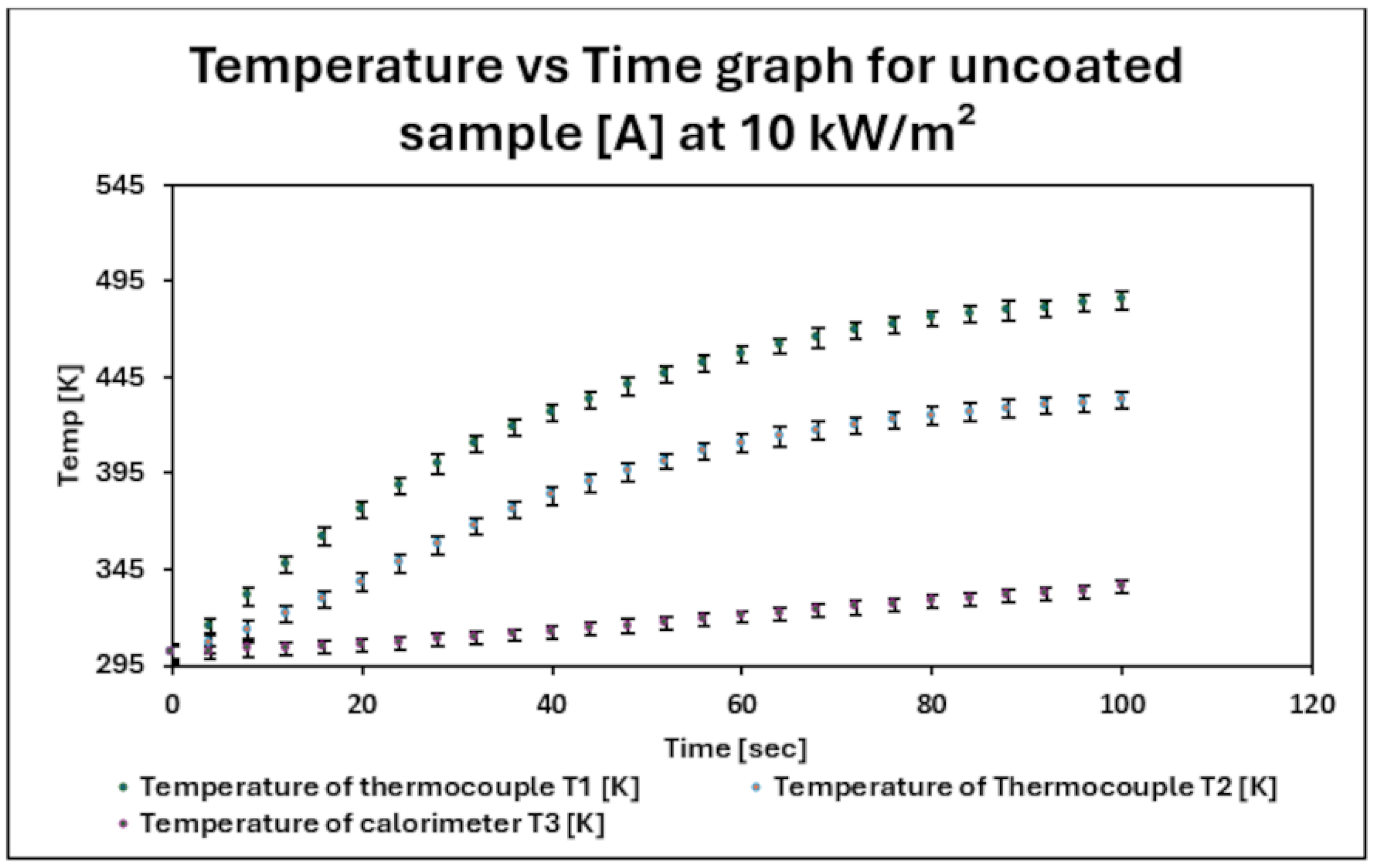
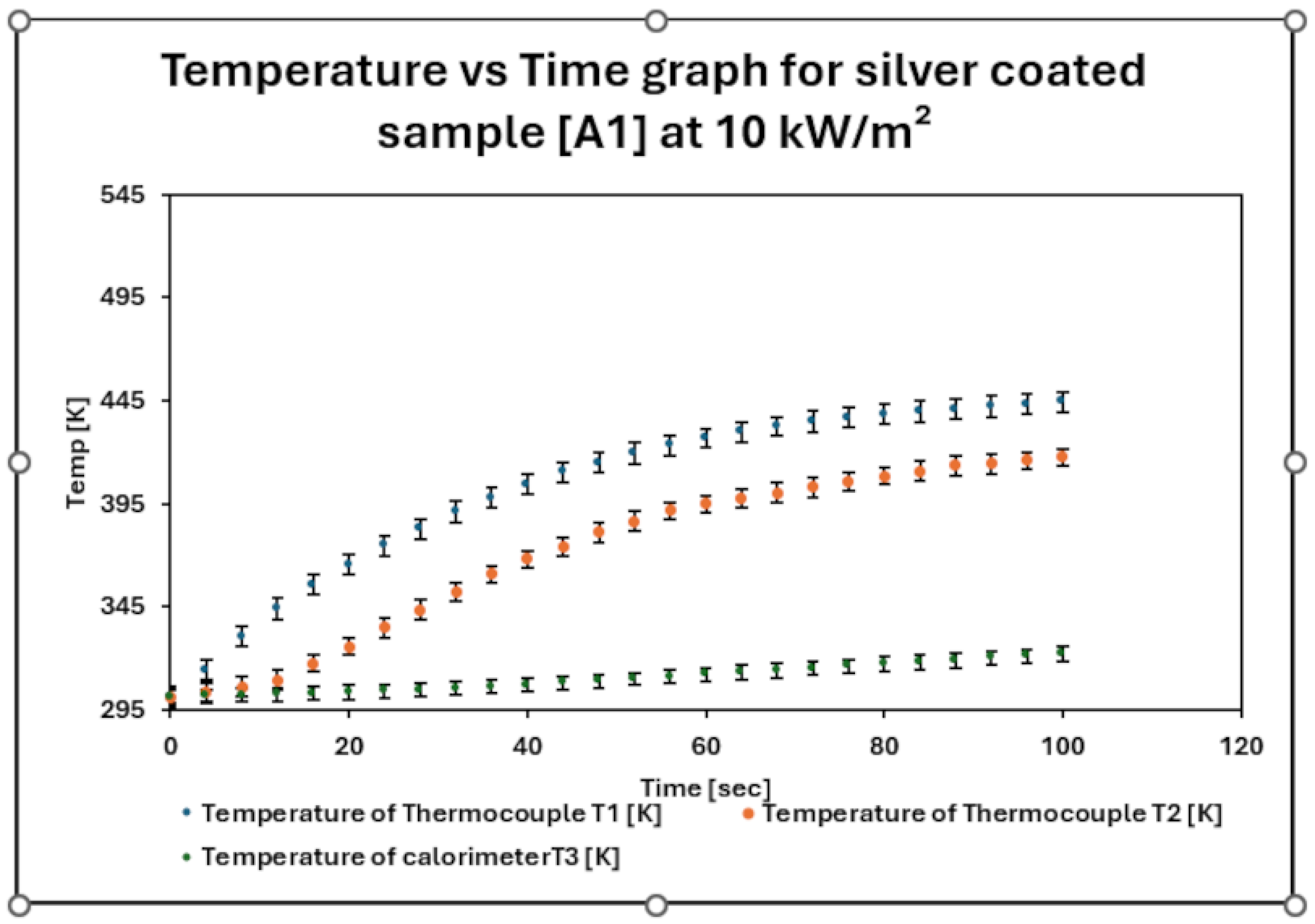
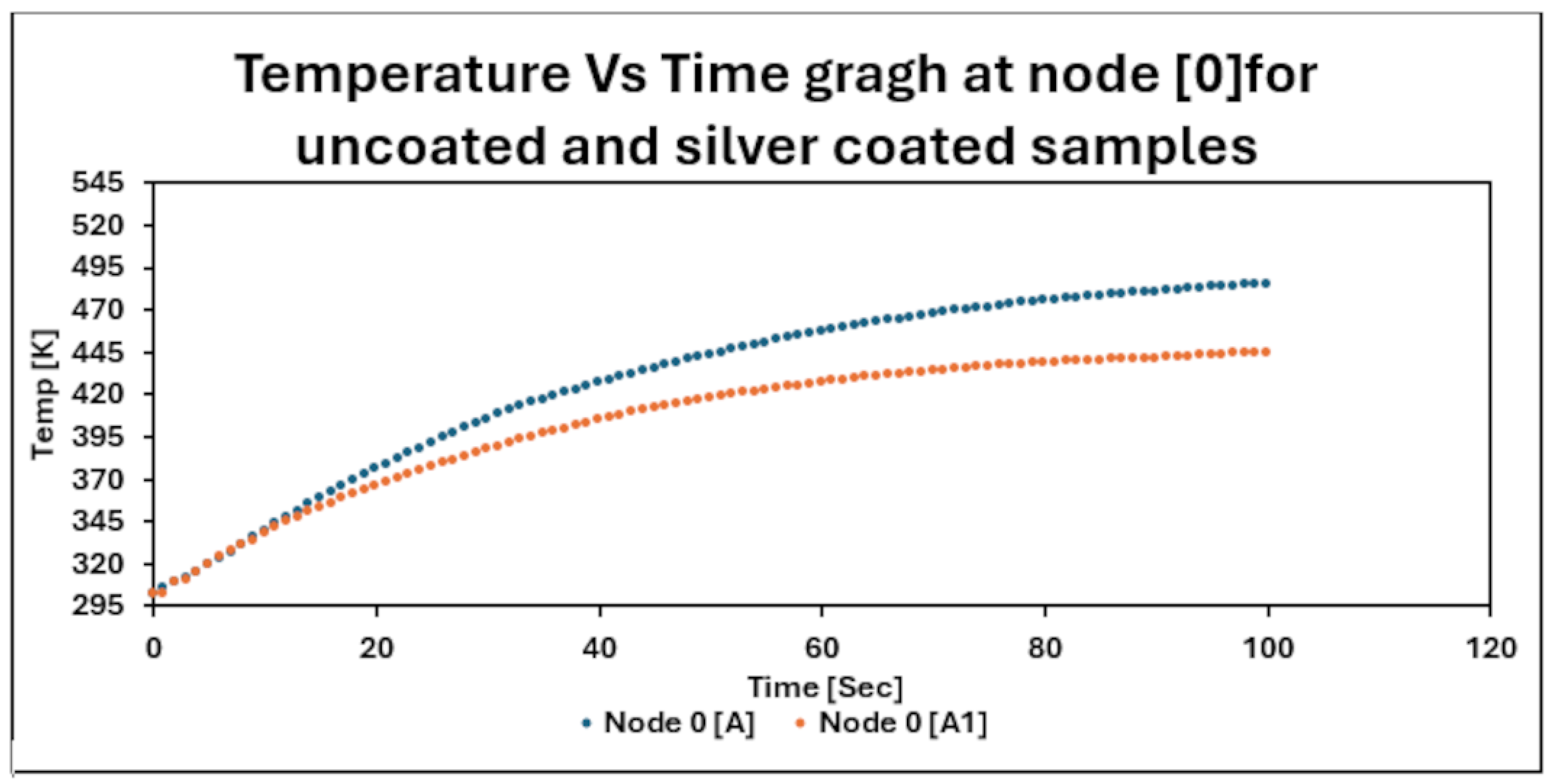
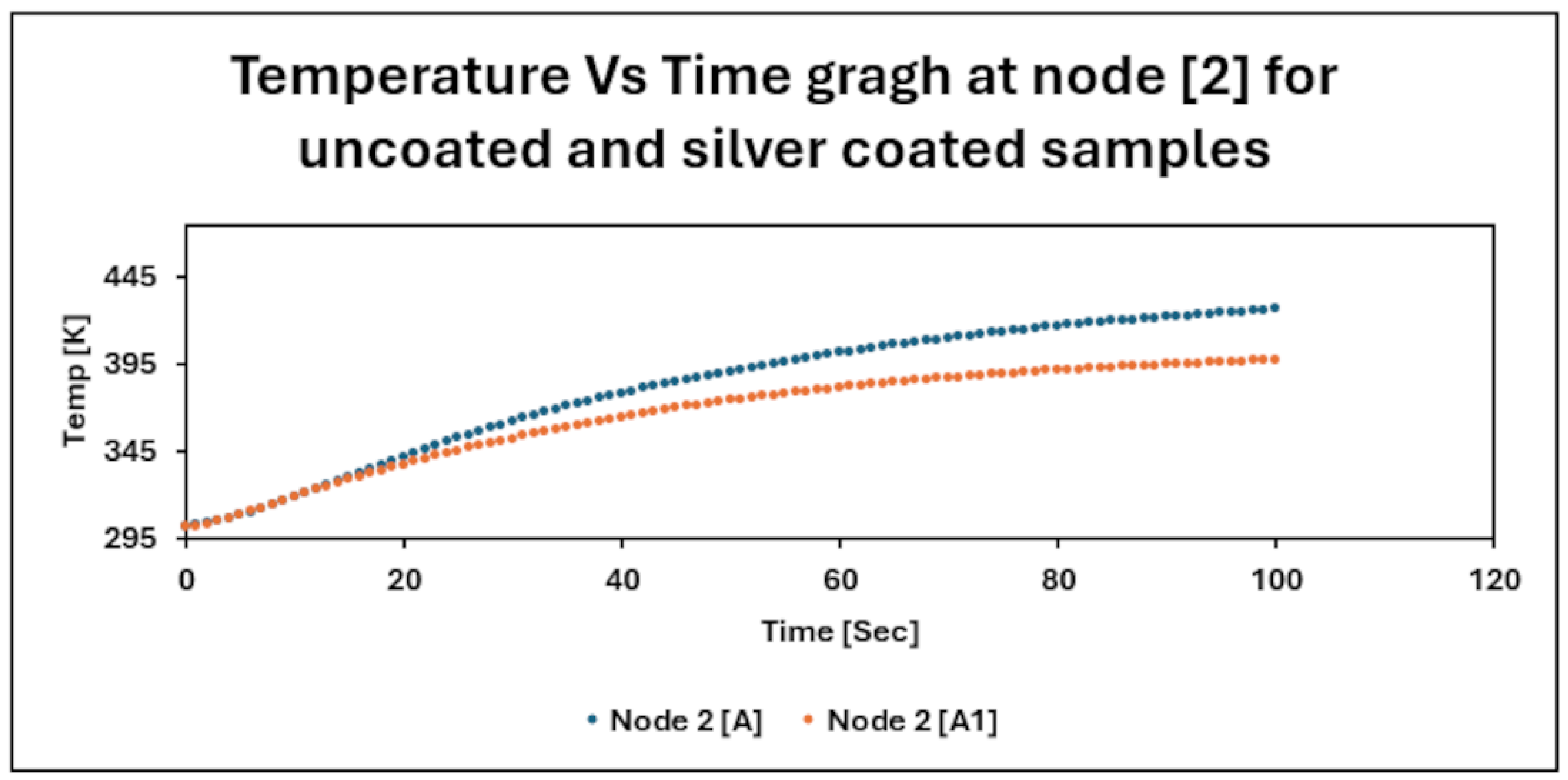
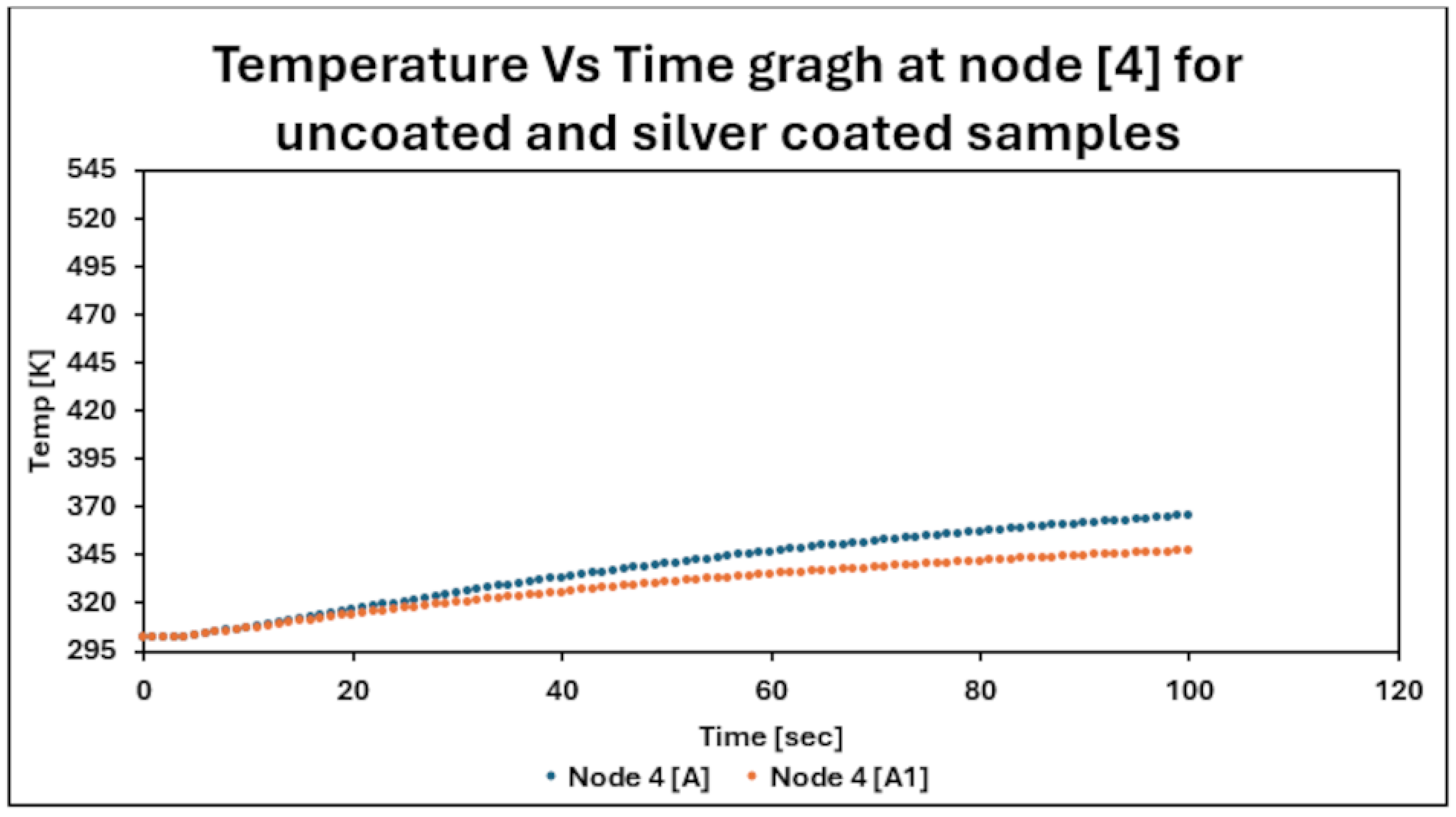
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holmer, I. How is performance in heat affected by clothing. Text. Bioeng. Inform. Symp. Proc. 2008, 1, 700–705. [Google Scholar]
- Keiser, C.; Rossi, R.M. Temperature analysis for the prediction of steam formation and transfer in multilayer thermal protective clothing at low level thermal radiation. Text. Res. J. 2008, 78, 1025–1035. [Google Scholar] [CrossRef]
- Bajaj, P.; Sengupta, A.K. Protective clothing. Text. Prog. 1992, 22, 1–110. [Google Scholar] [CrossRef]
- Jin, L.; Hong, K.; Yoon, K. Effect of Aerogel on Thermal Protective Performance of Fire-Fighter Clothing. J. Fiber Bioeng. Inform. 2013, 6, 315–324. [Google Scholar]
- Nayak, R.; Houshyar, S.; Padhye, R. Recent trends and future scope in the protection and comfort of fire-fighters’ personal protective clothing. Fire Sci. Rev. 2014, 1, 2014. [Google Scholar] [CrossRef]
- Song, G.; Paskaluk, S.; Sati, R.; Crown, E.M.; Dou, J. Thermal protective performance of protective clothing used for low radiant heat protection. Text. Res. J. 2010, 81, 311–323. [Google Scholar] [CrossRef]
- Mäkinen, H. Firefighter Protective Clothing. In Textile for Protection; Woodhead Publishing: Sawston, UK, 2005; pp. 622–647. [Google Scholar]
- Song, G.; Chitrphiromsri, P.; Ding, D. Numerical Simulations of Heat and Moisture Transport in Thermal Protective Clothing Under Flash Fire Conditions. Int. J. Occup. Saf. Ergon. 2008, 14, 89–106. [Google Scholar] [CrossRef] [PubMed]
- Fu, M.; Weng, W.; Yuan, H. Thermal Insulations of multilayer clothing systems measured by a bench scale test in low level heat exposures. Int. J. Cloth. Sci. Technol. 2013, 26, 412–423. [Google Scholar] [CrossRef]
- Min, K.; Son, Y.; Kim, C.; Lee, K.; Hong, K. Heat and moisture transfer from skin to environment through fabrics: A mathematical model. Int. J. Heat Mass Transf. 2007, 50, 5292–5304. [Google Scholar] [CrossRef]
- Venkataraman, M.; Mishra, R.; Kotresh, T.M.; Sako, T. Effect of compressibility on heat transport phenomena in aerogel-treated nonwoven fabrics. J. Text. Inst. 2016, 107, 1150–1158. [Google Scholar] [CrossRef]
- Stabkovic, S.B.; Popvic, D.; Poparic, G.B. Thermal properties of textile fabrics made of natural and regenerated cellulose fibers. Polym. Test. 2008, 27, 41–48. [Google Scholar] [CrossRef]
- Jin, L.; Cao, M.L.; Yu, W.; Hu, J.Y.; Yoon, K.J.; Park, P.K.; Li, Y. New approaches to evaluate performance of firefighter protective clothing. Fire Technol. 2018, 54, 1283–1307. [Google Scholar] [CrossRef]
- Fu, M.; Weng, W.; Yuan, H. Effects of multiple air gaps on the thermal performance of firefighter protective clothing under low-level heat exposure. Text. Res. J. 2013, 84, 968–978. [Google Scholar] [CrossRef]
- Shaid, A.; Wang, L.; Padhye, R. The thermal protection and comfort properties of aerogel and PCM-coated fabric for firefighter garment. J. Ind. Text. 2015, 45, 611–625. [Google Scholar] [CrossRef]
- Ali, A.H.M.; Mohmmed, R. A review of the firefighting fabrics for flashover temperature. Int. J. Eng. Sci. Res. Technol. 2015, 4, 247–257. [Google Scholar]
- Raslan, W.M. Ultraviolet Protection, Flame Retardancy and Antibacterial Properties of Treated Polyester Fabric Using Plasma-Nano Technology. Mater. Sci. Appl. 2011, 2, 1432–1442. [Google Scholar] [CrossRef]
- Azom, “Silver (Ag), Properties and Applications,” Azo Materials. 2013. Available online: https://www.azom.com/article.aspx?ArticleID=9282 (accessed on 24 June 2023).
- Negawao, T.A. Analyzing and Modelling of Comfort and Protection Properties of Firefighters Protective Clothing. Master’s Thesis, Istanbul Technical University, Istanbul, Turkey, 2015. [Google Scholar]
- ISO 6942; Protective Clothing—Protection against Heat and Fire—Method of Test: Evaluation of Materials and Material Assemblies when Exposed to a Source of Radiant Heat. International Organization for Standardization: Geneva, Switzerland, 2002.
- Torvi, D. Heat Transfer in Thin Fibrous Materials under High Heat Flux Conditions. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1997. [Google Scholar]
- Kukuck, S.; Prasad, K. Thermal Performance of Fire Fighters’ Protective Clothing. 3. Simulating a TPP Test for Single-Layered Fabrics; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2003. [Google Scholar]
- Zhu, F.L.; Zhang, W.; Song, G. Heat transfer in a cylinder sheathed by flame-resistant fabrics exposed to convective and radiant heat flux. Fire Saf. J. 2008, 43, 401–409. [Google Scholar] [CrossRef]
- Mercer, G.N.; Sidhu, H. A theoretical investigation into phase change clothing benefits for firefighters under extreme conditions. Chem. Prod. Process Model. 2003, 4, 289–305. [Google Scholar] [CrossRef]
- Song, G.; Barker, R.L.; Hamouda, H.; Kuznetsov, V. Modeling the thermal protective performance of heat resistant garments in flash fire exposures. Text. Res. J. 2004, 74, 1033–1040. [Google Scholar] [CrossRef]
- Ghazy, A.; Bergstrom, D.J. Numerical simulation of heat transfer in firefighters’ protective clothing with multiple air gaps during flash fire exposure. Numer. Heat Transf. Part A Appl. 2012, 61, 569–593. [Google Scholar] [CrossRef]
- Su, Y.; He, J.; Li, J. Modelling transmitted and stored energy in multilayer protective clothing under low level radiant exposure. Appl. Therm. Eng. 2016, 93, 1295–1303. [Google Scholar] [CrossRef]
- Su, Y.; He, J.; Li, J. A model of heat transfer in firefighting protective clothing during compression after radiant heat exposure. J. Ind. Text. 2016, 47, 2128–2152. [Google Scholar] [CrossRef]
- Su, Y.; Li, R.; Song, R.; Li, J.; Xiang, C. Modeling steam heat transfer in thermal protective clothing under hot steam exposure. Int. J. Heat Mass Transf. 2018, 120, 818–829. [Google Scholar] [CrossRef]
- Ackerman, M.; Crown, E.; Dale, J.; Murtaza, G.; Gonzalese, J. Development of a test apparatus/method and material specifications for protection from steam under pressure. In Performance of Protective Clothing and Equipment Emerging Issues and Technologies; ASTM International: West Conshohocken, PA, USA, 2012; Volume 9. [Google Scholar]
- Yoo, H.; Hu, S.; Kim, E.A. Effects of heat and moisture transport in fabrics and garments determined with a vertical plates wearing skin model. Text. Res. J. 2000, 70, 542–549. [Google Scholar] [CrossRef]
- Desruelle, A.V.; Schmid, B. The steam laboratory of the Institut de Médecine Navale du Service de Santé des Armées: A set of tools in the service of the French Navy. Eur. J. Appl. Physiol. 2004, 92, 630–635. [Google Scholar] [CrossRef] [PubMed]
- Sati, R.; Crown, E.M.; Ackerman, E.M.; Gonzalez, J. Protection from steam at high pressures: Development of a test device and protocol. Int. J. Occup. Saf. Ergon. JOSE 2008, 14, 29–41. [Google Scholar] [CrossRef][Green Version]
- Zhu, R.; Zhang, W. Modeling heat transfer for heat-resistant fabrics considering pyrolysis effect under an external heat flux. J. Fire Sci. 2009, 27, 81–96. [Google Scholar] [CrossRef]
- Yang, J.; Su, Y.; Song, G.; Li, R.; Xiang, C. A new approach to predict heat stress and skin burn of firefighter under lowlevel thermal radiation. Int. J. Therm. Sci. 2019, 145, 106021. [Google Scholar] [CrossRef]
- Shakeriaski, F.; Ghodrat, M.; James, D. Experimental and numerical studies on efficiency characterization of firefighters’ protective clothing: A review. J. Text. Inst. 2022, 113, 2549–2568. [Google Scholar] [CrossRef]
- Mandal, S.; Annaheim, S.; Greve, J. Modeling for predicting the thermal protective and thermo-physiological comfort performance of fabrics used in firefighters’ clothing. Text. Res. J. 2018, 89, 2836–2849. [Google Scholar] [CrossRef]
- Puszkarz, A.K.; Machnowski, W. Simulations of heat transfer through multilayer protective clothing exposed to flame. AUTEX Res. J. 2022, 22, 298–304. [Google Scholar] [CrossRef]
- Fonseca Malaquias, A.; Neves, S.; Camp, J.B.L.M. The impact of water on firefighter protective clothing thermal performance and steam burn occurrence in firefighters. Fire Saf. J. 2022, 127, 103506. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M. A robust Bézier based solution for nonlinear vibration and post-buckling of random checkerboard graphene nano-platelets reinforced composite beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature powerful new technique for analysis of composite structure. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Su, Y.; He, J.; Li, J. Numerical simulation of heat transfer in protective clothing with various heat exposures distances. J. Text. Inst. 2016, 108, 1412–1420. [Google Scholar] [CrossRef]
- Naeem, J. Thermal Protetcive Performance of Fitrefighter Protective Clothing. Ph.D. Thesis, Technical University of Liberec, Liberec, Czech Republic, 2020. [Google Scholar]
- Anon, “Magnetron Sputtering”. 2018. Available online: https://angstromengineering.com/tech/magnetron-sputtering/ (accessed on 24 June 2022).
- Anon, “Magnetron Sputtering Solutions”. 2020. Available online: https://www.dentonvacuum.com/products-technologies/magnetron-sputtering/ (accessed on 24 June 2022).
- Shohet, J.L. Metal Deposition: Plasma-Based Processes. In Encyclopedia of Plasma Technology, 1st ed.; Taylor and Francis: New York, NY, USA, 2016; p. 726. [Google Scholar]
- Shi, F. Introductory Chapter: Basic Theory of Magnetron Sputtering; IntechOpen: London, UK, 2018; Volume 93, pp. 1295–1303. [Google Scholar]
- Dr.-Ing. Georg Wazau Meß- + Prüfsysteme GmbH. Combustion Behavior Test Equipment; Wazau: Berlin, Germany, 2002. [Google Scholar]
- Cengel, Y.A.; Ghajar, A.; Ma, H. Heat and Mass Transfer Fundamentals and Applications, 4th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Feistauer, M.; Najzar, K. Finite Element Approximation of a Problem with a Nonlinear Boundary Condition. Numer. Math. 1998, 78, 403–425. [Google Scholar] [CrossRef]
- Mlýnek, J.; Knobloch, R. Model of Shell Metal Mould Heating in the Automotive Industry. J. Appl. Math. 2018, 63, 111–124. [Google Scholar]
- Křížek, M.; Liu, L. Finite Element Analysisof a Radiation Heat Transfer Problem. J. Comput. Math. 1998, 6, 327–336. [Google Scholar]
- Martinez, I. “Radiative View Factors”. 1995. Available online: http://imartinez.etsiae.upm.es/~isidoro/tc3/Radiation%20View%20factors.pdf (accessed on 25 April 2022).
- Modest, M.F. Radiative Heat Transfer; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- ASTM F2731; Test Method for Measuring the Transmitted and Stored Energy of Firefighter Protective Clothing Systems. American Standard for Testing Materials: West Conshohocken, PA, USA, 2011.
- Higham, N.J. Accuracy and Stability of Numerical Algorithms, 2nd ed.; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Fanghor, H. Solving Partial Differential Equations, Engineering and Environment. Lectures, University of South Hampton, UK, 2012. Available online: https://www.southampton.ac.uk/~fangohr/teaching/comp6024/comp6024-pdes.pdf (accessed on 25 April 2022).


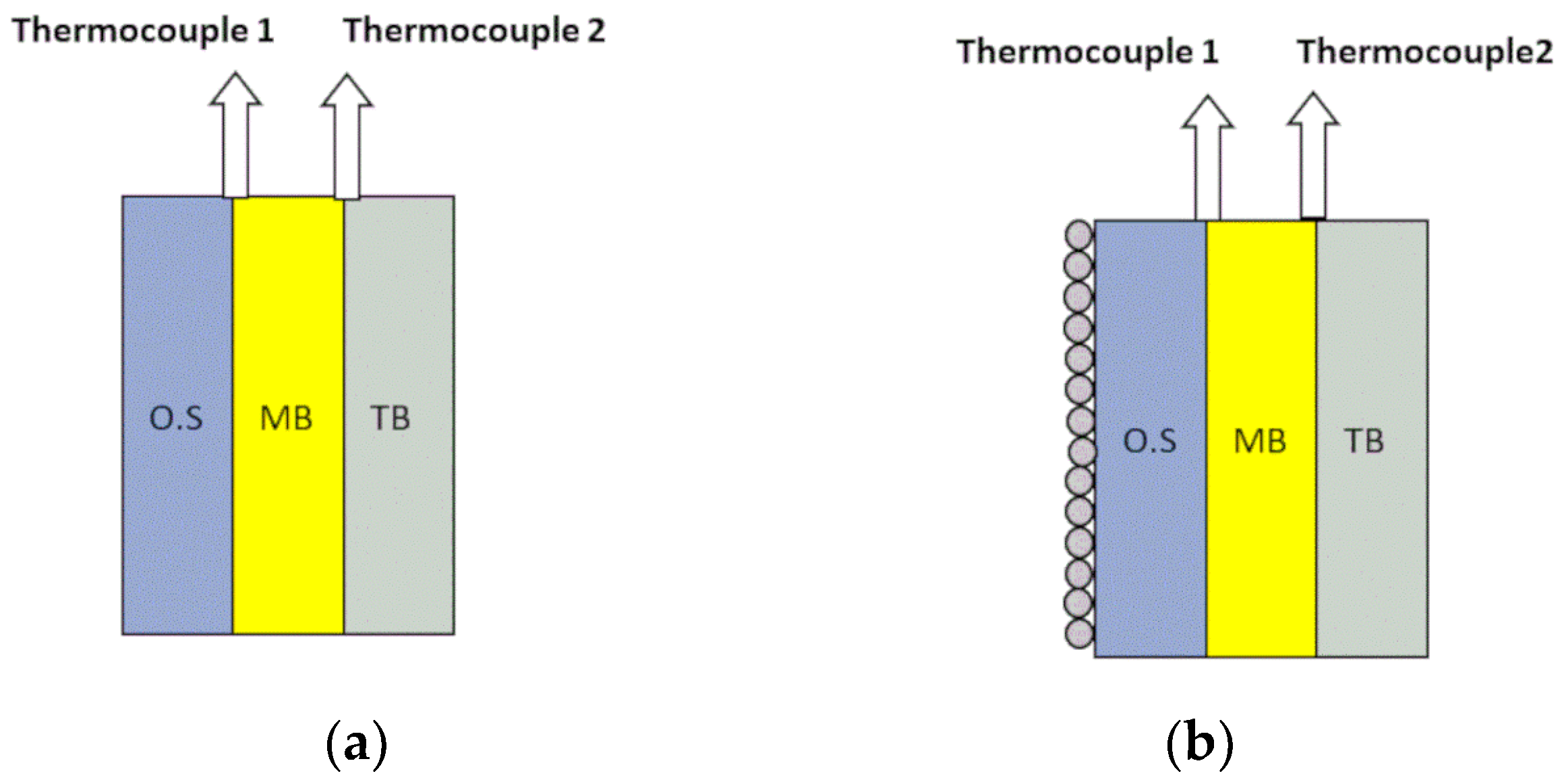
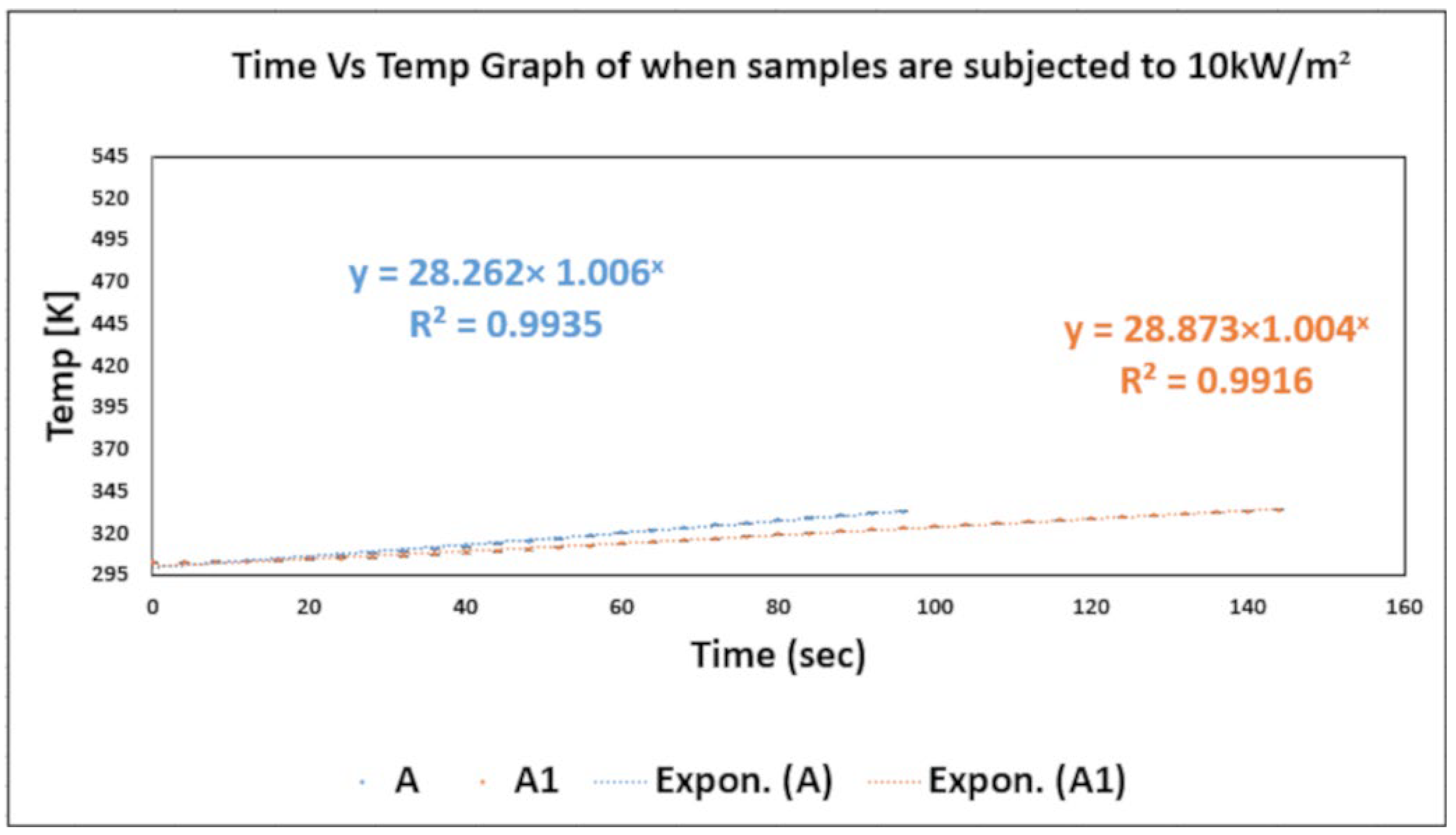





| Sr No | Name of Sample | Code | Material Specification | Weave Design | GSM [g/m2] | Thickness [mm] |
|---|---|---|---|---|---|---|
| 1 | Outer shell | O | 70% Conex, 23% Lenzing FR, 5% Twaron, 2% Beltron | Rip stop | 225 ± 2.1 | 0.44 ± 0.01 |
| 2 | Outer shell (1 μm thickness) | O (1) | 70% Conex, 23% Lenzing FR, 5% Twaron, 2% Beltron | Rip stop | 234 ± 1.8 | 0.441 ± 0.02 |
| 3 | Moisture barrier | MB | Face fabric, 50%/50% Kermel/viscose FR, PTFE membrane | Non-woven | 120 ± 1.8 | 0.55 ± 0.01 |
| 4 | Thermal barrier | TB | Thermo: Para Aramid Inner futter: 50% Meta aramid, 50% viscose | Non-woven | 200 ± 2.3 | 1.8 ± 0.02 |
| Sr No | Fabric Assembly | Fabric Code | Fabric Weight [g/m2] | Thickness [mm] |
|---|---|---|---|---|
| 1 | Outer shell (O) + moisture barrier (MB) + thermal barrier (TB) | A | 545 ± 3.1 | 2.79 ± 0.02 |
| 2 | Outer shell (O1) + moisture barrier (MB) + thermal barrier (TB) | A1 | 554 ± 3.5 | 2.791 ± 0.03 |
| Sr No | Samples | Qo [kW/m2] | RHTI 12 [sec] | RHTI 24 [sec] | RHTI24-RHTI 12 [sec] | Qc [kW/ m2] | [%] Age TF Qo | Reflectivity |
|---|---|---|---|---|---|---|---|---|
| 1 | A | 10.0 | 46.30 ± 0.94 | 77.20 ± 0.92 | 30.90 | 2.153 ± 0.001 | 21.60 | [0.09] |
| 2 | A1 | 10.0 | 63.3 ± 0.86 | 110.50 ± 0.72 | 47.20 | 1.415 ± 0.003 | 14.20 | [0.46] |
| Symbols | Values |
|---|---|
| (uncoated) | 0.86 |
| (silver coated) | 0.52 |
| 0.98 [55] | |
| 0.002826 m2 | |
| 0.0397 m2 | |
| 0.0065 | |
| 0.091 | |
| 0.909 | |
| τ (uncoated shell) | 0.01 |
| τ (silver shell) | 0.007 |
| Cp (uncoated fabric) | 1241.5 j/kg.K |
| Cp (silver coated) | 1221.5 j/kg.K |
| ρ of fabric (uncoated) | 195.3 kg/m3 |
| ρ of fabric (silver coated) | 198.1 kg/m3 |
| λ of fabric (uncoated) | 0.036 W/[m.K] |
| λ of fabric (silver coated) | 0.039 W/[m.K] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naeem, J.; Mazari, A.; Kus, Z.; Havelka, A.; Abdelkader, M. Implementation of Numerical Model for Prediction of Temperature Distribution for Metallic-Coated Firefighter Protective Clothing. Micro 2024, 4, 368-386. https://doi.org/10.3390/micro4020023
Naeem J, Mazari A, Kus Z, Havelka A, Abdelkader M. Implementation of Numerical Model for Prediction of Temperature Distribution for Metallic-Coated Firefighter Protective Clothing. Micro. 2024; 4(2):368-386. https://doi.org/10.3390/micro4020023
Chicago/Turabian StyleNaeem, Jawad, Adnan Mazari, Zdenek Kus, Antonin Havelka, and Mohamed Abdelkader. 2024. "Implementation of Numerical Model for Prediction of Temperature Distribution for Metallic-Coated Firefighter Protective Clothing" Micro 4, no. 2: 368-386. https://doi.org/10.3390/micro4020023
APA StyleNaeem, J., Mazari, A., Kus, Z., Havelka, A., & Abdelkader, M. (2024). Implementation of Numerical Model for Prediction of Temperature Distribution for Metallic-Coated Firefighter Protective Clothing. Micro, 4(2), 368-386. https://doi.org/10.3390/micro4020023