Dielectric Behaviour and Electrical Conductivity of α-BiNbO4 and β-BiNbO4 Ceramics
Abstract
1. Introduction
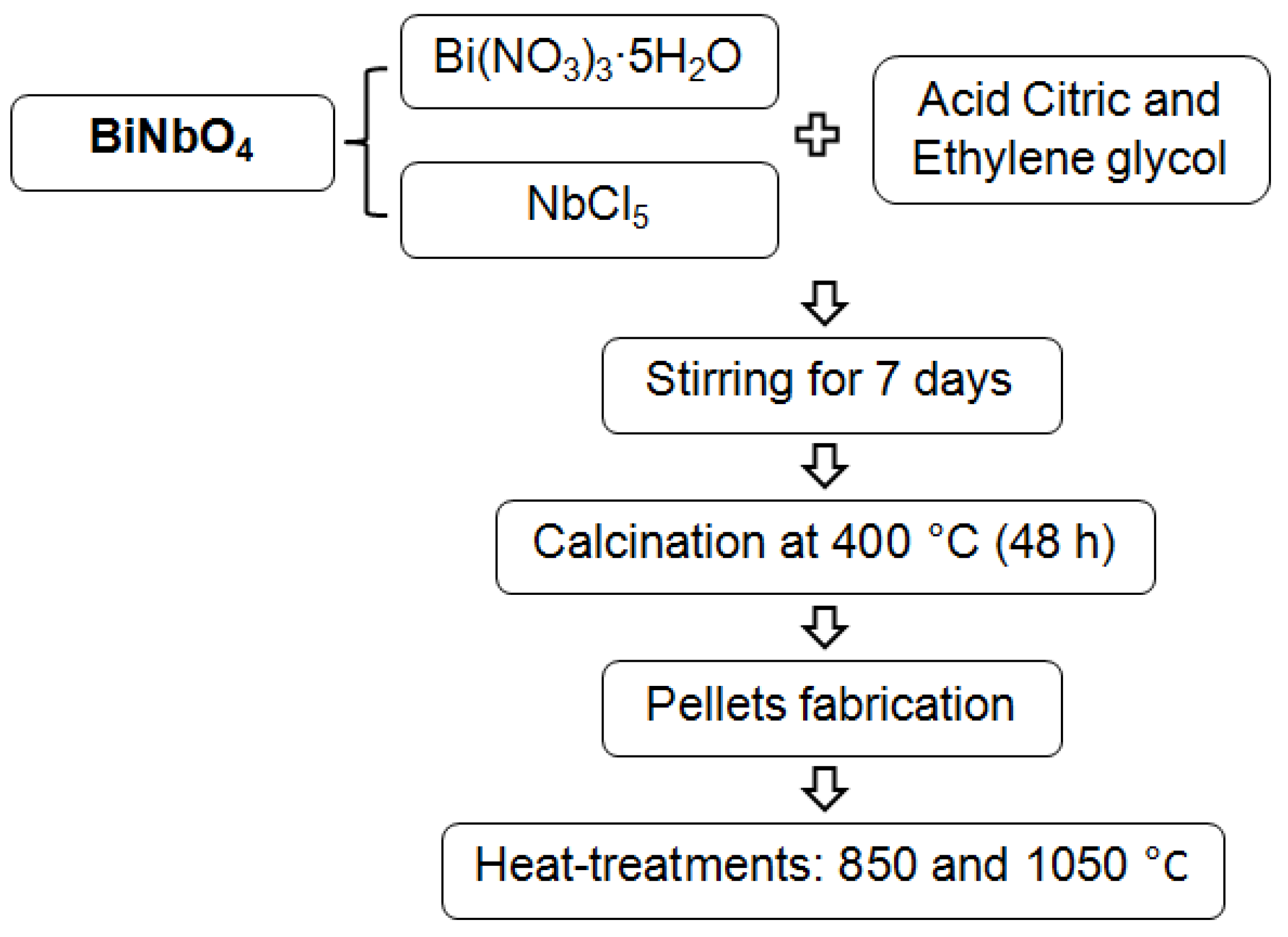
2. Experimental
3. Results and Discussion
3.1. Structural Characterisation
3.2. Morphological Characterisation
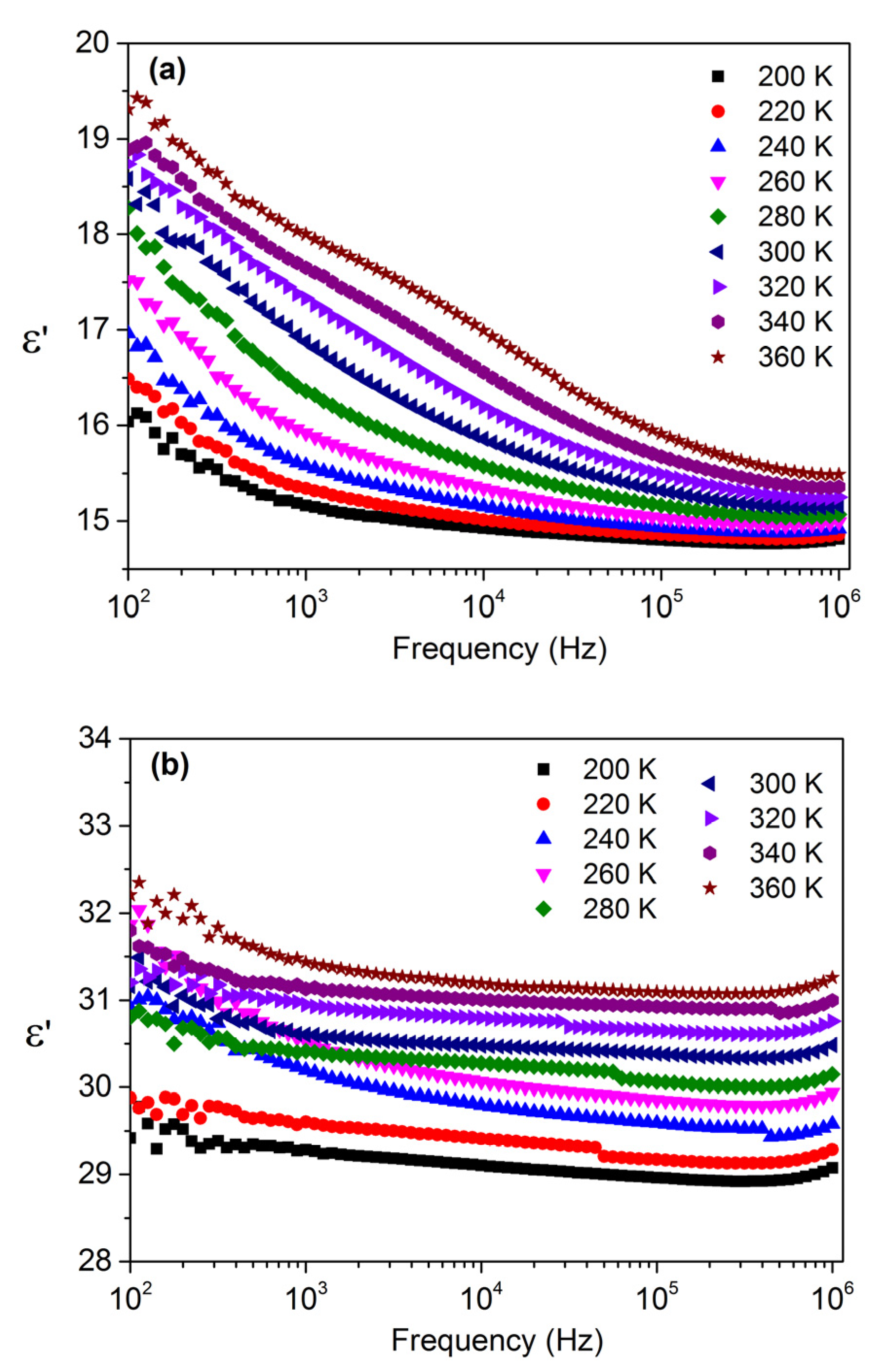
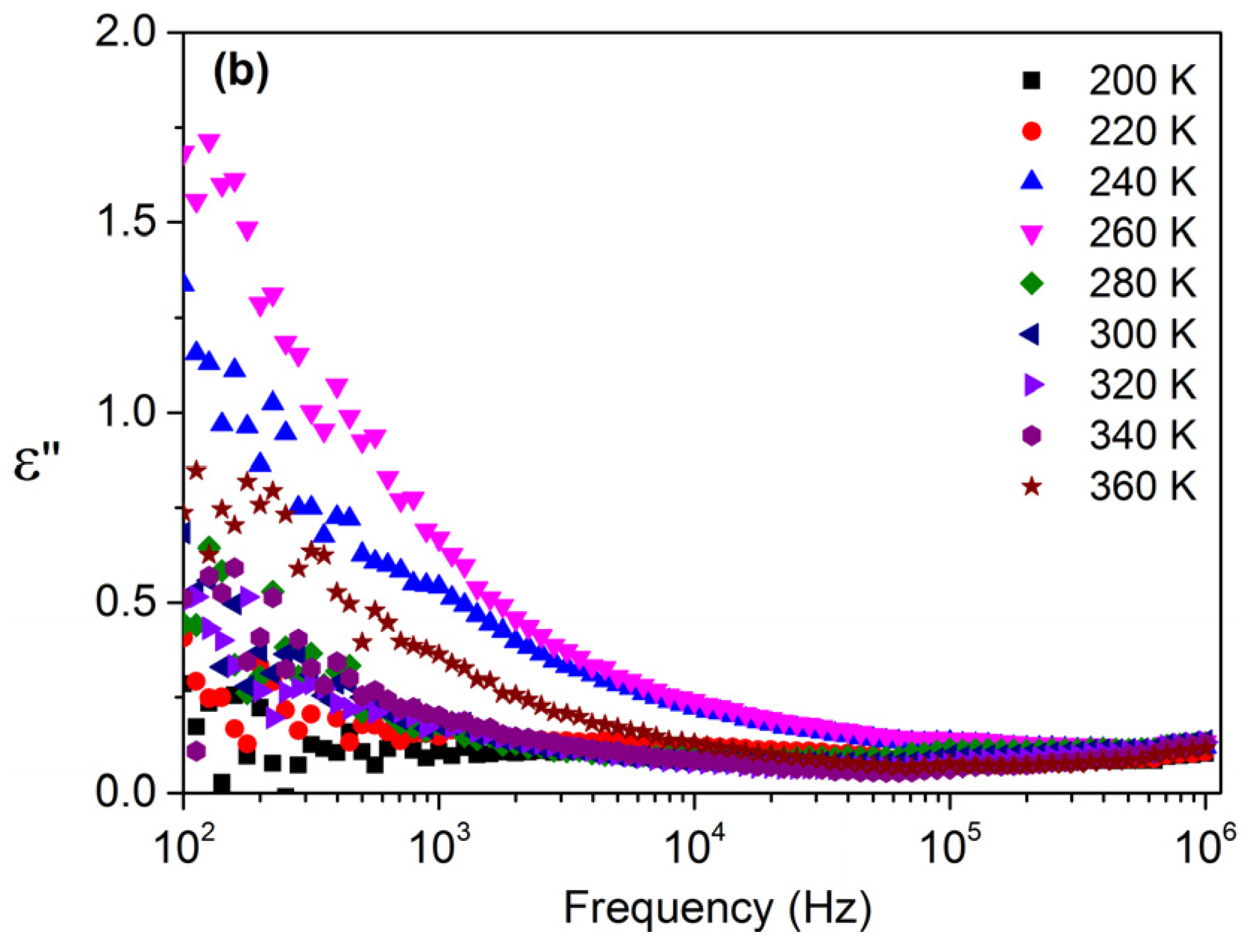
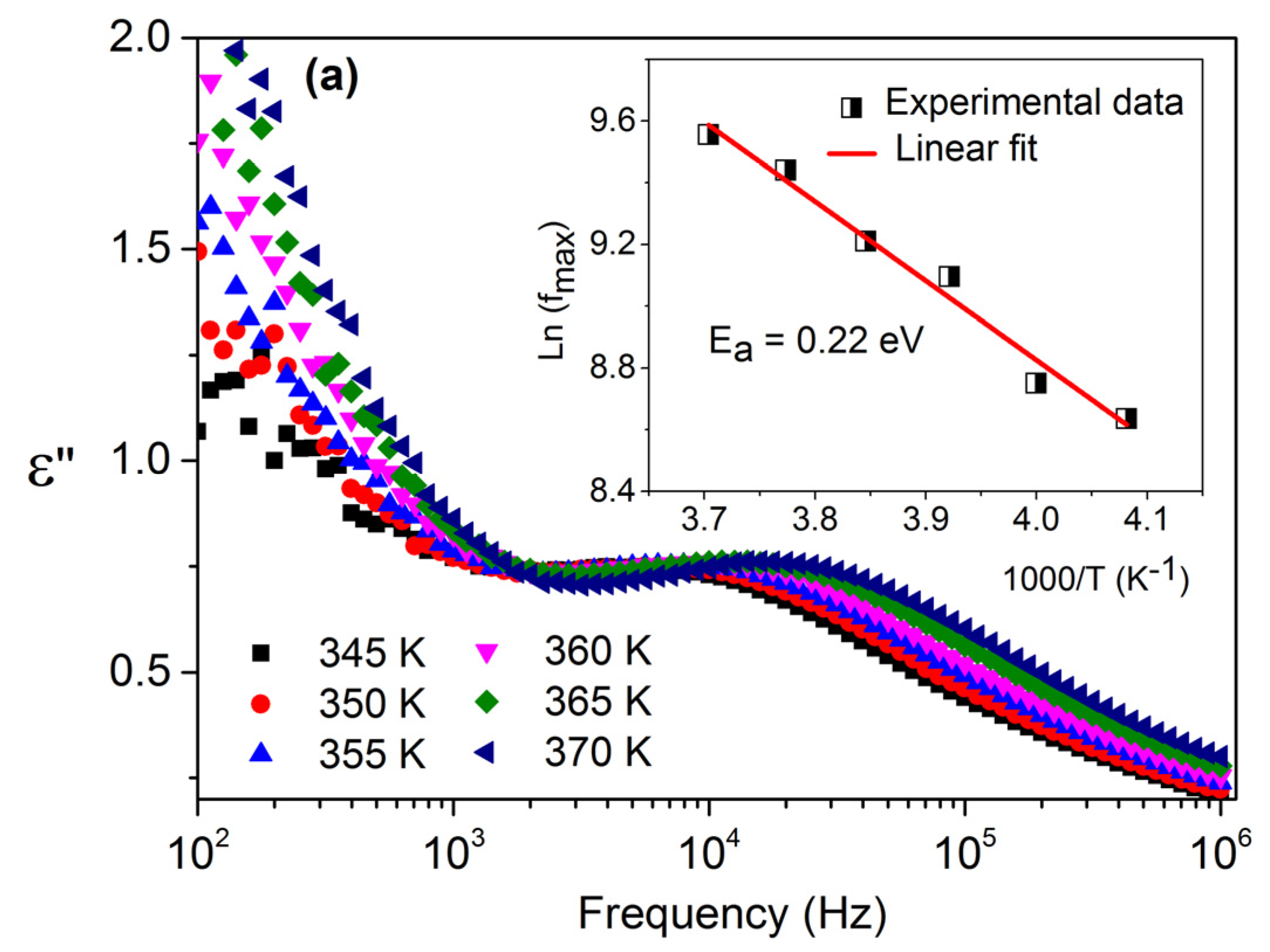
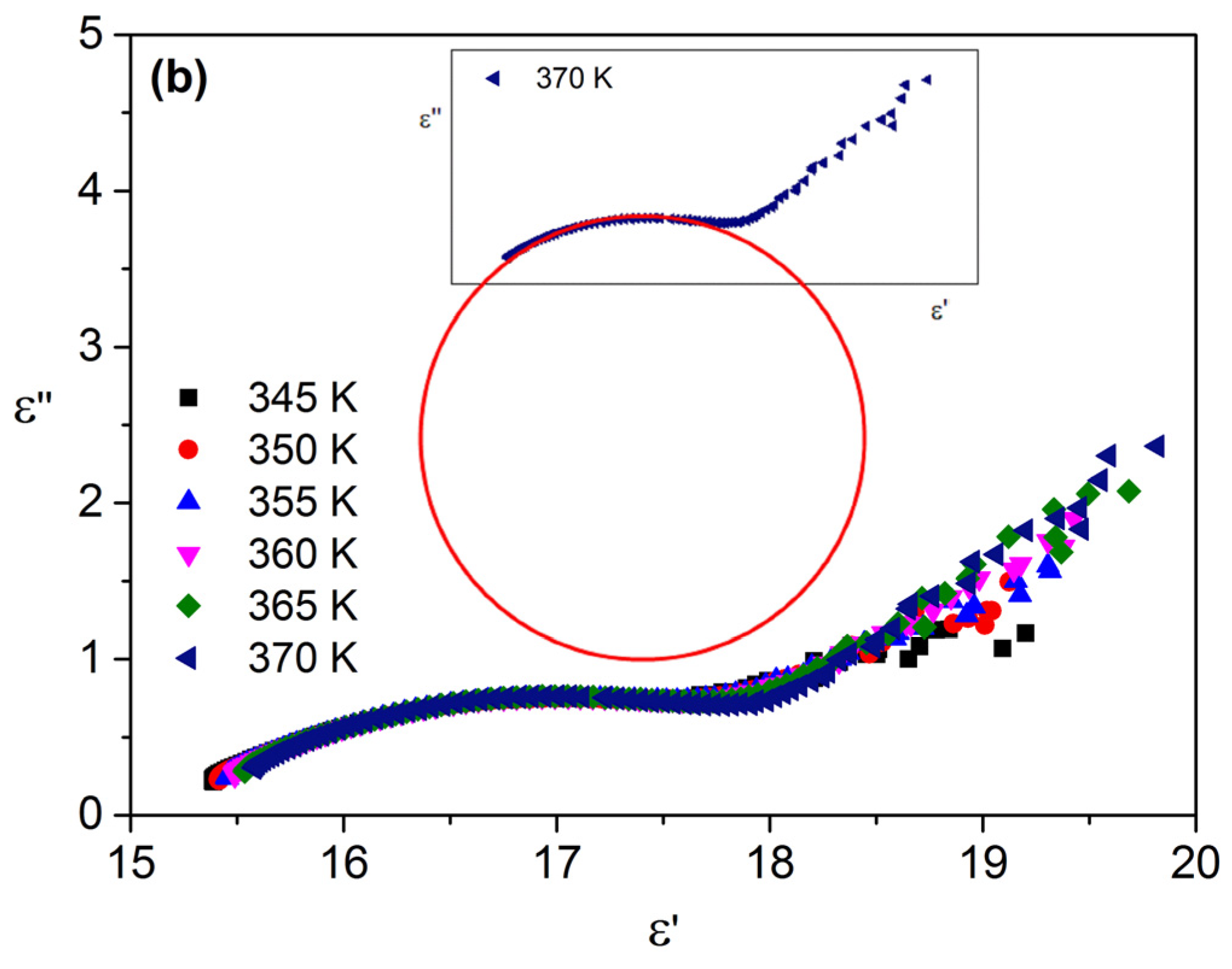
3.3. Dielectric Properties
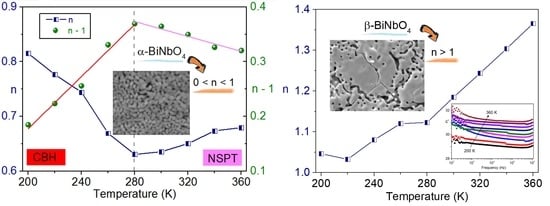
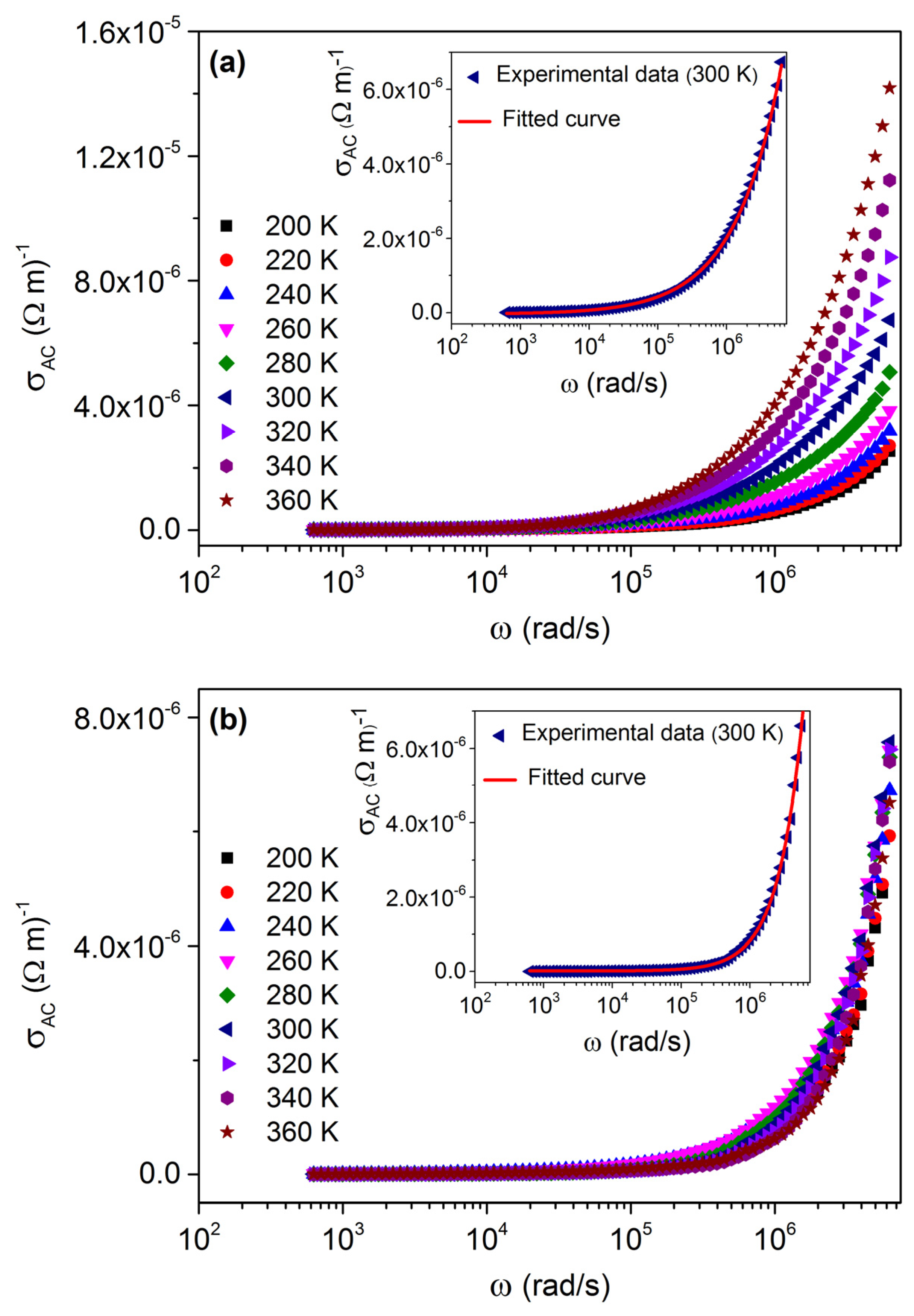
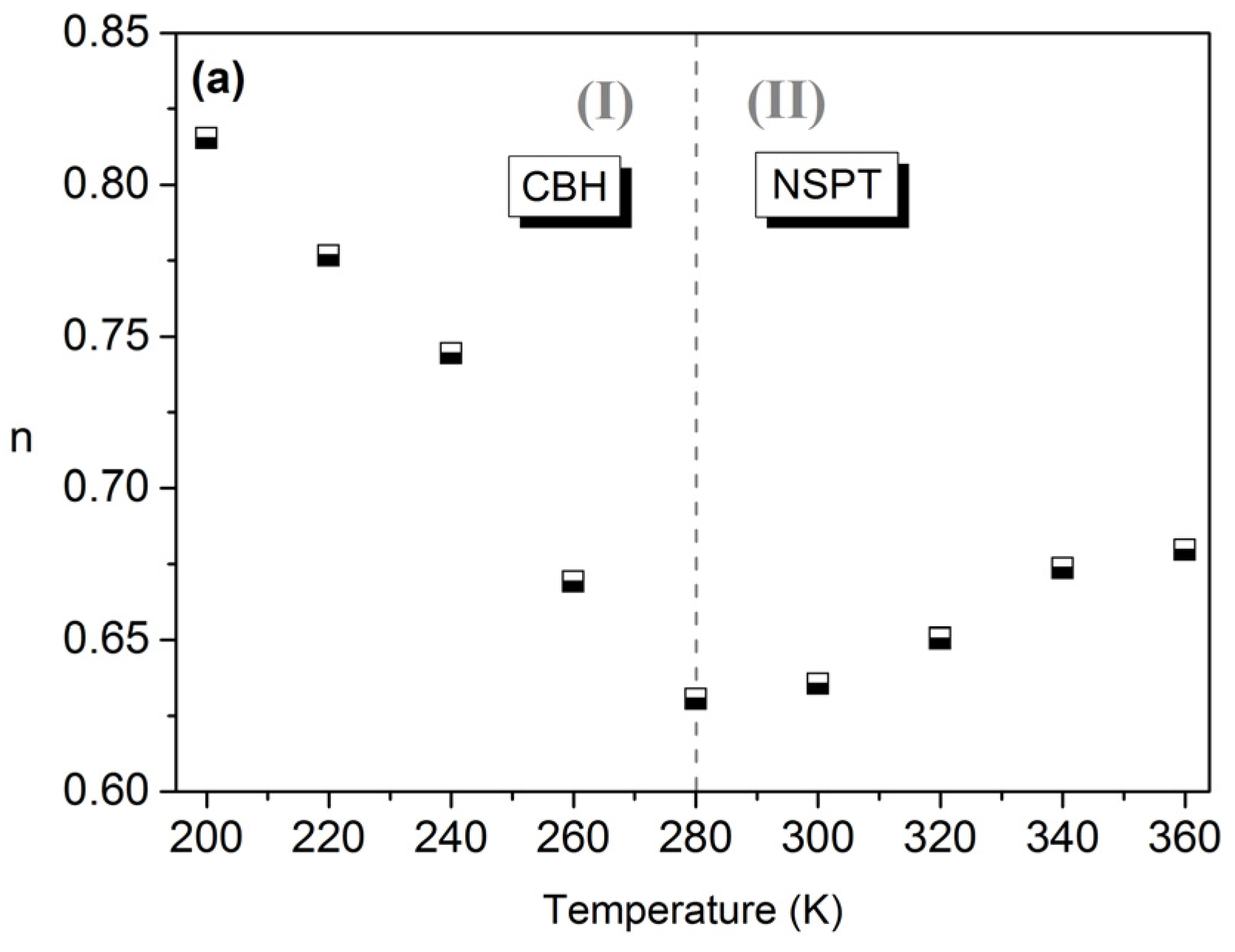
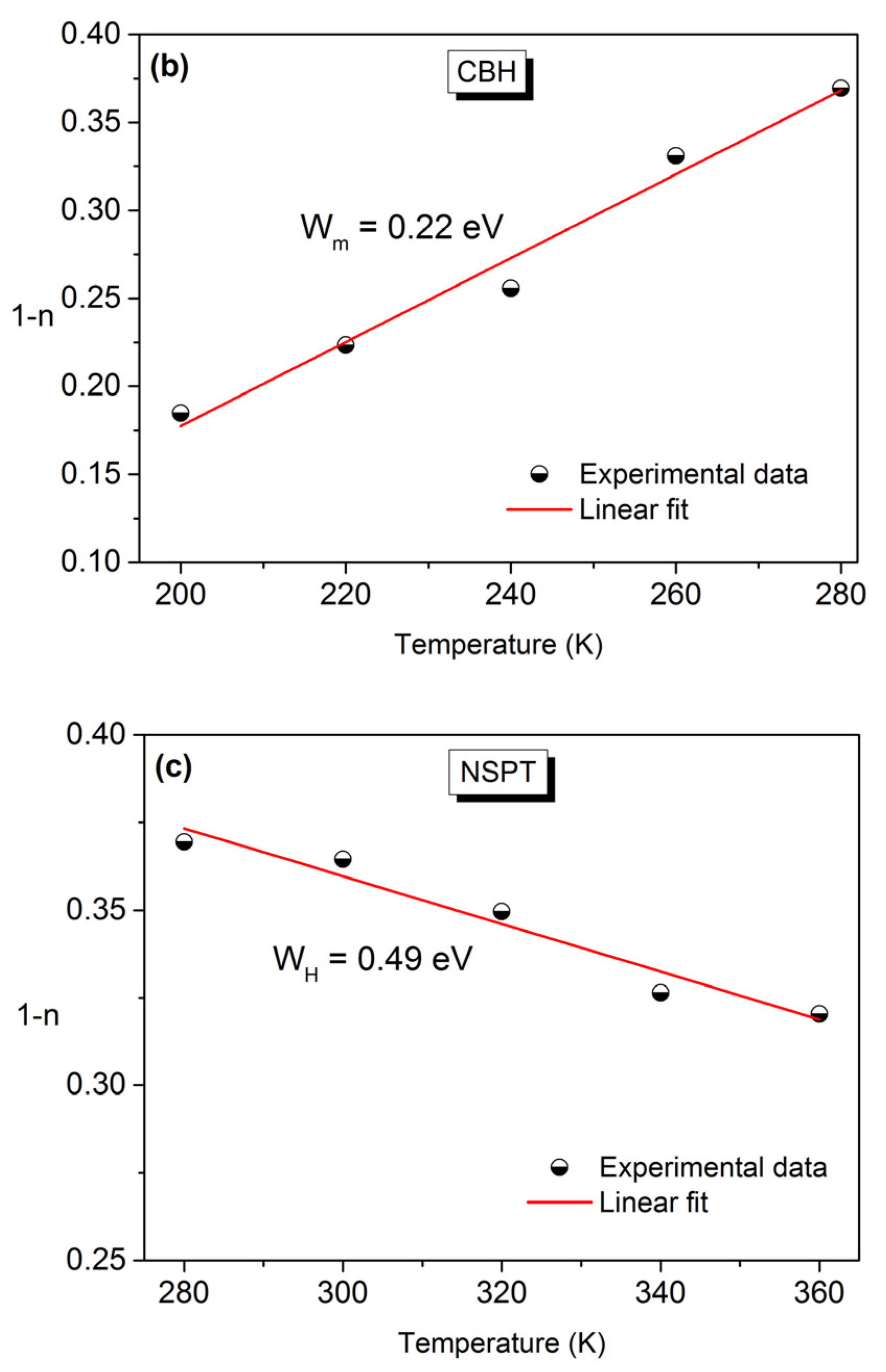
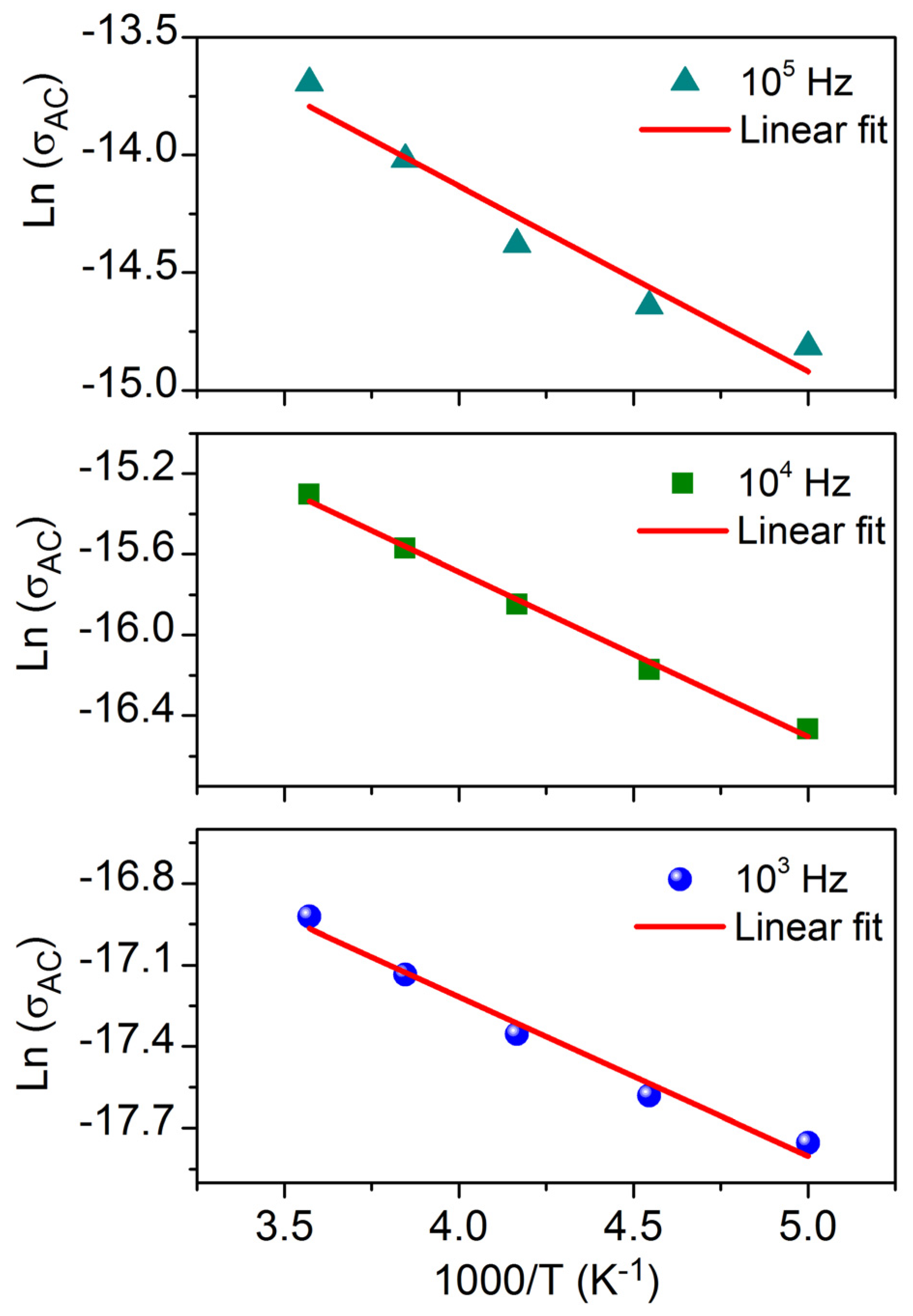
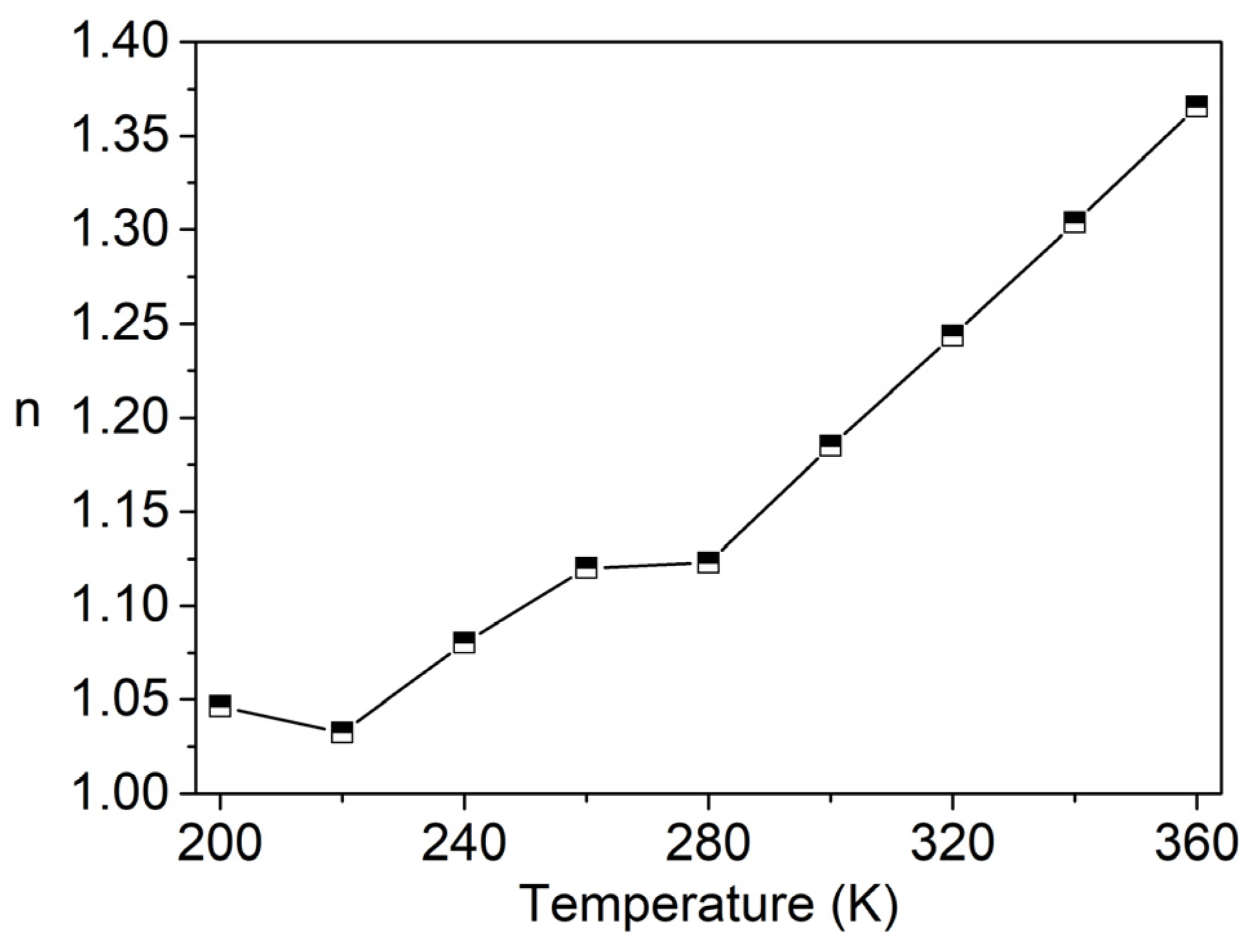
3.4. Conductivity Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dhahri, A.; Dhahri, E.; Hlil, E.K. Electrical conductivity and dielectric behaviour of nanocrystalline La0.6Gd0.1Sr0.3Mn0.75Si0.25O3. RSC Adv. 2018, 8, 9103–9111. [Google Scholar] [CrossRef] [PubMed]
- Siqueira, K.P.F.; Moreira, R.L.; Dias, A. Synthesis and Crystal Structure of Lanthanide Orthoniobates Studied by Vibrational Spectroscopy. Chem. Mater. 2010, 22, 2668–2674. [Google Scholar] [CrossRef]
- Theissmann, R.; Ehrenberg, H.; Weitzel, H.; Fuess, H. Nanostructured cation distribution in FeNbO4: A synchrotron powder diffraction and transmission electron microscopy investigation. J. Mater. Sci. 2002, 37, 4431–4436. [Google Scholar] [CrossRef]
- Zhou, D.; Pang, L.-X.; Wang, H.; Yao, X. Phase composition and phase transformation in Bi(Sb,Nb,Ta)O4 system. Solid State Sci. 2009, 11, 1894–1897. [Google Scholar] [CrossRef]
- Hou, J.; Chen, Q.; Gao, C.; Dai, R.; Zhang, J.; Wang, Z.; Zhang, Z.; Ding, Z. Raman and luminescence studies on phase transition of EuNbO4 under high pressure. J. Rare Earths 2014, 32, 787–791. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Shugurov, S.M.; Krzhizhanovskaya, M.G.; Belyy, V.A.; Sekushin, N.A.; Makeev, B.A.; Nekipelov, S.V.; Beznosikov, D.S.; Busargina, Y.A. The effect of CuO on the microstructure, spectral characteristics, thermal and electrical properties of BiNbO4 ceramics. J. Alloys Compd. 2020, 822, 153619. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Zhang, J.-W.; He, D.-W.; Xu, C.; Hu, Q.-W.; Qi, L.; Liang, A.-K. Exploring the compression behavior of HP-BiNbO4 under high pressure. Chin. Phys. B 2017, 26, 116202. [Google Scholar] [CrossRef]
- Xu, C.; He, D.; Liu, C.; Wang, H.; Zhang, L.; Wang, P.; Yin, S. High pressure and high temperature study the phase transitions of BiNbO4. Solid State Commun. 2013, 156, 21–24. [Google Scholar] [CrossRef]
- Dunkle, S.S.; Suslick, K.S. Photodegradation of BiNbO4 Powder during Photocatalytic Reactions. J. Phys. Chem. C 2009, 113, 10341–10345. [Google Scholar] [CrossRef]
- Ayyub, P.; Multani, M.S.; Palkar, V.R.; Vijayaraghavan, R. Vibrational spectroscopic study of ferroelectric SbNbO4, antiferroelectric BiNbO4, and their solid solutions. Phys. Rev. B 1986, 34, 8137–8140. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Wang, H.; Yao, X.; Wei, X.; Xiang, F.; Pang, L. Phase transformation in BiNbO4 ceramics. Appl. Phys. Lett. 2007, 90, 172910. [Google Scholar] [CrossRef]
- Radha, R.; Muthurajan, H.; Rao, N.K.; Pradhan, S.; Gupta, U.; Jha, R.; Mirji, S.; Ravi, V. Low temperature synthesis and characterization of BiNbO4 powders. Mater. Charact. 2008, 59, 1083–1087. [Google Scholar] [CrossRef]
- Devesa, S.; Graça, M.P.; Costa, L.C. Sol-Gel Synthesis, Structural Characterization and Microwave Dielectric Properties of Bismuth Niobate Modified by Iron Inclusion. In Recent Applications in Sol-Gel Synthesis; Chandra, U., Ed.; IntechOpen: Rijeka, Croatia, 2017; p. 63. [Google Scholar]
- Sebastian, M.; Jantunen, H. Low loss dielectric materials for LTCC applications: A review. Int. Mater. Rev. 2008, 53, 57–90. [Google Scholar] [CrossRef]
- Devesa, S.; Graça MP, F.; Costa, L.C. Dielectric Properties of Bismuth Niobate Ceramics. In Bismuth—Advanced Applications and Defects Characterization; Zhou, Y., Dong, F., Jin, S., Eds.; IntechOpen: London, UK, 2018; p. 93. [Google Scholar]
- El-Mallah, H. AC Electrical Conductivity and Dielectric Properties of Perovskite (Pb,Ca)TiO3Ceramic. Acta Phys. Pol. A 2012, 122, 174–179. [Google Scholar] [CrossRef]
- Jebli, M.; Rayssi, C.; Dhahri, J.; Khirouni, K. Investigation of electrical properties and conduction mechanism using CBH model of Ba0.97La0.02Ti1−xNb4x/5O3 (x = 0.00 and 0.02) compounds. Appl. Phys. A 2020, 126, 1–16. [Google Scholar] [CrossRef]
- Akgul, U.; Ergin, Z.; Sekerci, M.; Atici, Y. AC conductivity and dielectric behavior of [Cd(phen)2(SCN)2]. Vacuum 2007, 82, 340–345. [Google Scholar] [CrossRef]
- Kahouli, A.; Sylvestre, A.; Jomni, F.; Yangui, B.; Legrand, J. Experimental and Theoretical Study of AC Electrical Conduction Mechanisms of Semicrystalline Parylene C Thin Films. J. Phys. Chem. A 2012, 116, 1051–1058. [Google Scholar] [CrossRef] [PubMed]
- Ben Taher, Y.; Moutia, N.; Oueslati, A.; Gargouri, M. Electrical properties, conduction mechanism and modulus of diphosphate compounds. RSC Adv. 2016, 6, 39750–39757. [Google Scholar] [CrossRef]
- Ncib, W.; Kharrat, A.B.J.; Saadi, M.; Khirouni, K.; Chniba-Boudjada, N.; Boujelben, W. Structural, AC conductivity, conduction mechanism and dielectric properties of La0.62Eu0.05Ba0.33Mn0.85Fe0.15O3 ceramic compound. J. Mater. Sci. Mater. Electron. 2019, 30, 18391–18404. [Google Scholar] [CrossRef]
- Devesa, S.; Graça, M.; Costa, L. Structural, morphological and dielectric properties of BiNbO4 ceramics prepared by the sol-gel method. Mater. Res. Bull. 2016, 78, 128–133. [Google Scholar] [CrossRef]
- Devesa, S.; Graça, M.; Henry, F.; Costa, L. Dielectric properties of FeNbO4 ceramics prepared by the sol-gel method. Solid State Sci. 2016, 61, 44–50. [Google Scholar] [CrossRef]
- Subramanian, M.; Calabrese, J. Crystal structure of the low temperature form of bismuth niobium oxide [α-BiNbO4]. Mater. Res. Bull. 1993, 28, 523–529. [Google Scholar] [CrossRef]
- Muktha, B.; Darriet, J.; Madras, G.; Row, T.G. Crystal structures and photocatalysis of the triclinic polymorphs of BiNbO4 and BiTaO4. J. Solid State Chem. 2006, 179, 3919–3925. [Google Scholar] [CrossRef]
- Doebelin, N.; Kleeberg, R. Profex: A graphical user interface for the Rietveld refinement program BGMN. J. Appl. Crystallogr. 2015, 48, 1573–1580. [Google Scholar] [CrossRef] [PubMed]
- Toby, B.H. R factors in Rietveld analysis: How good is good enough? Powder Diffr. 2006, 21, 67–70. [Google Scholar] [CrossRef]
- Standard E112-10; Standard Test Methods for Determining Average Grain Size. ASTM International: West Conshohocken, PA, USA, 2010.
- Zhao, C.; Zhao, C.Z.; Werner, M.; Taylor, S.; Chalker, P. Dielectric relaxation of high-k oxides. Nanoscale Res. Lett. 2013, 8, 456. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.M.; Pires, G.F.M., Jr.; Terezo, A.J.; Graça, M.P.F.; Sombra, A.S.B. Impedance and modulus studies of magnetic ceramic oxide Ba2Co2Fe12O22 (Co2Y) doped with Bi2O3. J. Appl. Phys. 2011, 110, 34107. [Google Scholar] [CrossRef]
- Rouahi, A.; Kahouli, A.; Challali, F.; Besland, M.-P.; Vallée, C.; Yangui, B.; Salimy, S.; Goullet, A.; Sylvestre, A. Impedance and electric modulus study of amorphous TiTaO thin films: Highlight of the interphase effect. J. Phys. D Appl. Phys. 2013, 46, 65308. [Google Scholar] [CrossRef]
- Arya, S.K.; Danewalia, S.S.; Arora, M.; Singh, K. Effect of Variable Oxidation States of Vanadium on the Structural, Optical, and Dielectric Properties of B2O3–Li2O–ZnO–V2O5 Glasses. J. Phys. Chem. B 2016, 120, 12168–12176. [Google Scholar] [CrossRef] [PubMed]
- Badapanda, T.; Harichandan, R.K.; Nayak, S.S.; Mishra, A.; Anwar, S. Frequency and temperature dependence behaviour of impedance, modulus and conductivity of BaBi4Ti4O15 aurivillius ceramic. Process. Appl. Ceram. 2014, 8, 145–153. [Google Scholar] [CrossRef]
- Mohamed, R.I. AC conductivity and dielectric constant of poly (vinyl alcohol) doped with MnSO4. J. Phys. Chem. Solids 2000, 61, 1357. [Google Scholar] [CrossRef]
- Ncib, W.; Kharrat, A.B.J.; Wederni, M.; Chniba-Boudjada, N.; Khirouni, K.; Boujelben, W. Investigation of structural, electrical and dielectric properties of sol-gel prepared La0.67−xEuxBa0.33Mn0.85Fe0.15O3 (x = 0.0, 0.1) manganites. J. Alloys Compd. 2018, 768, 249–262. [Google Scholar] [CrossRef]
- Jellibi, A.; Chaabane, I.; Guidara, K. Experimental and theoretical study of AC electrical conduction mechanisms of Organic–inorganic hybrid compound Bis (4-acetylanilinium) tetrachlorocadmiate (II). Phys. E Low-Dimens. Syst. Nanostruct. 2016, 80, 155–162. [Google Scholar] [CrossRef]
- Khadhraoui, S.; Triki, A.; Hcini, S.; Zemni, S.; Oumezzine, M. Variable-range-hopping conduction and dielectric relaxation in Pr0.6Sr0.4Mn0.6Ti0.4O3±δ perovskite. J. Magn. Magn. Mater. 2014, 371, 69–76. [Google Scholar] [CrossRef]
- Oumezzine, E.; Hcini, S.; Rhouma, F.; Oumezzine, M. Frequency and temperature dependence of conductance, impedance and electrical modulus studies of Ni0.6Cu0.4Fe2O4 spinel ferrite. J. Alloys Compd. 2017, 726, 187–194. [Google Scholar] [CrossRef]
- Saranya, S.; Selvan, R.K.; Priyadharsini, N. Synthesis and characterization of polyaniline/MnWO4 nanocomposites as electrodes for pseudocapacitors. Appl. Surf. Sci. 2012, 258, 4881–4887. [Google Scholar] [CrossRef]
- Shanmugapriya, S.; Surendran, S.; Nithya, P. Saravanan and Selvan R K undefined Temperature dependent electrical and magnetic properties of CoWO4 nanoparticles synthesized by sonochemical method. J. Alloys Compd. 2016, 214, 57. [Google Scholar]



| Cell Lengths (Å) | Cell Angles (º) | D (nm) | R-Factor | χ2 | |
|---|---|---|---|---|---|
| α-BiNbO4 | a 5.6816 b 11.7139 c 4.9838 | __________ | 110.4 | Rwp 8.00 Rexp 2.81 | 8.11 |
| ICDD 04-010-5422 [24] | a 5.6730 b 11.7140 c 4.9780 | α 90 β 90 γ 90 | __________ | ||
| β-BiNbO4 | a 5.5412 b 7.6192 c 7.9326 | α 102.511 β 90.148 γ 92.814 | 130.6 | Rwp 5.21 Rexp 2.62 | 3.88 |
| ICDD 04-013-6357 [25] | a 5.5376 b 7.6184 c 7.9324 | α 102.565 β 90.143 γ 92.788 | __________ |
| Method | Line Number | Number of Grains Intersected | Grain Average Diameter per Line (nm) | |
|---|---|---|---|---|
| Heyn Lineal Intercept | 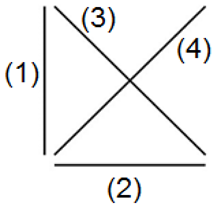 | 1 | 38 | 514 |
| 2 | 52 | 503 | ||
| 3 | 65 | 503 | ||
| 4 | 70 | 467 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devesa, S.; Graça, M.P.; Costa, L.C. Dielectric Behaviour and Electrical Conductivity of α-BiNbO4 and β-BiNbO4 Ceramics. Micro 2022, 2, 549-563. https://doi.org/10.3390/micro2040036
Devesa S, Graça MP, Costa LC. Dielectric Behaviour and Electrical Conductivity of α-BiNbO4 and β-BiNbO4 Ceramics. Micro. 2022; 2(4):549-563. https://doi.org/10.3390/micro2040036
Chicago/Turabian StyleDevesa, S., M. P. Graça, and L. C. Costa. 2022. "Dielectric Behaviour and Electrical Conductivity of α-BiNbO4 and β-BiNbO4 Ceramics" Micro 2, no. 4: 549-563. https://doi.org/10.3390/micro2040036
APA StyleDevesa, S., Graça, M. P., & Costa, L. C. (2022). Dielectric Behaviour and Electrical Conductivity of α-BiNbO4 and β-BiNbO4 Ceramics. Micro, 2(4), 549-563. https://doi.org/10.3390/micro2040036