Abstract
Clove oil is an essential oil used in food and pharmaceutical applications, with a market value of 300+ million dollars per year. Microemulsions have been used as effective clove oil delivery vehicles and could also be used to develop new extraction processes from clove buds. Eugenol, the main component of clove oil, is a polar oil that behaves as a surfactant and as an oil. This bifunctional behavior makes formulating clove oil microemulsions a challenging task. Here, we used a version of the Hydrophilic–Lipophilic Difference (HLD) + Net-Average Curvature (NAC) model that incorporates the bifunctional polar oil model to predict and fit the phase behavior of lecithin (surfactant) + polyglycerol-10 caprylate (hydrophilic linker) microemulsions using mixtures of heptane and clove oil as the oil phase. Using HLD-NAC parameters from the literature, the predicted HLD-NAC curves reproduced the expected phase transitions and the trends in Eugenol segregation toward the surfactant layer. Using these literature parameters as an initial guess to fit the experimental phase volumes produced accurate calculated phase volumes, and predicted interfacial tensions. This work demonstrates the application of heuristics and databases of HLD-NAC parameters in predicting the complex phase behavior of surfactant–oil–water (SOW) systems.
Keywords:
microemulsions; surfactants; polar oils; solubilization; interfacial tension; eugenol; essential oil; fragrance; flavor 1. Introduction
Clove oil is extracted from clove buds and is a natural source of phenolic compounds such as flavonoids, hydroxybenzoic acids, hydroxyphenyl propane, and terpenoids. Clove oil is mainly composed of eugenol (70–90%), a phenylpropanoid phytochemical and its derivatives, mainly eugenol acetate. Clove oil has many pharmacological applications, such as an anesthetic, anti-inflammatory, antioxidant, and antimicrobial agent, among others [1,2,3]. The global clove market (including clove oil) has been estimated at more than 300 million US dollars in 2025, with an annual growth of around 5% [4].
Due to the pharmacological applications of eugenol (the main component in clove oil), there has been research on the formulation of eugenol and clove oil microemulsions (μEs) to use these formulations as delivery systems in oral, buccal, parenteral, and topical delivery applications [5,6,7,8,9]. Microemulsions can also be used as extraction media for vegetable oils, where the oil solubilization capacity and interfacial tension (IFT) of the system are the parameters that control the extraction efficiency [10]. Connecting the formulation of eugenol μEs with their solubilization capacity and IFT (via HLD-NAC) is necessary for the design of the μE-based extraction processes of clove oil [11].
The formulation of μEs containing eugenol and other polar essential oils, which are often used as flavoring agents and fragrances, is a complex task due to the surfactant-like and oil-like behavior of these molecules [12]. Polar oils, in the context of HLD-guided μE formulations, have low aqueous solubility (less than 0.1 wt%), a nonzero polar surface area, a dipole moment, the ability to segregate toward the oil/water interface, and at least one polar group that can form hydrogen bonds (e.g., -OH, -COOH, etc.) [13].
The complexity in formulating polar oil μEs is reflected in the trial-and-error approach used with these microemulsions. In most cases, these formulations contain short-chain alcohols and a relatively high concentration of polyethylene glycol (PEG)-based surfactants. To prevent the potential side effects of alcohol and PEG-based formulations [14], lecithin-linker μEs (LLMs) have been introduced as alternatives that use lecithin (phosphatidyl cholines) as surfactant and glycerol esters (polyglycerol caprylate/caprate) as hydrophilic linkers (highly hydrophilic surfactants with 8 to 10 carbons in their tail) [15,16,17].
The objective of this work was to develop LLMs for an oil phase consisting of heptane and clove oil, guided by the Hydrophilic–Lipophilic Difference (HLD) + Net-Average Curvature (NAC) model. Using mixtures of heptane and clove oil helps differentiate the polar oil behavior of eugenol (from clove oil) from the non-polar oil behavior of heptane. Furthermore, the μE-based extraction of clove oil uses heptane as a cosolvent [11].
The HLD is a set of correlation equations that quantify the proximity-to-surfactant phase inversion point (PIP) in surfactant–oil–water (SOW) systems as a function of formulation variables such as electrolyte concentration (salinity S, expressed in g NaCl/100 mL of aqueous solution); temperature (T, Celsius); hydrophobicity of the oil expressed as the equivalent alkane carbon number of the oil (EACN, e.g., for n-heptane, EACN = 7); surfactant hydrophobicity expressed as the characteristic curvature (Cc, positive for more hydrophobic surfactants); and others [18,19,20]. The HLD is best interpreted in saturated conditions (when there is at least one excess phase) and at a water-to-oil volume ratio (WOR) of ~1. In such a case, at negative HLDs, the surfactant tends to form micelles in water that contain solubilized oil and an excess oil phase, producing systems known as Type I μEs; at positive HLDs, the surfactant tends to form reverse micelles in oil that contain solubilized water and an excess aqueous phase, producing systems known as Type II μEs; and at near-zero or zero HLD, the surfactant tends to form bicontinuous middle-phase μEs containing interpenetrating channels of solubilized oil and water, in the presence of excess aqueous and oil phases, producing systems known as Type III μEs. The set of HLD correlation equations for ionic and nonionic surfactants is as follows [20]:
where the terms k, b, and αT, cT are constants that depend on the surfactant head group and the electrolyte used (e.g., b = 0.13 for NaCl, k~0.16 for most surfactants). The terms f(A) and Φ(A) are empirical (often linear) equations that account for the volume fraction of a short- or medium-chain alcohol or other cosolvent in the aqueous phase.
The Net-Average Curvature (NAC) model uses a simplified definition of the radius of solubilization, Rs~3 V/As, where V is the volume of the solubilized phase and As is the interfacial area provided by the surfactant. This definition of solubilization radius does not apply to bicontinuous systems; therefore, NAC uses a mathematical approximation of two coexisting states to represent SOW systems. In one state, water is solubilized in a continuous oil phase, with a solubilization radius, Rw = 3(φw/φs)(vs/as), where φw is the volume fraction of water in the μE, φs is the volume fraction of the surfactant in the μE, and vs/as is the molecular volume to interfacial area ratio of the surfactant. In the second state, oil is solubilized in a continuous aqueous phase, with a solubilization radius, Ro = 3(φo/φs)(vs/as), where φo is the volume fraction of oil in the μE. These radii define two statistical descriptors of the interface curvature in µEs, with the net (Hn) and average (Ha) curvatures, calculated as follows [21,22]:
The term L is the length parameter, which is proportional to the extended length of the surfactant tail (L~1.4·surfactant tail length for nonionic surfactants). The term ξH is the μE “size”, interpreted as the radius of a sphere that has the same volume-to-area ratio as the μE. At HLD~0, the value of ξH reaches a maximum value “ξ”, known as the characteristic length of the microemulsion [22].
Nouraei and Acosta used the HLD–NAC framework to formulate drug delivery systems for ibuprofen, a polar oil, in lecithin-linker µEs or LLMs [16]. To account for the polar nature of ibuprofen in the HLD–NAC, the authors made the simplifying assumption that, at low concentrations, the polar oil acts only as a surfactant, neglecting the partition of ibuprofen into the bulk oil phase. While that simplification was enough to get apparent HLD parameters for ibuprofen, such an approach is insufficient to understand the partition of the polar oil in the oil, which is important when µEs are used as extraction media for polar oils (e.g., clove oil). This work adapts the lecithin–linker–ibuprofen system of Nouraei and Acosta, replacing ibuprofen with eugenol (the main component of clove oil) as the polar oil. The HLD–NAC model in this work considers the more complex case where polar oil has a significant partition in the oil phase, and the dual behavior of the polar oil (both oil-like and surfactant-like) is taken into account. This work also introduces the use of recent HLD-NAC database tables to produce full predictions of the phase behavior, which are later used as a first guess in the fitting of phase behavior studies.
2. Model Development
2.1. Algorithm
Figure 1 presents the HLD-NAC bifunctional polar oil algorithm applied to a mixture of a surfactant (surfactant 1, lecithin), a hydrophilic linker (surfactant 2, polyglycerol-10 caprylate), and a polar oil (eugenol) in the presence of a non-polar oil (heptane). This algorithm has been adapted from previous HLD-NAC bifunctional algorithms that have been introduced in the literature to consider crude oil microemulsions that contain naphthenic acids as polar oils [23,24,25].
Block B1 in Figure 1 summarizes the required inputs, including the temperature (T, Celsius), characteristic curvatures of lecithin (Cc1), hydrophilic linker polyglycerol caprylate/caprate (PG10C) (Cc2), and polar oil (eugenol) (Ccpo); the EACN of the non-polar oil (heptane) (EACNnp) and polar oil (eugenol) (EACNpo); the surfactant’s volume to interfacial area ratio for lecithin ((vs/as)1) and PG10C ((vs/as)2). The polar oil is not considered to contribute to the interfacial area (thus no vs/as) based on neutron scattering studies where the introduction of dodecanol (a polar oil) in μEs, used as a lipophilic linker, did not increase the interfacial area of the system [26]. The HLD constants b, k, and cT were considered to be similar between lecithin and PG10C; therefore, only a single set of parameters was used. If those parameters differed significantly between the two surfactants, then the appropriate mixing rules should have been used [20]. The surfactant tail length parameter L is different for lecithin and PG10C, and L for the mixed surfactant system will be first estimated using a linear mixing rule, but later, this value will be set based on previous experience with lecithin-linker μEs (LLMs) [15]. The characteristic length ξ is often used as a fitting parameter; however, in this case, an initial guess will be introduced based on the Overlap Factor Theory (OFT) [22]. Similarly, the polar oil’s Langmuir segregation constants: Km the partition constant (L/mol) and the maximum segregation ratio qmax (moles of polar oil segregated/mol of surfactants) have been previously used as fitting parameters for polar oils [23], but in this case, the initial guess for Km, and the set value for qmax will be obtained from recent heuristics [13]. The input block also considered the concentration (Cs, mol/L), molecular weight (MW, g/mol), and density (ρ, g/mL) of surfactant 1 (lecithin) and 2 (PG10C), as well as the polar oil. For the polar oil, Ci,po is its initial molar concentration in the oil phase, before it segregates between the surfactant molecules. One important assumption of the algorithm in Figure 1 is that the water-to-oil volume ratio (WOR) is one. As such, the initial aqueous concentrations of the surfactant in the aqueous phase (Cs) can be approximated as its equivalent concentration in the oil phase (this is the oil-equivalent surfactant concentration).


Figure 1.
Bifunctional HLD-NAC algorithm for surfactant mixtures with a polar oil. An open-source Excel-based implementation of the algorithm is available (https://tinyurl.com/bifunctionalHLDNAC, accessed 28 August 2025) [27].
Block B2 includes the polar oil calculations. Equation A1 is used to determine the concentration of the polar in equilibrium (Ce,po) after a portion of that polar oil segregates between the surfactant tails [23]. Equation A2 is the Langmuir equation used to determine the segregation of surfactant (q, moles of polar oil segregated per mol of surfactant mixture). Equation A3 gives the molar fraction of the polar oil segregated at the surfactant interface (xpo). Equation A4 gives the volume fraction of polar oil in the oil phase (ypo).
Block B3 focuses on calculating the HLD parameters. Equations A5 and A6 calculate the molar fractions of surfactants 1 and 2 (x1 and x2), respectively, in the surfactant interface (calculated assuming ideal solutions). Equation A7 calculates the characteristic curvature of the mixed surfactant system (Ccmix). Equation A8 calculates the mixed volume-to-area ratio ((vs/as)mix) considering the composition of the surfactant interface. Equation A9 calculates the EACN of the mixture between the polar and the non-polar oil.
Block B4 calculates the NAC parameters. Equation A10 calculates the HLD of the system. Equation A11 calculates the volume fraction of the surfactant (φs for surfactant 1+ surfactant 2). Equations A12 and A13 calculate the solubilization radius in the case that water (Rwcont) or in the case that oil (Rocont) is the continuous phase of the μE, respectively. Equations A12 and A13 are equal because the water-to-oil ratio (WOR) is 1 (for this algorithm), making the surfactant volume fraction in the continuous phase (φs, as if all the surfactant partitions in that phase) the same; otherwise, the expressions should account for the volume of the surfactant, and the continuous phase, Rphase,cont = 3(vs/as) × Volume of the continuous phase/volume of the surfactant. Equations A14 and A15 calculate the HLD at the μE Type I-III (HLDI-III) and Type III-II (HLDIII-II) transitions, respectively.
The dashed line box considers the paths that lead to the determination of Ro and Rw for any HLD. If the HLD from A10 is more negative than HLDI-III, then (at WOR~1) one has a Type I μE, and the HLD-NAC calculations follow block B5, where Ro is obtained from the net curvature equation, and Rw is Rwcont. If the HLD is more positive than HLDIII-II, then (at WOR~1) one has a Type II μE, and the HLD-NAC calculations follow block B6, where Ro is Rocont, and Rw is obtained from the net curvature equation. For HLD that is greater (more positive) than HLDI-III but smaller than HLDIII-II, (at WOR~1) one has a Type III (bicontinuous) μE, and the net and average curvature equations are solved simultaneously for Ro and Rw, as shown in block B7.
In any of the three scenarios described in the previous paragraph, one is left with the solubilization radii for oil (Ro) and water (Rw). These two radii are then used in block B8 to calculate the lower (LL) and upper (UL) limits (expressed as fractions of the total volume of the system) of the μE phase. These calculated limits can then be compared to the limits or boundaries obtained experimentally, and block B9 can be used to fit the necessary HLD-NAC parameters (Km, ξ).
2.2. Inputs
Table 1 summarizes the inputs of the bifunctional HLD-NAC algorithm of Figure 1. The characteristic curvature of lecithin (Cc1) reported in the HLD-NAC database [20] is +5.5; however, in our experience, surfactants obtained from natural sources have different Cc values, depending on the source and the extraction method. The lecithin used in this work is the same as that used by Doratt-Mendoza et al., who assessed the lecithin Cc using the phase scans of mixtures of lecithin and an alkyl ethoxylate reference surfactant, C9E5 [17]. Similarly, the Cc2 for polyglyceryl-10-caprylate (PG10C) is reported in the HLD-NAC database as −7.4. However, the value determined experimentally in the work of Doratt-Mendoza et al. was −5.4. Although polyglycerol esters of fatty acids are synthetic molecules obtained from renewable raw materials, their polydispersity in the degree of glycerol polymerization and the way that the glycerol polymerizes (ranging from linear to branch and dendritic structures) leads to differences in Cc between products that are nominally the same, and sometimes even batch-to-batch variations of the same product. The PG10C used in this work is not the same product as that used by Doratt-Mendoza et al., nor the same batch of the product cited in the HLD-NAC database. As a result, an average between the reported values was used.

Table 1.
Input table for the bifunctional HLD-NAC algorithm.
For eugenol, there is no Cc that has been previously determined. However, for polar oils such as hydrophobic alcohols (e.g., eugenol), there is a shortcut (heuristic) method to assess a preliminary value of Cc [13]:
For eugenol, the logarithm of the octanol–water partition coefficient (logP) is, according to the DrugBank database, logPeugenol = 2.66, and from Equation (5), Cceugenol = +3.7. For the EACN of polar oils, one can also estimate the value using a shortcut equation, suitable for hydrocarbons and oxygenated hydrocarbons [13]:
The density of eugenol, reported by the supplier of the standard, is ρeugenol = 1.06 g/mL, and introducing this density and logPeugenol = 2.66 in Equation (6), EACN = −5.0. For the EACN of n-heptane, we simply use EACNn-heptane = 7 for the number of carbons of this n-alkane.
The surfactant volume-to-area ratio (vs/as) and the tail volume-to-area ratio (vt/as) for surfactant “1” (lecithin) and surfactant “2” (PG10C) were obtained from the HLD-NAC database table [20]. The tail lengths (Lt) for surfactants “1” and “2” were also obtained from the HLD-NAC database table, and the tail length parameter (L) for a mixture of surfactants (with molar fractions x1, x2 = 1 − x1) can be estimated as follows [20,22]:
L~1.4·(x1·Lt1 + x2·Lt2)
For the initial phase behavior prediction, the length parameter (L) was estimated using Equation (7) and the composition of each tube; however, for fitting purposes, L was set to 90 Å because in mixtures of lecithin and hydrophilic linkers, such as PG10C, a synergistic effect has been observed where L achieves this unexpected high value [15,16]. A potential explanation for this high L value has been recently discussed, considering the derivation of the net curvature (Equation (3)) from the free energy form of the Kelvin equation and interpreting the HLD as the difference in chemical potential between surfactant monomers in water and in oil [22]. Based on that derivation, the L parameter is proportional to the volume of the surfactant tail. For straight single-tailed systems, this L parameter is proportional to the tail length, but for straight double-tailed surfactants, this value should be twice that of a single straight tail. For lecithin, this would mean L~72 Å, considering L~1.4·Lt. The same derivation indicates that the factor 1.4·Lt could be as large as 2.3·Lt, meaning that the maximum theoretical value of L for lecithin could be 118 Å.
The parameters b and K correspond to the typical parameters for nonionic surfactants. Lecithin, while having an amphoteric functionality, at pH ranges between 5 and 10 (pH of the systems considered was pH~6–7), has a net zero charge, and it can be treated as a nonionic surfactant [15,20].
The shortcut method for polar oils suggests that when using a nonionic surfactant, Km = 5 M−1, and that qmax ranges from 0.6 to 10, when the polar oil-to-surfactant molar ratio is low and high, respectively [13]. In this work, given the wide range of PG10C concentrations, both extremes are encountered. Between the extremes, qmax was set as the ratio of the initial (added) molar concentration of polar oil to the total molar concentration of the surfactant mixture.
The density and molecular weight of the surfactants and polar oil were obtained from the suppliers or estimated from the HLD-NAC database when not available from the supplier. All other parameters in Table 1 were obtained from the experimental conditions.
3. Materials and Methods
3.1. Materials
Table 2 lists the chemicals used to determine the HLD parameters and those used to formulate the µE formulation for clove oil extraction. All the chemicals were used without further purification.

Table 2.
List of chemicals, sources, and purity.
3.2. Methods
3.2.1. Salinity Scans to Assess Clove Oil’s Characteristic Curvature (Cc)
A simplified method of determining the Cc of a surfactant via emulsion stability was used in this work. The method was adapted from the work of Zarate et al. [28]. The method requires conducting several salinity scans (one for each test surfactant concentration) with mixtures of a reference surfactant (C9E5 in this work) and a test surfactant (clove oil, considered as a single species with the molecular weight of eugenol). Using the simplifying assumption that clove oil behaves only as a surfactant, the apparent Cc is determined by plotting the “optimal” salinity, or phase inversion salinity point (S*), vs. the molar fraction of clove oil (xclove oil) in the mixture with the reference surfactant. The salinity scans were produced with a 1:1 phase volume ratio, at 3 mL each phase, in a 2-dram vial at room temperature (23 ± 1 °C). The aqueous phase contained 7% w/v of the reference surfactant, C9E5, the specified concentration of clove oil, varying salinity (S, in g NaCl/100 mL), and cyclohexane as the oil phase. For every selected clove oil concentration, a phase inversion from Type I (o/w) to Type III (bicontinuous) to Type II (w/o) µE was observed. The optimal salinity (S*) was identified in each scan by the system, which produced a Type III µE or the middle phase, with an equal volume of aqueous and oil excess phases.
3.2.2. Hydrophilic Linker (HL, PG10C) Scans for Clove Oil Systems
Phase behavior scans of lecithin (the main surfactant), PG10C (HL), heptane, and clove oil µEs were conducted by increasing the HL concentration from one vial to the next. The HL scans consisted of a surfactant mixture of HL and 0.1, 0.2, and 0.5% w/v soybean lecithin (lec) in the presence of 0.2% w/v NaCl, both in the aqueous phase and 5% v/v technical grade clove oil in the oil phase. The HL concentration was scanned from 0 to 10% w/v in the aqueous phase. The % Le and %PG10C reported in this work represent % w/v added to the aqueous phase. The required amounts were pipetted into 10 mL flat-bottom vials with Teflon-lined screwcaps (Fisher Scientific, Newark, NJ, USA) at a 1:1 phase volume ratio (Vo/Vw = 1). The vials were then wrist-twisted at room temperature (23 ± 1 °C) for 100 s and then left at room temperature to equilibrate for at least two weeks. Note that while one week is the minimum recommended time for systems that separate quickly (visually separated phases within one week), this time can expand to two weeks (as in this work) or months for some systems, especially those with high interfacial rigidity [20].
3.2.3. High-Performance Liquid Chromatography (HPLC) Analysis
An HLPC (Waters, Mississauga, ON, Canada), equipped with a Waters 717 plus autosampler, a Waters 1525 binary HPLC pump, and a Waters 2487 absorbance detector, was used to quantify the amount of clove oil present in the excess (bulk) oil phase after equilibrium had been reached. The samples were fractionated with a Waters C18, 4 µL column (L 150 mm, ID 4.6 mm), and the absorbance was registered at a wavelength of 280 nm.
The HPLC standards were prepared by diluting a stock solution of clove oil in heptane in a series of steps. First, 100 µL of the standards and the oil samples were pipetted into a 1 mL vial and diluted with 900 µL of HPLC-grade methanol, and wrist-shaken 10 times to obtain a uniform mixture. Then, 10 µL of the standard and samples were injected into the HPLC with a run time of 6 min. The mobile phase was 100% methanol, with a flow rate of 1 mL/min. The area under the curve (AUC) was integrated and used to construct a linear calibration curve with a concentration range from 0 to 8% v/v clove oil in cyclohexane with R2 = 0.9984 and heptane with R2 = 0.9976. The peaks’ areas obtained via HPLC from salinity and HL scans were used to calculate their respective clove oil concentrations.
3.2.4. Interfacial Tension (IFT) Measurements
A spinning drop tensiometer (Grace Instrument, M6500, Houston, TX, USA) equipped with a digital camera (2.0 MP live resolution, 1/3” optical format, 16 mm focusable lens) and ToupView 3.7 image processing software was used to determine the IFT (γ, mN/m) between the aqueous and oil phase. The IFT measurements were obtained at room temperature, where a drop of the light oil phase was placed into a spinning drop capillary glass tube that was already filled with the heavy aqueous phase. The diameter of the deformed droplet was measured at three different points along the drop length using the imaging processing software. The drop diameter was used to calculate IFT via the Vonnegut equation [29].
3.2.5. Estimation of Eugenol Content in Clove Oil
The eugenol content in clove oil was estimated as the ratio of the absorbance at 280 nm of 100 ppm (10 μL of clove oil/100 mL of solution with methanol) of clove oil to the absorbance of 100 ppm of the eugenol standard (99.9% purity).
4. Results
4.1. Assessment of Eugenol Cc via the Surfactant-Only Simplifying Assumption
Figure 2 presents the optimal salinities (S*, the salinity that makes HLD = 0) against the mole fraction (x) of clove oil in mixtures with C9E5, assuming that all clove oil components (assumed to be eugenol) accumulate at the interface, behaving as a surfactant. The S* vs. x data in Figure 2 is fairly linear, which, in principle, supports the surfactant-only behavior hypothesis for eugenol and has little influence on the EACN of the oil phase [23]. For mixtures of a nonionic test and reference surfactant, the Cc of the test surfactant (eugenol in this case) is as follows [28]:
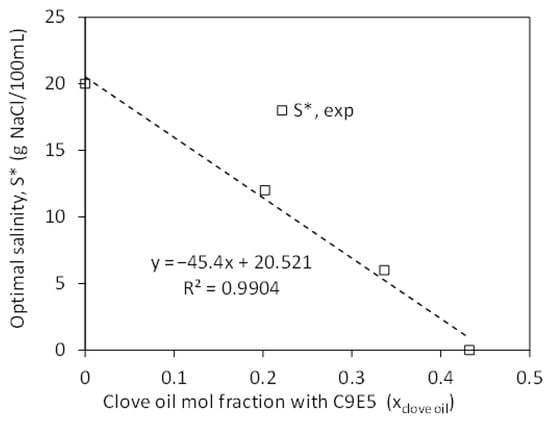
Figure 2.
Optimal salinity (S*) vs. clove oil mol fraction (xclove oil) in a mixture with 7% w/v of the nonionic reference surfactant C9E5 and cyclohexane as the oil phase. The data points correspond to 0%, 1%, 2%, and 3% v/v of clove oil added to the oil phase.
Considering the slope of the S* vs. xclove oil (dS*/dxclove oil = −45.4 ± 13.6), T~25 °C, no co-solvent (f(A) = 0), k = 0.16, b = 0.13, EACN = 3 (for cyclohexane), a Ccref for C9E5 = −2.1 (from HLD = 0 at S* and Equation (2)), and Equation (8), then one obtains Ccclove oil~+3.8 ± 1.8. This estimated value of Cc for clove oil is close to that predicted by the shortcut method (Ccclove oil~+3.7), particularly considering the uncertainty (the ± intervals reported in this work correspond to the 95% confidence interval). In the calculation, this experimentally assessed Cceugenol will be rounded to 4.
4.2. Prediction of Phase Behavior of Eugenol–Heptane μEs in LLMs (0.5% Lecithin)
Figure 3A presents the HLD-NAC-predicted phase volumes obtained with 0.5% lecithin, and PG10C concentrations ranging from 0% to 10%, using the algorithm described in Figure 1 (without the fitting feedback loop) and the inputs listed in Table 1. The length parameter (L) input was assessed considering the composition of each vial, Lt1 and Lt2 parameters in Table 1, and the linear molar mixing rule for L (Equation (7)) [30]. The characteristic length (ξ) input was assessed using the Overlap Factor Theory (OFT) [22]:

Figure 3.
Microemulsion (μE) phase volumes showing the lower (yellow) and upper (orange) limits of the μEs. (A) Eugenol concentration in the excess oil (B), and interfacial tension (IFT) (C) as a function of the concentration of the hydrophilic linker, polyglycerol-10-caprylate (PG10C), (vials 1–11 corresponding to 0–10% w/v of PG10C in the aqueous phase) for systems containing 0.5% w/v lecithin, and 5% v/v clove oil/95% v/v heptane as the oil phase. The circles represent experimental values, and the solid lines represent the predicted values obtained using the HLD-NAC algorithm from Figure 1, with parameters from Table 1 and those in the inset table in Figure 3A.
Given that we used a mixture of lecithin with (vt/as)1 = 10.4 Å, and PG10C with (vt/as)2 = 2.5 Å, one could assess the mixed tail volume to area using a linear molar mixing rule using the intermediate composition of 0.5% lecithin and 5% PG10C (vial 5 composition), where x2 = 0.896. In that case, (vt/as)mix = 0.896 × 2.5 + 0.104 × 10.4 = 3.32 Å. The term Vmoil in Equation (9) is the molecular volume of the oil. In this work, the oil was mostly heptane (~95% by volume), with a molecular weight of 100.2 g/mol and a density of 0.684 g/mL, then Vmoil = (100 g/mol)/(0.684 g/mL)·(1 E + 24 Å3/mL)/(6.022 E + 23 molecules/mol) = 243Å3. Implementing Equation (9), ξ = 1.5Å·exp(5·3.32/(243(1/3)))~21Å. This value was used to generate the fully predicted phase volumes in Figure 3A; however, the introduction of polar oils increases the characteristic length of μEs [23], suggesting that ξ > 21 Å.
The fully predicted phase volumes in Figure 3A are shown with solid lines; the single solid line represents the predicted upper limit (UL) of the μE phase, and the double line represents the lower limit (LL) of the phase. The model correctly predicts that vial 1 is a Type II (water-swollen reverse micelles in oil) μE, and that vials 10 and 11 are Type I (oil-swollen micelles in water) μEs. However, the model severely underpredicted the volume of Type III (bicontinuous middle phase systems) μEs and overpredicted the span of the Type III composition window. The underprediction of the Type III μE volume is directly related to a low predicted “ξ”, which is not surprising given that polar oils are known to increase this value, and this factor was not considered in the prediction. An over-prediction of eugenol segregated (Figure 3B, solid blue line) also meant an under-prediction of the leftover eugenol concentration in the excess of the oil phase (Cepo(eugenol), obtained from Equation A1), reflected in the experiment (red circles) vs. model (red solid line) comparison in Figure 3B. Another issue with the prediction is that the solubilization of oil in Type I μEs was under-predicted, which is related to a low tail length parameter, “L”.
While the discussion of hits and misses is useful for future predictions and the upcoming fitting exercise, the essential question is, why model in the first place? The answer can be different for different people, but in this work, this modeling effort was part of a larger project on clove oil extraction using heptane μEs that could solubilize or displace the oil from crushed clove buds. We were looking for systems in the Type I–III boundary with high solubilization capacity (high Ro) and low interfacial tension (IFT) [11]. Confident in our experience with lecithin-linker μEs (LLMs), we started hydrophilic linker (PG10C in this case) scans, similar to those in Figure 3A, but without any modeling, using our experience in formulating LLMs with ibuprofen (a polar oil) [16]. However, this approach became chaotic when it came to pinpointing a formulation that could produce the largest Ro and the lowest IFT while using the lowest possible PG10C content. At that point, HLD-NAC was implemented to guide this optimization exercise. At the time the work was completed, there were no heuristics to predict polar oil parameters (Km, qmax, EACNpo, Ccpo), and the fitting of these parameters had substantial uncertainties and biases, as the error function (equation A24 in the algorithm) could be minimized using different combinations of parameters. The full prediction, illustrated by the solid lines in Figure 3, not only provides a starting point for the formulation scans but also produces a reasonable initial guess for the fitting exercise. More importantly, it may also guide surfactant selection before a single test tube is prepared, for example, using surfactants with larger vt/as for larger characteristic length (ξ), or surfactants with longer L parameter. One aspect not covered by the HLD-NAC prediction is the potential formation of precipitates, gels, or liquid crystals, which are commonly obtained with surfactants having high vt/as and L. Nevertheless, this predictive HLD-NAC provides the formulator with a starting point for surfactant selection.
The last aspect of this predictive exercise is assessing the interfacial tension (IFT) of the formulations. The IFT is not included in the algorithm of Figure 1, but is calculated from the solubilization radius of oil (Ro) and water (Rw) obtained in the algorithm [22]:
The interfacial rigidity, Er, is another parameter that is required for IFT prediction. In systems with hydrophilic linkers, the interfacial rigidity is in the order of thermal energy, Er~1 KBT, with KB being Boltzmann’s constant, and T the absolute temperature [31]. The predicted IFT in Figure 3C was calculated using Er = 1 KBT. Types I and II μEs have only one interface, and therefore only one IFT that can be predicted by Equation (10). Type III μEs have three possible interfaces: μE (middle phase) + eO (excess oil), μE + eW (excess water), and eW + eO. For Type III μEs, Equation (10) predicts the IFT of the eW + eO interface, which is often the most relevant IFT in practical applications. The IFTmodel/IFTexp ratio ranged from 9 to 133, with an average of 36 in Figure 3C. The overestimation of IFTmodel is likely due to the underestimation of ξ and L. However, the model does predict a dip in IFT.
4.3. Fitting the Phase Behavior of Eugenol–Heptane μEs
As discussed earlier, the characteristic curvature of the polar oil (Ccpo), the partition or segregation constant (Km), the tail length parameter (L), and the characteristic length of the μE (ξ) are all parameters that have a profound impact on the μE phase behavior and could be tuned to improve the accuracy of the HLD-NAC model. Figure 4 shows this optimized HLD-NAC model, using Ccpo = +4 (rounded value from the Cc assessment in Figure 2) and L = 90 Å (this value was reported for other lecithin-linker μEs [15]) as set parameters. The only fitted parameters were Km and ξ.
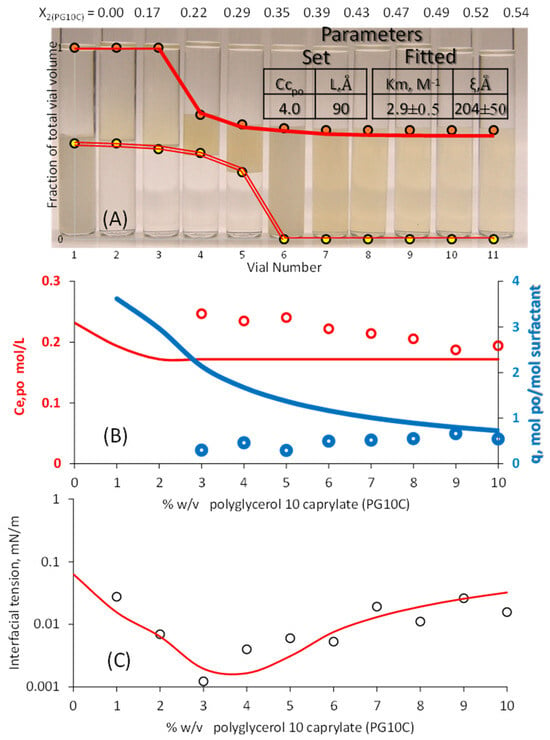
Figure 4.
μE phase volumes. (A) Eugenol concentration in the excess oil (B), and interfacial tension (IFT) (C) as a function of PG10C concentration (0.5% w/v lecithin). The solid lines in frame A represent the HLD-NAC phase volumes calculated with the algorithm of Figure 1, the parameters of Table 1, and the set and fitted parameters in the inset table in Figure 4A. The solid lines in frames (B,C) were fully predicted using the fitted parameters obtained in frame A. The ± interval reflects the 95% confidence interval.
The fitted phase volumes in Figure 4A required a lower Km (lower segregation of the polar oil toward the interface) and a higher characteristic length (a higher ξ leads to a larger middle phase volume). The slightly higher Cc (set at +4) produced an earlier transition into the middle phase, and the higher L (set at 90 Å) was able to produce a larger Type I and II μE volumes. The concentration of eugenol in excess oil after segregation (Ce,po_eugenol) in Figure 4B was fully predicted using the fitted parameters from the phase volumes in Figure 4A. This prediction was accurate with a PG10C of more than 5%. The interfacial tension (IFT) in Figure 4C was also predicted using Er = 1 KBT, yielding an IFTmodel/IFTexp ratio ranging from 0.4 to 2.1, with an average of 1.1
Figure 5 and Figure 6 present a similar fitting exercise for systems prepared with 0.2% lecithin and 0.1% lecithin, respectively. The Km values for each of these systems are similar to the value obtained with 0.5% lecithin in Figure 4 (considering the 95% confidence interval). The characteristic length (ξ), however, substantially decreases with decreasing lecithin content, which can be explained by a lower vt/as for mixtures with a lower lecithin content. For example, for 0.1% lecithin, vial 4 (3% PG10C) in Figure 6, x2 = 0.96, then vt/as = 0.96 × 2.5 + 0.04 × 10.4 = 2.8 Å, and from Equation (9), ξ = 1.5Å·exp(5·2.8/(243(1/3)))~14Å. The ratio for 0.5% lecithin, ξfitted/ξpredicted = 204/21 = 9.7, and for 0.1% lecithin, ξfitted/ξpredicted = 132/14 = 9.4, suggesting that the ratio ξfitted/ξpredicted remains approximately constant.

Figure 5.
μE phase volumes. (A) Eugenol concentration in the excess oil (B), and interfacial tension (IFT) (C) as a function of PG10C concentration (0.2% w/v lecithin). The solid lines in frame A represent the HLD-NAC phase volumes calculated using the algorithm in Figure 1, the parameters in Table 1, and the set and fitted parameters in the inset table of Figure 5A. The solid lines in frames (B,C) were fully predicted using the fitted parameters obtained in frame A. The ± interval reflects the 95% confidence interval.
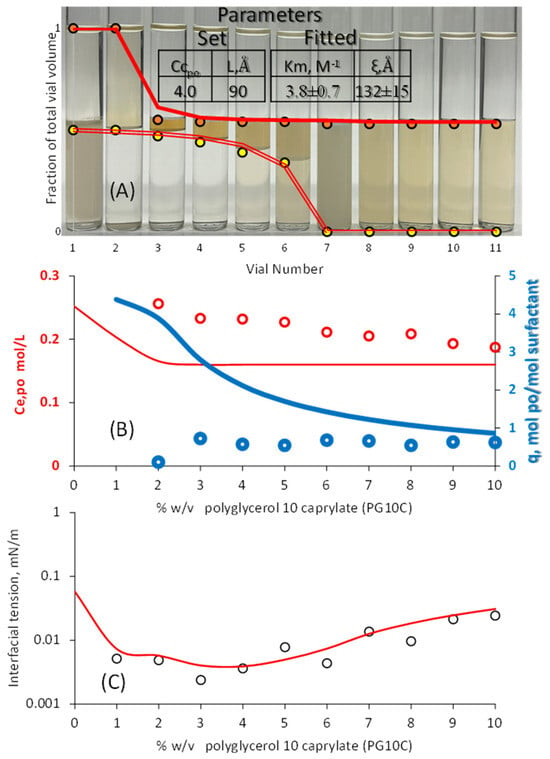
Figure 6.
μE phase volumes. (A) Eugenol concentration in the excess oil (B), and interfacial tension (IFT) (C) as a function of PG10C concentration (0.1% w/v lecithin). The solid lines in frame A represent the HLD-NAC phase volumes calculated using the algorithm in Figure 1, the parameters in Table 1, and the set and fitted parameters in the inset table of Figure 6A. The solid lines in frames (B,C) were fully predicted using the fitted parameters obtained in frame A. The ± interval reflects the 95% confidence interval.
The prediction of eugenol in excess oil after segregation (Ce,po_eugenol) in Figure 5B and Figure 6B slightly improved compared to the prediction in Figure 4B. The prediction of IFT in Figure 5C (IFTmodel/IFTexp~1.5 ± 1.3) is less accurate than that in Figure 4C (IFTmodel/IFTexp~1.1 ± 0.6) and 6C (IFTmodel/IFTexp~1.3 ± 0.4), but the largest deviations in IFT from the prediction in Figure 5C are likely due to experimental deviations. The lowest IFT obtained in Figure 6C is higher than the lowest IFT in Figure 4C, which is explained by the fact that the characteristic length (ξ) of the 0.5% lecithin μE is larger than that of the 0.1% lecithin μE.
4.4. Prediction of Characteristic Length (ξ) in Polar Oil Systems
The results and discussion above illustrate the use and utility of heuristics in predicting qmax, Km, EACNpo, and Ccpo for polar oils, while highlighting the poor accuracy of ξ prediction when neglecting the influence of polar oils. Ghayour et al. established that the addition of polar oils produced an increase in characteristic length, expressed as ξ/ξ0 (ξ0 is the characteristic length in the absence of polar oils), and produced a positive shift in HLD (HLDpo-HLDref) that seemed correlated with the changes in ξ/ξ0 [23], which could be explained by the HLD-based Overlap Factor Theory (OFT) [22]:
This form of the OFT uses a given oil (e.g., octane) with molecular volume (Vmref) and room temperature as the reference condition, and the term HLD-HLDref represents the shift from the reference condition to the actual oil and temperature at which the phase inversion point is obtained. One could extrapolate Equation (11) to conditions where the reference condition is the μE without polar oil (to produce HLDref), and the condition where polar oil is added (HLDpo). If the characteristic length in the absence of a polar oil is ξ0, then applying Equation (11), one would arrive at a new expression:
To calculate the polar oil HLD shift (HLDpo − HLDref), one calculates the HLD of a tube (containing the polar) that has a middle-phase μE, for example, vial 5 in Figure 4A. Using the open-source Excel file (https://tinyurl.com/bifunctionalHLDNAC, accessed 28 August 2025) [27] used to produce Figure 4, the HLD of vial 5 was −0.21 (cellY24 in that sheet). This is HLDpo because it was obtained considering the presence of the polar oil (Cell A24). Setting the concentration of polar oil in cell A24 to zero produced an HLD (Cell Y24) of −5.55, which is HLDref. The HLD shift was −0.21 − (−5.55) = 5.34. However, Figure 4 was already fitted, so what would the HLD shift be for vial 5 using the conditions of Figure 3 (fully predicted)? Following the same steps but using the predicted inputs for Figure 3, one obtains (HLDpo − HLDref) = 5.5, which is close enough for an initial estimation on the effect of polar oils on ξ.
The solid line in Figure 7 illustrates the OFT-predicted (Equation (12)) changes in characteristic length ratio (ξ/ξ0) as a function of the HLD shift observed with the introduction of the polar oil. The experimental data for the systems of SDHS-NA (sodium dihexyl sulfosuccinate surfactant and naphthenic acid as polar oil), C9PhE-NA (nonylphenol ethoxylate and naphthenic acid), and SDHS-C12OH (SDHS and dodecanol as polar oil) reported by Ghayour et al. [23] are consistent with the OFT prediction.
The ξ/ξ0 ratios calculated earlier for the eugenol systems (eugenol LLMs in Figure 7) are not consistent with the ratios predicted by the OFT. There are three potential explanations for this inconsistency: first, the solubilization enhancement plateaus at ξ/ξ0~10; second, the method to estimate ξ0 for surfactant mixture, through (vt/as)mix, might not be appropriate; and third, perhaps not all the hydrophilic linker (PG10C) participates in the middle-phase μE. This last possibility would produce lower HLD shifts and higher fitted ξ values, which, combined, would lead to experimental ξ/ξ0 points closer to the predicted OFT line. Previous work with hydrophilic linkers has postulated that the participation of the hydrophilic linker in the middle phase could range from 30 to 70% of the total hydrophilic linker added to the system [32]. Future efforts in this area should consider the combined hydrophilic linker and polar oil segregation in μEs.
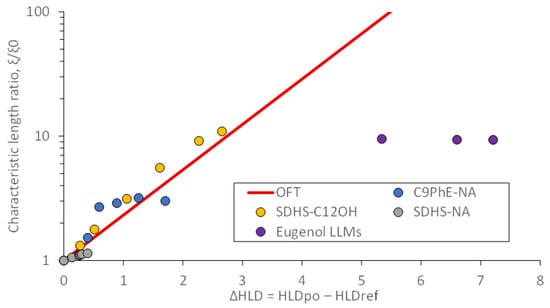

Figure 7.
Ratio of the characteristic length of systems containing polar oils to the corresponding polar oil-free microemulsions (ξ/ξ0) versus the shift in HLD produced by the introduction of the polar oil. The experimental ratios for SDHS-NA, C9PhE-NA, and SDHS-C12OH were obtained from Ghayour et al. [23]. The solid line represents the ratio predicted by the overlap factor theory (OFT) using Equation (12).
5. Conclusions
The central objective of this work was to reproduce the phase behavior of lecithin-linker microemulsions (LLMs) containing eugenol and heptane. This was accomplished in two steps. The first step used existing heuristics for eugenol (polar oil) constants (Km, qmax, Ccpo, and EACNpo) and the Overlap Factor Theory (OFT) to predict the characteristic length (ξ) of the polar oil-free μEs. This first step produced an under-estimation of the μE volumes and an over-estimation of the composition window for Type III μEs. The main factors affecting these predictions were a slight over-estimation of the partition “Km” constant, and the underprediction of the tail length parameter “L” and the characteristic length ξ for the systems with polar oil. The second step involved optimizing the values of “Km” and “ξ” to minimize the difference between the bifunctional HLD-NAC (Figure 1)-predicted phase volumes and the experimental phase volumes obtained with the systems containing eugenol. This optimization used set values of “Ccpo” and “L” obtained experimentally from phase behaviors with other surfactant–oil systems. After fitting “Km” and “ξ”, the bifunctional HLD-NAC model produced adequate predictions of residual eugenol in the bulk oil phase (Cepo) and interfacial tension (IFT) for systems containing 0.1%, 0.2%, and 0.5% w/v lecithin.
It was noted that the characteristic length (ξ) showed the largest deviation between the predicted and fitted values. Using the HLD-based OFT equation, a new expression was introduced for the prediction of ξ for polar oils using the shift in HLD introduced by the polar oil. While the expression introduced more reasonable values, it also highlighted the gap in understanding the potential role of hydrophilic linker segregation and the fact that the field is still in its early stages in terms of predicting ξ for surfactant mixtures.
The workflow introduced in this work for predicting and fitting the phase behavior of clove oil can be extrapolated to other polar oils. This workflow could facilitate the formulation of drugs, flavoring components, and fragrances, as most of these components have a polar oil structure.
Author Contributions
Conceptualization by J.-X.T. and E.A.; methodology development and implementation by J.-X.T.; Excel programming by J.-X.T. and E.A.; Validation by J.-X.T.; formal analysis by J.-X.T. and E.A.; Investigation by J.-X.T. and E.A.; Writing—original draft preparation by J.-X.T.; Writing—review and editing by E.A.; Visualization by J.-X.T. and E.A.; Supervision by E.A.; Project administration by E.A. Funding acquisition by E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a MITACS Accelerate grant, “Microemulsion technologies for the extraction and delivery of herbal oils and oleoresins”, with support from Micellae Deliver Systems, Inc. This is an invited article, with APC fees waived by the journal.
Data Availability Statement
The data for the base case scenario (0.5% lecithin and PG10C scan) and the implementation of the bifunctional HLD-NAC model are available at the following link: https://tinyurl.com/bifunctionalHLDNAC, accessed 28 August 2025.
Acknowledgments
The authors acknowledge the kind donations of surfactant samples.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Cc | Characteristic curvature |
| Ci,po | Initial concentration of the polar oil in the oil phase |
| Ce,po | Concentration, at equilibrium, of the polar oil in the oil phase after segregation |
| Cs | Surfactant concentration (assumed to be the concentration in the oil phase as if all the surfactant was introduced through the oil phase) (in mol/L or M) |
| EACN | Equivalent alkane carbon number of the oil |
| Er | Interfacial rigidity (expressed as thermal energy, KBT) |
| Ha | Average curvature |
| Hn | Net curvature |
| HLD | Hydrophilic–lipophilic difference |
| IFT | Interfacial tension |
| Km | Segregation (Partition) constant (in M−1) |
| LLM | Lecithin-linker microemulsions |
| L | Surfactant tail length parameter (1.4 times extended tail length) (in Å) |
| NAC | Net-average curvature |
| OFT | Overlap Factor Theory |
| PG10C | Propylene glycol-10 caprylate |
| q | Molar ratio of polar oil segregated/surfactant at the interface |
| qmax | Maximum molar ratio of polar oil segregated/surfactant at the interface |
| Vm | Molecular volume of the oil |
| vs/as | Volume-to-neck area ratio for one surfactant molecule |
| vt/as | Tail volume-to-neck area ratio for one surfactant molecule |
| xi | Molar fraction of surfactant “i” in the surfactant mixture |
| μE | Microemulsion |
| ξ | Characteristic length (maximum μE size) |
| ξH | μE size (=1/Ha) |
| ρ | Density (in g/mL) |
References
- Kamatou, G.P.; Vermaak, I.; Viljoen, A.M. Eugenol—From the remote Maluku Islands to the international market place: A review of a remarkable and versatile molecule. Molecules 2012, 17, 6953–6981. [Google Scholar] [CrossRef]
- Li, Y.X.; Erhunmwunsee, F.; Liu, M.; Yang, K.; Zheng, W.; Tian, J. Antimicrobial mechanisms of spice essential oils and application in food industry. Food Chem. 2022, 382, 132312. [Google Scholar] [CrossRef]
- Alma, M.H.; Ertaş, M.; Nitz, S.; Kollmannsberger, H. Chemical composition and content of essential oil from the bud of cultivated Turkish clove (Syzygium aromaticum L.). BioResources 2007, 2, 265–269. [Google Scholar] [CrossRef]
- Future Market Insights Inc. Cloves Market Analysis by Form, Application, Distribution Channel and End Use Through 2035. Reports. 2025. Available online: https://www.futuremarketinsights.com/reports/cloves-market (accessed on 23 May 2025).
- Gaysinsky, S.; Taylor, T.M.; Davidson, P.M.; Bruce, B.D.; Weiss, J. Antimicrobial efficacy of eugenol microemulsions in milk against Listeria monocytogenes and Escherichia coli O157:H7. J. Food Prot. 2007, 70, 2631–2637. [Google Scholar] [CrossRef] [PubMed]
- Al-Okbi, S.Y.; Mohamed, D.A.; Hamed, T.E.; Edris, A.E. Protective effect of clove oil and eugenol microemulsions on fatty liver and dyslipidemia as components of metabolic syndrome. J. Med. Food 2014, 17, 764–771. [Google Scholar] [CrossRef] [PubMed]
- Kheawfu, K.; Pikulkaew, S.; Rades, T.; Müllertz, A.; Okonogi, S. Development and characterization of clove oil nanoemulsions and self-microemulsifying drug delivery systems. J. Drug Deliv. Sci. Technol. 2018, 46, 330–338. [Google Scholar] [CrossRef]
- Gross, I.P.; Lima, A.L.; Sousa, E.C.; Souza, M.S.; Cunha-Filho, M.; da Silva, I.C.R.; Orsi, D.C.; Sá-Barreto, L.L. Antimicrobial and acaricide sanitizer tablets produced by wet granulation of spray-dried soap and clove oil-loaded microemulsion. PLoS ONE 2024, 19, e0313517. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Chen, D.; Gao, P.; Ding, P.; Li, K. Synthesis of ibuprofen eugenol ester and its microemulsion formulation for parenteral delivery. Chem. Pharm. Bull. 2005, 53, 1246–1250. [Google Scholar] [CrossRef]
- Acosta, E.J.; Gangopadhyay, K.; Chan, J.; Sabatini, D.A. HLD-guided design of vegetable oil extraction technology. In Surfactant Formulation Engineering Using HLD and NAC, 1st ed.; Acosta, E.J., Harwell, J.H., Sabatini, D.A., Eds.; Academic Press: Cambridge, MA, USA, 2025; pp. 151–166. [Google Scholar]
- Tan, J.X. Extraction of Clove Oil with Lecithin-Based Microemulsions Guided by the Hydrophilic-Lipophilic-Difference (HLD) and Net-Average-Curvature (NAC) Model. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2022. [Google Scholar]
- Tchakalova, V.; Testard, F.; Wong, K.; Parker, A.; Benczédi, D.; Zemb, T. Solubilization and interfacial curvature in microemulsions. I. Interfacial expansion and co-extraction of oil. Colloids Surf. A Physicochem. Eng. Asp. 2008, 331, 31–39. [Google Scholar] [CrossRef]
- Acosta, E.J.; Ghayour, A.; Boza-Troncoso, A.; Hill, R.; Harwell, J.H. Effect of oils and additives on the hydrophilic-lipophilic difference (HLD). In Surfactant Formulation Engineering Using HLD and NAC, 1st ed.; Acosta, E.J., Harwell, J.H., Sabatini, D.A., Eds.; Academic Press: Cambridge, MA, USA, 2025; pp. 49–98. ISBN 9780128214824. [Google Scholar]
- Sellaturay, P.; Nasser, S.; Islam, S.; Gurugama, P.; Ewan, P.W. Polyethylene glycol (PEG) is a cause of anaphylaxis to the Pfizer/BioNTech mRNA COVID-19 vaccine. Clin. Exp. Allergy 2021, 51, 861–863. [Google Scholar] [CrossRef]
- Nouraei, M.; Acosta, E.J. Predicting solubilisation features of ternary phase diagrams of fully dilutable lecithin linker microemulsions. J. Colloid Interface Sci. 2017, 495, 178–190. [Google Scholar] [CrossRef]
- Nouraei, M.; Collymore, C.; Diosady, L.; Acosta, E. HLD-NAC design and evaluation of a fully dilutable lecithin-linker SMEDDS for ibuprofen. Int. J. Pharm. 2021, 610, 121237. [Google Scholar] [CrossRef]
- Doratt Mendoza, J.; Ding, J.; Acosta Alvarez, M.; Acosta, E. Yeast Viability in HLD–NAC-Designed Fully Dilutable Lecithin-Linker Microemulsions. Molecules 2025, 30, 921. [Google Scholar] [CrossRef]
- Salager, J.L. Physico-Chemical Properties of Surfactant-Water-Oil Mixtures: Phase Behavior, Microemulsion Formation and Interfacial Tension. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1977. [Google Scholar]
- Salager, J.L.; Marquez, N.; Graciaa, A.; Lachaise, J. Partitioning of ethoxylated octylphenol surfactants in microemulsion-oil-water systems: Influence of temperature and relation between partitioning coefficient and physicochemical formulation. Langmuir 2000, 16, 5534–5539. [Google Scholar] [CrossRef]
- Acosta, E.; Perez-Franco, R.; Zhuotao, L.; Cordeiro, B.; Tan, J.X.; Boza-Troncoso, A.; Hammond, C.; Zarate-Muñoz, S.; Harwel, J. The hydrophobicity of surfactants and surfactant-oil-water (SOW) systems. In Surfactant Formulation Engineering Using HLD and NAC, 1st ed.; Acosta, E.J., Harwell, J.H., Sabatini, D.A., Eds.; Academic Press: Cambridge, MA, USA, 2025; pp. 1–48. [Google Scholar]
- Acosta, E.J.; Szekeres, E.; Sabatini, D.A.; Harwell, J.H. Net-average curvature model for solubilization and supersolubilization in surfactant microemulsions. Langmuir 2003, 19, 186–195. [Google Scholar] [CrossRef]
- Acosta, E.J.; Harwell, J.H. Net-Average Curvature (NAC) fundamentals. In Surfactant Formulation Engineering Using HLD and NAC, 1st ed.; Acosta, E.J., Harwell, J.H., Sabatini, D.A., Eds.; Academic Press: Cambridge, MA, USA, 2025; pp. 259–325. [Google Scholar]
- Ghayour, A.; Acosta, E. Characterizing the Oil-like and Surfactant-like Behavior of Polar Oils. Langmuir 2019, 35, 15038–15050. [Google Scholar] [CrossRef] [PubMed]
- Ghayour, A.; Perez, R.; Bhattacharya, S.; Acosta, E.J. Characterizing the Behavior of Bitumen-Water Systems with the Hydrophilic-Lipophilic Difference (HLD) framework. Energy Fuels 2022, 36, 14030–14041. [Google Scholar] [CrossRef]
- Perez-Franco, R.; Acosta, E. Zipper-Like Linker Self-Assembly to Obtain Low Interfacial Tensions with Partially Neutralized Naphthenic Acids. Energy Fuels 2024, 38, 1729–1743. [Google Scholar] [CrossRef]
- Acosta, E.J. Modeling and Formulation of Microemulsions: The Net-Average Curvature Model and the Combined Linker Effect. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2004. [Google Scholar]
- Acosta, E.J. Bifunctional HLD-NAC LLM Example. Available online: www.tinyurl.com/bifunctionalHLDNAC (accessed on 30 June 2025).
- Zarate-Muñoz, S.; Texeira De Vasconcelos, F.; Myint-Myat, K.; Minchom, J.; Acosta, E.J. A Simplified Methodology to Measure the Characteristic Curvature (Cc) of Alkyl Ethoxylate Nonionic Surfactants. J. Surfactants Deterg. 2016, 19, 249–263. [Google Scholar] [CrossRef]
- Princen, H.M.; Zia, I.Y.Z.; Mason, S.G. Measurement of interfacial tension from the shape of a rotating drop. J. Colloid Interface Sci. 1967, 23, 99–107. [Google Scholar] [CrossRef]
- Acosta, E.J.; Yuan, J.S.; Bhakta, A.S. The characteristic curvature of ionic surfactants. J. Surfactants Deterg. 2008, 11, 145–158. [Google Scholar] [CrossRef]
- Sabatini, D.A.; Acosta, E.; Harwell, J.H. Linker molecules in surfactant mixtures. Curr. Opin. Colloid Interface Sci. 2003, 8, 316–326. [Google Scholar] [CrossRef]
- Acosta, E.J.; Harwell, J.H.; Sabatini, D.A. Self-assembly in linker-modified microemulsions. J. Colloid Interface Sci. 2004, 274, 652–664. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).