Next Article in Journal / Special Issue
Quantum Chemical (QC) Calculations and Linear Solvation Energy Relationships (LSER): Hydrogen-Bonding Calculations with New QC-LSER Molecular Descriptors
Previous Article in Journal / Special Issue
Nanoheterogeneity in Protic and Aprotic Alkylimidazolium Bistriflimide Ionic Liquids
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Liquids
Volume 4
Issue 3
10.3390/liquids4030036
liquids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Intramolecular Hydrogen Bond Formation on the Abraham Model Solute Descriptors for Oxybenzone

by
Jocelyn Chen
,
Audrey Chen
,
Yixuan Yang
and
William E. Acree
*
Department of Chemistry, University of North Texas, Denton, TX 76203, USA
*
Author to whom correspondence should be addressed.
Liquids 2024, 4(3), 647-662; https://doi.org/10.3390/liquids4030036
Submission received: 27 July 2024 / Revised: 12 August 2024 / Accepted: 12 September 2024 / Published: 16 September 2024
(This article belongs to the Special Issue Recent Advances in the Behavior of Liquids in Honor of Prof. Dr. William Acree Jr.)
Browse Figures
Versions Notes

Abstract

:
Solute descriptors derived from experimental solubility data for oxybenzone dissolved in 21 different organic solvents indicate that the hydrogen atom on the hydroxyl functional group forms an intramolecular hydrogen bond with the lone electron pair on the oxygen atom of the neighboring >C=O functional group. Group contribution methods developed for estimating the Abraham model solute descriptors from the molecule’s Canonical SMILES code significantly over-estimate the Abraham model’s hydrogen bond acidity solute descriptor of oxybenzone. An informed user-modified Canonical SMILES code is proposed to identify which hydrogen atoms are involved in intramolecular H-bond formation. The identified hydrogen atom(s) can be used to define a new functional/fragment group and numerical group contribution value.

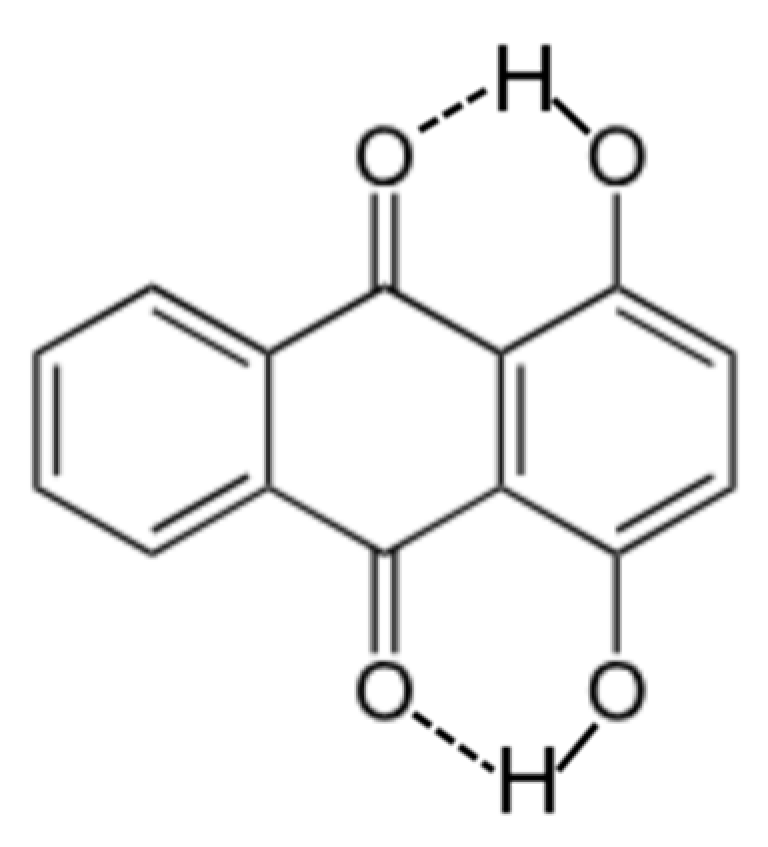
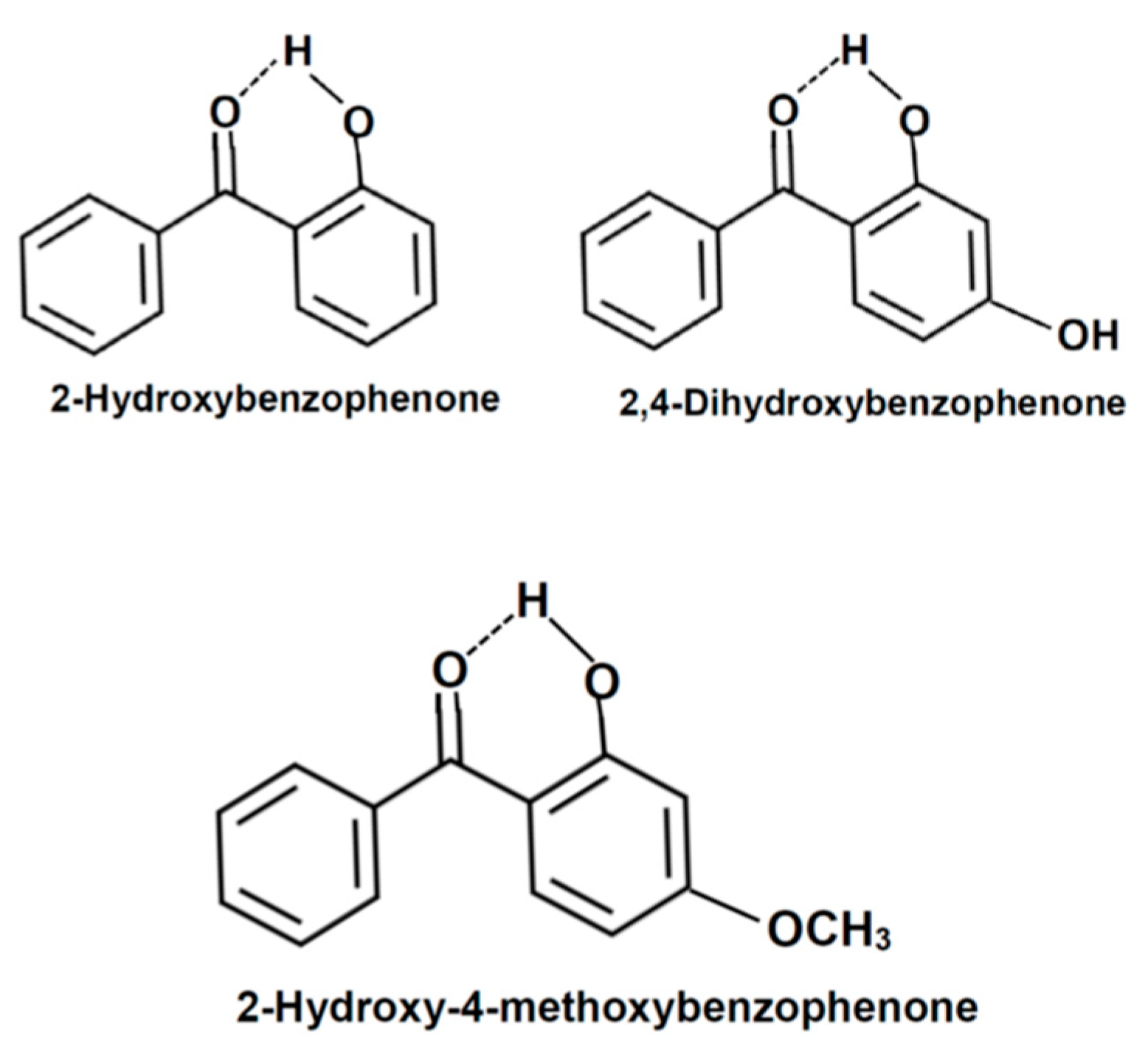
1. Introduction

The chemical manufacturing sector relies heavily on predictive methods to estimate the thermodynamic and physical properties of fluid mixtures, as experimental measurements cannot keep pace with the large number of new chemical compounds synthesized or discovered each year. Currently, experimental quantities are available for only a very small fraction of the multicomponent mixtures commonly encountered in industrial processes. Quantitative structure property/activity relationships (QSPRs/QSARs), linear free energy relationships (LFERs), and functional/fragment group contribution methods have been widely used by research scientists and design engineers to predict properties of both neat organic compounds and fluid mixtures based on the molecular structure of each individual compound or mixture component. The simpler predictive methods combine structural information, and easily measure property data to serve as required input parameters in mathematical correlations, while the more sophisticated predictive approaches utilize input parameters (such as atomic charges, atom–atom polarizabilities, molecular orbital energies, and frontier orbital densities) deduced from more theoretical quantum-mechanical computation methods. Binary interaction terms have even been incorporated in some methods to represent the various types of molecular interactions believed to be present. The introduction of machine learning and deep learning models has increased the applicability and predictive accuracy of the various estimation methods. Physical and thermodynamic properties that have been reasonably predicted by QSPR/QSAR, LFER, and group contribution approaches include vapor pressures [1,2], critical temperature [3], flash point temperatures [4,5], water-to-organic solvent partition coefficients [2,6,7,8], Gibbs energies of solvation and Ostwald solubility coefficients [9,10,11,12,13,14,15], liquid viscosities [16,17,18,19], surface tensions [20], enthalpies of combustion and enthalpies of formation [21,22,23,24], enthalpies of solvation [25,26], isobaric solid, liquid and gas molar heat capacities [27,28,29,30,31,32], enthalpies of vaporization and sublimation [33,34,35,36,37], total solid-to-liquid phase change entropies [38,39], and activity coefficients [40,41,42,43,44].
The focus of the current study is limited in scope to the group contribution and machine learning approaches that have been developed for estimating Abraham model solute descriptors based on inputting the solute molecule’s Canonical SMILES. Our recent experience has indicated that such methods often do not properly account for intramolecular hydrogen bond formation. For example, both the UFZ-LSER and MIT group contribution methods significantly overestimate the Abraham model hydrogen bond acidity solute descriptor. In the case of 1,4-dihydroxyanthraquinone (see Figure 1 for the molecular structure), the UFZ-LSER [45] and MIT [14,46] predictive software yielded values of A = 0.82 and A = 0.862, respectively. The two estimated values are significantly larger than the experiment-based value of A = 0.00 obtained by fitting the measured molar solubility of 1,4-dihydroxyanthraquinone in accordance with expressions derived from the Abraham model using measured solubility data for the organic solute dissolved in acetic acid, acetone, acetonitrile, 1-butanol and toluene [47].
In this study, we identify several molecules in our Abraham model solute descriptor database that are known to engage in intramolecular H-bond formation. We propose a relatively simple modification of the molecule’s Canonical SMILES code to indicate which -OH hydrogen atoms cannot act as H-bond donors in their interactions with surrounding solvent molecules. As part of this study, we also measured the mole fraction solubility of oxybenzone (more formally named 2-hydroxy-4-methoxybenzophenone) dissolved in hexane, heptane, octane, dodecane, cyclohexane, methylcyclohexane, 2,2,4-trimethylpentane, diisopropyl ether, propan-1-ol, butan-1-ol, pentan-1-ol, heptan-1-ol, octan-1-ol, 2-methylpropan-1-ol, butan-2-ol, 2-methylbutan-1-ol, 3-methylbutan-1-ol, 4-methylpentan-2-ol, 2-ethylhexan-1-ol, cyclopentanol, and ethylene glycol at 298.15 K. Oxybenzone was selected because we wished to report experiment-based solute descriptors for one additional organic compound that exhibits intramolecular H-bond formation. Published infrared [48,49], X-ray crystallographic [50,51], proton nuclear magnetic resonance chemical shift [48,52], and computational studies [53,54] have revealed that intramolecular H-bond formation occurs between the hydroxyl hydrogen atom in 2-hydroxybenzophenone derivatives and the lone electron pairs on the oxygen atom of the neighboring (>C=O) functional group, as depicted in Figure 2. Intramolecular H-bond formation does not prevent the second lone electron pair on the oxygen >C=O from forming an intermolecular hydrogen bond with protic solvents [55]. Several amphoteric alcohol solvents were included in the current study because of their ability to act both as a hydrogen bond donor and a hydrogen bond acceptor. Published studies [55,56,57,58] have suggested the possible formation of bifurcated three-center hydrogen bonds in several organic compounds that exhibit intramolecular H-bond formation, which is where the hydroxyl hydrogen atom is simultaneously involved in an internal H-bond as well as an external H-bond with a surrounding solvent molecule. The amphoteric nature of the alcohol solvents would allow us to explore this possibility through the magnitude of oxybenzone’s calculated A solute descriptor. A very small calculated A value near zero would suggest the negligible involvement of the hydroxyl hydrogen atom in external H-bond formation with the H-bond acceptor sites on neighboring solvent molecules considered in the current study.
We note that oxybenzone is widely used as a UV filter in a variety of personal sunscreen products to prevent sunburn, premature photoaging and skin cancer, or as a stabilizer in many commercial products (e.g., plastic surface coatings, outdoor building materials) to minimize photodegradation. It is reported that as many as 81% of the personal care products from both the U.S. and China contain oxybenzone [59,60]. The increased demand for UV filters has resulted in the substantial release of oxybenzone and other benzophenone-type filter materials into the environment, and a greater concern for the potential damage that these emerging contaminants might cause in aquatic and other living organisms [61]. To minimize adverse environmental effects, several countries now limit the amount of oxybenzone in sunscreen products [62], and Hawaii has even gone so far as to pass legislation banning the active chemical ingredients oxybenzone and octinoxate in sunscreens altogether so as to protect coral reefs from bleaching and disruptions of the ecosystem [63,64]. Laws banning the sale or use of sunscreen products containing oxybenzone have also been enacted in several Caribbean islands such as the U.S. Virgin Islands, Aruba and Bonaire [62].
The Abraham model experiment-based solute descriptors that are obtained from the solubility data measured in the current study, in combination with published Abraham model correlations, will allow researchers to evaluate potential biphasic aqueous–organic extraction systems and potential absorbent materials for the removal of oxybenzone from environmental waterways. At present, wastewater treatment facilities have problems removing UV filters [65].

2. Chemical Materials and Experimental Methodology

Oxybenzone was purchased from Sigma-Aldrich Chemical Company (Milwaukee, WI, USA, 0.98 mass fraction) in the highest purity available and was recrystallized three times from anhydrous methanol to remove any trace impurities that may have been present in the commercial sample. The recrystallized sample was further dried at 313 K for three days to remove any adsorbed methanol. Gas chromatographic analysis (thermal conductivity detector, carbowax stationary phase) indicated a purity of 0.995 mass fraction for the purified sample. The 21 different organic solvents were purchased from commercial chemical suppliers as follows: hexane (Aldrich Chemical Company, Milwaukee, WI, USA, 0.99+ mass fraction purity), heptane (Aldrich Chemical Company, anhydrous, 0.99 mass fraction), octane (Fluka Chemicals, Buchs, Switzerland, prem, 0.99+ mass fraction), dodecane (Aldrich Chemical Company, 0.99+ mass fraction), cyclohexane (Sigma-Aldrich Chemical Company, St. Louis, MO, USA, anhydrous, 0.995 mass fraction), methylcyclohexane (Aldrich Chemical Company, anhydrous, 0.99+ mass fraction), 2,2,4-trimethylpentane (Aldrich Chemical Company, anhydrous, 0.998 mass fraction), diisopropyl ether (Sigma-Aldrich Chemical Company, anhydrous, 0.99 mass fraction), propan-1-ol (Alfa Aesar, Ward Hill, MA, USA, anhydrous, 0.999 mass fraction), butan-1-ol (Aldrich Chemical Company, HPLC grade, 0.998 mass fraction), pentan-1-ol (Sigma-Aldrich Chemical Company, ACS Reagent, 0.99+ mass fraction), heptan-1-ol (Alfa Aesar, 0.99 mass fraction), octan-1-ol (Sigma-Aldrich Chemical Company, anhydrous, 0.99+ mass fraction), 2-methylpropan-1-ol (Sigma-Aldrich Chemical Company, anhydrous, 0.995 mass fraction), butan-2-ol (Aldrich Chemical Company, anhydrous, 0.995 mass fraction), 2-methylbutan-1-ol (Sigma-Aldrich Chemical Company, 0.99+ mass fraction), 3-methylbutan-1-ol (Sigma-Aldrich Chemical Company, anhydrous, 0.99+ mass fraction), 4-methylpentan-2-ol (Acros Organics, Morris Plains, NJ, USA, 0.99+ mass fraction), 2-ethylhexan-1-ol (Acros Organics, 0.99 mass fraction), cyclopentanol (Sigma-Aldrich Chemical Company, anhydrous, 0.995 mass fraction), and ethylene glycol (Aldrich Chemical Company, spectrophotometric grade, 99+%). The organic solvents were stored over activated molecular sieves, and distilled prior to use. Gas chromatographic analysis showed the solvent purities to be 0.997 mass fraction or higher.
Mole fraction solubilities were determined using a spectrophotometric method of chemical analysis by placing excess oxybenzone and 20 mL of the respective organic solvent in sealed amber glass bottles. The sealed bottles were allowed to equilibrate in a constant-temperature water bath at 298.15 K for three days with periodic shaking to facilitate dissolution. Known aliquots of the clear saturated solutions were transferred into pre-weighed volumetric flasks. The flasks containing the transferred aliquot were then re-weighed on an analytical balance in order to determine the mass of the saturated solution removed for chemical analysis. By determining the amount of transferred saturated solution in this fashion we can calculate the solubility of oxybenzone as a mass fraction, which can be accurately converted to mole fraction solubilities, XS,organic, without having to measure the density of each saturated solution. Many journals require that solubility data be reported in terms of mole fractions.
The transferred solutions were diluted quantitatively with propan-2-ol and their absorbances were recorded on a Milton Roy Spectronic 1000 Plus spectrophotometer (Milton Roy, Rochester, NY, USA) at an analysis wavelength of 284 nm. The 21 organic solvents were optically transparent at the analysis wavelength. The concentration of each diluted sample was obtained from a Beer–Lambert law graph prepared from the measured absorbances of nine standard solutions of known oxybenzone concentration. A new Beer–Lambert law graph was determined each day using nine freshly prepared standard solutions. The molar absorptivity coefficient, ε ≈ 14,000 L/(mole cm), was found to be nearly constant over the concentration range from 3.29 × 10−5 Molar to 1.10 × 10−4 Molar.
The measured absorbances of the dilute solutions prepared from saturated solutions were converted to mass fraction solubilities and then mole fraction solubilities using the molar masses of oxybenzone and the respective organic solvent, the mass of the saturated solution taken for analysis, the volume of the volumetric flasks, calculated molar absorption coefficient, and any dilutions that were required to place the measured absorbance within the linear region of the Beer–Lambert law curve. Repetitive experimental measurements were performed on select samples after an additional two days of equilibration to ensure that saturation conditions had been attained. Melting point temperatures were determined on the equilibrated solid phases recovered from each saturated solution to verify that the solid phase did not change during the course of experimental measurements. For each of the 21 oxybenzone–organic solvent combinations studied in the current communication, the melting point temperature of the equilibrated oxybenzone solid phase was within ±0.5 K of the melting point temperature of the recrystallized sample of oxybenzone prior to contact with the organic solvent. There was no evidence of solid-to-solid phase transitions or solvate formation.

3. Results and Discussion

The experimental mole fraction solubilities, XS,organic, of the oxybenzone dissolved in seven different linear, cyclic and branched alkanes, in 12 primary and secondary mono-alcohols, in ethylene glycol, and in diisopropyl ether at 298.15 K, are reported in the second and fourth columns of Table 1. Each numerical value represents the average of 6 to 10 independent measurements, including the follow-up determinations to ensure that the samples had attained equilibrium after the initial three-day equilibration time. The follow up studies confirmed that in all cases, equilibrium had been reached. The tabulated XS,organic values were reproducible to within ±2.5% (relative error). Our search of the published chemical and engineering literature unfortunately failed to find any experimental solubility data that could be used to compare our measured XS,organic values against. In fact, we found no experimental XS,organic data for oxybenzone dissolved in organic solvents. We did find a practical logarithm of a water-to-octanol partition coefficient of log P = 3.79 [66]; however, that could be used in computing oxybenzone’s Abraham model solute descriptors.
A major reason for performing experimental solubility measurements is to aid in selecting an organic mono-solvent or solvent mixture to serve as a reaction media for the synthesis of chemical compounds, for the purification of chemical products through either recrystallization or biphasic liquid–liquid extraction, or for dissolving medicinal drug compounds in controlled time-release drug formulations. The solubility data given in Table 1 provide useful oxybenzone solubility data for a very limited number of the solvents used in industrial manufacturing processes. The measurements become more useful if one discovers a way to utilize the XS,organic values given in Table 1 to predict oxybenzone solubilities in additional organic solvents. Linear free energy relationships and quantitative structure–property relationships provide a convenient means for researchers to extend their experimental studies by developing mathematical expressions to estimate additional physical and thermodynamic properties from a limited number of measured quantities. In the case of the current study, the measured XS,organic values in Table 1 can be used to calculate the Abraham model descriptor values of the dissolved oxybenzone solute molecule. The solute descriptors (E, S, A, B, V, and L) once calculated can be inserted into Equations (1) and (2) [67,68],
log P or log (CS,organic/CS,water) = cp + ep × E + sp × S + ap × A + bp × B + vp × V
log K or log (CS,organic/CS,gas) = ck + ek × E + sk × S + ak × A + bk × B + lk × L
thus allowing researchers to estimate the logarithm of the solute’s water-to-octanol partition coefficient, log P, the logarithm of the solute’s gas-to-organic solvent partition coefficient, log K, or the logarithm of the solute’s molar solubility ratios, log (CS,organic/CS,water) and log (CS,organic/CS,gas), in the more than 130 different organic solvents for which the solvent’s equation coefficients (cp, ep, sp, ap, bp, vp, ck, ek, sk, ak, bk, and lk) are known [67,68]. The phase to which each molar solute concentration refers is indicated by the subscripts “organic”, “water” and “gas”.
Each term on the right-hand side of Equations (1) and (2) represents a different type of solute–solvent interaction. The magnitude of the different molecular interactions is quantified by a solute property times the complementary solvent property. The solute descriptors are valuable regarding how the solute interacts with surrounding molecules. The solute descriptor E measures the molar refraction of the given solute in excess of that of a linear alkane with a comparable molecular size, which when multiplied by the complementary solvent property, ep and ek, describes the additional dispersion interactions possible for solute and solvent molecules with polarizable π-electrons and lone electron pairs. Intermolecular solute–solvent hydrogen-bonding interactions are quantified by the a × A + b × B terms on the right-hand side of Equations (1) and (2). In the first of the two respective terms, the oxybenzone solute molecule acts as the H-bond donor, while the solubilizing solvent medium acts as the H-bond acceptor. The roles of dissolved oxybenzone and the neighboring solvent molecules are reversed in the case of the two b × B terms.
The three remaining terms on the right-hand side of Equations (1) and (2) refer to contributions resulting from both orientation and induction dipole-type interactions (e.g., the s × S terms), and the breaking of solvent–solvent interactions needed in the creation of the solvent cavity wherein the dissolved oxybenzone solute molecule will reside (e.g., the vp × V and lk × L terms). The size of the created solvent cavity depends on the volume of the solute molecule (e.g., the McGowan V solute descriptor). The various solute descriptors and complementary solvent equation coefficients are described in greater detail in several very informative review and research articles [69,70,71,72,73].
The first step in determining oxybenzone’s solute descriptor values is to convert the measured XS,organic values to molar solubilities, CS,organic. This conversion is easily accomplished through Equation (3).
CS,organic ≈ XS,organic/[XS,organic VSolute + (1 − XS,organic) VSolvent]
The numerical values of XS,organic given in Table 1 are divided by the respective ideal molar volume of the respective saturated solution. A value of VSolute = 0.1948 L mol−1 was used for the molar volume of the hypothetical subcooled liquid hippuric acid. The mole fraction solubility of oxybenzone is sufficiently small in the studied organic solvents that any errors resulting from our estimation of oxybenzone’s hypothetical subcooled liquid molar volume, VSolute, or the ideal molar volume approximation should result in a negligible effect on each calculated CS,organic value.
The calculated molar solubilities (listed in Table 2), combined with the solvent equation coefficients (listed in Table 3), are substituted into Equations (1) and (2). They give 42 Abraham model expressions to use in our solute descriptor determination. Two additional expressions are obtained from the practical log P value contained in the published paper by Rodil and Moeder [66]. The equation coefficients that describe solute partitioning into a water-saturated octanol phase are identified by the word “wet”, which follows the name of the organic solvent. The remaining equation coefficients in Table 3 that are not identified as “wet” mean that the organic solvent does not contain enough water to significantly alter its solubilizing character. In other words, it is these equation coefficients that are used in conjunction with measured molar solubility data. The practical log P value for “wet” octan-1-ol is converted into the corresponding water-to-wet octan-1-ol partition coefficient, log K, as follows:
log K = log P + log (CS,water/CS,gas)
This uses oxybenzone’s aqueous molar solubility, CS,water, and molar gas phase concentration, CS,gas. The low solubility of 1-octanol in water allows “wet” log P values to be converted to log K in this fashion.
The Abraham model correlations that we have constructed contain the six solute descriptors (E, S, A, B, V and L) that we wish to calculate, as well as the values of CS,water and CS,gas. The latter two quantities will be floated and determined during the course of the solute description computation. Our search of the published literature did not find experimental solubility for oxybenzene in water. There are more than enough Abraham model expressions to calculate the eight desired quantities. The number of solute descriptors can be reduced to four by remembering that the values of both V and E can be obtained entirely from oxybenzone’s molecular structure. For example, the characteristic McGowan volume, V = 1.7391, is calculated from the number of chemical bonds, as well as the number and sizes of the individual hydrogen, carbon and oxygen atoms in oxybenzone [74]. An estimated value for the E solute descriptor, E = 1.500, is obtained by inputting the oxybenzone’s Canonical SMILES code, O=C(C=1C=CC=CC1)C2=CC=C(OC)C=C2O, into the estimation software program available on the UFZ-LSER website [45]. Our past experience with this software program is that this group contribution method provides a very good estimate of the E solute descriptor for organic molecules having few functional groups and relatively simple molecular structures. Estimated values of the S, A, B, and L solute descriptors for large, complex solute molecules containing multiple functional groups, however, can differ significantly from experiment-based solute descriptors deduced from measured molar solubilities and measured partition coefficients.
Preliminary regression analysis yielded a negative numerical value of A = −0.068 for oxybenzone’s overall hydrogen bond acidity solute descriptor. A negative numerical value of A was also obtained when we analyzed only the solubility in the 12 alcohol mono-solvents having a single hydroxyl functional group (A = −0.126). A negative value of the A solute descriptor is unrealistic, so we set the value to zero, and performed the regression analysis one more time to give the set of experiment-based descriptor values of E = 1.500, S = 1.413, A = 0.000, B = 0.617, V = 1.7391 and L = 8.660, as well as two logarithms of molar concentrations of oxybenzone—log CS,water = −4.558 and log CS,gas = −9.581. Only a very slight increase was noted in the overall standard deviation for the solute descriptor regression analysis, from SD = 0.094 log units to SD = 0.115 log units, by our setting A = 0.000. Small individual standard deviations of SD = 0.114 log units and SD = 0.118 log units were obtained for the 21 calculated and observed log (CS,organic/CS,water) values and the 21 calculated and observed log (CS,organic/CS,gas) values, respectively, indicating that either Abraham model could be used in predicting the molar solubilities of oxybenzene in additional organic solvents (See the last two columns of Table 2 for the back-calculated values of log CS,organiccalc based on Equations (1) and (2)).
Our private database of experiment-based Abraham model solute descriptors contains numerical values for relatively few hydroxybenzophenone derivatives: 2-hydroxybenzophenone (E = 1.54, S = 1.46, A = 0.00, B = 0.46, V = 1.5395, L = 7.7950); 4-hydroxybenzophenone (E = 1.59, S = 1.89, A = 0.81, B = 0.59, V = 1.5395, L = 8.802); and 2,4-dihydroxybenzophenone (E = 1.73, S = 2.03, A = 0.49, B = 0.70, V = 1.5982, L = 9.062). Oxybenzone and 2-hydroxybenzophenone have a single -OH functional group located in the 2-position on the aromatic phenyl ring, and the calculated A solute descriptor of both compounds is equal to zero, as would be expected for strong intramolecular H-bond formation. 4-Hydroxybenzophenone also has a single -OH function group; however, its A solute descriptor value is much larger, as the hydroxyl functional group is too far away from the carbonyl group to permit intramolecular H-bond formation. The hydrogen atom on the hydroxyl functional group on 4-hydroxybenzophenone is thus available to form intermolecular H-bonds with surrounding solvent molecules. 2,4-Dihydroxybenzophenone has two hydroxyl functional groups, one that engages in intramolecular H-bond formation (-OH group at the 2-ring position) and one that is capable of forming intermolecular hydrogen bonds (-OH group at the 4-ring position) with lone electron pairs on surrounding solvent molecules.
An Abraham model hydrogen bond acidity descriptor value of zero indicates that the hydrogen atom of the hydroxyl functional group is engaged in strong intramolecular hydrogen bond formation with one of the lone electron pairs on the oxygen atom of the >C=O. This observation would be consistent with published spectroscopic [48,49,50,51,52] and computation studies [53,54] that suggest the formation of intramolecular H-bonds in 2-hydroxybenzophenone derivatives. Moreover, a value of A = 0.000 rules out the possibility of a bifurcated H-bond between the intramolecular H-bonded hydrogen atom and a neighboring diisopropyl ether or alcohol molecule. A bifurcated H-bond should result in a small, nonzero A value.
As a reminder, one of the reasons for selecting oxybenzone was to determine if the compound engaged in intramolecular hydrogen bond formation, and to ascertain if the existing group contribution and machine learning models used for estimating the Abraham model solute descriptors would be able to recognize the possibility that the molecule could form intramolecular H-bonds. In the case of 1,4-dihydroxyanthraquinone, 1,8-dihydroxyanthraquinone, and 4,5-dihydroxyanthraquinone-2-carboxylic acids, the two-group contribution methods [45,46] significantly overestimated the A solute descriptor value [47,75]. The MIT machine learning method [46] was found to provide better estimates of the A solute descriptor value in these three compounds.
Oxybenzone has a very different molecular structure (2-hydroxybenzophenone versus hydroxyanthraquinone motif), and it will informative to compare the experiment-based solute descriptors to estimated values based on the UFZ-LSER and MIT group contribution methods, as well as the MIT and newly proposed AbraLlama machine learning models. Inputting the Canonical SMILES of oxybenzone, O=C(C=1C=CC=CC1)C2=CC=C(OC)C=C2O, into the respective computational software programs yielded the following four sets of Abraham model solute descriptor values:
  • Group contribution UFZ-LSER estimation [45]—E = 1.50, S = 1.66, A = 0.41, B = 0.71, V = 1.7391, and L = 9.214;
  • Group contribution MIT estimation [46]—E = 1.668, S = 1.898, A = 0.431, B = 0.832, V = 1.7391, and L = 9.354;
  • Machine learning MIT estimation [46]—E = 1.644, S = 1.714, A = 0.153, B = 0.697, V = 1.7391, and L = 8.915;
  • Machine learning AbraLlama estimation [76]—E = 1.467, S = 1.599, A = 0.175, B = 1.049, and V = 1.767.
Both group contribution methods significantly overestimated oxybenzone’s A solute descriptor. The two machine learning models performed much better in this regard. One must remember, however, that in comparing the different methods to estimate Abraham model solute descriptors, the goal is not simply to obtain a set of estimated values, but rather to obtain values that are of sufficient “quality” to be used in conjunction with existing Abraham model correlations to predict a solute’s physical and thermodynamic properties. To further assess the capability of the four estimation approaches for solute descriptors, we used the estimated values to predict the solubility of oxybenzone in the 21 organic solvents considered in the current study. As part of the comparison, we redetermined the numerical values of log CS,water and log CS,gas that were floated in our initial solute descriptor determination. The values of the two floated quantities need to be the ones that minimize the overall standard deviation for the predicted solute descriptors. The results of our calculations, which are summarized in Table 4, reveal that the four sets of estimated solute descriptors provide poor predictions for the solubility of oxybenzone when substituted into existing Abraham model log (CS,organic/CS,water) and log (CS,organic/CS,gas) correlations, as reflected in the much larger overall standard deviations. Slight differences between the experiment-based and estimated solute descriptor values can result in sizeable errors in the predicted physical and thermodynamic properties of the given solute molecule, particularly when the descriptor value is multiplied by a large complementary solvent equation coefficient.
The Canonical SMILES unfortunately does not incorporate all of the salient structural features that govern a molecule’s physical and thermodynamic properties. The SMILES code provides information regarding the numbers and various types of atoms, and how the individual atoms are arranged within the molecule. There are arrangements that give rise to special intramolecular interactions and to steric hinderance, which can inhibit a functional group from efficiently interacting with surrounding molecules. We believe that a better set of solute descriptors could be obtained if such information were used in the initial training of the group contribution or machine learning method. For example, if one knows from independent spectroscopic or computational studies that a specific hydroxyl hydrogen atom forms a strong intramolecular H-bond, would it not be better to reduce the contribution of this particular hydrogen atom from the overall H-bond acidity descriptor?
In the case of group contribution methods, it should be fairly easy to introduce a new functional group and associated group value to account for hydrogen atoms engaged in forming an intramolecular H-bond. The Canonical SMILES code of oxybenzone could be modified to include “hb” after the oxygen atom that is covalently bonded to the hydrogen atom involved in intramolecular hydrogen bonding. Our suggested “Informed User-Modified Canonical SMILES code” for oxybenzone would take the form of O=C(C=1C=CC=CC1)C2=CC=C(OC)C=C2Ohb. Modified SMILES codes for other select molecules and their experiment-based Abraham model solute descriptors are provided in Table 5 and Table 6, respectively. The tabulated information would provide a good starting point for anyone interested in incorporating intramolecular H-bond formation in the Abraham model solute descriptor predictions. The methodology can be extended to other structural features, such as intramolecular H-bond formation involving the hydrogen atom of a primary and/or secondary amine (Nhb) with lone electron pairs on neighboring oxygen or nitrogen atoms within the molecule [77,78]. Steric hindrance around an H-bond donor site (Osh and Nsh) could be introduced into the SMILES code as well. Each modification would permit the user of the predictive software to encode their knowledge of any special structural features that the solute molecule might possess that would affect the estimated Abraham model’s solute descriptors. We note that Gani and coworkers [79] accounted for intramolecular H-bond formation and other steric factors by introducing second-order and third-order groups into their group contribution approach. The challenge with implementing higher-order groups into existing software programs for estimating solute descriptors is that much of the computational program will need to be completely rewritten. On the other hand, our suggested approach would require the addition of only a few select functional groups and the retraining of the method with a sufficient number of compounds and their modified Canonical SMILES codes in order to obtain group values with good predictive accuracy.
Steric factors have been used in the past to explain the dissimilar solubility behaviors of 2-acetyl-1-naphthol and 1-acetyl-2-naphthol in saturated hydrocarbons versus in alcohol solvents [81,82]. The measured solubilities of 2-acetyl-1-naphthol are significantly larger in alcohol solvents than in saturated hydrocarbons. In contract, there is very little difference in the solubility of 1-acetyl-2-naphthol in these two solvent types. Both acetylnaphthols exhibit intramolecular H-bond formation, as indicated by UV-Vis absorption [83] and dielectric studies [84]. It is believed that the formation of an intermolecular solute–alcohol H-bond in the case of 1-acetyl-2-naphthol is capable of breaking the weak intramolecular H-bond [81]. Our suggested Informed User-Modified Canonical SMILES, if incorporated into group contribution methods, will enable researchers to calculate different sets of solute descriptors for 1-acetyl-2-naphthol depending upon whether they wish to include the intramolecular H-bond. In other words, one could use one set of Abraham model solute descriptors to predict the solubility of 1-acetyl-2-naphthol in saturated hydrocarbons and a second set of values to predict solubilities in alcohol solvents.

4. Summary

The Abraham general solvation parameter model has been shown to provide a reasonably accurate mathematical description of the observed solubility behavior of oxybenzone dissolved in hexane, heptane, octane, dodecane, cyclohexane, methylcyclohexane, 2,2,4-trimethylpentane, diisopropyl ether, propan-1-ol, butan-1-ol, pentan-1-ol, heptan-1-ol, octan-1-ol, 2-methylpropan-1-ol, butan-2-ol, 2-methylbutan-1-ol, 3-methylbutan-1-ol, 4-methylpentan-2-ol, 2-ethylhexan-1-ol, cyclopentanol, and ethylene glycol at 298.15 K. The solute descriptors calculated from experimental solubility data for oxybenzone dissolved in 21 different organic solvents indicate that the hydrogen atom on the hydroxyl functional group forms an intramolecular hydrogen bond with the lone electron pair on the oxygen atom of the neighboring >C=O functional group. This observation is consistent with published spectroscopic [48,49,50,51,52] and computation studies [53,54] that suggest the formation of intramolecular H-bonds in 2-hydroxybenzophenone derivatives. Moreover, the calculated value of A = 0.000 rules out the possibility that oxybenzone forms a bifurcated H-bond between the intramolecular H-bonded hydrogen atom and a neighboring diisopropyl ether or alcohol molecule. A bifurcated H-bond should result in a small, nonzero A value.
Two existing group contribution methods and two machine learning methods were used to estimate the Abraham model’s solute descriptors. Both group contribution methods were found to significantly overestimate oxybenzone’s A solute descriptor because the methods did not properly account for the formation of the intramolecular H-bond. The two machine learning models performed much better in this regard. An “Informed User-Modified Canonical SMILES code” was proposed as an input structural parameter to identify which hydrogen atoms are involved in intramolecular H-bond formation in the hopes of improving the group contribution methods that have already been developed to estimate Abraham model solute descriptors.

Author Contributions

Conceptualization and writing—original draft preparation, W.E.A.; data curation, J.C., A.C. and Y.Y.; formal analysis, J.C., A.C. and Y.Y.; writing—review and editing, J.C., A.C. and Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All experimental data are contained within the manuscript.

Acknowledgments

J.C. and A.C. thank the University of North Texas’s Texas Academy of Mathematics & Science (TAMS) program for providing a summer research scholarship to each student.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Katritzky, A.R.; Slavov, S.H.; Dobchev, D.A.; Karelson, M. Rapid QSPR model development technique for prediction of vapor pressure of organic compounds. Comp. Chem. Eng. 2007, 31, 1123–1130. [Google Scholar] [CrossRef]
  2. Zushi, Y. Direct prediction of physicochemical properties and toxicities of chemicals from analytical descriptors by GC-MS. Anal. Chem. 2022, 94, 9149–9157. [Google Scholar] [CrossRef] [PubMed]
  3. Carande, W.H.; Kazakov, A.; Muzny, C.; Frenkel, M. Quantitative structure-property relationship predictions of critical properties and acentric factors for pure compounds. J. Chem. Eng. Data 2015, 60, 1377–1387. [Google Scholar] [CrossRef]
  4. Katritzky, A.R.; Petrukhin, R.; Jain, R.; Karelson, M. QSPR analysis of flash points. J. Chem. Inf. Comp. Sci. 2001, 41, 1521–1530. [Google Scholar] [CrossRef] [PubMed]
  5. Katritzky, A.R.; Stoyanova-Slavova, I.B.; Dobchev, D.A.; Karelson, M. QSPR modeling of flash points: An update. J. Mol. Graph. Model. 2007, 26, 529–536. [Google Scholar] [CrossRef]
  6. Liu, Y.; Yu, X.; Chen, J. Quantitative structure-property relationship of distribution coefficients of organic compounds. SAR QSAR Environ. Res. 2020, 31, 585–596. [Google Scholar] [CrossRef]
  7. Fu, L.; Liu, L.; Yang, Z.-J.; Li, P.; Ding, J.-J.; Yun, Y.-H.; Lu, A.-P.; Hou, T.-J.; Cao, D.-S. Systematic modeling of log D7.4 based on ensemble machine learning, group contribution, and matched molecular pair analysis. J. Chem. Inf. Model. 2020, 60, 63–76. [Google Scholar] [CrossRef]
  8. Kang, X.; Hu, B.; Perdana, M.C.; Zhao, Y.; Chen, Z. Extreme learning machine models for predicting the n-octanol/water partition coefficient (Kow) data of organic compounds. J. Environ. Chem. Eng. 2022, 10, 108552. [Google Scholar] [CrossRef]
  9. Katritzky, A.R.; Oliferenko, A.A.; Oliferenko, P.V.; Petrukhin, R.; Tatham, D.B.; Maran, U.; Lomaka, A.; Acree, W.E., Jr. A general treatment of solubility. 2. QSPR prediction of free energies of solvation of specified solutes in ranges of solvents. J. Chem. Inf. Comp. Sci. 2003, 43, 1806–1814. [Google Scholar] [CrossRef]
  10. Katritzky, A.R.; Oliferenko, A.A.; Oliferenko, P.V.; Petrukhin, R.; Tatham, D.B.; Maran, U.; Lomaka, A.; Acree, W.E., Jr. A general treatment of solubility. 1. The QSPR correlation of solvation free energies of single solutes in series of solvents. J. Chem. Inf. Comp. Sci. 2003, 43, 1794–1805. [Google Scholar] [CrossRef]
  11. Brown, T.N. QSPRs for predicting equilibrium partitioning in solvent-air systems from the chemical structures of solutes and solvents. J. Solut. Chem. 2022, 51, 1101–1132. [Google Scholar] [CrossRef]
  12. Fu, Z.; Chen, J.; Li, X.; Wang, Y.; Yu, H. Comparison of prediction methods for octanol-air partition coefficients of diverse organic compounds. Chemosphere 2016, 148, 118–125. [Google Scholar] [CrossRef] [PubMed]
  13. Wang, Y.; Tang, W.; Xiao, Z.; Yang, W.; Peng, Y.; Chen, J.; Li, J. Novel quantitative structure activity relationship models for predicting hexadecane/air partition coefficients of organic compounds. J. Environ. Sci. 2023, 124, 98–104. [Google Scholar] [CrossRef] [PubMed]
  14. Chung, Y.; Vermeire, F.H.; Wu, H.; Walker, P.J.; Abraham, M.H.; Green, W.H. Group contribution and machine learning approaches to predict Abraham solute parameters, solvation free energy, and solvation enthalpy. J. Chem. Inf. Model. 2022, 62, 433–446. [Google Scholar] [CrossRef]
  15. Ebert, R.-U.; Kühne, R.; Schüürmann, G. Henry’s law constant—A general-purpose fragment model to predict Log Kaw from molecular structure. Environ. Sci. Technol. 2023, 57, 160–167. [Google Scholar] [CrossRef]
  16. Katritzky, A.R.; Chen, K.; Wang, Y.; Karelson, M.; Lucic, B.; Trinajstic, N.; Suzuki, T.; Schuurmann, G. Prediction of liquid viscosity for organic compounds by a quantitative structure-property relationship. J. Phys. Org. Chem. 2000, 13, 80–86. [Google Scholar] [CrossRef]
  17. Mirkhani, S.A.; Gharagheizi, F. Predictive quantitative structure-property relationship model for the estimation of ionic liquid viscosity. Ind. Eng. Chem. Res. 2012, 51, 2470–2477. [Google Scholar] [CrossRef]
  18. Paduszyński, K.; Domańska, U. Viscosity of ionic liquids: An extensive database and a new group contribution model based on a feed-forward artificial neural network. J. Chem. Inf. Model. 2014, 54, 1311–1324. [Google Scholar] [CrossRef] [PubMed]
  19. Das, S.; Ojha, P.K.; Roy, K. Development of a temperature dependent 2D-QSPR model for viscosity of diverse functional ionic liquids. J. Mol. Liq. 2017, 240, 454–467. [Google Scholar] [CrossRef]
  20. Lazzús, J.A.; Pulgar-Villarroel, G.; Cuturrufo, F.; Vega, P. Development of a group contribution method for estimating surface tension of ionic liquids over a wide range of temperatures. J. Mol. Liq. 2017, 240, 522–531. [Google Scholar] [CrossRef]
  21. Naef, R. A generally applicable computer algorithm based on the group additivity method for the calculation of seven molecular descriptors: Heat of combustion, log Po/w, log S, refractivity, polarizability, toxicity and log BB of organic compounds; scope and limits of applicability. Molecules 2015, 20, 18279–18351. [Google Scholar] [CrossRef] [PubMed]
  22. Gharagheizi, F.; Mirkhani, S.A.; Tofangchi Mahyari, A.R. Prediction of standard enthalpy of combustion of pure compounds using a very accurate group-contribution-based method. Energy Fuels 2011, 25, 2651–2654. [Google Scholar] [CrossRef]
  23. Cardozo, R.L. Prediction of the enthalpy of combustion of organic compounds. AIChE J. 1986, 32, 844–848. [Google Scholar] [CrossRef]
  24. Hukkerikar, A.S.; Meier, R.J.; Sina, G.; Gani, R. Method to estimate the enthalpy of formation of organic compounds with chemical accuracy. Fluid Phase Equilibria 2013, 348, 23–32. [Google Scholar] [CrossRef]
  25. Golmohammadi, H.; Dashtbozorgi, Z.; Gholam Samani, M.; Acree, W.E., Jr. QSPR prediction of gas-to-methanol solvation enthalpy of organic compounds using replacement method and support vector machine. Phys. Chem. Liq. 2015, 53, 46–66. [Google Scholar] [CrossRef]
  26. Toubaei, A.; Golmohammadi, H.; Dashtbozorgi, Z.; Acree, W.E., Jr. QSPR studies for predicting gas to acetone and gas to acetonitrile solvation enthalpies using support vector machine. J. Mol. Liq. 2012, 175, 24–32. [Google Scholar] [CrossRef]
  27. Khajeh, A.; Modarress, H. Quantitative structure–property relationship prediction of liquid heat capacity at 298.15 K for organic compounds. Ind. Eng. Chem. Res. 2012, 51, 6251–6255. [Google Scholar] [CrossRef]
  28. Khajeh, A.; Modarress, H. Quantitative structure-property relationship prediction of gas heat capacity for organic compounds. Ind. Eng. Chem. Res. 2012, 51, 13490–13495. [Google Scholar] [CrossRef]
  29. Naef, R. Calculation of the isobaric heat capacities of the liquid and solid phase of organic compounds at 298.15 K by means of the group-additivity method. Molecules 2020, 25, 1147. [Google Scholar] [CrossRef]
  30. Chickos, J.S.; Hesse, D.G.; Liebman, J.F. A group additivity approach for the estimation of heat capacities of organic liquids and solids at 298 K. Struct. Chem. 1993, 4, 261–269. [Google Scholar] [CrossRef]
  31. Acree, W.; Chickos, J.S. Phase transition enthalpy measurements of organic and organometallic compounds and ionic liquids. sublimation, vaporization, and fusion enthalpies from 1880 to 2015. Part 2. C11-C192. J. Phys. Chem. Ref. Data 2017, 46, 013104. [Google Scholar] [CrossRef]
  32. Kolska, Z.; Kukal, J.; Zabransky, M.; Ruazicka, V. Estimation of the heat capacity of organic liquids as a function of temperature by a three-level group contribution method. Ind. Eng. Chem. Res. 2008, 47, 2075–2085. [Google Scholar] [CrossRef]
  33. Naef, R.; Acree, W.E., Jr. Calculation of five thermodynamic molecular descriptors by means of a general computer algorithm based on the group-additivity method: Standard enthalpies of vaporization, sublimation and solvation, and entropy of fusion of ordinary organic molecules and total phase-change entropy of liquid crystals. Molecules 2017, 22, 1059. [Google Scholar] [CrossRef]
  34. Gharagheizi, F.; Ilani-Kashkouli, P.; Acree, W.E., Jr.; Mohammadi, A.H.; Ramjugernath, D. A group contribution model for determining the vaporization enthalpy of organic compounds at the standard reference temperature of 298 K. Fluid Phase Equilibria 2013, 360, 279–292. [Google Scholar] [CrossRef]
  35. Gharagheizi, F.; Ilani-Kashkouli, P.; Acree, W.E., Jr.; Mohammadi, A.H.; Ramjugernath, D. A group contribution model for determining the sublimation enthalpy of organic compounds at the standard reference temperature. Fluid Phase Equilibria 2013, 354, 265–285. [Google Scholar] [CrossRef]
  36. Dohnal, V. New QSPR molecular descriptors based on low-cost quantum chemistry computations using DFT/COSMO approach. J. Mol. Liq. 2024, 407, 125256. [Google Scholar] [CrossRef]
  37. Yan, X.; Lan, T.; Jia, Q.; Yan, F.; Wang, Q. A norm indexes-based QSPR model for predicting the standard vaporization enthalpy and formation enthalpy of organic compounds. Fluid Phase Equilibria 2020, 507, 112437. [Google Scholar] [CrossRef]
  38. Chickos, J.S.; Acree, W.E., Jr.; Liebman, J.F. Estimating solid-liquid phase change enthalpies and entropies. J. Phys. Chem. Ref. Data 1999, 28, 1535–1673. [Google Scholar] [CrossRef]
  39. Chickos, J.S.; Acree, W.E., Jr. Total phase change entropies and enthalpies. An update on fusion enthalpies and their estimation. Thermochim. Acta 2009, 495, 5–13. [Google Scholar] [CrossRef]
  40. Fredenslund, A.; Gmehling, J.; Michelsen, M.L.; Rasmussen, P.; Prausnitz, J.M. Computerized design of multicomponent distillation columns using the UNIFAC group contribution method for calculation of activity coefficients. Ind. Eng. Chem. Proc. Des. Dev. 1977, 16, 450–462. [Google Scholar] [CrossRef]
  41. Gmehling, J.; Tiegs, D.; Knipp, U. A comparison of the predictive capability of different group contribution methods. Fluid Phase Equilibria 1990, 54, 147–165. [Google Scholar] [CrossRef]
  42. Gmehling, J.; Lohmann, J.; Jakob, A.; Li, J.; Joh, R. A modified UNIFAC (Dortmund) model. 3. Revision and extension. Ind. Eng. Chem. Res. 1998, 37, 4876–4882. [Google Scholar] [CrossRef]
  43. Currier, R.P.; O’Connell, J.P. An analysis of the solution of groups method for component activity coefficients. Fluid Phase Equilibria 1987, 33, 245–265. [Google Scholar] [CrossRef]
  44. Tochigi, K.; Gmehling, J. Determination of ASOG parameters-extension and revision. J. Chem. Eng. Jpn. 2011, 44, 304–306. [Google Scholar] [CrossRef]
  45. Ulrich, N.; Endo, S.; Brown, T.N.; Watanabe, N.; Bronner, G.; Abraham, M.H.; Goss, K.-U. UFZ-LSER Database; v 3.2.1; Helmholtz Centre for Environmental Research-UFZ: Leipzig, Germany, 2017; Available online: http://www.ufz.de/lserd (accessed on 27 June 2024).
  46. Solvation Tools. Available online: https://rmg.mit.edu/database/solvation/search/ (accessed on 27 June 2024).
  47. Acree, W.E., Jr.; Smart, K.; Abraham, M.H. Abraham model solute descriptors reveal strong intramolecular hydrogen bonding in 1,4-dihydroxyanthraquinone and 1,8-dihydroxyanthraquinone. Phys. Chem. Liq. 2018, 56, 416–420. [Google Scholar] [CrossRef]
  48. Merrill, J.R. Measurements of intramolecular hydrogen bonding by nuclear magnetic resonance and infrared spectroscopy. J. Phys. Chem. 1961, 65, 2023–2026. [Google Scholar] [CrossRef]
  49. Strat, M.; Umreiko, D.S.; Khovratovich, N.N. Spectroscopic manifestation of an intramolecular hydrogen bond in 2-hydroxybenzophenone derivatives. Zhurnal Prikl. Spektrosk. 1973, 19, 103–108. [Google Scholar]
  50. Liebich, B.W.; Parthe, E. 2-Hydroxy-4-methoxybenzophenone. Acta Crystallogr. B 1974, 30B, 2522–2524. [Google Scholar] [CrossRef]
  51. Liebich, B.W. The crystal and molecular structure of 2,4-dihydroxybenzophenone (HHB). Acta Crystallogr. B 1979, B35, 1186–1190. [Google Scholar] [CrossRef]
  52. Baumstark, A.L.; Boykin, D.W. Oxygen-17 NMR spectroscopy: Multiple intramolecular hydrogen-bonded phenolic carbonyl systems. Nouv. J. Chim. 1992, 16, 357–360. [Google Scholar]
  53. Zahedi-Tabrizi, M.; Tayyari, S.F.; Badalkhani-Khamseh, F.; Ghomi, R.; Afshar-Qahremani, F. Molecular structure and intramolecular hydrogen bonding in 2-hydroxybenzophenones: A theoretical study. J. Chem. Sci. 2014, 126, 919–929. [Google Scholar] [CrossRef]
  54. Fang, Z.; Zhang, X.; Wu, F.; Huang, B.; Au, C.; Yi, B. Effect of substituent groups on the strength of intramolecular hydrogen bonds in 2,4-dihydroxybenzophenone UV absorbers. Molecules 2023, 28, 5017. [Google Scholar] [CrossRef] [PubMed]
  55. Baughman, B.M.; Stennett, E.; Lipner, R.E.; Rudawsky, A.C.; Schmidtke, S.J. Structural and spectroscopic studies of the photophysical properties of benzophenone derivatives. J. Phys. Chem. A 2009, 113, 8011–8019. [Google Scholar] [CrossRef]
  56. Litwinienko, G.; Di Labio, G.A.; Mulder, P.; Korth, H.-G.; Ingold, K.U. Intramolecular and intermolecular hydrogen bond formation by some ortho-substituted phenols: Some surprising results from an experimental and theoretical investigation. J. Phys. Chem. A 2009, 113, 6275–6288. [Google Scholar] [CrossRef]
  57. Bureiko, S.F.; Golubev, N.S.; Pihlaja, K. Spectroscopic studies of bifurcated hydrogen bonds in solution. J. Mol. Struct. 1999, 480–481, 297–301. [Google Scholar] [CrossRef]
  58. Bureiko, S.F.; Golubev, N.S.; Mattinen, J.; Pihlaja, K. On the existence of bifurcated hydrogen bond in liquids: Interaction of 2,6-disubstituted phenols with proton acceptors. J. Mol. Liq. 1990, 45, 139–145. [Google Scholar] [CrossRef]
  59. Liao, C.; Kannan, K. Widespread occurrence of benzophenone-type UV light filters in personal care products from China and the United States: An assessment of human exposure. Environ. Sci. Technol. 2014, 48, 4103–4109. [Google Scholar] [CrossRef] [PubMed]
  60. Scheele, A.; Sutter, K.; Karatum, O.; Danley-Thomson, A.A.; Redfern, L.K. Environmental impacts of the ultraviolet filter oxybenzone. Sci. Total Environ. 2023, 863, 160966. [Google Scholar] [CrossRef] [PubMed]
  61. Huang, Y.; Law, J.C.F.; Lam, T.K.; Leung, K.S.Y. Risks of organic UV filters: A review of environmental and human health concern studies. Sci. Total Environ. 2021, 755, 142486. [Google Scholar] [CrossRef]
  62. Downs, C.A.; Bishop, E.; Diaz-Cruz, M.S.; Haghshenas, S.A.; Stien, D.; Rodrigues, A.M.S.; Woodley, C.M.; Sunyer-Caldu, A.; Doust, S.N.; Espero, W.; et al. Oxybenzone contamination from sunscreen pollution and its ecological threat to Hanauma Bay, Oahu, Hawaii, U.S.A. Chemosphere 2022, 291, 132880. [Google Scholar] [CrossRef]
  63. Narla, S.; Lim, H.W. Sunscreen: FDA regulation, and environmental and health impact. Photochem. Photobiol. Sci. 2020, 19, 66–70. [Google Scholar] [CrossRef] [PubMed]
  64. Raffa, R.B.; Pergolizzi, J.V., Jr.; Taylor, R., Jr.; Kitzen, J.M. Sunscreen bans: Coral reefs and skin cancer. J. Clin. Pharm. Ther. 2019, 44, 134–139. [Google Scholar] [CrossRef] [PubMed]
  65. Schneider, S.L.; Lim, H.W. Review of environmental effects of oxybenzone and other sunscreen active ingredients. J. Am. Acad. Dermatol. 2019, 80, 266–271. [Google Scholar] [CrossRef] [PubMed]
  66. Rodil, R.; Moeder, M. Development of a method for the determination of UV filters in water samples using stir bar sorptive extraction and thermal desorption–gas chromatography–mass spectrometry. J. Chromatogr. A 2008, 1179, 81–88. [Google Scholar] [CrossRef] [PubMed]
  67. Abraham, M.H.; Smith, R.E.; Luchtefeld, R.; Boorem, A.J.; Luo, R.; Acree, W.E., Jr. Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 2010, 99, 1500–1515. [Google Scholar] [CrossRef]
  68. Acree, W.E., Jr.; Horton, M.Y.; Higgins, E.; Abraham, M.H. Abraham model linear free energy relationships as a means of extending solubility studies to include the estimation of solute solubilities in additional organic solvents. J. Chem. Thermodyn. 2016, 102, 392–397. [Google Scholar] [CrossRef]
  69. Jalan, A.; Ashcraft, R.W.; West, R.H.; Green, W.H. Predicting solvation energies for kinetic modeling. Annu. Rep. Prog. Chem Sec. C Phys. Chem. 2010, 106, 211–258. [Google Scholar] [CrossRef]
  70. Clarke, E.D. Beyond physical properties–application of Abraham descriptors and LFER analysis in agrochemical research. Bioorg. Med. Chem. 2009, 17, 4153–4159. [Google Scholar] [CrossRef]
  71. Poole, C.F.; Ariyasena, T.C.; Lenca, N. Estimation of the environmental properties of compounds from chromatographic properties and the solvation parameter method. J. Chromatogr. A 2013, 1317, 85–104. [Google Scholar] [CrossRef]
  72. Poole, C.F.; Atapattu, S.N. Recent advances for estimating environmental properties for small molecules from chromatographic measurements and the solvation parameter model. J. Chromatogr. A 2022, 1687, 463682. [Google Scholar] [CrossRef]
  73. Endo, S.; Goss, K.-U. Applications of polyparameter linear free energy relationships in environmental chemistry. Environ. Sci. Technol. 2014, 48, 12477–12491. [Google Scholar] [CrossRef] [PubMed]
  74. Abraham, M.H.; McGowan, J.C. The use of characteristic volumes to measure cavity terms in reversed phase liquid chromatography. Chromatographia 1987, 23, 243–246. [Google Scholar] [CrossRef]
  75. Sinha, S.; Yang, C.; Wu, E.; Acree, W.E., Jr. Abraham solvation parameter model: Examination of possible intramolecular hydrogen-bonding using calculated solute descriptors. Liquids 2022, 2, 131–146. [Google Scholar] [CrossRef]
  76. Lang, A.S.I.D.; Lee, Y. AbraLlama Hugging Face App: Predicting Abraham Model Solute Descriptors and Modified Solvent Parameters Using Llama. Available online: https://huggingface.co/spaces/ttmn/AbraLlama (accessed on 21 July 2024).
  77. Hansen, P.K. A Spectroscopic overview of intramolecular hydrogen bonds of NH…O,S,N type. Molecules 2021, 26, 2409. [Google Scholar] [CrossRef]
  78. Bertolasi, V.; Ferretti, V.; Gilli, P.; Gilli, G.; lssaI, Y.M.; Sherif, O.E. Intramolecular N-H O hydrogen bonding assisted by resonance. Part 2. Intercorrelation between structural and spectroscopic parameters for five 1.3-diketone arylhydrazones derived from dibenzoylmethane. J. Chem. Soc. Perkin Trans. 2 1993, 2223–2228. [Google Scholar] [CrossRef]
  79. Marrero, J.; Gani, R. Group-contribution based estimation of pure component properties. Fluid Phase Equilibria 2001, 183–184, 183–208. [Google Scholar] [CrossRef]
  80. SciFinder. Chemical Abstracts Service: Columbus, OH. Carbon-13 NMR Spectrum; Spectrum ID CC-03-C_SPC-3734; RN 50-52-2. Available online: https://scifinder.cas.org (accessed on 21 July 2024).
  81. Domanska, U. Solubility of acetyl-substituted naphthols in binary solvent mixtures. Fluid Phase Equilibria 1990, 55, 125–145. [Google Scholar] [CrossRef]
  82. Buchowski, H.; Domanska, U. Solubility and hydrogen bonding. Part VI. Evidence for intramolecular hydrogen bonds. Pol. J. Chem. 1980, 54, 97–102. [Google Scholar]
  83. Skulski, L. Studies on intramolecular hydrogen bonding by ultraviolet spectroscopy. VI. Ultraviolet absorption spectra of acetyl- and benzoyl-substituted naphthols. Bull. Acad. Polon. Sci. Ser. Sci. Chim. 1969, 17, 253–258. [Google Scholar]
  84. Skulski, L.; Waclawek, W. Studies on intramolecular hydrogen bonding by ultraviolet-visible absorption spectroscopy. VIII. Correlations between the spectral solvent effects and dioxane effect in the dipolometric measurements. Bull. Acad. Polon. Sci. Ser. Sci. Chim. 1971, 19, 277–286. [Google Scholar]
Liquids 04 00036 g001
Figure 1. Molecular structure of 1,4-dihydroxyanthraquinone showing the intramolecular hydrogen bonds (dashed lines).
Figure 1. Molecular structure of 1,4-dihydroxyanthraquinone showing the intramolecular hydrogen bonds (dashed lines).
Liquids 04 00036 g001
Liquids 04 00036 g002
Figure 2. Intramolecular hydrogen bond formation in three 2-hydroxybenzophenone compounds (e.g., 2-hydroxybenzophenone, 2,4-dihydroxybenzophenone and 2-hydroxy-4-methoxybenzophenone).
Figure 2. Intramolecular hydrogen bond formation in three 2-hydroxybenzophenone compounds (e.g., 2-hydroxybenzophenone, 2,4-dihydroxybenzophenone and 2-hydroxy-4-methoxybenzophenone).
Liquids 04 00036 g002
Table 1. Mole fraction solubilities, XS,organic, of oxybenzone dissolved in select organic solvents at a temperature of 298.15 K and ambient atmospheric pressure of 101 kPa a.
Table 1. Mole fraction solubilities, XS,organic, of oxybenzone dissolved in select organic solvents at a temperature of 298.15 K and ambient atmospheric pressure of 101 kPa a.
Organic SolventXS,organicChemical NameXS,organic
Hexane0.01298Heptan-1-ol0.03054
Heptane0.01467Octan-1-ol0.04069
Octane0.01554Butan-2-ol0.01698
Dodecane0.021012-Methylpropan-1-ol0.01161
Cyclohexane0.019942-Methylbutan-1-ol0.02262
Methylcyclohexane0.026043-Methylbutan-1-ol0.02313
2,2,4-Trimethylpentane0.012644-Methylpentan-2-ol0.02695
Diisopropyl ether0.06958Ethyl-1-hexan-1-ol0.02726
Propan-1-ol0.02016Cyclopentanol0.05380
Butan-1-ol0.01819Ethylene glycol0.000994
Pentan-1-ol0.01633
a Standard uncertainties and relative uncertainties are u(T) = 0.05 K; u(p) = 5 kPa; and ur(x) = 0.025.
Table 2. Comparison between inputted logarithms of the experimental molar solubility of oxybenzone dissolved in the 21 different organic mono-solvents, log CS,organic, and back-calculated values based for Equations (1) and (2).
Table 2. Comparison between inputted logarithms of the experimental molar solubility of oxybenzone dissolved in the 21 different organic mono-solvents, log CS,organic, and back-calculated values based for Equations (1) and (2).
SolventLog CS,organicexpLog CS,organiccalc; Equation (1) aLog CS,organiccalc; Equation (2) a
Hexane−1.008−1.102−1.077
Heptane−1.004−1.039−1.070
Octane−1.023−1.031−1.048
Dodecane−1.035−1.101−0.999
Cyclohexane−0.744−0.678−0.810
Methylcyclohexane−0.698−0.716−0.822
Isooctane−1.120−1.184−1.219
Propan-1-ol−0.585−0.659−0.700
Butan-1-ol−0.713−0.631−0.677
Pentan-1-ol−0.822−0.636−0.682
Heptan-1-ol−0.675−0.601−0.603
Octan-1-ol−0.594−0.613−0.627
2-Methylpropan-1-ol −0.908−0.703−0.732
Butan-2-ol−0.744−0.673−0.670
2-Methylbutan-1-ol−0.687−0.667−0.702
3-Methylbutan-1-ol−0.684−0.669−0.687
4-Methylpentan-2-ol−0.680−0.707−0.733
2-Ethylhexan-1-ol−0.764−0.677−0.653
Cyclopentanol−0.236−0.455−0.380
Ethylene glycol−1.751−1.554−1.581
Diisopropyl ether−0.324−0.533−0.491
a Calculated using numerical values of the solute descriptors of E = 1.500; S = 1.413; A = 0.000; B = 0.617; V = 1.7391; L = 8.660; and log CS,water = −4.558 and log CS,gas = −9.581.
Table 3. Equation coefficients for water solvent partition coefficients and air solvent partition coefficients, as log P and log K, and for molar solubility ratios, as log (CS,org/CS,water) and log (CS,org/CS,gas), at 298 K for the organic solvents considered in the current study.
Table 3. Equation coefficients for water solvent partition coefficients and air solvent partition coefficients, as log P and log K, and for molar solubility ratios, as log (CS,org/CS,water) and log (CS,org/CS,gas), at 298 K for the organic solvents considered in the current study.
Log (P or CS,org/CS,water)cpepspapbpvp
Octan-1-ol (wet)0.088 0.562 −1.054 0.034 −3.460 3.814
Hexane0.333 0.560 −1.710 −3.578 −4.939 4.463
Heptane0.297 0.634 −1.755 −3.571 −4.946 4.488
Octane0.241 0.690 −1.769 −3.545 −5.011 4.511
Dodecane0.114 0.668 −1.644 −3.545 −5.006 4.459
Cyclohexane0.159 0.784 −1.678 −3.740 −4.929 4.577
Methylcyclohexane0.246 0.782 −1.982 −3.517 −4.293 4.528
Isooctane0.318 0.555 −1.737 −3.677 −4.864 4.417
Air-to-water−0.994 0.577 2.549 3.813 4.841 −0.869
Propan-1-ol0.139 0.405 −1.029 0.247 −3.767 3.986
Butan-1-ol0.165 0.401 −1.011 0.056 −3.958 4.044
Pentan-1-ol0.150 0.536 −1.229 0.141 −3.864 4.077
Heptan-1-ol0.035 0.398 −1.063 0.002 −4.342 4.317
Octan-1-ol−0.034 0.489 −1.044 −0.024 −4.235 4.218
2-Methylpropan-1-ol 0.188 0.354 −1.127 0.016 −3.568 3.986
Butan-2-ol0.127 0.253 −0.976 0.158 −3.882 4.114
2-Methylbutan-1-ol0.1430.388−1.173−0.024−3.8174.129
3-Methylbutan-1-ol0.1110.337−1.1800.063−3.8804.218
4-Methylpentan-2-ol0.0960.301−1.1000.039−4.0814.242
2-Ethylhexan-1-ol−0.0330.566−1.233−0.068−3.9124.153
Cyclopentanol0.3320.522−1.034−0.106−3.7563.892
Ethylene glycol−0.270 0.578 −0.511 0.715 −2.619 2.729
Diisopropyl ether0.1810.285−0.954−0.956−5.0774.542
Log (K or CS,org/CS,gas)ckekskakbklk
Octan-1-ol (wet)−0.198 0.002 0.709 3.519 1.429 0.858
Hexane0.320 0.000 0.000 0.000 0.000 0.945
Heptane0.284 0.000 0.000 0.000 0.000 0.950
Octane0.219 0.000 0.000 0.000 0.000 0.960
Dodecane0.017 0.000 0.000 0.000 0.000 0.989
Cyclohexane0.163 −0.110 0.000 0.000 0.000 1.013
Methylcyclohexane0.318 −0.215 0.000 0.000 0.000 1.012
Isooctane0.264 −0.230 0.000 0.000 0.000 0.975
Air-to-water−1.271 0.822 2.743 3.904 4.814 −0.213
Propan-1-ol−0.042 −0.246 0.749 3.888 1.076 0.874
Butan-1-ol−0.004 −0.285 0.768 3.705 0.879 0.890
Pentan-1-ol−0.002 −0.161 0.535 3.778 0.960 0.900
Heptan-1-ol−0.056 −0.216 0.554 3.596 0.803 0.933
Octan-1-ol−0.147 −0.214 0.561 3.507 0.749 0.943
2-Methylpropan-1-ol−0.003 −0.357 0.699 3.595 1.247 0.881
Butan-2-ol−0.034 −0.387 0.719 3.736 1.088 0.905
2-Methylbutan-1-ol−0.055−0.3480.6013.5650.9960.925
3-Methylbutan-1-ol−0.040−0.4080.6483.5990.9050.932
4-Methylpentan-2-ol−0.013−0.6060.6873.6220.4360.985
2-Ethylhexan-1-ol−0.127−0.3390.5513.3970.7220.963
Cyclopentanol−0.151−0.3140.6933.5490.9140.956
Ethylene glycol−0.887 0.132 1.657 4.457 2.355 0.565
Diisopropyl ether0.139−0.4730.6102.5680.0001.016
Table 4. Comparison of the four different sets of estimated descriptor values used in predicting the molar solubility of oxybenzone in 21 organic mono-solvents.
Table 4. Comparison of the four different sets of estimated descriptor values used in predicting the molar solubility of oxybenzone in 21 organic mono-solvents.
Solute Descriptor Estimation MethodSD (Log Units)Log CS,waterLog CS,gas
Experiment-Based Values0.115−4.558−9.581
UFZ-LSER Group Contribution Model0.896−3.100−11.485
MIT Group Contribution Model1.025−2.642−11.551
MIT Machine Learning Model0.439−3.729−10.347
AbraLlama Machine Learning Model0.707 a−2.397 a
a Values for the AbraLlama machine learning model based only on Equation (1) because the predictive software does not calculate the Abraham model L solute descriptor.
Table 5. Solute molecules that exhibit intramolecular hydrogen bond formation and their proposed Informed User-Modified Canonical SMILES Codes.
Table 5. Solute molecules that exhibit intramolecular hydrogen bond formation and their proposed Informed User-Modified Canonical SMILES Codes.
SoluteInformed User-Modified Canonical SMILES Code a
OxybenzoneO=C(C=1C=CC=CC1)C2=CC=C(OC)C=C2Ohb
2-HydroxybenzophenoneO=C(C=1C=CC=CC1)C=2C=CC=CC2Ohb
2,4-DihydroxybenzophenoneO=C(C=1C=CC=CC1)C2=CC=C(O)C=C2Ohb
5-HydroxyflavoneO=C1C=C(OC=2C=CC=C(Ohb)C12)C=3C=CC=CC3
3,5-DihydroxyflavoneO=C1C(O)=C(OC=2C=CC=C(Ohb)C12)C=3C=CC=CC3
5,6-DihydroxyflavoneO=C1C=C(OC2=CC=C(O)C(Ohb)=C12)C=3C=CC=CC3
5,7-DihydroxyflavoneO=C1C=C(OC=2C=C(O)C=C(Ohb)C12)C=3C=CC=CC3
5,4′-DihydroxyflavoneO=C1C=C(OC=2C=CC=C(Ohb)C12)C=3C=CC(O)=CC3
5,2′-DihydroxyflavoneO=C1C=C(OC=2C=CC=C(Ohb)C12)C=3C=CC=CC3O
5,3′-DihydroxyflavoneO=C1C=C(OC=2C=CC=C(Ohb)C12)C=3C=CC=C(O)C3
5,4′-Dihydroxy-7-methoxyisoflavoneO=C1C(=COC=2C=C(OhbC)C=C(O)C12)C=3C=CC(O)=CC3
1-HydroxyanthraquinoneO=C1C=2C=CC=CC2C(=O)C=3C(Ohb)=CC=CC13
1,4-DihydroxyanthraquinoneO=C1C=2C=CC=CC2C(=O)C=3C(Ohb)=CC=C(Ohb)C13
1,8-DihydroxyanthraquinoneO=C1C=2C=CC=C(Ohb)C2C(=O)C=3C(Ohb)=CC=CC13
4,5-Dihydroxyanthraquinone-2-carboxylic acidO=C(O)C1=CC(Ohb)=C2C(=O)C=3C(Ohb)=CC=CC3C(=O)C2=C1
2′-HydroxyacetophenoneO=C(C=1C=CC=CC1Ohb)C
2-NitrophenolO=N(=O)C=1C=CC=CC1Ohb
2,4-DinitrophenolO=N(=O)C1=CC=C(Ohb)C(=C1)N(=O)=O
2,5-DinitrophenolO=N(=O)C1=CC=C(C(Ohb)=C1)N(=O)=O
2,6-DinitrophenolO=N(=O)C1=CC=CC(=C1Ohb)N(=O)=O
2-MethoxyphenolOhbC=1C=CC=CC1OC
2-Methyl-4,6-dinitrophenolO=N(=O)C=1C=C(C(Ohb)=C(C1)C)N(=O)=O
a The Informed User Canonical SMILES codes were obtained by modifying the compound’s SMILES codes taken from SciFinder Scholar [80].
Table 6. Experiment-based Abraham model solute descriptors for compounds that engage in intramolecular hydrogen bond formation.
Table 6. Experiment-based Abraham model solute descriptors for compounds that engage in intramolecular hydrogen bond formation.
SoluteESABVL
Oxybenzone1.5001.4130.0000.6171.73918.660
2-Hydroxybenzophenone1.541.460.000.461.53957.95
2,4-Dihydroxybenzophenone1.732.030.490.701.59829.062
5-Hydroxyflavone1.911.910.020.521.72849.41
5,3-Dihydroxyflavone2.092.070.370.731.787110.13
5,6-Dihydroxyflavone2.061.960.630.731.787110.08
5,7-Dihydroxyflavone2.131.980.690.731.787110.22
5,4′-Dihydroxyflavone2.141.940.710.981.787110.18
5,2′-Dihydroxyflavone2.141.900.420.841.787110.08
5,3′-Dihydroxyflavone2.141.900.670.851.787110.14
1-Hydroxyanthraquinone1.5041.4910.0500.5391.58749.075
1,4-Dihydroxyanthraquinone2.4551.7430.0000.6691.64629.919
1,8-Dihydroxyanthraquinone2.4551.7860.0000.5581.64629.907
4,5-Dihydroxyanthraquinone-2-carboxylic acid2.3402.1950.7550.5961.861511.073
2′-Hydroxyacetophenone0.9481.320.000.371.07265.341
2-Nitrophenol1.0151.050.060.350.94934.778
2,4-Dinitrophenol1.2001.570.090.541.12356.078
2,5-Dinitrophenol1.2001.460.140.511.12355.990
2,6-Dinitrophenol1.2202.110.160.451.12356.565
2-Methoxyphenol0.8370.920.160.540.97474.494
2-Methyl-4,6-dinitrophenol1.2001.590.040.521.26445.34
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, J.; Chen, A.; Yang, Y.; Acree, W.E. Effect of Intramolecular Hydrogen Bond Formation on the Abraham Model Solute Descriptors for Oxybenzone. Liquids 2024, 4, 647-662. https://doi.org/10.3390/liquids4030036

AMA Style

Chen J, Chen A, Yang Y, Acree WE. Effect of Intramolecular Hydrogen Bond Formation on the Abraham Model Solute Descriptors for Oxybenzone. Liquids. 2024; 4(3):647-662. https://doi.org/10.3390/liquids4030036

Chicago/Turabian Style

Chen, Jocelyn, Audrey Chen, Yixuan Yang, and William E. Acree. 2024. "Effect of Intramolecular Hydrogen Bond Formation on the Abraham Model Solute Descriptors for Oxybenzone" Liquids 4, no. 3: 647-662. https://doi.org/10.3390/liquids4030036

APA Style

Chen, J., Chen, A., Yang, Y., & Acree, W. E. (2024). Effect of Intramolecular Hydrogen Bond Formation on the Abraham Model Solute Descriptors for Oxybenzone. Liquids, 4(3), 647-662. https://doi.org/10.3390/liquids4030036

Article Metrics

Back to TopTop