Abstract
Many ionic liquids, including alkylimidazolium salts, form a nanoheterogeneous structure with polar and apolar domains in their liquid phase. Using molecular dynamics simulations, the influence of the structure of the cations of a series of aprotic ([CnC1Im][TFSI], [CnCnIm][TFSI]) and protic ([HCnIm][TFSI]) alkylimidazolium bistrilimides on the domain structure of their liquid phase was studied. The characteristic sizes of domains and the extent of domain segregation in different liquids have been compared. It has been shown that the latter, but not the former, is a key factor determining the magnitude of the Gibbs free energy of cavity formation in nanostructured ionic liquids, which in turn governs their solvation properties.
1. Introduction
Ionic liquids are salts that exist in a liquid state at relatively low temperatures. The vast number of potential combinations of cation and anion allows for the tailoring of ionic liquids for various tasks. Changes in the structure of the cation or anion affect the supramolecular organization of the liquid phase of these solvents. Ionic liquids containing apolar hydrocarbon chains in their cations often exhibit nanoscale segregation into polar and apolar domains [1,2,3]. Nanoheterogeneity affects various properties of ionic liquids including solvation behavior, conductivity, diffusion coefficients, viscosity, spectral properties, and so on.
Small- or wide-angle X-ray (SAXS, WAXS) or small-angle neutron (SANS) scattering methods can be used to obtain information about the nanostructure of ionic liquids [2,4,5]. Scattering data have been reported for quite a large number of ionic liquids, with a particular focus on the intensity peaks observed at values of the scattering vector modulus q below 1 Å−1. These peaks are indicative of the nanosegregated structure of ionic liquids. An increase in the first peak intensity and decrease in the value of q corresponding to its maximum is observed with increasing length of alkyl chain in cations [2,6,7,8] due to the growth of the distance between the charged groups separated by apolar domains. The introduction of polar groups, such as hydroxyls or ether moieties, into the cation results in a deterioration of hydrophobic interactions between alkyl residues, which in turn leads to a strong decrease or complete disruption of the structural heterogeneity [2,9]. These observations are consistent with other known properties of these liquids. For example, an increase in the alkyl size in alkylammonium ionic liquids leads to the growth of the solubility of hydrocarbons, which are preferentially solvated by apolar domains [10]. Conversely, the hydrocarbon solubility in 2-hydroxyethylammonium nitrate lacking domain segregation is much lower than in propyl- or ethylammonium nitrate [11].
Interesting comparisons of the structure of symmetric and asymmetric dialkylimidazolium bis(trifluoromethanesulfonyl)imides (bistriflimides) were performed by Xiao et al. [12] and Rocha et al. [6]. As follows from their scattering data, the size of the heterogeneous domains in these liquids is mainly determined by the longest alkyl chain. For example, it is similar in 1,3-dibutylimidazolium and 1-butyl-3-methylimidazolium bistriflimides but much larger in 1-methyl-3-heptylimidazolium bistriflimide. It was suggested that long alkyl chains interdigitate in apolar domains.
Another comparison that is important to understand the relationship between the nature of ions and the structure of the liquid phase is contrasting aprotic (AIL) and protic (PIL) ionic liquids. The presence of an acidic hydrogen can strengthen the interactions in polar domains between cation and anion due to the formation of hydrogen bonds, which influences the structure of the liquid phase. Martinelli et al. showed that protic 1-alkylimidazolium bistriflimides [7,13] show similar X-ray scattering patterns to the aprotic imidazolium bistriflimides [8] with the same length of an alkyl chain, namely similar peak positions but higher peak intensities in the case of PILs. This enhancement was attributed to the increase in the domain segregation in 1-alkylimidazolium PILs in comparison with 1,3-dialkylimidazolium AILs.
Computer simulations have been successfully used to study the nanoheterogeneous structure of ionic liquids. Molecular dynamics have been carried out in order to provide insights into the structure of alkylimidazolium [14,15], alkylammonium [10,16], alkylpyrrolidinium [17], and alkylphosphonium [18,19,20] ionic liquids. In addition to the scattering patterns, various computational approaches can be used to assess the spatial heterogeneity using molecular dynamics snapshots. The most common of them are calculation of radial distribution functions, cluster analysis, and Voronoi tessellation. In our recent work [16], we used Ripley’s functions, finite-volume integrals of radial distribution functions, and local atom density variance to identify the existence of a domain nanostructure in ionic liquids and characterize the domain length scale. In addition, we have shown that the Gibbs free energy of cavity formation in the liquid is sensitive to the presence of domain segregation and has much lower values in apolar than in polar domains [10,16]. This quantity is important to understand the influence of nanoheterogeneity on the solvation properties of a liquid.
In the present work, we study the structure of the liquid phase of 21 alkylimidazolium bistriflimides using molecular dynamics simulations. Three groups of bistriflimides are considered (Figure 1): aprotic symmetric ([CnCnIm][TFSI]) and asymmetric ([CnC1Im][TFSI]) 1,3-dialkylimidazolium salts, and protic 1-alkylimidazolium salts ([HCnIm][TFSI]). The characteristic size of segregated domains in the studied ionic liquids is assessed using different methods. The relationships between the nature of substituents, the presence and size of domains, and the cavity formation thermodynamics are analyzed.
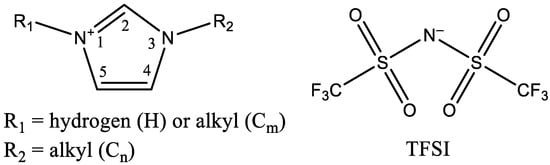
Figure 1.
Structures of cations (HCnIm and CnCmIm) and anion (TFSI) of the studied ILs.
2. Methodology
2.1. Molecular Dynamics Simulations
Molecular dynamics simulations were performed using the GROMACS 2022.5 package [21]. Topologies of cations and anions were created using the fftool program [22]. For all ions, the models developed by Canongia Lopes et al. were used [23,24,25,26]. The partial charges from these models were scaled by 0.8, which is the value used in a number of previous studies [27,28,29] in order to achieve the best agreement of simulation with the experimental properties of 1-alkyl-3-methylimidazolium salts. Charge scaling represents a computationally cheaper alternative for models with explicit atomic level polarizability which lead to more accurate results [30,31,32]. The cutoff distances for van der Waals and short-range electrostatic interactions were set to 1.2 nm. For long-range electrostatic interactions, the particle mesh Ewald method with an interpolation order of 4 and Fourier grid spacing of 0.12 nm was used. The covalent bonds with hydrogen atoms were constrained using the LINCS algorithm. The leapfrog integration algorithm with time step 1 fs was used.
Cubic simulation cells with periodic boundary conditions contained 500 pairs of cation and anion of IL. The v-rescale algorithm with a temperature coupling constant of 1 ps was used for temperature control. A constant pressure (1 bar) was maintained by the Parrinello–Rahman barostat with a pressure coupling constant of 5 ps. Before the production run, the simulation cell was energy minimized and equilibrated at 298 K. After this, five cycles of heating to high temperatures at constant volume and cooling to 298 K in NPT conditions were carried out to ensure the random configuration of ions and the absence of crystalline structures. Then, the cell was additionally equilibrated for 10 ns in NPT conditions before starting the production run. The 100 ns long production runs were recorded in NPT conditions at 298 K. The instantaneous configurations recorded every 1 ps were analyzed using programs written by authors as well as the standard GROMACS tools.
In simulations, we did not observe crystallization or the systematic drift of any properties calculated for different instantaneous configurations or blocks. The densities of ionic liquids from simulations agree well with the experimental values (Table 1).

Table 1.
Comparison of calculated and experimental values of the density (ρ) of ILs at 298 K.
2.2. Functions Characterizing Nanoheterogeneity
Various approaches can be used to analyze the structure of the liquid phase of ionic liquids. First of all, we compared the positions of peak maxima in the calculated and experimental SAXS curves. The calculation was carried out using the gmx saxs program from the GROMACS package, which uses the Cromer method [51].
The nanoheterogeneity of the liquid phase was also characterized using several functions discussed previously [16]. One of them is the finite-volume Kirkwood–Buff-like integral [16,52] of the radial distribution function for a given set of atoms with average number density ρ:
This function is calculated separately for the sets of all “polar” and “apolar” heavy atoms without distinguishing the atom or element type within the set. For a completely random (Poisson) distribution of points in space, the function equals zero at any R. The positive or negative values reflect the increased or decreased probability of finding atoms of the considered set at a given distance from another atom. Hence, clustering behavior results in positive values of at the length scales of the cluster diameter.
Another homogeneity-related function, , equals the difference in the density-normalized average number of atoms belonging to two different sets (domains), A and B, within radius R from an atom that belongs to one of these sets (A). The reference atom itself should be counted in order to expect a zero value in the case of a homogeneous spatial distribution of atoms in both sets. can be expressed through pairwise radial distribution functions:
If reference A comprises apolar fragments, this function shows the prevalence of apolar atoms in the vicinity of other apolar atoms. Otherwise, if A refers to the polar fragments, it shows the prevalence of polar atoms in the vicinity of other polar atoms.
The third function we use to characterize structural (in)homogeneity is the local atom number density variance inside the balls of radius R centered at random points.
Here,
is the average number of atom centers inside these balls, and is the variance of . This function has a large positive value if atoms tend to form clusters at the given length scale. It is calculated separately for polar and apolar atom sets.
2.3. The Gibbs Free Energy of Cavity Formation
The Gibbs free energy of the formation of small cavities in the solvent, which describes its solvation properties, can be calculated using a variation of the Widom test particle insertion method [53]. The formation of a cavity is considered as the insertion of a hard-sphere particle with an infinitely large interaction potential. This particle excludes all centers of solvent heavy (non-hydrogen) atoms within its radius R. Molecular dynamics is used to obtain instantaneous solvent configurations. A large number of insertions is performed into the random points of space for each configuration. Neglecting small fluctuations in the volume of the system, the Gibbs free energy of cavity formation can be related to the probability p(R) of successful insertion, i.e., the fraction of insertion attempts resulting in the absence of heavy atom centers within radius R:
The accuracy increases with the number of configurations and insertions, which becomes increasingly important for large cavity radii R. Hence, we produced long (100 ns) trajectories with instantaneous configurations recorded each 1 ps (105 configurations in total) and performed 105 insertions for each configuration, which results in 1010 insertions per liquid. This allows us to obtain values for R < 0.4 nm with the standard deviation below 0.5 kJ·mol−1 according to block analysis.
3. Results and Discussion
3.1. Scattering Curves Calculated from Simulations
X-ray scattering curves calculated from the MD trajectory snapshots are presented in Figure 2. As in experiments [6,7,8,12], up to three peaks are observed in these curves. Peak I corresponds to the smallest values of q and characterizes the separation distance between charged groups by the alkyl chain, i.e., the size of apolar domains. Its intensity and position depend on the length of the alkyl substituent. Peak I can appear as a shoulder in the case of short alkyl chains and is unnoticeable for substituents with fewer than four carbon atoms. Peak II observed around 9 nm−1 was reported [54] to describe the distance between polar groups of the same charge not separated by alkyl chains. The positions of the maxima of peaks I and II for calculated and experimental scattering curves are given in Table 2. Peak III is positioned near 14 nm−1 and is caused by ions located at close distances (about 0.45 nm). Its position and intensity are almost the same for different bistriflimides except for protic 1-methyl and 1-ethylimidazolium salts showing slightly lower q values of the peak maximum, in agreement with experimental observations [6,7].
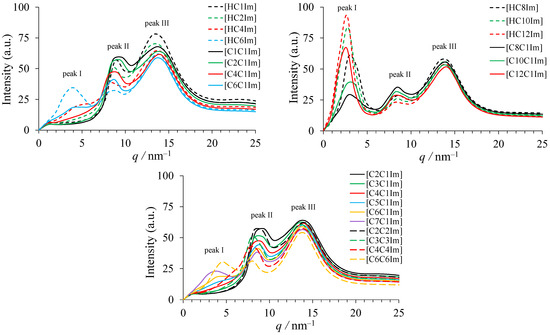
Figure 2.
Calculated X-ray scattering curves for the studied ionic liquids.

Table 2.
Positions of the maxima of peak I in calculated and experimental X-ray scattering curves.
The data in Table 2 indicate a general agreement between calculated and experimental [6,7,8,12] positions of peaks I and II as well. The values of q corresponding to the maximum of peak I significantly decrease with increasing alkyl chain length. Larger alkyl substituents also cause an increase in the intensity of peak I. This peak is not observed for [HC1Im][TFSI], [HC2Im][TFSI], [C1C1Im][TFSI], [C2C1Im][TFSI], [C3C1Im][TFSI], [C2C2Im][TFSI], and [C3C3Im][TFSI], indicating that there is no significant nanoheterogeneity in these ionic liquids. For [C4C1Im][TFSI] and [C4C4Im][TFSI], a small shoulder is observed. Protic ionic liquids ([HCnIm][TFSI]) have higher peak I intensity compared to their aprotic counterparts ([CnC1Im][TFSI]). This can be explained by the stabilization of domain structure by hydrogen bonds in the polar domain between the anion and NH group of the cation. A comparison of SAXS plots for ionic liquids with the same total number of carbon atoms in positions 1 and 3 of the imidazolium ring of the cation (e.g., [C4C4Im][TFSI] and [C7C1Im][TFSI]) shows that ionic liquids with long alkyl groups form larger domains corresponding to lower q and produce much more intensive scattering peaks. Asymmetric and symmetric ionic liquids with the same length of the alkyl chain (e.g., [C6C1Im][TFSI] and [C6C6Im][TFSI]) produce peaks with much closer positions corresponding to a similar domain size as pointed out previously [12].
Peak II undergoes a small shift to lower q with alkyl chain length growing from C2 to C4. This can also be explained by the emergence of the domain structure with the clusters of polar groups. Further growth of alkyl chain length does not change significantly the position of peak II.
3.2. Heterogeneity of Polar/Apolar Atom Distribution
For the analysis using functions described in Section 2.2, only the carbon atoms of the side chain of the imidazolium cation were considered as belonging to the apolar domain (also called apolar atoms below). The remaining heavy atoms, namely all the atoms in the anion and carbon and nitrogen atoms in the imidazolium ring of the cation, were attributed to the polar domain.
As stated above, RDF integrals G(R) and , and local density fluctuations can be calculated separately for the polar and apolar domains. This always resulted in a pair of curves sharing similar features. Most importantly, G(R) and had their first zero, and had its maximum at the close values of radii R for calculations with polar and apolar atoms. The same result was observed in the analysis of the structure of alkylammonium salts [16]. Hence, these functions characterize a general length scale of heterogeneities in ionic liquids. Below, only the results of calculations of G(R) and for the polar domain and for the polar atoms as reference are shown.
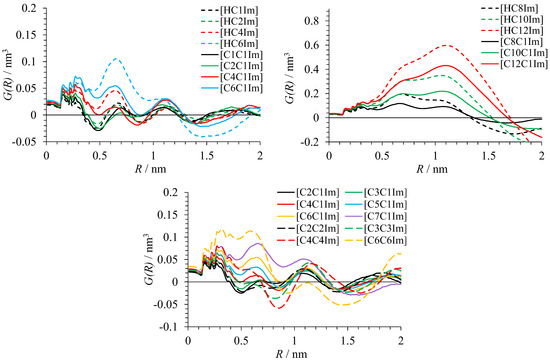
Figure 3.
Function characterizing inhomogeneity of heavy atom distribution in polar fragments of ILs.
Figure 4.
Function characterizing inhomogeneity of heavy atom distribution in ILs around polar atoms.
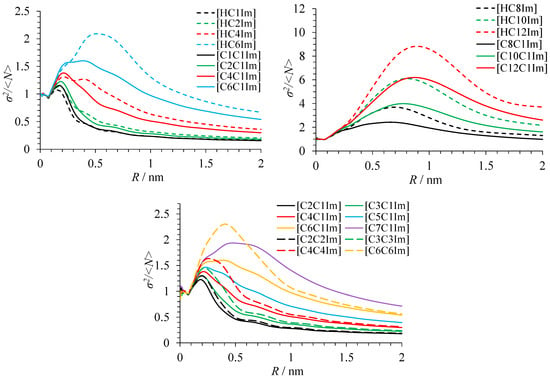
Figure 5.
The variance of the number density of polar atoms in ionic liquids.
G(R) and show the oscillating behavior typical for domainless liquids [16] in the case of bistriflimides with fewer than four carbon atoms in the alkyl substituent. For the liquids with seven or more carbon atoms in the substituent, large-period oscillations caused by well-defined domains are present. In the liquids from C4 to C6, progressive degradation of the first minimum of oscillations corresponding to the emergence and strengthening of domain structure is observed. From the curves in Figure 3 and Figure 4, it is clear that heterogeneous structure is more pronounced in protic than in aprotic ionic liquids with the same alkyl substituent. Analysis of the radial distribution function between the center of mass of the anion and N3 atom of the imidazolium ring shows that its first maximum is observed at the lower distance R for PILs such as [HC10C1Im][TFSI] than for AILs like [C10C1Im][TFSI] (Figure 6). A shoulder in the RDF for [HC10C1Im][TFSI] corresponds to the part of cations not involved in hydrogen bonding with anion.
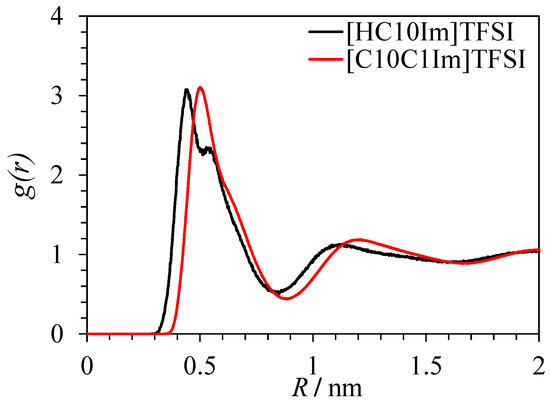
Figure 6.
Radial distribution function g(r) between the center of mass of the anion and N3 atom of imidazolium ring for [HC10Im][TFSI] and [C10C1Im][TFSI].
The above conclusions are fully supported by the curves of the variance of atom density shown in Figure 5. C1–C3 liquids have no maximum or even shoulder caused by the difference in the atom density inside and outside domains. Other liquids show signs of nanoheterogeneity. The variance is also larger for protic than for aprotic liquids. Symmetric ionic liquids [CnCnIm][TFSI] exhibit better segregation of polar and apolar domains than asymmetric liquids [CnC1Im][TFSI], which is also visible in the G(R) and curves.
The radii corresponding to the first zero of G(R) and as well as double of the radius of maximum of function for domain-forming bistriflimides are given in Table 3. All these quantities generally reflect the size of the domains. The values of R0 for G(R) and almost always coincide. They correspond to the radius of the sphere at which polar and apolar atoms become on average represented proportionally to their total number in the liquid, i.e., the sphere around a polar atom includes both polar and apolar domains. The value of maximum atom number variance Rmax is always much smaller. It would correspond to the radius of domains if they were spherical. The values of 2Rmax are usually closer to the values of R0.

Table 3.
Quantitative characteristics of domains in the studied ionic liquids: R0 is the radius corresponding to the first zero of G(R) or , 2Rmax is twice the radius corresponding to the maximum of .
The obtained results indicate that the size of domains rapidly grows in the liquids from C4 to C6. The values of R0 and 2Rmax can diverge for these liquids due to the presence of double peaks in the calculated curves, which is linked to the loose domain segregation. For the liquids with longer alkyl substituents, single sharp peaks and agreeing domain size characteristics were obtained, evidencing that they have well-defined nanostructure. The results obtained for [C6C1Im][TFSI] and [C6C6Im][TFSI] allow us to suggest that they form domains with a similar size. The size of domains coincides for protic and aprotic bistriflimides with the same alkyl group.
3.3. Gibbs Free Energy of Cavity Formation
The concept of cavity formation is widely used in studies of solvation processes. Solvation of any molecule can be considered as its accommodation in the cavity of the molecular size that has been pre-formed in a solvent. The free energy cost of cavity formation is determined by the solvent–solvent interactions. In ionic liquids with domain segregation, cavities predominantly form in apolar domains. This should lead to lower free energy of solvation and higher hydrocarbon solubility in such liquids.
Calculated values of the Gibbs free energy of cavity formation ΔcavG in the studied liquids are shown in Figure 7. ΔcavG always decreases with increasing length of the alkyl substituent. A rapid decrease is observed for C1–C6 liquids due to the emergence and strengthening of domain segregation. In contrast, only a small decrease occurs for C8–C12 liquids, in which well-defined domains are present, and cavities form predominantly in apolar domains with similar free energy cost for all liquids. At the same time, these liquids have a significantly different domain length scale, which has no huge effect on ΔcavG.
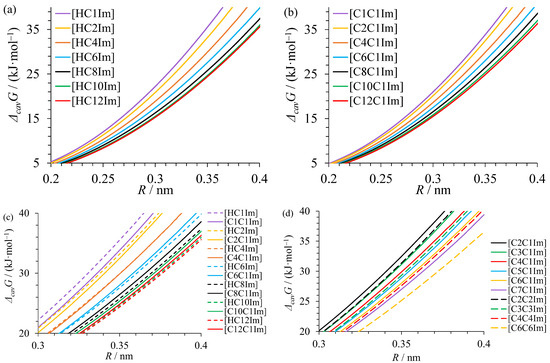
Figure 7.
The Gibbs free energy of cavity formation in alkylimidazolium bistriflimides at 298 K for spherical cavities with various radii R: (a,b) dependence on the alkyl substituent chain length; (c) comparison of protic and aprotic ionic liquids; (d) comparison of liquids with symmetrically and asymmetrically alkylated cations.
An interesting trend is observed for the difference in the cavity formation Gibbs free energy between protic and aprotic ionic liquids (Figure 7c). For liquids with fewer than four carbon atoms in the alkyl chain, ΔcavG is slightly higher in protic liquids. In the absence of a domain structure, hydrogen bonds formed between cations and anions in protic liquids impede cavity formation, similar to what was observed for the hydrogen-bonded molecular solvents [55]. For [HC4Im][TFSI] and [C4C1Im][TFSI], the values of ΔcavG become almost the same. Protic liquids with larger alkyl chains have lower ΔcavG values than aprotic liquids. In this case, hydrogen bonds are isolated in polar domains and improve domain segregation, which facilitates cavity formation in apolar domains.
A comparison of aprotic ionic liquids with symmetric and asymmetric cations (Figure 7d) indicates a similar cost of cavity formation for ionic liquids with the same total number of carbon atoms (e.g., [C3C3Im][TFSI] and [C5C1Im][TFSI]) but not for liquids with the same length of the alkyl groups ([C6C6Im][TFSI] and [C6C1Im][TFSI]) which were shown above to have a similar domain size. This is in part a result of a much higher fraction of liquid volume occupied by the apolar domains in ionic liquids with two alkyl groups than in those with a single group. A rough approximation with a two times higher fraction of apolar domain in [C6C6Im][TFSI] than in [C6C1Im][TFSI] leads to the difference ΔΔcavG = RTln2 = 1.7 kJ∙mol−1 if only the cavities in the apolar domain are considered. The observed difference is even larger due to the better segregation of polar and apolar domains in the liquids in symmetrical cations, which has been shown above. Hence, the solvation properties of such pairs of liquids will differ significantly despite the same domain length scale.
4. Conclusions
A nanoheterogeneous structure comprising polar and apolar domains is typical for ionic liquids with sufficiently long alkyl substituents. It has previously been shown that in the case of alkylammonium nitrates, even ethylammonium nitrate shows signs of nanoheterogeneity. In the case of alkylimidazolium bistriflimides ([HCnIm][TFSI] and [CnCmIm][TFSI]), our analysis of molecular dynamics snapshots as well as previously reported scattering data indicate domain segregation in the presence of butyl or longer alkyl substituents. As the length of the alkyl substituent increases, larger domain sizes and better segregation are observed. At the same time, ionic liquids with symmetric and asymmetric cations with the same alkyl substituent ([CnCnIm][TFSI] and [CnC1Im][TFSI]) have similar domain length scales, but better segregation is observed for symmetric cations. Protic alkylimidazolium bistriflimides [HCnIm][TFSI] have more pronounced nanoheterogeneity than aprotic salts [CnC1Im][TFSI] but do not differ from them in domain size. This is explained by hydrogen bonding between the acidic hydrogen in the cation and the anion.
The nanoheterogeneous structure can dramatically affect the solvation properties of ionic liquids. For the first time, we have analyzed the dependence of the Gibbs free energy of cavity formation in ionic liquids on both the domain length scale and the extent of domain segregation. We have shown that the latter, but not the former, plays a crucial role in determining the solvation properties of nanostructured ionic liquids. For example, a rather small decrease of the Gibbs free energy of cavity formation is observed from 1-octyl- to 1-undecyl-3-methylimidazolium bistriflimide despite an apparent increase in domain size. At the same time, increasing the alkyl substituent chain length by a single methylene group from C1 (no domain segregation) to C6 (clear evidence of nanoheterogeneity) liquids leads to a much more pronounced decrease in ΔcavG. In addition, cation–anion hydrogen bonding in aprotic ionic liquids strengthens the domain structure if it is present, and thus results in a higher propensity of cavity formation in [HCnIm][TFSI] liquids than in [CnC1Im][TFSI] liquids with n > 4. For the liquids with smaller alkyl substituents and no domain segregation, the situation is reversed: cation–anion hydrogen bonds increase the energy cost of cavity formation and result in larger ΔcavG values in AILs.
The most intriguing result of the work comes from the comparison of ionic liquids with symmetrically and asymmetrically substituted cations ([CnCnIm][TFSI], [CnC1Im][TFSI], and [C2n-1C1Im][TFSI]). The Gibbs free energies of cavity formation were found to be governed by the total number of carbon atoms in the substituents. The length scale of the domains again does not play a significant role, while the fraction of the volume occupied by the apolar domains and the extent of domain segregation are important.
Thus, it has been shown that the structure of the ionic liquid cation has complex relationships with the bulk phase properties such as cavity formation thermodynamics even for a series of structurally similar alkylimidazolium bistriflimides. This study once again highlights the links between the structure of the ions of different ionic liquids, the nanostructure of their liquid phase, and their solvation properties.
Author Contributions
Conceptualization, T.I.M. and I.A.S.; software, I.A.S.; investigation, T.I.M. and I.A.S.; data curation, T.I.M.; writing—original draft preparation, T.I.M. and I.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the Russian Science Foundation, project 24-13-00062.
Data Availability Statement
Data are contained within the article. The raw data are available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hayes, R.; Warr, G.G.; Atkin, R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [CrossRef] [PubMed]
- Greaves, T.L.; Kennedy, D.F.; Mudie, S.T.; Drummond, C.J. Diversity Observed in the Nanostructure of Protic Ionic Liquids. J. Phys. Chem. B 2010, 114, 10022–10031. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-L.; Li, B.; Sarman, S.; Mocci, F.; Lu, Z.-Y.; Yuan, J.; Laaksonen, A.; Fayer, M.D. Microstructural and Dynamical Heterogeneities in Ionic Liquids. Chem. Rev. 2020, 120, 5798–5877. [Google Scholar] [CrossRef] [PubMed]
- Triolo, A.; Russina, O.; Bleif, H.-J.; Di Cola, E. Nanoscale Segregation in Room Temperature Ionic Liquids. J. Phys. Chem. B 2007, 111, 4641–4644. [Google Scholar] [CrossRef] [PubMed]
- Atkin, R.; Warr, G.G. The Smallest Amphiphiles: Nanostructure in Protic Room-Temperature Ionic Liquids with Short Alkyl Groups. J. Phys. Chem. B 2008, 112, 4164–4166. [Google Scholar] [CrossRef]
- Rocha, M.A.A.; Neves, C.M.S.S.; Freire, M.G.; Russina, O.; Triolo, A.; Coutinho, J.A.P.; Santos, L.M.N.B.F. Alkylimidazolium Based Ionic Liquids: Impact of Cation Symmetry on Their Nanoscale Structural Organization. J. Phys. Chem. B 2013, 117, 10889–10897. [Google Scholar] [CrossRef]
- Abdurrokhman, I.; Elamin, K.; Danyliv, O.; Hasani, M.; Swenson, J.; Martinelli, A. Protic Ionic Liquids Based on the Alkyl-Imidazolium Cation: Effect of the Alkyl Chain Length on Structure and Dynamics. J. Phys. Chem. B 2019, 123, 4044–4054. [Google Scholar] [CrossRef]
- Martinelli, A.; Maréchal, M.; Östlund, Å.; Cambedouzou, J. Insights into the Interplay between Molecular Structure and Diffusional Motion in 1-Alkyl-3-Methylimidazolium Ionic Liquids: A Combined PFG NMR and X-Ray Scattering Study. Phys. Chem. Chem. Phys. 2013, 15, 5510. [Google Scholar] [CrossRef]
- Triolo, A.; Russina, O.; Caminiti, R.; Shirota, H.; Lee, H.Y.; Santos, C.S.; Murthy, N.S.; Castner, E.W., Jr. Comparing Intermediate Range Order for Alkyl- vs. Ether-Substituted Cations in Ionic Liquids. Chem. Commun. 2012, 48, 4959. [Google Scholar] [CrossRef] [PubMed]
- Sedov, I.A.; Magsumov, T.I.; Salikov, T.M.; Solomonov, B.N. Solvation of Apolar Compounds in Protic Ionic Liquids: The Non-Synergistic Effect of Electrostatic Interactions and Hydrogen Bonds. Phys. Chem. Chem. Phys. 2017, 19, 25352–25359. [Google Scholar] [CrossRef]
- Sedov, I.A.; Salikov, T.M.; Solomonov, B.N. Contrasting the Solvation Properties of Protic Ionic Liquids with Different Nanoscale Structure. J. Mol. Liq. 2019, 290, 111361. [Google Scholar] [CrossRef]
- Xiao, D.; Hines, L.G.; Li, S.; Bartsch, R.A.; Quitevis, E.L.; Russina, O.; Triolo, A. Effect of Cation Symmetry and Alkyl Chain Length on the Structure and Intermolecular Dynamics of 1,3-Dialkylimidazolium Bis(Trifluoromethanesulfonyl)Amide Ionic Liquids. J. Phys. Chem. B 2009, 113, 6426–6433. [Google Scholar] [CrossRef]
- Garaga, M.N.; Dracopoulos, V.; Werner-Zwanziger, U.; Zwanziger, J.W.; Maréchal, M.; Persson, M.; Nordstierna, L.; Martinelli, A. A Long-Chain Protic Ionic Liquid inside Silica Nanopores: Enhanced Proton Mobility Due to Efficient Self-Assembly and Decoupled Proton Transport. Nanoscale 2018, 10, 12337–12348. [Google Scholar] [CrossRef]
- Ghatee, M.H.; Zolghadr, A.R.; Moosavi, F.; Ansari, Y. Studies of Structural, Dynamical, and Interfacial Properties of 1-Alkyl-3-Methylimidazolium Iodide Ionic Liquids by Molecular Dynamics Simulation. J. Chem. Phys. 2012, 136, 124706. [Google Scholar] [CrossRef] [PubMed]
- Dudariev, D.; Koverga, V.; Kalugin, O.; Miannay, F.-A.; Polok, K.; Takamuku, T.; Jedlovszky, P.; Idrissi, A. Insight to the Local Structure of Mixtures of Imidazolium-Based Ionic Liquids and Molecular Solvents from Molecular Dynamics Simulations and Voronoi Analysis. J. Phys. Chem. B 2023, 127, 2534–2545. [Google Scholar] [CrossRef] [PubMed]
- Sedov, I.A.; Magsumov, T.I. Highlighting the Difference in Nanostructure between Domain-Forming and Domainless Protic Ionic Liquids. Phys. Chem. Chem. Phys. 2022, 24, 21477–21494. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Santos, C.S.; Murthy, N.S.; Hettige, J.J.; Kerr, K.; Ramati, S.; Gwon, J.; Gohdo, M.; Lall-Ramnarine, S.I.; Wishart, J.F.; et al. Structure of 1-Alkyl-1-Methylpyrrolidinium Bis(Trifluoromethylsulfonyl)Amide Ionic Liquids with Linear, Branched, and Cyclic Alkyl Groups. J. Phys. Chem. B 2013, 117, 15328–15337. [Google Scholar] [CrossRef]
- Gontrani, L.; Russina, O.; Lo Celso, F.; Caminiti, R.; Annat, G.; Triolo, A. Liquid Structure of Trihexyltetradecylphosphonium Chloride at Ambient Temperature: An X-Ray Scattering and Simulation Study. J. Phys. Chem. B 2009, 113, 9235–9240. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Li, B.; Sarman, S.; Laaksonen, A. Microstructures and Dynamics of Tetraalkylphosphonium Chloride Ionic Liquids. J. Chem. Phys. 2017, 147, 224502. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Y.; Zhang, X.; Zhou, G.; Zhang, S. Microstructures and Interaction Analyses of Phosphonium-Based Ionic Liquids: A Simulation Study. J. Phys. Chem. B 2012, 116, 4934–4942. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Padua, A. Fftool v1.0.0. 2015. Available online: https://zenodo.org/records/18618 (accessed on 15 May 2024).
- Canongia Lopes, J.N.; Pádua, A.A.H. Molecular Force Field for Ionic Liquids III: Imidazolium, Pyridinium, and Phosphonium Cations; Chloride, Bromide, and Dicyanamide Anions. J. Phys. Chem. B 2006, 110, 19586–19592. [Google Scholar] [CrossRef] [PubMed]
- Canongia Lopes, J.N.; Deschamps, J.; Pádua, A.A.H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Pádua, A.A.H. Molecular Force Field for Ionic Liquids Composed of Triflate or Bistriflylimide Anions. J. Phys. Chem. B 2004, 108, 16893–16898. [Google Scholar] [CrossRef]
- Gouveia, A.S.L.; Bernardes, C.E.S.; Tomé, L.C.; Lozinskaya, E.I.; Vygodskii, Y.S.; Shaplov, A.S.; Lopes, J.N.C.; Marrucho, I.M. Ionic Liquids with Anions Based on Fluorosulfonyl Derivatives: From Asymmetrical Substitutions to a Consistent Force Field Model. Phys. Chem. Chem. Phys. 2017, 19, 29617–29624. [Google Scholar] [CrossRef]
- Bhargava, B.L.; Balasubramanian, S. Refined Potential Model for Atomistic Simulations of Ionic Liquid [Bmim][PF6]. J. Chem. Phys. 2007, 127, 114510. [Google Scholar] [CrossRef] [PubMed]
- Chaban, V. Polarizability versus Mobility: Atomistic Force Field for Ionic Liquids. Phys. Chem. Chem. Phys. 2011, 13, 16055. [Google Scholar] [CrossRef]
- Doherty, B.; Zhong, X.; Gathiaka, S.; Li, B.; Acevedo, O. Revisiting OPLS Force Field Parameters for Ionic Liquid Simulations. J. Chem. Theory Comput. 2017, 13, 6131–6145. [Google Scholar] [CrossRef]
- Schröder, C. Comparing Reduced Partial Charge Models with Polarizable Simulations of Ionic Liquids. Phys. Chem. Chem. Phys. 2012, 14, 3089. [Google Scholar] [CrossRef]
- Son, C.Y.; McDaniel, J.G.; Schmidt, J.R.; Cui, Q.; Yethiraj, A. First-Principles United Atom Force Field for the Ionic Liquid BMIM+ BF4–: An Alternative to Charge Scaling. J. Phys. Chem. B 2016, 120, 3560–3568. [Google Scholar] [CrossRef]
- McDaniel, J.G.; Yethiraj, A. Influence of Electronic Polarization on the Structure of Ionic Liquids. J. Phys. Chem. Lett. 2018, 9, 4765–4770. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, H.; Doi, H.; Saito, S.; Matsugami, M.; Fujii, K.; Kanzaki, R.; Kameda, Y.; Umebayashi, Y. Hydrogen Bond in Imidazolium Based Protic and Aprotic Ionic Liquids. J. Mol. Liq. 2016, 217, 35–42. [Google Scholar] [CrossRef]
- Rodrigues, A.S.M.C.; Rocha, M.A.A.; Almeida, H.F.D.; Neves, C.M.S.S.; Lopes-da-Silva, J.A.; Freire, M.G.; Coutinho, J.A.P.; Santos, L.M.N.B.F. Effect of the Methylation and N–H Acidic Group on the Physicochemical Properties of Imidazolium-Based Ionic Liquids. J. Phys. Chem. B 2015, 119, 8781–8792. [Google Scholar] [CrossRef]
- Kolbeck, C.; Lehmann, J.; Lovelock, K.R.J.; Cremer, T.; Paape, N.; Wasserscheid, P.; Fröba, A.P.; Maier, F.; Steinrück, H.-P. Density and Surface Tension of Ionic Liquids. J. Phys. Chem. B 2010, 114, 17025–17036. [Google Scholar] [CrossRef]
- Součková, M.; Klomfar, J.; Pátek, J. Measurements and Group Contribution Analysis of 0.1MPa Densities for Still Poorly Studied Ionic Liquids with the [PF6] and [NTf2] Anions. J. Chem. Thermodyn. 2014, 77, 31–39. [Google Scholar] [CrossRef]
- Fröba, A.P.; Kremer, H.; Leipertz, A. Density, Refractive Index, Interfacial Tension, and Viscosity of Ionic Liquids [EMIM][EtSO4], [EMIM][NTf2], [EMIM][N(CN)2], and [OMA][NTf2] in Dependence on Temperature at Atmospheric Pressure. J. Phys. Chem. B 2008, 112, 12420–12430. [Google Scholar] [CrossRef]
- Zorębski, E.; Geppert-Rybczyńska, M.; Zorębski, M. Acoustics as a Tool for Better Characterization of Ionic Liquids: A Comparative Study of 1-Alkyl-3-Methylimidazolium Bis[(Trifluoromethyl)Sulfonyl]Imide Room-Temperature Ionic Liquids. J. Phys. Chem. B 2013, 117, 3867–3876. [Google Scholar] [CrossRef]
- Zorębski, M.; Zorębski, E.; Dzida, M.; Skowronek, J.; Jężak, S.; Goodrich, P.; Jacquemin, J. Ultrasonic Relaxation Study of 1-Alkyl-3-Methylimidazolium-Based Room-Temperature Ionic Liquids: Probing the Role of Alkyl Chain Length in the Cation. J. Phys. Chem. B 2016, 120, 3569–3581. [Google Scholar] [CrossRef] [PubMed]
- Esperança, J.M.S.S.; Visak, Z.P.; Plechkova, N.V.; Seddon, K.R.; Guedes, H.J.R.; Rebelo, L.P.N. Density, Speed of Sound, and Derived Thermodynamic Properties of Ionic Liquids over an Extended Pressure Range. 4. [C3Mim][NTf2] and [C5Mim][NTf2]. J. Chem. Eng. Data 2006, 51, 2009–2015. [Google Scholar] [CrossRef]
- Xue, L.; Gurung, E.; Tamas, G.; Koh, Y.P.; Shadeck, M.; Simon, S.L.; Maroncelli, M.; Quitevis, E.L. Effect of Alkyl Chain Branching on Physicochemical Properties of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2016, 61, 1078–1091. [Google Scholar] [CrossRef]
- Gomes De Azevedo, R.; Esperança, J.M.S.S.; Szydlowski, J.; Visak, Z.P.; Pires, P.F.; Guedes, H.J.R.; Rebelo, L.P.N. Thermophysical and Thermodynamic Properties of Ionic Liquids over an Extended Pressure Range: [Bmim][NTf2] and [Hmim][NTf2]. J. Chem. Thermodyn. 2005, 37, 888–899. [Google Scholar] [CrossRef]
- Zorębski, E.; Zorębski, M.; Dzida, M.; Goodrich, P.; Jacquemin, J. Isobaric and Isochoric Heat Capacities of Imidazolium-Based and Pyrrolidinium-Based Ionic Liquids as a Function of Temperature: Modeling of Isobaric Heat Capacity. Ind. Eng. Chem. Res. 2017, 56, 2592–2606. [Google Scholar] [CrossRef]
- Santos, D.; Santos, M.; Franceschi, E.; Dariva, C.; Barison, A.; Mattedi, S. Experimental Density of Ionic Liquids and Thermodynamic Modeling with Group Contribution Equation of State Based on the Lattice Fluid Theory. J. Chem. Eng. Data 2016, 61, 348–353. [Google Scholar] [CrossRef]
- Khalil, R.; Chaabene, N.; Azar, M.; Malham, I.B.; Turmine, M. Effect of the Chain Lengthening on Transport Properties of Imidazolium-Based Ionic Liquids. Fluid Phase Equilibria 2020, 503, 112316. [Google Scholar] [CrossRef]
- Lago, S.; Rodríguez, H.; Soto, A.; Arce, A. Deterpenation of Citrus Essential Oil by Liquid−Liquid Extraction with 1-Alkyl-3-Methylimidazolium Bis(Trifluoromethylsulfonyl)Amide Ionic Liquids. J. Chem. Eng. Data 2011, 56, 1273–1281. [Google Scholar] [CrossRef]
- Tariq, M.; Forte, P.A.S.; Gomes, M.F.C.; Lopes, J.N.C.; Rebelo, L.P.N. Densities and Refractive Indices of Imidazolium- and Phosphonium-Based Ionic Liquids: Effect of Temperature, Alkyl Chain Length, and Anion. J. Chem. Thermodyn. 2009, 41, 790–798. [Google Scholar] [CrossRef]
- Domańska, U.; Królikowski, M.; Wlazło, M.; Więckowski, M. Phase Equilibrium Investigation on 2-Phenylethanol in Binary and Ternary Systems: Influence of High Pressure on Density and Solid–Liquid Phase Equilibrium. J. Phys. Chem. B 2018, 122, 6188–6197. [Google Scholar] [CrossRef]
- Tomé, L.I.N.; Carvalho, P.J.; Freire, M.G.; Marrucho, I.M.; Fonseca, I.M.A.; Ferreira, A.G.M.; Coutinho, J.A.P.; Gardas, R.L. Measurements and Correlation of High-Pressure Densities of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2008, 53, 1914–1921. [Google Scholar] [CrossRef]
- Hasse, B.; Lehmann, J.; Assenbaum, D.; Wasserscheid, P.; Leipertz, A.; Fröba, A.P. Viscosity, Interfacial Tension, Density, and Refractive Index of Ionic Liquids [EMIM][MeSO3], [EMIM][MeOHPO2], [EMIM][OcSO4], and [BBIM][NTf2] in Dependence on Temperature at Atmospheric Pressure. J. Chem. Eng. Data 2009, 54, 2576–2583. [Google Scholar] [CrossRef]
- Cromer, D.T.; Mann, J.B. X-Ray Scattering Factors Computed from Numerical Hartree–Fock Wave Functions. Acta Crystallogr. A 1968, 24, 321–324. [Google Scholar] [CrossRef]
- Ben-Naim, A. The Kirkwood–Buff Integrals for One-Component Liquids. J. Chem. Phys. 2008, 128, 234501. [Google Scholar] [CrossRef] [PubMed]
- Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Annapureddy, H.V.R.; Kashyap, H.K.; De Biase, P.M.; Margulis, C.J. What Is the Origin of the Prepeak in the X-Ray Scattering of Imidazolium-Based Room-Temperature Ionic Liquids? J. Phys. Chem. B 2010, 114, 16838–16846. [Google Scholar] [CrossRef]
- Sedov, I.; Magsumov, T. The Gibbs Free Energy of Cavity Formation in a Diverse Set of Solvents. J. Chem. Phys. 2020, 153, 134501. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).