Abstract
We review the statistical mechanic foundations of the fundamental structure-making/breaking functions, leading to the rigorous description of the solute-induced perturbation of the solvent environment for the understanding of the solvation process of any species regardless of the type and nature of the solute–solvent interactions. Then, we highlight how these functions are linked to unambiguous thermodynamic responses resulting from changes in state conditions, composition, and solute–solvent intermolecular interaction asymmetries. Finally, we identify and illustrate the pitfalls behind the use of surrogate approaches to structure-making/breaking markers, including those based on Jones–Dole’s B-coefficient and Hepler’s isobaric-thermal expansivity, while highlighting their ambiguities and lack of consistency and the sources of misinterpretations.
Keywords:
solute-induced microstructural perturbation; fundamental structure-making/breaking functions; aqueous electrolyte solutions; solution non-idealities; solute–solvent intermolecular asymmetries; Hepler’s criterion; Jones–Dole’s B-coefficient-based criterion; preferential solvation function; Krichevskii parameter; second osmotic virial coefficients 1. Introduction
Since the early days of the molecular modeling of fluid mixtures, the main effort has focused on drawing formal (albeit rigorous) connections between the microstructural features of the system of interest and their macroscopic manifestation as thermodynamic properties. This approach follows logically from a pair of fundamental facts, namely: (a) the microstructure of a system arises from the presence of interparticle interactions, where an ideal gas represents the complete absence of them so that non-zero (statistical mechanic) pair correlation functions reflect the deviations of the actual pair distribution functions from the (ideal gas) uniform distribution counterpart triggered by the strength of the interactions; and (b) the microstructure of the mixture stems from the differences (e.g., asymmetries) between the unlike-pair interactions, giving rise to contrasting pair correlation functions [1]. Consequently, the macroscopic manifestations of these microscopic behaviors become described by the thermodynamic residual properties as deviations from those of the ideal gas model in the (a)-case and by the thermodynamic excess properties as deviation from a precisely-defined ideal solution reference in the (b)-case [2,3]. These two fundamental concepts become the blueprint for building the rigorous microscopic-to-macroscopic understanding of solvation processes, one based on the analysis of the solute-induced perturbation of the surrounding environment, leading to the unambiguous definition of the fundamental structure-making/breaking functions [4].
In fact, the isobaric–isothermal solute-induced microstructural distortion described as a local solvent-density perturbation (direct effect) caused by the intermolecular interaction asymmetry between the strength of the original solvent–solvent and the resulting solute–solvent interactions and propagating across the system up to a (correlation length) distance from the perturbing center (indirect effect) [5,6] leads to its macroscopic interpretation in terms of thermodynamics of solution non-ideality [7,8,9,10,11,12,13,14]. Thus, a great deal of effort in solution thermodynamics has been placed on the development of experimental methods to extract the structural information of aqueous electrolyte and non-electrolyte solutions from scattering experiments, such as X-ray (including XANES and EXAFS) [15,16,17,18,19,20,21,22], neutron diffraction with isotope substitution (NDIS) [20,23,24,25,26], hybrid empirical microstructural refinement techniques [27,28,29,30,31,32,33], and the molecular simulation-based interpretation of NDIS raw data [34,35,36,37,38,39,40], frequently complemented with infrared [41,42], Raman [43,44,45,46,47], NMR [48,49], and femtosecond pump-probe spectroscopies [50,51].
This research effort has often led to loose interpretations of the solvation behavior of solutes as either structure-makers or structure-breakers [52,53,54,55,56], followed by the more pretentious kosmotrope (order-maker) and chaotrope (disorder-maker) descriptors [57], usually used as an interchangeable alternative notation for structure-makers and structure-breakers, respectively [57,58,59,60,61,62], i.e., an unfortunate circumstance that introduced additional ambiguities and confusion into the reported interpretation of the solvation behavior of solutes. In fact, this sentiment was vented earlier as “Concepts like ‘structure-breaking’ and ‘structure-promoting’ solutes appear almost in every discussion of the physicochemical properties of aqueous solutions…Yet in spite of the great number of articles written on this subject, the very basic questions of how to define the ‘structure of water’ and which experiment should be done to measure the extent of ‘structural changes in the solvent’ were left unanswered. Almost invariably, these concepts slip into the discussion in a somewhat qualitative manner, i.e., it is assumed that they are already understood intuitively and no further clarification or elaboration is needed.” [63].
The common source of ambiguity around the concept of structure-maker/breaker solutes (or kosmotropes/chaotropes, for that matter) has been the lack of an explicit identification of the structure-making/breaking (kosmotrope/chaotrope) signature, and consequently, the absence of any definite formal link between the microstructural effect of the solute on the surrounding solvent environment—the solute-induced local density perturbation—and the corresponding macroscopic response whose magnitude can be measured experimentally [54,64]. Moreover, the alluded restructuring process highlights a few essential requirements to avoid the frequently used vague language while facilitating the interpretation of solvation phenomena, e.g., the need for (i) a meaningful unambiguous account for the microstructural perturbation of the environment around any species, (ii) the development of precisely defined descriptors of the solvation phenomena, and (iii) the identification of the corresponding macroscopic responses as thermodynamic signatures of the species solvation leading to the solution of thermodynamic non-ideality.
Based on the discussed scenario, the main goal of this manuscript is twofold: first, review the fundamentals underlying the rigorous and unambiguous interpretation of the solute-induced structure-making/breaking phenomena indicated in the title, and second, identify the myths, verities, and misuses of the structure-making/breaking markers in solvation thermodynamics, as emphasized in the subtitle of this manuscript. Given the scope of the current manuscript, and to keep the discussion on focus, this review mainly comprises our own developments on the matter while being illustrated with the analysis of data from numerous sources from the literature and aims to raise awareness on what can and cannot be construed from frequently invoked markers of structure-making/breaking phenomena.
For that purpose, we start reviewing the statistical mechanic foundations underlying the solute-induced distortion of the solvent environment in Section 2, where we discuss the interplay of two length scales in the solvation process associated with the microstructural perturbation and its propagation, leading to the explicit unambiguous and natural definition of the fundamental structure-making/breaking functions. In the process, we show how these functions become rigorously linked to thermodynamic responses, including the isochoric–isothermal pressure change upon solvation, the osmotic second virial coefficient, and a number of frequently invoked thermodynamic preferential solvation parameters. In Section 3, we discuss the responses of the fundamental structure-making/breaking functions to changes in state conditions, composition, and solute–solvent intermolecular interaction asymmetries. Then, in Section 4, we argue and illustrate the pitfalls behind the use of surrogate approaches, including those based on Jones–Dole’s B coefficient and Hepler’s isobaric-thermal expansivity, while highlighting their ambiguities and lack of consistency and fulfillment of required constraints, as well as identifying the sources of misinterpretations.
2. Rigorous Definition of Solute-Induced Microstructural Perturbation of the Solvent Environment
As indicated in the introduction, we must fulfill a few essential requirements in the microscopic characterization of the solvation process, including the unambiguous and precise description of the perturbation of the solvent environment upon solute solvation at the prevailing state conditions of the solution, and the rigorous linking of the microscopic behavior to the corresponding macroscopic manifestations leading to the experimental measurements [4]. For that purpose, we review the statistical mechanical-based foundations for the fundamental structure-making/breaking concept as a thermodynamic state function, link it to the pressure perturbation counterparts and preferential solvation phenomena, and discuss its attributes, including the universality of the definition.
2.1. Fundamental Split between Short- and Long-Range Contributions to the Solvation Behavior of Solutes
The solvation of any solute (electrolyte or otherwise) entails a disruption of the system microstructure resulting from the solute–solvent intermolecular interaction asymmetry, described formally and unambiguously as a finite local density perturbation (i.e., a short-range or direct effect) whose propagation across the system (i.e., a longer-range or indirect effect) is felt up to a distance given by the correlation length of the environment and scales with its isothermal compressibility [65]. Note that the local density perturbation associated with the solvation process remains finite even under special thermodynamic conditions, such as in the solvation of a solute at infinite dilution in a solvent at its critical conditions where the correlation length becomes divergent [12,66]. More importantly, the alluded split is rigorously described by the Ornstein–Zernike equation [67], and therefore, the local density perturbation becomes naturally linked to the direct correlation functions, while the ensuing propagation becomes linked to the indirect correlation functions [5,68,69]. This feature provides the means to unravel the rigorous connections between the species-induced microstructural perturbation in a solution, its propagation across the system, and the driving force underlying the solvation of any species at any state condition or composition. This formal characterization becomes more powerful through their reinterpretation according to the species’ molecular-based fundamental structure-making/breaking functions [4].
2.2. Definition and Attributes of the Fundamental Structure-Making/Breaking Functions
To dissipate the controversy underlying the meaning of the structure-making/breaking concept, we must (i) identify the precise link between the microstructural impact of the solute species on its surrounding environment, i.e., the induced local density perturbation and the ensuing macroscopic manifestation to be ultimately measured, (ii) provide a direct path for the calculation of the magnitude of the microstructural perturbation of the system according to an explicit, general, and rigorous molecular-based thermodynamic formalism, and (iii) be able to apply the concept equally and consistently to any solute–solvent intermolecular interaction asymmetry regardless of either the state conditions, number of components, or system composition [4].
The magnitude of the local density perturbation of the j-solvent environment around the i-solute can be rigorously measured in terms of Kirkwood–Buff [70] total correlation function integrals (TCFI) as follows [4,71]:
where describes the absolute average number of j-solvent molecules around any central i-solute at the prevailing state conditions and system composition. Note that the TCFIs in Equation (1), , are volume integrals over the pair correlation function , where depicts the spatial pair distribution function as the statistical mechanical microstructural descriptor, represents an orientational average, describes the orientation of the -species, and defines the distance between the centers of mass of the two species. In other words, characterizes the average number of j-solvent molecules around the central i-solute in excess (deficit) to that around any j-solvent and comprises the key microscopic information required to assess the magnitude of the i-induced microstructural perturbation of the j-solvent environment, i.e.,
where the arrow highlights the microstructural evolution of the solvent environment from the original TCFI, , to the final TCFI, . This microstructural perturbation becomes characterized by three possible outcomes according to the sign of the difference as follows:
Therefore, according to Equations (1)–(3), the solute-induced solvent perturbation becomes unambiguously described as a strengthening of the solvent environment around the i-solute when , i.e., , as the i-solute behaves as a structure-maker species. Conversely, the solvent perturbation weakens the solvent environment around the i-solute when , i.e., , as the i-solute exhibits a structure-breaking effect. As we will discuss below, the j-solvent environment might remain unperturbed despite the presence of the i-solute as , i.e., . Note that the unperturbed condition represents also the signature of a special case of Lewis–Randall solution ideality because describes the scenario where the i-solute behaves as the j-solvent, as well as the more general solution ideality condition , leading to [72,73].
At this point, we fulfilled the first requirement (i), and now we must provide a direct path for the calculation of the magnitude of the microstructural perturbation described by the three conditions in Equation (3), i.e., requirement (ii). For that purpose, we have invoked Kirkwood–Buff fluctuation formalism [70] and derived the following expressions for the general type of (electrolyte or non-electrolyte) i-solute at any system composition including infinite dilution [1,4]:
where is the stoichiometric coefficient of the electrolyte i-solute, denotes its partial molar volume, is the molar density of the solution, and describes the material stability coefficient in terms of the composition slope of the activity coefficient of the j-solvent [74]. In other words, given the pair of volumetric properties and the stability coefficient , Equation (4) describes the thermodynamic response to the solute-induced effects on the microstructure of the fluid mixture and rigorously and unambiguously reveals the possible behaviors of the i-solute without requiring any explicit microstructural information of the system.
Finally, requirement (iii) is automatically satisfied given the absence of any constraint on the type of interactions, nature of the species, and number of components in the solution underlying the generality of the Kirkwood–Buff formalism. In fact, a universal and fundamentally based structure-making/breaking function (aka criterion or marker) must apply equally to species such as a non-interacting ideal gas i-solute [14,75], any i-species behaving identically to the j-solvent [12], and either weakly or strongly interacting i-electrolyte solutes, regardless of the type and description of the solute–solvent interactions. Therefore, the structure-making/breaking criterion must be able to identify the null solute-induced effect when the solute–solvent interaction asymmetry crosses the transition boundary between the solute-induced structure-making and the structure-breaking perturbations. Note that this transition condition might portray two significantly different scenarios, namely: (i) one characterized as a special cases of Lewis–Randall solution ideality, either when the interacting solute species behaves just as another solvent species and therefore keeps the solvent environment unperturbed [76], or (ii) when a non-interacting ideal gas species () is solvated by a real j-solvent along the thermodynamic path [14,71]. In fact, from (4) and the fact that with , we find that . Likewise, because [14] it follows immediately that , i.e., when the actual compressibility of the system becomes equal to that of the system behaving as an ideal gas environment, (e.g., see Figure 6 and Appendix A of Ref. [71]).
2.3. Link between , the Isochoric-Isothermal Pressure Perturbation upon Solvation and Krichevskii’s Parameter
The isobaric–isothermal change of residual () partial molar Gibbs free energy for the solvation of a -dissociable i-solute in a j-solvent can be expressed as follows,
where denotes the partial molar fugacity coefficient of the -species in solution at the prevailing state conditions and composition, while the isochoric-isothermal pressure perturbation becomes the thermodynamic response to the microstructural reorganization of the system upon solvation, which in turn can be expressed in terms of the species partial molar volumes and the isothermal compressibility of the system as follows [4,12],
Equations (5) and (6) provide the macroscopic-to-microscopic rigorous link between the solvation-induced pressure perturbation and the resulting microstructural response of the system,
where we have invoked the following identities,
With the diffusional stability coefficient [74], and
As well as,
Which define the partial molar volumes of the species, and the corresponding isothermal compressibility of the system with and , according to the inversion of the Kirkwood-Buff formalism [1].
From Equations (1) and (6) we immediately find the explicit connection between the pressure perturbation upon solvation and the microstructural responses, i.e.,
where the phase stability requires and [74] so that,
Leading finally to,
Note that the pressure perturbation upon solvation in a stable phase is always finite regardless of the state condition and composition, even though the right-hand-side of Equation (11) involves potentially divergent compressibility-driven contributions [12,77]. In fact, for the binary system comprising an infinitely dilute i-solute at the critical point of the pure j-solvent, the partial molar volume of the solute at infinite dilution will diverge at the same rate as the isothermal compressibility of the pure solvent, yet,
where the so-called Krichevskii parameter [77] becomes defined in terms of the limiting behavior of the structure-making/breaking function of the i-solute, i.e., [78]
The finiteness of the alluded limiting function becomes more obvious after recalling that , with where denotes the short-range or solvation contribution to the property [79].
2.4. Link between and the Second Osmotic Virial Coefficient of the Solute
The second osmotic virial coefficients derive from the isothermal solute-density expansion of the solute activity along different thermodynamic -paths including (see e.g., Figure 4 and discussed in section SI-A of the Supplementary Information of Ref. [71]). According to the Lewis-Randall (LR) solution ideality reference, the structure-making/breaking function can be rigorously linked to the three distinctive types of second osmotic virial coefficients [71]. In fact, after invoking the limiting composition slope [80], and recalling the definition of the isobaric–isothermal second osmotic virial coefficient, , it has been demonstrated that
Likewise, from the definition of the isothermal iso osmotic second virial coefficient, [81], follows immediately that,
And therefore,
where
And,
Moreover, from the definition of the isochoric-isothermal second osmotic virial coefficient [81], and subsequent interpretation in terms of Kirkwood-Buff integrals [75], follows that [71],
We must highlight that the derived relationships are all rigorous expressions involving neither approximations nor constraints on the type of solute, nature of the solvent, and magnitude of the intermolecular interactions asymmetries. However, for i-solutes whose non-idealities follows the functionality, as in the case of gases in aqueous and organic solutions, [75,82] the limiting composition slope becomes . Consequently, the fundamental structure-making/breaking function and the three osmotic second virial coefficients become related as follows,
While we have illustrated the links for a non-electrolyte solute, similar connections can be drawn for a dissociative solute as described explicitly for electrolyte species in Ref. [83].
2.5. Preferential Solvation Phenomenon as a Balance among Structure-Making/Breaking Effects
Preferential solvation usually refers to the effect of a third species (aka cosolvent) on the solubility of a solute, a phenomenon of great interest for the understanding of the thermodynamics underlying the solubility enhancement of low-solubility species in highly compressible environments [10,84,85,86,87], and the manipulation of the relative volatility of species to improve separations [88,89]. The behavior of these systems has been frequently interpreted by a diversity of thermodynamic preferential interaction parameters leading to a number of non-equivalent microscopic markers for the preferential solvation phenomenon [90,91]. The common denominator underlying this scenario is again the lack of an explicit microscopic definition of the underlying marker as previously highlighted, i.e., “how do we measure the of a given solute in a given mixture?” leading to “what are the molecular reasons that cause a solute to prefer one component over the other and, hence, alter the composition in its local environment?” [92].
To confront this issue, we have recently introduced a universal preferential solvation (state) function, [91], as unique microscopic measure of how much different the j-solvent environment around the i-solute is in comparison to the k-solvent environment counterpart, where . Thus, accounts unambiguously for the solvation of an infinitely dilute i-solute species in a mixed-solvent (i.e., a j-solvent plus a k-cosolvent) environment at fixed state conditions in terms of the solute-induced microstructural perturbations of the solvent and cosolvent environments resulting from the species intermolecular interaction asymmetries. This solute-induced differential microstructural perturbation, caused by the disparity of affinities between the i-solute and each of the solvents species, becomes more revealing when written explicitly written in terms of Kirkwood-Buff integrals [70] as follows,
where , and represents the average number of -solvent molecules around the infinitely dilute -solute in either excess or deficit to that of the -ideal gas uniform distribution. From Equation (25) follows immediately that for two precisely-defined scenarios; namely: (a) for any interacting i-solute species at infinite dilution, where the j-solvent and the k-cosolvent behave identically as a single pure solvent leading to , and (b) for the solvation of a non-interacting i-solute (ideal gas) species at infinite dilution in a mixed -real solvent.
On the one hand, note that implies that , in other words, describes the average deviation of the mixed-solvent distribution around the i-solute at infinite dilution from that of the corresponding uniform bulk-phase value. On the other hand, highlights the microstructural response of the system to the solute–solvent and solute-cosolvent interaction asymmetries, leading to the differential affinities of the solute with the solvent, whose macroscopic responses translate into thermodynamic excess properties describing the solution thermodynamic non-idealities [74]. Moreover, given the fact that the ternary system under consideration becomes fully characterized either by five Kirkwood-Buff integrals (, , , , ), or four fundamental structure-making/breaking functions, (, , , ), where and with . In other words, this ternary system becomes fully described by two independent fundamental structure-making/breaking functions, and consequently, the interpretation of preferential solvation phenomena based on , Equation (25), becomes entirely described in terms of a linear combination of four fundamental structure-making/breaking functions as follows [82,91],
We must emphasize that Equations (25) and (26) are exact statistical mechanical expressions for the alluded ternary system regardless of the type or nature of the species involved, while Equation (26) explicitly identifies the formal contribution of the relevant fundamental structure-making/breaking functions. Moreover, this expression becomes rigorously connected to the thermodynamic preferential solvation parameter in the isothermal–isobaric closed system (often identified as , i.e., in Refs. ([93,94]) for , as follows:
where . Thus, by invoking the Gibbs–Duhem relation for the -binary mixture, we find the complementary thermodynamic link,
indicating that the isothermal–isobaric closed system comprises formally similar behaviors for the diffusible -species, resulting from the combined i-solute-induced perturbations of the j-solvent and k-cosolvent, as described by a linear combination of the four structure-making/breaking functions .
3. Microstructural Responses to Intermolecular Interaction Asymmetries, Environmental State Conditions, and Composition
Because the solvation process comprises the solute-induced effect on the solution microstructure at the prevailing state conditions and composition, it becomes instructive to evaluate how the solute–solvent molecular asymmetry, as well as individual perturbations of pressure, temperature, and composition, can modify the solvent microstructure around a solute species.
3.1. Response to Solute–Solvent Molecular Asymmetry
As a state function, the behavior of the fundamental structure-making/breaking function , Equation (1) of a stable fluid mixture becomes a continuous function of the magnitude of the solute–solvent interaction asymmetry, as well as the state conditions and system composition. Typically, the idea of structure-making/breaking behavior has been applied to solutes at infinite dilution [57,95], and therefore, we review first this limiting behavior for a binary fluid mixture, i.e., . For the sake of generality, we start with Equation (1), written as follows:
whose isochoric-isothermal pressure perturbation upon solvation becomes [4]
Equations (29) and (30) comprise two remarkable attributes: (a) the first indicates that the structure-making/breaking functions scale with the partial molar volume of the solute at infinite dilution, and consequently, with the magnitude of the solute–solvent intermolecular interaction asymmetry, and (b) the second provides an alternative avenue to experimentally measure the degree of dissimilarity between the solute and the solvent, i.e., the source of thermodynamic non-ideality of the resulting mixture.
In fact, Equation (30) indicates that an i-solute behaves as a structure-maker when , i.e., conventionally known as non-volatile [77] or attractive solutes [7]. Conversely, an i-solute behaves as a structure-breaker if , i.e., characterized as volatile [77] or weakly-attractive and repulsive [7] in the jargon of supercritical fluid solutions [12,85]. Obviously, nature presents a wide and continuous range of solute–solvent interaction asymmetries in binary fluid solutions. For instance, for a particular real j-solvent, we might consider a non-interaction (ideal gas) i-solute, , characterized by so that [96]
and a finite . By cranking up the solute–solvent interactions, such as that of an inert gas solute, , the binary system can be characterized by the second virial coefficients and while keeping the solvent-solvent interactions unchanged, i.e., [4]
and
This expression indicates that when the unlike-pair interaction second virial coefficient , and consequently, the solute induces an additional microstructural perturbation on the surrounding solvent, over that of the ideal gas solute, and becomes a structure-making solute. Otherwise, when , there are two possible alternatives: either giving rise to a structure-maker with or resulting in a structure-breaker. Note that at a specific state condition at which , Equation (34) indicates that the solute does not perturb the microstructure of the j-solvent.
Should we keep increasing the magnitude solute–solvent interactions, up to the point that the solute–solvent interactions become equal to the corresponding solvent-solvent interactions, then we would have reached the null solute–solvent asymmetry, i.e., , and the i-solute would not perturb the surrounding solvent environment. Not surprisingly, the most frequent scenario comprises systems with solute–solvent interactions different (either weaker or stronger) from the solvent–solvent interactions. When , such as in the case of non-polar gases in water, we expect and so that , i.e., the i-solute behaves as a structure-breaker species. Conversely, when , such as in the case of strongly interactive solutes including strong electrolytes, we observe and so that , i.e., the i-solute becomes a structure-maker. Note, however, that the inequality can be satisfied by , i.e., by either or , as illustrated in Figure 1 below, where we provide a schematic with the discussed relationships among , , and while highlighting the relevant boundaries.
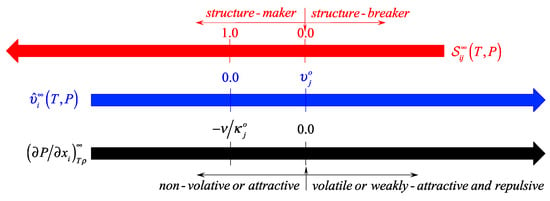
Figure 1.
Relationships among , , and , including some relevant boundaries.
3.2. Response to Changes in State Conditions
From Equation (29), we immediately have the following temperature and pressure derivatives:
and
where and identify the isothermal compressibility and isobaric thermal expansivity of the species at the limiting composition condition , i.e., either pure component or infinite dilution . Consequently, the magnitude and sign of the response to changes in either temperature or pressure depends on the product of two differences, i.e., either or , respectively. In fact, for a structure-making () solute, , characterized by the following condition:
There are four distinctive responses to changes in temperature,
And another four distinctive responses to changes in pressure,
Otherwise, for a structure-breaking () solute, , is characterized by the following conditions:
There are only two possible responses to changes in temperature
and another two possible responses to changes in pressure
In summary, Equations (38)–(42) indicate contrasting solvent microstructural responses to changes in system pressure and temperature regardless of the structure-making/breaking nature of the i-solute. In fact, according to the thermodynamic relation with , the microstructural response to either a pressure increase or temperature decrease accentuates both the intrinsic nature of the original structure-making when and structure-breaking solutes whenever the isothermal compressibility and the isobaric thermal expansivity of the pure solvent are both larger than those corresponding to the infinite dilute solute. Otherwise, when , the same changes in state conditions will weaken the intrinsic nature of the original structure-making and structure-breaking solutes whenever the isothermal compressibility and isobaric thermal expansivity of the pure solvent are both smaller than those of the infinite dilute solute.
Note that, according to the analysis of Section 3.1, we immediately find that
For which , i.e., when a solute behaves identically as a solvent species, the structure-making/breaking function and its responses to -perturbations are all zero. Moreover, for the non-interacting ideal gas solute, for which we have , we have
The sign and magnitude of the responses to -perturbations caused by a non-interacting solute in real solvents depend on how different and are from its ideal gas values. Note that the authors have erroneously assumed in Ref. [4] that and , i.e., equivalent to assume that .
3.3. Response to Changes of State Conditions at Finite Composition
For the binary system forming a thermodynamic stable phase at finite compositions, i.e., exhibiting a finite -coefficient, we deal with two fundamental structure-making/breaking functions, i.e., , whose isothermal–isobaric composition dependence has been derived elsewhere [1]
and
Therefore,
with , , while identifies the partial molar volume of the -species, and
with so that [74]
where denotes the partial molar enthalpy of the j-species at the prevailing state conditions and composition.
Likewise,
where , , and
with
while denotes the partial molar volume of the j-species at the prevailing state conditions and composition.
As expected, these expressions converge into the corresponding ones derived for the case of the i-species becoming infinitely dilute in the j-species. In fact, considering that , the limiting behavior of Equation (46) becomes Equation (29) while . Similarly, Equations (48) and (51) become identical to Equations (35) and (36) given that , , , and , while Equations (49) and (52) become null because . Consequently, as for the case of the infinite dilution, the magnitude and sign of the response to changes in either temperature or pressure depend on two factors, and , and give rise to either two sets of four possible outcomes for or two sets for . For example, for , we have that so that
Otherwise, for we have that so that there are only two possible responses to isobaric changes in temperature
and another two possible responses to changes in pressure
Note that, according to the analysis of Section 3.1, we immediately find that
for which , i.e., when a solute behaves identically as a solvent species, the fundamental structure-making/breaking function and its responses to -perturbations are all zero. Moreover, for the system comprising a non-interacting finite composition ideal gas solute in a real j-solvent, there is only one structure-making/breaking function, (see Appendix A), i.e.,
And therefore,
whose isobaric temperature derivative results in the following expression:
Moreover, for the isothermal pressure derivative, we find
Note that (61)–(62) converge into (44)–(45) when the i-solute becomes infinitely dilute in the j-solvent.
4. Pitfalls from Surrogate Experimental Techniques
Researchers have often invoked surrogate experimental techniques to investigate the solvent environment around a solute and searched for correlations between the observed thermodynamic manifestations and the corresponding responses from different microscopic probes hoping to gain some understanding of the effect of a solute on the microstructure of the solution. Unfortunately, these research tools frequently provide a rather limited (i.e., short-ranged and/or orientational) view of the solute-induced effects, might invoke solvent-specific (e.g., water or other hydrogen-bonding species) approaches, or would depend on other markers to conjecture microscopic-to-macroscopic correspondence while overlooking that correspondence does not necessarily means cause-effect connection [97,98].
In what follows, we review two examples of these surrogate approaches, i.e., the conjectured markers associated with the behavior of the B-coefficient in Jones–Dole’s equation [99] together with its isobaric temperature derivative, and the isobaric-thermal expansivity of the solute in solution [95], whose misguided use has perpetuated their involvement as structure-making/breaking markers as if they had already been proven adequate for this purpose.
4.1. Myths and Verities about the Use of Jones–Dole’s B- and -Coefficients as Structure Markers and Their Connection to the Fundamental Structure-Making/Breaking Function
The empirical Jones–Dole’s equation for the relative viscosity of the dilute solution reads as follows:
where with , denotes the molar concentration of the i-solute, and the coefficients and account for the direct ion-ion and the (ion) solute–solvent interactions, respectively [99]. If we assume that Jones–Dole’s equation provides an accurate representation of the shear viscosity of a dilute solution, the B-coefficient becomes determined from the limiting isothermal–isobaric composition slope, i.e.,
leading to . Because the B-coefficient is the coefficient of the linear concentration term in Jones–Dole’s equation, this coefficient has been associated with the solvent-mediated solute–solute interactions, and therefore, with the conjectured for a structure-maker species and for a structure-breaker species [53,100,101,102], later supplemented with the alternative isobaric temperature derivative [57,103,104,105,106,107,108,109,110].
Despite early warnings, e.g., “This type of coefficient is therefore probably related to the disturbance of the structure which is present in such liquids…No general theory has yet been developed for the B-coefficient but important qualitative explanations have been advanced in terms of ion-solvent interactions…Interesting as these various correlations are, it should be emphasized that they are, as yet, qualitative in nature and a quantitative theory for the B-coefficient still awaits development” [111] that would have prompted legitimate questions, as identified below, there was instead a proliferation of rather convoluted claims involving unproven connections between the signs of either the B-coefficient or its temperature derivative and the solute-induced perturbation of the solvent microstructure, as if the alluded links were either self-evident or already established and validated. In other words, instead of addressing some genuine issues including whether Jones–Dole’s B-coefficient contains any embedded microstructural information, whether we could assign any definite foundation to the widely used assumption about the sign of the B-coefficient and its structure-making/breaking trend, and whether we could find a rational justification for the use of the sign of as a structure-making/breaking marker, unfortunately, the literature has been flooded with conjectures born on dicey narratives, including “A positive B-coefficient indicates that the ions tend to order the solvent structure and increase the viscosity of the solution while a negative B-coefficient indicates disordering and a decrease of viscosity” [102] and “the values of temperature coefficient of , i.e., for the solute can provide direct evidence regarding their structure-making or breaking effect in solution. The values of are positive for hydrophilic structure-breaking groups. For hydrophobic structure-making groups, the value of is negative” [112], and a number of variations, as quoted in the Supporting Information of Ref. [113].
In a series of recent publications [4,71,113,114], we have addressed the issues identified above to test the validity and consistency of the outcomes from the application of the B-coefficient and/or its temperature derivative as structure-making/breaking markers. While all outcomes pointed to the lack of uniqueness of these markers, as clearly illustrated in Table 1, where we observe that the same sign-pair combination could represent opposite structure-making/breaking parameter and, consequently, confirm the lack of uniqueness of the sign-pair combination as a structure-making/breaking marker.

Table 1.
Representative systems illustrating the eight sign-pair combinations and their resulting structure-making/breaking parameter for infinitely dilute solutes at ambient conditions.
To trace back the microscopic origin for such behavior according to explicit statistical mechanics arguments, we have interpreted the plausible links between the behavior of the B-coefficient (and/or its temperature derivative ) and the (electrolyte or non-electrolyte) solute-induced perturbation of the solvent environment. For that purpose, we invoked Feakins et al.’s [118,119] rigorous expression for the B-coefficient, derived according to the transition state theory [120], as follows:
for the infinitely dilute i-solute where with for non-electrolyte solutes. and denote the molar Gibbs free energy of activation of viscous flow and the corresponding partial molar volume for the -species, respectively, at the -composition condition, i.e., either infinite dilution or pure component. Equation (65) contributes two terms to the B-coefficient, namely the change of Gibbs free energy of activation for the viscous flow, and the volumetric change when -solvent molecules are alchemically mutated into a solute during the formation of an i-solute at infinite dilution in an otherwise pure j-solvent, . This volumetric term provides direct access to the microstructural perturbation during the solvation process since, according to the rigorous definition of the structure-making/breaking parameter , as described by Equation (4), and Equation (65) becomes
Equation (66) warrants the following important observations: (i) the B-coefficient must be defined by the limiting condition of infinite dilution, vide supra Equation (64), to be consistent with its TS-based interpretation, and (ii) the TS-based interpretation clearly illustrates that the B-coefficient results from the combination of the solute-induced perturbation of the solvent structure and the corresponding induced difference between the Gibbs free energy of activation for the viscous flow of the solute and the solvent. Consequently, Equation (66) not only confirms that the B-coefficient comprises some information about the solute-induced effect on the solvent microstructure but also suggests that the sign of the B-coefficient cannot unambiguously describe the structure-making/breaking nature of the dilute i-solute, contrary to the widespread practice in the literature [53,57,100,102,112,121,122,123,124,125,126,127,128].
To illustrate the lack of uniqueness of the B-coefficient and/or its temperature derivative as markers for the structure-making/breaking behavior, we first test the behavior of a prototypical solute (see Equation (15) of [113]) and then introduce a novel statistical mechanics proof. (Equation (15) of [114]). For example, in Ref. [113], we have determined the conditions at which the B-coefficient for the non-interacting ideal gas solute () might predict either a structure-making, , a structure-breaking, , or an unperturbed microstructure, , as illustrated below.
This straightforward and rigorous thermodynamic analysis illustrates the lack of uniqueness of the B-coefficient as a structure-making/breaking marker, in that either or could represent a structure-making, , and simultaneously a structure-breaking, , behavior depending on the state conditions of the pure solvent (see Table 1).
Moreover, for the non-interacting ideal gas solute, the system comprises , [120], and [4] so that its -coefficient would read as follows:
with [120], where and denote the shear viscosity and molar volume of the pure j-solvent, while and identify Planck and Avogadro constants, respectively. Therefore, from Equation (68), we immediately find that
emphasizing that the condition of the null solute-induced effect on the viscosity of the dilute solution, , represents two contrasting structure-making/breaking scenarios. The first one, the top line of Equation (69), indicates a non-zero solute-induced effect on the structure of a real solvent, , whose sign depends on the condition. The second one, the bottom line of Equation (69), predicts an unperturbed structure of the solvent or , a condition highly unlikely to occur in real solvents, as illustrated in Table 2 for a series of condensed solvents.

Table 2.
Representative systems illustrating the sign-pair combinations and their resulting structure-making/breaking parameter for and infinitely dilute ideal gas solute in a variety of solvents mostly at ambient conditions (according to tabulated data from Ref. [129]).
According to the isobaric temperature derivative of Equation (66), Ref. [113] discusses the ability of the coefficient to discriminate between structure-making and structure-breaking solutes, under the four categories introduced by Tsangaris and Martin [103]. The resulting expression is
where the second line of Equation (70) highlights the replacement of with its corresponding explicit form previously derived [4]. Equation (70) indicates that the behavior (i.e., magnitude and sign) of depends on those of , , and , as well as the differences , , and giving rise to sixteen possible structure-making/breaking outcomes, as discussed in the Supporting Information of Ref. [113].
In brief, there are eight possible sign-pair combinations that could lead to a structure-making outcome , with four exhibiting and another four exhibiting , while the remaining eight combinations could result in a structure-breaking outcome , with four exhibiting and another four exhibiting . In other words, the sign of as a structure-making/breaking marker cannot distinguish between structure-making () solutes and structure-breaking (). In summary, neither the alone nor the sign-pair combination can provide a unique one-to-one correspondence between their signs and the structure-making/breaking nature of the i-solute described here by the molecular-based parameter , rendering these criteria deceptive markers of structure-making/breaking trends despite their widespread use in the literature, as illustrated in Table 3 below.

Table 3.
Experimentally based structure-making/breaking parameter for aqueous infinitely dilute solutes at ambient conditions in comparison with predictions based on Hepler’s isobaric-thermal expansivity marker as well as Jones–Dole’s B-coefficient and derivative criteria.
Table 2 and Table 3 highlight the fact that, despite the lack of uniqueness, the structure-making/breaking marker based on the signs of have been regularly invoked in combination with, or as an alternative to, the isobaric expansivity-based criterion to be discussed in Section 4.3 [107,109,110,137,139,151,152,153,154,155,156,157,158,159,160,161,162,163].
4.2. Sources of Ambiguities Underlying the Use of Jones–Dole’s B- and -Coefficients as Structure Markers
Having illustrated the lack of uniqueness of the B-, -, or any sign-pair combination as structure-making/breaking markers, the last piece of the puzzle to be solved was the origin of such behavior. For that purpose, Ref. [114] presented an alternative, yet equivalent, representation of Feakins’ TST approach by rewriting the first term of Equation (65) as follows:
which, after invoking the mean-value theorem for integrals [164], provided a more informative version of the link between the B-coefficient and the microstructure of the solvent around the solute as described by the fundamental structure-making/breaking function ,
where identifies the compressibility factor of the pure j-solvent at the prevailing state conditions, and the horizontal bar on the RHS of Equation (72) describes the mean value of the function between parenthesis within the range.
Equation (72) highlights the interplay between microstructural perturbations at two different levels, the ground state and the transition state, where the perturbation associated with the activated state for the viscous flow is incorporated as a pressure integral, which defines the activation molar Gibbs free energy. Consequently, Feakins’ TST-based analysis of the B-coefficient describes a combination of disparate structure-making/breaking quantities, i.e., ground state versus transition state, which becomes the most obvious and direct theoretical attributes giving rise to the unavoidable drawback of the B-coefficient as a structure-making/breaking marker, beyond the ones previously discussed in detail elsewhere [78,113]. Likewise, under the same approach, the isobaric temperature derivative of Equation (72) led to
With the isobaric–isothermal residual thermal expansivity , where the isobaric temperature derivatives and are simple functions of by the exact relations [4]
and
In other words, as in the case of the B-coefficient, involves solute-induced microstructural perturbations, and their temperature derivative, at not only the ground- but also the activated-state conditions. Consequently, neither the B-coefficient, , nor any of its sign-pair combinations can unequivocally describe the actual solute-induced perturbation of the solvent microstructure at the ground state conditions, a conclusion that applies to any value of the stoichiometric coefficient .
4.3. Frequent Pitfalls in the Application of Feakins’ TST Approach to the Study of B-Coefficients for Electrolytes
A persisting oversight in the application of Feakins’ TST approach to the B-coefficients involving electrolyte systems is the omission of the stoichiometric coefficient [165] in Equation (66) and related expressions associated with the transition-state properties. This omission amounts to using in Equation (66) and leads to the corruption of the reported transition state thermodynamic quantities and their interpretation, given that it introduces significant errors in the values of the molar Gibbs free energy of activation for aqueous electrolytes involving [109,141,166,167,168,169,170,171,172,173,174] depending on the magnitude of the ratio and becoming even larger with increasing [175,176,177,178,179]. As a matter of fact, according to the tabulated data from Ref. [124], it becomes evident the significantly large error introduced when assuming rather than the correct as illustrated in Table 4, which translates into . In other words, the erroneous estimations of the molar Gibbs free energy of activation when assuming are carried over to the representation of the i-solute-induced perturbation of the j-solvent microstructure and its corresponding -derivatives, i.e.,

Table 4.
Magnitude of the error in the calculated Gibbs free energy of activation when wrongly assuming in Equation (66) instead of the correct .
4.4. Myths and Verities about Hepler’s Isobaric-Thermal Expansivity as Structure-Making/Breaking Marker
Another surrogate tool frequently invoked for the assessment of the structure-making/breaking ability of a solute has been proposed by Hepler [95], who suggested a marker based on the conjecture that “since increasing pressure would also break up the bulky aggregates, the same reasoning suggests that the heat capacity of pure water should decrease with increasing pressure” and that this behavior could be extended to species in solution at infinite dilution. Hepler’s criterion is based on the sign of the isothermal pressure dependence of its partial molar heat capacity , or its more easily accessible Maxwell equivalent expression . More specifically, this criterion states that whenever or , the i-solute behaves as a structure-maker, and conversely, if or , the i-solute behaves as a structure-breaker.
Unfortunately, as for the case of the B-coefficients, the lack of an explicit unambiguous cause-effect connection between either or and the solute-induced perturbation of the solvent microstructure [1,4,71,78] makes any attempt to determine either the latter from volumetric data or the former from pressure perturbation calorimetry pointless [180,181,182,183]. Moreover, this so-called Hepler’s criterion immediately fails the compliance of two simple constraints associated with the behavior of a system comprising either the largest or the null solute–solvent intermolecular asymmetry.
For the largest solute–solvent intermolecular asymmetry we have the solute, characterized by [96,184], leading to the exact expression for its structure-making/breaking function [4]
Consequently, from Equation (4), we expect to observe
The significance of Equation (80) can be summarized as follows: (i) at ambient conditions, the in a real j-solvent exhibits a structure-making behavior, (ii) the microstructure of the pure j-solvent remains unperturbed along the states where the solvent behavior follows the condition, and (iii) after crossing this boundary, the ideal gas solute becomes a structure-breaker (e.g., see Figures 8 and 9 of Ref. [14] for the solvent water and the Lennard-Jones fluid, respectively).
Hepler’s criterion cannot account for the behavior described by Equation (80), in particular, the inability of the isobaric-thermal expansivity-based criterion to cross the line, as described by in Hepler’s marker. In fact, it has been shown that ; in other words, Hepler’s criterion cannot describe the structure-making-to-breaking transition for the ideal gas solute in a real j-solvent along the -line. Moreover, for the null solute–solvent intermolecular asymmetry, as characterized by an i-solute behaving as a j-solvent and regardless of the definition of structure-making/breaking, the outcome must be an unperturbed solvent structure depicted by in the schematic Equation (3). While the physical representation for the null solute–solvent intermolecular asymmetry is characterized by [72], its simplest and most advantageous case occurs when the Kirkwood-Buff integrals obey the condition. In other words, this condition is not only the microstructural signature of a pure j-solvent [96] but also the prototypical fingerprint for the microstructural transition between structure-making and structure-breaking processes driven by the solute–solvent intermolecular interaction asymmetry. This general and rigorous condition for the structure-making/breaking transition provides another opportunity to test the validity of the thermal expansivity-based criterion, which in Hepler’s terms becomes described by .
It becomes immediately obvious that, given the condition for pure j-solvents at normal (around ambient), these fluids would describe the boundary and its crossing only if they meet at least two rather unlikely properties, namely an isobaric thermal expansivity independent of the state conditions, i.e., , and an isobaric-linear temperature-dependent isothermal compressibility, i.e., . We are not aware of any real pure solvent following this bizarre behavior, and consequently, we must conclude that Hepler’s criterion cannot possibly describe and/or predict the transition between structure-making and structure-breaking events involving common solvents (in particular water which was the target of Hepler’s analysis). In summary, according to the above discussion and the evidence in Table 3, Hepler’s conjectured marker cannot account for the solute-induced perturbation of the solvent microstructure of infinitely dilute solution comprising any solute–solvent intermolecular asymmetries, i.e., either the smallest (zero, for the special case of ) or the largest (for the solute).
5. Concluding Remarks and Outlook
The usefulness of the structure-making/breaking concept has been previously challenged due to its lack of uniqueness [64], i.e., forged by the absence of a precise definition for what is meant by structure, and how to measure its perturbation. In addressing this challenge, we have argued that any criterion or marker for the structure-making/breaking ability of a solute must represent a state function and apply to any type and magnitude of solute–solvent molecular interaction asymmetry and should comply with some fundamental molecular thermodynamic constraints. More importantly, we have emphasized that the uniqueness does not (and cannot) depend on the criterion or probe used for the test of the type of solute-induced perturbation of the solvent microstructure.
On the one hand, we have reviewed the approaches to rigorously describe the ability of a solute species to perturb the solvent environment, to assign a precise statistical mechanics meaning to the structure-making/breaking event, and to rigorously link it to its thermodynamic responses, including quantitative measures of solution thermodynamic non-ideality which can be assessed experimentally. On the other hand, we have lent true molecular thermodynamic support for the testability, and eventual falsifiability, of a pair of popular conjectured structure-making/breaking markers whose validity has never been established but assumed in the current literature.
Supported by rigorous statistical thermodynamics, we discussed the proper interpretation of the role played by the species-induced microstructural perturbations of the solvent, their response to environmental state conditions and composition, as well as our ability to probe the system and test all conjectures in the development of a causative explanation for a variety of solvation phenomena. In other words, “…if a theory is testable, then it implies that events of a certain kind cannot happen; and so, it asserts something about reality. This is why we demand that the more conjectural a theory is, the higher should be its degree of testability.” [185].
In closing, we must stress that often times, authors attempt to add value to their experimental data by introducing hand-waving interpretations of the trends in the observed thermodynamic properties based on umbrella concepts of structure-making/breaking as if, by placing names to unsupported or conjectured ideas, they provide additional understanding. In fact, in the words of Richard Feynman, [186] we should always recognize “… the difference between knowing the name of something and knowing something”.
Funding
This research received no external funding.
Data Availability Statement
All data are available from the cited references.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Structure-Making/Breaking Function for a Non-Interacting Finite Composition Ideal Gas in a Real Solvent
Starting with the isothermal–isobaric composition evolution of the system microstructure, i.e., [80]
where for the general case , though here, .
Likewise, from the Kirkwood–Buff expressions for the partial molar volumes [70], we obtain the following equations for the real j-species and the ideal gas i-species [14]
with the isobaric-thermal expansivity , i.e.,
From Equations (A2)–(A4), we immediately find
And from Equations (3) and (4), we determine the composition dependence of , i.e.,
Consequently, from (A8) and Equation (6) follows that
with the system isothermal compressibility written accordingly
Moreover,
so that its isobaric temperature derivative becomes
with , whose rearrangement leads to
Likewise, the isothermal pressure derivative results in the following expression
with .
References
- Chialvo, A.A. On the Elusive Links between Solution Microstructure, Dynamics, and Solvation Thermodynamics: Demystifying the Path through a Bridge over Troubled Conjectures and Misinterpretations. J. Phys. Chem. B 2023, 127, 10792–10813. [Google Scholar] [CrossRef] [PubMed]
- Abbott, M.M.; Nass, K.K. Equations of State and Classical Solution Thermodynamics—Survey of the Connections. ACS Symp. Ser. 1986, 300, 2–40. [Google Scholar]
- Chialvo, A.A. Accurate Calculation of Excess Thermal, Infinite Dilution, and Related Properties of Liquid Mixtures Via Molecular-Based Simulation. Fluid Phase Equilibria 1993, 83, 23–32. [Google Scholar] [CrossRef]
- Chialvo, A.A. On the Solute-Induced Structure-Making/Breaking Effect: Rigorous Links among Microscopic Behavior, Solvation Properties, and Solution Non-Ideality. J. Phys. Chem. B 2019, 123, 2930–2947. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Cummings, P.T. Solute-induced Effects on the Structure and the Thermodynamics of Infinitely Dilute Mixtures. Aiche J. 1994, 40, 1558–1573. [Google Scholar] [CrossRef]
- Levelt Sengers, J.M.H. Supercritical Fluids: Their Properties and Applications. In Supercritical Fluids: Fundamentals and Applications; Kiran, E., Debenedetti Pablo, G., Peters Cor, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000; pp. 1–29. [Google Scholar]
- Debenedetti, P.G.; Mohamed, R.S. Attractive, Weakly Attractive and Repulsive Near-Critical Systems. J. Chem. Phys. 1989, 90, 4528–4536. [Google Scholar] [CrossRef]
- Petsche, I.B.; Debenedetti, P.G. Influence of Solute-Solvent Asymmetry upon the Behavior of Dilute Supercritical Mixtures. J. Phys. Chem. 1991, 95, 386–399. [Google Scholar] [CrossRef]
- O’Connell, J.P.; Liu, H.Q. Thermodynamic modelling of near-critical solutions. Fluid Phase Equilibria 1998, 144, 1–12. [Google Scholar] [CrossRef]
- Mazo, R.M. Salting out near the critical point. J. Phys. Chem. B 2007, 111, 7288–7290. [Google Scholar] [CrossRef] [PubMed]
- Gee, M.B.; Smith, P.E. Kirkwood-Buff theory of molecular and protein association, aggregation, and cellular crowding. J. Chem. Phys. 2009, 131, 165101. [Google Scholar] [CrossRef]
- Chialvo, A.A. Solvation Phenomena in Dilute Solutions: Formal, Experimental Evidence, and Modeling Implications. In Fluctuation Theory of Solutions: Applications in Chemistry, Chemical Engineering and Biophysics, 1st ed.; Matteoli, E., O’Connell, J.P., Smith, P.E., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 191–224. [Google Scholar]
- Pallewela, G.N.; Smith, P.E. Preferential Solvation in Binary and Ternary Mixtures. J. Phys. Chem. B 2015, 119, 15706–15717. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, A.A. On the Solvation Thermodynamics Involving Species with Large Intermolecular Asymmetries: A Rigorous Molecular-Based Approach to Simple Systems with Unconventionally Complex Behaviors. J. Phys. Chem. B 2020, 124, 7879–7896. [Google Scholar] [CrossRef] [PubMed]
- Enderby, J.E. Neutron and X-ray Scattering from Aqueous Solutions. Proc. R. Soc. Lond. 1975, 345, 107–117. [Google Scholar]
- Nishikawa, K.; Iijima, T. Small-Angle X-rays Scattering Study of Fluctuations in Ethanol and Water Mixtures. J. Phys. Chem. 1993, 97, 10824–10828. [Google Scholar] [CrossRef]
- Yamanaka, K.; Yamagami, M.; Takamuku, T.; Yamaguchi, T.; Wakita, H. X-Ray-Diffraction Study on Aqueous Lithium-Chloride Solution in the Temperature-Range 138-373-K. J. Phys. Chem. 1993, 97, 10835–10839. [Google Scholar] [CrossRef]
- Fulton, J.L.; Heald, S.M.; Badyal, Y.S.; Simonson, J.M. Understanding the Effects of Concentration on the Solvation Structure of Ca+2 in Aqueous Solution. I. The Perspective on Local Structure from EXAFS and XANES. J. Phys. Chem. A 2003, 107, 4688–4696. [Google Scholar] [CrossRef]
- D’Angelo, P.; Roscioni, O.M.; Chillemi, G.; Della Longa, S.; Benfatto, M. Detection of second hydration shells in ionic solutions by XANES: Computed spectra for Ni2+ in water based on molecular dynamics. J. Am. Chem. Soc. 2006, 128, 1853–1858. [Google Scholar] [CrossRef]
- Ansell, S.; Barnes, A.C.; Mason, P.E.; Neilson, G.W.; Ramos, S. X-ray and neutron scattering studies of the hydration structure of alkali ions in concentrated aqueous solutions. Biophys. Chem. 2006, 124, 171–179. [Google Scholar] [CrossRef]
- Antalek, M.; Pace, E.; Hedman, B.; Hodgson, K.O.; Chillemi, G.; Benfatto, M.; Sarangi, R.; Frank, P. Solvation structure of the halides from x-ray absorption spectroscopy. J. Chem. Phys. 2016, 145, 044318. [Google Scholar] [CrossRef]
- Zitolo, A.; Chillemi, G.; D’Angelo, P. X-ray Absorption Study of the Solvation Structure of Cu2+ in Methanol and Dimethyl Sulfoxide. Inorg. Chem. 2012, 51, 8827–8833. [Google Scholar] [CrossRef]
- Enderby, J.E. Ion Solvation via Neutron Scattering. Chem. Soc. Rev. 1995, 24, 159–168. [Google Scholar] [CrossRef]
- Badyal, Y.S.; Barnes, A.C.; Cuello, G.J.; Simonson, J.M. Understanding the effects of concentration on the solvation structure of Ca2+ in aqueous solutions. II: Insights into longer range order from neutron diffraction isotope substitution. J. Phys. Chem. A 2004, 108, 11819–11827. [Google Scholar] [CrossRef]
- Mancinelli, R.; Botti, A.; Bruni, F.; Ricci, M.A.; Soper, A.K. Hydration of sodium, potassium, and chloride ions in solution and the concept of structure maker/breaker. J. Phys. Chem. B 2007, 111, 13570–13577. [Google Scholar] [CrossRef]
- Bruni, F.; Imberti, S.; Mancinelli, R.; Ricci, M.A. Aqueous solutions of divalent chlorides: Ions hydration shell and water structure. J. Chem. Phys. 2012, 136, 064520. [Google Scholar] [CrossRef] [PubMed]
- Pusztai, L.; McGreevy, R.L. MCGR: An inverse method for deriving the pair correlation function from the structure factor. Physica 1997, 234, 357–358. [Google Scholar] [CrossRef]
- Pusztai, L. Partial pair correlation functions of liquid water. Phys. Rev. B 1999, 60, 11851–11854. [Google Scholar] [CrossRef]
- Soper, A.K. Tests of the empirical potential structure refinement method and a new method of application to neutron diffraction data on water. Mol. Phys. 2001, 99, 1503–1516. [Google Scholar] [CrossRef]
- Soper, A.K. Joint structure refinement of x-ray and neutron diffraction data on disordered materials: Application to liquid water. J. Phys. Condens. Matter 2007, 19, 335206. [Google Scholar] [CrossRef]
- Harsanyi, I.; Pusztai, L. Hydration structure in concentrated aqueous lithium chloride solutions: A reverse Monte Carlo based combination of molecular dynamics simulations and diffraction data. J. Chem. Phys. 2012, 137, 204503–204509. [Google Scholar] [CrossRef]
- Mile, V.; Gereben, O.; Kohara, S.; Pusztai, L. On the Structure of Aqueous Cesium Fluoride and Cesium Iodide Solutions: Diffraction Experiments, Molecular Dynamics Simulations, and Reverse Monte Carlo Modeling. J. Phys. Chem. B 2012, 116, 9758–9767. [Google Scholar] [CrossRef]
- Pethes, I.; Pusztai, L. Reverse Monte Carlo modeling of liquid water with the explicit use of the SPC/E interatomic potential. J. Chem. Phys. 2017, 146, 064506. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Simonson, J.M. The Structure of Concentrated NiCl2 Aqueous Solutions. What is Molecular Simulation Revealing about the Neutron Scattering Methodologies? Mol. Phys. 2002, 100, 2307–2315. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Simonson, J.M. The Structure of CaCl2 Aqueous Solutions over a Wide Range of Concentrations. Interpretation of Difraction Experiments Via Molecular Simulation. J. Chem. Phys. 2003, 119, 8052–8061. [Google Scholar] [CrossRef]
- Mason, P.E.; Neilson, G.W.; Dempsey, C.E.; Brady, J.W. Neutron diffraction and simulation studies of CsNO3 and Cs2CO3 solutions. J. Am. Chem. Soc. 2006, 128, 15136–15144. [Google Scholar] [CrossRef] [PubMed]
- Pluharova, E.; Fischer, H.E.; Mason, P.E.; Jungwirth, P. Hydration of the chloride ion in concentrated aqueous solutions using neutron scattering and molecular dynamics. Mol. Phys. 2014, 112, 1230–1240. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Vlcek, L. NO3– Coordination in Aqueous Solutions by 15N/14N and 18O/natO Isotopic Substitution: What Can We Learn from Molecular Simulation? J. Phys. Chem. B 2015, 119, 519–531. [Google Scholar] [CrossRef]
- Kohagen, M.; Pluhařová, E.; Mason, P.E.; Jungwirth, P. Exploring Ion–Ion Interactions in Aqueous Solutions by a Combination of Molecular Dynamics and Neutron Scattering. J. Phys. Chem. Lett. 2015, 6, 1563–1567. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Vlcek, L. “Thought experiments” as dry-runs for “tough experiments”: Novel approaches to the hydration behavior of oxyanions. Pure Appl. Chem. 2016, 88, 163–176. [Google Scholar] [CrossRef]
- Max, J.J.; Chapados, C. Infrared spectroscopy of aqueous ionic salt mixtures at low concentrations: Ion pairing in water. J. Chem. Phys. 2007, 127, 114509. [Google Scholar] [CrossRef]
- Nickolov, Z.S.; Miller, J.D. Water structure in aqueous solutions of alkali halide salts: FTIR spectroscopy of the OD stretching band. J. Colloid Interface Sci. 2005, 287, 572–580. [Google Scholar] [CrossRef] [PubMed]
- Dillon, S.R.; Dougherty, R.C. Raman studies of the solution structure of univalent electrolytes in water. J. Phys. Chem. A 2002, 106, 7647–7650. [Google Scholar] [CrossRef]
- Smith, J.D.; Saykally, R.J.; Geissler, P.L. The effects of dissolved halide anions on hydrogen bonding in liquid water. J. Am. Chem. Soc. 2007, 129, 13847–13856. [Google Scholar] [CrossRef]
- Rinne, K.F.; Gekle, S.; Netz, R.R. Ion-Specific Solvation Water Dynamics: Single Water versus Collective Water Effects. J. Phys. Chem. A 2014, 118, 11667–11677. [Google Scholar] [CrossRef] [PubMed]
- Shalit, A.; Ahmed, S.; Savolainen, J.; Hamm, P. Terahertz echoes reveal the inhomogeneity of aqueous salt solutions. Nat. Chem. 2017, 9, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Balos, V.; Imoto, S.; Netz, R.R.; Bonn, M.; Bonthuis, D.J.; Nagata, Y.; Hunger, J. Macroscopic conductivity of aqueous electrolyte solutions scales with ultrafast microscopic ion motions. Nat. Commun. 2020, 11, 1611. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Wu, Z.; Morrow, A.R.; Yethiraj, A.; Yethiraj, A. Self-Diffusion and Viscosity in Electrolyte Solutions. J. Phys. Chem. B 2012, 116, 12007–12013. [Google Scholar] [CrossRef]
- Ma, K.; Zhao, L. The Opposite Effect of Metal Ions on Short-/Long-Range Water Structure: A Multiple Characterization Study. Int. J. Mol. Sci. 2016, 17, 602. [Google Scholar] [CrossRef]
- Tielrooij, K.J.; Garcia-Araez, N.; Bonn, M.; Bakker, H.J. Cooperativity in Ion Hydration. Science 2010, 328, 1006–1009. [Google Scholar] [CrossRef]
- Choi, J.H.; Cho, M. Ion aggregation in high salt solutions. VI. Spectral graph analysis of chaotropic ion aggregates. J. Chem. Phys. 2016, 145, 174501. [Google Scholar] [CrossRef]
- Bernal, J.D.; Fowler, R.H. A Theory of Water and Ionic Solution, with Particular Reference to Hydrogen and Hydroxyl Ions. J. Chem. Phys. 1933, 1, 515–548. [Google Scholar] [CrossRef]
- Frank, H.S.; Evans, M.W. Free Volume and Entropy in Condensed Systems.3. Entropy in Binary Liquid Mixtures—Partial Molal Entropy in Dilute Solutions—Structure and Thermodynamics in Aqueous Electrolytes. J. Chem. Phys. 1945, 13, 507–532. [Google Scholar] [CrossRef]
- Ben-Naim, A. Structure-Breaking and Structure-Promoting Processes in Aqueous-Solutions. J. Phys. Chem. 1975, 79, 1268–1274. [Google Scholar] [CrossRef]
- Collins, K.D. Sticky Ions in Biological-Systems. Proc. Natl. Acad. Sci. USA 1995, 92, 5553–5557. [Google Scholar] [CrossRef]
- Waluyo, I.; Nordlund, D.; Bergmann, U.; Schlesinger, D.; Pettersson, L.G.M.; Nilsson, A. A different view of structure-making and structure-breaking in alkali halide aqueous solutions through X-ray absorption spectroscopy. J. Chem. Phys. 2014, 140, 244506. [Google Scholar] [CrossRef]
- Marcus, Y. Effect of Ions on the Structure of Water: Structure Making and Breaking. Chem. Rev. 2009, 109, 1346–1370. [Google Scholar] [CrossRef] [PubMed]
- Russo, D. The impact of kosmotropes and chaotropes on bulk and hydration shell water dynamics in a model peptide solution. Chem. Phys. 2008, 345, 200–211. [Google Scholar] [CrossRef]
- Vranes, M.; Tot, A.; Papovic, S.; Panic, J.; Gadzuric, S. Is choline kosmotrope or chaotrope? J. Chem. Thermodyn. 2018, 124, 65–73. [Google Scholar] [CrossRef]
- Ben Ishai, P.; Mamontov, E.; Nickels, J.D.; Sokolov, A.P. Influence of Ions on Water Diffusion—A Neutron Scattering Study. J. Phys. Chem. B 2013, 117, 7724–7728. [Google Scholar] [CrossRef]
- Bonetti, M.; Nakamae, S.; Roger, M.; Guenoun, P. Huge Seebeck coefficients in nonaqueous electrolytes. J. Chem. Phys. 2011, 134, 114513. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Vlcek, L. Toward the understanding of hydration phenomena in aqueous electrolytes from the interplay of theory, molecular simulation, and experiment. Fluid Phase Equilibria 2016, 407, 84–104. [Google Scholar] [CrossRef][Green Version]
- Ben-Naim, A. Solubility, Hydrophobic Interactions and Structural Changes in the Solvent. In Chemistry and Physics of Aqueous Gas Solutions; Adams, W.A., Ed.; Electrochemical Society: Princeton, NJ, USA, 1975; pp. 8–18. [Google Scholar]
- Ball, P.; Hallsworth, J.E. Water structure and chaotropicity: Their uses, abuses and biological implications. Phys. Chem. Chem. Phys. 2015, 17, 8297–8305. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967, 30, 615–730. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Chialvo, A.A. Solute-Solute Correlations in Infinitely Dilute Supercritical Mixtures. J. Chem. Phys. 1992, 97, 504–507. [Google Scholar] [CrossRef]
- Gray, C.G.; Gubbins, K.E. Theory of Molecular Fluids; Oxford University Press: Oxford, UK, 1985; Volume 1. [Google Scholar]
- Chialvo, A.A.; Cummings, P.T.; Simonson, J.M.; Mesmer, R.E. Solvation in High-Temperature Electrolyte Solutions. II. Some Formal Results. J. Chem. Phys. 1999, 110, 1075–1086. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Kusalik, P.G.; Cummings, P.T.; Simonson, J.M.; Mesmer, R.E. Molecular approach to high-temperature solvation. Formal, integral equation and experimental results. J. Phys. Condens. Matter 2000, 12, 3585–3593. [Google Scholar] [CrossRef]
- Kirkwood, J.G.; Buff, F.P. The Statistical Mechanical Theory of Solution. I. J. Chem. Phys. 1951, 19, 774–777. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Crisalle, O.D. Osmolyte-induced Effects on the Hydration Behavior and the Osmotic Second Virial Coefficients of Alkyl-Substituted Urea Derivatives. Critical assessment of their structure-making/breaking behavior. J. Phys. Chem. B 2021, 125, 6231–6243. [Google Scholar] [CrossRef]
- Mazo, R.M. Statistical Mechanical Theory of Solutions. J. Chem. Phys. 1958, 29, 1122–1128. [Google Scholar] [CrossRef]
- Ben-Naim, A. Molecular Theory of Solutions; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- O’Connell, J.P.; Haile, J.M. Thermodynamics: Fundamentals for Applications; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Chialvo, A.A.; Crisalle, O.D. On the behavior of the osmotic second virial coefficients of gases in aqueous solutions: Rigorous results, accurate approximations, and experimental evidence. J. Chem. Phys. 2019, 150, 124503. [Google Scholar] [CrossRef]
- Chialvo, A.A. Determination of Excess Gibbs Free Energy from Computer Simulation Via the Single Charging-integral Approach. I. Theory. J. Chem. Phys. 1990, 92, 673–679. [Google Scholar] [CrossRef]
- Levelt Sengers, J.M.H. Solubility Near the Solvent’s Critical Point. J. Supercrit. Fluids 1991, 4, 215–222. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Crisalle, O.D. Solute-Induced Perturbation of the Solvent Microstructure in Aqueous Electrolyte Solutions: Some Uses and Misuses of Structure Making/Breaking Criteria. Liquids 2022, 2, 106–130. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Crisalle, O.D. On the Molecular-Based Thermodynamics of Dilute Solutions Along Orthobaric Conditions Concise review of the fundamental microscopic constraints, rigorous formal results, and macroscopic modeling implications. J. Mol. Liq. 2023, 390, 122901. [Google Scholar] [CrossRef]
- Chialvo, A.A. Alternative Approach to Modeling Excess Gibbs Free Energy in Terms of Kirkwood-Buff Integrals. In Advances in Thermodynamics; Matteoli, E., Mansoori, G.A., Eds.; Taylor & Francis: New York, NY, USA, 1990; Volume 2, pp. 131–173. [Google Scholar]
- Koga, K.; Holten, V.; Widom, B. Deriving Second Osmotic Virial Coefficients from Equations of State and from Experiment. J. Phys. Chem. B 2015, 119, 13391–13397. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, A.A.; Crisalle, O.D. Gas Solubility and Preferential Solvation Phenomena in Mixed-Solvents; Rigorous relations between microscopic behavior, solvation properties, and solution non-ideality. Fluid Phase Equilibria 2024, 581, 114081. [Google Scholar] [CrossRef]
- Chialvo, A.A. Molecular-Based Description of the Osmotic Second Virial Coefficients of Electrolytes: Rigorous Formal Links to Solute−Solvent Interaction Asymmetry, Virial Expansion Paths, and Experimental Evidence. J. Phys. Chem. B 2022, 126, 4339–4353. [Google Scholar] [CrossRef]
- Schmitt, W.J.; Reid, R.C. The Use of Entrainers in Modifying the Solubility of Phenanthrene and Benzoic Acid in Supercritical Carbon Dioxide and Ethane. Fluid Phase Equilibria 1986, 32, 77–99. [Google Scholar] [CrossRef]
- Chialvo, A.A. Solute-Solute and Solute-Solvent Correlations in Dilute Near-Critical Ternary Mixtures: Mixed Solute and Entrainer Effects. J. Phys. Chem. 1993, 97, 2740–2744. [Google Scholar] [CrossRef]
- Gutkowski, K.I.; Fernandez-Prini, R.; Japas, M.L. Solubility of solids in near-critical conditions: Effect of a third component. J. Phys. Chem. B 2008, 112, 5671–5679. [Google Scholar] [CrossRef]
- Shimizu, S.; Abbott, S. How Entrainers Enhance Solubility in Supercritical Carbon Dioxide. J. Phys. Chem. B 2016, 120, 3713–3723. [Google Scholar] [CrossRef]
- Lei, Z.G.; Wang, H.Y.; Zhou, R.Q.; Duan, Z.T. Influence of salt added to solvent on extractive distillation. Chem. Eng. J. 2002, 87, 149–156. [Google Scholar] [CrossRef]
- Zhao, J.; Dong, C.C.; Li, C.X.; Meng, H.; Wang, Z.H. Isobaric vapor-liquid equilibria for ethanol-water system containing different ionic liquids at atmospheric pressure. Fluid Phase Equilibria 2006, 242, 147–153. [Google Scholar] [CrossRef]
- Smith, P.E. Equilibrium dialysis data and the relationships between preferential interaction parameters for biological systems in terms of Kirkwood-Buff integrals. J. Phys. Chem. B 2006, 110, 2862–2868. [Google Scholar] [CrossRef]
- Chialvo, A.A. Preferential Solvation Phenomena as Solute-induced Structure-Making/Breaking Processes: Linking thermodynamic preferential interaction parameters to fundamental structure making/breaking functions. J. Phys. Chem. B 2024, 128, 5228–5245. [Google Scholar] [CrossRef]
- Ben-Naim, A. Theory of Preferential Solvation of Non-Electrolytes. Cell Biophys. 1988, 12, 255–269. [Google Scholar] [CrossRef]
- Shimizu, S.; Matubayasi, N. Preferential hydration of proteins: A Kirkwood-Buff approach. Chem. Phys. Lett. 2006, 420, 518–522. [Google Scholar] [CrossRef]
- Smiatek, J. Aqueous ionic liquids and their effects on protein structures: An overview on recent theoretical and experimental results. J. Phys. Condens. Matter 2017, 29, 233001. [Google Scholar] [CrossRef]
- Hepler, L.G. Thermal Expansion and Structure in Water and Aqueous Solutions. Can. J. Chem. 1969, 47, 4613–4617. [Google Scholar] [CrossRef]
- Chialvo, A.A. Gas Solubility in Dilute Solutions: A Novel Molecular Thermodynamic Perspective. J. Chem. Phys. 2018, 148, 174502. [Google Scholar] [CrossRef]
- Jani, A.; Malfait, B.; Morineau, D. On the coupling between ionic conduction and dipolar relaxation in deep eutectic solvents: Influence of hydration and glassy dynamics. J. Chem. Phys. 2021, 154, 164508. [Google Scholar] [CrossRef]
- Balos, V.; Kaliannan, N.K.; Elgabarty, H.; Wolf, M.; Kuhne, T.D.; Sajadi, M. Time-resolved terahertz-Raman spectroscopy reveals that cations and anions distinctly modify intermolecular interactions of water. Nat. Chem. 2022, 14, 1031–1104. [Google Scholar] [CrossRef]
- Jones, G.; Dole, M. The viscosity of aqueous solutions of strong electrolytes with special reference to barium chloride. J. Am. Chem. Soc. 1929, 51, 2950–2964. [Google Scholar] [CrossRef]
- Gurney, R.W. Ionic Processes in Solution; McGraw Hill: New York, NY, USA, 1953. [Google Scholar]
- Kaminsky, M. Ion-Solvent Interaction and the Viscosity of Strong Electrolyte Solutions. Discuss. Faraday Soc. 1957, 24, 171–179. [Google Scholar] [CrossRef]
- Nightingale, E.R. Phenomenological Theory of Ion Solvation: Effective Radii of Hydrated Ions. J. Phys. Chem. 1959, 63, 1381–1387. [Google Scholar] [CrossRef]
- Tsangaris, J.M.; Martin, R.B. Viscosities of Aqueous Solutions of Dipolar Ions. Arch. Biochem. Biophys. 1965, 112, 267–272. [Google Scholar] [CrossRef]
- Out, D.J.P.; Los, J.M. Viscosity of aqueous solutions of univalent electrolytes from 5 to 95 °C. J. Solut. Chem. 1980, 9, 19–35. [Google Scholar] [CrossRef]
- Hertz, H.G.; Maurer, R.; Killie, S. An NMR-Study of Dynamics in Aqueous Strong Acid Solutions. 1. The B’ Coefficients. Z. Phys. Chem. Int. J. Res. Phys. Chem. Chem. Phys. 1991, 172, 157–183. [Google Scholar]
- Jenkins, H.D.B.; Marcus, Y. Viscosity B-coefficients of ions in solution. Chem. Rev. 1995, 95, 2695–2724. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Ren, X.F.; Ma, Y.G. Densities and Viscosities of Amino Acid plus Xylitol plus Water Solutions at 293.15 <= T/K <= 323.15. J. Chem. Eng. Data 2017, 62, 477–490. [Google Scholar]
- Gupta, J.; Nain, A.K. Physicochemical study of solute-solute and solute-solvent interactions of homologous series of alpha-amino acids in aqueous-isoniazid solutions at temperatures from 293.15 to 318.15 K. J. Mol. Liq. 2019, 278, 262–278. [Google Scholar] [CrossRef]
- Rani, R.; Kumar, A.; Sharma, T.; Sharma, T.; Bamezai, R.K. Volumetric, acoustic and transport properties of ternary solutions of L-serine and L-arginine in aqueous solutions of thiamine hydrochloride at different temperatures. J. Chem. Thermodyn. 2019, 135, 260–277. [Google Scholar] [CrossRef]
- Sawhney, N.; Kumar, M.; Sandarve; Sharma, P.; Sharma, A.K.; Sharma, M. Structure-making behaviour of L-arginine in aqueous solution of drug ketorolac tromethamine: Volumetric, compressibility and viscometric studies. Phys. Chem. Liq. 2019, 57, 184–203. [Google Scholar] [CrossRef]
- Stokes, R.H.; Mills, R. Viscosity of Electrolytes and Related Properties; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Dhondge, S.S.; Zodape, S.P.; Parwate, D.V. Volumetric and viscometric studies of some drugs in aqueous solutions at different temperatures. J. Chem. Thermodyn. 2012, 48, 207–212. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Crisalle, O.D. Can Jones-Dole’s B-coefficient Be a Consistent Structure Making/Breaking Marker? Rigorous molecular-based analysis and critical assessment of its marker uniqueness. J. Phys. Chem. B 2021, 125, 12028–12041. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Crisalle, O.D. On the Transition-State theory approach to the Jones-Dole’s viscosity B-coefficient: A novel molecular-based interpretation, assessment of its implications, and experimental evidence. J. Mol. Liq. 2023, 379, 121548. [Google Scholar] [CrossRef]
- Abdulagatov, I.M.; Zeinalova, A.B.; Azizov, N.D. Viscosity of aqueous Ni(NO3)2 solutions at temperatures from (297 to 475) K and at pressures up to 30 MPa and concentration between (0.050 and 2.246) mol·kg−1. J. Chem. Thermodyn. 2006, 38, 179–189. [Google Scholar] [CrossRef]
- Abdulagatov, I.; Azizov, N. Experimental Study of the Effect of Temperature, Pressure, and Concentration on the Viscosity of Aqueous KBr Solutions. J. Solut. Chem. 2008, 37, 3–26. [Google Scholar] [CrossRef]
- Liu, Q.; Dai, H.; Chi, H.; Shi, K.; Zheng, Q.; Qi, Y. The density and dynamic viscosity for dilute solutions of [Emim][NTf2] [Bmim][NTf2], and [Bmmim][NTf2] in ethylene glycol. J. Mol. Liq. 2023, 371, 121080. [Google Scholar] [CrossRef]
- Feakins, D.; Freemantle, D.J.; Lawrence, K.G. Transition-State Treatment of Relative Viscosity of Electrolyte Solutions: Applications to Aqueous, Non-Aqueous and Metanol+Water Systems. J. Chem. Soc. Faraday Trans. I 1974, 70, 795–806. [Google Scholar] [CrossRef]
- Feakins, D.; Waghorne, W.E.; Lawrence, K.G. The Viscosity and Structure of Solutions. 1. A New Theory of the Jones-Dole B-coefficient and the Related Activation Parameters—Applications to Aqueous Solutions. J. Chem. Soc. Faraday Trans. I 1986, 82, 563–568. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.J.; Eyring, H. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena; McGraw-Hill Book Company, Inc.: Chicago, IL, USA, 1941. [Google Scholar]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd (revised) ed.; Butterworths: London, UK, 1970. [Google Scholar]
- Conway, B.E. Ionic Hydration in Chemistry and Biophysics; Elsevier: Amsterdam, The Netherlands, 1981; Volume 12. [Google Scholar]
- Franks, F. Water: A Matrix of Life; Royal Society of Chemistry: London, UK, 2000. [Google Scholar]
- Waghorne, W.E. Viscosities of electrolyte solutions. Philos. Trans. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci. 2001, 359, 1529–1543. [Google Scholar] [CrossRef]
- Hammadi, A. Electrical Conductance, Density, and Viscosity in Mixtures of Alkali-Metal Halides and Glycerol. Int. J. Thermophys. 2004, 25, 89–111. [Google Scholar] [CrossRef]
- Jindal, R.; Singla, M.; Kumar, H. Transport behavior of aliphatic amino acids glycine/L-alanine/L-valine and hydroxyl amino acids L-serine/L-threonine in aqueous trilithium citrate solutions at different temperatures. J. Mol. Liq. 2015, 206, 343–349. [Google Scholar] [CrossRef]
- Gadzuric, S.; Tot, A.; Armakovic, S.; Armakovic, S.; Panic, J.; Jovic, B.; Vranes, M. Uncommon structure making/breaking behaviour of cholinium taurate in water. J. Chem. Thermodyn. 2017, 107, 58–64. [Google Scholar] [CrossRef]
- Zafarani-Moattar, M.T.; Shekaari, H.; Mostafavi, H.; Jafari, P. Thermodynamic and transport properties of aqueous solutions containing cholinium L-alaninate and polyethylene glycol dimethyl ether 250: Evaluation of solute-solvent interactions and phase separation. J. Chem. Thermodyn. 2019, 132, 9–22. [Google Scholar] [CrossRef]
- Marcus, Y. Ions in Solution and Their Solvation; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Batchelor, J.D.; Olteanu, A.; Tripathy, A.; Pielak, G.J. Impact of protein denaturants and stabilizers on water structure. J. Am. Chem. Soc. 2004, 126, 1958–1961. [Google Scholar] [CrossRef]
- Hood, G.R. The viscosity of urea in aqueous solution. Phys. A J. Gen. Appl. Phys. 1933, 4, 211–214. [Google Scholar] [CrossRef]
- Herskovits, T.T.; Kelly, T.M. Viscosity Studies of Aqueous Solutions of Alcohols, ureas, and Amides. J. Phys. Chem. 1973, 77, 381–388. [Google Scholar] [CrossRef]
- Egorov, G.I.; Makarov, D.M. Densities and Volumetric Properties of Aqueous Solutions of {Water (1) + N-Methylurea (2)} Mixtures at Temperatures of 274.15-333.15 K and at Pressures up to 100 MPa. J. Chem. Eng. Data 2017, 62, 4383–4394. [Google Scholar] [CrossRef]
- Singh, M.; Kumar, A. Hydrophobic interactions of methylureas in aqueous solutions estimated with density, molal volume, viscosity and surface tension from 293.15 to 303.15 K. J. Solut. Chem. 2006, 35, 567–582. [Google Scholar] [CrossRef]
- Panic, J.; Vranes, M.; Tot, A.; Ostojic, S.; Gadzuric, S. The organisation of water around creatine and creatinine molecules. J. Chem. Thermodyn. 2019, 128, 103–109. [Google Scholar] [CrossRef]
- Richu; Kumar, A. A Comprehensive Study on Molecular Interactions of l-Ascorbic Acid/Nicotinic Acid in Aqueous [BMIm]Br at Varying Temperatures and Compositions: Spectroscopic and Thermodynamic Insights. J. Chem. Eng. Data 2021, 66, 3859–3880. [Google Scholar] [CrossRef]
- Sharma, R.; Thakur, R.C.; Kumar, H. Study of viscometric properties of L-ascorbic acid in binary aqueous mixtures of D-glucose and D-fructose. Phys. Chem. Liq. 2018, 57, 139–150. [Google Scholar] [CrossRef]
- Hossain, M.F.; Biswas, T.K.; Islam, M.N.; Huque, M.E. Volumetric and viscometric studies on dodecyltrimethylammonium bromide in aqueous and in aqueous amino acid solutions in premicellar region. Monatshefte Chem. 2010, 141, 1297–1308. [Google Scholar] [CrossRef][Green Version]
- Banipal, T.S.; Beni, A.; Kaur, N.; Banipal, P.K. Volumetric, Viscometric and Spectroscopic Approach to Study the Solvation Behavior of Xanthine Drugs in Aqueous Solutions of NaCl at T = 288.15-318.15 K and at p = 101.325 kPa. J. Chem. Eng. Data 2017, 62, 20–34. [Google Scholar] [CrossRef]
- Vranes, M.; Tot, A.; Jankovic, N.; Gadzuric, S. What is the taste of vitamin-based ionic liquids? J. Mol. Liq. 2019, 276, 902–909. [Google Scholar] [CrossRef]
- Rudan-Tasic, D.; Klofutar, C.; Horvat, J. Viscosity of aqueous solutions of some alkali cyclohexylsulfamates at 25.0 degrees C. Food Chem. 2004, 86, 161–167. [Google Scholar] [CrossRef]
- Horvat, J.; Bester-Rogac, M.; Klofutar, C.; Rudan-Tasic, D. Viscosity of aqueous solutions of lithium, sodium, potassium, rubidium and caesium cyclohexylsulfamates from 293.15 to 323.15 k. J. Solut. Chem. 2008, 37, 1329–1342. [Google Scholar] [CrossRef]
- Dunn, L.A. Apparent Molar Volumes of Electrolytes.3: Some 1-1 and 2-1 Electrolytes in Aqueous Solution at 0, 5. 15. 35, 45, 55, and 65 Degrees C. Trans. Faraday Soc. 1968, 64, 2951–2961. [Google Scholar] [CrossRef]
- Abdulagatov, I.M.; Azizov, N.D. Viscosity of aqueous calcium chloride solutions at high temperatures and high pressures. Fluid Phase Equilibria 2006, 240, 204–219. [Google Scholar] [CrossRef]
- Herrington, T.M.; Roffey, M.G.; Smith, D.P. Densities of Aqueous Electrolytes MnCl2, CoCl2, NiCl2, ZnCl2, and CdCl2 from 25 degrees to 72 degrees at 1 atm. J. Chem. Eng. Data 1986, 31, 221–225. [Google Scholar] [CrossRef]
- Sonika; Thakur, R.C.; Chauhan, S.; Singh, K. Molecular Interactions of Transition Metal Chlorides in Water and Water–Ethanol Mixtures at 298–318 K on Viscometric Data. Russ. J. Phys. Chem. A 2018, 92, 2701–2709. [Google Scholar] [CrossRef]
- Apelblat, A. A new two-parameter equation for correlation and prediction of densities as a function of concentration and temperature in binary aqueous solutions. J. Mol. Liq. 2016, 219, 313–331. [Google Scholar] [CrossRef]
- Clegg, S.L.; Wexler, A.S. Densities and Apparent Molar Volumes of Atmospherically Important Electrolyte Solutions. 1. The Solutes H2SO4, HNO3, HCl, Na2SO4, NaNO3, NaCl, (NH4)(2)SO4, NH4NO3, and NH4Cl from 0 to 50 degrees C, Including Extrapolations to Very Low Temperature and to the Pure Liquid State, and NaHSO4, NaOH, and NH3 at 25 degrees C. J. Phys. Chem. A 2011, 115, 3393–3460. [Google Scholar]
- Campbell, A.N.; Friesen, R.J. Conductance in the Range of Medium Concentration. Can. J. Chem.-Rev. Can. Chim. 1959, 37, 1288–1293. [Google Scholar] [CrossRef]
- Laliberte, M.; Cooper, W.E. Model for calculating the density of aqueous electrolyte solutions. J. Chem. Eng. Data 2004, 49, 1141–1151. [Google Scholar] [CrossRef]
- Sarma, T.S.; Ahluwalia, J.C. Experimental Studies on Structure of Aqueous Solutions of Hydrophobic Solutes. Chem. Soc. Rev. 1973, 2, 203–232. [Google Scholar] [CrossRef]
- Sanyal, S.K.; Mandal, S.K. Viscosity B-Coefficients of Alkyl Carboxylates. Electrochim. Acta 1983, 28, 1875–1876. [Google Scholar]
- Tamaki, K.; Ohara, Y.; Watanabe, S. Solution Properties of Sodium Perfluoralkanoates. Heats of Solution, Viscosity B-coefficients, and Surface Tensions. Bull. Chem. Soc. Jpn. 1989, 62, 2497–2501. [Google Scholar] [CrossRef]
- Zhao, H. Viscosity B-coefficients and standard partial molar volumes of amino acids, and their roles in interpreting the protein (enzyme) stabilization. Biophys. Chem. 2006, 122, 157–183. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jayabalakrishnan, S.S. Volumetric, ultrasonic speed, and viscometric studies of salbutamol sulphate in aqueous methanol solution at different temperatures. J. Chem. Thermodyn. 2010, 42, 984–993. [Google Scholar] [CrossRef]
- Kabiraz, D.C.; Biswas, T.K.; Huque, M.E. Physico-chemical properties of some electrolytes in water and aqueous sodiumdodecyl sulfate solutions at different temperatures. J. Chem. Thermodyn. 2011, 43, 1917–1923. [Google Scholar] [CrossRef]
- Banipal, T.S.; Kaur, N.; Kaur, A.; Gupta, M.; Banipal, P.K. Effect of food preservatives on the hydration properties and taste behavior of amino acids: A volumetric and viscometric approach. Food Chem. 2015, 181, 339–346. [Google Scholar] [CrossRef]
- Kumar, K.; Patial, B.S.; Chauhan, S. Interactions of Saccharides in Aqueous Glycine and Leucine Solutions at Different Temperatures of (293.15 to 313.15) K: A Viscometric Study. J. Chem. Eng. Data 2015, 60, 47–56. [Google Scholar] [CrossRef]
- Sharma, S.K.; Singh, G.; Kumar, H.; Kataria, R. Densities, Sound Speed, and Viscosities of Some Amino Acids with Aqueous Tetra-Butyl Ammonium Iodide Solutions at Different Temperatures. J. Chem. Eng. Data 2015, 60, 2600–2611. [Google Scholar] [CrossRef]
- Sarmad, S.; Zafarani-Moattar, M.T.; Nikjoo, D.; Mikkola, J.P. How Different Electrolytes Can Influence the Aqueous Solution Behavior of 1-Ethyl-3-Methylimidazolium Chloride: A Volumetric, Viscometric, and Infrared Spectroscopy Approach. Front. Chem. 2020, 8, 593786. [Google Scholar] [CrossRef]
- Nain, A.K. Insight into solute-solute and solute-solvent interactions of l-proline in aqueous-D-xylose/L-arabinose solutions by using physicochemical methods at temperatures from 293.15 to 318.15 K. J. Mol. Liq. 2020, 318, 114190. [Google Scholar] [CrossRef]
- Rajput, P.; Richu; Sharma, T.; Kumar, A. Temperature dependent physicochemical investigations of some nucleic acid bases (uracil, thymine and adenine) in aqueous inositol solutions. J. Mol. Liq. 2021, 326, 115210. [Google Scholar] [CrossRef]
- Brinzei, M.; Ciocirlan, O. Volumetric and transport properties of ternary solutions of L-serine and L-valine in aqueous NaCl solutions in the temperature range (293.15–323.15) K. J. Chem. Thermodyn. 2021, 154, 106335. [Google Scholar] [CrossRef]
- Bronshtein, I.N.; Semendyayev, A.K. Handbook of Mathematics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Feakins, D.; Bates, F.M.; Waghorne, W.E.; Lawrence, K.G. Relative Viscosities and Quasi-Thermodynamics of Solutions of Ter-Butyl Alcohol in the Methanol-Water System—A Different View of the Alkyl Water Interaction. J. Chem. Soc. Faraday Trans. 1993, 89, 3381–3388. [Google Scholar] [CrossRef]
- Haldar, P.; Das, B. Viscosities of some tetraalkylammonium bromides in 2-ethoxyethanol at 308.15, 313.15, 318.15, and 323.15 K. Can. J. Chem. 2005, 83, 499–504. [Google Scholar] [CrossRef]
- Xu, W.G.; Qi, W.S.; Zhang, Z.H.; Tong, J. Volumetric and viscometric investigation of aqueous solution of Bmim BF4 from 288.15 to 318.15 K. J. Mol. Liq. 2019, 278, 600–606. [Google Scholar] [CrossRef]
- Gupta, J.; Chand, D.; Nain, A.K. Study to reconnoiter solvation consequences of l-arginine/l-histidine and sodium salicylate in aqueous environment probed by physicochemical approach in the temperature range (293.15–318.15) K. J. Mol. Liq. 2020, 305, 112848. [Google Scholar] [CrossRef]
- Ankita; Nain, A.K. Solute-solute and solute-solvent interactions of drug sodium salicylate in aqueous-glucose/sucrose solutions at temperatures from 293.15 to 318.15 K: A physicochemical study. J. Mol. Liq. 2020, 298, 112006. [Google Scholar] [CrossRef]
- Vraneš, M.; Rackov, S.; Papović, S.; Pilić, B. The study of interactions in aqueous solutions of 1-alkyl-3-(3-butenyl)imidazolium bromide ionic liquids. J. Chem. Thermodyn. 2021, 159, 106479. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, L.Q.; Xiong, D.G.; Zhang, Z.; Yu, J.; Cai, J.X.; Yang, Z.Y. Density and viscosity behaviour of EBPBF4, TBPBF4 and HBPBF4 in acetonitrile solutions at different temperatures at T = (293.15–323.15) K. J. Chem. Thermodyn. 2021, 158, 106467. [Google Scholar] [CrossRef]
- Sharma, T.; Bandral, A.; Bamezai, R.K.; Kumar, A. Interaction behavior of sucrose in aqueous tributylmethylammonium chloride solutions at various temperatures: A volumetric, ultrasonic and viscometric study. Chem. Thermodyn. Therm. Anal. 2022, 6, 100043. [Google Scholar] [CrossRef]
- Yao, D.D.; Tang, P.C.; Song, P.; Sun, Z. Viscosities and Densities of Mixed Aqueous Alkali Metal Nitrate Solutions at T = (293.15–333.15) K. J. Chem. Eng. Data 2022, 67, 2088–2097. [Google Scholar] [CrossRef]
- Tong, J.; Zheng, X.; Li, H.; Tong, J.; Liu, Q.S. Densities and Viscosities of Aqueous Amino Acid Ionic Liquids C(n)mim Ala (n = 3, 4, 5). J. Chem. Eng. Data 2017, 62, 2501–2508. [Google Scholar] [CrossRef]
- Li, X.R.; Qin, Y.; Xu, W.G.; Liu, J.G.; Yang, J.Z.; Xu, Q.; Yan, C.W. Investigation of electrolytes of the vanadium redox flow battery (IV): Measurement and prediction of viscosity of aqueous VOSO4 solution at 283.15 to 323.15 K. J. Mol. Liq. 2016, 224, 893–899. [Google Scholar] [CrossRef]
- Banipal, T.S.; Singh, K.; Banipal, P.K.; Sood, A.K.; Singh, P.; Singh, G.; Patyar, P. Volumetric and Viscometric Studies of Some Metal Acetates in Aqueous Solutions at T = (288.15 to 318.15) K. J. Chem. Eng. Data 2008, 53, 2758–2765. [Google Scholar] [CrossRef]
- Roy, M.N.; Sah, R.S.; Pradhan, P.P.; Roy, P.K. Ion-Solvent and Ion-Ion Interactions of Phosphomolybdic Acid in Aqueous Solution of Catechol at 298.15, 308.15, and 318.15 K. Russ. J. Phys. Chem. A 2009, 83, 1887–1895. [Google Scholar] [CrossRef]
- Ameta, R.K.; Singh, M. Surface tension, viscosity, apparent molal volume, activation viscous flow energy and entropic changes of water plus alkali metal phosphates at T = (298.15, 303.15, 308.15) K. J. Mol. Liq. 2015, 203, 29–38. [Google Scholar] [CrossRef]
- Gupta, J.; Nain, A.K. Molecular interactions of gentamicin sulphate in aqueous-l-asparagine/l-glutamine solutions at different temperatures: Volumetric, acoustic and viscometric properties. J. Mol. Liq. 2019, 293, 111547. [Google Scholar] [CrossRef]
- Lin, L.N.; Brandts, J.F.; Brandts, J.M.; Plotnikov, V. Determination of the volumetric properties of proteins and other solutes using pressure perturbation calorimetry. Anal. Biochem. 2002, 302, 144–160. [Google Scholar] [CrossRef]
- Mitra, L.; Smolin, N.; Ravindra, R.; Royer, C.; Winter, R. Pressure perturbation calorimetric studies of the solvation properties and the thermal unfolding of proteins in solution—Experiments and theoretical interpretation. Phys. Chem. Chem. Phys. 2006, 8, 1249–1265. [Google Scholar] [CrossRef]
- Zhai, Y.; Okoro, L.; Cooper, A.; Winter, R. Applications of pressure perturbation calorimetry in biophysical studies. Biophys. Chem. 2011, 156, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Suladze, S.; Kahse, M.; Erwin, N.; Tomazic, D.; Winter, R. Probing volumetric properties of biomolecular systems by pressure perturbation calorimetry (PPC)—The effects of hydration, cosolvents and crowding. Methods 2015, 76, 67–77. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Cummings, P.T.; Kalyuzhnyi, Y.V. Solvation effect on kinetic rate constant of reactions in supercritical solvents. Aiche J. 1998, 44, 667–680. [Google Scholar] [CrossRef]
- Popper, K.R. Conjectures and Refutations: The Growth of Scientific Knowledge; Routledge: Oxfordshire, UK, 2002. [Google Scholar]
- Feynman, R.P. What Do You Care What Other People Think?: Further Adventures of a Curious Character; Norton & Company, Incorporated: New York, NY, USA, 1988. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).