Polarity of Aqueous Solutions
Abstract
1. Introduction
N = 61; r2 = 0.99991; SD = 0.014; F = 3,369,994,
2. Solvent Features Characterize the Physicochemical Properties of Aqueous Solutions
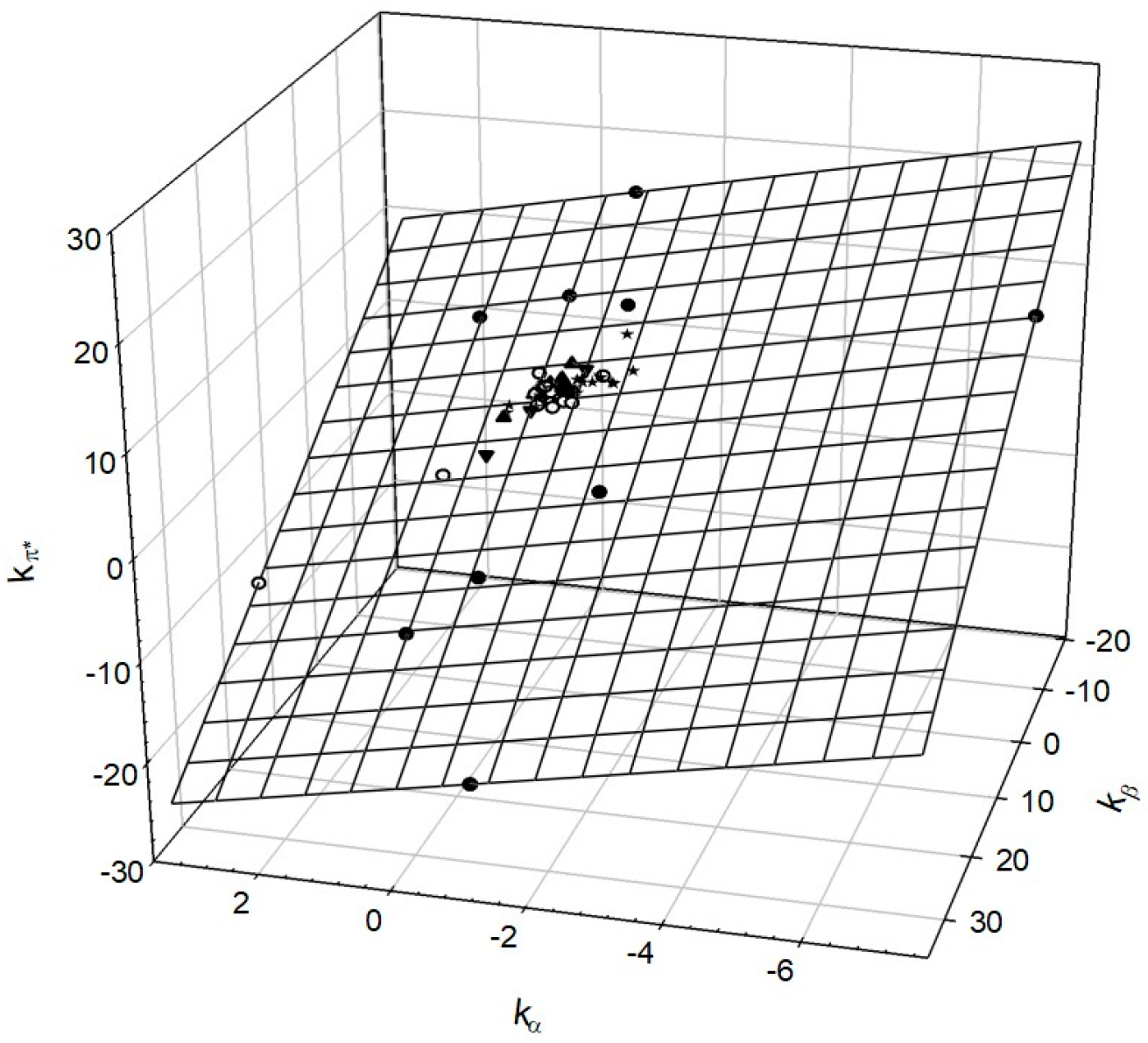
3. Solvent Properties of Aqueous Solutions Are Due to Rearrangement of Hydrogen Bonds
N = 7; r2 = 0.9976; SD = 0.004; F = 1973,
N = 7; r2 = 0.9901; SD = 0.006; F = 199,
N = 7; r2 = 0.9709; SD = 0.001; F = 167,
4. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guan, Y.; Lilley, T.H.; Treffry, T.E. A new excluded volume theory and its application to the coexistence curves of aqueous polymer two-phase systems. Macromolecules 1993, 26, 3971–3979. [Google Scholar] [CrossRef]
- Zaslavsky, B.Y.; Ferreira, L.A.; Uversky, V.N. Driving Forces of Liquid-Liquid Phase Separation in Biological Systems. Biomolecules 2019, 9, 473. [Google Scholar] [CrossRef]
- Boudh-Hir, M.-E.; Mansoori, G.A. Theory for interfacial tension of partially miscible liquids. Phys. A Stat. Mech. Its Appl. 1991, 179, 219–231. [Google Scholar] [CrossRef]
- Atefi, E.; Mann, J.A., Jr.; Tavana, H. Ultralow interfacial tensions of aqueous two-phase systems measured using drop shape. Langmuir 2014, 30, 9691–9699. [Google Scholar] [CrossRef] [PubMed]
- Bamberger, S.; Seaman, G.V.; Sharp, K.; Brooks, D.E. The effects of salts on the interfacial tension of aqueous dextran poly (ethylene glycol) phase systems. J. Colloid Interface Sci. 1984, 99, 194–200. [Google Scholar] [CrossRef]
- Forciniti, D.; Hall, C.; Kula, M. Interfacial tension of polyethyleneglycol-dextran-water systems: Influence of temperature and polymer molecular weight. J. Biotechnol. 1990, 16, 279–296. [Google Scholar] [CrossRef]
- Ryden, J.; Albertsson, P.-Å. Interfacial tension of dextran—Polyethylene glycol—Water two—Phase systems. J. Colloid Interface Sci. 1971, 37, 219–222. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Uversky, V.N.; Zaslavsky, B.Y. Modified binodal model describes phase separation in aqueous two-phase systems in terms of the effects of phase-forming components on the solvent features of water. J. Chromatogr. A 2018, 1567, 226–232. [Google Scholar] [CrossRef]
- da Silva, N.R.; Ferreira, L.A.; Madeira, P.P.; Teixeira, J.A.; Uversky, V.N.; Zaslavsky, B.Y. Analysis of partitioning of organic compounds and proteins in aqueous polyethylene glycol-sodium sulfate aqueous two-phase systems in terms of solute-solvent interactions. J. Chromatogr. A 2015, 1415, 1–10. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Fan, X.; Madeira, P.P.; Kurgan, L.; Uversky, V.N.; Zaslavsky, B.Y. Analyzing the effects of protecting osmolytes on solute–water interactions by solvatochromic comparison method: II. Globular proteins. RSC Adv. 2015, 5, 59780–59791. [Google Scholar] [CrossRef]
- Madeira, P.P.; Bessa, A.; Teixeira, M.A.; Alvares-Ribeiro, L.; Aires-Barros, M.R.; Rodrigues, A.E.; Zaslavsky, B.Y. Study of organic compounds-water interactions by partition in aqueous two-phase systems. J. Chromatogr. A 2013, 1322, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Tompa, H. Polymer Solutions; Butterworth Science Publications: London, UK, 1956. [Google Scholar]
- Minton, A.P. Influence of macromolecular crowding upon the stability and state of association of proteins: Predictions and observations. J. Pharm. Sci. 2005, 94, 1668–1675. [Google Scholar] [CrossRef]
- Zhou, H.X.; Rivas, G.; Minton, A.P. Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008, 37, 375–397. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. Explicit Incorporation of Hard and Soft Protein-Protein Interactions into Models for Crowding Effects in Protein Mixtures. 2. Effects of Varying Hard and Soft Interactions upon Prototypical Chemical Equilibria. J. Phys. Chem. B 2017, 121, 5515–5522. [Google Scholar] [CrossRef]
- Ando, T.; Yu, I.; Feig, M.; Sugita, Y. Thermodynamics of Macromolecular Association in Heterogeneous Crowding Environments: Theoretical and Simulation Studies with a Simplified Model. J. Phys. Chem. B 2016, 120, 11856–11865. [Google Scholar] [CrossRef]
- Hoppe, T.; Minton, A.P. Incorporation of Hard and Soft Protein-Protein Interactions into Models for Crowding Effects in Binary and Ternary Protein Mixtures. Comparison of Approximate Analytical Solutions with Numerical Simulation. J. Phys. Chem. B 2016, 120, 11866–11872. [Google Scholar] [CrossRef] [PubMed]
- Gnutt, D.; Gao, M.; Brylski, O.; Heyden, M.; Ebbinghaus, S. Excluded-volume effects in living cells. Angew. Chem. Int. Ed. 2015, 54, 2548–2551. [Google Scholar] [CrossRef]
- Wang, Y.; Sarkar, M.; Smith, A.E.; Krois, A.S.; Pielak, G.J. Macromolecular crowding and protein stability. J. Am. Chem. Soc. 2012, 134, 16614–16618. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Madeira, P.P.; Breydo, L.; Reichardt, C.; Uversky, V.N.; Zaslavsky, B.Y. Role of solvent properties of aqueous media in macromolecular crowding effects. J. Biomol. Struct. Dyn. 2016, 34, 92–103. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Uversky, V.N.; Zaslavsky, B.Y. Role of solvent properties of water in crowding effects induced by macromolecular agents and osmolytes. Mol. Biosyst. 2017, 13, 2551–2563. [Google Scholar] [CrossRef]
- Madeira, P.P.; Reis, C.A.; Rodrigues, A.E.; Mikheeva, L.M.; Zaslavsky, B.Y. Solvent properties governing solute partitioning in polymer/polymer aqueous two-phase systems: Nonionic compounds. J. Phys. Chem. B 2010, 114, 457–462. [Google Scholar] [CrossRef] [PubMed]
- Madeira, P.P.; Bessa, A.; de Barros, D.P.; Teixeira, M.A.; Alvares-Ribeiro, L.; Aires-Barros, M.R.; Rodrigues, A.E.; Chait, A.; Zaslavsky, B.Y. Solvatochromic relationship: Prediction of distribution of ionic solutes in aqueous two-phase systems. J. Chromatogr. A 2013, 1271, 10–16. [Google Scholar] [CrossRef]
- Marcus, Y. Effect of ions on the structure of water: Structure making and breaking. Chem. Rev. 2009, 109, 1346–1370. [Google Scholar] [CrossRef] [PubMed]
- Ball, P.; Hallsworth, J.E. Water structure and chaotropicity: Their uses, abuses and biological implications. Phys. Chem. Chem. Phys. 2015, 17, 8297–8305. [Google Scholar] [CrossRef]
- Zhang, Y.; Cremer, P.S. Interactions between macromolecules and ions: The Hofmeister series. Curr. Opin. Chem. Biol. 2006, 10, 658–663. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water as an active constituent in cell biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef]
- Titus, A.R.; Ferreira, L.A.; Belgovskiy, A.I.; Kooijman, E.E.; Mann, E.K.; Mann, J.A., Jr.; Meyer, W.V.; Smart, A.E.; Uversky, V.N.; Zaslavsky, B.Y. Interfacial tension and mechanism of liquid-liquid phase separation in aqueous media. Phys. Chem. Chem. Phys. 2020, 22, 4574–4580. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Gusev, N.B.; Uversky, V.N.; Zaslavsky, B.Y. Effect of human heat shock protein HspB6 on the solvent features of water in aqueous solutions. J. Biomol. Struct. Dyn. 2018, 36, 1520–1528. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Walczyk Mooradally, A.; Zaslavsky, B.; Uversky, V.N.; Graether, S.P. Effect of an Intrinsically Disordered Plant Stress Protein on the Properties of Water. Biophys. J. 2018, 115, 1696–1706. [Google Scholar] [CrossRef]
- Titus, A.R.; Madeira, P.P.; Ferreira, L.A.; Belgovskiy, A.I.; Mann, E.K.; Mann, J.A., Jr.; Meyer, W.V.; Smart, A.E.; Uversky, V.N.; Zaslavsky, B.Y. Arrangement of Hydrogen Bonds in Aqueous Solutions of Different Globular Proteins. Int. J. Mol. Sci. 2022, 23, 11381. [Google Scholar] [CrossRef]
- Madeira, P.P.; Passos, H.; Gomes, J.; Coutinho, J.A.P.; Freire, M.G. Alternative probe for the determination of the hydrogen-bond acidity of ionic liquids and their aqueous solutions. Phys. Chem. Chem. Phys. 2017, 19, 11011–11016. [Google Scholar] [CrossRef]
- Uversky, V.N. Natively unfolded proteins: A point where biology waits for physics. Protein Sci. 2002, 11, 739–756. [Google Scholar] [CrossRef]
- Tanford, C. The hydrophobic effect and the organization of living matter. Science 1978, 200, 1012–1018. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.D. The behavior of ions in water is controlled by their water affinity. Q Rev. Biophys. 2019, 52, e11. [Google Scholar] [CrossRef]
- Politi, R.; Sapir, L.; Harries, D. The impact of polyols on water structure in solution: A computational study. J. Phys. Chem. A 2009, 113, 7548–7555. [Google Scholar] [CrossRef] [PubMed]
- Perry, J.M.; Kanasaki, Y.N.; Karadakov, P.B.; Shimizu, S. Mechanism of dye solubilization and de-aggregation by urea. Dye. Pigment. 2021, 193, 109530. [Google Scholar] [CrossRef]
- Arakawa, T.; Uozaki, M.; Hajime Koyama, A. Modulation of small molecule solubility and protein binding by arginine. Mol. Med. Rep. 2010, 3, 833–836. [Google Scholar] [CrossRef]
- Hirano, A.; Kameda, T.; Arakawa, T.; Shiraki, K. Arginine-assisted solubilization system for drug substances: Solubility experiment and simulation. J. Phys. Chem. B 2010, 114, 13455–13462. [Google Scholar] [CrossRef]
- Garekani, H.A.; Sadeghi, F.; Ghazi, A. Increasing the aqueous solubility of acetaminophen in the presence of polyvinylpyrrolidone and investigation of the mechanisms involved. Drug Dev. Ind. Pharm. 2003, 29, 173–179. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ab Rani, M.A.; Brant, A.; Crowhurst, L.; Dolan, A.; Lui, M.; Hassan, N.H.; Hallett, J.P.; Hunt, P.A.; Niedermeyer, H.; Perez-Arlandis, J.M.; et al. Understanding the polarity of ionic liquids. Phys. Chem. Chem. Phys. 2011, 13, 16831–16840. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Abboud, J.L.; Taft, R.W. Solvatochromic Comparison Method. 6. Pi-Star Scale of Solvent Polarities. J. Am. Chem. Soc. 1977, 99, 6027–6038. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Taft, R.W. Solvatochromic Comparison Method. 1. Beta-Scale of Solvent Hydrogen-Bond Acceptor (Hba) Basicities. J. Am. Chem. Soc. 1976, 98, 377–383. [Google Scholar] [CrossRef]
- Taft, R.W.; Kamlet, M.J. Solvatochromic Comparison Method. 2. Alpha-Scale of Solvent Hydrogen-Bond Donor (Hbd) Acidities. J. Am. Chem. Soc. 1976, 98, 2886–2894. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Loureiro, J.A.; Gomes, J.; Uversky, V.N.; Madeira, P.P.; Zaslavsky, B.Y. Why physicochemical properties of aqueous solutions of various compounds are linearly interrelated. J. Mol. Liq. 2016, 221, 116–123. [Google Scholar] [CrossRef]
- Badyal, Y.; Saboungi, M.-L.; Price, D.; Shastri, S.; Haeffner, D.; Soper, A. Electron distribution in water. J. Chem. Phys. 2000, 112, 9206–9208. [Google Scholar] [CrossRef]
- Kemp, D.D.; Gordon, M.S. An interpretation of the enhancement of the water dipole moment due to the presence of other water molecules. J. Phys. Chem. A 2008, 112, 4885–4894. [Google Scholar] [CrossRef]
- Lakshmi, T.; Nandi, P. Effects of sugar solutions on the activity coefficients of aromatic amino acids and their N-acetyl ethyl esters. J. Phys. Chem. 1976, 80, 249–252. [Google Scholar] [CrossRef]
- Gekko, K. Mechanism of polyol-induced protein stabilization: Solubility of amino acids and diglycine in aqueous polyol solutions. J. Biochem. 1981, 90, 1633–1641. [Google Scholar] [CrossRef]
- Nozaki, Y.; Tanford, C. The Solubility of Amino Acids and Related Compounds in Aqueous Urea Solutions. J. Biol. Chem. 1963, 238, 4074–4081. [Google Scholar] [CrossRef]
- Heyden, M.; Brundermann, E.; Heugen, U.; Niehues, G.; Leitner, D.M.; Havenith, M. Long-range influence of carbohydrates on the solvation dynamics of water—Answers from terahertz absorption measurements and molecular modeling simulations. J. Am. Chem. Soc. 2008, 130, 5773–5779. [Google Scholar] [CrossRef]
- Arakawa, T.; Kita, Y.; Koyama, A.H. Solubility enhancement of gluten and organic compounds by arginine. Int. J. Pharm. 2008, 355, 220–223. [Google Scholar] [CrossRef] [PubMed]
- Malmberg, C.G.; Maryott, A.A. Dielectric constants of aqueous solutions of dextrose and sucrose. J. Res. Natl. Bur. Stand. 1950, 45, 299–303. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Uversky, V.N.; Zaslavsky, B.Y. Effects of amino acids on solvent properties of water. J. Mol. Liq. 2019, 277, 123–131. [Google Scholar] [CrossRef]
- Sasahara, K.; Uedaira, H. Solubility of amino acids in aqueous poly (ethylene glycol) solutions. Colloid Polym. Sci. 1993, 271, 1035–1041. [Google Scholar] [CrossRef]
- Tinjacá, D.A.; Muñoz, M.M.; Rahimpour, E.; Jouyban, A.; Martínez, F.; Acree, W.E., Jr. Solubility and apparent specific volume of sucrose in some aqueous polyethylene glycol mixtures at 298.2 K. Pharm. Sci. 2018, 24, 163–167. [Google Scholar] [CrossRef]
- Rytting, E.; Lentz, K.A.; Chen, X.-Q.; Qian, F.; Venkatesh, S. Aqueous and cosolvent solubility data for drug-like organic compounds. AAPS J. 2005, 7, E78–E105. [Google Scholar] [CrossRef] [PubMed]
- Atha, D.H.; Ingham, K.C. Mechanism of precipitation of proteins by polyethylene glycols. Analysis in terms of excluded volume. J. Biol. Chem. 1981, 256, 12108–12117. [Google Scholar] [CrossRef]
- Nayak, A.K.; Panigrahi, P.P. Solubility enhancement of etoricoxib by cosolvency approach. ISRN Phys. Chem. 2012, 2012, 820653. [Google Scholar] [CrossRef]
- Okubo, T.; Chen, S.-X.; Ise, N. Solubility of alkyl bromides in aqueous polymer solutions. Bull. Chem. Soc. Jpn. 1973, 46, 397–400. [Google Scholar] [CrossRef]
- Guptat, R.; Kumar, R.; Singla, A. Enhanced dissolution and absorption of trimethoprim from coprecipitates with polyethylene glycols and polyvinylpyrrolidone. Drug Dev. Ind. Pharm. 1991, 17, 463–468. [Google Scholar] [CrossRef]
- Bettinetti, G.; Mura, P.A.; Liguori, A.U.; Bramanti, G.; Giordano, F. Solubilization and interaction of naproxen with polyvinyl-pyrrolidone in aqueous solution and in the solid state. IL FARMACO. EDIZIONE PRATICA 1988, 43, 331–343. [Google Scholar] [PubMed]
- Ariki, R.; Hirano, A.; Arakawa, T.; Shiraki, K. Arginine increases the solubility of alkyl gallates through interaction with the aromatic ring. J. Biochem. 2011, 149, 389–394. [Google Scholar] [CrossRef]
- Arakawa, T.; Timasheff, S.N. Mechanism of poly(ethylene glycol) interaction with proteins. Biochemistry 1985, 24, 6756–6762. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Singh, J.; Gill, B.; Harikumar, S. SMEDDS: A novel approach for lipophilic drugs. Int. J. Pharm. Sci. Res. 2012, 3, 2441. [Google Scholar]
- Zaslavsky, B.Y.; Ferreira, L.A.; Uversky, V.N. Biophysical principles of liquid–liquid phase separation. In Droplets of Life; Academic Press: Cambridge, MA, USA, 2023; pp. 3–82. [Google Scholar]
- Rossi, S.; Lo Nostro, P.; Lagi, M.; Ninham, B.W.; Baglioni, P. Specific anion effects on the optical rotation of alpha-amino acids. J. Phys. Chem. B 2007, 111, 10510–10519. [Google Scholar] [CrossRef] [PubMed]
- Lo Nostro, P.; Ninham, B.W.; Milani, S.; Fratoni, L.; Baglioni, P. Specific anion effects on the optical rotation of glucose and serine. Biopolymers 2006, 81, 136–148. [Google Scholar] [CrossRef]
- Collander, R.; Lindholm, M.; Haug, C.M. The partition of organic compounds between higher alcohols and water. Acta Chem. Scand 1951, 5, 774–780. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A. Exploring QSAR.: Fundamentals and Applications in Chemistry and Biology; American Chemical Society: Washington, DC, USA, 1995; Volume 1. [Google Scholar]
- Ferreira, L.; Chervenak, A.; Placko, S.; Kestranek, A.; Madeira, P.; Zaslavsky, B. Responses of polar organic compounds to different ionic environments in aqueous media are interrelated. Phys. Chem. Chem. Phys. 2014, 16, 23347–23354. [Google Scholar] [CrossRef]
- Ferreira, L.A.; Chervenak, A.; Placko, S.; Kestranek, A.; Madeira, P.P.; Zaslavsky, B.Y. Effect of ionic composition on the partitioning of organic compounds in octanol–buffer systems. RSC Adv. 2015, 5, 20574–20582. [Google Scholar] [CrossRef]
- Masuda, K.; Haramaki, T.; Nakashima, S.; Habert, B.; Martinez, I.; Kashiwabara, S. Structural change of water with solutes and temperature up to 100 degrees C in aqueous solutions as revealed by attenuated total reflectance infrared spectroscopy. Appl. Spectrosc. 2003, 57, 274–281. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.-H.; Zhao, L.-J. ATR-FTIR spectroscopic studies on aqueous LiClO4, NaClO4, and Mg(ClO4)2 solutions. Phys. Chem. Chem. Phys. 2004, 6, 537–542. [Google Scholar] [CrossRef]
- Kitadai, N.; Sawai, T.; Tonoue, R.; Nakashima, S.; Katsura, M.; Fukushi, K. Effects of ions on the OH stretching band of water as revealed by ATR-IR spectroscopy. J. Solut. Chem. 2014, 43, 1055–1077. [Google Scholar] [CrossRef]
- Pavelec, J.; DiGuiseppi, D.; Zavlavsky, B.Y.; Uversky, V.N.; Schweitzer-Stenner, R. Perturbation of water structure by water-polymer interactions probed by FTIR and polarized Raman spectroscopy. J. Mol. Liq. 2019, 275, 463–473. [Google Scholar] [CrossRef]
- Kataoka, Y.; Kitadai, N.; Hisatomi, O.; Nakashima, S. Nature of hydrogen bonding of water molecules in aqueous solutions of glycerol by attenuated total reflection (ATR) infrared spectroscopy. Appl. Spectrosc. 2011, 65, 436–441. [Google Scholar] [CrossRef]
- Guo, Y.-C.; Li, X.-H.; Zhao, L.-J.; Zhang, Y.-H. Drawing out the structural information about the first hydration layer of the isolated Cl− anion through the FTIR-ATR difference spectra. J. Solut. Chem. 2013, 42, 459–469. [Google Scholar] [CrossRef]
- da Silva, N.; Ferreira, L.A.; Belgovskiy, A.I.; Madeira, P.P.; Teixeira, J.A.; Mann, E.K.; Mann, J.A., Jr.; Meyer, W.V.; Smart, A.E.; Chernyak, V.Y.; et al. Effects of different solutes on the physical chemical properties of aqueous solutions via rearrangement of hydrogen bonds in water. J. Mol. Liq. 2021, 335, 116288. [Google Scholar] [CrossRef]
- Brini, E.; Fennell, C.J.; Fernandez-Serra, M.; Hribar-Lee, B.; Luksic, M.; Dill, K.A. How Water’s Properties Are Encoded in Its Molecular Structure and Energies. Chem. Rev. 2017, 117, 12385–12414. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madeira, P.P.; Ferreira, L.A.; Uversky, V.N.; Zaslavsky, B.Y. Polarity of Aqueous Solutions. Liquids 2024, 4, 107-116. https://doi.org/10.3390/liquids4010005
Madeira PP, Ferreira LA, Uversky VN, Zaslavsky BY. Polarity of Aqueous Solutions. Liquids. 2024; 4(1):107-116. https://doi.org/10.3390/liquids4010005
Chicago/Turabian StyleMadeira, Pedro P., Luisa A. Ferreira, Vladimir N. Uversky, and Boris Y. Zaslavsky. 2024. "Polarity of Aqueous Solutions" Liquids 4, no. 1: 107-116. https://doi.org/10.3390/liquids4010005
APA StyleMadeira, P. P., Ferreira, L. A., Uversky, V. N., & Zaslavsky, B. Y. (2024). Polarity of Aqueous Solutions. Liquids, 4(1), 107-116. https://doi.org/10.3390/liquids4010005








