The Relevance of Cavity Creation for Several Phenomena Occurring in Water
Abstract
1. Introduction
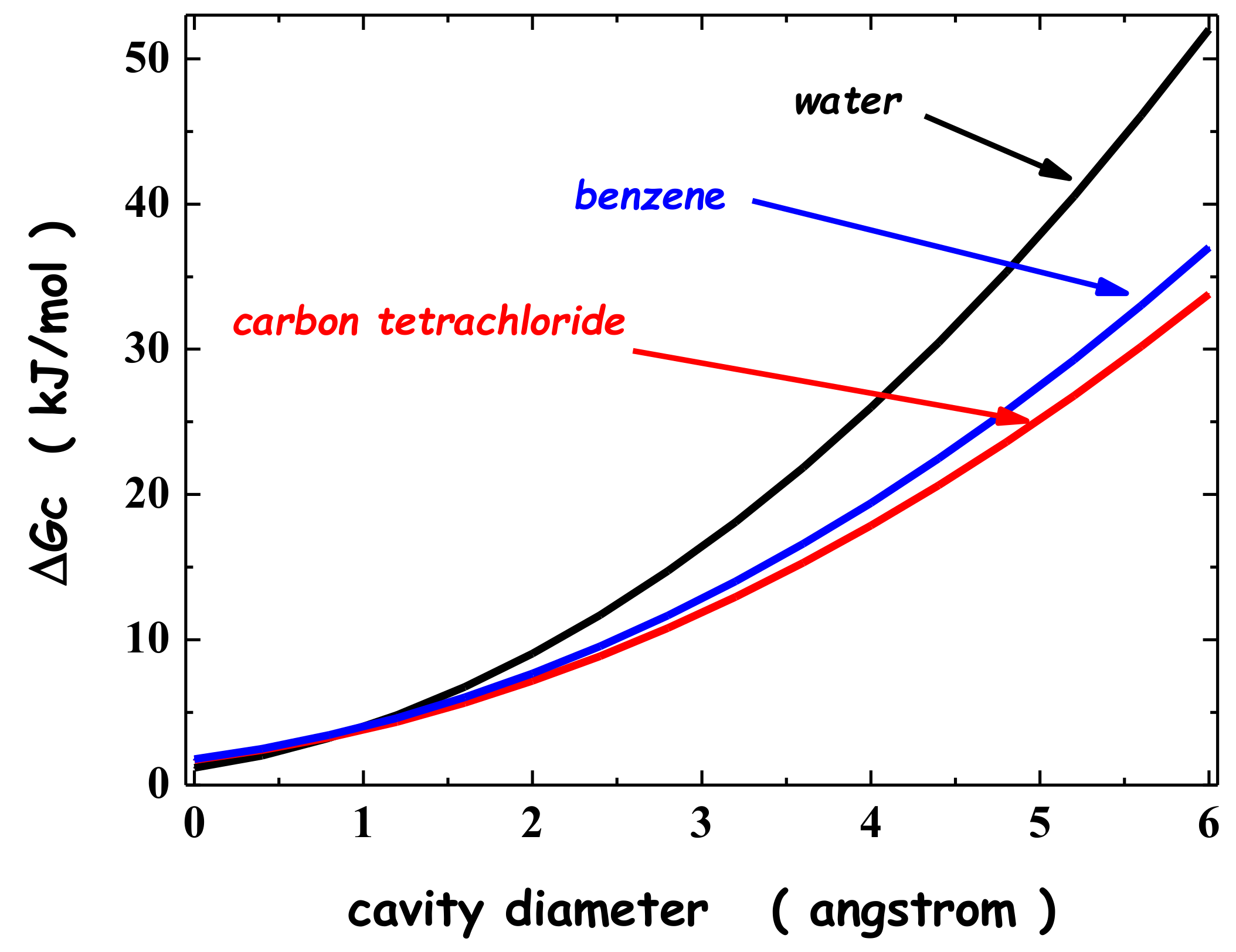
2. Solvation of Noble Gases
3. Formation of Host–Guest Complexes
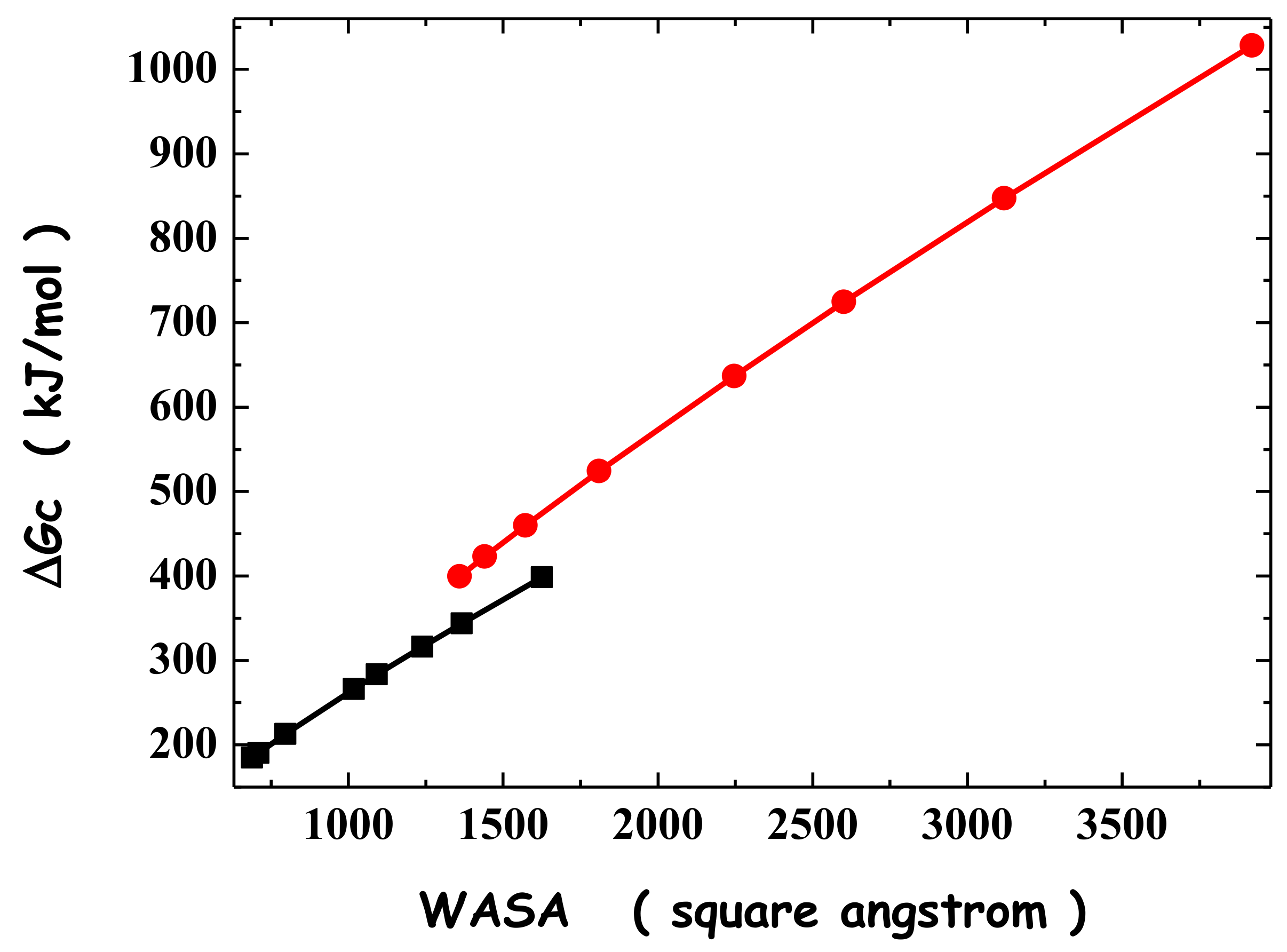
4. Conformational Stability of Globular Proteins
5. Conclusions
Funding
Conflicts of Interest
References
- Ben-Naim, A. Water and Aqueous Solutions; Springer US: Boston, MA, USA, 1974. [Google Scholar]
- Pratt, L.R.; Chandler, D. Theory of the hydrophobic effect. J. Chem. Phys. 1977, 67, 3683–3704. [Google Scholar] [CrossRef]
- Lee, B. The physical origin of the low solubility of nonpolar solutes in water. Biopolymers 1985, 24, 813–823. [Google Scholar] [CrossRef]
- Ben-Naim, A. Solvation Thermodynamics; Plenum Press: New York, NY, USA, 1987. [Google Scholar]
- Yu, H.; Karplus, M. A thermodynamic analysis of solvation. J. Chem. Phys. 1988, 89, 2366–2379. [Google Scholar] [CrossRef]
- Pohorille, A.; Pratt, L.R. Cavities in molecular liquids and the theory of hydrophobic solubilities. J. Am. Chem. Soc. 1990, 112, 5066–5074. [Google Scholar] [CrossRef]
- Blokzijl, W.; Engberts, J.B.F.N. Hydrophobic Effects. Opinions and Facts. Angew. Chem. Int. Ed. 1993, 32, 1545–1579. [Google Scholar] [CrossRef]
- Guillot, B.; Guissani, Y. A computer simulation study of the temperature dependence of the hydrophobic hydration. J. Chem. Phys. 1993, 99, 8075–8094. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Beutler, T.C.; Béguelin, D.R.; van Gunsteren, W.F. Free energy of cavity formation in solvent: Computational, methodological, and physical aspects. J. Chem. Phys. 1995, 102, 3787–3793. [Google Scholar] [CrossRef]
- Hummer, G.; Garde, S.; García, A.E.; Paulaitis, M.E.; Pratt, L.R. Hydrophobic Effects on a Molecular Scale. J. Phys. Chem. B 1998, 102, 10469–10482. [Google Scholar] [CrossRef]
- Lum, K.; Chandler, D.; Weeks, J.D. Hydrophobicity at Small and Large Length Scales. J. Phys. Chem. B 1999, 103, 4570–4577. [Google Scholar] [CrossRef]
- Lazaridis, T. Solvent Size vs Cohesive Energy as the Origin of Hydrophobicity. Acc. Chem. Res. 2001, 34, 931–937. [Google Scholar] [CrossRef]
- Southall, N.T.; Dill, K.A.; Haymet, A.D.J. A View of the Hydrophobic Effect. J. Phys. Chem. B 2002, 106, 521–533. [Google Scholar] [CrossRef]
- Pratt, L.R.; Pohorille, A. Hydrophobic Effects and Modeling of Biophysical Aqueous Solution Interfaces. Chem. Rev. 2002, 102, 2671–2692. [Google Scholar] [CrossRef]
- Benzi, C.; Cossi, M.; Improta, R.; Barone, V. Building cavities in a fluid of spherical or rod-like particles: A contribution to the solvation free energy in isotropic and anisotropic polarizable continuum model. J. Comput. Chem. 2005, 26, 1096–1105. [Google Scholar] [CrossRef]
- Chandler, D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Pratt, L.R. Contrasting Nonaqueous against Aqueous Solvation on the Basis of Scaled-Particle Theory. J. Phys. Chem. B 2007, 111, 9330–9336. [Google Scholar] [CrossRef]
- Ben-Amotz, D.; Underwood, R. Unraveling Water’s Entropic Mysteries: A Unified View of Nonpolar, Polar, and Ionic Hydration. Acc. Chem. Res. 2008, 41, 957–967. [Google Scholar] [CrossRef]
- Otto, S. The role of solvent cohesion in nonpolar solvation. Chem. Sci. 2013, 4, 2953–2959. [Google Scholar] [CrossRef]
- Ben-Amotz, D. Water-Mediated Hydrophobic Interactions. Annu. Rev. Phys. Chem. 2016, 67, 617–638. [Google Scholar] [CrossRef]
- Soda, K. Solvent Exclusion Effect Predicted by the Scaled Particle Theory as an Important Factor of the Hydrophobic Effect. J. Phys. Soc. Jpn. 1993, 62, 1782–1793. [Google Scholar] [CrossRef]
- Tang, K.E.; Bloomfield, V.A. Excluded Volume in Solvation: Sensitivity of Scaled-Particle Theory to Solvent Size and Density. Biophys. J. 2000, 79, 2222–2234. [Google Scholar] [CrossRef] [PubMed]
- Merlino, A.; Pontillo, N.; Graziano, G. A driving force for polypeptide and protein collapse. Phys. Chem. Chem. Phys. 2017, 19, 751–756. [Google Scholar] [CrossRef]
- Graziano, G. On the mechanism of cold denaturation. Phys. Chem. Chem. Phys. 2014, 16, 21755–21767. [Google Scholar] [CrossRef]
- Lee, B.; Richards, F. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 1971, 55, 379-IN4. [Google Scholar] [CrossRef]
- Reiss, H. Scaled Particle Methods in the Statistical Thermodynamics of Fluids. In Advances in Chemical Physics; Prigogine, I., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 1–84. [Google Scholar]
- Lebowitz, J.L.; Helfand, E.; Praestgaard, E. Scaled Particle Theory of Fluid Mixtures. J. Chem. Phys. 1965, 43, 774–779. [Google Scholar] [CrossRef]
- Pierotti, R.A. A scaled particle theory of aqueous and nonaqueous solutions. Chem. Rev. 1976, 76, 717–726. [Google Scholar] [CrossRef]
- Gallicchio, E.; Kubo, M.M.; Levy, R.M. Enthalpy−Entropy and Cavity Decomposition of Alkane Hydration Free Energies: Numerical Results and Implications for Theories of Hydrophobic Solvation. J. Phys. Chem. B 2000, 104, 6271–6285. [Google Scholar] [CrossRef]
- Graziano, G. Contrasting the hydration thermodynamics of methane and methanol. Phys. Chem. Chem. Phys. 2019, 21, 21418–21430. [Google Scholar] [CrossRef]
- Wilhelm, E.; Battino, R. Thermodynamic functions of the solubilities of gases in liquids at 25. deg. Chem. Rev. 1973, 73, 1–9. [Google Scholar] [CrossRef]
- Krause, D.; Benson, B.B. The solubility and isotopic fractionation of gases in dilute aqueous solution. IIa. solubilities of the noble gases. J. Solut. Chem. 1989, 18, 823–873. [Google Scholar] [CrossRef]
- Graziano, G. On the temperature dependence of hydration thermodynamics for noble gases. Phys. Chem. Chem. Phys. 1999, 1, 1877–1886. [Google Scholar] [CrossRef]
- Wilhelm, E.; Battino, R. Estimation of Lennard-Jones (6,12) Pair Potential Parameters from Gas Solubility Data. J. Chem. Phys. 1971, 55, 4012–4017. [Google Scholar] [CrossRef]
- Graziano, G. Salting out of methane by sodium chloride: A scaled particle theory study. J. Chem. Phys. 2008, 129, 084506. [Google Scholar] [CrossRef] [PubMed]
- Graziano, G. Scaled Particle Theory Study of the Length Scale Dependence of Cavity Thermodynamics in Different Liquids. J. Phys. Chem. B 2006, 110, 11421–11426. [Google Scholar] [CrossRef] [PubMed]
- Head-Gordon, T.; Hura, G. Water Structure from Scattering Experiments and Simulation. Chem. Rev. 2002, 102, 2651–2670. [Google Scholar] [CrossRef] [PubMed]
- Sedov, I.; Magsumov, T. The Gibbs free energy of cavity formation in a diverse set of solvents. J. Chem. Phys. 2020, 153, 134501. [Google Scholar] [CrossRef]
- Buchanan, P.; Aldiwan, N.; Soper, A.; Creek, J.; Koh, C. Decreased structure on dissolving methane in water. Chem. Phys. Lett. 2005, 415, 89–93. [Google Scholar] [CrossRef]
- Graziano, G.; Lee, B. On the Intactness of Hydrogen Bonds around Nonpolar Solutes Dissolved in Water. J. Phys. Chem. B 2005, 109, 8103–8107. [Google Scholar] [CrossRef]
- Bowron, D.T.; Filipponi, A.; Lobban, C.; Finney, J.L. Temperature-induced disordering of the hydrophobic hydration shell of Kr and Xe. Chem. Phys. Lett. 1998, 293, 33–37. [Google Scholar] [CrossRef]
- Kim, J.; Tian, Y.; Wu, J. Thermodynamic and Structural Evidence for Reduced Hydrogen Bonding among Water Molecules near Small Hydrophobic Solutes. J. Phys. Chem. B 2015, 119, 12108–12116. [Google Scholar] [CrossRef]
- Irudayam, S.J.; Henchman, R. Solvation theory to provide a molecular interpretation of the hydrophobic entropy loss of noble-gas hydration. J. Phys. Condens. Matter 2010, 22, 284108. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Besford, Q.A.; Mulvaney, T.; Gray-Weale, A. Order and correlation contributions to the entropy of hydrophobic solvation. J. Chem. Phys. 2015, 142, 114117. [Google Scholar] [CrossRef] [PubMed]
- Lee, B. A procedure for calculating thermodynamic functions of cavity formation from the pure solvent simulation data. J. Chem. Phys. 1985, 83, 2421–2425. [Google Scholar] [CrossRef]
- He, S.; Biedermann, F.; Vankova, N.; Zhechkov, L.; Heine, T.; Hoffman, R.E.; De Simone, A.; Duignan, T.T.; Nau, W.M. Cavitation energies can outperform dispersion interactions. Nat. Chem. 2018, 10, 1252–1257. [Google Scholar] [CrossRef]
- Biedermann, F.; Uzunova, V.D.; Scherman, O.A.; Nau, W.M.; De Simone, A. Release of High-Energy Water as an Essential Driving Force for the High-Affinity Binding of Cucurbit[n]urils. J. Am. Chem. Soc. 2012, 134, 15318–15323. [Google Scholar] [CrossRef] [PubMed]
- Biedermann, F.; Nau, W.; Schneider, H.-J. The Hydrophobic Effect Revisited-Studies with Supramolecular Complexes Imply High-Energy Water as a Noncovalent Driving Force. Angew. Chem. Int. Ed. 2014, 53, 11158–11171. [Google Scholar] [CrossRef]
- Setny, P.; Baron, R.; McCammon, J.A. How Can Hydrophobic Association Be Enthalpy Driven? J. Chem. Theory Comput. 2010, 6, 2866–2871. [Google Scholar] [CrossRef]
- Dzubiella, J. How Interface Geometry Dictates Water’s Thermodynamic Signature in Hydrophobic Association. J. Stat. Phys. 2011, 145, 227–239. [Google Scholar] [CrossRef]
- Graziano, G. Molecular driving forces of the pocket–ligand hydrophobic association. Chem. Phys. Lett. 2012, 533, 95–99. [Google Scholar] [CrossRef]
- Graziano, G. The Gibbs energy cost of cavity creation depends on geometry. J. Mol. Liq. 2015, 211, 1047–1051. [Google Scholar] [CrossRef]
- Wallqvist, A.; Berne, B.J. Molecular Dynamics Study of the Dependence of Water Solvation Free Energy on Solute Curvature and Surface Area. J. Phys. Chem. 1995, 99, 2885–2892. [Google Scholar] [CrossRef]
- Patel, A.; Varilly, P.; Chandler, D. Fluctuations of Water near Extended Hydrophobic and Hydrophilic Surfaces. J. Phys. Chem. B 2010, 114, 1632–1637. [Google Scholar] [CrossRef]
- Sosso, G.C.; Caravati, S.; Rotskoff, G.; Vaikuntanathan, S.; Hassanali, A. On the Role of Nonspherical Cavities in Short Length-Scale Density Fluctuations in Water. J. Phys. Chem. A 2016, 121, 370–380. [Google Scholar] [CrossRef]
- Ansari, N.; Laio, A.; Hassanali, A.A. Spontaneously Forming Dendritic Voids in Liquid Water Can Host Small Polymers. J. Phys. Chem. Lett. 2019, 10, 5585–5591. [Google Scholar] [CrossRef]
- Azizi, K.; Laio, A.; Hassanali, A. Model Folded Hydrophobic Polymers Reside in Highly Branched Voids. J. Phys. Chem. Lett. 2022, 13, 183–189. [Google Scholar] [CrossRef]
- Royer, C.A. Revisiting volume changes in pressure-induced protein unfolding. Biochim. et Biophys. Acta (BBA)—Protein Struct. Mol. Enzym. 2002, 1595, 201–209. [Google Scholar] [CrossRef]
- Chalikian, T.V. Volumetric Properties of Proteins. Annu. Rev. Biophys. Biomol. Struct. 2003, 32, 207–235. [Google Scholar] [CrossRef]

| σ Å | ε/k K | ΔH∙ kJ mol−1 | ΔS∙ J K−1mol−1 | ΔG∙ kJ mol−1 | ΔGC kJ mol−1 | Ea kJ mol−1 | ΔGC + Ea kJ mol−1 | ||
|---|---|---|---|---|---|---|---|---|---|
| a | He | 2.6 | 6 | 1.8 | −32.5 | 11.5 | 13.2 | −1.6 | 11.6 |
| Ne | 2.8 | 28 | −1.3 | −41.9 | 11.2 | 14.7 | −3.9 | 10.8 | |
| Ar | 3.4 | 125 | −9.6 | −60.4 | 8.4 | 20.0 | −11.3 | 8.7 | |
| Kr | 3.7 | 175 | −13.0 | −66.7 | 6.9 | 22.9 | −15.4 | 7.5 | |
| Xe | 4.0 | 230 | −16.8 | −74.8 | 5.5 | 26.0 | −20.2 | 5.8 | |
| b | Ar | 3.4 | 110 | 2.1 | −2.0 | 2.7 | 14.1 | −11.7 | 2.4 |
| c | Ar | 3.4 | 110 | 2.8 | −2.3 | 3.5 | 15.3 | −12.3 | 3.0 |
| Kr | 3.7 | 165 | −0.2 | −3.0 | 0.7 | 17.3 | −16.6 | 0.7 | |
| Xe | 3.4 | 240 | −5.5 | −8.7 | −2.9 | 19.4 | −22.1 | −2.7 |
| ΔHC kJ·mol−1 | ΔH∙ − Ea kJ·mol−1 | ΔSC J·K−1·mol−1 | ΔS∙ J·K−1·mol−1 | ||
|---|---|---|---|---|---|
| a | He | 2.1 | 3.4 | −37.2 | −32.5 |
| Ne | 2.3 | 2.6 | −41.6 | −41.9 | |
| Ar | 3.2 | 2.1 | −56.0 | −60.4 | |
| Kr | 3.7 | 2.4 | −64.1 | −66.7 | |
| Xe | 4.3 | 3.4 | −72.8 | −74.8 | |
| b | Ar | 13.4 | 13.8 | −2.3 | −2.0 |
| c | Ar | 14.9 | 15.1 | −1.3 | −2.3 |
| Kr | 17.1 | 16.4 | −0.7 | −3.0 | |
| Xe | 19.5 | 16.6 | 0.3 | −8.7 |
| a Å | l Å | WASAC Å2 | ΔGC kJ mol−1 | |
|---|---|---|---|---|
| A | 6.0 | - - | 688.1 | 184.7 |
| 5.0 | 4.85 | 709.7 | 190.5 | |
| 4.0 | 12.67 | 796.3 | 212.8 | |
| 3.0 | 28.00 | 1017.4 | 266.1 | |
| 2.8 | 33.00 | 1092.5 | 283.4 | |
| 2.5 | 42.75 | 1238.7 | 316.1 | |
| 2.3 | 51.37 | 1366.3 | 343.9 | |
| 2.0 | 69.31 | 1625.9 | 398.3 | |
| B | 9.0 | - - | 1359.2 | 399.3 |
| 7.0 | 10.50 | 1440.9 | 422.9 | |
| 6.0 | 19.00 | 1571.5 | 459.6 | |
| 5.0 | 32.21 | 1810.0 | 524.2 | |
| 4.0 | 55.41 | 2246.5 | 636.9 | |
| 3.5 | 74.69 | 2601.2 | 724.5 | |
| 3.0 | 104.01 | 3118.7 | 847.3 | |
| 2.5 | 152.15 | 3919.5 | 1028.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graziano, G. The Relevance of Cavity Creation for Several Phenomena Occurring in Water. Liquids 2023, 3, 57-65. https://doi.org/10.3390/liquids3010006
Graziano G. The Relevance of Cavity Creation for Several Phenomena Occurring in Water. Liquids. 2023; 3(1):57-65. https://doi.org/10.3390/liquids3010006
Chicago/Turabian StyleGraziano, Giuseppe. 2023. "The Relevance of Cavity Creation for Several Phenomena Occurring in Water" Liquids 3, no. 1: 57-65. https://doi.org/10.3390/liquids3010006
APA StyleGraziano, G. (2023). The Relevance of Cavity Creation for Several Phenomena Occurring in Water. Liquids, 3(1), 57-65. https://doi.org/10.3390/liquids3010006






