Abstract
Evaluating the temperature dependence of the fusion enthalpy is no trivial task, as any compound melts at a unique temperature. At the same time, knowledge of the fusion enthalpies under some common conditions, particularly at the reference temperature of 298.15 K, would substantially facilitate the comparative analysis and development of the predictive schemes. In this work, we continue our investigations of the temperature dependence of the fusion enthalpy of organic non-electrolytes using solution calorimetry. As an object of study, n-octadecanophenone, an arylaliphatic compound was chosen. The solvent appropriate for evaluating the fusion enthalpy at 298.15 K from the solution enthalpy of crystal was selected: p-xylene. The heat capacity and fusion enthalpy at the melting temperature were measured by differential scanning calorimetry to derive the fusion enthalpy at 298.15 K from the Kirchhoff’s law of Thermochemistry. An agreement between the independently determined values was demonstrated. This particular result opens a perspective for further studies of the fusion thermochemistry of arylaliphatic compounds at 298.15 K by solution calorimetry.
1. Introduction
The studies of phase transition thermodynamics of organic non-electrolytes have more than a 150-year-old history. A lot of efforts have been paid to develop increasingly precise experimental techniques [1], as well as predictive methods. Quantitative structure-property relationships proposed so far to characterize the fusion process, particularly its enthalpy, remain relatively less accurate [2,3,4,5,6,7], compared with the vaporization and sublimation [7,8,9,10,11,12]. Among the obstacles to establishing the relationships of the fusion enthalpy with the molecular structure and descriptors, one can distinguish the fact that it is measured at the melting point (Tm), which is unique for each compound. This impedes the comparative analysis, in contrast with the vaporization and sublimation processes, whose thermodynamic parameters can be determined under the common conditions (e.g., 298.15 K) for numerous systems. Adjustment of the fusion enthalpies (ΔcrlH) to 298.15 K would require knowledge of its temperature dependence. The temperature dependence of the fusion enthalpy is also of interest when applying the ideal solubility equation [13,14,15,16,17], and analyzing nucleation and crystallization kinetics [18,19].
ΔcrlH at 298.15 K can be found from Kirchhoff’s law of Thermochemistry (Equation (1)):
where is the heat capacity change on melting. Generally speaking, it also depends on temperature and this dependence can sometimes significantly contribute to ΔcrlH(298.15 K) [20]. Experimental determination of this value below Tm would require supercooling the melt, which is rarely possible.
In a recent cycle of works [21,22] we proposed a method for determining the fusion enthalpies of organic non-electrolytes based on solution calorimetry, based on Hess’s law (Equation (2)):
ΔsolnH(cr, 298.15 K) = ΔcrlH(298.15 K) + ΔsolnH(l, 298.15 K)
According to Equation (2), the solution enthalpy of the crystal in a certain solvent ΔsolnH(cr, 298.15 K) is equal to a sum of ΔcrlH(298.15 K) and the solution enthalpy of the quasi-equilibrium melt in the same solvent at 298.15 K. In many solute-solvent systems (e.g., aromatic compounds incapable of self-association in benzene [21] or alkanes in heptane [23]) the latter is nearly 0, so ΔcrlH(298.15 K) can be found directly from ΔsolnH(cr, 298.15 K).
Combining Equations (1) and (2), we independently tracked the temperature dependence of the supercooled liquid heat capacity between 298.15 K and Tm:
Analyzing the relationship between the enthalpies of fusion and solution, we established that an agreement between the left and right sides of Equation (3) is achieved when the temperature dependence of the heat capacity of the liquid determined above Tm is extrapolated down to 298.15 K as a linear function of temperature [21].
Equation (2) provides a useful alternative to Equation (1), replacing a laborious procedure of heat capacity measurement with solution calorimetry. However, it requires searching for the solvent, in which ΔsolnH(l, 298.15 K) can be accurately evaluated based on the molecular structure. Previously we mainly focused on aromatic (both hydrogen-bonded [22] and non-hydrogen-bonded [21]) and aliphatic [23] systems but did not concern alkylaromatic compounds. For alkylarenes, the solution enthalpy in benzene significantly grows with the chain length increase, while the solution enthalpy in heptane can be significantly influenced by the presence of any substituent, except for the alkyl group. In this work we tested if p-xylene, which contains both aromatic core and alkyl groups, can be used as an “athermal” solvent for a long-chain alkylaromatic solute, n-octadecanophenone, to determine its fusion enthalpy at 298.15 K.
2. Materials and Methods
2.1. Materials
p-Xylene (CAS № 106-42-3, C8H10, Acros, Thermo Fisher Scientific, Waltham, MA, USA), n-octanophenone (CAS № 1674-37-9, C14H20O, TCI Chemicals, Tokyo, Japan), and n-octadecanophenone (CAS № 6786-36-3, C24H40O, Alfa Aesar, Haverhill, MA, USA) were of commercial origin with a purity more than 0.99 (mole fraction), as it was stated in the certificate of analysis (determined by gas chromatography). Water content in p-xylene was determined by Fischer titration and equaled 0.01% (mole fraction). Before the measurements, n-octanophenone and n-octadecanophenone were dried in vacuo to remove any traces of moisture.
The samples were used without further purification.
2.2. Differential Scanning Calorimetry
The specific heat capacity of crystal, enthalpy, and temperature of fusion of n-octadecanophenone were measured using DSC 8500 (Perkin Elmer, Waltham, MA, USA). Prior to the experiment, aluminum crucibles were annealed at 200 °C. DSC was calibrated according to the manufacturer’s recommendation using the standard samples of Indium and Zinc. Each value (onset temperature and area of the peak) was determined three times. The reproducibilities of heat flow and temperature calibration (0.95 level of confidence, coverage factor 2.0) were equal to 1% and 0.1 K, respectively. The correctness of the determination of the heat capacity and heat effects was checked as previously [24]. The agreement with the reference values was within 2%.
The samples were placed in a 50 μL aluminum crucible in an inert atmosphere. Two samples were studied to determine each value. Experiments were performed in a nitrogen dynamic atmosphere (30 mL min−1) with a heating/cooling rate of 5 K min−1. Two cycles of ‘‘heating–cooling” from room temperature to a temperature 40 K higher than the melting point were carried out to determine the enthalpy and temperature of fusion. The samples crystallized completely on cooling. Experimental results from DSC measurements are presented in Table 1. An exemplary melting peak of n-octadecanophenone obtained by DSC is shown in Figure 1. An agreement between the fusion enthalpies obtained in each experiment was within a typical reproducibility of the DSC technique (2–3%).

Table 1.
The enthalpies and temperatures of fusion of n-octadecanophenone determined in this work by DSC at 0.1 MPa a.
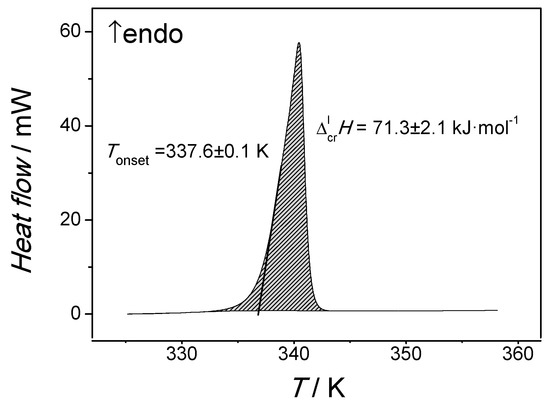
Figure 1.
Melting peak of n-octadecanophenone obtained by DSC in this work.
The measurement of specific heat capacity was performed according to the isothermal step method as previously [25]. The procedure included three steps. First, the baseline was determined using empty crucibles. Then, using the baseline, a standard sample (sapphire) with a weight of 33.79 mg and a sample of n-octadecanophenone were each measured in the same crucible. This procedure was repeated twice for two samples of n-octadecanophenone, whose fusion enthalpies were measured. The temperature program included a dynamic segment between 320 K and 325 K and two isothermal segments at 320 K and 325 K. The resulting heat capacity of solid n-octadecanophenone at 322.5 K was 622 ± 18 J·K−1·mol−1 (the uncertainty includes the standard deviation of the mean and the standard calibration uncertainty both multiplied by the coverage factor k ≈ 2.0 (expanded uncertainty of the mean U; 0.95 level of confidence)).
2.3. Solution Calorimetry
The solution enthalpies of n-octadecanophenone and n-octanophenone in p-xylene were measured at 298.15 K in the concentration range from 1.39 to 6.37 mmol kg−1 using TAM III precision solution calorimeter (TA Instruments, New Castle, DE, USA). Crystal n-octadecanophenone was dissolved by breaking a glass ampule filled with ~50 mg of the studied sample in a glass cell containing 90 mL of the pure solvent. Liquid n-octanophenone was injected in ~50 μL portions using an electronically operated syringe equipped with a long gold cannula immersed in the solvent. The details of the solution calorimetry procedure have been described elsewhere [26]. The conditions corresponding to an infinite dilution, which was confirmed by an absence of the concentration dependence of the solution enthalpy. The experimental values are provided in Table 2.

Table 2.
The solution enthalpies of phenones in p-xylene measured in this work at 298.15 K and 0.1 MPa a.
3. Results
In Ref. [27] the molar heat capacity of liquid n-octadecanophenone was determined as a function of temperature between 373 and 418 K with an uncertainty of 2% (Equation (4)):
Cp,m/(J·K−1·mol−1) = 297.5 + 1.238 ∙ (T/K)
In this work, Cp,m(cr, 322.5 K) = 622 ± 18 J·K−1·mol−1 was determined. The extrapolated Cp,m(l, 322.5 K) value equals 697 ± 30 J·K−1·mol−1 (uncertainty evaluated according to Ref. [20]). Thus, ΔcrlCp,m (322.5 K) = 75 ± 35 J·K−1·mol−1. Within the temperature range of Equation (4) (298.15–337.6 K), it is reasonable to assume that ΔcrlCp,m slightly depends on temperature. Then = ΔcrlCp,m · (298.15 K − Tm) = −3.0 ± 1.4 kJ·mol−1. Therefore, from Equation (1) one can obtain ΔcrlH(298.15 K) = 68.3 ± 2.5 kJ·mol−1.
Evaluation of ΔcrlH(298.15 K) is also possible using the experimental value of ΔsolnH of crystal n-octadecanophenone (71.0 ± 0.5 kJ·mol−1) and Equation (2). The solution enthalpies of liquid alkanes in p-xylene are notably less than in benzene, which has been previously used as a solvent for aromatic compounds. For example, ΔsolnH(l, 298.15 K) of hexadecane in benzene is equal to 11.3 kJ·mol−1 [28] and in p-xylene to 3.1 kJ·mol−1 [29]. Those of heptane equal 5.6 [28] and 1.4 kJ·mol−1 [29], respectively. ΔsolnH(l, 298.15 K) of n-octanophenone in p-xylene determined in this work equaled −0.4 kJ·mol−1. Thus, it is reasonable to assume that ΔsolnH(l, 298.15 K) of n-octadecanophenone in p-xylene is in the range from −0.4 to 3.1 kJ·mol−1, or 1.4 ± 1.8 kJ·mol−1, which is not quite wide, taking in mind the absolute values of ΔsolnH(cr, 298.15 K) and ΔcrlH(Tm). Further elaboration of this value is possible if additional measurements of the solution enthalpies of alkylarenes is performed to understand the regularities met in this series. Then, from Equation (2), one obtains ΔcrlH(298.15 K) = 69.6 ± 1.9 kJ·mol−1.
4. Discussion
The above-obtained ΔcrlH(298.15 K) values of 68.3 ± 2.5 and 69.6 ± 1.9 kJ·mol−1 agree within the limits of the propagated errors. Such an agreement confirms the validity of the assumptions made during the ΔsolnH(l, 298.15 K) evaluation. Thus, the fusion enthalpies of alkylarenes and their derivatives can actually be determined using solution calorimetry and p-xylene as an “athermal” solvent. It is worth noting that, due to an extrapolation uncertainty, the error of the enthalpy correction to 298.15 K according to Kirchhoff’s law may attain ~50% of its value. In this paper, this error was comparable with the fusion and solution enthalpies uncertainties. However, when the temperature range of adjustment and heat capacity integral increase, its contribution can become crucial. This highlights the advantages of the solution calorimetry approach, which enables to evaluation of the fusion enthalpy directly at 298.15 K, with an uncertainty independent of the melting temperature and tendency to supercooling.
Further quantification of the regularities, especially tracking the effects of the chain length, branching, and substituents on ΔsolnH(l, 298.15 K) in p-xylene is anticipated to obtain more accurate results for a wider range of compounds. This finding echoes with the previously denoted “molecule-additivity” of the vaporization enthalpies of alkylaromatic compounds [30], which can be associated with instantaneous nanoheterogeneities in such systems, i.e., aromatic-aromatic and aliphatic-aliphatic interactions are more frequent than aromatic-aliphatic ones. Such distinction can be enough to minimize the significant endothermic effects met when studying benzene-alkanes systems under infinite dilution conditions [28].
Author Contributions
Conceptualization, M.I.Y.; methodology, M.I.Y.; investigation, I.S.B. and A.A.S.; writing—original draft preparation, M.I.Y.; writing—review and editing, B.N.S. All authors have read and agreed to the published version of the manuscript.
Funding
This paper has been supported by the Kazan Federal University Strategic Academic Leadership Program (‘PRIORITY-2030′).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weir, R.D.; de Loos, T.W. Measurement of the Thermodynamic Properties of Multiple Phases; Gulf Professional Publishing: Woburn, MA, USA, 2005. [Google Scholar]
- Dannenfelser, R.-M.; Yalkowsky, S.H. Estimation of Entropy of Melting from Molecular Structure: A Non-Group Contribution Method. Ind. Eng. Chem. Res. 1996, 35, 1483–1486. [Google Scholar] [CrossRef]
- Jain, A.; Yang, G.; Yalkowsky, S.H. Estimation of Melting Points of Organic Compounds. Ind. Eng. Chem. Res. 2004, 43, 7618–7621. [Google Scholar] [CrossRef]
- Wu, M.; Yalkowsky, S. Estimation of the molar heat capacity change on melting of organic compounds. Ind. Eng. Chem. Res. 2008, 48, 1063–1066. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E. Total phase change entropies and enthalpies. An update on fusion enthalpies and their estimation. Thermochim. Acta 2009, 495, 5–13. [Google Scholar] [CrossRef]
- Bondi, A. A Correlation of the Entropy of Fusion of Molecular Crystals with Molecular Structure. Chem. Rev. 1967, 67, 565–580. [Google Scholar] [CrossRef]
- Naef, R.; Acree, W.E. Calculation of five thermodynamic molecular descriptors by means of a general computer algorithm based on the group-additivity method: Standard enthalpies of vaporization, sublimation and solvation, and entropy of fusion of ordinary organic molecules and total phase-change entropy of liquid crystals. Molecules 2017, 22, 1059. [Google Scholar] [PubMed]
- Gharagheizi, F.; Babaie, O.; Mazdeyasna, S. Prediction of vaporization enthalpy of pure compounds using a group contribution-based method. Ind. Eng. Chem. Res. 2011, 50, 6503–6507. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadina, I.; Parra, M.I. Comparison of corresponding-states-based correlations for the prediction of the vaporization enthalpy of fluids. Ind. Eng. Chem. Res. 2008, 47, 7903–7916. [Google Scholar] [CrossRef]
- Solomonov, B.N.; Yagofarov, M.I. An approach for the calculation of vaporization enthalpies of aromatic and heteroaromatic compounds at 298.15 K applicable to supercooled liquids. J. Mol. Liq. 2020, 319, 114330. [Google Scholar] [CrossRef]
- Solomonov, B.N.; Yagofarov, M.I. Compensation relationship in Thermodynamics of solvation and vaporization: Features and applications. I. Non-hydrogen-bonded systems. J. Mol. Liq. 2022. submitted. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree Jr, W.E. Estimation of enthalpies of sublimation of organic, organometallic and inorganic compounds. Fluid Phase Equilibria 2020, 515, 112575. [Google Scholar] [CrossRef]
- Bustamante, P.; Peña, M.A.; Barra, J. Partial-solubility Parameters of Naproxen and Sodium Diclofenac. J. Pharm. Pharmacol. 2011, 50, 975–982. [Google Scholar] [CrossRef] [PubMed]
- Cheuk, D.; Svärd, M.; Rasmuson, Å.C. Thermodynamics of the Enantiotropic Pharmaceutical Compound Benzocaine and Solubility in Pure Organic Solvents. J. Pharm. Sci. 2020, 109, 3370–3377. [Google Scholar] [CrossRef] [PubMed]
- Neau, S.H.; Bhandarkar, S.V.; Hellmuth, E.W. Differential molar heat capacities to test ideal solubility estimations. Pharm. Res. 1997, 14, 601–605. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, P.A.; Paruta, A.N. Solution thermodynamics of alkyl p-aminobenzoates. J. Pharm. Sci. 1976, 65, 252–257. [Google Scholar] [CrossRef]
- Pappa, G.D.; Voutsas, E.C.; Magoulas, K.; Tassios, D.P. Estimation of the differential molar heat capacities of organic compounds at their melting point. Ind. Eng. Chem. Res. 2005, 44, 3799–3806. [Google Scholar] [CrossRef]
- Hoffman, J.D. Thermodynamic driving force in nucleation and growth processes. J. Chem. Phys. 1958, 29, 1192–1193. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Z.; Gui, Y.; Shi, C.; Zhang, G.G.; Yu, L. Crystal nucleation rates in glass-forming molecular liquids: D-sorbitol, d-arabitol, d-xylitol, and glycerol. J. Chem. Phys. 2018, 149, 054503. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Solomonov, B.N. Calculation of the fusion enthalpy temperature dependence of polyaromatic hydrocarbons from the molecular structure: Old and new approaches. J. Chem. Thermodyn. 2021, 152, 106278. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Nagrimanov, R.N.; Solomonov, B.N. New aspects in the thermochemistry of solid-liquid phase transitions of organic non-electrolytes. J. Mol. Liq. 2018, 256, 58–66. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Lapuk, S.E.; Mukhametzyanov, T.A.; Ziganshin, M.A.; Valiakhmetov, T.F.; Solomonov, B.N. The fusion thermochemistry of self-associated aromatic compounds at 298.15 K studied by solution calorimetry. J. Chem. Thermodyn. 2019, 137, 43–47. [Google Scholar] [CrossRef]
- Nagrimanov, R.N.; Samatov, A.A.; Solomonov, B.N. Additive scheme of solvation enthalpy for linear, cyclic and branched-chain aliphatic compounds at 298.15 K. J. Mol. Liq. 2019, 292, 111365. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Sokolov, A.A.; Gerasimov, A.V.; Solomonov, B.N.; Stepurko, E.N.; Yurkshtovich, Y.N. Thermodynamic Properties of Thioxanthone between 80 and 540 K. J. Chem. Eng. Data 2022, in press. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Bolmatenkov, D.N.; Solomonov, B.N. Relationship between the vaporization enthalpies of aromatic compounds and the difference between liquid and ideal gas heat capacities. J. Chem. Thermodyn. 2021, 158, 106443. [Google Scholar] [CrossRef]
- Solomonov, B.N.; Varfolomeev, M.A.; Nagrimanov, R.N.; Novikov, V.B.; Zaitsau, D.H.; Verevkin, S.P. Solution calorimetry as a complementary tool for the determination of enthalpies of vaporization and sublimation of low volatile compounds at 298.15 K. Thermochim. Acta 2014, 589, 164–173. [Google Scholar] [CrossRef]
- Bolmatenkov, D.N.; Notfullin, A.A.; Yagofarov, M.I.; Nagrimanov, R.N.; Italmasov, A.R.; Solomonov, B.N. Vaporization thermodynamics of normal alkyl phenones. J. Mol. Liq. 2023, 370, 121000. [Google Scholar] [CrossRef]
- Lu, J.Z.; Acree, W.E.; Abraham, M.H. Updated Abraham model correlations for enthalpies of solvation of organic solutes dissolved in benzene and acetonitrile. Phys. Chem. Liq. 2019, 57, 84–99. [Google Scholar] [CrossRef]
- Varfolomeev, M.A.; Rakipov, I.T.; Acree, W.E., Jr.; Brumfield, M.; Abraham, M.H. Examination of hydrogen-bonding interactions between dissolved solutes and alkylbenzene solvents based on Abraham model correlations derived from measured enthalpies of solvation. Thermochim. Acta 2014, 594, 68–79. [Google Scholar] [CrossRef]
- Solomonov, B.N.; Yagofarov, M.I.; Nagrimanov, R.N. Additivity of vaporization enthalpy: Group and molecular contributions exemplified by alkylaromatic compounds and their derivatives. J. Mol. Liq. 2021, 342, 117472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).