Thermodynamic Scaling of the Shear Viscosity of Lennard-Jones Chains of Variable Rigidity
Abstract
:1. Introduction
2. Models and Theory
2.1. The Lennard-Jones Chains Fluid Model
2.2. Simulation Context
2.2.1. Numerical Methods and Parameters
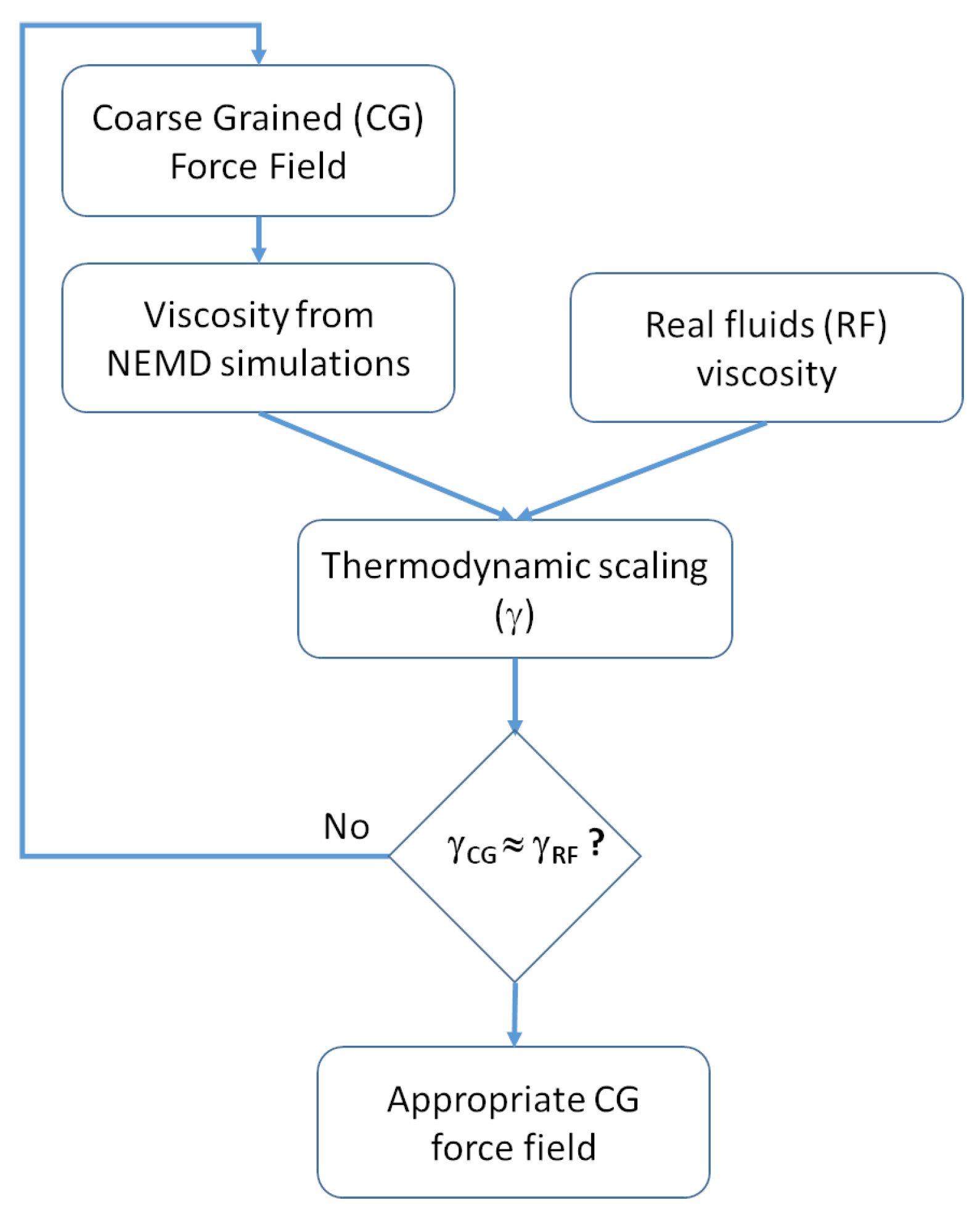
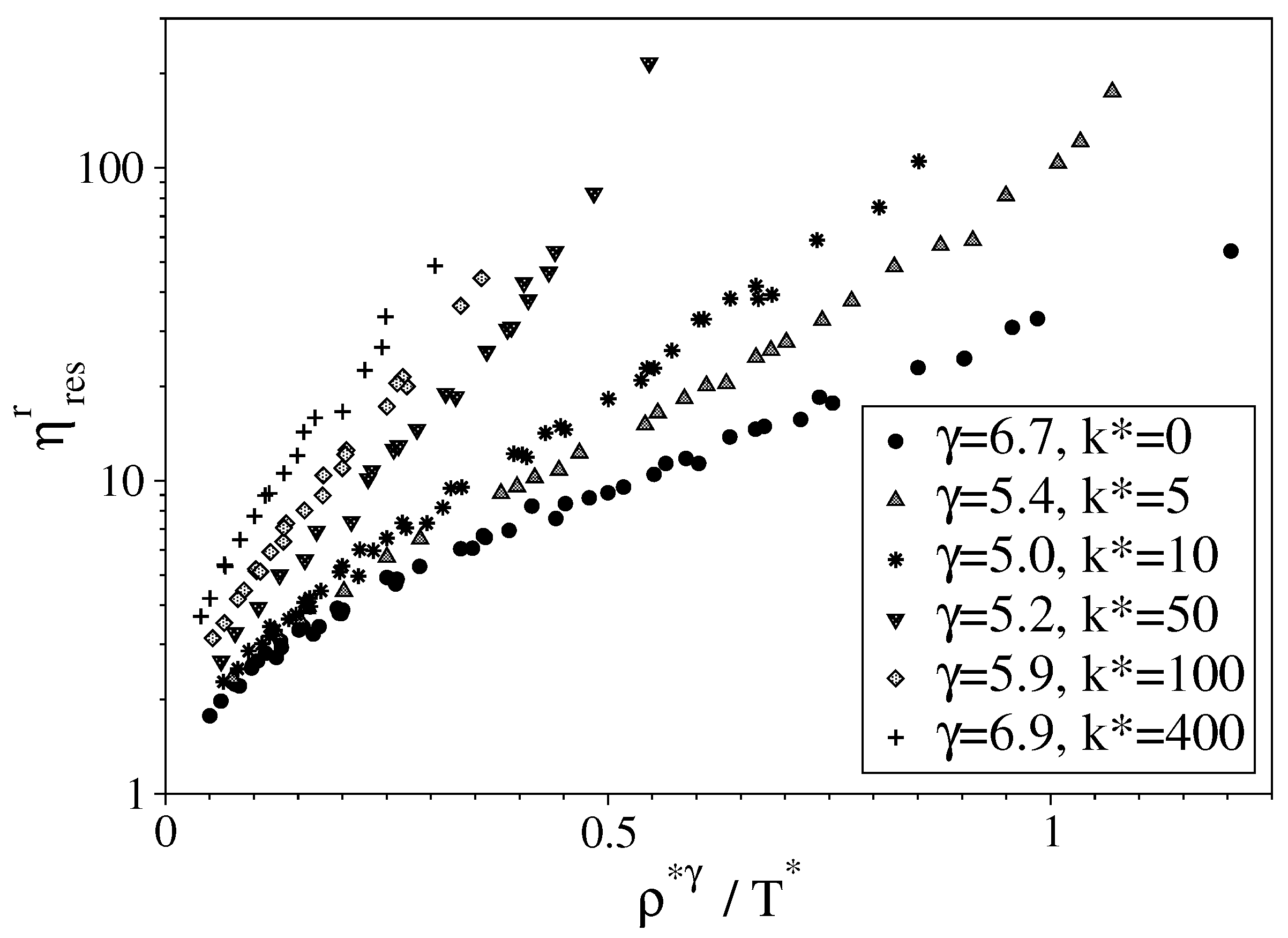
2.2.2. Viscosity Modeling and Thermodynamic Scaling
3. Results
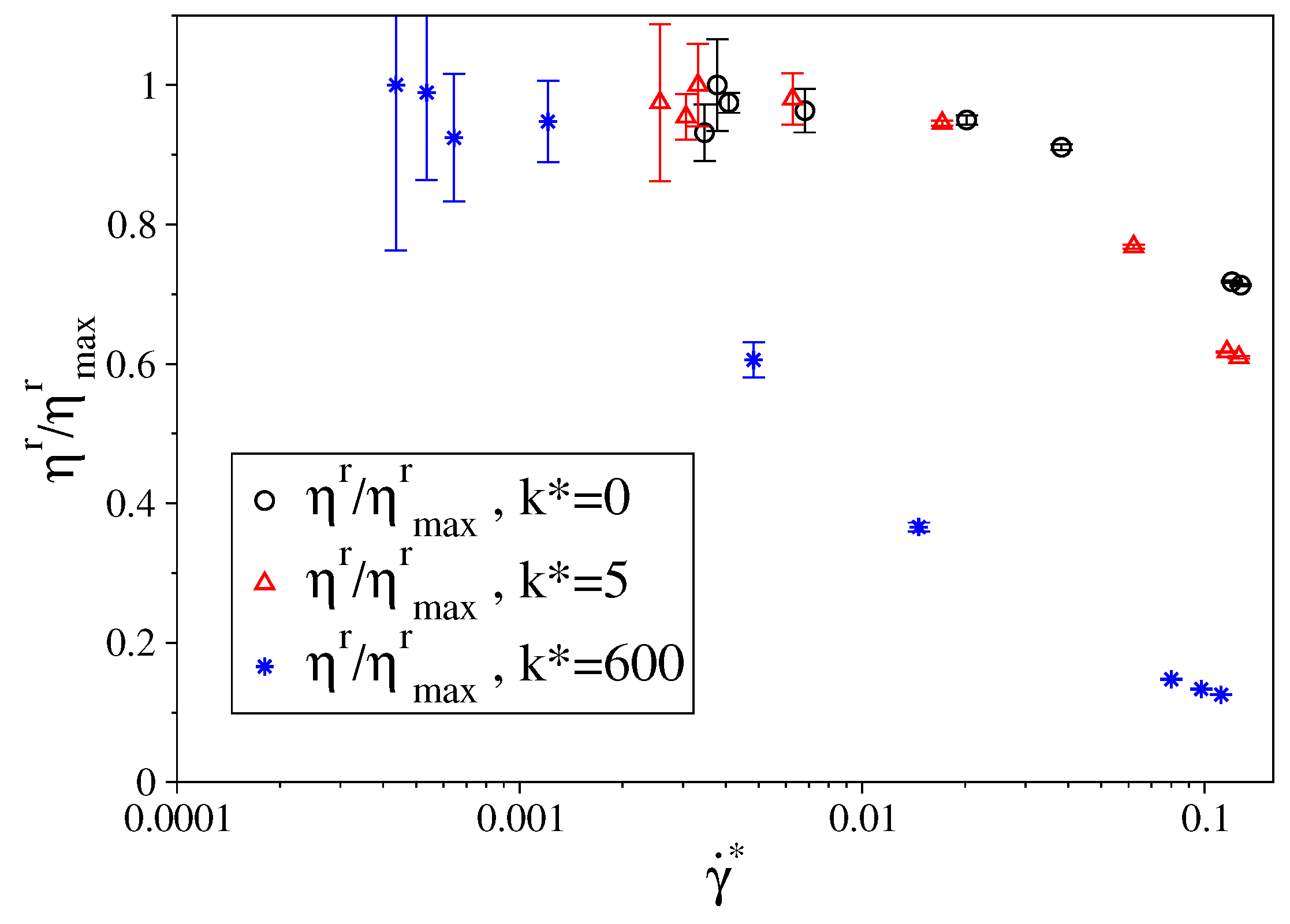
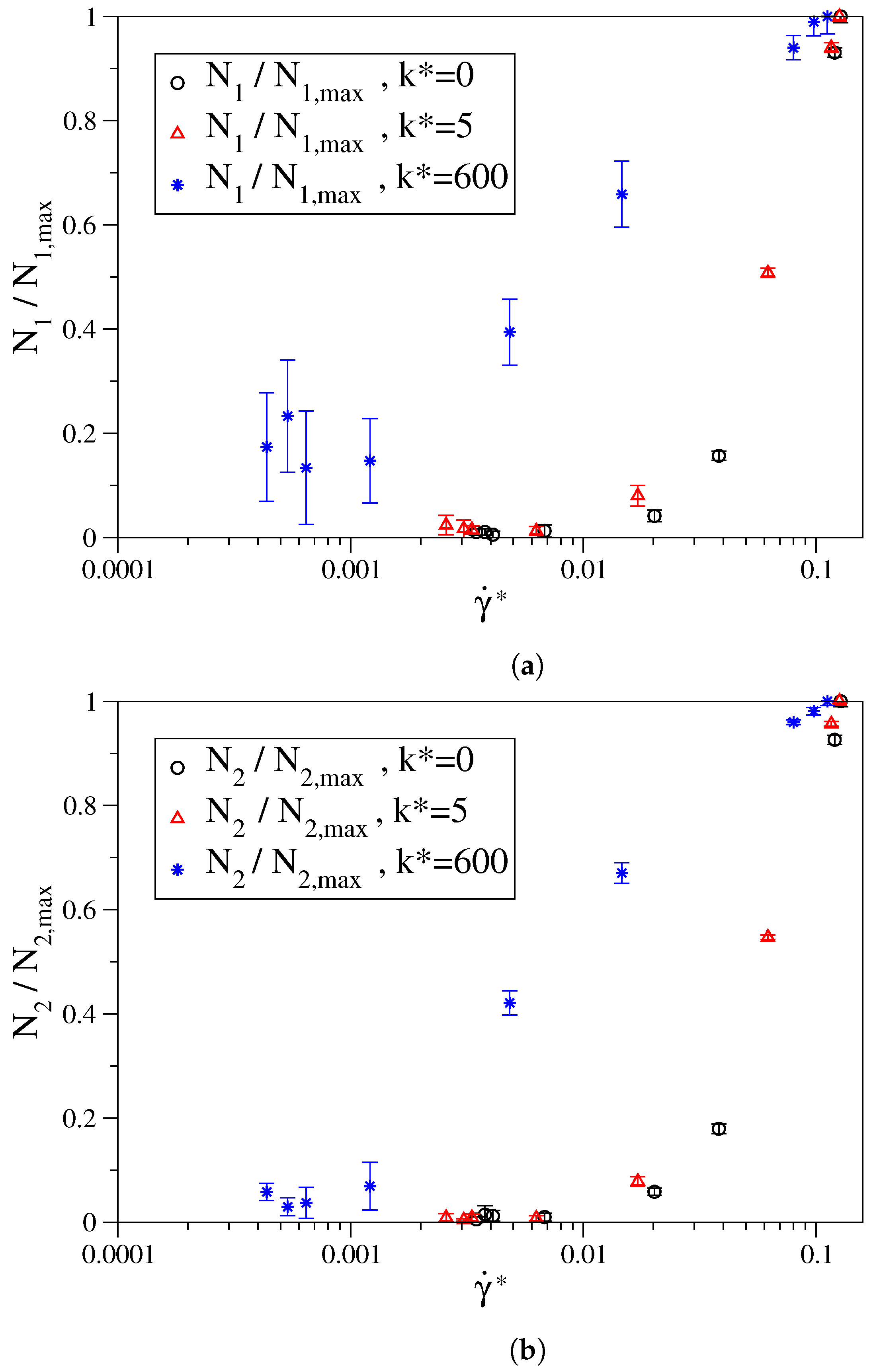
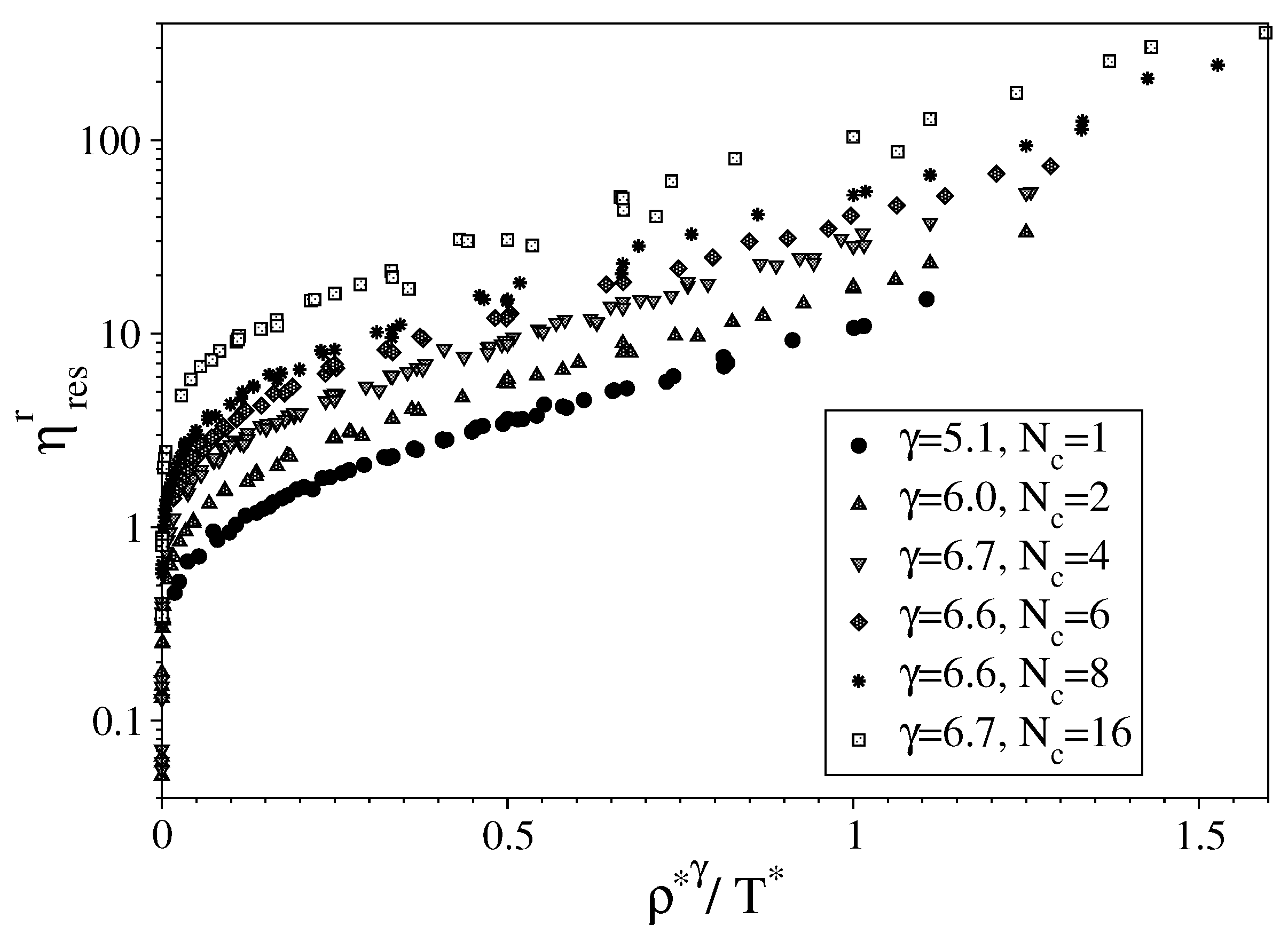
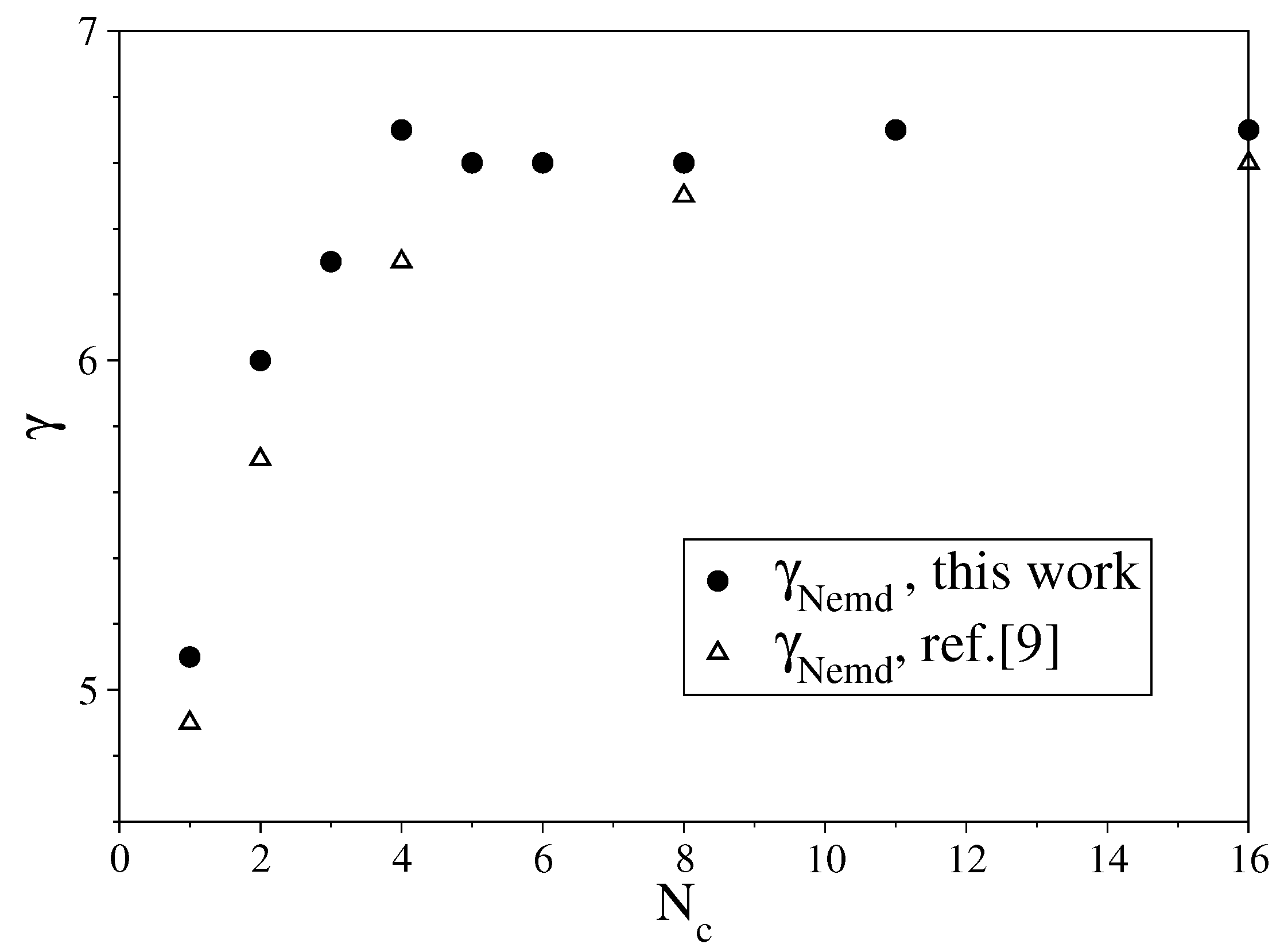
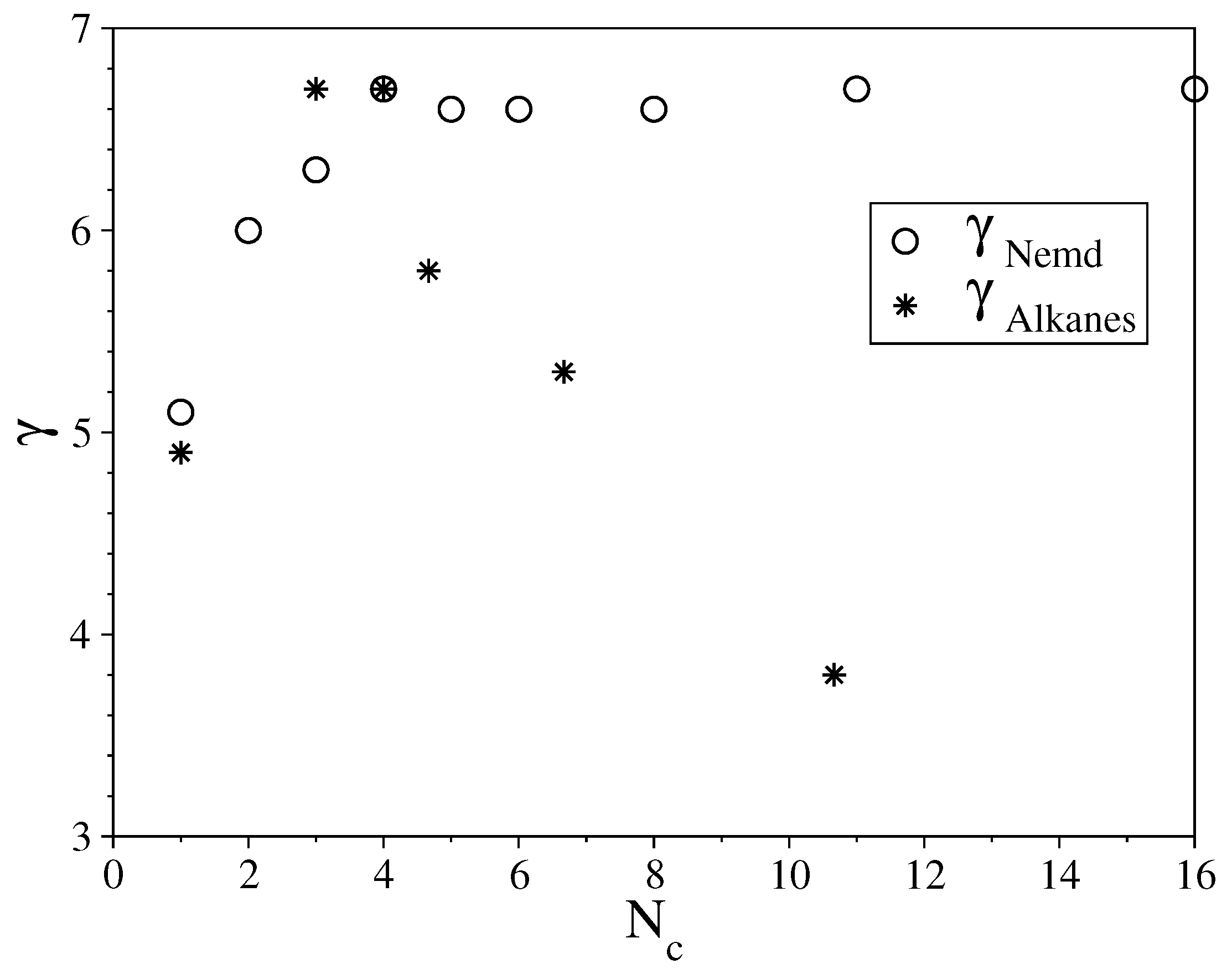
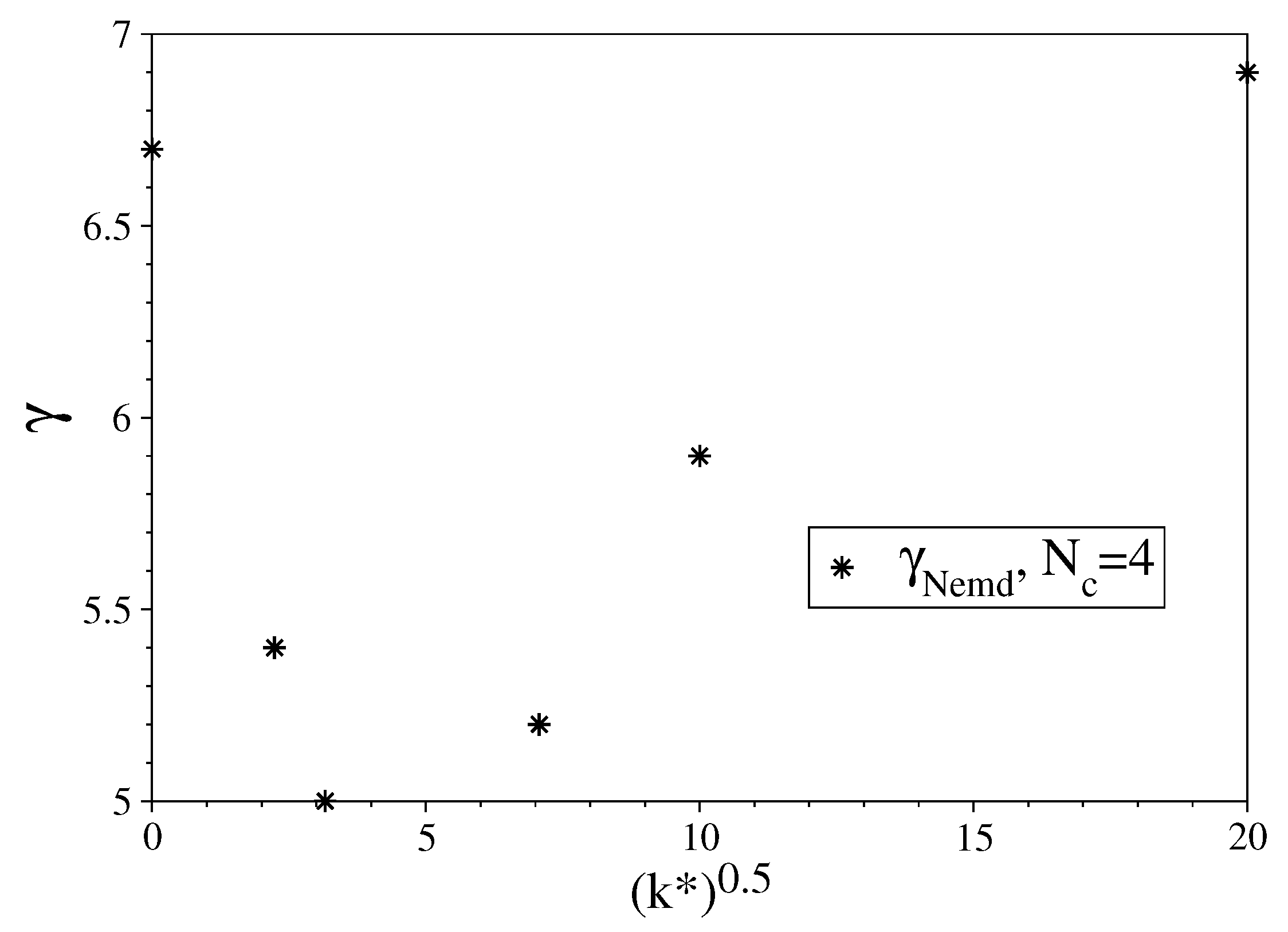
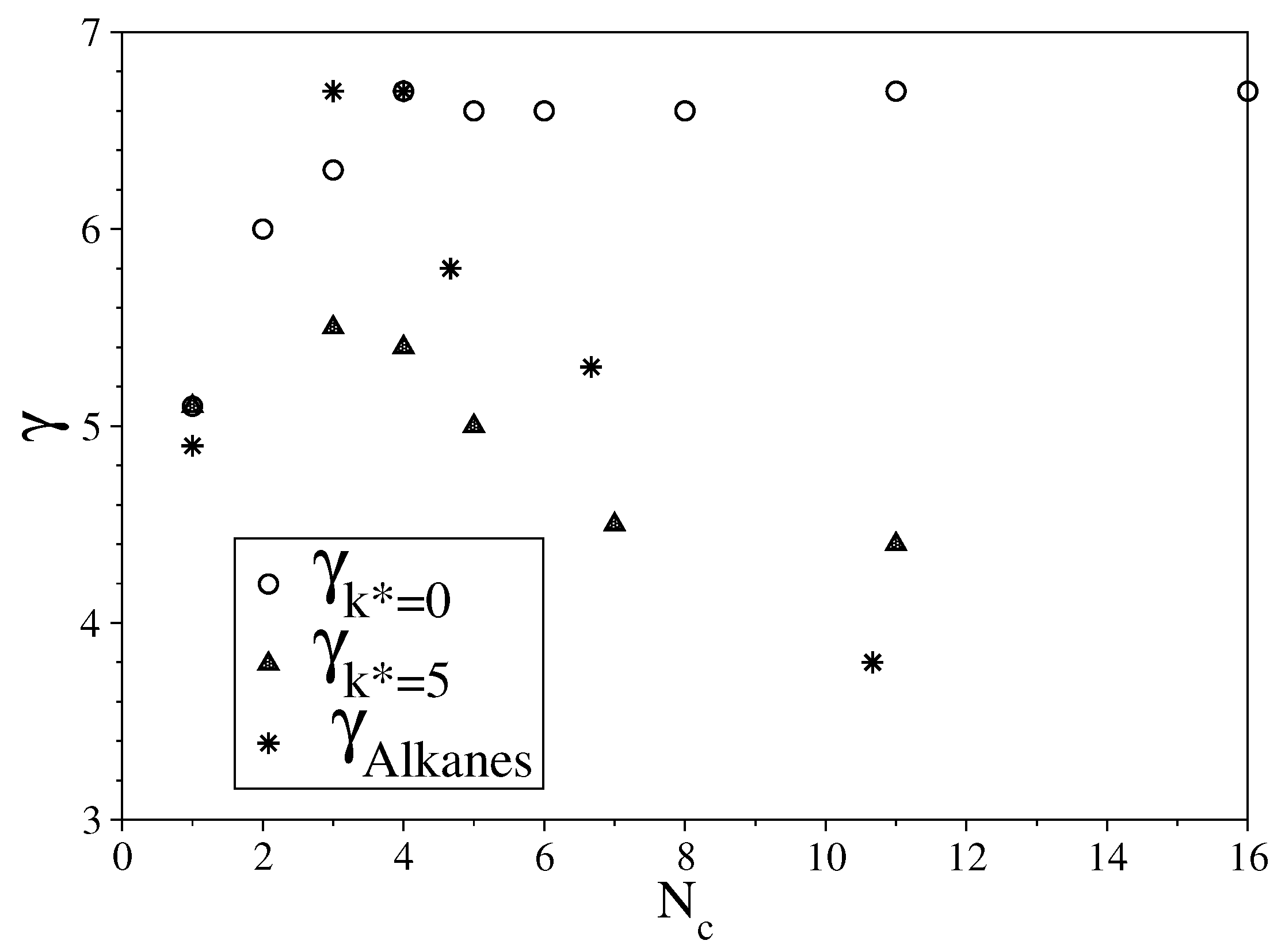
3.1. Fully Flexible LJ Chains Model for Alkanes
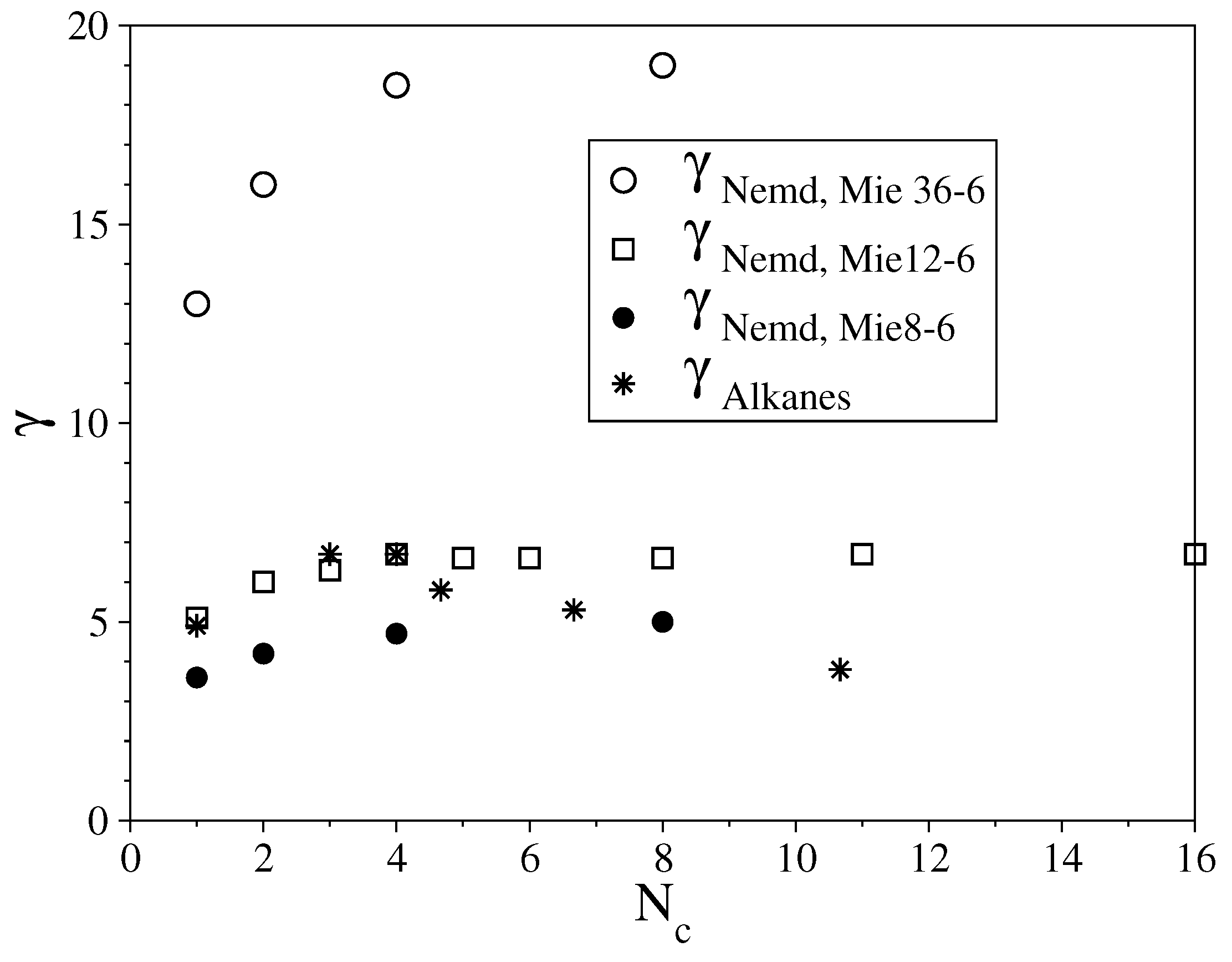
3.2. Semi-Rigid LJ Chains Model for Alkanes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LJ | Lennard-Jones |
| NEMD | Non-Equilibrium Molecular Dynamics |
| NIST | National Institute of Standards and Technology |
| TS | Thermodynamic Scaling |
References
- Hendriks, E.; Kontogeorgis, G.; Dohrn, R.; de Hemptinne, J.C.; Economou, I.; Žilnik, L.; Vesovic, V. Industrial Requirements for Thermodynamics and Transport Properties. Ind. Eng. Chem. Res. 2010, 49, 11131–11141. [Google Scholar] [CrossRef]
- Kontogeorgis, G.; Dohrn, R.; Economou, I.; de Hemptinne, J.C.; Ten Kate, A.; Kuitunen, S.; Mooijer, M.; Žilnik, L.; Vesovic, V. Industrial Requirements for Thermodynamic and Transport Properties: 2020. Ind. Eng. Chem. Res. 2021, 60, 4987–5013. [Google Scholar] [CrossRef]
- Assael, M.; Dymond, J.; Papadaki, M.; Patterson, P. Correlation and prediction of dense fluid transport coefficients. I. n-alkanes. Int. J. Thermophys. 1992, 13, 269–281. [Google Scholar] [CrossRef]
- Poling, B.; Prausnitz, J.; O’Connell, J. The Properties of Gases and Liquids; Mcgraw-Hill: New York, NY, USA, 2001; Volume 5. [Google Scholar]
- de Wijn, A.S.; Vesovic, V.; Jackson, G.; Trusler, J.M. A kinetic theory description of the viscosity of dense fluids consisting of chain molecules. J. Chem. Phys. 2008, 128, 204901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vesovic, V.; Trusler, J.P.M.; Assael, M.; Riesco, N.; Quiñones-Cisneros, S.E. Dense Fluids: Viscosity: Experimental Thermodynamics Volume IX: Advances in Transport Properties of Fluids; Assael, M.J., Goodwin, A.R.H., Vesovic, V., Wakeham, W.A., Eds.; Royal Society of Chemistry: London, UK, 2014; Chapter 8. [Google Scholar]
- Quiñones-Cisneros, S.; Zéberg-Mikkelsen, C.; Stenby, E. The friction theory (f-theory) for viscosity modeling. Fluid Phase Equilibria 2000, 169, 249–276. [Google Scholar] [CrossRef]
- Quiñones-Cisneros, S.; Deiters, U. Generalization of the friction theory for viscosity modeling. J. Phys. Chem. B 2006, 110, 12820–12834. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, Y. A quasi-universal scaling law for atomic transport in simple fluids. J. Phys. Condens. Matter 1999, 11, 5415–5427. [Google Scholar] [CrossRef]
- Galliero, G.; Boned, C.; Fernandez, J. Scaling of the viscosity of the Lennard-Jones chain fluid model, argon, and some normal alkanes. J. Chem. Phys. 2011, 134, 064505. [Google Scholar] [CrossRef]
- Lötgering-Lin, O.; Gross, J. Group contribution method for viscosities based on entropy scaling using the perturbed-chain polar statistical associating fluid theory. Ind. Eng. Chem. Res. 2015, 54, 7942–7952. [Google Scholar] [CrossRef]
- Dyre, J. Perspective: Excess-entropy scaling. J. Chem. Phys. 2018, 149, 210901. [Google Scholar] [CrossRef] [Green Version]
- Bell, I.; Messerly, R.; Thol, M.; Costigliola, L.; Dyre, J. Modified entropy scaling of the transport properties of the Lennard-Jones fluid. J. Phys. Chem. B 2019, 123, 6345–6363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dyre, J. Isomorphs, hidden scale invariance, and quasiuniversality. Phys. Rev. E 2013, 88, 042139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dyre, J. Hidden Scale Invariance in Condensed Matter. J. Phys. Chem. B 2014, 118, 10007–10024. [Google Scholar] [CrossRef]
- Bacher, A.; Schrøder, T.B.; Dyre, J. Explaining why simple liquids are quasi-universal. Nat. Commun. 2014, 5, 5424. [Google Scholar] [CrossRef] [Green Version]
- Ashurst, W.T.; Hoover, W.G. Dense-fluid shear viscosity via nonequilibrium molecular dynamics. Phys. Rev. A 1975, 11, 658–678. [Google Scholar] [CrossRef]
- Grzybowski, A.; Paluch, M.; Grzybowska, K.; Haracz, S. Communication: Relationships between Intermolecular potential, thermodynamics, and dynamic scaling in viscous systems. J. Chem. Phys. 2010, 133, 161101. [Google Scholar] [CrossRef] [Green Version]
- Roland, C.; Bair, S.; Casalini, R. Thermodynamic scaling of the viscosity of van der Waals, H-bonded, and ionic liquids. J. Chem. Phys. 2006, 125, 124508. [Google Scholar] [CrossRef]
- Bøhling, L.; Ingebrigtsen, T.; Grzybowski, A.; Paluch, M.; Dyre, J.; Schrøder, T. Scaling of viscous dynamics in simple liquids: Theory, simulation and experiment. New J. Phys. 2012, 14, 113035. [Google Scholar] [CrossRef]
- Delage-Santacreu, S.; Galliero, G.; Hoang, H.; Bazile, J.P.; Boned, C.; Fernandez, J. Thermodynamic scaling of the shear viscosity of Mie n-6 fluids and their binary mixtures. Chem. Phys. 2015, 142, 174501. [Google Scholar] [CrossRef] [PubMed]
- Bøhling, L.; Bailey, N.; Schrøder, T.; Dyre, J. Estimating the density-scaling exponent of a monatomic liquid from its pair potential. J. Chem. Phys. 2014, 140, 124510. [Google Scholar] [CrossRef] [Green Version]
- Veldhorst, A.; Dyre, J.; Schrøder, T. Scaling of the dynamics of flexible Lennard-Jones chains: Effects of harmonic bonds. J. Chem. Phys. 2015, 143, 194503. [Google Scholar] [CrossRef] [Green Version]
- Puosi, F.; Chulkin, O.; Bernini, S.; Capaccioli, S.; Leporini, D. Thermodynamic scaling of vibrational dynamics and relaxation. J. Chem. Phys. 2016, 145, 234904. [Google Scholar] [CrossRef] [PubMed]
- Douglas, J.; Xu, W.S. Equation of State and Entropy Theory Approach to Thermodynamic Scaling in Polymeric Glass-Forming Liquids. Macromolecules 2021, 54, 3247–3269. [Google Scholar] [CrossRef]
- Comuñas, M.J.; Paredes, X.; Gaciño, F.; Fernández, J.; Bazile, J.P.; Boned, C.; Daridon, J.L.; Galliero, G.; Pauly, J.; Harris, K. Viscosity measurements for squalane at high pressures to 350 MPa from T = (293.15 to 363.15) K. J. Chem. Thermodyn. 2014, 69, 201–208. [Google Scholar] [CrossRef]
- Johnson, J.K.; Mueller, E.A.; Gubbins, K.E. Equation of state for Lennard-Jones chains. J. Phys. Chem. 1994, 98, 6413–6419. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Oxford Science Publications; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Griebel, M.; Knapek, S.; Zumbusch, G. Numerical Simulation in Molecular Dynamics, Texts in Computational Science and Engineering; Springer: Berlin, Germany, 2007. [Google Scholar]
- Maginn, E.; Elliott, J. Historical perspective and current outlook for molecular dynamics as a chemical engineering tool. Ind. Eng. Chem. Res. 2010, 49, 3059–3078. [Google Scholar] [CrossRef]
- Galliero, G.; Boned, C. Shear viscosity of the Lennard-Jones chain fluid in its gaseous, supercritical, and liquid states. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 021201. [Google Scholar] [CrossRef]
- Delage Santacreu, S.; Galliero, G.; Odunlami, M.; Boned, C. Low density shear viscosity of Lennard-Jones chains of variable rigidities. J. Chem. Phys. 2012, 137, 204306. [Google Scholar] [CrossRef] [PubMed]
- Hoang, H.; Delage-Santacreu, S.; Galliero, G. Simultaneous Description of Equilibrium, Interfacial, and Transport Properties of Fluids Using a Mie Chain Coarse-Grained Force Field. Ind. Eng. Chem. Res. 2017, 56, 9213–9226. [Google Scholar] [CrossRef]
- Andersen, H.C. Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 1983, 52, 24–34. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Müller-Plathe, F. Reversing the perturbation in nonequilibrium molecular dynamics: An easy way to calculate the shear viscosity of fluids. Phys. Rev. E 1999, 59, 4894–4898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kröger, M. Simple models for complex nonequilibrium fluids. Phys. Rep. 2004, 390, 453–551. [Google Scholar] [CrossRef]
- Ramírez-González, P.V.; Escobar-Barrios, V.A. Viscosity and normal stress forces of Lennard-Jones chains using reverse non-equilibrium molecular dynamics. Mol. Phys. 2017, 115, 2970–2977. [Google Scholar] [CrossRef]
- Fernandez, J.; Lopez, E. Density Scaling Approach: Experimental Thermodynamics Volume IX: Advances in Transport Properties of Fluids; Assael, M.J., Goodwin, A.R.H., Vesovic, V., Wakeham, W.A., Eds.; Royal Society of Chemistry: London, UK, 2014; Chapter 9.3. [Google Scholar]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Galliero, G. Equilibrium, interfacial and transport properties of n-alkanes: Towards the simplest coarse grained molecular model. Chem. Eng. Res. Des. 2014, 92, 2031–2037. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Reference Fluid Thermodynamic and Transport Properties. In NIST Standard Reference Database 23; Refprop Version 8.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Baled, H.O.; Xing, D.; Katz, H.; Tapriyal, D.; Gamwo, I.K.; Soong, Y.; Bamgbade, B.A.; Wu, Y.; Liu, K.; McHugh, M.A.; et al. Viscosity of n-hexadecane, n-octadecane and n-eicosane at pressures up to 243 MPa and temperatures up to 534 K. J. Chem. Thermodyn. 2014, 72, 108–116. [Google Scholar] [CrossRef]
- Llovell, F.; Pàmies, J.C.; Vega, L.F. Thermodynamic properties of Lennard-Jones chain molecules: Renormalization-group corrections to a modified statistical associating fluid theory. J. Chem. Phys. 2004, 121, 10715–10724. [Google Scholar] [CrossRef]
- Lafitte, T.; Apostolakou, A.; Avendaño, C.; Galindo, A.; Adjiman, C.S.; Müller, E.A.; Jackson, G. Accurate statistical associating fluid theory for chain molecules formed from Mie segments. J. Chem. Phys. 2013, 139, 154504. [Google Scholar] [CrossRef]
- Mejia, A.; Herdes, C.; Muller, E.A. Force fields for coarse-grained molecular simulations from a corresponding states correlation. Ind. Eng. Chem. Res. 2014, 53, 4131–4141. [Google Scholar] [CrossRef]
- Oyarzún Rivera, B.; van Westen, T.; Vlugt, T.J.H. Liquid-crystal phase equilibria of Lennard-Jones chains. Mol. Phys. 2016, 114, 895–908. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delage Santacreu, S.; Hoang, H.; Khennache, S.; Galliero, G. Thermodynamic Scaling of the Shear Viscosity of Lennard-Jones Chains of Variable Rigidity. Liquids 2021, 1, 96-108. https://doi.org/10.3390/liquids1010008
Delage Santacreu S, Hoang H, Khennache S, Galliero G. Thermodynamic Scaling of the Shear Viscosity of Lennard-Jones Chains of Variable Rigidity. Liquids. 2021; 1(1):96-108. https://doi.org/10.3390/liquids1010008
Chicago/Turabian StyleDelage Santacreu, Stephanie, Hai Hoang, Samy Khennache, and Guillaume Galliero. 2021. "Thermodynamic Scaling of the Shear Viscosity of Lennard-Jones Chains of Variable Rigidity" Liquids 1, no. 1: 96-108. https://doi.org/10.3390/liquids1010008
APA StyleDelage Santacreu, S., Hoang, H., Khennache, S., & Galliero, G. (2021). Thermodynamic Scaling of the Shear Viscosity of Lennard-Jones Chains of Variable Rigidity. Liquids, 1(1), 96-108. https://doi.org/10.3390/liquids1010008






