Isochoric Specific Heat in the Dual Model of Liquids

Abstract

We continue in this paper to illustrate the implications of the dual model of liquids (DML) by deriving the expression for the isochoric specific heat as a function of the collective degree of freedom available at a given temperature and analyzing its dependence on temperature. Two main tasks have been accomplished. First, we show that the expression obtained for the isochoric specific heat in the DML is in line with the experimental results. Second, the expression has been compared with the analogous one obtained in another theoretical dual model of the liquid state, the phonon theory of liquid thermodynamics. This comparison allows providing interesting insights about the number of collective degrees of freedom available in a liquid and the value of the isobaric thermal expansion coefficient, two quantities that are related to each other in this framework.

1. Introduction

In a previous paper [1], the dual model of liquids (DML) has been introduced. It is a mesoscopic model that assumes a liquid to be a system made up of molecules arranged in solid-like dynamic structures in continuous rearrangement, swimming in an ocean of amorphous liquid. These solid-like aggregates, which we like to call liquid particles, (or also icebergs) interact with lattice particles, the phonons, present in liquids and responsible for the propagation of elastic and thermal energy. As a consequence of the interactions, the dynamic solid-like aggregates of molecules and the phonons exchange energy and momentum with each other. 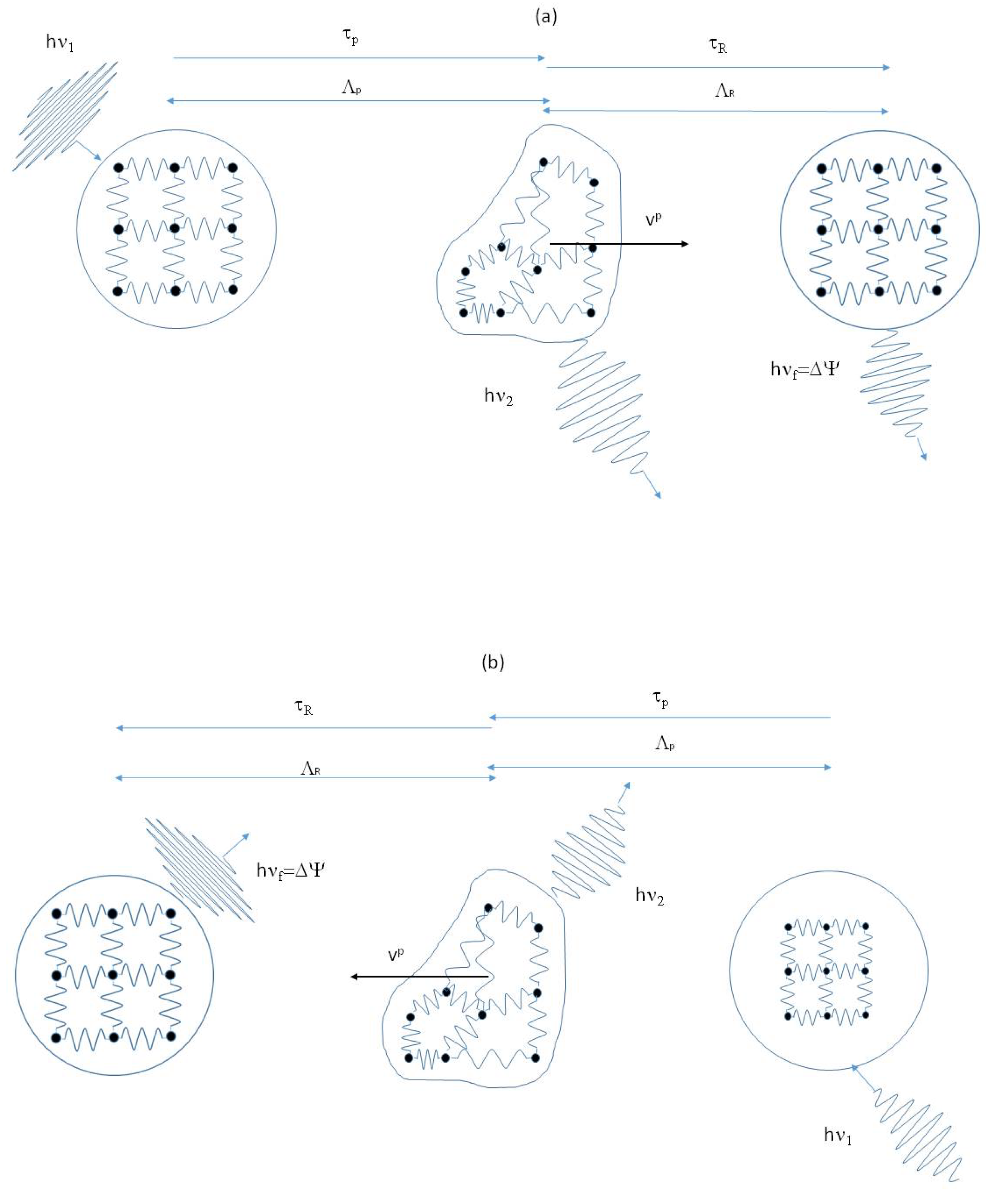This interaction is described in Figure 1, where the two elementary events at the base of the DML are represented. One of the most important aspects is that, involving wave-packets and not harmonic waves, the interaction with the liquid particle takes a finite time $\langle {\tau }_p\rangle$, during which the cluster is displaced by $\langle {\Lambda }_p\rangle$ (here and in the rest of the paper, the two brackets $\langle \rangle$ indicate the average over a statistical ensemble of the quantity inside them). During the interaction, both energy and momentum are exchanged between the phonon and the liquid particle. In an event of type (a), an energetic wave-packet collide with a dynamic iceberg, transferring to it the energy $\Delta {\epsilon }^{wp}$ and momentum $\Delta p^{wp}$, given by:

$$\Delta {\epsilon }^{wp}=h\langle {\nu }_1\rangle -h\langle {\nu }_2\rangle =\Delta E_p^k+\Delta {\Psi }_p=f^{th}\cdot \langle {\Lambda }_p\rangle$$

(1)

$$\Delta p^{wp}=f^{th}\cdot \langle {\tau }_p\rangle .$$

(2)

where $\langle {\nu }_1\rangle$ and $\langle {\nu }_2\rangle$ represent the wave-packet frequency before and after the collision, respectively; $\Delta E_p^k$ is the kinetic energy acquired by the liquid particle, while $\Delta {\Psi }_p$ is that part of the energy lost by the wave-packet in the inelastic interaction and converted into the potential energy of the internal collective Degrees of Freedom (DoF) of the solid-like cluster; $f^{th}$ is the interaction term between the wave-packet and the liquid particle. The wave-packet emerges from the collision with reduced energy and momentum, while the cluster acquires the energy and momentum lost by the phonon. The effect is of having converted the energy carried by the wave-packet into the kinetic and potential energy of the cluster. The power developed during the interaction is given by $W=f^{th}\cdot \frac{\langle {\Lambda }_p\rangle }{\langle {\tau }_p\rangle }$. The kinetic energy is dissipated as friction against the liquid. The liquid particle will begin to relax the potential energy $\Delta {\Psi }_p$, once the interaction is completed, i.e., after $\langle {\tau }_p\rangle$, having dissipated it during a time lapse $\langle {\tau }_R\rangle$, and travelled over a distance $\langle {\Lambda }_R\rangle$, at the end of which this residual energy stored into the internal DoF is returned to the liquid pool. The total duration of the process and the total displacement of the particle are shown in Equations (3) and (4), respectively:

$$\langle \tau \rangle =\langle {\tau }_p\rangle +\langle {\tau }_R\rangle ,$$

(3)

$$\langle \Lambda \rangle =\langle {\Lambda }_p\rangle +\langle {\Lambda }_R\rangle .$$

(4)

The overall effect of the interaction is that the energy subtracted from the phonon’ pool returns into it a time interval $\langle \tau \rangle$ later and a step $\langle \Lambda \rangle$ forward, alike in a tunnel effect. The event of type (b) is just the opposite: an energetic cluster collides with a wave-packet and transfers to it energy and momentum. The wave-packet will emerge from the scattering with increased energy and momentum. The net effect is that of having increased the liquid thermal energy carried by wave-packets at the expense of the kinetic and internal energy of the liquid particle.

The two events (a) and (b) are commuted one into the other by time reversal. These interactions are proposed in the DML as the basis of the Onsager’s reversibility principle [2,3]; furthermore, they are responsible for the propagation of momentum, energy, and mass in a liquid, and in this framework, thermal energy is seen as a form of elastic energy [1]. In equilibrium conditions, events of type (a) will alternate with events of type (b), to maintain the balance of the two energy pools unaltered. Besides, the macroscopic equilibrium is the consequence of the mesoscopic equilibrium; events such as those in Figure 1 will be equally probable along any direction to have a null average over time and space. On the contrary, if a symmetry breaking is present, for instance a temperature or a concentration gradient, one type of event will prevail over the other along the direction of the gradient.

The wave-pack–particle interaction gives a propagative character to the advancement of the thermo-elastic wave rather than a diffusive one, the ratio between $\langle \Lambda \rangle$ and $\langle \tau \rangle$ representing the propagation velocity:

$$\langle v_s\rangle =\frac{\langle \Lambda \rangle }{\langle \tau \rangle }.$$

(5)

Figure 1. Schematic representation of inelastic collisions between wave-packets and liquid particles. The event represented in (a), in which an energetic wave-packet transfers energy and momentum to a liquid particle, is commuted upon time reversal into the one represented in (b), where a liquid particle transfers energy and momentum to a wave-packet. The particle changes the velocity and the frequency of the wave-packet is shifted by the amount $\left({\nu }_2-{\nu }_1\right)$. Due to its time symmetry, we assume this mechanism is the equivalent of Onsager’ reciprocity law at the microscopic level [1,2,3]. In a pure isothermal liquid, energy and momentum exchanged among the icebergs are statistically equivalent, and no net effects are produced. Events of type (a) will alternate with events of type (b), to keep the balance of the two energy pools unaltered. Besides, the macroscopic equilibrium will ensure also the mesoscopic equilibrium; events (a,b) will be equally probable along any direction, to have a zero average over time and space. On the contrary, if a symmetry breaking is introduced, for instance a temperature or a concentration gradient, one type of event will prevail over the other along a preferential direction.

Figure 1. Schematic representation of inelastic collisions between wave-packets and liquid particles. The event represented in (a), in which an energetic wave-packet transfers energy and momentum to a liquid particle, is commuted upon time reversal into the one represented in (b), where a liquid particle transfers energy and momentum to a wave-packet. The particle changes the velocity and the frequency of the wave-packet is shifted by the amount $\left({\nu }_2-{\nu }_1\right)$. Due to its time symmetry, we assume this mechanism is the equivalent of Onsager’ reciprocity law at the microscopic level [1,2,3]. In a pure isothermal liquid, energy and momentum exchanged among the icebergs are statistically equivalent, and no net effects are produced. Events of type (a) will alternate with events of type (b), to keep the balance of the two energy pools unaltered. Besides, the macroscopic equilibrium will ensure also the mesoscopic equilibrium; events (a,b) will be equally probable along any direction, to have a zero average over time and space. On the contrary, if a symmetry breaking is introduced, for instance a temperature or a concentration gradient, one type of event will prevail over the other along a preferential direction.

The elementary interaction is subdivided into two parts. Taking for instance event (a). The first part is the process in which the lattice particle (the wave-packet) collides with the liquid particle and transfers to it momentum and energy, a fraction of which is transformed in the kinetic energy of the liquid particle, and the remaining in the potential energy of its internal DoF. This first part lasts $\langle {\tau }_p\rangle$ and the particle travels by $\langle {\Lambda }_p\rangle$, at the end of which the second part begins, the liquid particle relaxes and the energy is returned to the thermal pool through a lattice particle, alike in a tunnel effect. This second part lasts $\langle {\tau }_R\rangle$, during which the particle travels by $\langle {\Lambda }_R\rangle$. 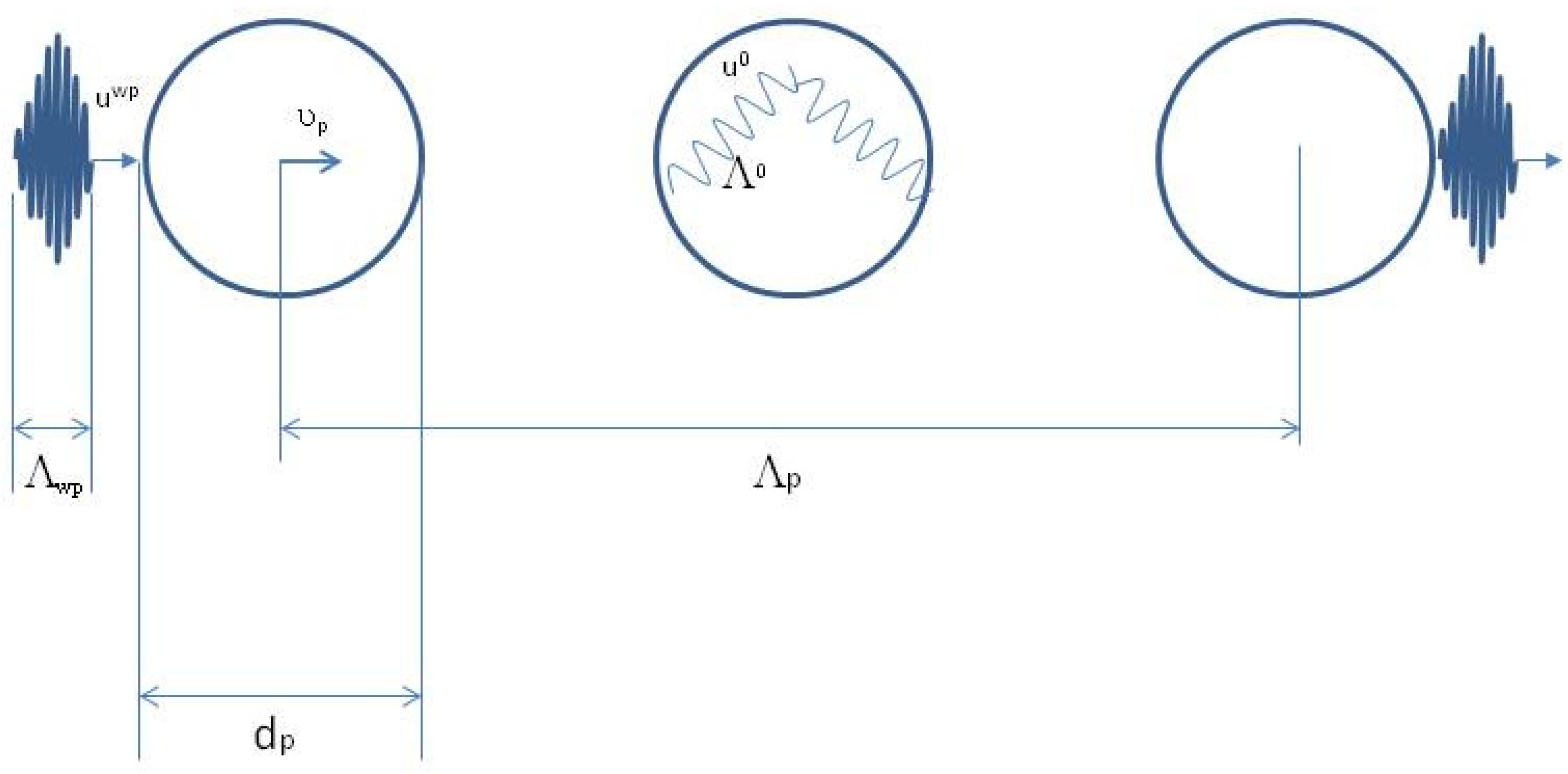Figure 2 is a close-up of the first event, which lasts ${\tau }_p$, of the wave-packet $\leftrightarrow$ liquid particle interaction shown in Figure 1a. $\langle {\Lambda }_{wp}\rangle$ is the size of the wave-packet and $\langle d_p\rangle$ is the diameter of the liquid particle [1].

Starting from these considerations and applying a simple kinetic model, we calculated, among others, the expressions for several macroscopic quantities in terms of elementary parameters. Examples are the thermal conductivity, the thermal diffusivity, the specific heat, etc. The order of magnitude of the particle and the wave-packet mean free paths and in particular the relaxation times involved in their interactions were also calculated [1].

The internal energy associated to the pool of wave-packets, $q_T^{wp}$, is represented in the DML as a fraction of the total one, $q_T$:

$$q_T^{wp}=m{q}_T=m{\displaystyle \underset{0}{\overset{T}{\int }}\rho C_{V}d\theta =}{{\rm N}}^{wp}\langle {\epsilon }^{wp}\rangle ,$$

(6)

where the classical expression for $q_T$, where $\rho$ is the medium density and $C_V$ is the isochoric specific heat per unit mass, is now multiplied by $m$; ${{\rm N}}^{wp}$ is the number of wave-packets per unit of volume (${{\rm N}}^{wp}$ is the average density of the wave-packets statistical distribution and is represented by a Bose–Einstein distribution function) and $\langle {\epsilon }^{wp}\rangle$ is their average energy. The dynamics described above occurs at high frequencies and involves only the DoF of the lattice; parameter m that we have introduced accounts for the ratio between the number of the collective DoF surviving at temperature T and the total number of the available DoF. We will return on the meaning and values of $m$ in the course of the paper, for now it is relevant to note that $0\le m\le 1$.

Figure 1a shows that the energy acquired by the liquid particle is given back to the pool of elastic excitation a $\langle \Lambda \rangle =\langle {\Lambda }_p\rangle +\langle {\Lambda }_R\rangle$ step forward and a $\langle \tau \rangle =\langle {\tau }_p\rangle +\langle {\tau }_R\rangle$ time lapse later, alike in a tunnel effect, as pointed out before, with $\langle \tau \rangle$ assuming also the role of a relaxation time [1]. One of the immediate consequences of this model is that thermal (and elastic) energy spread in liquids is naturally described by a propagation equation, such as the Cattaneo equation, rather than by a diffusion equation, such as the Fourier [4], the delay time introduced into the propagation equation being physically interpreted as the time taken by the thermal energy to reappear in a different place, or by the icebergs to move from a place to the next, as in Figure 1.

Very interestingly, in the last few years, several papers have appeared in international journals devoted to the liquid modelling, in particular the “phonon theory of liquid thermodynamics” (PLT) [5,6,7,8,9,10,11,12,13,14,15], the theory of dissipative systems with k-gaps [16,17], and a theory of specific heat derived by means of an analytical form of the vibrational density of states of liquids based on the existence of instantaneous normal modes [18,19].

The PLT, like the DML, is a theoretical model that assumes liquids as dual systems. In the PLT, the energy content of a liquid is described by a solid-like Hamiltonian, modified to account for the presence in liquids of anharmonic DoF. One of the main achievements of the PLT is that the Hamiltonian provides an expression for isochoric specific heat $C_V$ covering the solid, glassy, liquid, gas, and quantum liquids states of matter. Two expressions are obtained for the specific heat, with one in harmonic approximation and the other including anharmonic contributions to the pool of energy. The theoretical expressions have been confirmed experimentally in 21 different liquids. Moreover, the PLT has also provided a theoretical interpretation of the elastic, visco-elastic and viscous behavior response of matter to external disturbances due to the value of the product $\nu \tau$ (this product is normally reported as $\omega \tau$ by many authors, instead of $\nu \tau$. It is clear that there is no ambiguity between the two definitions), where $\nu$ is the frequency of the excitation of the DoF and $\tau$ is the relaxation time as defined above. It depends on whether $\nu$ is larger, comparable or smaller than $1/\tau$ [1,5,6,7,8,9,10,11,12,13,14,15].

Microscopically, the gap in the k-space in liquids can be related to a finite propagation length of shear waves; indeed, the gap in the momentum space in liquids emerges only in the transverse spectrum, while the longitudinal one remains gapless. One needs two essential ingredients for the k-gap to emerge in the wave spectrum. First, we need a wave-like component enabling wave propagation; this is represented in the DML by the wave-packets. Second, we need a dissipative effect, the process that disrupts the wave continuity and dissipates it over a certain distance, thus destroying waves with long wavelengths and giving origin to the gap in the k-space. The last is obviously represented by the “wave-packet–liquid particle” interaction, which is the source of dissipation, and works displacing the wave-packets from one place, where it is absorbed by the liquid particle, to another, where it returns to the system’ energy pool, alike in a tunnel effect. If $\langle \tau \rangle$ introduced above is the time during which the shear stress relaxes, then $\langle \Lambda \rangle =\langle v_s\rangle \cdot \langle \tau \rangle$ gives the shear wave propagation length (or liquid elasticity length) [1].

The solution to the fundamental law of density of states (DoS) in liquids [18] allows calculating an expression for the specific heat of liquids based on the instantaneous normal modes (INMs) [19], a concept extended from solids to liquids in view of the experimental evidence that INMs dominate the low- and intermediate-frequency ranges of the DoS in liquids.

The paper is organized as follows. In Section 2, the expression for isochoric specific heat $C_V$ in the frame of the reference of the DML is obtained as a function of the number of collective DoF available at a given temperature, $m$. Then, $C_V$ is compared with the analogous expression in the PLT [5,6,7,8,9,10,11,12,13,14,15], and their similarities, insights, and implications are discussed, in particular the limiting values of the collective DoF, and that of the isobaric thermal expansion coefficient of the liquid, $\alpha$, two quantities that are related to each other in this framework. In Section 3, the DML is shortly summarized and compared with the PLT. Finally, in Section 4, some further consequences and comparisons between the two theories are discussed.

2. Isochoric Specific Heat in the DML and the PLT Models: Similarities and Insights

The scope of this section is first to calculate the expression for the isochoric specific heat obtained in the DML and then to compare it with that acquired by the PLT. The same physical quantity is indeed obtained with two different approaches, namely a thermodynamic approach for the PLT and a mesoscopic-statistical approach for the DML. Consequently, the comparison between the two expressions could shed light on some parameters adopted in their derivation. This is actually the case for $m$ used in the DML approach and for $\alpha$ used in the PLT model. For both these quantities, some limits are deduced from the comparison of the two expressions for $C_V$.

The first step to accomplish the task is to calculate the specific heat in the frame of the DML [1]. Let us return to Equation (6), which can be re-written as follows:

$$q_T^{wp}=m{q}_T={{\rm N}}^{wp}\langle {\epsilon }^{wp}\rangle =m^{*}\rho C_{V}T,$$

(7)

where the quantity $m^{*}=m\frac{{\displaystyle \underset{0}{\overset{T}{\int }}\rho C_{V}d\theta }}{\rho C_{V}T}$ depends on the nature of the liquid and is introduced for the sake of simplifying the expression; $q_T^{wp}$ allows for calculating the phonon specific heat $C_V^{DML}$ contribution to the total one, $C_V$:

$$\{\begin{array}{ll}\rho C_V^{DML}& =\frac{\partial q_T^{wp}}{\partial T}=\frac{\partial }{\partial T}\left(m{q}_T\right)=q_T\frac{dm}{dT}+m\frac{\partial q_T}{\partial T}=q_T\frac{dm}{dT}+m\rho C_V\\ & =m\rho C_V\left[\frac{q_T}{m\rho C_V}\frac{dm}{dT}+1\right]=m\rho C_V\left[\frac{m^{*}}{m^2}\frac{dm}{dT}T+1\right]\end{array}.$$

(8)

Let us evaluate the quantity in square brackets at the last member. Because

$$\rho C_V^{DML}=\frac{\partial q_T^{wp}}{\partial T}\ge 0,$$

(9)

and $0\le m\le 1$, which implies that $\left[\frac{m^{*}}{m^2}\frac{dm}{dT}T+1\right]\ge 0$. As for the temperature dependence of $m$, the basis for the reasoning is the experimental evidence of the presence in liquids of transversal modes [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] active for the propagation of elastic energy by means of shear waves working in the solid phase. These modes, however, persist in the liquid phase, as long as solid-like structures survive. Experiments have shown that the two transversal modes disappear when the system approaches the critical point, where only the longitudinal collective modes survive accounting for the compression and expansion waves responsible for hydrodynamic modes propagation. This topic has been extensively discussed elsewhere [1]. Here, it is important to have in mind that the number of the collective DoF defined by $m$ decreases with temperature, so that $\frac{dm}{dT}<0$. Consequently, $\frac{m^{*}}{m^2}\frac{dm}{dT}T\ge -1$, and this defines the lower limit for $\frac{m^{*}}{m^2}\frac{dm}{dT}T$. As for the upper limit, because of the fact that $\frac{dm}{dT}<0$ and $\left[\frac{m^{*}}{m^2}\frac{dm}{dT}T+1\right]\ge 0$, we obtain the maximum value $\frac{m^{*}}{m^2}\frac{dm}{dT}T\le 0$. Definitively, we may conclude that:

$$0\le \left[\frac{m^{*}}{m^2}\frac{dm}{dT}T+1\right]\le 1,$$

(10)

and finally

$$C_V^{DML}\le C_V,$$

(11)

as one would have expected.

One of the most important results of the PLT is providing for the first time an expression for isochoric specific heat $C_V$ of liquids that is shown to be valid for the solid, glassy, liquid, gas, and quantum liquids states of matter [5,6,7,8,9,10,11,12,13,14,15]. To obtain this expression, the authors proposed a solid-like Hamiltonian of the system, in which only harmonic terms are included because of the harmonic character of the interactions in a solid lattice. In order to tailoring the Hamiltonian for the liquid structure, it has been modified to account also for inelastic interactions, thus including the anharmonic contributions to the pool of energy. The theoretical expressions of $C_V$ have been confirmed experimentally in 21 different liquids. Without entering into the details of the calculations, it is enough for our purposes to quote the expressions of the specific heat as obtained from the PLT accounting for both harmonic $C_V^H$ and anharmonic $C_V^A$ contributions, which can be written as:

$$C_V^H=\frac{1}{N}{\left(\frac{\partial q_T{}^H}{\partial T}\right)}_V=3-{\left(\frac{{\tau }_D{G}_{\infty }}{\eta }\right)}^3+\frac{3T}{2\eta }{\left(\frac{{\tau }_D{G}_{\infty }}{\eta }\right)}^3\frac{d\eta }{dT},$$

(12)

$$C_V^A=\frac{1}{N}{\left(\frac{\partial q_T{}^A}{\partial T}\right)}_V=3\alpha T-\alpha T{\left(\frac{{\tau }_D{G}_{\infty }}{\eta }\right)}^3+\frac{3\alpha T^2}{2\eta }{\left(\frac{{\tau }_D{G}_{\infty }}{\eta }\right)}^3\frac{d\eta }{dT}=\alpha T{C}_V^H,$$

(13)

from which we obtain:

$$C_V^{PLT}=C_V^H+C_V^A=C_V^H\left(1+\alpha T\right),$$

(14)

where indexes “H” and “A” stay for harmonic and anharmonic, respectively, while q_T is the total heat content of the liquid defined in Equation (6); The remaining terms have the same meanings as those quoted in [5,7], i.e., $\alpha$ is the coefficient of isobaric thermal expansion of the liquid, $\eta$ is its viscosity, ${\tau }_D$ is the Debye vibration period, and $G_{\infty }$ is the instantaneous shear modulus. The scope of the present section is to compare the expression given by Equation (14) for the total specific heat $C_V^{PLT}$ due to collective oscillations (phonons) as calculated in the PLT with the corresponding one calculated in the DML frame as the reference, $C_V^{DML}$, obtained from Equation (8) [1]:

$$C_V^{DML}=m{C}_V\left[\frac{m^{*}}{m^2}\frac{dm}{dT}T+1\right].$$

(15)

As pointed out before, $C_V$ is the total specific heat of the liquid. This last definition should not surprise the reader; indeed, notwithstanding in the DML the exchange of energy and momentum is due to the presence of collective oscillations, this picture nevertheless changes gradually, as temperature increases. If at the triple point all the energy is supposed to be propagated by means of phonons and wave-packets, as the temperature increases the solid phase gives progressively way to dynamic icebergs swimming in an ocean of amorphous liquid; the number and size of icebergs decrease and the amount of amorphous liquid increases to the point where it reaches the pure liquid at the Frenkel line. Thus, at the triple point one has $m\cong 1$, while $m$ decreases progressively to zero at the Frenkel line, so that $\frac{dm}{dT}<0$. The result at the mesoscopic scale is that the energy propagation by means of wave-packets becomes less and less important as the temperature increases. This is in line with Equation (11). Ultimately, we may assume that in a liquid the total specific heat $C_V$ is written as:

$$C_V=C_V^M+C_V^H+C_V^A=C_V^M+C_V^{DML}=C_V^M+C_V^H\left(1+\alpha T\right),$$

(16)

where $C_V^M$ is the classical contribution due to molecular interactions, and the last two members are obtained using Equation (14).

We are now ready to accomplish the task by comparing Equations (14) and (15) as:

$$C_V^{DML}\equiv C_V^{PLT}\Rightarrow m{C}_V\left[\frac{m^{*}}{m^2}\frac{dm}{dT}T+1\right]=C_V^H\left(1+\alpha T\right).$$

(17)

We can derive the expression for $\frac{dm}{dT}$:

$$\frac{dm}{dT}=\frac{C_V^H\left(1+\alpha T-m\right)-m\left(C_V-C_V^H\right)}{C_V\frac{m^{*}}{m}T}<0.$$

(18)

Because the quantities at the denominator are all positive, the above relation reduces to discuss the algebraic sign of the numerator. Two possibilities may be considered and described as:

$$\begin{array}{l}(\mathrm{A})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_V^H\left(1+\alpha T-m\right)<0\\ (\mathrm{B})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\{\begin{array}{c}(\mathrm{a})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_V^H\left(1+\alpha T-m\right)>0\\ (\mathrm{b})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_V^H\left(1+\alpha T-m\right)<m\left(C_V-C_V^H\right)\end{array}\end{array}$$

(19)

The case (A) is, however, not acceptable because of the definition $0\le m\le 1$; therefore we will discuss case (B) only. Because $C_V^H$ is a positive quantity, we have:

$$\{\begin{array}{c}(\mathrm{a})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1+\alpha T-m>0\\ (\mathrm{b})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1+\alpha T-m<m\left(\frac{C_{\mathrm{V}}}{C_V^H}-1\right)\end{array},$$

(20)

from which we easily get

$$\{\begin{array}{c}(\mathrm{a})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1+\alpha T>m\\ (\mathrm{b})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1+\alpha T<m\frac{C_{\mathrm{V}}}{C_V^H}\end{array}.$$

(21)

Equation (21) allows us to identify specific limits for parameter $m$:

$$\frac{C_V^H}{C_{\mathrm{V}}}\left(1+\alpha T\right)<m<\left(1+\alpha T\right).$$

(22)

We then see that parameter $m$ is strictly linked to $\alpha$. In the general case in which $\alpha >0$, Equation (22) becomes:

$$\frac{C_V^H}{C_{\mathrm{V}}}\left(1+\alpha T\right)<m<1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha >0.$$

(23)

The lower limit goes to zero as $C_V^H$. This conclusion is in line with the hypothesis of the DML. In fact, at high temperature, icebergs melt and disappear from the liquid, and with them also the collective DoF contributes to $C_V^H$.

There are, however, very few cases in nature where $\alpha <0$, for instance the water in the temperature range $\left(0<T<4\right)$ °C at atmospheric pressure. In these cases, the assumption introduced in Equation (23) cannot be adopted.

There are other interesting insights that can be deduced from (b) in Equation (21). Remembering that it is valid for $\frac{dm}{dT}<0$, an upper limit can be deduced for $\alpha$:

$$\alpha <\frac{1}{T}\left(m\frac{C_V}{C_V^H}-1\right);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{dm}{dT}<0.$$

(24)

Because usually it is also $\alpha >0$, we get the following relation holding for the specific heat:

$$C_V^H<m{C}_V,$$

(25)

which represents in turn an upper limit for $C_V^H$, providing the maximum thermal energy that can be stored into the harmonic DoF of icebergs. Incidentally, this is also in line with the limits imposed to the total specific heat $C_V^{DML}$ (see Equations (15) and (17) and the related validity range). Compiling Equations (17) and (25), we obtain the following expression for the lower limit of $\alpha$:

$$\alpha >\frac{m^{*}}{m^2}\frac{dm}{dT},$$

(26)

where the second member is a negative quantity. Thus, also in the very few cases in which $\alpha <0$, there is a minimum value of $\alpha$ as a function of the number of collective excitations present in the liquid. The complete range holding for $\alpha$ is obtained compiling Equations (24) and (26):

$$\frac{m^{*}}{m^2}\frac{dm}{dT}<\alpha <\frac{1}{T}\left(m\frac{C_V}{C_V^H}-1\right).$$

(27)

3. DML Comparison with Other Recent Liquid Models: The Same Scenario Seen from Different Perspectives

The liquid state was initially dealt with as a sort of extension of the gaseous one, mainly because of its property of flowing such as gases, the lacking of the capability of transmitting shear stresses, and adapting to the shapes of their containers. However, this approach has never allowed going very far in the formulation of theories that are able to provide a fairly general picture of physical quantities characterizing the liquid state. Let us take for instance the specific heat, for which a strong theoretical basis exists for gaseous and solid states, but not for the liquid one.

The alternative approach to considering the liquid state in the same way as the solid state has illustrious predecessors, such as Debye [36,37], Brillouin [38,39], and Frenkel [40]. However, they have never gone so far as to provide a model that goes beyond an intuitive description, probably because of the lack of experimental evidences that could guide and/or validate it. Nevertheless, recent measurements have given credit again to the ideas of Frenkel and Brillouin. At low frequencies, i.e., large wavelengths, it is not possible to "see" the mesoscopic structure of liquids. The entire liquid oscillates, compressing and expanding under the effect of pressure waves, which travel at the speed of sound. When one investigates the behavior of a liquid at very high frequencies and therefore at small wavelengths, it is discovered that it has a mesoscopic structure organized by means of solid-like dynamic aggregates, although ephemeral, which are identified here in a picturesque and imaginative way with icebergs, elsewhere simply called pseudo-crystalline structures (see for instance [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]).

The first experimental evidence, although indirect, that on short-time- and length-scale liquids are organized by means of solid-like local structures with a pseudo-periodicity, was obtained in 1996 [27], when Ruocco and Sette conducted Inelastic X-ray Scattering IXS experiments to measure the propagation speed of elastic waves at high frequencies in liquid water at ambient conditions. They found it equal to 3200 m/s, i.e., more than double that known at traditional frequencies, 1500 m/s, and very close to that of solid water, 4000 m/s. Starting from the results of experiments performed on various liquids with Inelastic Neutron Scattering INS and IXS techniques, [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35], the idea that pseudo-crystalline structures “exist and persist” in liquids on short time-scale and length-scale has gradually consolidated, with their size and number depending on the liquid temperature (and pressure). The presence of these ephemeral dynamical structures can obviously be deduced, only when high-frequency measurements are carried out, typical of INS and IXS techniques, and the wavelengths of the radiation involved are small enough to interfere with them. In the DML, these pseudo-crystalline structures within which elastic energy is propagated by means of (quasi) harmonic waves (phonons) interact with the rest of the (amorphous) liquid through anharmonic interactions, represented by wave-packets, which arise at their border. Ultimately, a quasi-elastic propagation within icebergs is transmitted to the amorphous matrix in the form of anharmonic wave-packets, and vice-versa. Unlike in crystalline solids, the anharmonicity allows a non-infinitesimal duration of the interactions, with the consequent transport of both energy and momentum and furthermore the exchange of energy with the internal DoF of the icebergs. 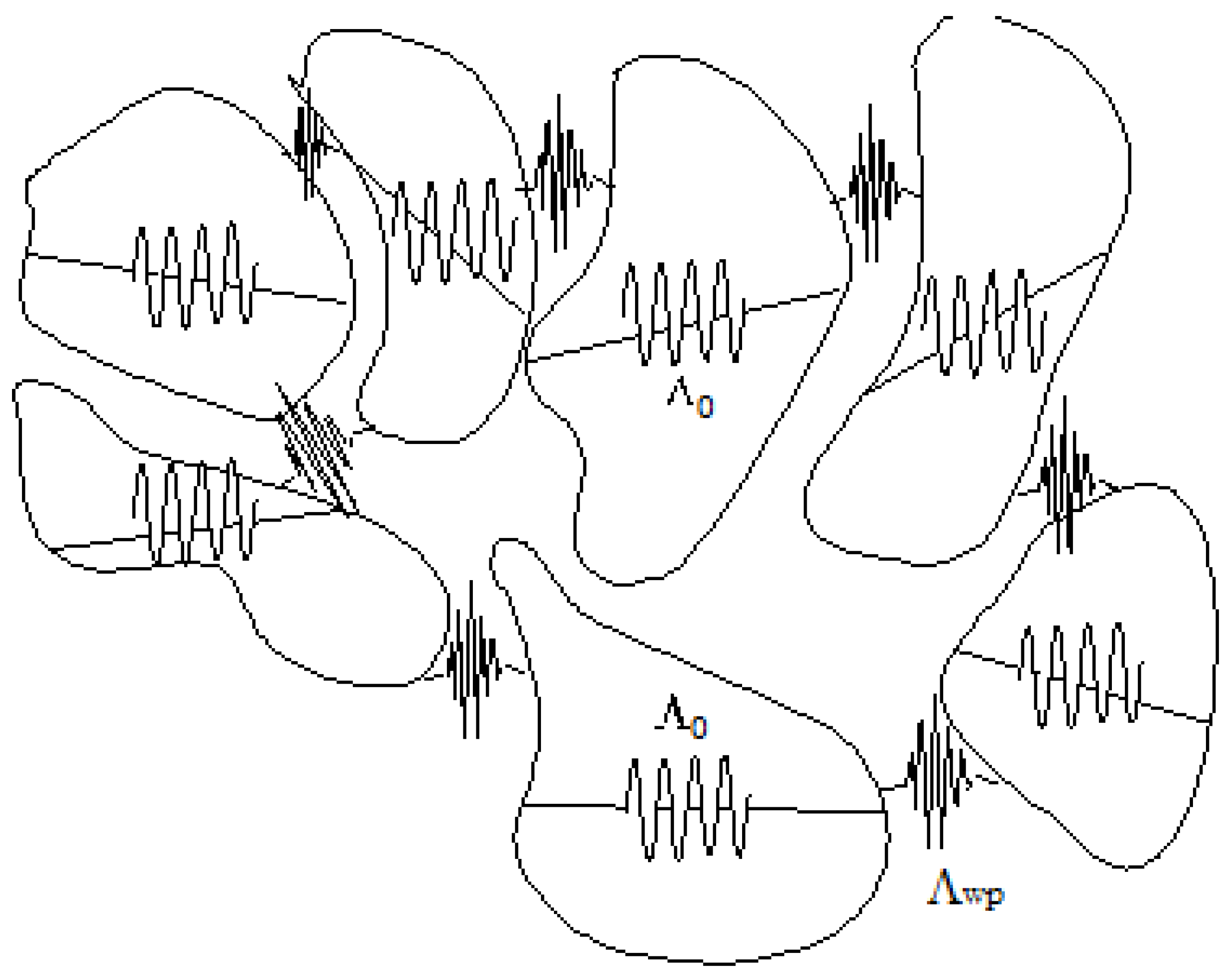Figure 3 shows the process described above.

How is the liquid state organized in the DML and how does it evolve? At the triple point, the solid structure is abruptly lost. The liquid state resembles an ocean where pieces of solid, in continuous rearrangement, continue to exist and participate in the propagation of energy and momentum. Being solid-like, they are able to transmit not only longitudinal compressions and expansions of the medium, but also shear stresses. As the temperature rises, the fusion is not instantaneous, the solid phase giving a progressive way to solid-like dynamic structures in continuous evolution (the icebergs) swimming in an ocean of amorphous liquids; the number and size of the solid-like structures decrease and the amount of amorphous liquid increases to the point where it reaches the pure liquid at the Frenkel line. On the other hand, it would not be surprising if the transition from the solid to the liquid phase takes place over a wide range of temperature and pressure rather than over a restricted interval around the triple point.

This vision of liquids is not entirely new; from a historical point of view, besides the pioneering ideas of Debye and Brillouin, Frenkel proposed that liquids are constituted by a very large number of randomly oriented crystals of submicroscopic size, which he defined as cybotactic groups (In his book [40], Frenkel actually affirms that this idea was introduced by Stewart around 1930s; Stewart proposed to denote such submicroscopic crystals, consisting of few tens of molecules, at most, by the term “cybotactic group” (or regions), and assumed them to be connected with each other by thin layers of the wholly amorphous phase). The concept of relaxation time was early introduced by Maxwell in the liquid dynamics as a phenomenological concept related to the visco-elastic nature of liquid [41]. Frenkel, trying to compile a solid-like vision of liquids with their peculiarity of flowing, recovered the concept of relaxation time by giving it a microscopic interpretation as “the average time between particle jumps at one point in space in a liquid” [40]. Its inverse, ${\nu }_F=1/{\tau }_F$, is the frequency of occurrence of particle jumps. In the Frenkel model, the way of distinguishing a liquid from a solid or a gas goes around the value of the relaxation time ${\tau }_F$. If at a given temperature the characteristic time t of a perturbation propagating in the liquid is much shorter than ${\tau }_F$ (or the frequency f is much larger than ${\nu }_F$), over the time interval t, the medium is seen by the perturbation as a solid, because the particles do not have enough time to rearrange. The dynamic response is a free recoil of the liquid particle after the collision with the probe. Incidentally, this figure matches the interdependence between the relaxation time and the excitation frequency introduced in Introduction.

The value obtained experimentally for the speed of sound in liquid water [25,26,27,32] proves that, in the range of momentum exchange examined and during the time lapse of the relaxation time, water behaves as a rigid network of molecules and intermolecular forces are the same as in ice. Indeed, the energy of the acoustic wave generated after the collision of the probe with the target particle of the medium increases from the viscous to the elastic regime, i.e., upon frequency increase, due to the decrease of the acoustic dissipation. The same trend holds for the speed of sound, which manifests a positive dispersion versus frequency (PSD), while the opposite is true for the viscosity. Consequently, fingerprints of relaxation phenomena typical of collective dynamics can be found by examining the trend of the liquid physical parameters with frequency [22]. Surprisingly, this is the demonstration of their ingenious intuitions. This conclusion is exactly the same as those reported by Brillouin and Frenkel in their pioneering works [38,39,40], which anticipated what has been experimentally assessed on the structure of liquids only a century later.

The presence of relaxation time is a distinguishing aspect of liquids vs. gases; in the latter, every collision is independent, and every collision is equal to the previous and successive ones. The heat motion in liquids close to the crystallization point has the same characteristics as in solids, consisting of oscillations of molecules around their equilibrium positions. The positions of atoms in liquids are not permanent but temporary. After performing a number of oscillations around a given position, the atom can jump to another equilibrium position, far $\delta$ from the previous, where $\delta$ is of the same order of magnitude as the average distance among molecules in the liquid. This step-by-step wandering, lasting time ${\tau }_F$, is a sort of self-diffusion motion, leading to a gradual mix-up of all the atoms [see for instance [42,43]]. It must proceed much faster in liquids than in solids and must have a simpler characteristic because of the absence of definite lattice sites. Figure 3 illustrates the scenario.

Relaxation time ${\tau }_F$ has two intrinsic limits [see for instance [5,6,15,23]. The upper limit is at low temperatures above the crystallization point, to leave the atoms the possibility to jump between two equilibrium positions. This limit corresponds to time intervals ${\tau }_F\approx {10}^2÷{10}^3 s$, typical of the glass transition. The lower limit at high temperature corresponds to the minimum value of the Debye vibration period, ${\tau }_F={\tau }_D=1/{\nu }_D\approx 0.1ps$, and the time interval between two successive jumps, the relaxation time, becomes comparable with the shortest vibration period. Thus, one way of distinguishing a liquid from a solid or a gas goes around the values of relaxation time ${\tau }_F$. If at a given temperature characteristic time $t$ of a perturbation propagating in the liquid is much shorter than ${\tau }_F$ (or the frequency $f$ much larger than ${\nu }_F$), over the time interval $t$ the medium is seen by the perturbation as a solid and the particles have no time to rearrange. The dynamic response is a free recoil of the liquid particle after the elastic collision with the probe (neutron or X-ray photon). The emerging spectrum is that of a solid being determined by the classical Maxwell–Boltzmann distribution [24], while the speed of sound is much higher. This case is that of “fast sound”, of which the velocity for water of $\approx 3200\hspace{0.17em}m/s$ obtained experimentally [25,26,27,32] is very close to the sound velocity found in crystalline ice Ih of ≈ 4000 m/s, confirming that, in the explored range of temperature, water is in the visco-elastic regime, i.e., they combine viscous and solid-like elastic properties, as early suggested by Maxwell [41] and subsequently by Frenkel [40]. In this configuration, the medium supports one longitudinal mode and two transversal modes. At time significantly longer than $t$, the opposite is true, the system is seen as a viscous medium, and it supports only one longitudinal mode. More precisely, liquids support two transversal and one longitudinal modes at low temperature; as far as the temperature increases, approaching the liquid-to-gas transition, the capability of supporting shear stresses is lost and only the longitudinal mode survives (however, the fact that flat waves are not intrinsic excitations in disordered media such as liquids inevitably leads to mixing longitudinal and transverse excitations. Unlike in crystals, these types of excitations are not orthogonal). This limit provides the borderline between purely diffusive motions and vibratory or oscillatory motions.

What described above is equivalent to assert that liquids and solids differ only quantitatively, not qualitatively [10], with the borderline being the frequency ${\nu }_F$ the relaxation time ${\tau }_F$, as guessed by Frenkel [40]. This concept, i.e., the distinction between liquids and solids is quantitative rather than qualitative, was introduced for the first time by Eckart [44,45] in his famous papers on the theory of “anelastic fluid”. Eckart demonstrated also that the propagation velocity of isentropic longitudinal waves is a complex number because it depends on frequency. He also faced in his model the problem of the relaxation times occurring in the dissipative processes. He ignored all the possible causes of dissipation, except the collision process (as in the DML), which results in viscous forces, and considered the type of dissipative process that is characteristic of anelastic media, either solid and liquid. This process depends on the fact that the anelastic variations of strain can occur, independently of changes in density.

On the one hand, liquids of relaxation times distinguish them from gases. On the other hand, the thermal unrest in liquids has the same characteristic as in solids, consisting of oscillations of molecules around their equilibrium positions. As in solids, a liquid particle may oscillate along with three preferred directions, one longitudinal (L) and two transversal (T). At low temperatures, therefore, liquids manifest also the capability of reacting to shear stresses, with this behavior being explained by the presence of the icebergs. Because of the progressive disappearance of icebergs, the capability of liquids to react to shear stresses by means of transversal DoF is progressively lost, as it approaches the Frenkel line. This is in line with the structural cross-over existing in liquids [8,23]. Consequently, the number $m$ of the lattice collective DoF available in a liquid, introduced in Equation (6), decreases, as the temperature increases, $dm/dT<0$. Indeed, at low temperatures, energy and momentum in liquids are propagated also by means of transversal DoF, because the propagation mechanism involves a structural relaxation of the pseudo-crystalline structure. As the temperature increases, this property is progressively lost and energy and momentum are propagated only by means of longitudinal DoF, because only collisional mechanisms are involved. Therefore, at low temperatures, $m$ approaches unity, while it decreases by increasing the temperature because the number of the lattice collective DoF decreases with increasing T, $0\le m\le 1$ (at the Frenkel line only the longitudinal DoF survives). This is a fundamental point of the DML. It is worth noting that, apart from the hypothesis of the mesoscopic organizations of liquids by means of dynamic icebergs, this figure matches that of the PLT, with DML representing its mesoscopic counterpart. The above argument related to the variation with temperature (and pressure) of the number of DoF is supported also by measurements [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,46].

A very interesting insight has emerged from the comparison with recent developments in theoretical models in systems exhibiting k-gaps [16]. Baggioli et al. [16] used a two-field Lagrangian to describe, from the theoretical point of view, systems with k-gaps composed of two mutually interacting sub-systems (which we identify with the wave-packets and the liquid particles in the DML). They used a two-scalar fields, ${\varphi }_1$ and ${\varphi }_2$, to represent velocities or displacements, from which the Lagrangian is built up, instead of a single-scalar field. Without entering into the details of the mathematical formalism, which is out of the scope here, what matters is that the equations of motion for the two scalar fields decouple; the development of the Lagrangian leads to two separate Cattaneo-like equations (Frenkel [40] already deduced a Cattaneo-like propagation equation introduced into the Navier–Stokes equation due to the shear in a liquid, although he did not solve the equation) for both ${\varphi }_1$ and ${\varphi }_2$, which can be written as:

$$\{\begin{array}{l}{\varphi }_1={\varphi }_0\exp \left(-\frac{t}{2\langle \tau \rangle }\right)\cos \left(kx-\omega t\right)\\ {\varphi }_2={\varphi }_0\exp \left(\frac{t}{2\langle \tau \rangle }\right)\cos \left(kx-\omega t\right)\end{array}.$$

(28)

The solution for such a system shows many interesting key-points. The more relevant for our purposes are as follows:

(1)

The interaction potential is an oscillating function (see Figure 5 in [16]), which is the two-scalar fields, and therefore the two interacting sub-systems exchange energy among them: ${\varphi }_1$ and ${\varphi }_2$ reduce and grow over time $\langle \tau \rangle$, respectively. This process is not dissimilar from phonon scattering in crystals due to defects or anharmonicity where a plane-wave phonon (${\varphi }_1$) decays into other phonons (represented by ${\varphi }_2$) [16] and acquires a finite lifetime $\langle \tau \rangle$.

(2)

Being the total-scalar field of the product of ${\varphi }_1$ and ${\varphi }_2$, the total energy of the composite system does not have exponential terms depending on time due to their cancellation; consequently, the total energy is a constant of motion.

(3)

The motion described by the solutions of the two-scalar fields or by the function represented in Figure 5 in [16] is a typical dissipative hydrodynamic motion. If the anharmonic interaction described by the Lagrangian (i.e., the wave-packet–liquid particle interaction in the DML) has a double-well (or multi-well) form, the field can move from one minimum to another (tunnel effect) in addition to oscillating in a single well.

(4)

This motion is analogous to diffusive particle jumps in the liquid and represents a possible origin for the viscosity. The motion is indeed a sort of hopping motion of the field via thermal activation or tunnelling between different wells with frequency ${\nu }_F=1/{\tau }_F$. It is worth noticing that the dissipation concerns the propagation of plane waves in the anharmonic field described by the two-scalar fields of the Lagrangian. The dissipation varies as ${\nu }_F=1/{\tau }_F$: large $\langle \tau \rangle$ corresponds to rare transitions of the field between different potential minima.

A distinct effect of dissipation is related to a situation where the energy of the system is not changed overall but the propagation range of a collective mode (e.g., phonon) acquires a finite range. No dissipation takes place, when a plane wave propagates in a crystal where the wave is an eigenstate. However, a plane wave dissipates in systems with structural and dynamical disorder, such as liquids. Particle dynamics in liquids involves both solid-like oscillatory motion at quasi-equilibrium positions and diffusive jumps into neighboring locations [7,9,15,16,40,47]. The first allows liquids to show solid-like parameters when experimentally investigated over mesoscopic scales, while the jumps enable liquids to flow and associate them with viscosity. However, describing this dynamics needs the consideration of a non-linear interaction, allowing for both oscillation and jumps activated over potential barrier of the inter-particle potential. This problem does not originate in solids and gases. The smallness of atomic displacements in solids and the weakness of interactions in gases simplify their theoretical descriptions, as already pointed out above. Liquids do not have those simplifying features: they combine large displacements with strong interactions (liquids do not have small parameters). For this reason, liquids are not described by theoretical tools at the same level as gases and solids [48].

There are interesting features that associate the presence of k-gaps in liquids with the fast sound or PSD, the increase with frequency of the measured speed of sound over its hydrodynamic value. As first noted by Frenkel, a non-zero shear modulus of liquids implies that the propagation velocity crosses over from its hydrodynamic value $v=\sqrt{B/\rho }$ to the solid-like elastic value $v=\sqrt{\left(B+4/3G\right)/\rho }$, where B and G are bulk and shear moduli, respectively. According to the above, shear modes become propagating at high k values, implying PSD at these k points. This further implies that PSD should disappear with temperature starting from small k, because the k-gap increases with temperature [16].

The positions of atoms of liquid particles in fluids are not permanent, but temporary, as in solids. This is explained by the fact that kinetic energy, $E_p^k$, of a liquid particle is comparable with potential energy, ${\Psi }_p$, that keeps it to a definite lattice point. Unlike in solids, where obviously ${\Psi }_p>>E_p^k$, or in gases, where the opposite holds, ${\Psi }_p<<E_p^k$, in liquids, the intermediate situations is true, ${\Psi }_p\approx E_p^k$. This step-by-step wandering, totally lasting time ${\tau }_F$ for each jump, must proceed much faster in liquids than in solids and must have a simpler characteristic because of the absence of definite lattice sites.

The arrangement of liquid molecules on the mesoscopic scale, along with local lattices, justifies the experimental value found for the speed of sound in water (and in other liquids) close to that of the corresponding solid form [20,21,22,23,24,25,26,27,28,29,30,31,32,33,35]. Liquid molecules are bounded to the local dynamic lattice, the iceberg; as far as thermal perturbations propagate inside an iceberg, they behave as in solids. When perturbations cross the boundary between two such local lattices, inertial effects develop, giving rise to momentum transport, as in the Frenkel model. The interactions are accompanied by the propagation of elastic energy in the form of wave-packets because of the anharmonicity of the potential field [1]. The anharmonic characteristic of the collisions generated at the border between two nearest-neighbor icebergs makes the interaction time non-negligible, thus allowing also momentum transport. This gives origin to the displacement of icebergs and consequently to their diffusion. When wave-packets propagate in the amorphous phase, the speed of sound decreases and the same happens for the other liquid parameters. Incidentally, this figure provides a qualitative explanation of the PSD observed in liquids at high frequencies.

It is clear from above that what we usually mean as a “liquid” is not a liquid at all in the DML, but a mixture of solid-like dynamic structures and an amorphous phase, i.e., liquid phase in its common sense. As a consequence, any liquid parameter, of which the magnitude is experimentally measured at temperatures and pressures where a usual liquid phase exists, is actually a pondered average of a solid/liquid value, in particular at those frequencies where the duality of liquids phase emerges [1,5,7,8,10,11,12,13,14,15].

It is very interesting to compare the DML with the PLT. The PLT describes the liquid from a statistical-thermodynamic point of view; therefore, it cannot provide a direct answer on “why” liquid particles oscillate. The DML, instead, faces the problem from an opposite, mesoscopic point of view, starting from the elementary wave packet $\leftrightarrow$ liquid particle collision that gives rise to the harmonic and anharmonic contributions present even in the PLT. The DML provides and analyzes the microscopic elementary mechanism by which elastic and thermal energy, as well as momentum, are exchanged between liquid particles and lattice particles (phonons) and show that this scenario is in agreement with that of the PLT. One of the junction points between the two approaches, PLT and DML, is the relaxation times involved in the elementary interactions. Because of the thermodynamic-statistical nature of the theory, the PLT from its side is only able to provide an indication of the variation range of the relaxation time through the value of the product $\nu \tau$. On the other side, the DML is a mesoscopic model and analyzes the intimate mechanism of the interaction of liquid particles with lattice modes; this provides both the answer to the question of “why” liquid particles oscillate and a way for calculating the order of magnitude of $\tau$ in ordinary liquids [1]. We have shown [1] that the attained values of $\tau$ and the product $\nu \tau$ are in the range foreseen on thermodynamic statistical basis from the PLT. The relaxation time is one of the key points of both models, and because the only common argument of PLT and DML is the assumption that thermal energy in liquids is transported by means of collective lattice excitations, both harmonic and anharmonic, the mutual agreement shows that both of them look at the model of the liquid state in the same way although from different observation points.

Another similarity of the PLT and the DML is the presence of harmonic and anharmonic contributions to the pool of energy. From a statistical-thermodynamic point of view, this fact is accounted for in the PLT by considering bcontributions to the Hamiltonian of a liquid, giving rise in turn to the expression for the specific heat (the Hamiltonian adopted in the PLT has, however, many other interesting consequences, which are not discussed here because they are out of the specific topic of the present paper). On the other side, harmonic and anharmonic oscillations in the DML are believed to be responsible for the propagation of energy and momentum within a liquid. In fact, energy is supposed to propagate inside the solid-like aggregates by means of harmonic oscillations. Liquid particles communicate among them and with the disordered liquid by means of anharmonic wave-packets, capable to exchange not only energy, but also momentum. In such a way, the macroscopic phenomena of diffusion (and thermal diffusion) may be easily interpreted in the DML.

The duality of liquids, supposed by both the DML and the PLT, however, does not exclude classical mechanisms of intermolecular interactions, as in Section 2 when discussing the similarities of isochoric specific heat expressions and their implications. The propagation of energy in a condensed medium through inter-molecular interactions and interactions between wave-packets and pseudo-crystalline structures may be supposed to work simultaneously and uniformly at the mesoscopic level. Which of the two prevails over the other depends on the thermodynamic conditions of the system. In a solid, only the phononic part will be present. When the solid melts, the molecules begin to arrange in local solid-like lattices, phononic propagation gradually leaves a way for propagation through molecular interactions, until the former completely disappears when the gaseous state is reached, with only the molecular one remaining. While in solids there are always three modes of vibration, two transversal and one longitudinal, in liquids the transverse modes will be active only for frequencies higher than ${\omega }_F$, $\omega >{\omega }_F=\frac{2\pi }{{\tau }_F}$, where ${\tau }_F$ is the relaxation time. In other words, for interaction times lower than the relaxation time, liquids behave as solids, while for times longer than ${\tau }_F$, liquids lose the ability to support transversal ways, as in the classical approach.

An alternative—or rather complementary—expression for the liquid specific heat has recently emerged from another model proposed by Baggioli and Zaccone [19]. Starting from the solution they found for the vibrational DoS in liquids [18], they have obtained an expression of $C_V$ due to the only contribution of the experimentally proven presence in liquids of INMs, neglecting the contribution of the “traditional” normal modes, on which the PLT is based. INMs are indeed not normal modes in the traditional meaning, but rather pure imagery modes due to the anharmonic interaction potential typical of liquids. As such, they are absent in solids. Their comparison with the expressions of $C_V$ provided by the DML and the PLT is not straightforward.

4. Further Discussion and Conclusions

The hypotheses behind the DML, duly described in [1] and which the reader is referred to for an in-depth study, are actually two, and both have an experimental background. The first is that experiments performed with IXS and INS techniques [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] have made it possible to highlight that the mesoscopic structure of liquids is characterized by the (ephemeral) presence of solid-like, pseudo-crystalline structures, of which the size is a few molecular diameters and of which the mass is equal to those of a few molecules, within which the elastic waves propagate as in the corresponding solid phase. The number and size of these structures varies with the temperature and pressure of the liquid. The second hypothesis is a direct consequence of the first. It consists in the assumption that elastic energy and momentum in liquids propagate by means of collective oscillations or wave-packets in a similar way as in crystalline solids. The perturbation propagates inside the solid-like structure by means of (quasi)harmonic waves; when it crosses the boundary, they leave a way to anharmonic wave-packets, responsible for the propagation among solid-like structures and with the surrounding amorphous liquid phase. This scheme and the DML may be obtained by gathering the early pictures of liquids of Debye [36,37] Brillouin [38,39], and Frenkel [40] in the light even of what is known today from high-frequency scattering experiments. In fact, as a result of the interaction described in Figure 1, being the icebergs in continuous rearrangement, molecules continuously move from an iceberg to the nearest neighbor and icebergs jump in the liquid from one site to the nearest-neighbor one, as hypothesized by Frenkel for the cybotactic groups introduced in [40].

Here, in this paper and also elsewhere [1], we have largely discussed and commented the intimate similitude and differences of the DML and PLT. In particular, both of them are dual models of liquids, consider the presence of harmonic and anharmonic oscillations, give a pivotal role to relaxation times, etc. All these arguments bring the obvious conclusion that the two models show an evident visual identity: in the liquid state, both harmonic modes, typical of the solid state, and anharmonic modes, typical of non-crystalline structures, are simultaneously present. The comparison of the two expressions for the specific heat provides interesting information about the degree of excitation of vibratory modes in liquids. Besides, we have also pointed out the central role of relaxation times in both models; in particular, their role has the consequence, among others, that heat propagation in liquids is described by a propagation (Cattaneo) equation, instead of a diffusive equation [4].

As outlined above and duly discussed in [1], the key point of the DML is that the liquid is composed of two systems, the liquid particles and the lattice particles; they interact with each other through a harmonic potential inside the iceberg and through an anharmonic potential outside. The presence of k-gaps reinforces this point, and also the fact that not only longitudinal but also transversal modes are allowed in liquids. As far as the system is in thermodynamic equilibrium, the same holds for the two subsystems; however, when a non-equilibrium state is imposed, even the two populations reach two distinct equilibria. The anharmonic characteristic of the interaction allows the two populations to exchange among them not only energy, but also momentum. This is another key point of the model, because the interaction represents a mechanism through which energy is dissipated. A possible application of the DML is providing an elementary mechanism to explain the viscosity, which is a dissipative phenomenon present in liquids [49]. In a physical model for the viscosity of liquids, the exchange of momentum and energy among the two subsystems—liquid particles and lattice particles—should be indeed accounted for, for instance with a suitable modification of the Navier–Stokes equation by using a two-field Lagrangian. Another interesting topic to be investigated is the transition from inviscid liquid to gas.

If the elementary wave-packet ↔ liquid particle interactions would be perfectly elastic, all the energy (and momentum) lost by the wave-packet in an event shown in Figure 1a would be acquired by the particle and converted into kinetic energy, with only the translational DoF being involved in the scattering process. Nevertheless, being the interaction anharmonic, it is not instantaneous, and the momentum exchanged between the wave-packet and the particle is proportional to the duration of the interaction, $\langle {\tau }_p\rangle$ (i.e., to the time-length of the wave-packet), but also the energy lost by a wave-packet in an event of type (a) of Figure 1 is only partially converted into the kinetic energy of the particle. The remaining part is converted into internal molecular energy, exciting the corresponding DoF. This is an important point of the model, which introduces the exchange of energy with the internal vibratory DoF of the molecular cluster in a phononic model of liquid. It is possible to define an “effective heat capacity” $C_{eff}$ for the total heat absorbed by (or given to) a liquid particle, taking into account the two branches of DoF. $C_{eff}$ is a complex quantity, of which the real part is the static contribution pertaining to the external translational DoF while the imaginary part depends on that pertaining to the internal vibratory (quantized) DoF on the frequency and on the relaxation time [50]. The pool of energy stored in the cluster will be released after a time lag $\langle {\tau }_R\rangle$. Depending on the order of magnitude of such a time interval, the events of Figure 1 can be considered elastic, quasi-elastic, or inelastic [1,5,15,23].

One of the peculiarities of the interactions between wave-packets and liquid particles is to work as a tunnel effect, by moving quantities of energy from one place to another in a well-defined time interval, the relaxation time, during which it is kept out of the heat current. The role of relaxation times is important in all the situations in which transport phenomena are influenced by a delay occurring in the microscopic transport processes. One of these cases is that of the heat transport in non-stationary conditions, where such delays play a relevant role in the correct identification of the physical process and the related mathematical equations describing the heat propagation in condensed media. It is well-known that in non-stationary conditions a Cattaneo-like hyperbolic equation should be used to describe the heat propagation, instead of a Fourier-like parabolic one to describe the heat diffusion.

Some final remarks are in order about the comparison of the expression for isochoric specific heat deduced from the PLT and the DML. This comparison has provided very interesting information about the physical limits of parameter $m$ and the coefficient of isobaric thermal expansion $\alpha$. An additional relation is also deduced for the ratio between the harmonic contribution to specific heat, $C_V^H$, and the total specific heat of the liquid. Besides the intrinsic information, which is not supported by experimental confirmation, all the attained expressions and limits are internally consistent with the model, and with other limits provided on different bases. Having found limiting values for these quantities stimulates our reasoning on the fact that other authors [51,52,53,54,55] have identified limiting values although for different physical quantities. However, an answer to such a comparison is still premature, although not absurd in principle.

However, today, there are many questions on the nature of liquids that are still unanswered, as well as a deficit of experiments. Performing experiments at the onset of a temperature gradient may allow investigating how liquid parameters evolve from equilibrium to non-equilibrium conditions. It could be possible, for instance, to investigate the evolution of correlations lengths, sound velocity, thermal conductivity, etc. In addition, very interesting could be the investigation of whether and how a temperature gradient affects the viscous coupling between two liquids. Such experiments could be performed, for instance, by applying a temperature gradient to a stabilized isothermal liquid, provided that the average temperature of the system remains unchanged, preventing the convection instability and performing light scattering experiments, until a stationary temperature gradient is reached, i.e., during the transient, exactly the situation that is normally avoided in all the experiments. An alternative way to heat a small volume of liquids could be hitting the liquids with a focalized high-power laser beam.

A second type of experiments could be aimed at investigating glassy and liquid-to-solid transitions. Starting from a stationary temperature gradient, both temperatures could be lowered, thus decreasing the average temperature until the liquid solidifies. Light scattering experiments performed during the non-stationary phase should allow investigating the dynamics of the system when the glassy and liquid-to-solid transitions are crossed. In particular, the local domains should be oriented following the external temperature gradient, thus allowing the increases of the correlation lengths, sound velocity, thermal conductivity, etc., along the preferential direction of the external temperature gradient. A difference between the same parameters when measured along the direction of the temperature gradient with respect to those measured along a different direction should be evident from the experimental data collected. This technique could in some way introduce a sort of anisotropy into the liquid matrix, becoming an anisotropic solid phase.

In all the above experimental setups, one could fruitfully exploit the characteristics of a special environment such a microgravity laboratory on orbiting platforms, where the above measurements could be pursuit without disturbance and often overwhelming effects due to the presence of the Earth’s gravity.