Generation of Multiple Types of Driving Scenarios with Variational Autoencoders for Autonomous Driving

Abstract

Generating realistic and diverse driving scenarios is essential for effective scenario-based testing and validation in autonomous driving and the development of driver assistance systems. Traditionally, parametric models are used as standard approaches for scenario generation, but they require detailed domain expertise, suffer from scalability issues, and often introduce biases due to idealizations. Recent research has demonstrated that AI models can generate more realistic driving scenarios with reduced manual effort. However, these models typically focused on single scenario types, such as cut-in maneuvers, which limits their applicability to diverse real-world driving situations. This paper, therefore, proposes a unified generative framework that can simultaneously generate multiple types of driving scenarios, including cut-in, cut-out, and cut-through maneuvers from both directions, thus covering six distinct driving behaviors. The model not only learns to generate realistic trajectories but also reflects the same statistical properties as observed in real-world data, which is essential for risk assessment. Comprehensive evaluations, including quantitative metrics and visualizations from detailed latent and physical space analyses, demonstrate that the unified model achieves comparable performance to individually trained models. The shown approach reduces modeling complexity and offers a scalable solution for generating diverse, safety-relevant driving scenarios, supporting robust testing and validation.

1. Introduction

Recent advances in autonomous driving research, particularly in deep reinforcement learning and transfer learning, have significantly improved end-to-end decision making and perception capabilities [1,2,3,4]. These developments highlight the growing complexity and adaptiveness of modern ADAS and autonomous systems, emphasizing the need for more comprehensive and systematic validation approaches [5]. Among the various testing strategies, scenario-based testing has become a widely used and effective method [6,7]. It provides a structured way to evaluate system behavior across a range of driving conditions, allowing test engineers to assess performance in realistic and potentially critical situations [8,9]. However, the reliability and effectiveness of this approach depends heavily on the quality of the used test scenarios [10]. In particular, scenarios must reflect the variability in and complexity of real-world traffic in order to provide meaningful and robust evaluations [11].

Traditional methods for generating test scenarios are often based on parametric, rule-based models [12]. In these approaches, specific maneuver types are defined using expert knowledge and a set of fixed parameters. While such models are easy to interpret, they have several limitations. Firstly, they are time-consuming and expensive to design, as they require manual modeling and expert input for each maneuver type. Secondly, they are difficult to extend to new or rare scenarios. Finally, as each new behavior typically requires its own model, the overall validation system becomes complex and hard to manage.

To overcome these limitations, recent research turned to deep generative models for data-driven scenario generation, which learn directly from real-world or simulated data [13,14,15,16,17,18,19,20,21]. This enables them to capture even complex behavior patterns that are hard to model analytically. Autoregressive and heuristic methods such as [13,14] construct multi-agent scenes by sequentially adding agents, where [14] relies on secondary modules for motion forecasting. Ref. [15] employs a GAN to generate Birds-Eye View (BEV) occupancy maps, followed by post-processing steps to identify agent positions and synthesize their trajectories, resulting in a two-stage, non-end-to-end pipeline.

VAE-based methods such as [16,17,18] learn latent spaces for trajectory generation and often give stable results but are trained as single-maneuver models and do not scale well across behaviors. Without explicit controls, they may also shift from dataset-level statistics. Conditional variants can generate many behaviors in one model by using scene and agent context, but they still need care to preserve statistical fidelity. Ref. [19] uses a graph-based CVAE prior to create realistic but rare cases, but it assumes perfect perception, attacks only the planner, and does not ensure dataset-level statistics. Diffusion-based models like [20,21] have shown strong potential for expressive and controllable scenario synthesis. Ref. [20] incorporates token conditioning to generate structured urban scenes, while [21] uses guided diffusion to model rich multi-agent interactions. However, both rely on bounding-box or occupancy-based inputs and focus primarily on urban scenarios, limiting their applicability to ego-centric or highway driving contexts.

The above challenges highlight the need for a unified generative model that can jointly learn multiple maneuver types within a single framework while maintaining the statistical distributions observed in real traffic data. Such a model simplifies training and maintenance by replacing several specialized networks with one consistent architecture, making it easier to scale and adapt to new data. By learning all scenario types together, it enables shared learning across behaviors, capturing similarities, variations, and smooth transitions between maneuvers. This shared representation produces more coherent traffic situations and ensures that the generated data remain statistically faithful to real-world proportions. Maintaining these correct proportions is essential for risk assessment, since an incorrect representation of how often certain critical events occur can lead to biased estimates of system safety.

In this paper, we present a generative framework based on VAE that learns from six different maneuver types: cut-in (CI), cut-out (CO), and cut-through (CT), each in the left (L) and right (R) directions. The model is trained on real-world trajectory data and is designed to generate realistic, diverse, and statistically consistent driving maneuvers. Ref. Section 2 introduces the corresponding dataset used for training. As a reference, Section 3 describes a VAE architecture for modeling the individual scenarios separately, while Section 4 details the proposed unified model. Ref. Section 5 evaluates the trajectories generated by the unified model in the physical space by comparing their spatial distributions and statistical properties to the real data. Finally, Section 6 concludes the paper with a summary of key findings and future research directions.

2. Measured Cut-In, Cut-Out, and Cut-Through Scenarios

The dataset used in this work is based on real-world driving data, as described in [18]. It combines signals from the Electronic Control Unit (ECU) of the ego vehicle, with sensor data describing the surrounding traffic. All measurements are recorded at a sampling rate of 50 Hz, where the considered variables include the relative longitudinal and lateral positions $s\left(t\right),d\left(t\right)$, and the absolute speed $v\left(t\right)$ of nearby vehicles, see Figure 1.

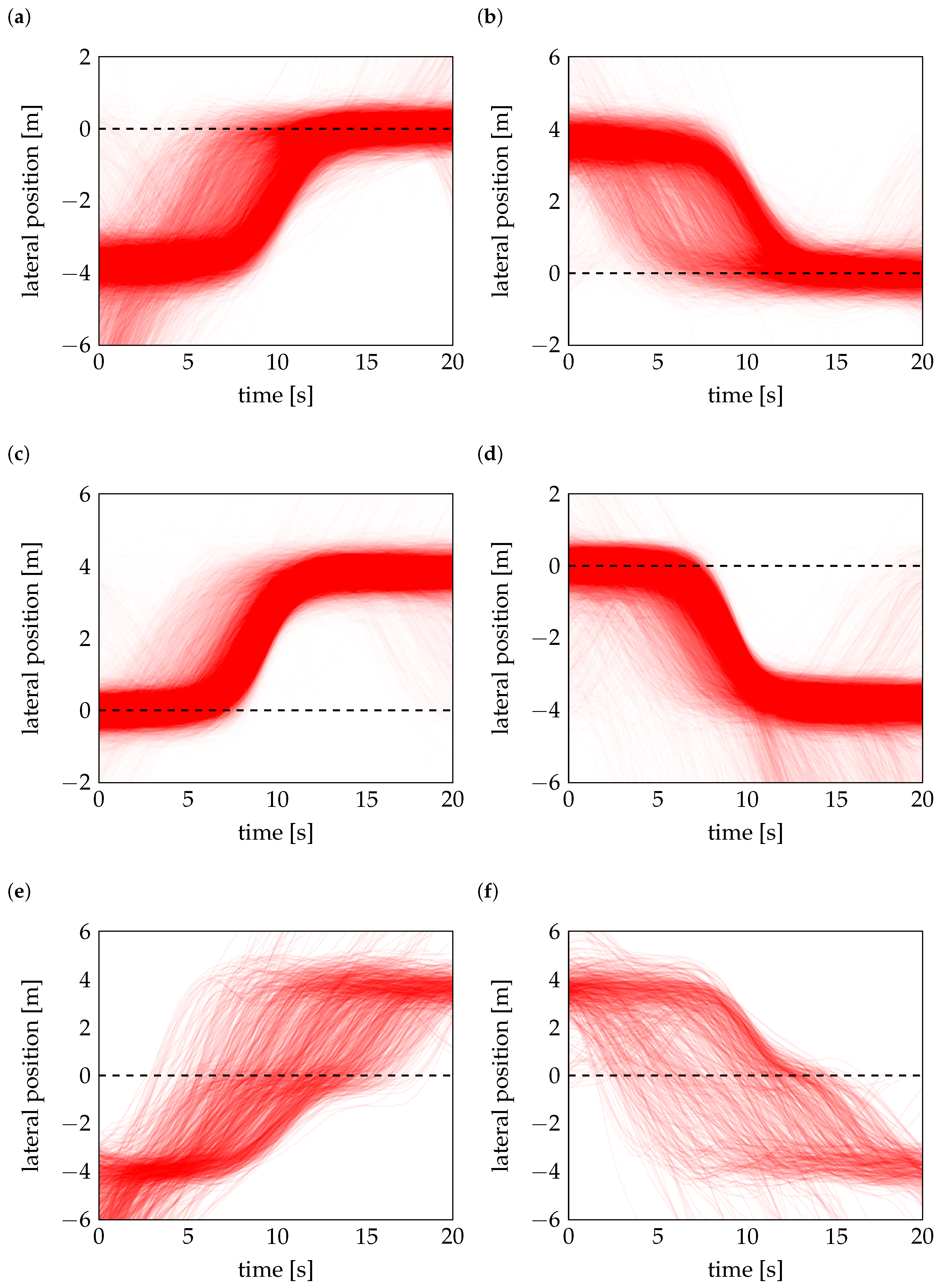
In this analysis, measurements of six maneuver types are considered, representing common, yet safety-critical, traffic situations for autonomous vehicle (AV) validation: cut-in towards left (CIL) and right (CIR), cut-out to the left (COL) and right (COR), as well as cut-through to the left (CTL) and right (CTR), as shown in Figure 1. Cut-in maneuvers involve a nearby vehicle merging into the ego lane, requiring the AV to react to sudden intrusions. Cut-out events occur when a vehicle suddenly leaves the ego lane, creating unexpected gaps in traffic, which can be dangerous especially ahead of a traffic jam. Cut-through maneuvers involve a vehicle crossing multiple lanes in a single motion, introducing more complex lateral dynamics and interactions.

To prepare the labeled dataset with each maneuver type, we adopt the two-stage classification framework introduced in [22], which combines initial rule-based filtering with a Time-Series Forest (TSF) model [23]. The rule-based classification uses the longitudinal distance $s\left(t\right)$ to initially identify the scenarios, and TSF uses the lateral distance $d\left(t\right)$ for secondary classification or validation of identified scenarios. Data preprocessing steps are applied before giving the identified scenarios to the TSF classifier, which include steps like dropout removal, road curvature correction, and smoothening [18].

The resulting dataset is structured as refined time-series data, where the combined sample contains $N_s$ sample trajectories in total across all six maneuver types over $N_t$ discrete time steps. Each trajectory datum includes a scenario label

$$L^{\left(i\right)}\in \{1,2,3,4,5,6\}\mathrm{where}{L}^{\left(i\right)}=\left\{\begin{array}{cc}\hfill 1& \stackrel{\wedge }{=}\mathrm{cut-in}\mathrm{left},\hfill \\ \hfill 2& \stackrel{\wedge }{=}\mathrm{cut-in}\mathrm{right},\hfill \\ \hfill 3& \stackrel{\wedge }{=}\mathrm{cut-out}\mathrm{left},\hfill \\ \hfill 4& \stackrel{\wedge }{=}\mathrm{cut-out}\mathrm{right},\hfill \\ \hfill 5& \stackrel{\wedge }{=}\mathrm{cut-through}\mathrm{left},\hfill \\ \hfill 6& \stackrel{\wedge }{=}\mathrm{cut-through}\mathrm{right},\hfill \end{array}\right.$$

(1)

time instances, and two motion features: lateral position $d\left(t\right)$ and longitudinal velocity $v\left(t\right)$, measured at discrete time steps $t_k$:

$$\left(L^{\left(i\right)},t_k^{\left(i\right)},d_k^{\left(i\right)},v_k^{\left(i\right)}\right),i=1,\dots ,N_S,k=1,\dots ,N_t.$$

(2)

For each trajectory segment i, the motion features are concatenated into a matrix, where columns are related to features:

$${\mathbf{x}}^{\left(i\right)}=\left[\begin{array}{c}[t_k^{\left(i\right)}],[d_k^{\left(i\right)}],[v_k^{\left(i\right)}]\end{array}\right],i=1,\dots ,N_S,k=1,\dots ,N_t.$$

(3)

The dataset contains $N_S\approx \mathrm{44,600}$ labeled trajectories, as shown in the heatmap of measured lateral position $d\left(t\right)$ combining all six scenarios in Figure 2a. On German highways, the different maneuver types do not occur equally often, as the frequency of occurrence in Figure 2b demonstrates. In order to obtain a correct risk assessment [23], the intended generative model has to reflect this probability distribution, which is why it is implicitly included in the aggregated data in Figure 2a used for training the unified generative model. This can be better observed in Figure 3, presenting individual heatmaps of measured lateral position $d\left(t\right)$ for each scenario type, where the number of trajectories is different for different scenario types. Additionally, a representative trajectory is overlaid to illustrate typical maneuver characteristics. These separate scenario data subsets are used to train individual generative models for each scenario type. For illustration purposes, we show only the lateral position, but the models are trained using both lateral position $d\left(t\right)$ and longitudinal velocity $v\left(t\right)$, as defined in Equation (3).

3. Variational Autoencoders for Generating Single-Type Scenarios

A detailed comparison of different generative models in [22] has shown the superior performance of VAE over Generative Adversarial Networks (GANs). Therefore, the VAE introduced in [18] and indicated in black in Figure 4 is also used here for generating individual types of maneuvers. In contrast to [18], it is not restricted to cut-in maneuvers in the rightward direction but also trained for the other five scenarios. Each maneuver class $L\in \{1,2,\dots ,6\}$ is modeled using a dedicated VAE, where measured trajectories $\mathbf{x}\in {\mathbb{R}}^{100\times 3}$ are encoded into latent variables $\mathbf{z}\in {\mathbb{R}}^d$ and reconstructed as $\tilde{\mathbf{x}}\in {\mathbb{R}}^{100\times 3}$. This setup provides a scenario-specific baseline for later evaluating the unified VAE model.

A VAE models high-dimensional data by learning a probability distribution over a lower-dimensional latent space, enabling the generation of diverse and realistic samples [24]. The encoder network estimates the mean $\mathit{\mu }$ and variance ${\mathit{\sigma }}^2$ of the latent variable vector $\mathbf{z}$, forming an approximate posterior distribution $q_{{\mathit{\theta }}_E}\left(\mathbf{z}\right|\mathbf{x})$. To generate $\mathbf{z}$ from this distribution while enabling backpropagation, reparameterization is applied, i.e., an auxiliary variable $\mathit{\epsilon }\sim \mathcal{N}(\mathbf{0},\mathbf{I})$ is sampled from a multivariate standard Gaussian distribution, and the latent vector is obtained as

$$\mathbf{z}=\mathit{\mu }+\mathit{\sigma }\otimes \mathit{\epsilon },$$

(4)

where ⊗ denotes element-wise multiplication. The decoder reconstructs the measured input by modeling the likelihood $p_{{\mathit{\theta }}_D}\left(\tilde{\mathbf{x}}\right|\mathbf{z})$ of producing an output trajectory $\tilde{\mathbf{x}}$. Training the VAE involves optimizing the neural network parameters ${\mathit{\theta }}_E$ and ${\mathit{\theta }}_D$ with respect to two objectives: minimizing the reconstruction loss and regularizing the latent space. The reconstruction loss is defined as the mean squared error (MSE) between the measured input and reconstructed output, i.e.,

$$\mathrm{MSE}(\tilde{\mathbf{x}},\mathbf{x})={\displaystyle \frac{1}{N_s}}\sum _{i=1}^{N_s}{\parallel {\tilde{\mathbf{x}}}^{\left(i\right)}-{\mathbf{x}}^{\left(i\right)}\parallel }^2,$$

(5)

while the regularization term minimizes the Kullback–Leibler (KL) divergence

$$D_{\mathrm{KL}}\left(q\left(\mathbf{z}\right) \parallel p\left(\mathbf{z}\right)\right)=\mathbb{E}\left[log{\displaystyle \frac{q\left(\mathbf{z}\right)}{p\left(\mathbf{z}\right)}}\right]$$

(6)

between the approximate posterior distribution $q\left(\mathbf{z}\right)$ resulting from the encoder and the assumed prior $p\left(\mathbf{z}\right)=\mathcal{N}(\mathit{\mu },\mathrm{diag}\left({\mathit{\sigma }}^2\right))$ being a multivariate Gaussian distribution. The total loss function is

$$\mathcal{L}({\mathit{\theta }}_E,{\mathit{\theta }}_D)=\mathrm{MSE}(\tilde{\mathbf{x}},\mathbf{x})+\beta D_{\mathrm{KL}}\left(q\left(\mathbf{z}\right) \parallel p\left(\mathbf{z}\right)\right),$$

(7)

where the weighting factor $\beta$ balances reconstruction fidelity and latent space regularization. It is typically adjusted such that the KL term is prevented from overwhelming the reconstruction loss, especially in early training stages.

The architecture of the variational autoencoder (VAE) used in this paper is detailed in

Table 1. VAE encoder and decoder architecture for both individual scenario generation (black) and unified model, where the red part shows the additional layers for label prediction.

Encoder Layer	Output Shape	Decoder Layer	Output Shape
Input	100 × 3	Input	10
Conv, ReLU	100 × 25	Dense, ReLU	1000
Conv, ReLU	100 × 50	Reshape	100 × 100
Conv, ReLU	100 × 100	DeConv, ReLU	100 × 50
Flatten	10,000	DeConv, ReLU	100 × 25
Dense (2x), ReLU	10	Flatten	2500
Lambda	10	Dense	300
—	—	Reshape	100 × 3
—		Input	10
—		Dense, Softmax	1 × 6

. The encoder uses convolutional (Conv) layers that progressively extract and refine temporal and spatial features from trajectory data. They are followed by a flattening (Flatten) layer and fully connected (Dense) layers that reorder and reduce the representation to a compact latent vector. A Lambda layer is then used to perform sampling from the latent distribution using reparameterization for enabling gradient-based optimization during training. The latent space dimensionality is fixed at $d=10$. The decoder mirrors the encoder in reverse, a Dense layer expands the latent representation, which is then reshaped and passed through transposed convolutional (DeConv) layers to reconstruct the input sequence. Flatten and Reshape layers are used to reorganize the data. The rectified linear unit (ReLU) is used as a non-linear activation function.

All scenario-specific VAE models were trained on an NVIDIA Quadro P4000 GPU, with approximately 227,603 trainable parameters. A grid search was conducted over key hyperparameters, including batch size, KL divergence weight ($\beta$), and learning rate.

Table 2. VAE hyperparameters for each model. Values are inherited from default unless explicitly stated.

Model	Batch Size	Epochs	$\mathit{\beta }$	Learning Rate	Optimizer
Default	32	1000	$1\times {10}^{-3}$	$1\times {10}^{-5}$	Adam
$VA{E}_{\mathrm{CTL}}$	16	–	–	–	–
$VA{E}_{\mathrm{CTR}}$	16	–	–	–	–

lists the hyperparameter settings selected for each model. Most scenario types used a common default configuration, but the CTL and CTR classes, which are less frequent in the dataset, were trained with smaller batch sizes, which yielded a modest reduction in validation loss.

Once trained, each scenario-specific VAE learns its own latent space distributions, i.e., distributions of mean $\mathit{\mu }$ and the natural logarithm of variance ${\mathit{\sigma }}^2$ for each of the 10 latent parameters using a Kernel Density Estimation (KDE)-based sampling strategy superposing Gaussian kernels [25,26]. To generate a new synthetic trajectory j, latent variables are sampled from these scenario-specific latent distributions as

$$z_k^{\left(j\right)}={\mu }_k^{\left(j\right)}+{\sigma }_k^{\left(j\right)}{\epsilon }_k^{\left(j\right)},k=1,2,\dots ,10,$$

(8)

where ${\mu }_k^{\left(j\right)}$ and ${\sigma }_k^{\left(j\right)}$ are chosen randomly according to the learned distributions of the VAE model, and ${\epsilon }_k^{\left(j\right)}$ is an independent random number drawn from a standard multivariate Gaussian. The corresponding decoder is then used to map ${\mathbf{z}}^{\left(j\right)}=[z_1^{\left(j\right)},z_2^{\left(j\right)},\dots ,z_{10}^{\left(j\right)}]$ to a synthetic trajectory ${\tilde{\mathbf{x}}}^{\left(j\right)}$, as shown by the framed part in Figure 4.

In the following, the scenario-specific VAE models are evaluated using a structured combination of qualitative (heatmaps and trajectory-level comparison), quantitative (MSE loss on validation data), and statistical (KDE) [27,28] analyses to provide a comprehensive understanding of model performance. Each of these methods has a distinct purpose:

• Qualitative heatmaps reveal spatial coverage and overall alignment with real trajectories;
• Quantitative metrics indicate whether the model has learned generalizable patterns rather than simply memorizing the training data;
• Statistical comparisons assess whether the generated data preserve the underlying distribution of the real samples, which is essential for evaluation of failure probability of Advanced Driver Assistance Systems (ADASs);
• Trajectory-level matching demonstrates the model’s ability to generate realistic samples.

Together, these evaluations confirm that the trained models effectively capture both global spatiotemporal trends and fine-grained maneuver characteristics.

For the analysis, the models generate the same number of trajectories as the corresponding measured samples in the dataset. By comparing the heatmaps of the generated trajectories in Figure 5 with those of the real data in Figure 3, this reveals a strong spatial alignment across all six maneuver types, indicating that the models effectively capture the key spatiotemporal patterns of the original trajectories.

Quantitative evaluation used the MSE (5) as a measure of reconstruction error on a held-out validation set (30% of measured trajectories). In this case, unseen maneuvers were fed as inputs to the trained VAE to reconstruct a corresponding output trajectory. The consistently low MSE values in column 2 in

Table 3. Quantitative analysis of individual and unified VAE models across all six maneuver types.

Maneuvers	Individual VAE	Unified VAE
	Validation MSE	Validation MSE	Classification Error
Cut-in left	$2.79\times {10}^{-2}$	$4.26\times {10}^{-2}$	$0\times {10}^0$
Cut-in right	$2.32\times {10}^{-2}$	$2.82\times {10}^{-2}$	$1\times {10}^{-2}$
Cut-out left	$2.28\times {10}^{-2}$	$3.06\times {10}^{-2}$	$0\times {10}^0$
Cut-out right	$5.79\times {10}^{-2}$	$4.64\times {10}^{-2}$	$0\times {10}^0$
Cut-through left	$6.28\times {10}^{-2}$	$6.19\times {10}^{-2}$	$0\times {10}^0$
Cut-through right	$3.38\times {10}^{-2}$	$6.01\times {10}^{-2}$	$1\times {10}^{-2}$
Overall		$3.80\times {10}^{-2}$	$1\times {10}^{-2}$

across all classes demonstrate accurate reconstruction of input trajectories. Slightly elevated errors in the CT classes appear to be influenced more by training dynamics, particularly the early stopping patience, than by dataset size, suggesting sensitivity to optimization behavior rather than data imbalance. Nevertheless, these deviations remain small and do not impact the model’s ability to generate realistic and reliable trajectories.

For checking the statistical similarity, the lateral position distributions $p\left(\mathbf{d}\right)$ are estimated separately for measured and generated trajectories using KDE. As shown in Figure 6, the resulting density curves align closely for all six models, capturing the dominant peaks and overall shape of the real distributions. Minor differences in peak values are observed but remain below 0.05, confirming that the generative models preserve the statistical properties of the measured data.

Finally, trajectory-level comparison is conducted by identifying closest matches for the highlighted measured trajectories in Figure 3. This is achieved by computing the mean square error,

$$\mathrm{MSE}({\mathbf{d}}^{\left(i\right)},{\tilde{\mathbf{d}}}^{\left(j\right)})={\displaystyle \frac{1}{N_t}}\sum _k{\left(d_k^{\left(i\right)}-{\tilde{d}}_k^{\left(j\right)}\right)}^2$$

(9)

between the specific measured trajectory i in Figure 3 and all randomly generated trajectories j in Figure 5. The closest matches with minimum MSEs are shown in Figure 7. It is important to note that these matches are not reconstructions but a selection from random samples generated independently by the model. As Figure 7 illustrates, there is always a closely matching generated sample with the same characteristics as the corresponding measured maneuver.

4. Variational Autoencoder for Unified Scenario Generation

Rather than modeling each scenario type with a separate model, we now propose a unified VAE that jointly learns to represent all six maneuver classes within a common latent space. As illustrated in Figure 4 and Table 1, the same base architecture is used here, and only the additional layers highlighted in red are added to the decoder for predicting the maneuver class information. Importantly, the class label L is not fed to the encoder and, therefore, not directly encoded into the latent representation $\mathbf{z}$, but it is only used to supervise learning of the class prediction through an auxiliary classification loss. A dense layer with softmax activation predicts $\tilde{\mathbf{l}}$ from $\mathbf{z}$, and the resulting cross-entropy loss is added to the VAE objective. This encourages the latent space to remain informative of the maneuver type while preserving the unsupervised nature of the core VAE training.

To be more precise, the training dataset (3) now comprises mixed scenario trajectories ${\mathbf{x}}^{\left(i\right)}$ annotated with scenario type labels $L^{\left(i\right)}$. To incorporate this label into the training objective, $L^{\left(i\right)}$ is first converted into a one-hot-encoded vector ${\mathbf{l}}^{\left(i\right)}=[l_1^{\left(i\right)},l_2^{\left(i\right)},\dots ,l_6^{\left(i\right)}]\in {\{0,1\}}^6$, where $l_c^{\left(i\right)}=1$ if the true class is c and zero otherwise. This one-hot vector serves as a categorical probability distribution representing the ground truth maneuver class. The model outputs predicted class probabilities ${\tilde{\mathbf{l}}}^{\left(i\right)}=[{\tilde{l}}_1^{\left(i\right)},{\tilde{l}}_2^{\left(i\right)},\dots ,{\tilde{l}}_6^{\left(i\right)}]\in {[0,1]}^6$ by applying a softmax layer, which guarantees that the predicted probabilities form a valid distribution, such that

$$\sum _{c=1}^6{\tilde{l}}_c^{\left(i\right)}=1.$$

(10)

The components ${\tilde{l}}_c^{\left(i\right)}$ of ${\tilde{\mathbf{l}}}^{\left(i\right)}\in {\mathbb{R}}^6$ then indicate probabilities that the generated maneuver ${\tilde{\mathbf{x}}}^{\left(i\right)}$ belongs to class c, as defined in Equation (1).

To measure the discrepancy between the predicted and true distributions, we use the categorical cross-entropy loss resulting from scalar products between vectors ${\mathbf{l}}^{\left(i\right)}$ and ${\tilde{\mathbf{l}}}^{\left(i\right)}$:

$${\mathcal{L}}_{\mathrm{pred}}(\mathbf{l},\tilde{\mathbf{l}})=-\sum _{i=1}^{N_S}{\mathbf{l}}^{\left(i\right)\top }log\left({\tilde{\mathbf{l}}}^{\left(i\right)}\right).$$

(11)

This is added to loss function (7), resulting in

$$\mathcal{L}\left({\mathit{\theta }}_E,{\mathit{\theta }}_D\right)=\mathrm{MSE}(\tilde{\mathbf{x}},\mathbf{x})+\beta D_{\mathrm{KL}}\left(q\left(\mathbf{z}\right) \parallel p\left(\mathbf{z}\right)\right)+{\lambda }_{\mathrm{pred}}·{\mathcal{L}}_{\mathrm{pred}}(\mathbf{l},\tilde{\mathbf{l}}).$$

(12)

Minimizing this total loss leads to a latent representation that is both generative, i.e., capable of generating realistic trajectories, and discriminative, i.e., informative of its maneuver class.

Training was performed on an NVIDIA Quadro P4000 GPU. The unified model shares the same base architecture as the individual VAEs, with the addition of a classification layer, resulting in only 66 extra trainable parameters. To determine the optimal configuration, we conducted a grid search over key hyperparameters, including batch size, learning rate, KL divergence weight ($\beta$), and classification loss weight (${\lambda }_{\mathrm{pred}}$). The final setting of ${\lambda }_{\mathrm{pred}}=1$ with the default settings for other parameters in Table 2 provided the most consistent performance. Keeping the classification loss at full strength ensures that the latent space becomes semantically meaningful and maneuver-discriminative which is evident from the latent space analysis later shown.

The unified model was trained from scratch in approximately 23 min, compared to around 10 min per model for the individually trained VAEs. Although the joint model takes longer than a single VAE, it achieves broader coverage with a single pass, avoiding the cumulative cost and management overhead of training six separate models. At inference, it is about 40 times faster per sample than the individual models, which corresponds to about a 98% reduction in latency making the unified approach more scalable and suitable for real time scenario generation.

To generate new trajectories, the same sampling procedure as described in Section 3 is followed. The only difference is that the unified model now generates both trajectories ${\tilde{\mathbf{x}}}^{\left(j\right)}$ and maneuver label probabilities ${\tilde{\mathbf{l}}}^{\left(j\right)}$. The predicted class label ${\tilde{L}}^{\left(j\right)}$ is obtained as maximum component of ${\tilde{\mathbf{l}}}^{\left(j\right)}$:

$${\tilde{L}}^{\left(j\right)}=arg\underset{c}{max}{\tilde{\mathbf{l}}}_c^{\left(j\right)}.$$

(13)

By analyzing the measured and generated samples, it can be seen that the occurrence distribution of the different maneuver types is well captured. In Figure 8, the frequencies of occurrence of the six maneuver classes are nearly identical between the measured (blue) and generated (red) trajectories. This consistency arises from the structure of the learned latent space. Although $\mathbf{z}$ is sampled randomly, the class-wise proportions are preserved because the latent space reflects the distribution of maneuver types observed during training. As a result, the generative model accurately reproduces these frequencies without any explicit enforcement, which is important for a correct risk assessment.

This property can be further examined by investigating how maneuver classes are organized in the latent space. To visualize this, a t-distributed stochastic neighbor embedding (t-SNE) [29,30] projection is applied to the ten-dimensional latent space $\mathbf{z}$, reducing it to a two-dimensional representation, as shown in Figure 9. Six distinct clusters corresponding to the six maneuver types can be clearly observed. Notably, cut-in and cut-out maneuvers form clearly separated clusters even across direction-specific variations. The cut-through maneuvers, which inherently combine features of both cut-in and cut-out, appear between these clusters, indicating their intermediate nature.

This clustering structure highlights the model’s ability to encode class-relevant information in the latent space. Consequently, generating representative and diverse trajectories becomes straightforward. In principle, class-specific new samples could also be intentionally obtained by drawing $\mathbf{z}$ from different cluster regions. This allows for targeted exploration by generating more instances of a specific maneuver type by sampling additional latent codes near its corresponding cluster center.

5. Physical Space Analysis of Maneuvers Generated by the Unified VAE

The realism of the generated scenarios may be further examined in the physical space using the same evaluation techniques as introduced in Section 3, i.e., heatmaps, KDE, trajectory level comparisons, and quantification of reconstruction errors computed for validation data. The physical space refers to the observable motion, where trajectories are represented by their spatial and kinematic variables over time. Analyzing the generated maneuvers at this trajectory level enables direct evaluation of their physical realism, feasibility, and class consistency across the unified VAE’s multiple maneuver types. Additionally, dimensionality reduction by t-SNE and Principal Component Analysis (PCA) [31] is applied. Since the unified model generates scenarios across multiple maneuver classes, the classification error is included as an additional part of the quantitative analysis.

The heatmap of generated trajectories in Figure 10 exhibits strong resemblance to that of the measured data in Figure 2a, indicating that the generated maneuvers cover the relevant regions of the physical space. All six maneuver types are distinctly represented, and the density of generated trajectories matches that of the measured ones. Dense clusters of trajectories are observed around lane boundaries and the ego lane, consistent with the spatial patterns of measured trajectories. This forms an initial qualitative confirmation of realism, suggesting that the model has not only learned to reproduce spatial distributions but also to respect the semantic structure inherent in driving scenarios.

In Figure 11, the KDEs of the lateral positions of the combined scenarios reveal high similarity between the distributions of measured and generated data. The probability distribution of the whole sample in Figure 11a has three prominent peaks aligned with the high densities of curves within the three participating lanes. The central peak corresponds to the ego lane and has the highest density, reflecting the fact that all maneuvers either start, pass through, or end in this lane. The other two peaks, associated with the left and right lanes, appear at lower values, corresponding to the contributions of cut-in, cut-out, and cut-through maneuvers. Also, the separate analysis of KDEs for each maneuver type labeled in Figure 11b–g remains consistent with that of the measured data, indicating that the statistical structure of each maneuver type is preserved and that the generated data accurately reflect class-specific distributions.

As shown in column 3 in Table 3, the reconstruction errors across each scenario type for the unified VAE model remain almost as low as those of the individual VAEs. Although the unified model exhibits slightly higher errors, the overall reconstruction quality is still well preserved. This indicates that the joint training across maneuver types does not significantly compromise fidelity while offering a more scalable and unified representation. Moreover, the classification error in column 4 remains very low, validating the model’s ability to correctly predict maneuver types. The predicted labels for generated trajectories are almost always correct, with false prediction rates being either zero or near zero for all six maneuver types. This ensures that no invalid classes are produced, further confirming the reliability of the unified generation approach.

Trajectory-level comparison may be performed similarly to Figure 7. For each maneuver type, the highlighted measured trajectory in Figure 3 and its closest counterpart found from generated samples in Figure 10 are shown in Figure 12. As before, ${\tilde{\mathbf{x}}}^{\left(j\right)}$ is not a reconstruction of ${\mathbf{x}}^{\left(i\right)}$ but a randomly generated sample from the latent space. The resulting differences are expected, as they demonstrate the model’s ability to produce diverse, yet plausible, trajectories within the same maneuver class. The comparison confirms that generated maneuvers maintain realistic structure, dynamics, and alignment with measured vehicle behavior.

Finally, the clustering structure of the generated samples is examined in the physical space using two-dimensional projections of the trajectories. The t-SNE in Figure 13 shows that the generated samples are organized into six well-separated clusters corresponding to the six maneuver types. Cut-in and cut-out clusters are clearly distinct for both directions, and the cut-through samples form a bridge like in Figure 9. While t-SNE introduces some randomness in cluster locations, the shape and size of the clusters are consistent and proportional to their frequency of occurrence. By applying PCA in Figure 14, which provides a deterministic view of the first two principal components, cluster locations are preserved, resulting in a total consistency of cluster arrangements for measured and generated trajectories.

6. Conclusions

The proposed unified VAE framework is able to effectively model different driving scenarios within a single generative architecture, maintaining high fidelity while reducing overall modeling complexity. Experimental results show that the unified model achieves the same high performance as individually trained models while preserving correct probabilities of occurrence of the different maneuver types. This is achieved by a well-structured clustering in the latent space, which may support a scalable generalization regarding the number of different maneuver types.

Limitations

• The model’s performance is influenced by the diversity of the training data. Incorporating more varied and rare driving situations could further improve generalization.
• The current framework does not enforce explicit physical or kinematic constraints. Adding such constraints could ensure the generated trajectories remain dynamically feasible and no post-processing needed.
• Improving the controllability and interpretability of the latent space could enable more targeted and meaningful scenario generation.
• Additional evaluation under unseen traffic conditions and more complex multi-agent interactions is needed to improve the robustness of the approach.

Future work will focus on enhancing the controllability of maneuver types by linking physical parameters to latent variables. For example, this may enable targeted scenario synthesis by allowing one of the latent parameters to learn and smoothly interpolate between different behaviors. In addition, accurately modeling interactions between multiple vehicles remains a key challenge. Future work should also incorporate multi-agent dynamics to better represent realistic traffic conditions.