Transportation Link Risk Analysis Through Stochastic Link Fundamental Flow Diagram
Abstract
1. Introduction
2. Deterministic and Stochastic Link Fundamental Diagram
- f ≥ 0 is the (vehicular) flow;
- k ≥ 0 is the (vehicular) density;
- v ≥ 0 is the (space average) speed;
- fMAX is the capacity (f ≤ fMAX is commonly assumed as a function of geometrical characteristics of the infrastructure [7] or calibrated against read data);
- kMAX is the maximum density (k ≤ kMAX, depending on (average) vehicle length and minimum safety distance or calibration against read data);
- v0 is the zero-flow or free-flow or maximum speed (v ≤ v0 is commonly assumed as a function of geometrical characteristics of the infrastructure, as well as weather and light conditions),
- kC is the critical density, the density giving the maximum flow f(kC) = fMAX;
- vC = vK(kC) is the critical speed, the speed at critical density.
- A stable regime, with high speed and low density, in which v(f) is monotonically decreasing;
- An unstable regime, with low speed and high density, in which v(f) is monotonically increasing.
3. Transportation Link Risk Analysis
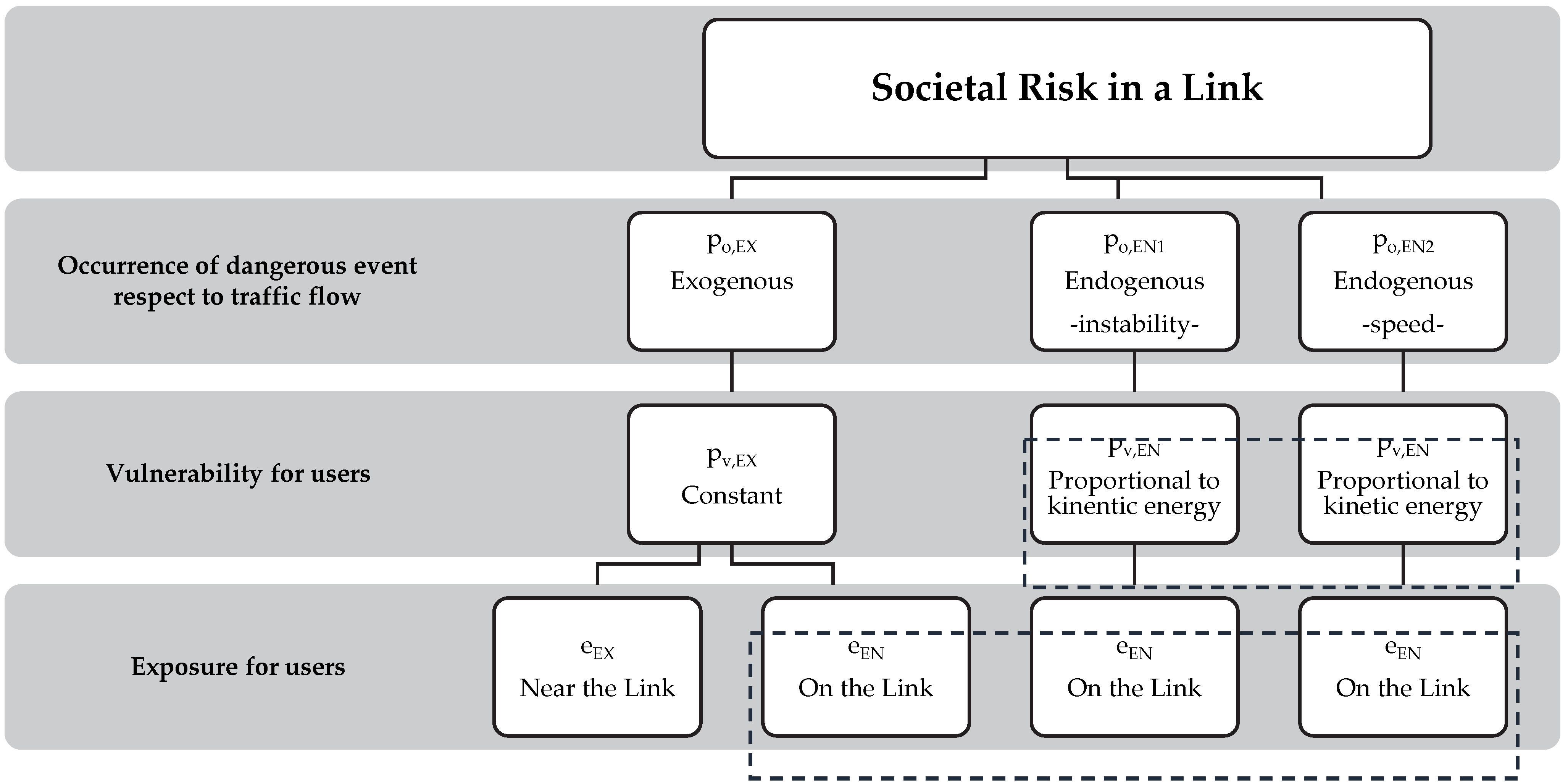
- Occurrence. In the context of a transport system, a dangerous occurrence refers to an event, either accidental or intentional, that has the potential to cause serious harm, injury, or damage, and is often subject to specific reporting requirements. The occurrence of dangerous events in a transport system can be classified into two categories with respect to the vehicular flow:
- o
- Exogenous: these events originate from external sources and, as a result, are not affected by congestion; some examples of this kind of event are floods and earthquakes;
- o
- Endogenous: these events are generated by vehicle flow and congestion and thus depend on traffic conditions; examples of such events include vehicular accidents.
- Vulnerability. In a transport system, vulnerability to dangerous events refers to the susceptibility of the system to disruptions and negative impacts caused by unforeseen or hazardous occurrences. The impact energy applied to users in the aftermath of a dangerous event can be quantified as follows:
- o
- For an exogenous event occurring within the flow, the energy does not depend on the traffic flow variables;
- o
- For endogenous events, the energy depends on the traffic flow variables and is mainly a function of the kinetic energy of the vehicles involved in the impact.
- Exposure. In a transport system, exposure to dangerous events refers to the number of users (and the quantity of goods) on the link and in the proximity of the link who are affected by the hazardous event. The model is composed of two components:
- o
- The first category of users is those situated close to the link, for example, residents, who could potentially be affected by the dangerous event;
- o
- The second category of users is those utilizing the transport link; this category of users is dependent on traffic conditions.
- v be the (space average) speed;
- pO be the probability of the occurrence of a hazardous event;
- pO,EX be the probability of the occurrence of an exogenous hazardous event;
- pO,EN1 be the probability of the occurrence of an endogenous dangerous event in an unstable flow region;
- pO,EN2 be the probability of the occurrence of an endogenous dangerous event in a stable flow region;
- pV be the vulnerability, the conditional probability that the users of the transport system will suffer negative effects given the occurrence of the dangerous event;
- pV,EX be the vulnerability, the conditional probability given the occurrence of the dangerous exogenous event;
- pV,EN be the vulnerability, the conditional probability given the occurrence of the dangerous endogenous event;
- e be the exposure, the number of people (and the quantity of goods) exposed to exogenous (eEX) and endogenous (eEN) events.
4. Transportation Link Risk Analysis Through Stochastic Fundamental Diagram
4.1. Deterministic Approach
- x = f/fMAX be the (dimensionless) degree of saturation;
- y = v/v0 be the (dimensionless) speed ratio.
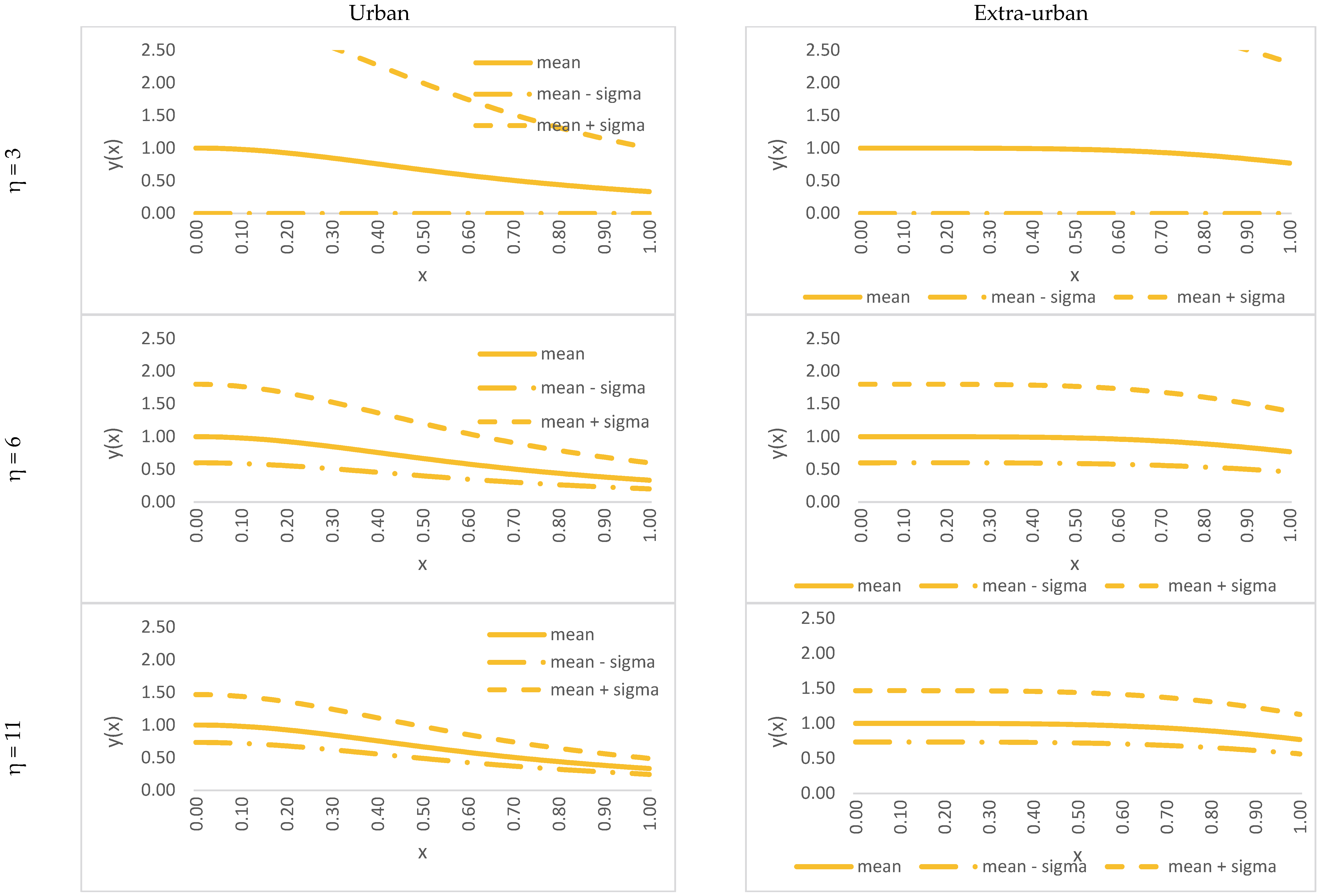
4.2. Stochastic Approach
- Defined over the nonnegative real line;
- Defined by at least scale and shape parameters, so that mean and variance are independent;
- Unimodal;
- Has an easily defined unimodal inverse describing the travel time randomness, stable with respect to the sum, thus allowing the modeling of route travel time as a random variable of known distribution.
- η is the shape parameter;
- θV is the scale parameter.
5. Numerical Experimentation
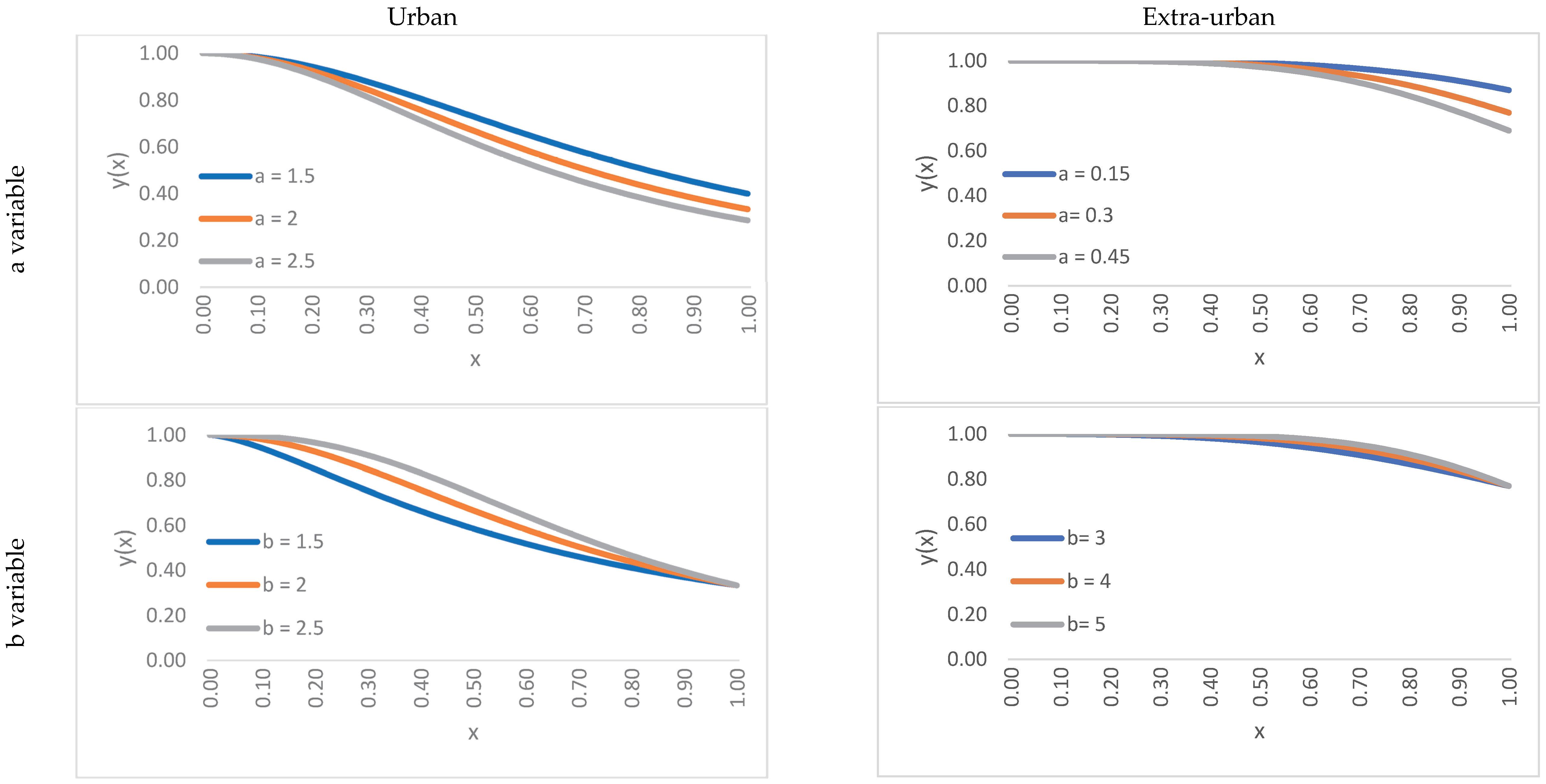
5.1. Speed–Flow Function Specification
- t is the travel time needed to traverse the link;
- L is the length of the link;
- t0 = L/v0 is the null flow travel time needed to traverse the link;
- a > 1 is the congestion factor, such that 1 + a = t(fMAX)/t0;
- b ≥ 1 is a shape coefficient (b = 1, meaning it is a linear function).
- a = 0.15, b = 4, v0 = 120 km/h for extra-urban application [in this case Equation (21) mainly plays the role of a capacity constraint];
- a = 2, b = 2, v0 = 60 km/h for urban application.
- x = f/fMAX is the degree of saturation;
- y = v/v0 is the speed ratio.
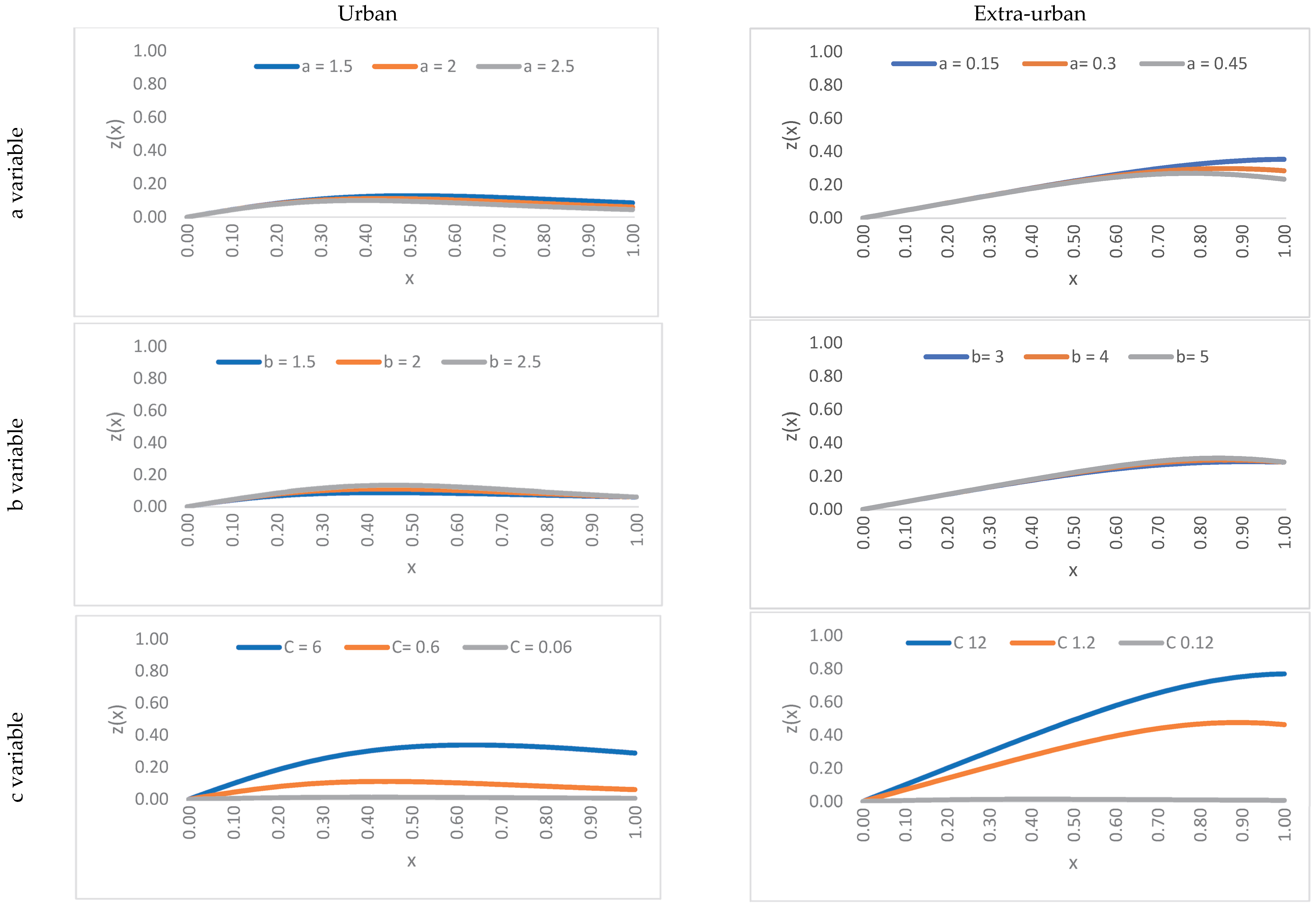
5.2. Risk Function Specification
= (α · L/v02) · (1 − exp(−β · v(f))) · v(f) · f =
= (α · L · fMAX/v0) (1 − exp(−β · v0 · v(f)/v0)) · (v(f)/v0) · (f/fMAX)
- x = f/fMAX ∈ [0,1] is the degree of saturation (usually a value of fMAX = 2000 veic/h for a standard lane);
- y = v/v0 ∈ [0, 1] is the speed ratio (usually values of v0 = 80–120 km/h x-urb, 30–60 km/h urb);
- z = r/(α · L/v0 · fMAX) ∈ [0,1] is the risk index (L is the highway length; α is to be calibrated).
5.3. Numerical Results and Comments
5.3.1. Deterministic Risk Analysis
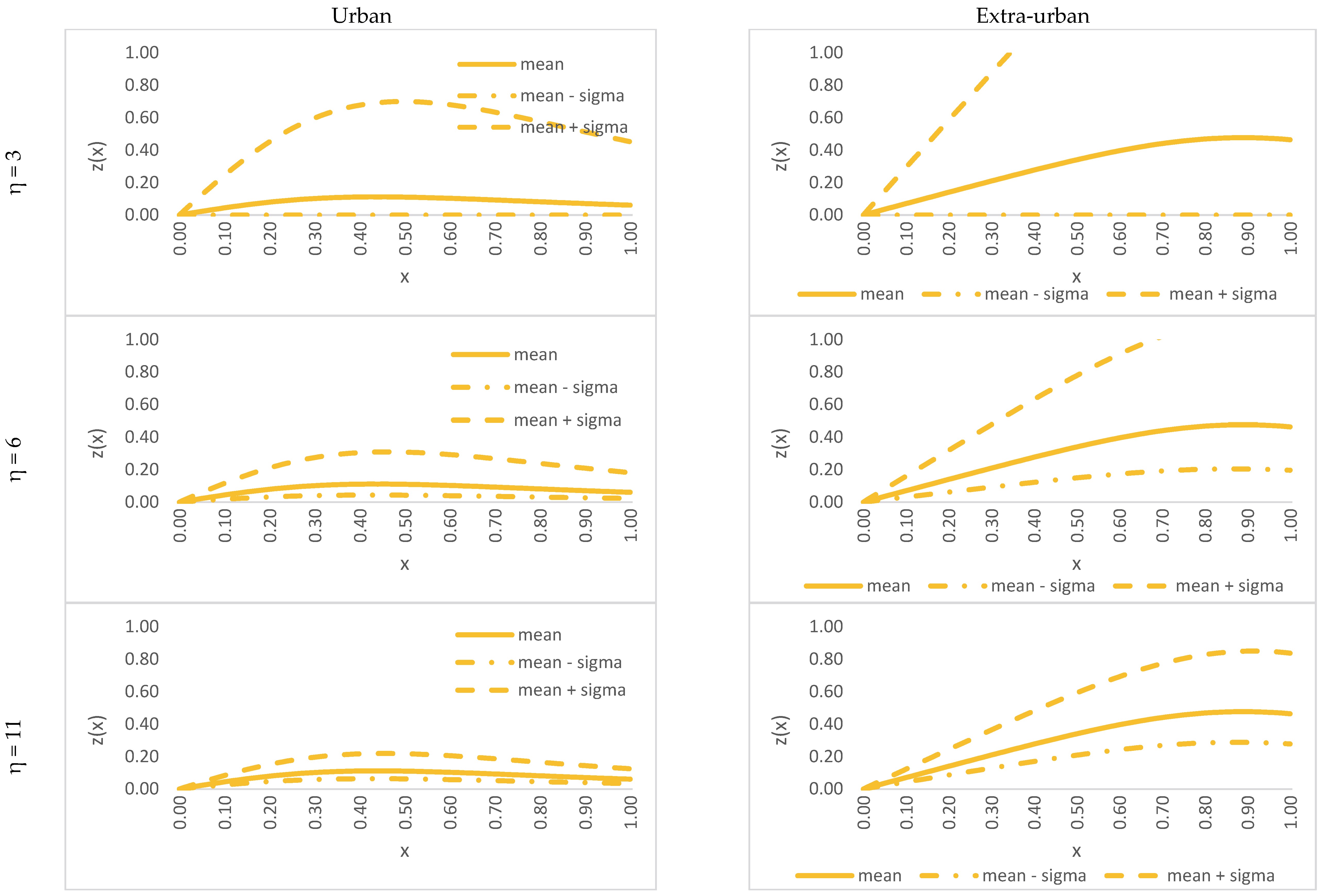
5.3.2. Stochastic Risk Analysis
6. Conclusions
- the specification of a more precise modeling approach based on the definition of the risk index distribution from Equation (12) and the distribution of the speed as an InvGamma. Since a closed-form formulation seems hard to derive, presumably Monte Carlo techniques need to be applied.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.; Xu, J.; Gao, C.; Mu, M.; E, G.; Gu, C. Review of Research on Road Traffic Operation Risk Prevention and Control. Int. J. Environ. Res. Public Health 2022, 19, 12115. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Chang, X.; Xie, T.; Fujita, H.; Wu, J. Unsupervised anomaly detection based method of risk evaluation for road traffic accident. Appl. Intell. 2023, 53, 369–384. [Google Scholar] [CrossRef]
- Berdica, K. An introduction to road vulnerability: What has been done, is done and should be done. Transp. Policy 2002, 9, 117–127. [Google Scholar] [CrossRef]
- Elvik, R. Some implications of an event-based definition of exposure to the risk of road accident. Accid. Anal. Prev. 2015, 76, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Greenshields, B.D. A Study of Traffic Capacity. Highw. Res. Board Proc. 1935, 14, 448–477. [Google Scholar]
- Treiber, M.; Kesting, A. Traffic Flow Dynamics. In Traffic Flow Dynamics: Data, Models and Simulation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- HCM. Highway Capacity Manual VI Edition, Transportation Research Board (TRB); National Academy of Sciences: Washington, DC, USA, 2016. [Google Scholar]
- Cantarella, G.E.; Watling, D.; De Luca, S.; Di Pace, R. Traffic Flow Theory. In Dynamics and Stochasticity in Transportation Systems; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Cantarella, G.E.; Cipriani, E.; Gemma, A.; Giannattasio, O.; Mannini, L. Stochastic Fundamental Diagram Consistent with Transportation Systems Theory. In Proceedings of the 4th Symposium on Management of Future Motorway and Urban Traffic Systems 2022 (MFTS2022), Dresden, Germany, 30 November–2 December 2022. [Google Scholar]
- Cantarella, G.E.; Cipriani, E.; Gemma, A.; Giannattasio, O.; Mannini, L. Stochastic Fundamental Diagram: For motorway traffic modelling and emission estimation. Transp. Res. Procedia 2023, 12–18. [Google Scholar]
- Di Pace, R.; Cantarella, G.E. (Eds.) Urban Traffic Analysis and Control: The Key Challenges in the Era of ITS; IET: Stevenage, UK, 2025. [Google Scholar]
- Cascetta, E. Transportation Systems Analysis: Models and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 29. [Google Scholar]
- Quddus, M.A.; Wang, C.; Ison, S.G. Road traffic congestion and crash severity: Econometric analysis using ordered response models. J. Transp. Eng. 2010, 136, 424–435. [Google Scholar] [CrossRef]
- De Luca, S. Choice Modelling Theories. Appendix 1 in Cantarella et al. In Dynamics and Stochasticity in Transportation Systems: Tools for Transportation Network Modelling; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- May, A.D. Traffic Flow Fundamentals; Prentice Hall: Hoboken, NJ, USA, 1990. [Google Scholar]
- Hauer, E. Safety review of highway 407: Confronting two myths. Transp. Res. Rec. 1999, 1693, 9–12. [Google Scholar] [CrossRef]
- Kerner, B.S. The Physics of Traffic: Empirical Freeway Pattern Features, Engineering Applications, and Theory; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Wier, M.; Weintraub, J.; Humphreys, E.H.; Seto, E.; Bhatia, R. An Area-Level Model of Vehicle-Pedestrian Collisions with Implications for Land Use and Transportation Planning. Accid. Anal. Prev. 2009, 41, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Tarawneh, M.A.; Muromachi, Y. Vulnerability assessment by speed profiles. J. Traffic Transp. Eng. 2011, 11, 123–131. [Google Scholar]
- Vitetta, A. Influence of vehicular flow instability in a transport network on risk reduction: Test in a two-link network. J. Adv. Transp. 2025, 2025, 7966144. [Google Scholar] [CrossRef]
- Wardrop, J.G. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. 1952, 2, 325–378. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Watling, D.P.; de Luca, S.; Di Pace, R. Dynamics and Stochasticity in Transportation Systems: Tools for Transportation Network Modelling; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Cantarella, G.E.; Fiori, C.; Mussone, L. Dynamics and Stochasticity in Transportation Systems: Equations and Examples; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
| Symbol/Term | Description |
|---|---|
| T | Speed random variable |
| V | Travel time random variable |
| η | Shape parameter of the gamma and inverse gamma distribution |
| θT | Scale parameter of the inverse gamma distribution |
| θV | Scale parameter of the inverse gamma distribution |
| x | Degree of saturation (dimensionless), ratio between flow and capacity |
| y | Speed ratio (dimensionless), ratio between speed and free flow speed |
| Parameter | Urban | Extra-Urban |
|---|---|---|
| v0 [km/h] | 60 | 120 |
| fMAX [veic/h] | 2000 | 2000 |
| a | 2 | 0.3 |
| b | 2 | 4 |
| β | 0.01 | 0.01 |
| c = β · v0 | 0.6 | 1.2 |
| Saturation Level x | Risk Index z(x) | Parameter c | Elasticity εc |
|---|---|---|---|
| 0.2 | 0.015 | 0.85 | −0.42 |
| 0.5 | 0.038 | 0.85 | −0.67 |
| 0.8 | 0.021 | 0.85 | −0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannattasio, O.; Vitetta, A. Transportation Link Risk Analysis Through Stochastic Link Fundamental Flow Diagram. Future Transp. 2025, 5, 150. https://doi.org/10.3390/futuretransp5040150
Giannattasio O, Vitetta A. Transportation Link Risk Analysis Through Stochastic Link Fundamental Flow Diagram. Future Transportation. 2025; 5(4):150. https://doi.org/10.3390/futuretransp5040150
Chicago/Turabian StyleGiannattasio, Orlando, and Antonino Vitetta. 2025. "Transportation Link Risk Analysis Through Stochastic Link Fundamental Flow Diagram" Future Transportation 5, no. 4: 150. https://doi.org/10.3390/futuretransp5040150
APA StyleGiannattasio, O., & Vitetta, A. (2025). Transportation Link Risk Analysis Through Stochastic Link Fundamental Flow Diagram. Future Transportation, 5(4), 150. https://doi.org/10.3390/futuretransp5040150







