Improvement of the Hybrid Renewable Energy System for a Sustainable Power Supply of Transportation Infrastructure Objects

Abstract

This paper shows that using renewable energy sources in the power supply of transportation infrastructure is gradually becoming a new trend. Renewable energy systems are already valuable for railway and automotive infrastructure in various countries; however, this use is limited. This paper examines the improvement of control in a grid-connected, hybrid renewable energy system to meet the needs of a railway transportation infrastructure object by utilizing an additional diesel generator in autonomous mode. The aim is to reduce the depth of battery discharge and limit energy consumption from the grid during peak demand hours, considering the wide fluctuations in power consumption of the object and deviations in renewable energy generation relative to the forecast. Additionally, the task of ensuring long-term autonomous operation of the system is addressed. A control system is proposed based on the deviation of the battery’s state of charge relative to a set schedule, which is determined according to the forecast using an additional variable that sets the power consumption limit. This ensures the minimum possible depth of discharge and peak consumption, taking into account the generation of renewable energy sources, with a power-increase factor ranging from 1 to 1.5 relative to the calculated value. In autonomous mode, the task of minimizing energy consumption by the diesel generator is addressed. Solutions have been developed to implement control in grid and autonomous modes with the corresponding calculation algorithm. The system is not sensitive to the load schedule, and the battery’s depth of discharge limitations are maintained even when renewable energy generation is below the forecast by up to 20%. When generating renewable energy sources below the average monthly value in summer, it is possible to maintain a DoD of no less than 60%.

1. Introduction

Railway and automotive transportation infrastructure is the largest consumer of electrical energy. Electricity consumption is expected to increase with the further development of transportation infrastructure objects, such as new stations, depots, parking facilities, logistics centers, charging stations, level crossings, and stopping points.

The construction of new objects of transportation infrastructure and the development of the existing ones involve their geographical connection to existing distribution grids or the laying of new power transmission lines, which is associated with significant capital costs. Increasing the reliability of transportation infrastructure objects’ power supply and reducing maintenance costs requires new approaches. One such approach is the use of renewable energy sources (RESs).

In recent years, there has been a significant increase in the installed renewable energy capacity across various industries. For example, in 2023, according to Ref. [1], the world’s installed solar energy capacity amounted to 1418.97 GW. The use of RES on transportation infrastructure objects is expanding in these conditions. It is proposed to install RES, in particular photovoltaic panels, on the roofs of stations, as well as on wind and rain shelters of stations [2]; in depots [3]; at automatic railway crossings [4]; in protective zones on both sides of highways or railway lines [5]; etc. However, the use of RES in transportation infrastructure remains limited.

RES have recently been associated with ensuring a reliable energy supply and safety for railway transportation infrastructure while reducing the cost of electricity consumed from the grid. When using existing distribution systems with limited power, the issue of increasing object power beyond the grid’s supply limit can also be addressed. Such applications are justified for infrastructure objects located far from transformer substations.

Certain opportunities for compensating the uneven generation of renewable energy over time and seasons are provided by grid-connected hybrid systems (HRESs), combining photovoltaic panels (PVs), wind turbines (WGs), and storage batteries (SBs) or other energy storage systems (ESSs). When the grid is disconnected or there is energy insufficiency, diesel generators (DGs) or other generators are used. The potential of hybrid systems with RES in various sectors is currently unquestionable. However, the possibility of implementing such systems in transportation infrastructure objects is still insufficiently studied.

Therefore, the task of improving the implementation of hybrid systems, particularly through the use of renewable energy generation forecasting, which enhances their efficiency, is relevant.

The rest of this article is organized as follows: Section 2 provides a detailed overview of the relevant literature and problem statement. Section 3 details the research methodology. Section 4 outlines the load profile and the structure of the HRES, investigates situations such as grid-tied operation and autonomous operation mode, and presents the modeling results. Section 5 discusses the research results. Finally, Section 6 concludes this article.

2. Literature Review and Problem Statement

The management of energy consumption in HRES has been the subject of various review studies, such as those by Refs. [6,7]. According to Ref. [8], there is a need for specific control systems to manage the energy in HRES configurations that consist of DG, ESS, and PV. In a comprehensive review by Ref. [9], optimization methods and configurations of HRES are explored for a wide range of applications. This work presents various techniques to enhance the flexibility and efficiency of hybrid systems, ensuring they can meet diverse energy needs under different environmental conditions. Work [10] addresses the gaps in the literature regarding photovoltaic/wind systems, emphasizing the need for further research on new technologies and the environmental challenges posed by such systems. In another study by Ref. [11], various types of RESs—such as photovoltaic systems (PVS), wind turbines (WG), and fuel cells—were analyzed under different environmental conditions. This study also examined how diesel generators are used for standalone energy generation in cases where the primary power system fails.

The technological and economic feasibility of combining PV, WG, DG, and SB into a hybrid energy source is discussed in Ref. [12]. It is shown that the HRES option with 2 kW of photovoltaic energy, 1 kW of wind energy, 1 kW of generator energy, 1 kW of energy converter, and five batteries yielded the best results during modeling. This option was recommended for use in a proposed residential building. In Ref. [13], the optimal size of HRES is analyzed, taking into account the degradation of sources.

The control algorithm for HRES, consisting of DG, ESS, and PVS, which addresses issues of battery protection, storing excess energy, preventing power shortages in the grid, and using DG during critical moments, is discussed in Ref. [8]. The application of auxiliary WG in combination with PVS to increase the overall generation level while reducing energy consumption during seasons when PV generation is low and wind speed increases is considered in Refs. [14,15]. The use of HRES to increase power capacity beyond the consumption limit during modernization is presented in Ref. [16].

Regarding the implementation structures of HRES, two approaches can be highlighted. In Ref. [15], a system structure with a single grid inverter and the connection of PV, WG, and SB to a common DC bus is considered. In Ref. [17], the microgrid combines solar panels, a wind turbine system, a lithium-ion battery storage system, an electric vehicle (EV), and a DC load. All elements are connected to the DC bus via power electronic converters and are connected to the AC grid through an inverter (DC/AC).

The structure of a standalone HRES with PV, WG, SB, and DG connected to a DC bus with an autonomous inverter for powering the load is presented in Ref. [18]. An AC/DC converter is used at DG output, which must be regulated to ensure power balance in the system. This results in double energy conversion from the DG, leading to corresponding energy losses.

Currently, combined inverter solutions are not widely available. Modern hybrid grid-tied inverters are designed for use in PV systems with battery storage. For instance, in work [19], for a grid-connected system, the PV and fuel cell are connected to the DC bus, while the WG is connected to the AC bus. DG is not used in this structure. This configuration allows for the use of standard hybrid grid inverter solutions.

An essential component of HRES is the energy storage system, typically SB. However, this is also the most unreliable and expensive part of the system. Modern batteries, particularly LiFePO4, have high charge/discharge currents, allow for deep discharge, and have a significant lifespan. However, using a depth of discharge (DoD) of 80% provides 3000 discharge cycles [20], while at a DoD of 50%, the number of cycles increases to 5000. Thus, limiting the DoD is a crucial consideration. In Ref. [21], the focus is on minimizing electricity costs while simultaneously extending the lifespan of the ESS. An optimization method is employed to determine the optimal parameters of the ESS, including size and DoD, taking into account installation costs, the levelized cost of storage, winter and summer conditions, energy consumption profiles, and energy prices. It is noted that DoD plays a significant role in the operation of ESS and deeply affects its lifecycle.

Battery charging strategies in industrial applications for reducing peak loads are discussed in Ref. [22]. In Ref. [23], related to a microgrid consisting of a PV, DG, and an ESS, energy consumption management is considered based on a model predictive control approach. The aim is to ensure a reliable and safe energy supply, minimize the operational costs of the microgrid, and extend the lifespan of the ESS. In Ref. [18], one of the management tasks is to maintain the battery charge level to prevent power outages and extend the overall battery lifespan. In Ref. [24], it is argued that the advantage of intelligent control lies in its ability to accurately monitor the State of Charge (SoC) of the battery in five different states, which is unattainable with traditional control methods that rely only on two SoC levels (SoC_min, SoC_max).

A key issue is limiting the use of DG. In Ref. [25], an energy management algorithm for HRES, consisting of a PVS, SB, and DG, is discussed. The algorithm focuses on optimizing energy usage, protecting the batteries from damage, and preventing energy shortages. To limit the operating time of the DG, the energy stored in the battery is utilized. The efficiency of DG use is determined by its load. To assess DG fuel consumption (C in L/h), in Ref. [26], the linear dependence on output power (P_DG) is used: C = 0.0845P_R + 0.246P_DG, where P_R is rated power. In this case, at P_DG = 0.5P_R, the relative fuel consumption is 1.257; at P_DG = P_R/3, consumption increases by 1.513. Therefore, it is desirable to exclude the DG operation at low load.

In Ref. [27], a PVS with SB and four converters sharing a common DC link is examined. A proportional-integral (PI) voltage controller (VC) is used in the DC link. The controller sets the value of the currents of the battery and the supercapacitor. The “multiconverter” ensures the following: specified active power with appropriate power quality, operation of the PV with maximum power point tracking (MPPT), and extended battery lifespan through the use of a hybrid storage system. In Ref. [15], the structure of a control system for a multifunctional inverter in a PVS with SB, with voltage stabilization in the DC link using three PI VCs, is discussed. The VCs control the currents of the battery, the PV, and the current at the grid’s common connection point (PCC). The structure adapts to the operating mode, and only one VC is used at a time. As the number of sources increases, the HRES control system becomes more complex to ensure power balance. To limit the number of controlled variables, in Ref. [16], the WG operates independently with its controller.

Modern hybrid grid inverter solutions for PVS with SB, used for powering local facilities, such as those produced in Ref. [28], are available in capacities ranging from 2 to 50 kW. These inverters come with built-in controllers for connecting PV, SB, and DG. They offer a wide range of functions, including limiting power consumption from the grid, zero export to the grid, and grid-based charging. This enables the management of energy consumption using standard features. However, the capability for forecast-based energy management is not provided.

The autonomous operation mode (AOM) is considered the primary mode for HRES in the works [18,23]. For grid-connected HRES, this aspect receives insufficient attention, particularly regarding the interaction between RES and DG.

The use of forecasting can significantly improve the efficiency of energy consumption management. The use of real-time meteorological data for an intelligent energy management system in an autonomous hybrid photovoltaic/wind/biomass/battery energy storage system is discussed in Ref. [29]. In Ref. [30], an energy management system is considered that is based on the state of charge of the battery, supercapacitor, and hydrogen reservoir, as well as forecasts of solar radiation, wind speed, and load for the next day.

A significant number of studies are dedicated to forecasting RES generation using neural networks [31]. In Ref. [32], a wavelet-neural network-based genetic algorithm is proposed to optimize photovoltaic (PV) generation forecasting. Additionally, there are now several web resources [33,34,35] that provide information on PV generation and wind speed for a given object’s coordinates. The forecast discreteness interval can range from 1 h to 15 min.

However, forecast errors are inevitable. In Ref. [36], it is noted that the error can reach up to 15–20%. A similar margin of error is mentioned in Ref. [37]. An underestimated forecast leads to reduced utilization of renewable energy, while an overestimated forecast results in an increased DoD. This also applies to deviations in load relative to the calculated (planned) values.

Load planning is an effective way to increase the utilization of renewable energy for consumption. However, in practice, it is difficult to implement due to fluctuations in consumption caused by weather conditions, changes in technological processes, and other factors. As a result, the load can vary within quite a wide range. In Ref. [38], for an HRES consisting of PV, WG, a bio generator, and SB, future development scenarios are considered to account for these variations.

The use of correcting the value of power consumed from the grid P_g to compensate for deviations in the forecasted generation of RES and load relative to calculated values is considered in Ref. [39]. In this approach, a calculated schedule of the battery’s state of charge, SoC_R(t), is formed based on the deviation of SoC. According to the deviation of SoC, the power setpoint P_g is corrected. This allows the system to operate when the average load power deviates (0.877–1) relative to the calculated value and the generation deviation is ±10%. However, this is not always sufficient. The possibility of increasing the load power is not considered.

Peak demand is a problem for energy systems. In Ref. [40], peak demand limitation is addressed by using SB to store energy during off-peak hours and supply it during peak hours. The use of night and daytime battery charging to avoid consumption during peak hours is also discussed in Refs. [15,16,17]. In Ref. [41], scenarios are considered that involve reducing consumption during peak demand hours by pricing policies. In Ref. [42], multi-objective optimization of microgrid operation is performed using eight scenarios, incorporating RES and an additional DG.

Thus, several issues related to the implementation of hybrid systems remain insufficiently studied. These include forecast-based management, taking into account deviations in actual RES generation and load from calculated values, with the possibility of increasing consumption beyond the limit; ensuring the reduction in DoD and peak grid consumption; and reducing grid and DG consumption in AOM.

The purpose of this article is to improve the control of a grid-connected hybrid solar–wind system with SB and DG by reducing DoD and limiting peak consumption in cases of load power and RES generation deviations from calculated (forecasted) values, both in grid-connected and autonomous operating modes.

The following tasks have been set:

-

Justify a control mechanism using a forecast of RES generation, which will ensure a reduction in the DoD of the battery and limitation of consumption from the grid during peak demand hours when the load changes by up to 1.5 times with the possibility of increasing it above the limit.

-

Develop calculation and control algorithms with the formation of a given SoC schedule according to the deviation of the SoC value at the minimum possible DoD value and peak consumption for the actual generation of renewable energy.

-

Justify control in the AOM with a limitation within setting limits of the value power DG, with maximum consumption of RES energy and a reduction in fuel consumption.

-

Perform modeling to evaluate the proposed solutions.

3. Methods of Research

The classical methods of energy process analysis in electrical circuits are used. The hypothesis was adopted in the implementation that the total energy consumed in the daily cycle with a specific generation of RES and the object’s load is unchanged. At the same time, a decrease in the value of DoD = (100 − SoC)% = (100 − Q*min) (Q* = 100Q/Q_R, Q = ∫I_Bdt, Q_R = C_B, C_B—capacitance of SB, I_B—current of SB) at the end of the evening peak of the load is achieved by increasing daytime consumption with a corresponding decrease in nighttime consumption. This reduces energy losses in the daily cycle and helps to reduce grid consumption.

The limitation of the battery’s DoD and energy consumption from the grid during peak demand hours, when the object power consumption changes with the possibility of increasing it above the limit, was based on setting the SoC_R(t) battery charge state graph based on the RES forecast. There is a redistribution of consumption over time intervals with a shift to daylight time. In this case, an additional variable, P_R, is used, the value of which is set by time intervals, taking into account the limit of consumption power from the grid and the possible degree of change in load power.

When substantiating the reduction in the negative impact of deviations in the forecast of PV generation and load, emphasis is placed on the formation of the battery SoC schedule as a regulated parameter. A closed control system was used to set the power consumed from the grid by the deviation of SoC. It provides accounting for the actual load power and RES generation. Since the rate of change in the SoC is small, the regulation is carried out with a discreteness of 0.5 h.

In AOM, restrictions on DG use were provided to reduce the number of switches and fuel consumption with a corresponding reduction in emissions into the atmosphere.

Energy processes in terms of active power were analyzed in the daily cycle without taking into account transient processes. The efficiency factor is used to account for energy losses in the system elements. Archival data on renewable energy generation were used in the simulation. The mathematical model uses analytical expressions that correspond to generally accepted calculation methods. In the battery model, the charging characteristic was taken into account, taking into account the charge zone with a constant voltage.

To facilitate the comparison of results, a specific use case of the PV-WG system, as presented in the works [14,16,39], was considered. The overall calculation methodology was retained, utilizing the load profile normalized to a rated RES capacity of 1 kW. The power ratio of P_PV/P_W/P_L = 6/0.4/1 = 0.6/0.08/0.2 kW (where the maximum load power P_L = P_LIM) was applied, as accepted in Ref. [39]. For example, if the value of P_LIM = 5 kW, recalculation gives P_PV = 15 kW, P_W = 2 kW (similarly to Ref. [39], the use of a low-power vertical-axis WG was considered). A diesel generator with a capacity of P_DG = 3 kW can be used in combination with this equipment. Thus, the power ratio becomes P_PV/P_W/P_DG/P_L = 6/0.4/0.6/1.

4. Results of Research

4.1. Calculated Load Profile and the HRES Structure

In the implementation, the hypothesis assumes that the total energy consumed during the daily cycle for a specific RES generation and object load remains constant. Reducing the DoD by the end of the evening peak load is achieved by increasing consumption during the daytime and correspondingly reducing consumption at night. Some variation in consumed energy is attributed to losses in the battery storage system.

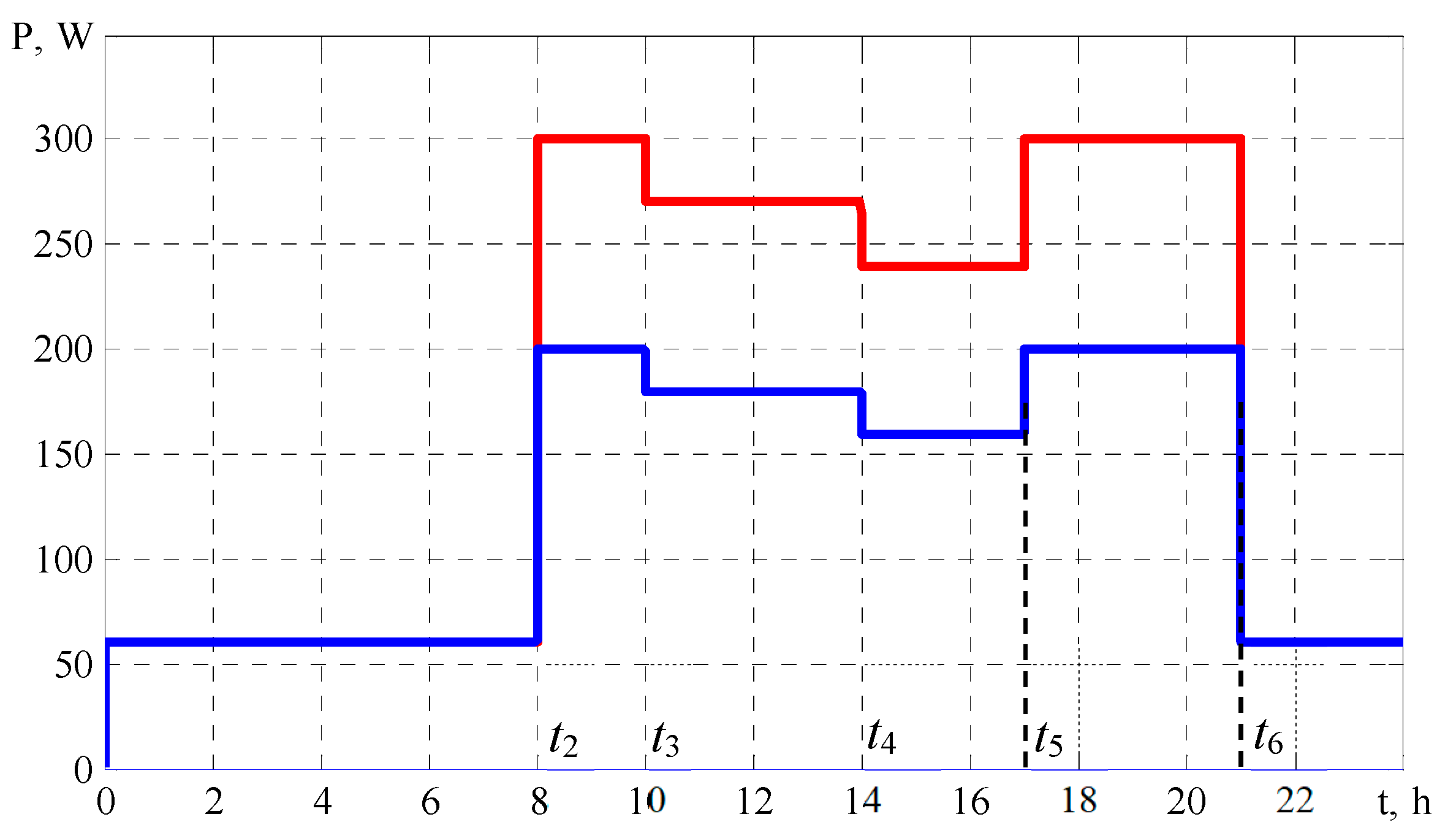
The same calculated load profile from Ref. [39] is used for the average load power P_L(t) over time intervals (Figure 1). The graph in Figure 1 represents the load profile for the winter period. The intervals (t₂, t₃) and (t₅, t₆) correspond to peak demand periods. To some extent, this load profile is idealized, and changes in this profile will result in changes in the RES power values. However, the overall principles of management implementation remain consistent. However, the overall principles of management implementation remain consistent. In Figure 1, the blue line represents the calculated load profile P_L(t), while the red line shows the profile when the load is increased by 1.5 times. The goal is to ensure system operation while maintaining the DoD value within the specified limits under varying load conditions. When the actual load is less than the calculated value, the DoD = (100 − Q₆) decreases, potentially resulting in underutilization of the available RES energy.

The HRES structure (Figure 2) is designed with the use of standard inverter solutions. A hybrid grid inverter (HGI) is used for the PV and SB, with the PV and SB connected through DC/DC converters. A grid inverter (GI) is used for the WG, which is connected through an AC/DC converter that also provides MPPT. The internal AC grid, including the load, is connected to the external distribution grid via an active energy meter (CT), automatic circuit breaker (QF1), and contactor (K1). The contactor K1 disconnects the internal grid when the external grid loses voltage, allowing the system to operate autonomously. The DG is connected to the grid on the CT input side and has a remote start function. The system includes the measurement of active power consumption PL from the load, power consumed from the grid P_g or DG P_DG, P_V generation P_PV, and WG generation P_W. The overall system control is handled by a control unit (CU) with a Wi-Fi module. Forecasted P_V generation, wind speed, measured power values, and battery SoC are processed by the CU, which generates control signals for the HGI. WG control is not utilized. The regulation system is based on the principles discussed in Ref. [14], and it includes three regulation channels: battery current I_B, PV current I_PV (to limit generation and prevent excess energy export to the grid), and current at the grid connection point (CT) Igm (active power consumption from the grid P_g). In this case, only I_B or I_PV is regulated during battery charging with constant voltage. The value of P_g is predefined.

The calculation of the battery capacity W_B = U_BC_B (U_B—the battery voltage) is based on the following conditions: it must be sufficient to consume the energy generated by RES during the daytime charging interval, based on average monthly generation in summer, and to be able to compensate for load consumption during the evening peak. During daytime charging in the interval (t₂, t₄), the increase in the state of charge of the battery ΔQ*₂₄ = Q*₄ − Q*₂ is calculated as follows:

$$\mathsf{\Delta }Q{*}_{24}={\displaystyle \frac{W_{RES24}\cdot {\mathrm{\eta }}_C-W_{L24}+W_{g24}}{0.01W_B}}{\mathrm{\eta }}_C\cdot {\mathrm{\eta }}_B,$$

(1)

where W_RES24 is the energy generated by RES, W_L24 is the energy consumed by the load, W_g24 is the energy consumed from the grid, η_C is the efficiency of the energy converter in the DC link and the grid inverter, and η_B is the efficiency of the battery.

In this case, consumption from the grid is not required, and W_g24 = 0.

During battery discharge in the evening peak, the following expression is used:

$$\mathsf{\Delta }Q{*}_{56}={\displaystyle \frac{W_{RES56}\cdot {\mathrm{\eta }}_C-W_{L56}}{0.01W_B\cdot {\mathrm{\eta }}_C\cdot {\mathrm{\eta }}_B}},$$

(2)

We accept the limit values ΔQ*₂₄ = 70% and, during the evening peak, ΔQ*₅₆ = (Q*₅ − Q*₆) = 50%. Thus, for the given consumption profile and taking into account the RES generation values for Kyiv, we can assume that the battery capacity is W_B = 1178 Wh.

The calculation of the DG power was carried out under the condition of ensuring operation during the daytime in winter (interval (t₂, t₆) corresponds to 13 h) in the absence of RES generation (W_RES = 0) and with a maximum DoD = 80%:

P_DG = W_DG26/(t₆ − t₂) = (W_L26 − ΔWB₂₆)/(t₆ − t₂),

(3)

Here, ΔW_B26 = 0.01ΔQ*₂₆·W_B·η_C·η is the energy supplied by the battery, where Q*₂ = 100%.

4.2. Grid Operation

Here, we estimate the potential degree of load variation (increase relative to P_LIM) in grid-connected operation, where ρ ≥ 1. When W_RES = 0, we have the following expression:

$$\rho ={\displaystyle \frac{\mathsf{\Delta }{W}_{B26}+W_{g26}}{W_{L26}}},$$

(4)

where W_g26 is the energy consumed from the grid.

In the limiting case, when W_g26 = W_LIM26 = P_LIM(t₆ − t₂), with Q*₂ = 100% and DoD₆ = 80% (Q*₆ = 20%), for the application under consideration, we have ρ = 1.43. With the presence of RES generation, the value of ρ can be higher.

The control is implemented by setting the power P_gR consumed from the grid. A closed-loop control system is considered, which forms the state of charge of the battery, Q*_R(t). The system is discrete, determining the value of power P_gR based on the deviation of Q* over the interval Δt using a proportional power controller. Unlike in Ref. [34], the calculation of P_gR is not performed. In calculating Q*_R(t), the variable P_R is used, which determines the limit of the power consumed from the grid (P_gR = (P_L − P_R) ≤ P_LIM).

The graph Q*_R(t) is set according to the forecasted value of RES generation P_RESF(t) and the value P_R(t). The formation of Q*_R(t) is carried out according to the accepted time discreteness Δt for the interval (t₂, t₆), taking into account the measured value Q*_2M at time t₂:

$$Q*=Q{*}_{2M}+{\displaystyle \sum _{i=1}^n\mathsf{\Delta }Q{*}_{Ri}},$$

(5)

where ΔQ*_Ri is the increment of Q*_R at the i-th time interval Δt, starting from t₂, and n = (t₆ − t₂)/Δt.

The value of ΔQ*_Ri, which is determined by the power P_R, is calculated as follows:

$$\mathsf{\Delta }Q{*}_{Ri}=B{\displaystyle \underset{0}{\overset{\mathsf{\Delta }t}{\int }}{P}_{B}dt=}B{\displaystyle \underset{0}{\overset{\mathsf{\Delta }t}{\int }}(P_{RESF}·{\mathrm{\eta }}_C-}{P}_R)dt,$$

(6)

where B is the coefficient that takes a specific value $B={\displaystyle \frac{{\eta }_C·{\eta }_B}{0.01W_B}}$ is during battery charging and $B={\displaystyle \frac{1}{0.01W_B·{\eta }_C·{\eta }_B}}$ during battery discharging, and P_B is the battery power.

The value of P_B, taking into account the battery charging characteristics in the constant voltage charging mode, which occurs when Q* ≥ Q*_d (Q*_d = (80–90)%), is determined by the following relationship:

$$P_B=\left\{\begin{array}{l}{P}_B, if Q*<Q{*}_d,\\ U_B\cdot C_B\cdot I{*}_B(Q*), if O*\ge Q{*}_d,\end{array}\right.$$

(7)

where I*_B(Q*) is the charging characteristic in the constant voltage charging region in per-unit values.

At the same time, the graphs Q*_R(t) and Q*_M(t) have a stepped shape with the given time discreteness Δt.

At time t₂, Q*_R = Q*_M, and in the first interval Δt, the deviation Δq_i = (Q*_Ri − Q*_Mi) = 0; thus, the power setpoint P_gRi = 0. In subsequent intervals, when Δq_i > 0, P_gRi > 0 (the state of charge of the battery increases and approaches Q*_R); when Δq_i ≤ 0, P_gRi = 0. The value of P_gRi in the case of using a proportional controller is P_gRi = Δq_i·K. The maximum deviation value occurs when P_gRi = P_LIM:

$$\mathsf{\Delta }{q}_M={\displaystyle \frac{P_{LIM}\cdot \mathsf{\Delta }t}{0.01W_B{\mathrm{\eta }}_C\cdot {\mathrm{\eta }}_B}}.$$

(8)

The value of the power controller transfer coefficient is obtained through the following expression:

$$K={\displaystyle \frac{P_{LIM}}{\mathsf{\Delta }{q}_M}}.$$

(9)

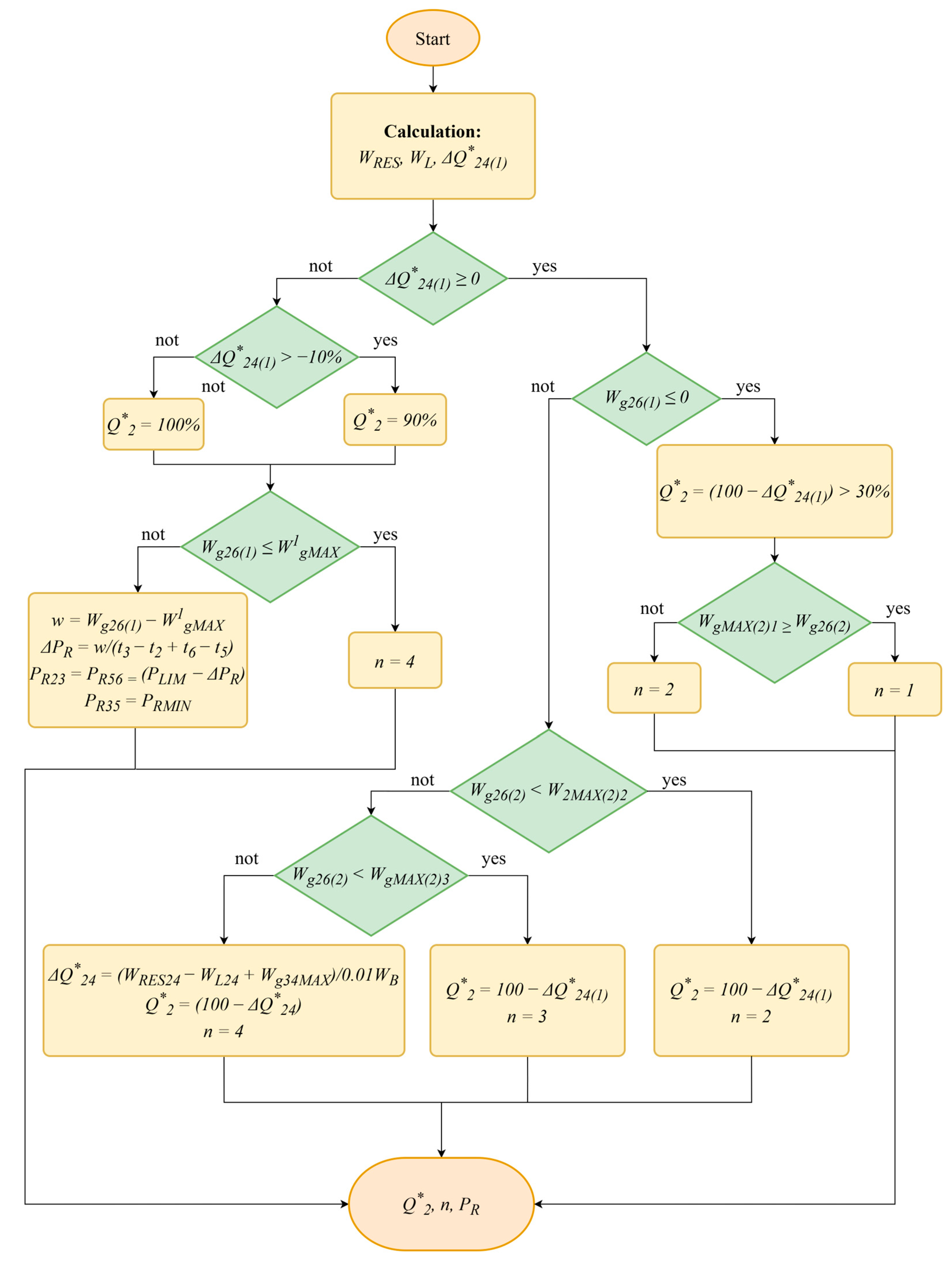
The block diagram for calculating Q*₂ and assigning combinations of P_R values over time intervals is shown in Figure 3. The input data are the forecasted RES generation P_RESF(t) and the calculated load profile P_L(t). The calculation is initially performed for ρ = 1, with subsequent refinement for the maximum value of ρ = 1.5. The increment in the state of charge over the interval (t₂, t₄) battery ΔQ*₂₄₍₁₎ at ρ = 1 is determined without accounting for energy consumption from the grid.

$$\Delta Q{*}_{24(1)}={\displaystyle \frac{W_{RES24}\cdot {\eta }_C-W_{L24}}{0.01W_B}}{\eta }_B\cdot {\eta }_C,$$

(10)

where W_RES24 and W_L24 are the energy from RES and the load, respectively, during the interval (t₂, t₄).

In this case, a limited set of P_R values is used. The description of the combinations of P_R values over time intervals is provided in

Table 1. The combinations of the used P_R values.

n	PR23	PR34	PR45	PR56	WgMAX(2)n
1	ρM·PLIM	ρM·PLIM	PRMIN	ρM·PLIM	WgMAX(2)1
2	PLIM	PLIM	PRMIN	PLIM + (ρM − 1)PLIM	WgMAX(2)2
3	PLIM	PLIM	PRMIN	PLIM	WgMAX(2)3
4	PLIM	PRMIN	PRMIN	PLIM	WgMAX(2)4

(n—combination number, with P_RMAX = P_LIM, P_RMIN = (ρP_LMIN − P_LIM). The values of W_gMAX(2)n are calculated according to the following expression:

W_gMAX(2)n = P_g23(t₃ − t₂) + P_g34(t₄ − t₃) + P_g45(t₅ − t₄) + P_g56(t₆ − t₅),

(11)

where P_gi(1) = (P_Li − P_Ri) and P_gi(2) = (ρ_M·P_Li − P_Ri) represent power values over time intervals for ρ = 1 and ρ = 1.5; and ρ_M is the maximum value of ρ.

$$P_{gi}=\left\{\begin{array}{l}{P}_{gi}, if 0\le P_{gi}<P_{LIM},\\ P_{LIM}, if P_{gi}\ge P_{LIM},\\ 0, if P_{gi}<0.\end{array}\right.$$

(12)

The energy consumed from the grid during the daytime (interval (t₂, t₆)) at ρ = 1 is obtained as follows:

W_g26(1) = W_L26 − W_RES26·η_C − ΔW_B26,

(13)

In the case where ΔQ*₂₄₍₁₎ < 0, it is assumed that Q*₆ = 40%, which corresponds to the DoD limit ≤60%; if ΔQ*₂₄₍₁₎ ≥ 0, it is assumed that ΔW_B26 = 0.

The energy consumed from the grid during the interval (t₂, t₆) when ρ_M = 1.5 is obtained as follows:

W_g26(2) = ρ_М·W_L26 − W_RES26·η_C − ΔW_B26,

(14)

The values are as follows: W¹_gMAX = W_RMAX(2)4 − (ρ_M − 1)W_L26 and W¹_g34MAX = (P_L34 − P_RMIN)(t₄ − t₃).

A deviation in RES generation (decrease) relative to the forecast inevitably leads to an increase in grid consumption to compensate for the shortfall and raises the DoD. There is an opportunity to correct the P_R values based on the actual RES generation. This applies to the values of P_R23 and P_R56.

4.3. Autonomous Operation Mode

The AOM is activated in the event of a grid power outage. The contactor K1 disconnects the object’s grid from the external AC grid. The PV hybrid inverter switches to autonomous mode, while the WG inverter continues operating in grid-connected mode. Based on the forecast for RES generation, a decision is made to start the DG if P_g > P_DGMIN. Depending on RES energy generation, the system may operate either without the DG or with it. When the DG is used alongside RES, the generator sets the grid voltage, which is used to synchronize both inverters in the system. The power consumption from the grid (from the DG) is also set within specified limits. The implementation of this mode is discussed below. The value of P_LIM in this case is set according to the DG power P_DG.

Naturally, in AOM, there is a load limitation at the level determined by the RES generation and DG power. An increase in load is allowed only if there is sufficient RES generation. If W_RES26·η_C = 0, the system operates solely on the DG and battery energy. In this case, the equation (ρW_L26 − ΔW_B26 − W_DG26 − W_RES26·η_C) = 0 applies. For the given parameters and load, when W_DG26 = P_DGMAX(t₆ − t₂) and ρ = 1 during the winter period, the battery discharge degree ΔQ*₂₆ ≥ 80%. However, when W_RES26·η_C ≥ 0.1W_RES26AV·η_C (W_RES26AV is the average monthly value), and ρ = 1, the value of ΔQ*₂₆ ≤ 70% (DoD ≥ 30%).

The AOM during the interval (t₂, t₆) is possible without using the DG (W_DG26 = 0) if the generation satisfies the following condition:

W_RES26·η_С > (ρW_L26 − ΔW_B26) = W¹.

(15)

We assume that Q*₂→100% and Q*₆ = 40%. For these parameters, at ρ = 1 in winter, W¹ = 1764 Wh, and at ρ = 1.5, W¹ = 2964 Wh. This means that the possibility of operating in winter conditions in Kyiv at ρ = 1.5 is practically excluded. In the summer period, at ρ = 1.5, W¹ = 3474 Wh, which is slightly below the average generation level. If W_RES26·η_C > W¹ for all time intervals, the value of P_Ri = ρ·P_Li is set.

A feature of setting the P_R value is maintaining the DG power Pg = P_DG ≥ P_DGMIN. This limits the DG’s operation in a mode close to idle, where efficiency is low. For the regulator, the constraint P_DGMIN ≤ P_DG ≤ P_DGMAX is used.

The energy required to ensure AOM from the DG is expressed as follows:

W_DG = (W¹ − W_RES26·η_С).

(16)

The following are two options for supplying this energy:

(a)

With uniform distribution over time, the average power of the DG is P_DGAV = WDG/(t₆ − t₂). In this case, the value of P_Ri for the corresponding time intervals is P_Ri = (ρ·P_Li − P_DGAV).

(b)

By concentrating the DG’s energy in the interval (t₄, t₅) with the set P_R45 = P_RMIN. In this case, the DG power is limited to the maximum value P_DG45 = (ρ·P_L45 − P_R45) = 120 W and W_DG45 = P_DG45(t₅ − t₄).

In option (a), the value of P_DGAV may be at the level of P_DGMIN, which will lead to periodic shutdowns of the DG during the interval Δt and reactivation in the next interval with a higher value of P_DG. In this case, the value of ΔQ*₂₄, considering DG energy, is expressed as follows:

$$\Delta Q{*}_{24}={\displaystyle \frac{W_{RES24}\cdot {\eta }_C+P_{DGAV}(t_4-t_2)-W_{L24}}{0.01W_B}}{\eta }_B\cdot {\eta }_C.$$

(17)

If, according to Equation (1), ΔQ*₂₄₍₁₎ < 0 and the value of Q*₂ = 100% is accepted, then by Equation (3), a situation may arise where Q*₂ > 100%. In this case, during the interval (t₄, t₅), there is excess energy that cannot be consumed, which would require reducing the generation from the PV system or the DG. However, this would violate conditions in Equation (2), leading to an increase in the DoD. Therefore, in this case, it is more appropriate to use option (b). The threshold value for switching to setting P_R45 = P_RMIN is expressed as follows:

Р¹_DGAV = W_DG45/(t₆ − t₂) at Р¹_DGAV > P_DGMIN.

(18)

In this case, with P_R45 = P_RMIN = 40 W, the DG power is limited to a maximum value of P_DG45 = (ρ·P_L45 − P_R45) = 120 W and W_DG45 = P_DG45(t₅ − t₄) ≤ 360 Wh. The threshold value is P_1DGAV = 27.7 W.

Thus, for the average generation in December, W_RES26AV·η_C = 1156 Wh and ρ· = 1, the required DG energy for AOM is W_DG = (W¹ − W_RES26·η_C) = 608 Wh, with an average power of P_DGAV = W_DG/(t₆ − t₂) = 47 W. Additional opportunities to increase ρ in this case, without increasing the DoD, can be achieved by setting P_R45 = P_RMIN = 40 W and accordingly increasing P_DG45 to P_DGMAX, provided W_DG ≤ W_DGMAX. When using the DG at maximum power, we have W_DGMAX = 1560 W and the maximum value ρ_MAX = (W_DGMAX + W_RES26AV ·η_C + ΔW_B26)/W_L26 = 1.4. It is worth noting that the value of P_Ri remains constant, and when the load (ρ) decreases, the value of Q*₆ slightly increases as W_DG decreases.

With average generation in February, W_RES26·η_C = 1538 Wh, the value of W_DG = 226 Wh corresponds to an average power of P_DGAV = 17 W, and the maximum value of ρ_MAX = 1.55. Setting P_R45 = P_RMIN also provides the possibility of increasing the load without significantly increasing the DoD.

During prolonged grid outages, an important issue is ensuring operation during nighttime while setting the required battery charge Q*_2R+1 for the next day based on the forecast of RES generation. Additional opportunities arise from controlling the values of P_R56 and Q*₆ according to the actual value of Q*₅. In cases of high RES generation forecasted for the next day, when Q*₂ < 50% and is close to Q*₆ (the average monthly RES value or higher for the May–September period), DG activation at night can be avoided. According to the forecast, the energy ΔW_g62 = (W_L62 − W_RES62·η_C) is determined, and if ΔWg62 > 0, the battery discharge ΔQ*₆₂ = ΔW_g62/0.01W_B·η_C·η_B. The required value of Q*₆ is then Q*₁₆ = Q*_2R + 1 + ΔQ*₆₂. Assuming the set value of Q*₆ = 40%, we find the battery charge increment during the interval (t₅, t₆) ΔQ* = Q*₁₆ − Q*₆, and the DG energy needed to achieve this ΔW_DG56 = 0.01ΔQ*·W_B/η_C·η_B. The DG power increment is ΔP_DG56 = ΔW_DG56/(t₆ − t₅), and P_R56 = P_RMAX − ΔP_DG56.

When ΔW_g62 ≤ 0 (which occurs during high wind speeds, although this is not typical for the summer period), the battery charges to the corresponding value ΔQ*₆₂. In this case, there may be a situation where Q*_2R+1 exceeds the calculated value, which would result in a reduced utilization of RES energy.

With low RES generation forecasted for the next day, when Q*₂ > 50% and Q*_2R+1 > Q*₆, increasing Q*₆ allows for a reduction in DG energy consumption over the daily cycle by reducing energy losses ΔW during the battery’s charge–discharge process:

$$\mathsf{\Delta }W=0.01\mathsf{\Delta }Q*\cdot W_B({\displaystyle \frac{1}{{\mathrm{\eta }}_B\cdot {\mathrm{\eta }}_C}}-{\mathrm{\eta }}_B\cdot {\mathrm{\eta }}_C).$$

(19)

where ΔQ* is the degree of battery charge increase by time t₆.

In the daily cycle, the total energy consumed remains practically unchanged but is redistributed over time. Thus, when Q*₆ increases, more energy is consumed during the interval (t₂, t₆), while consumption decreases during the interval (t₆, t₂). The reduction in energy losses leads to a decrease in DG fuel consumption. Simultaneously, the goal of reducing the DoD of the battery is achieved. Increasing Q*₆ is possible by increasing DG power during the interval (t₅, t₆) P_DG56. For instance, by decreasing P_R56 = 140 W when P_R56MAX = 200 W and ρ = 1, the DG energy W_DG will increase by 180 Wh over the 3-h interval. This allows Q*₆ to increase by ΔQ* = ΔW_DG56/0.01W_B·η_C·η_B = 17%.

The formation of battery charge during nighttime was considered using power correction based on the deviation of Q* from the target schedule Q*_R(t). The schedule Q*_R(t) is set according to the values of Q*₆ and Q*_2R+1.

4.4. Results of Modeling

The mathematical modeling of energy processes for the daily system operation cycle was performed using the principles outlined in Ref. [36]. The following system parameters were used: P_PV = 0.6 kW, P_W = 0.08 kW, P_DG = 0.12 kW (P_DGMIN = 0.02 kW), and W_B = 1178 Wh. The discretization interval was Δt = 0.5 h. RES generation was based on archival data for Kyiv. The load schedule was set according to time intervals, according to Figure 1. In this case, the determining factor is the energy consumed by the load at the intervals.

An evaluation of energy consumption in grid-connected mode was conducted based on the chosen value of Q*₆. The results for days with different RES generations are presented in Table 2, where the following are recorded:

-

W*_g represents the ratio of energy consumption values for the given increase in Q*₆.

-

W*_RES = W_RES/W_RESMAX (W_RES and W_RESMAX) are the daily energy generation from RES and the maximum RES generation for a clear day.

-

k₃, k₂, k₁ denotes the reduction in costs for consumed grid electricity under fixed-time tariff pricing (three tariffs, two tariffs, and one tariff). The following tariff ratios were assumed: for three tariffs—night (discounted)/semi-peak (day)/peak: 0.4/1/1.5 and for two tariffs—night/day: 0.5/1. When Q*₆ increases, grid energy consumption decreases; however, there is some worsening in terms of cost reduction under two- and three-tariff systems. The difference decreases as ρ increases.

Table 2. Simulation results for different Q*₆ values in grid-connected mode.

ρ, p.u.	W*RES, p.u.	Q*2, %	Q*6, %	k3, p.u.	k2, p.u.	k1, p.u.	W*g, p.u.
1	0.6 (summer)	70	43	5.656	4.898	3.955	0.989
1	0.6 (summer)	70	23.2	6.731	5.649	3.912
1.5	0.6 (summer)	70	42.5	2.427	2.298	2.165	0.999
1.5	0.6 (summer)	70	23.4	2.56	2.41	2.163
1	0.4 (winter)	100	42.6	3.68	3.304	2.43	0.983
1	0.4 (winter)	100	30	4.145	3.225	2.389
1.5	0.4 (winter)	100	41.5	2.111	1.95	1.763	0.98
1.5	0.4 (winter)	100	26.5	2.178	1.977	1.728
1	0.3 (winter)	100	44	2.798	2.297	1.943	1.006
1	0.3 (winter)	100	30	2.961	2.385	1.955
1.5	0.3 (winter)	100	40	1.861	1.693	1.563	0.968
1.5	0.3 (winter)	100	26	1.878	1.692	1.531

Table 2. Simulation results for different Q*₆ values in grid-connected mode.

ρ, p.u.	W*RES, p.u.	Q*2, %	Q*6, %	k3, p.u.	k2, p.u.	k1, p.u.	W*g, p.u.
1	0.6 (summer)	70	43	5.656	4.898	3.955	0.989
1	0.6 (summer)	70	23.2	6.731	5.649	3.912
1.5	0.6 (summer)	70	42.5	2.427	2.298	2.165	0.999
1.5	0.6 (summer)	70	23.4	2.56	2.41	2.163
1	0.4 (winter)	100	42.6	3.68	3.304	2.43	0.983
1	0.4 (winter)	100	30	4.145	3.225	2.389
1.5	0.4 (winter)	100	41.5	2.111	1.95	1.763	0.98
1.5	0.4 (winter)	100	26.5	2.178	1.977	1.728
1	0.3 (winter)	100	44	2.798	2.297	1.943	1.006
1	0.3 (winter)	100	30	2.961	2.385	1.955
1.5	0.3 (winter)	100	40	1.861	1.693	1.563	0.968
1.5	0.3 (winter)	100	26	1.878	1.692	1.531

With full use of renewable energy and a 15% deviation in renewable energy generation and load, the system performance indicators are similar to those presented in Refs. [16,39]. Therefore, the main emphasis was placed on critical deviations (20% for generation and 150% for load) when known solutions are inoperative and there is a complete discharge of the battery (DoD = 100%) or when the DoD is limited (cutoff) and the consumption from the grid exceeds the limit.

The main indicators of system operation with the grid are presented in

Table 3. Main indicators based on simulation results in grid-connected mode.

ρ, p.u.	P*RES, p.u.	n	W*RES, p.u.	PLAV, W	Q*2, %	Q*6, %	Pg23AV, W	Pg56AV, W	k3, p.u.	k2, p.u.	k1, p.u.
1	1	1	1 (summer)	178	33	37.4	0	0	37	32.4	21.4
1.5	1	1	1 (summer)	274	33	26	0	57.3	9.14	9	8.36
1	1	2	0.71 (summer)	178	50	45.2	1.5	19.6	10.33	9.5	7.87
1.5	1	2	0.71 (summer)	274	50	39	88	81	2.904	2.824	2.766
1	1	3	0.6 (summer)	178	70	43.2	0	20.1	5.55	4.8	3.86
1.5	1	3	0.6 (summer)	274	70	42.5	66.6	116.4	2.468	2.341	2.194
1	1	4	0.4 (summer)	178	100	53.3	0	33	2.985	2.551	2.09
1.5	1	4	0.4 (summer)	274	100	49.5	80.4	129	1.89	1.753	1.6
1	1	4	0.33 (summer)	178	100	52	0	27.4	2.36	2	1.72
1.5	1	4	0.33 (summer)	274	100	48.3	81.7	124.4	1.742	1.6	1.47
1.5	0.8	4	0.33 (summer)	274	100	48	90.8	129.2	1.652	1.52	1.4
1.5/1	1	4	0.33 (summer)	214.7	100	52	81.7	27.4	2.02	1.79	1.55
1.5/1	0.8	4	0.33 (summer)	214.7	100	51.5	90.8	33.4	1.8	1.59	1.433
1	1	4	0.3 (winter)	184.6	100	43	0	18.8	2.768	2.27	1.95
1.5	1	4	0.3 (winter)	276.9	100	41	72.66	118	1.85	1.684	1.565
1.5/1	1	4	0.3 (winter)	214.7	100	43	72.66	18.7	2.19	1.884	1.688
1.5	0.8	4	0.3 (winter)	276.9	100	39	85.7	126.8	1.7	1.55	1.42
1.5	0.8	4 *	0.18 (winter)	276.9	100	23	84.6	118.6	1.623	1.463	1.326
1.5	0.8	4 *(c)	0.18 (winter)	276.9	100	37	94.3	146.3	1.517	1.38	1.269
1	1	4 *	0.06 (winter)	184.6	100	50	92.6	121.3	1.257	1.154	1.042
1.5	1	4 *	0.06 (winter)	276.9	100	46	144	200	1.287	1.204	1.112
1.5	0.8	4 *	0.06 (winter)	276.9	100	46	145	200	1.282	1.2	1.106

* The relative value of the variable.

. Days with different RES generations were considered, using all combinations of the P_R setpoints. Combination 4* corresponds to the correction of P_R23 and P_R56. Table 3 includes the following: P*_RES = P_RES/P_RESF—the deviation of RES generation relative to the forecast P_RESF; P_LAV—the average load power over the interval (t₂, t₆); P_g23AV and P_g56AV—the average power consumed from the grid during peak demand hours; and ρ = 1.5/1 represents the load variation in the middle of the day. Changing the load schedule while maintaining the energy consumed during the interval has virtually no effect on the resulting indicators.

When RES generation is above average (W*_RES ≥ 0.71), the increase in DoD is necessary, as the goal is to maximize the battery’s energy capacity to consume excess energy.

The deviation of RES generation from the forecast leads to an increase in DoD, especially with low RES generation. For example, with W*_RES = 0.18 (winter) and P*_RES = 0.8, the value of Q*₆ = 23% (Table 3). By applying corrections to P_R23 and P_R56 based on actual RES generation (from 9:00, set P_R23 = P_R56 = 168), the value of Q*₆ = 37% (4*(c)_B Table 3) is obtained. However, this also leads to an increase in peak consumption and overall grid consumption (values of k₁ − k₃ decrease). Therefore, the necessity of such corrections is not always obvious.

Plots of power P_RES, P_L, Pg, state of charge Q*, and battery current I_B during grid-connected operation for a December day with average RES generation are shown in Figure 4a for ρ = 1 and P*_RES = 1, in Figure 4b for ρ = 1.5 and P*_RES = 1, in Figure 4c with ρ varying during the day from 1.5 to 1 and P*_RES = 1, and in Figure 4d for P*_RES = 0.8 and ρ = 1.5.

The performance indicators in AOM for the daily cycle from 8:00 to 8:00 are presented in

Table 4. Main indicators based on simulation results in autonomous mode.

ρ, p.u.	P*RES, p.u.	W*RES, p.u.	PR23/PR34/PR45/PR56/, W	Q*2, %	Q*6, %	WDG26, Wh	WDG62, Wh
1	1	0.71 (summer)	200/200/40/200	50	47.6	168.5	247.6
1.25	1	0.71 (summer)	200/200/40/200	50	52	869.3	182.9
1.25	0.8	0.71 (summer)	200/200/40/200	50	52.2	1398	273.2
1.5	1	0.71 (summer)	200/200/40/200	50	40.2	1411	315.9
1	1	0.4 (winter)	182/162/142/182	100	31.8	138	1198
1	1	0.4 (winter)	200/200/40/200	100	42.6	235.8	1051
1	1	0.4 (winter)	200/200/40/140	100	60	426	802.4
1	0.8	0.4 (winter)	200/200/40/140	100	35.7	451	1191
1.25	1	0.4 (winter)	200/200/40/140	100	55.1	972.1	864.1
1.4	1	0.4 (winter)	200/200/40/140	100	38.1	1142	1086

. Plots of RES power in MPPT mode P_RESM and accounting for PV power regulation P_RES, P_L, P_DG, Q*, for a winter day with W*_RES = 0.4 (February) are shown, with the battery charged to 100%.

In Figure 5a, the P_R values over the intervals are 182/162/142/182, with a limit of P_RMIN = 20 W and ρ = 1. In this case, during the interval (t₂, t₆), there are multiple DG starts with incomplete utilization of RES energy (shown as a dashed line for P_RES). In Figure 5b, similar graphs are shown with PR over the intervals set to 200/200/40/200 and ρ = 1. Here, full utilization of RES energy is achieved, and there is only one DG start during the day. For ρ = 1, using power values of 200/200/40/200 reduces DG energy consumption by 3.8%. When switching to power values of 200/200/40/140, the reduction reaches 8.7%, with an increase in Q*₆ to 60%. The increase in Q*₆ (DoD < 65%) is achieved even with W*_RES = 0.8.

5. Discussion of Research Results

Limiting the DoD of the battery and energy consumption from the grid during peak demand hours when the power consumption of the object changes, including increasing the power above the limit for consumption from the grid, is possible due to the following:

-

RES generation forecast-based control. In this case, reducing DoD and grid energy consumption during peak demand hours is accomplished by redistributing consumption over time, shifting it towards the daytime.

-

Setting the battery’s state of charge schedule SoC_R(t) based on the RES generation forecast, using an additional variable P_R, whose value is assigned over time intervals, considering the grid consumption power limit.

-

Forming SoC_R(t) using a closed-loop control system based on the deviation of SoC(t) from SoC_R(t). In this case, the value of P_R is set considering the possible variation in load power (up to 1.5 times in this application), and the value of grid power P_g is adjusted based on the SoC deviation, taking into account actual load power and RES generation. This ensures non-critical operation even with load power changes and deviations in RES generation from the forecast.

-

Increasing the SoC by the end of the evening peak load to reduce energy losses over the daily cycle, which in turn helps lower grid consumption.

Ensuring long-term operation in autonomous mode with the use of a diesel generator while increasing the utilization of RES energy, optimizing battery DoD, and reducing DG energy consumption and fuel is achieved through the following means:

-

Using a control system based on the deviation of SoC(t), with set values of P_R and correction of the setpoint during the evening peak.

-

Limiting DG power within specified limits, which prevents operation close to idle mode and helps reduce the number of DG starts.

-

Reducing DoD by the end of the evening peak load, which creates the opportunity to lower DG energy consumption.

This work is a development of the studies [16,39], where the control of a PV-WG system was considered based on the forecast of RES generation, with the setting of active power consumed from the grid. The use of power setpoint correction based on the deviation of SoC from the reference value allowed for a functional system even when there were deviations in the load from the accepted schedule and discrepancies between actual and forecasted RES generation. However, the control was rigidly tied to the load schedule, and only load deviations towards a reduction to 0.877 of the calculated value were considered. In real-world conditions, the load may vary within a broader range. Additionally, the limitation of DoD ≤ 80% only applied to the value at the evening peak.

A key feature of the proposed solutions is ensuring the maximum reduction in DoD and peak consumption with actual RES generation, considering potential load changes up to 1.5 times. The system’s capabilities are practically independent of the load schedule. This is achieved by using a closed-loop control system with the introduction of an additional variable, which accounts for the range of load power changes and the grid consumption limit. In autonomous mode, the system also provides the possibility of reducing DG energy consumption.

6. Conclusions

About the HRES of the infrastructure object, a control mechanism using the RES generation forecast and using a closed control system for forming a specified schedule of the battery state of charge SoC_R(t) is justified. The SoC_R(t) schedule is calculated using the RES generation forecast and an additional variable, P_R, which is set over time intervals, taking into account the grid consumption power limit and the battery’s charging characteristics. Discrete regulation is applied based on the deviation of SoC, with a discretization interval of 0.5 h. The deviation of SoC determines the setpoint for active power consumed from the grid. The battery current is set by a PI controller to maintain the power balance in the system.

An algorithm has been developed for calculating the reference SoC schedule with a defined set of combinations for the variable P_R over time intervals for grid-connected operation. A control mechanism for autonomous operation has been substantiated, with power consumption from DG limited within set boundaries, maximizing RES energy usage while reducing DG (fuel) energy consumption.

The simulation results show that for specific applications in grid-connected mode, it is possible to reduce the DoD and grid energy consumption during peak hours, even with load variations up to 1.5 times the calculated load and the power limit. This also applies in cases where RES generation deviates from the forecast. When the RES generation is below the average monthly value in summer (for the Kyiv region), it is possible to maintain a DoD of no more than 60%. Increasing the DoD to 70% during periods of RES generation above the monthly average in summer is related to maximizing the use of RES energy for consumption. When RES generation is below the average levels from September to April, only one deep discharge of the battery occurs per day. In autonomous mode, the possibility of reducing DoD remains, along with the potential to save DG energy.

The limitations regarding the use of the results of this work include the following:

• The consideration of a single-shift (daytime) operation mode of the object.
• Load power limitations in AOM when RES generation decreases.
• The results were obtained without accounting for the measurement error of the battery state.

The solution suggests further research into the impact of battery state measurement errors and the potential for improving system performance by increasing the number of combinations for the P_R setpoints.