Figure 1.
Vehicle approximation using Single Track Model.
Figure 1.
Vehicle approximation using Single Track Model.
Figure 2.
(a) Duration of active CBF constraint for varying OV velocities at AV reference velocity of 17.5 m/s. (b) Duration of active CBF constraint for varying OV velocities at AV reference velocity of 25 m/s. (c) Threshold OV overtaking velocities for different AV reference velocities. (d) Distance traveled by the AV under the influence of different OV velocities, with AV reference velocity of 25 m/s. (e) Distance traveled by the AV under the influence of different OV velocities, with AV reference velocity of 17.5 m/s.
Figure 2.
(a) Duration of active CBF constraint for varying OV velocities at AV reference velocity of 17.5 m/s. (b) Duration of active CBF constraint for varying OV velocities at AV reference velocity of 25 m/s. (c) Threshold OV overtaking velocities for different AV reference velocities. (d) Distance traveled by the AV under the influence of different OV velocities, with AV reference velocity of 25 m/s. (e) Distance traveled by the AV under the influence of different OV velocities, with AV reference velocity of 17.5 m/s.
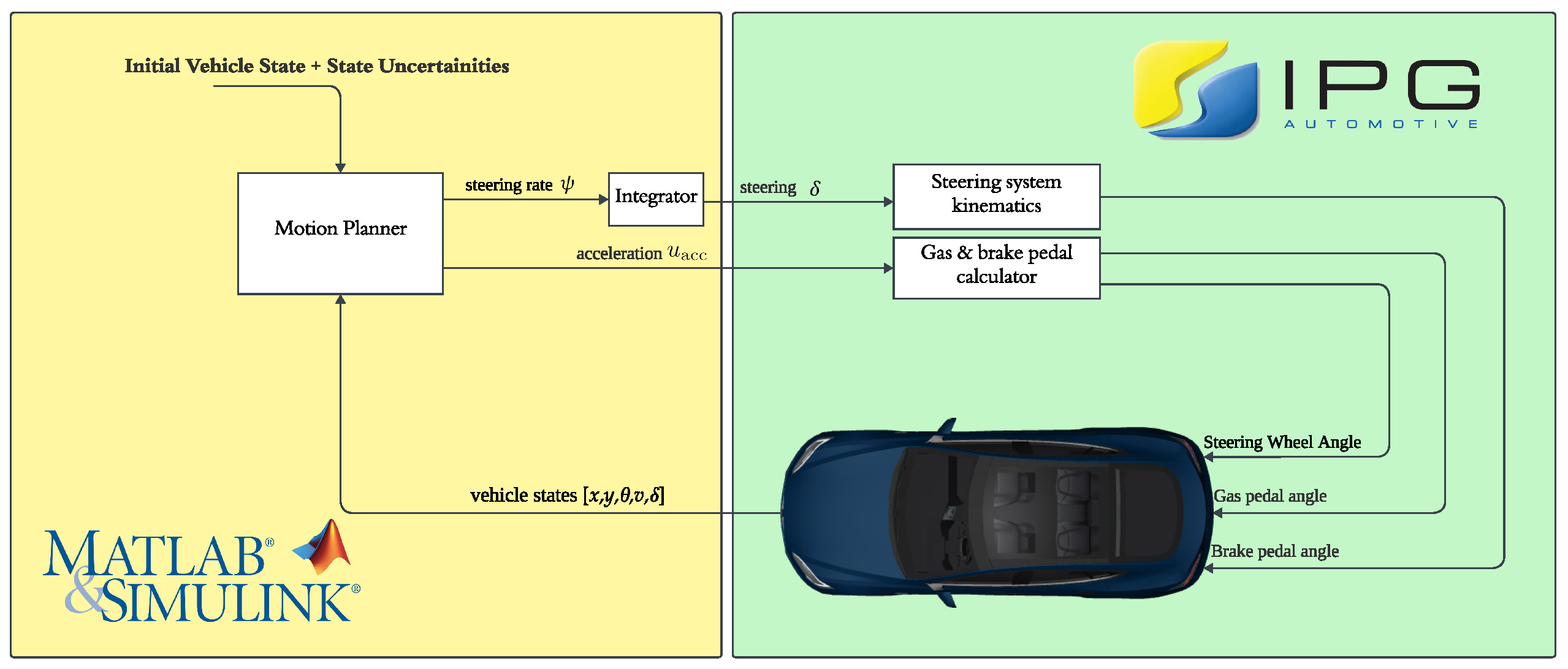
Figure 3.
Layout of feedback loop established between the developed motion planner and the high-fidelity simulation software.
Figure 3.
Layout of feedback loop established between the developed motion planner and the high-fidelity simulation software.
Figure 4.
Uncertain cases (obstacle-avoidance set): robust for nominal case of 95 m relative distance and fewer failures as distance decreases.
Figure 4.
Uncertain cases (obstacle-avoidance set): robust for nominal case of 95 m relative distance and fewer failures as distance decreases.
Figure 5.
(a) Nominal cases for stationary OV case (obstacle-avoidance set): failures visible for high-speed scenarios but more robust under uncertainties. (b) Nominal cases for stationary OV case (path-following set): all pass but performs poorly under uncertainties in position information.
Figure 5.
(a) Nominal cases for stationary OV case (obstacle-avoidance set): failures visible for high-speed scenarios but more robust under uncertainties. (b) Nominal cases for stationary OV case (path-following set): all pass but performs poorly under uncertainties in position information.
Figure 6.
Uncertain cases (path-following set): failures at all distances, failure modes are different from the first set of weights.
Figure 6.
Uncertain cases (path-following set): failures at all distances, failure modes are different from the first set of weights.
Figure 7.
obstacle-avoidance set simulation results: spread of scenarios with respect to starting position and heading.
Figure 7.
obstacle-avoidance set simulation results: spread of scenarios with respect to starting position and heading.
Figure 8.
obstacle-avoidance set simulation results: scenario spread with respect to initial position and initial velocity.
Figure 8.
obstacle-avoidance set simulation results: scenario spread with respect to initial position and initial velocity.
Figure 9.
obstacle-avoidance set simulation results: scenario spread with respect to initial position and reference velocity.
Figure 9.
obstacle-avoidance set simulation results: scenario spread with respect to initial position and reference velocity.
Figure 10.
Nominal cases for moving-OV case under AV of 17.5 m/s—all nominal cases pass successfully. Failures occur only in the presence of uncertainties, especially when increases with a decrease in .
Figure 10.
Nominal cases for moving-OV case under AV of 17.5 m/s—all nominal cases pass successfully. Failures occur only in the presence of uncertainties, especially when increases with a decrease in .
Figure 11.
AV trajectory RMSE under moving-OV scenario for AV of 17.5 m/s—failures only when increases with decreases in .
Figure 11.
AV trajectory RMSE under moving-OV scenario for AV of 17.5 m/s—failures only when increases with decreases in .
Figure 12.
Simulation results for the moving OV case under AV of 17.5 m/s: (a) vs. vs. most failures occur when increases with decreases in and is at the edge of the region; (b) vs. vs. heading most failures occur when increases with at the right edge of the region and with the initial heading angle to the right lane boundary.
Figure 12.
Simulation results for the moving OV case under AV of 17.5 m/s: (a) vs. vs. most failures occur when increases with decreases in and is at the edge of the region; (b) vs. vs. heading most failures occur when increases with at the right edge of the region and with the initial heading angle to the right lane boundary.
Figure 13.
Nominal cases for moving-OV case under AV of 25 m/s—all nominal cases pass successfully. Failures occur only in the presence of uncertainties, especially when increases with a decrease in .
Figure 13.
Nominal cases for moving-OV case under AV of 25 m/s—all nominal cases pass successfully. Failures occur only in the presence of uncertainties, especially when increases with a decrease in .
Figure 14.
AV trajectory RMSE under moving-OV scenario for AV of 25 m/s—failures only when increases with decreases in .
Figure 14.
AV trajectory RMSE under moving-OV scenario for AV of 25 m/s—failures only when increases with decreases in .
Figure 15.
Simulation results for the moving—OV case under AV of 25 m/s: (a) vs. vs. —most failures occur when increases with increases in and is invariant of ; (b) vs. vs. heading —most failures occur when increases and is invariant of and .
Figure 15.
Simulation results for the moving—OV case under AV of 25 m/s: (a) vs. vs. —most failures occur when increases with increases in and is invariant of ; (b) vs. vs. heading —most failures occur when increases and is invariant of and .
Figure 16.
Nominal cases for safety-critical stopping scenario—failures occur when increases with attributed to the shorter distance available for the AV to safely stop behind OV.
Figure 16.
Nominal cases for safety-critical stopping scenario—failures occur when increases with attributed to the shorter distance available for the AV to safely stop behind OV.
Figure 17.
AV trajectory RMSE under safety-critical scenario—failures occur when increases with failed case percentage increasing with increase in .
Figure 17.
AV trajectory RMSE under safety-critical scenario—failures occur when increases with failed case percentage increasing with increase in .
Figure 18.
Simulation results for the safety stop case: (a) vs. vs. —all the simulations corresponding to the failed nominal case failed too, i.e., the ones starting at 50 m and having a- velocity of 25 m/s; (b) vs. vs. heading —the failures occur when the AV starts nearest to the OV, i.e., 50 m and is invariant of and .
Figure 18.
Simulation results for the safety stop case: (a) vs. vs. —all the simulations corresponding to the failed nominal case failed too, i.e., the ones starting at 50 m and having a- velocity of 25 m/s; (b) vs. vs. heading —the failures occur when the AV starts nearest to the OV, i.e., 50 m and is invariant of and .
Table 1.
Parameters and their ranges for the concrete and logical scenario description.
Table 1.
Parameters and their ranges for the concrete and logical scenario description.
| Parameter Description | Symbol | Unit | Range | Uncertainty |
|---|
| AV x initial position | | [m] | [0, 0] | |
| AV y initial position | | [m] | [0, 50] | |
| OV initial position | (,) | [m] | [(0,100), (0,100)] | |
| AV heading | | [°] | [0, 0] | [−2, 2] |
| AV initial velocity | | [m/s] | [0, 25] | |
| AV reference position | | [m/s] | [10, 25] | |
| OV velocity | | [m/s] | [0, 24] | |
Table 2.
Parameter set for static obstacle logical scenario.
Table 2.
Parameter set for static obstacle logical scenario.
| Parameter | Unit | Value | Nominal | Uncertainty | Uncertain |
|---|
| [m] | [0] | ×1 | | |
| [m] | [5,20,35,50] | ×4 | | ×25 |
| (heading) | [°] | [0] | ×1 | [−2,0,2] | ×3 |
| [m/s] | [0,3,6] | ×3 | | |
| [m/s] | [10,17.5,25] | ×3 | | |
| [m/s] | [0] | ×1 | | |
| Total Simulations | | | 36 | × | 75 = 2700 |
Table 3.
obstacle-avoidance set simulation results: heading v/s .
Table 3.
obstacle-avoidance set simulation results: heading v/s .
| | | 5 | 20 | 35 | 50 |
|---|
| Heading | |
|---|
| −2 | 100% | 72% | 78% | 32% |
| 0 | 100% | 85% | 80% | 35% |
| 2 | 100% | 92% | 72% | 45% |
Table 4.
obstacle-avoidance set simulation results: v/s .
Table 4.
obstacle-avoidance set simulation results: v/s .
| | | 5 | 20 | 35 | 50 |
|---|
| |
|---|
| 0 | 100% | 85% | 75% | 36% |
| 3 | 100% | 83% | 73% | 40% |
| 6 | 100% | 80% | 82% | 37% |
Table 5.
obstacle-avoidance set simulation results: v/s .
Table 5.
obstacle-avoidance set simulation results: v/s .
| | | 5 | 20 | 35 | 50 |
|---|
| |
|---|
| 10 | 100% | 88% | 88% | 50% |
| 17.5 | 100% | 61% | 45% | 52% |
| 25 | 100% | 100% | 97% | 11% |
Table 6.
Parameter set for the moving-obstacle logical scenario at = 17.5 m/s.
Table 6.
Parameter set for the moving-obstacle logical scenario at = 17.5 m/s.
| Parameter | Unit | Value | Nominal | Uncertainty | Uncertain |
|---|
| [m] | [0] | ×1 | | |
| [m] | [5,20,35,50] | ×4 | | ×25 |
| (heading) | [°] | [0] | ×1 | [−2,0,2] | ×3 |
| [m/s] | | ×1 | | |
| [m/s] | [17.5] | ×1 | | |
| [m/s] | [6,9,12,15] | ×4 | | |
| Total Simulations | | | 16 | × | 75 = 1200 |
Table 7.
Simulation results for moving-OV case under AV of 17.5 m/s— vs. —number of failures increases when increases with a decrease in attributed to the shorter distance available for the AV to react to the OV.
Table 7.
Simulation results for moving-OV case under AV of 17.5 m/s— vs. —number of failures increases when increases with a decrease in attributed to the shorter distance available for the AV to react to the OV.
| | | 5 | 20 | 35 | 50 |
|---|
| |
|---|
| 6 | 100% | 100% | 76% | 65% |
| 9 | 100% | 100% | 100% | 81% |
| 12 | 100% | 100% | 100% | 100% |
| 15 | 100% | 100% | 100% | 99% |
Table 8.
Parameter set for moving-obstacle logical scenario at = 25 m/s.
Table 8.
Parameter set for moving-obstacle logical scenario at = 25 m/s.
| Parameter | Unit | Value | Nominal | Uncertainty | Uncertain |
|---|
| [m] | [0] | ×1 | | |
| [m] | [5,20,35,50] | ×4 | | ×25 |
| (heading) | [°] | [0] | ×1 | [−2,0,2] | ×3 |
| [m/s] | | ×1 | | |
| [m/s] | [25] | ×1 | | |
| [m/s] | [6,12,18,24] | ×4 | | |
| Total Simulations | | | 16 | × | 75 = 1200 |
Table 9.
Simulation results for moving-OV case under AV of 25 m/s— vs. —number of failures increases when increases with a decrease in attributed to the shorter distance available for the AV to react to the OV.
Table 9.
Simulation results for moving-OV case under AV of 25 m/s— vs. —number of failures increases when increases with a decrease in attributed to the shorter distance available for the AV to react to the OV.
| | | 5 | 20 | 35 | 50 |
|---|
| |
|---|
| 6 | 100% | 100% | 100% | 67% |
| 12 | 100% | 100% | 76% | 52% |
| 18 | 100% | 100% | 100% | 75% |
| 24 | 100% | 100% | 100% | 95% |
Table 10.
Parameter set for safety-critical scenario.
Table 10.
Parameter set for safety-critical scenario.
| Parameter | Unit | Value | Nominal | Uncertainty | Uncertain |
|---|
| [m] | [0] | ×1 | | |
| [m] | [5,20,35,50] | ×4 | | ×25 |
| (heading) | [°] | [0] | ×1 | [−2,0,2] | ×3 |
| [m/s] | | | | |
| [m/s] | [10,17.5,25] | ×3 | | |
| [m/s] | [0] | ×1 | | |
| Total Simulations | | | 12 | × | 75 = 900 |
Table 11.
Simulation results for safety-critical stopping scenario— vs. —failures occur when increases with attributed to the shorter distance available for the AV to safely stop behind OV with more cases failing when increases.
Table 11.
Simulation results for safety-critical stopping scenario— vs. —failures occur when increases with attributed to the shorter distance available for the AV to safely stop behind OV with more cases failing when increases.
| | | 5 | 20 | 35 | 50 |
|---|
| |
|---|
| 10 | 99% | 100% | 100% | 83% |
| 17.5 | 99% | 100% | 100% | 67% |
| 25 | 98% | 99% | 100% | 0% |