Identification of Aggregate Urban Mobility Patterns of Nonregular Travellers from Mobile Phone Data
Abstract
1. Introduction
- We argue that estimating origin–destination matrices of nonregular users is pointless due to representativity issues and focus instead on estimating total travelled distances.
- We define a methodology to select CDR users with reliable mobility information.
- We develop a cost-efficient method to infer travelled distances based on origin and destination positions and detour ratio.
- We test the method on two months of data covering the Colombian city of Santiago de Cali and evidence macroscopic patterns in the daily total travelled distances of nonregular travellers, including weekly seasonality and longer-term trends.
- We additionally explore the macroscopic patterns of the overall population and draw research perspectives from the results.
2. Methodology
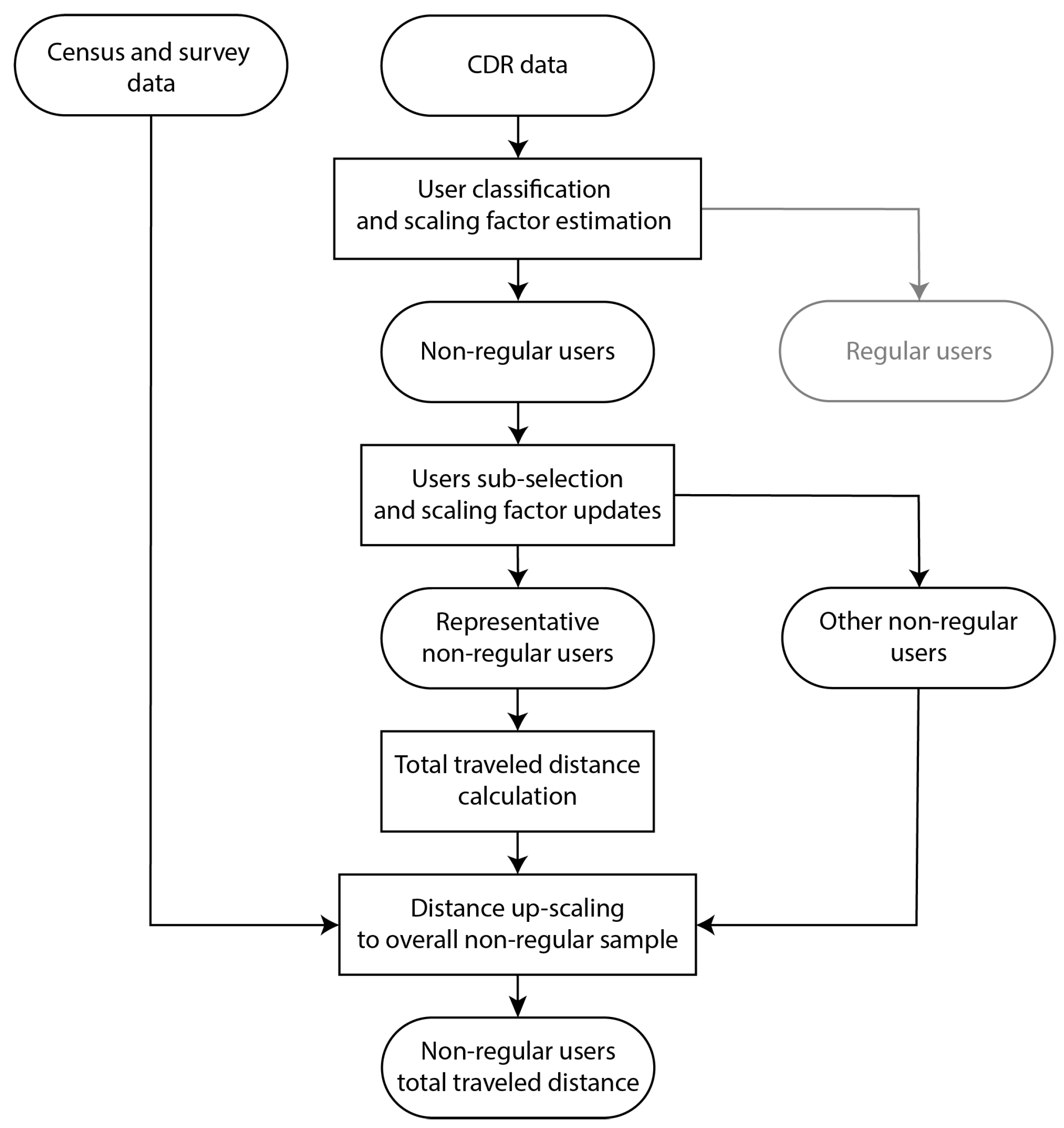
2.1. Design and Method Outline
2.2. Nonregular Travellers Extraction
2.3. Subsample Selection for Collective Mobility Reconstruction
2.4. Travel Distance Calculation
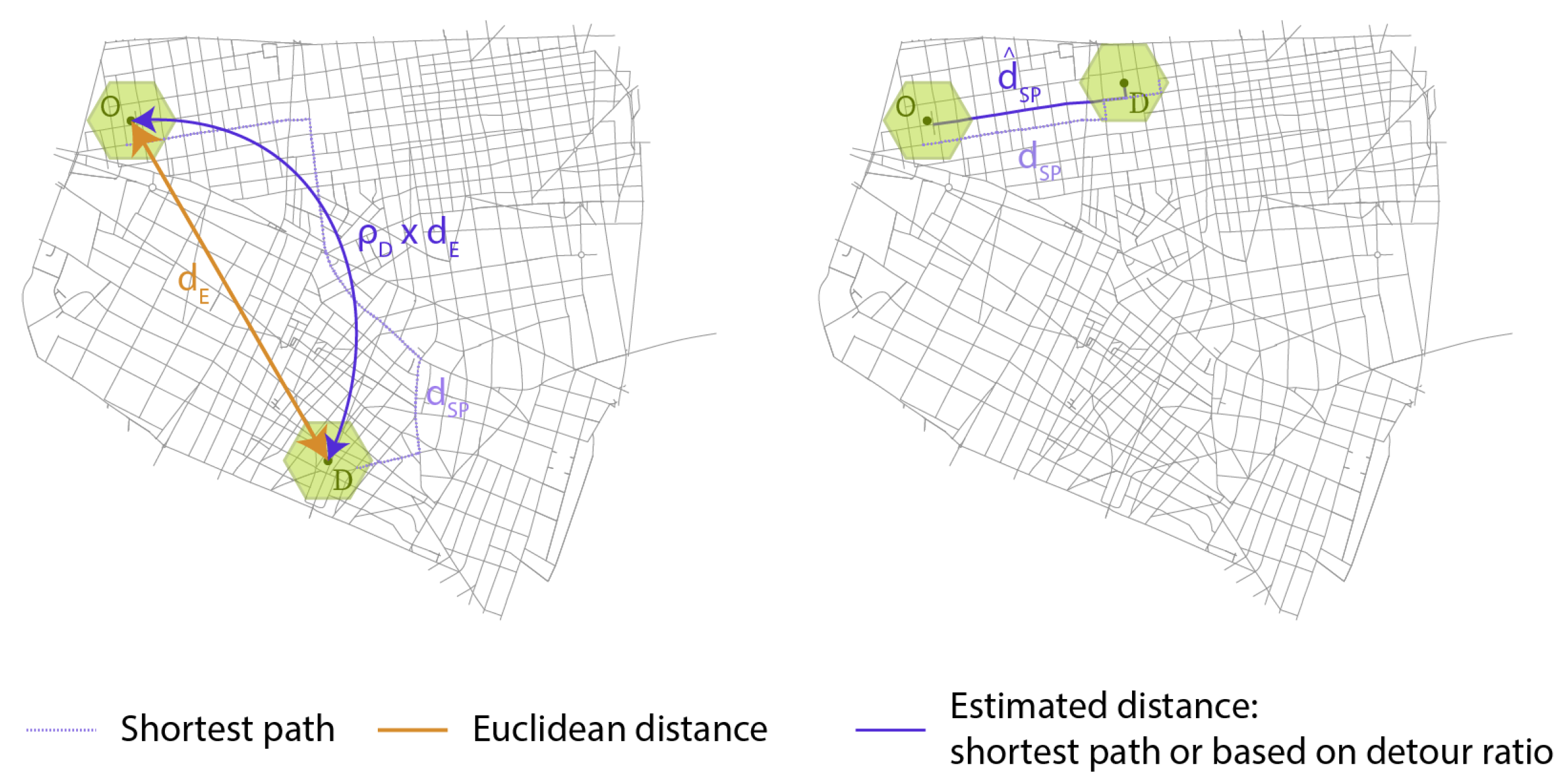
2.4.1. Metric Definition
2.4.2. Validation
2.5. Distance Upscaling
3. Case Study
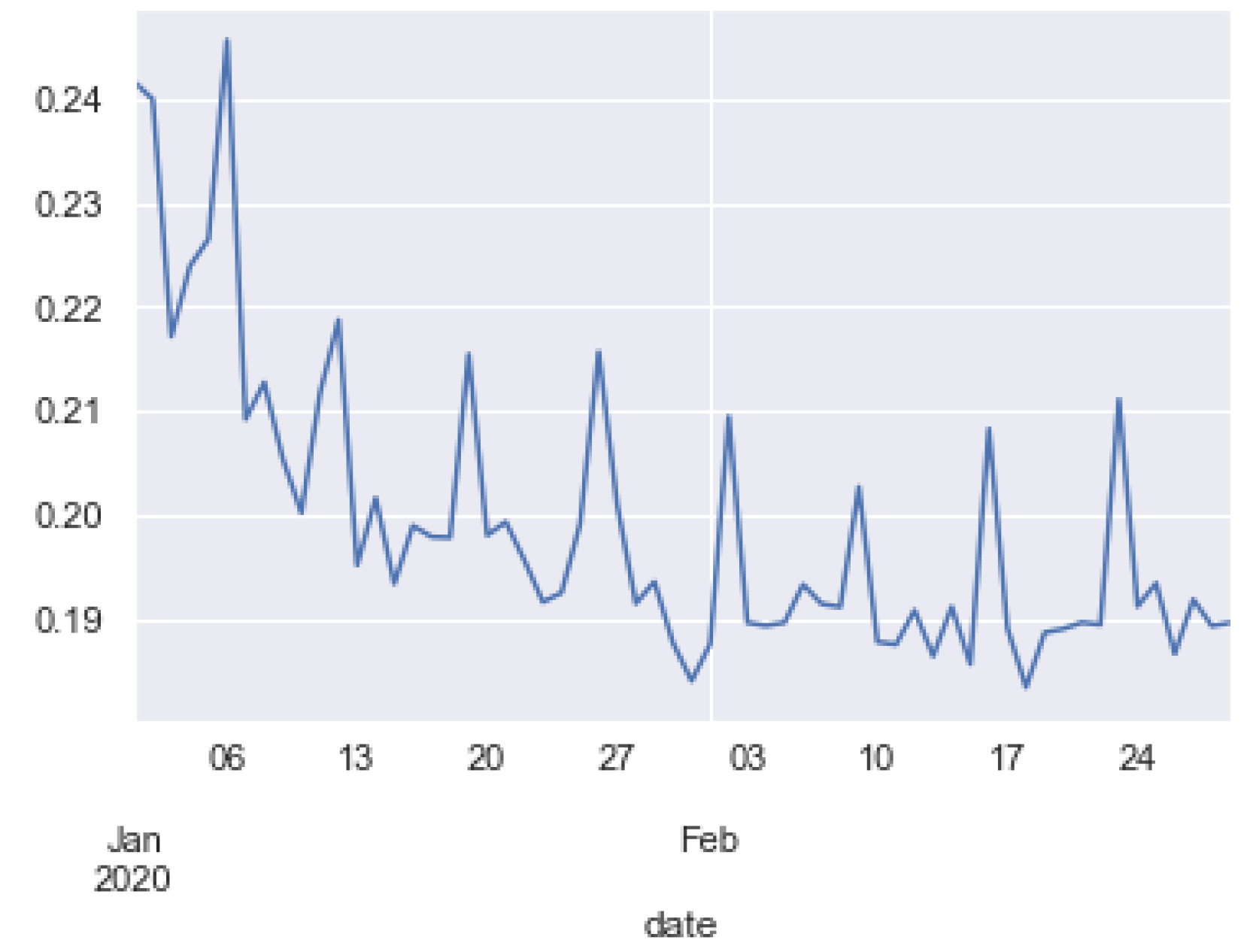
4. Results
- the calibration of the detour ratio function required to set up the parameters of ;
- the evaluation of the approximations implied by ;
- the determination of a reasonable individual data completeness threshold for selecting nonregular travellers used for mobility reconstruction.
4.1. Detour Ratio Calibration
4.2. Hybrid Distance Metric Evaluation
4.3. Sensitivity Analysis
4.4. Application Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Residents R: individuals living in the area covered by the antennas;
- Commuters C: individuals that live outside of the area but enter it on a frequent basis;
- Visitors V: individuals that mainly live and work outside of the area, but may visit the studied territory, either for touristic reasons with a dense stay, or from time to time with shorter stays.
Appendix A.1. A Binning Approach
- : the number of days of observation in the area;
- : the number of weekdays of observation in the area;
- : the number of nights with observation in the area;
- : the shortest stay (in number of consecutive days) observed over the historical period.
| Binning Rules | Role | |||
|---|---|---|---|---|
| Present at night | ||||
| Residents | or | and | or | present at day (w/ softer night condition) |
| or | or | has at least a long stay | ||
| Commuters | Present at day | |||
| and not a resident | ||||
| Visitors | User is not a resident | Other users | ||
| nor a commuter. |

Appendix A.2. Threshold Calibration
- the penetration rates of the mobile technology within and are identical;
- the penetration rates of the mobile technology within and are identical.
References
- Toch, E.; Lerner, B.; Ben-Zion, E.; Ben-Gal, I. Analyzing large-scale human mobility data: A survey of machine learning methods and applications. Knowl. Inf. Syst. 2018, 58, 501–523. [Google Scholar] [CrossRef]
- Bonnetain, L.; Furno, A.; El Faouzi, N.E.; Fiore, M.; Stanica, R.; Smoreda, Z.; Ziemlicki, C. TRANSIT: Fine-grained human mobility trajectory inference at scale with mobile network signaling data. Transp. Res. Part C Emerg. Technol. 2021, 130, 103257. [Google Scholar] [CrossRef]
- Paipuri, M.; Xu, Y.; González, M.C.; Leclercq, L. Estimating MFDs, trip lengths and path flow distributions in a multi-region setting using mobile phone data. Transp. Res. Part C Emerg. Technol. 2020, 118, 102709. [Google Scholar] [CrossRef]
- Seppecher, M.; Leclercq, L.; Furno, A.; Lejri, D.; Vieira da Rocha, T. Estimation of urban zonal speed dynamics from user-activity-dependent positioning data and regional paths. Transp. Res. Part C Emerg. Technol. 2021, 129, 103183. [Google Scholar] [CrossRef]
- Hoteit, S.; Chen, G.; Viana, A.C.; Fiore, M.C. Spatio-Temporal Completion of Call Detail Records for Human Mobility Analysis. In Proceedings of the Rencontres Francophones sur la Conception de Protocoles, l’Évaluation de Performance et l’Expérimentation des Réseaux de Communication, Quiberon, France, 29 May–2 June 2017. [Google Scholar]
- Chen, G.; Hoteit, S.; Carneiro Viana, A.; Fiore, M.; Sarraute, C. Enriching sparse mobility information in Call Detail Records. Comput. Commun. 2018, 122, 44–58. [Google Scholar] [CrossRef]
- Zhao, Z.; Koutsopoulos, H.N.; Zhao, J. Identifying Hidden Visits from Sparse Call Detail Record Data. Trans. Urban Data Sci. Technol. 2021, 1, 121–141. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Choudhury, C.F.; Wang, P.; González, M.C. Development of origin–destination matrices using mobile phone call data. Transp. Res. Part C Emerg. Technol. 2014, 40, 63–74. [Google Scholar] [CrossRef]
- Alexander, L.; Jiang, S.; Murga, M.; González, M.C. Origin–destination trips by purpose and time of day inferred from mobile phone data. Transp. Res. Part C Emerg. Technol. 2015, 58, 240–250. [Google Scholar] [CrossRef]
- Toole, J.L.; Çolak, S.; Sturt, B.; Alexander, L.P.; Evsukoff, A.; González, M.C. The path most traveled: Travel demand estimation using big data resources. Transp. Res. Part C Emerg. Technol. 2015, 58, 162–177. [Google Scholar] [CrossRef]
- Nanni, M.; Trasarti, R.; Furletti, B.; Gabrielli, L.; Van Der Mede, P.; De Bruijn, J.; De Romph, E.; Bruil, G. Transportation Planning Based on GSM Traces: A Case Study on Ivory Coast. In Proceedings of the Citizen in Sensor Networks, Barcelona, Spain, 19 September 2013; Nin, J., Villatoro, D., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 15–25. [Google Scholar]
- Çolak, S.; Alexander, L.P.; Alvim, B.G.; Mehndiratta, S.R.; González, M.C. Analyzing cell phone location data for urban travel: Current methods, limitations, and opportunities. Transp. Res. Rec. J. Transp. Res. Board 2015, 2526, 126–135. [Google Scholar] [CrossRef]
- Chen, G.; Viana, A.C.; Fiore, M.; Sarraute, C. Complete trajectory reconstruction from sparse mobile phone data. EPJ Data Sci. 2019, 8, 30. [Google Scholar] [CrossRef]
- Nilbe, K.; Ahas, R.; Silm, S. Evaluating the Travel Distances of Events Visitors and Regular Visitors Using Mobile Positioning Data: The Case of Estonia. J. Urban Technol. 2014, 21, 91–107. [Google Scholar] [CrossRef]
- Sikder, R.; Uddin, M.J.; Halder, S. An efficient approach of identifying tourist by call detail record analysis. In Proceedings of the 2016 International Workshop on Computational Intelligence (IWCI), Dhaka, Bangladesh, 12–13 December 2016; pp. 136–141. [Google Scholar] [CrossRef]
- Arai, A.; Fan, Z.; Matekenya, D.; Shibasaki, R. Comparative Perspective of Human Behavior Patterns to Uncover Ownership Bias among Mobile Phone Users. ISPRS Int. J. Geo-Inf. 2016, 5, 85. [Google Scholar] [CrossRef]
- Arai, A.; Witayangkurn, A.; Kanasugi, H.; Fan, Z.; Ohira, W.; Cumbane, S.; Miyazawa, S.; Ranjit, S.; Batran, M.; Shibasaki, R. Building a Data Ecosystem for Using Telecom Data to Inform the COVID-19 Response Efforts; Zenodo: Geneva, Switzerland, 2020. [Google Scholar] [CrossRef]
- Yang, H.; Ke, J.; Ye, J. A universal distribution law of network detour ratios. Transp. Res. Part C Emerg. Technol. 2018, 96, 22–37. [Google Scholar] [CrossRef]
- Furletti, B.; Gabrielli, L.; Renso, C.; Rinzivillo, S. Identifying Users Profiles from Mobile Calls Habits. In Proceedings of the ACM SIGKDD International Workshop on Urban Computing, Beijing, China, 12 August 2012; ACM: New York, NY, USA, 2012; pp. 17–24. [Google Scholar] [CrossRef]
- Furletti, B.; Gabrielli, L.; Renso, C.; Rinzivillo, S. Analysis of GSM calls data for understanding user mobility behavior. In Proceedings of the 2013 IEEE International Conference on Big Data, Santa Clara, CA, USA, 6–9 October 2013; pp. 550–555. [Google Scholar] [CrossRef]
- Gabrielli, L.; Furletti, B.; Trasarti, R.; Giannotti, F.; Pedreschi, D. City users’ classification with mobile phone data. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 1007–1012. [Google Scholar] [CrossRef]
- Mamei, M.; Colonna, M. Analysis of tourist classification from cellular network data. J. Locat. Based Serv. 2018, 12, 19–39. [Google Scholar] [CrossRef]
- Thuillier, E.; Moalic, L.; Lamrous, S.A.; Caminada, A. Clustering Weekly Patterns of Human Mobility Through Mobile Phone Data. IEEE Trans. Mob. Comput. 2018, 17, 817–830. [Google Scholar] [CrossRef]
- Seppecher, M. Mining Call Detail Records to Reconstruct Global Urban Mobility Patterns for Large Scale Emissions Calculation. Ph.D. Thesis, ENTPE, Univ. Gustave Eiffel, Univ. Lyon, Citepa, Paris, France, 2022. [Google Scholar]
- Song, C.; Qu, Z.; Blumm, N.; Barabasi, A.L. Limits of Predictability in Human Mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef]
- Lin, Z.; Lyu, S.; Cao, H.; Xu, F.; Wei, Y.; Samet, H.; Li, Y. HealthWalks: Sensing Fine-Grained Individual Health Condition via Mobility Data. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 1–26. [Google Scholar] [CrossRef]
- Jiang, S.; Fiore, G.A.; Yang, Y.; Ferreira, J.; Frazzoli, E.; González, M.C. A review of urban computing for mobile phone traces: Current methods, challenges and opportunities. In Proceedings of the UrbComp@KDD, Chicago, IL, USA, 11 August 2013. [Google Scholar]
- Candia, J.; González, M.C.; Wang, P.; Schoenharl, T.; Madey, G.; Barabási, A.L. Uncovering individual and collective human dynamics from mobile phone records. J. Phys. A Math. Theor. 2008, 41, 224015. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Calabrese, F.; Di Lorenzo, G.; Liu, L.; Ratti, C. Estimating Origin-Destination flows using opportunistically collected mobile phone location data from one million users in Boston Metropolitan Area. IEEE Pervasive Comput. 2011, 10, 36–44. [Google Scholar] [CrossRef]
- Armitage Cadavid, M.; Londoño Gomez, E.; Cancelado Sanchez, U.D.; Escobar Morales, G.; Perilla Galvis, D.M. Cali en cifras 2018–2019; Technical Report; Departamento Administrativo de Planeacion, Alcadia de Santiago de Cali: Santiago de Cali, Colombia, 2019.
- Möller, R. Movilidad de personas, transporte urbano y desarrollo sostenible en Santiago de Cali, Colombia. Ph.D. Thesis, Kassel University, Kassel, Germany, 2003. [Google Scholar]
- Ma, D.; Wu, X.; Sun, X.; Zhang, S.; Yin, H.; Ding, Y.; Wu, Y. The Characteristics of Light-Duty Passenger Vehicle Mileage and Impact Analysis in China from a Big Data Perspective. Atmosphere 2022, 13, 1984. [Google Scholar] [CrossRef]
- Guillon, N.; Wemelbeke, G.; Dubujet, F. Bilan Annuel des Transports en 2019: Bilan de la Circulation; Technical Report; Ministère Français de la Transition Ecologique: Paris, France, 2019.
- FHA. Highway Statistics; Technical Report; Federal Highway Adminstration, U.S. Department of Transportation: Washington, DC, USA. Available online: https://www.fhwa.dot.gov/policyinformation/statistics.cfm (accessed on 14 February 2022).
- Couronne, T.; Smoreda, Z.; Olteanu, A.M. Chatty Mobiles: Individual mobility and communication patterns. arXiv 2013, arXiv:1301.655. [Google Scholar]
- DANE. Proyecciones DE Población; Technical Report; Departamento Administrativo Nacional de Estadística: Bogota, Colombia, 2020.
- Metro Cali. Encuesta de Movilidad; Technical Report; Metro Cali S.A.: Santiago de Cali, Colombia, 2015.











| User ID | Base Station | Timestamp | Event Type | Technology | Emission/Reception |
|---|---|---|---|---|---|
| A | 09:10 | sms | 3G | incoming | |
| A | 09:20 | sms | 3G | outgoing | |
| A | 17:40 | call | 3G | outgoing | |
| A | 21:30 | data | 4G | incoming |
| User ID | Base Station | First Timestamp | Last Timestamp | # of Events |
|---|---|---|---|---|
| A | 09:10 | 17:40 | 3 | |
| A | 21:30 | 21:30 | 1 |
| Total Municipality | ||||||
|---|---|---|---|---|---|---|
| Jamundi | Yumbo | Cali Total | Urban Area | Rural Area | ||
| Population (mil.) | 2.72 | 0.13 | 0.13 | 2.46 | 2.43 | 0.03 |
| Area (km2) | 1434 | 632 | 234 | 569 | 123 | 446 |
| # of BS | 440 | 26 | 41 | 371 | 339 | 32 |
| # of BS per km2 | 0.36 | 0.04 | 0.18 | 0.65 | 2.79 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seppecher, M.; Leclercq, L.; Furno, A.; Vieira da Rocha, T.; André, J.-M.; Boutang, J. Identification of Aggregate Urban Mobility Patterns of Nonregular Travellers from Mobile Phone Data. Future Transp. 2023, 3, 254-273. https://doi.org/10.3390/futuretransp3010015
Seppecher M, Leclercq L, Furno A, Vieira da Rocha T, André J-M, Boutang J. Identification of Aggregate Urban Mobility Patterns of Nonregular Travellers from Mobile Phone Data. Future Transportation. 2023; 3(1):254-273. https://doi.org/10.3390/futuretransp3010015
Chicago/Turabian StyleSeppecher, Manon, Ludovic Leclercq, Angelo Furno, Thamara Vieira da Rocha, Jean-Marc André, and Jérôme Boutang. 2023. "Identification of Aggregate Urban Mobility Patterns of Nonregular Travellers from Mobile Phone Data" Future Transportation 3, no. 1: 254-273. https://doi.org/10.3390/futuretransp3010015
APA StyleSeppecher, M., Leclercq, L., Furno, A., Vieira da Rocha, T., André, J.-M., & Boutang, J. (2023). Identification of Aggregate Urban Mobility Patterns of Nonregular Travellers from Mobile Phone Data. Future Transportation, 3(1), 254-273. https://doi.org/10.3390/futuretransp3010015






