Calibration of the Microsimulation Traffic Model Using Different Neural Network Applications
Abstract
1. Introduction
2. Literature Review
3. Calibration Methods
3.1. Basic Premises of the Calibration Procedure
- P1
- Simulation resolution (time steps per simulation second) in the range {3, 9} by step 1;
- P2
- Number of observed proceeding vehicles in the range {2, 4} by step 1;
- P3
- Maximum looking ahead distance (m) in the range {100, 300} by step 1;
- P4
- Minimum looking ahead distance (m) in the range {0, 20} by step 1;
- P5
- Average standstill distance (m) in the range {1, 3} by step 0.1;
- P6
- Additive part of the desired safety distance (m) in the range {1, 5} by step 0.1;
- P7
- Multiplicative part of the desired safety distance (m) in the range {1, 6} by step 0.1;
- P8
- Desired speed in the range {30, 50} by step 10.
- Average standstill distance (ax)—defines the average desired distance between stopped cars (P5);
- Additive part of the desired safety distance (bx_add) (P6);
- Multiplicative part of the desired safety distance (bx_mult) (P7).
- Traveling time between the measurement points; and
- Queue parameters: maximum queue at the entrance (m), number of stoppings at the intersection entrance.
3.2. Comparison of the Different Methods of Computer Program Calibration
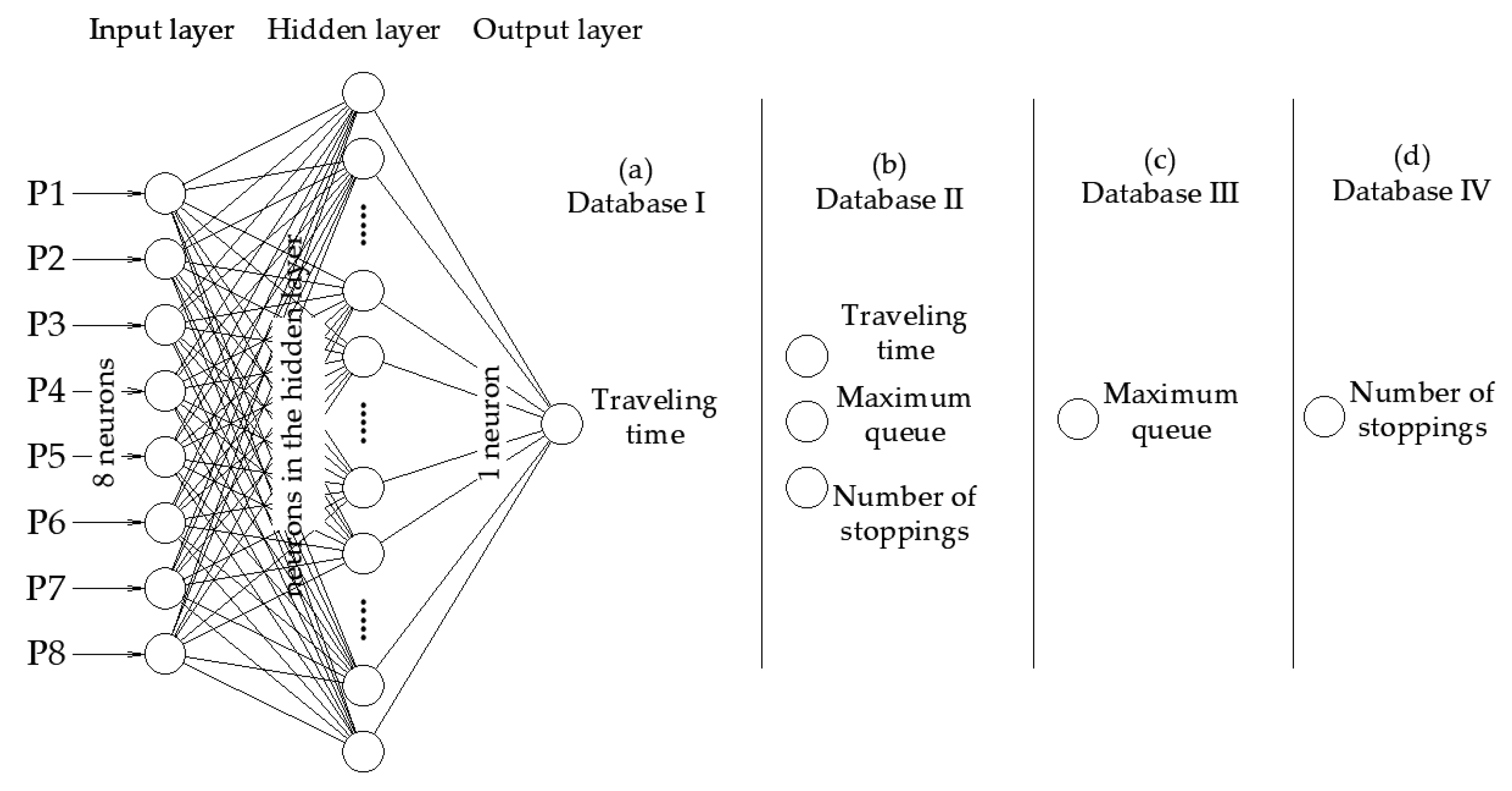
Use of Neural Networks Prediction of the VISSIM Simulation
- Database I: General regression type networks, one hidden layer with 5500 neurons, modified activation function in the logistic function, an iterative type of network (GR5500-logist IT) (Figure 3a);
- Database II: General regression type networks, one hidden layer with 2500 neurons, modified activation function in logistic function, an iterative type of network (GR2500-logist IT) (Figure 3b);
- Database III: General regression type networks, one hidden layer with 2500 neurons, scale function-non, genetic, adaptive type of network, genetic breeding pool size 100 (GR2500-non AD100) (Figure 3c);
- Database IV: General regression type networks, one hidden layer with 2500 neurons, scale function-non, genetic, adaptive type of network, genetic breeding pool size 100 (GR2500-non AD100) (Figure 3d).
4. Results
4.1. Testing of the Output Program Results in VISSIM
4.2. Methods Validation by Comparison of VISSIM Simulation Results and Measured Indicators
4.3. Statistical Comparison of the Raw Datasets of the Simulated and Measured Data
5. Discussion
6. Conclusions
- The first combination of input parameters values of Method I satisfied the statistical criteria set by expression (4) for all validation procedures;
- Results of the simulated values of the output indicator, travel time, satisfied the statistical criteria by expression (3) according to all methods; and
- Simulation results with default values of input parameters least corresponded with the measured values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flötteröd, G.; Bierlaire, M.; Nagel, K. Bayesian demand calibration for dynamic traffic simulations. Transp. Sci. 2012, 45, 541–561. [Google Scholar] [CrossRef]
- Shahdah, U.; Saccomanno, F.; Persaud, B. Application of traffic microsimulation for evaluating safety performance of urban signalized intersections. Transp. Res. Part C Emerg. Technol. 2015, 60, 96–104. [Google Scholar] [CrossRef]
- Llorca, C.; Moreno, A.T.; Lenorzer, A.J. Casas and A. Garcia. Development of a new microscopic passing manoeuvre model for two-lane rural roads. Transp. Res. Part C Emerg. Technol. 2015, 52, 157–172. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, X.; Liu, H.; Ren, G.; Zhang, Y.; Liu, X. Assessing the Influence of Adverse Weather on Traffic Flow Characteristics Using a Driving Simulator and VISSIM. Sustainability 2019, 11, 830. [Google Scholar] [CrossRef]
- Fang, X.; Li, H.; Tettamanti, T.; Eichberger, A.; Fellendorf, M. Effects of Automated Vehicle Models at the Mixed Traffic Situation on a Motorway Scenario. Energies 2022, 15, 2008. [Google Scholar] [CrossRef]
- Park, B.; Qi, H. Development and Evaluation of Simulation Model Calibration Procedure. Transp. Res Rec. 2005, 1934, 208–217. [Google Scholar] [CrossRef]
- Kim, S.J. Simultaneous Calibration of a Microscopic Traffic Simulation Model and OD Matrix. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2006. [Google Scholar]
- Paz, A.; Molano, V.; Martinez, E.; Gaviria, C.; Arteaga, C. Calibration of traffic flow models using a memetic algorithm. Transp. Res. Part C Emerg. Technol. 2015, 55, 432–443. [Google Scholar] [CrossRef]
- Chiappone, S.; Giuffrè, O.; Granà, A.; Mauro, R.; Sferlazza, A. Traffic simulation models calibration using speed–density relationship: An automated procedure based on genetic algorithm. Expert Syst. Appl. 2016, 44, 147–155. [Google Scholar] [CrossRef]
- Yu, M.; Wei, D.F. Calibration of microscopic traffic simulation models using metaheuristic algorithms. Int. J. Transp. Sci. Technol. 2017, 6, 63–77. [Google Scholar] [CrossRef]
- Sacks, J.; Rouphail, N.; Park, B.; Thakuriah, P. Statistically Based Validation of Computer Simulation Models in Traffic Operations and Management. J. Transp. Stat. 2002, 5, 1–24. [Google Scholar]
- Toledo, T.; Ben-Akiva, M.E.; Darda, D.; Jha, M.N.; Koutsopoulos, H.N. Calibration of microscopic traffic simulation models with aggregate data. Transp. Res. Rec. 2004, 1876, 10–19. [Google Scholar] [CrossRef]
- Cunto, F.; Saccomanno, F.F. Calibration and validation of simulated vehicle safety performance at signalized intersections. Accid. Anal. Prev. 2008, 40, 1171–1179. [Google Scholar] [CrossRef] [PubMed]
- Flötteröd, G.; Chen, Y.; Nagel, K. Behavioral calibration and analysis of a large-scale travel microsimulation. Netw. Spat. Econ. 2011, 12, 481–502. [Google Scholar] [CrossRef]
- Ištoka Otković, I.; Tollazzi, T.; Šraml., M. Calibration of microsimulation traffic model using neural network approach. Expert Syst. Appl. 2013, 40, 5965–5974. [Google Scholar] [CrossRef]
- Severino, A.; Pappalardo, G.; Curto, S.; Trubia, S.; Olayode, I.O. Safety Evaluation of Flower Roundabout Considering Autonomous Vehicles Operation. Sustainability 2021, 13, 10120. [Google Scholar] [CrossRef]
- Tollazzi, T.; Renčelj, M.; Turnšek, S. New type of roundabout: Roundabout with “depressed” lanes for right turning-“Flower roundabout”. Promet-Traffic Transp. 2011, 23, 353–358. [Google Scholar] [CrossRef]
- Pan, B.; Luo, S.; Ying, J.; Shao, Y.; Liu, S.; Li, X.; Lei, J. Evaluation and Analysis of CFI Schemes with Different Length of Displaced Left-Turn Lanes with Entropy Method. Sustainability 2021, 13, 6917. [Google Scholar] [CrossRef]
- Ištoka Otković, I. Using Neural Networks in the Process of Calibrating the Microsimulation Models in the Analysis and Design of Roundabouts in Urban Areas. Ph.D. Thesis, University of Maribor, Faculty of Civil Engineering, Maribor, Slovenia, 2011. [Google Scholar]
- Ištoka Otković, I.; Varevac, D.; Šraml., M. Analysis of neural network responses in calibration of microsimulation traffic model. Adv. Civ. Eng. 2015, 6, 67–76. [Google Scholar] [CrossRef]
- Hollander, Y.; Liu, R. The principles of calibrating traffic microsimulation models. TRANS 2008, 35, 347–362. [Google Scholar] [CrossRef]



| Authors | Traffic Network Segment | Software | Algorithm | Metric |
|---|---|---|---|---|
| Toledo et al.,2004 [12] | Intersections, freeways | MITSIMLab | Box’s complex algorithm | O–D flows, travel time |
| Park and Qi, 2005 [6] | Signalized intersection | VISSIM | Genetic algorithm | Travel time |
| Kim, 2006 [7] | Urban arterial and freeway | VISSIM | Genetic algorithm | Travel time and the O–D matrix |
| Cunto et al., 2008 [13] | Signalized intersections | VISSIM | Genetic algorithm | Vehicle tracking data |
| Ištoka Otković et al., 2013 [15] | Urban roundabouts | VISSIM | Neural networks | Travel time, queue parameters |
| Llorca et al., 2015 [3] | Two-lane rural roads | AIMSUN | Manual calibration procedure using mathematical tools | Passing maneuvers tracking data, traffic flow, percent followers and number of passing maneuvers |
| Paz et al., 2015 [8] | Arterial road links | CORSIM | Memetic algorithm | Vehicle count and speed |
| Chiappone et al., 2016 [9] | freeway | AIMSUN | Genetic algorithm | speed–density relationships |
| Yu and Wei, 2017 [10] | Urban freeway | VISSIM | Metaheuristic algorithms | Traffic flow and speed |
| Chen et al., 2019 [4] | Urban expressway | VISSIM | Experimental driving simulator data | Driving behavior data, speed |
| Severino et al., 2021 [16] | Flower roundabout | VISSIM | Statistical methods (GEH) | Traffic flow data |
| Pan et al., 2021 [18] | Intersection | VISSIM | Statistical method (MAPE) | Traffic flow data, capacity |
| Fang et al., 2022 [5] | Motorway | VISSIM | Programming code for the co-simulation framework | Average speed, traveltime, average delay |
| First Roundabout | Second Roundabout | |||
|---|---|---|---|---|
| 3 March 15:00–16:00 | 3 March 16:00–17:00 | 14 July 14:00–15:00. | 14 July 08:00–09:00 | |
| Mean value of traveling time (s) | 21.8 | 19.9 | 18.1 | 13.3 |
| Maximum queue (m) | 26 | 21 | 15.5 | 23 |
| Number of stops at the entrance | 89 | 61 | 54 | 56 |
| Methods | Database of VISSIM Simulations | Input Parameters | Output Traffic Indicators | Neural Network | Response of Neural Network (Correlations) 1 |
|---|---|---|---|---|---|
| Method I | Database I | 8 | 1 (Travel time) | 1 | 88% |
| Method II | Database II | 8 | 3 (Travel time, max. queue, no. of stops) | 1 | 83% 52% 45% |
| Method III | Database III | 8 | 1 (Max. queue) | 1 | 40% |
| Method IV | Database IV | 8 | 1 (No. of stops) | 1 | 52% |
| Method V | Database I, III and IV | 8 | 3 (Travel time, max. queue, no. of stops) | 3 | 88% 40% 52% |
| Combination of the Input Parameters | Neural Net. Prediction | VISSIM Result | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | T | T | Qmax | STOP |
| 6 | 4 | 164 | 8 | 2.4 | 2 | 3.3 | 40 | 21.267 | 20.8 | 25 | 86 |
| 6 | 4 | 172 | 8 | 2.4 | 1.9 | 3.4 | 40 | 21.303 | 20.8 | 25 | 90 |
| 6 | 4 | 172 | 8 | 2.4 | 1.9 | 3.5 | 40 | 21.295 | 20.9 | 25 | 89 |
| 6 | 4 | 172 | 8 | 2.5 | 1.9 | 3.3 | 40 | 21.295 | 20.8 | 25 | 86 |
| 6 | 4 | 172 | 12 | 2.4 | 1.9 | 3.4 | 40 | 21.271 | 20.8 | 25 | 90 |
| 6 | 4 | 172 | 12 | 2.4 | 1.9 | 3.5 | 40 | 21.264 | 20.9 | 25 | 89 |
| 6 | 4 | 172 | 12 | 2.5 | 1.9 | 3.3 | 40 | 21.283 | 20.8 | 25 | 86 |
| 6 | 4 | 173 | 8 | 2.4 | 1.9 | 3.4 | 40 | 21.298 | 21.1 | 25 | 85 |
| 6 | 4 | 173 | 12 | 2.4 | 1.9 | 3.4 | 40 | 21.298 | 21.1 | 25 | 85 |
| 6 | 4 | 175 | 8 | 2.5 | 1.9 | 3.5 | 40 | 21.262 | 21.0 | 25 | 85 |
| 6 | 4 | 176 | 8 | 2.4 | 1.8 | 3.5 | 40 | 21.275 | 21.4 | 27 | 88 |
| 6 | 4 | 176 | 8 | 2.5 | 1.8 | 3.4 | 40 | 21.273 | 20.9 | 27 | 90 |
| 6 | 4 | 176 | 12 | 2.5 | 1.8 | 3.4 | 40 | 21.273 | 20.9 | 27 | 90 |
| Combination of the Input Parameters | Neural Network Prediction | VISSIM Result | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | T | Qmax | STOP | T | Qmax | STOP |
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 3.8 | 40 | 20.18 | 24.72 | 80.13 | 20.9 | 25 | 87 |
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 4.0 | 40 | 20.20 | 24.72 | 80.16 | 20.8 | 25 | 87 |
| Combination of the Input Parameters | Neural Network Prediction | VISSIM Result | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | T | Qmax | STOP | T | Qmax | STOP |
| 9 | 2 | 247 | 8 | 2.1 | 2.7 | 4.3 | 40 | 20.94 | 24.71 | 85.31 | 20.8 | 27 | 88 |
| 9 | 2 | 266 | 8 | 2.1 | 2.8 | 4.3 | 40 | 20.94 | 24.71 | 85.31 | 21.0 | 25 | 86 |
| 9 | 2 | 272 | 8 | 2.1 | 2.9 | 4.2 | 40 | 20.93 | 24.71 | 85.96 | 21.3 | 25 | 87 |
| 9 | 2 | 264 | 8 | 2.1 | 2.8 | 4.2 | 40 | 20.93 | 24.71 | 85.96 | 20.9 | 25 | 85 |
| 9 | 2 | 254 | 8 | 2.1 | 2.8 | 4.3 | 40 | 20.92 | 24.751 | 85.31 | 20.8 | 25 | 87 |
| 9 | 2 | 264 | 8 | 2.1 | 3.1 | 4.3 | 40 | 20.92 | 24.71 | 85.31 | 21.3 | 25 | 91 |
| 9 | 2 | 255 | 8 | 2.1 | 2.7 | 4.2 | 40 | 20.92 | 24.71 | 85.96 | 21.3 | 25 | 86 |
| Input Parameters of the VISSIM Model | Traffic Indicators | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | T | Qmax | STOP |
| Measured Values | ||||||||||
| 19.9 | 21 | 61 | ||||||||
| Values Obtained by the VISSIM Model Simulations | ||||||||||
| Default Values of the Input Parameters | ||||||||||
| 5 | 2 | 250 | 0 | 2 | 2 | 3 | 40 | 20.3 | 15 | 60 |
| Method I | ||||||||||
| 6 | 4 | 176 | 8 | 2.4 | 1.8 | 3.5 | 40 | 19.8 | 22 | 58 |
| 6 | 4 | 173 | 8 | 2.4 | 1.9 | 3.4 | 40 | 20.2 | 15 | 63 |
| Method II | ||||||||||
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 3.8 | 40 | 19.9 | 19 | 63 |
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 4.0 | 40 | 20.0 | 15 | 55 |
| Method V | ||||||||||
| 9 | 2 | 272 | 8 | 2.1 | 2.9 | 4.2 | 40 | 20.2 | 15 | 57 |
| 9 | 2 | 255 | 8 | 2.1 | 2.7 | 4.2 | 40 | 19.6 | 15 | 52 |
| Input Parameters of the VISSIM Model | Traffic Indicators | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | T | Qmax | STOP |
| Measured Values | ||||||||||
| 18.1 | 15.5 | 54 | ||||||||
| Values Obtained by the VISSIM Model Simulations | ||||||||||
| Default Values of the Input Parameters | ||||||||||
| 5 | 2 | 250 | 0 | 2 | 2 | 3 | 40 | 17.6 | 23 | 50 |
| Method I | ||||||||||
| 6 | 4 | 176 | 8 | 2.4 | 1.8 | 3.5 | 40 | 17.6 | 15 | 52 |
| 6 | 4 | 173 | 8 | 2.4 | 1.9 | 3.4 | 40 | 17.8 | 15 | 53 |
| Method II | ||||||||||
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 3.8 | 40 | 17.6 | 24 | 46 |
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 4.0 | 40 | 17.5 | 24 | 44 |
| Method V | ||||||||||
| 9 | 2 | 272 | 8 | 2.1 | 2.9 | 4.2 | 40 | 18.0 | 24 | 50 |
| 9 | 2 | 255 | 8 | 2.1 | 2.7 | 4.2 | 40 | 18.3 | 24 | 52 |
| Input Parameters of the VISSIM Model | Traffic Indicators | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | T | Qmax | STOP |
| Measured Values | ||||||||||
| 13.3 | 23 | 56 | ||||||||
| Values Obtained by the VISSIM Model Simulations | ||||||||||
| Default Values of the Input Parameters | ||||||||||
| 5 | 2 | 250 | 0 | 2 | 2 | 3 | 40 | 13.1 | 27 | 50 |
| Method I | ||||||||||
| 6 | 4 | 176 | 8 | 2.4 | 1.8 | 3.5 | 40 | 13.1 | 22 | 58 |
| 6 | 4 | 173 | 8 | 2.4 | 1.9 | 3.4 | 40 | 13.1 | 22 | 54 |
| Method II | ||||||||||
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 3.8 | 40 | 13.6 | 21 | 62 |
| 9 | 4 | 250 | 0 | 2.1 | 3.1 | 4.0 | 40 | 13.7 | 21 | 64 |
| Method V | ||||||||||
| 9 | 2 | 272 | 8 | 2.1 | 2.9 | 4.2 | 40 | 13.6 | 20 | 63 |
| 9 | 2 | 255 | 8 | 2.1 | 2.7 | 4.2 | 40 | 13.6 | 22 | 65 |
| Default | Method I | Mathod II | Method V | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | Queue | Time | Queue | Time | Queue | Time | Queue | ||||||||||||||
| T | Qmax | STOP | T | Qmax | STOP | T | Qmax | STOP | T | Qmax | STOP | ||||||||||
| 1 1 | 2 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | ||||
| Calibration | ✕ | ✕ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Validation I | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✕ | ✓ | ✓ | ✕ | ✕ | ✕ | ✕ |
| Validation II | ✓ | ✕ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✕ | ✕ | ✓ | ✓ | ✕ | ✕ | ✕ | ✓ |
| Validation III | ✓ | ✕ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✕ | ✕ |
| Optimal Values of the VISSIM Model Input Parameters | |
|---|---|
| 6 |
| 4 |
| 176 |
| 8 |
| 2.4 |
| 1.8 |
| 3.5 |
| 40 |
| N | Mean | StDev | Median | Min | Max | A–D Test | p-Value | |
|---|---|---|---|---|---|---|---|---|
| Measured | 135 | 21.8 | 6.046 | 21.00 | 12.00 | 43.00 | 2.952 | <0.005 |
| Simulated | 135 | 21.4 | 5.875 | 20.00 | 12.00 | 40.00 | 4.306 | <0.005 |
| StDev | Ratio | Variance | Ratio | |
|---|---|---|---|---|
| Measured | 6.046 | 1.029 | 36.549 | 1.059 |
| Simulated | 5.875 | 34.510 |
| Method | Statistic Test | p-Value | CI for StDev Ratio | CI for the Variance Ratio |
|---|---|---|---|---|
| Bonett | 0.06 | 0.806 | 0.816; 1.302 | 0.666; 1.695 |
| Levene | 0.43 | 0.514 | 0.857; 1.369 | 0.735; 1.874 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ištoka Otković, I.; Tollazzi, T.; Šraml, M.; Varevac, D. Calibration of the Microsimulation Traffic Model Using Different Neural Network Applications. Future Transp. 2023, 3, 150-168. https://doi.org/10.3390/futuretransp3010010
Ištoka Otković I, Tollazzi T, Šraml M, Varevac D. Calibration of the Microsimulation Traffic Model Using Different Neural Network Applications. Future Transportation. 2023; 3(1):150-168. https://doi.org/10.3390/futuretransp3010010
Chicago/Turabian StyleIštoka Otković, Irena, Tomaž Tollazzi, Matjaž Šraml, and Damir Varevac. 2023. "Calibration of the Microsimulation Traffic Model Using Different Neural Network Applications" Future Transportation 3, no. 1: 150-168. https://doi.org/10.3390/futuretransp3010010
APA StyleIštoka Otković, I., Tollazzi, T., Šraml, M., & Varevac, D. (2023). Calibration of the Microsimulation Traffic Model Using Different Neural Network Applications. Future Transportation, 3(1), 150-168. https://doi.org/10.3390/futuretransp3010010










