Winter Road Friction Estimations via Multi-Source Road Weather Data—A Case Study of Alberta, Canada

Abstract

Road friction has long been recognized as one of the most effective winter road maintenance (WRM) performance measures. It allows WRM personnel to make more informed decisions to improve their services and helps road users make trip-related decisions. In this paper, a machine-learning-based methodological framework was developed to model road friction using inputs from mobile road weather information systems (RWIS) that collect spatially continuous road weather data and road grip. This study also attempts to estimate friction using data from stationary RWIS that are installed far from each other, thereby leaving large areas unmonitored. To fill in the spatial gaps, a kriging interpolator was developed to create a continuous friction map. Slippery road risk levels were classified to provide an overview of road conditions via a risk warning map. The proposed method was evaluated with a selected highway segment in Alberta, Canada. Results show that the models developed herein are highly accurate (93.3%) in estimating friction and identifying dangerous road segments via a color-coded risk map. Given its high performance, the developed model has the potential for large-scale implementation to facilitate more efficient WRM services while also improving the safety and mobility of the traveling public.

1. Introduction

Every year, snowfall and freezing rain create adverse road conditions that severely hinder both traffic mobility and safety, the main culprit being slippery road surfaces due to snow and ice buildup. During times like these, drivers choose to travel at significantly lower speeds out of concern that they will not be able to stop in a timely manner [1,2]. Research shows that the traveling speed is reduced by 30–40% on snowy or slushy pavement [2], resulting in up to 50% increase in travel delays [3]. One would expect that a reduction in traveling speed could result in safety improvements, but unfortunately, this is not the case. Vehicle collisions during the winter typically increase by 3.1–4.7% [4], and it was also found that 27.7% of all casualty collisions occurred on roads covered with slush, snow, or ice [5]. Therefore, it is critical that jurisdictions actively combat winter weather through well-organized maintenance operations.

Recognizing the importance of proactively combating adverse road conditions, countries that experience winter weather allocate significant capital toward winter maintenance operations (WRM) to improve mobility and public wellbeing. The U.S. state governments, for instance, currently allocate roughly 20% of their maintenance budget to WRM, with over $2.3 billion spent annually on snow and ice control operations [6]. Given its high cost, transportation agencies have long been searching for cost-effective strategies to maximize the return of investment [7]. One necessary component in creating such a strategy is the availability of spatially diverse road surface conditions (RSC) information. RSC information allows maintenance personnel to understand the state of their road network and develop an effective treatment strategy. However, before jurisdictions can start collecting RSC information en masse, they must first select an appropriate RSC measure. Currently, there are several methods of describing RSC: visual indicators, time to normal (or bare pavement regain time), traffic speed regain time, and road friction levels [8]. Visual indicators are easy to comprehend but very subjective and are not continuous measurements. In comparison, the time-to-normal and traffic speed regain times are continuous measurements but do not account for road conditions during inclement weather events. Among the various methods, road friction is the most adopted and intuitive; defined as the rubbing of vehicles’ tires against the road, it provides continuous and non-subjective measurements, expressed as the coefficient of friction ranging from 0 to 1. In addition, friction measurements during and after a storm events can further be used to measure road maintenance performance. Due to its popularity, it was chosen as the measurement of choice in this study.

Upon choosing a representative RSC measure (road friction in our case), the next step is determining a measurement method. Most jurisdictions collect road friction values manually, providing a limited amount of information because the collection process is not only time-consuming but also labor-intensive. By definition, the road friction can be affected by various factors including, but not limited to the texture of tires and pavement, and the contaminants on road surface [9]. Besides, it has also been found that road friction is highly dependent on environmental factors [10,11,12,13,14,15,16,17,18], which can subsequently be estimated using weather information from Road Weather Information Systems (RWIS) [19]. RWIS has been considered one of the most important highway intelligent transportation system (ITS) infrastructures as it provides real-time weather, environmental, and generalized road conditions information. There are two main types of RWIS: stationary RWIS (sRWIS) and mobile RWIS (mRWIS). Variable values from sRWIS are continuously monitored by the various environmental sensor stations (ESS) installed, resulting in high-quality long-term data measurements. However, these stations do not provide road friction measurement directly and suffer from coverage issues due to the large spacing between adjacent stations. Therefore, mRWIS equipped with road friction measurement gauges are commonly used to supplement the information collected by sRWIS. As the mRWIS travels along the network, it provides spatially continuous measurements of road friction values and the surrounding weather/environmental conditions. Nevertheless, given that the mRWIS has to travel through the road network, data collected suffer from time lag due to travel time, leading to temporal gaps between adjacent data points. To obtain a temporally stable and spatially continuous measure of road friction values, a method that makes use of both stationary and mobile RWIS data is of significant importance.

With accurate road weather data, previous investigations have implemented diverse approaches to the estimation of road surface friction. The Finnish meteorological society and road administration proposed a road friction classification by determining friction intervals based on road surface contaminates (i.e., wet ice, icy, packed snow, rough ice/packed snow, clear and wet, and clear and dry) [20], where the road friction estimation was derived by following a proposed criterion based on weather elements, such as air temperature, precipitation, humidity, and wind. Ilkka [21] applied a linear regression analysis to develop an estimation model but the simple linear assumption was insufficient to capture the varying road conditions. As such, this method was later improved by introducing three sub-models based on three different road surface conditions: snow and ice, water, and dry. On snow and ice, and water laden roads, the depth of these moisture deposits was the main contributing factor for reduced friction, whereas on dry roads, the friction was considered as a constant of 0.82. In another study [22], a non-parametric supervised learning algorithm (k-nearest neighbor (k-NN)) was applied to classify road surface conditions into dry, wet, salty-wet, and icy. The model’s accuracy reached 90%, demonstrating the efficiency of the developed model for classifying road surface conditions. Takasaki [23] classified road surface into dry, wet, slushy, and snowy to estimate road surface snow conditions with combined weather conditions and traffic volume. The model was constructed by random forest, with an accuracy of 95%. However, the road condition classification methods mentioned above are based on individual visual assessment which is subjective and unconvincing. Unlike the previous studies, Minges [24] developed two Neural Network (NN) models, where one used vehicle sensor data and the other added road weather data on top of vehicle sensor data. Their results showed that adding weather information increased accuracy by 3.7%, illustrating the impact of including weather data for road friction estimations. The issue with this approach is that the NN algorithm is a black-boxed method that lacks transparency and cannot be easily vetted.

Although these aforementioned friction estimation studies contributed immensely to deepening our understanding of how frictions can be inferred, they mostly focused on model development and lacked discussions or examples of their practical applications. In addition, no prior studies have yet to attempt to use multi-source weather data to further improve the accuracy of the model performance, and more importantly, an easy-to-implement winter road risk map that both road users and winter road maintenance personnel can use to make more informed trip and maintenance related decisions. Therefore, this paper proposes innovative method for developing a road friction model throughout a road network using multi-source weather data. First, a regression tree model was developed using mRWIS collected environmental and friction data to determine which RWIS factors provide the most accurate road friction estimates. Next, the selected factors were extracted from the sRWIS and spatially interpolated to generate continuous environmental data. Finally, the sRWIS interpolated data are inputted into the friction model developed in the first step to create a friction map of the entire study area. Ultimately, the goal is to obtain an accurate spatially continuous road friction map solely based on sRWIS data that maintenance agencies can use to plan, manage, and assess their work.

2. Study Area

The province of Alberta lies between 49° and 60° north latitude and 110° and 120° west longitude with a total area of 661,848 km². Alberta’s northerly location makes it prone to Arctic weather systems, leading to extreme winter conditions. The movement of fronts between air masses leads to rapidly changing arctic air masses that can produce extreme temperatures as low as −54 °C.

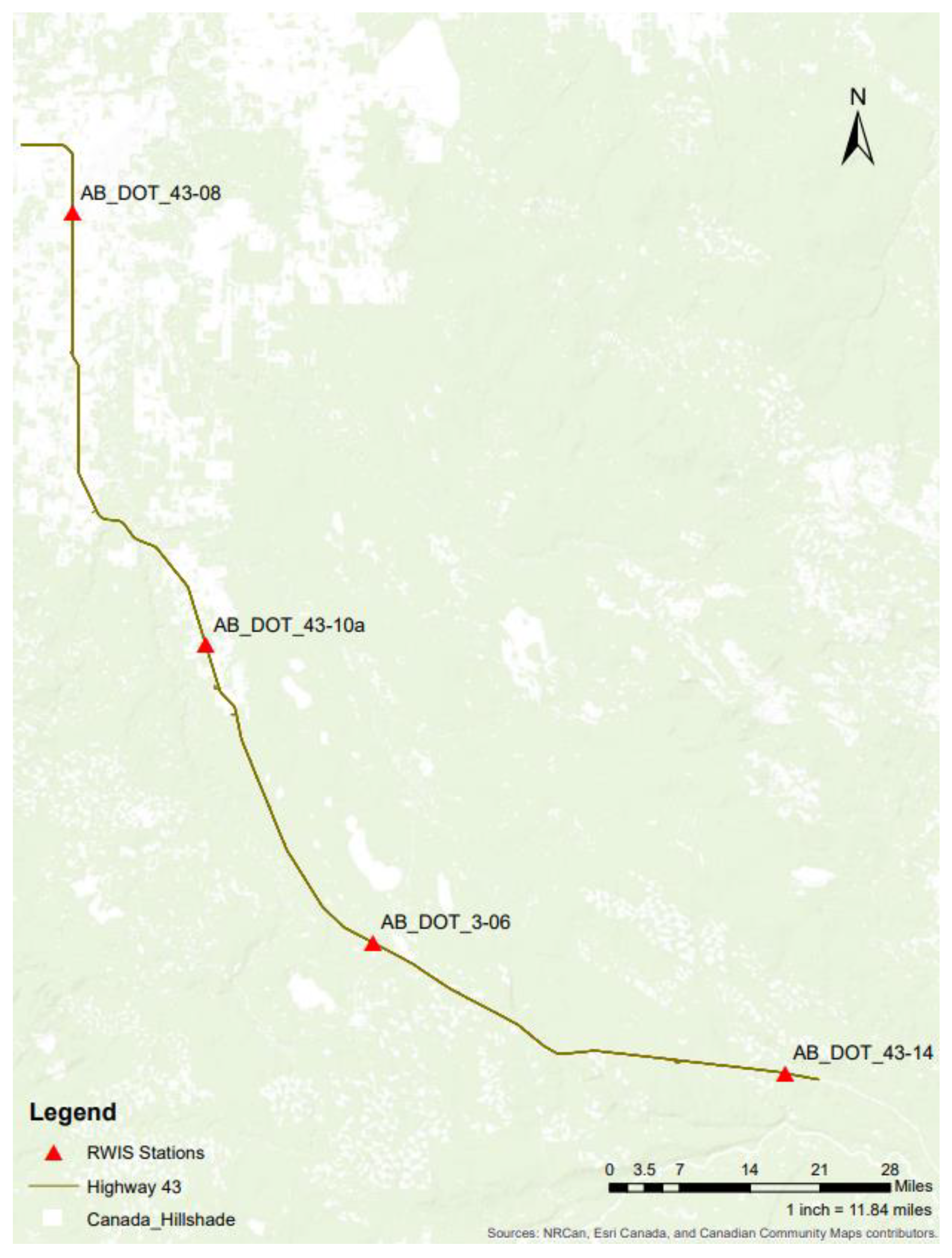
The study area is a 127 km segment of Highway 43 between Valleyview and Whitecourt that runs from the northeast to the southwest. Currently, there are 4 RWIS stations evenly deployed along this route: AB_DOT_43-08, AB_DOT_43-10a, AB_DOT_3-06, and AB_DOT_43-14 as illustrated in Figure 1 below. This highway segment was selected as the study area for its high geographic variation (i.e., vegetation, terrain types, and altitude) and data distribution along the road segment.

3. Data Description

The data used in this study comes from both mobile RWIS (mRWIS) and stationary RWIS (sRWIS). The testing vehicle was equipped with non-invasive Vaisala Condition Patrol DSP 310 to collect mRWIS data every 3 s, including air temperature, relative humidity, dewpoint, surface temperature, water depth, snow depth, ice depth, and friction that are all time and location tagged. Road surface states (i.e., layer thickness and friction) in particular, were measured by the remote sensor DSC111 that uses the spectroscopic measuring principle to collect road condition information. Since it is costly and laborious to collect mRWIS data, the data used in this paper were collected in one direction only during inclement weather events that occurred between November 2014 and February 2015, with 93,101 data points in total. Meanwhile, sRWIS recorded its environmental data every 20 min at their respective locations. Environmental data collected includes air temperature, average wind speed, average wind direction, dewpoint temperature, relative humidity, 1 h precipitation, 3 h precipitation, surface temperature, water depth, freeze point, and maximum and minimum temperatures as well as its station ID and data recording times with a total of 7344 sRWIS data points collected and used in this study. Because sRWIS data are used for friction estimation, to compare with actual values, the data extracted from the sRWIS stations matched the date, time, and location of the mRWIS passing by; therefore, sRWIS data between 5 and 7 p.m. on 22 November 2014 were selected for model application.

The two RWIS data sources were used for separate purposes. The mRWIS data was used to develop and calibrate the friction estimation model by using the collected environmental data with the corresponding friction outcome. The sRWIS data was then employed to evaluate the model’s applicability by providing weather information to spatial interpolate friction values. It is important to note that there are some subtle differences in the measurement values between mRWIS and sRWIS due to differences in measurement technique and sensor mounting locations. For example, sRWIS are slower in measuring changes in surface temperatures as their sensors are embedded into the ground, whereas mRWIS sensors are installed on the vehicle above the road surface. This difference results in a ±1 °C difference in recorded temperature values. Therefore, care should be taken to ensure data consistency when comparing mobile and stationary RWIS data. Additionally, only matching variables recorded by both RWIS formats were used as input model parameters. These variables are latitude, longitude, altitude, air temperature, relative humidity, dewpoint, surface temperature, and water depth. The friction value from mRWIS is used as the target variable in the modeling process.

Among the weather factors collected by both forms of RWIS, temperature has a remarkable effect on friction. If the temperature drops below 0 °C, any rain or thin snow layer will turn into ice, drastically decreasing road surface friction. Another critical parameter is dewpoint—the temperature at which water vapor in the air turns into dew or frost deposits. If the temperature is below dewpoint, moisture will form on the road surface, causing a decrease in road friction. Besides temperature and dewpoint, relative humidity is also important, as higher humidity levels mean a higher likelihood of precipitation, resulting in friction-reducing precipitant on the road surface. In addition to these weather factors, geography also contributes to the changes in friction. Since the amount of solar radiation reaching the surface lessens towards the poles, a higher latitude region will experience lower air temperatures than lower altitudes. Furthermore, local temperatures also vary vertically because higher altitudes receive less ground radiation and experience less insulation, causing temperatures to decrease by about 9.8 °C every 1000 m above sea level. As such, these variables are used to model highly accurate and spatially rich road surface frictions.

4. Methodology

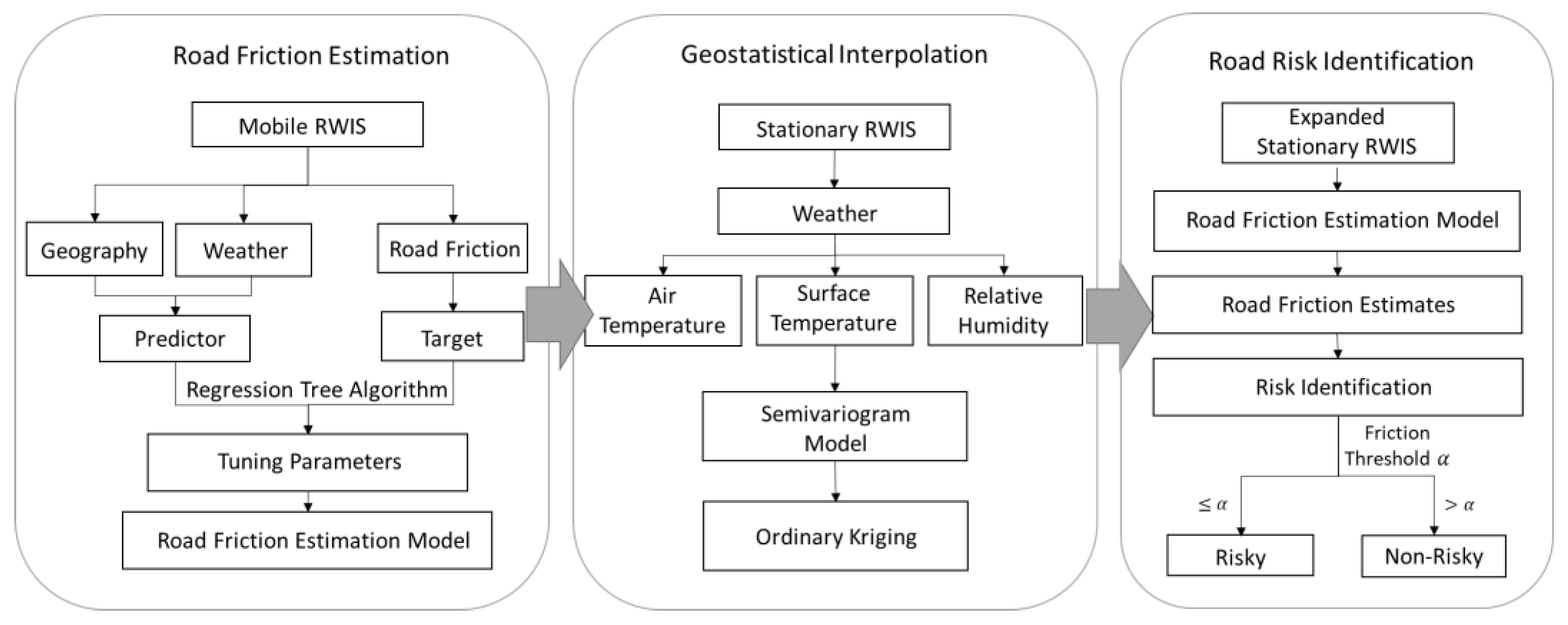
Our proposed methodology contains three parts: first, a friction estimation model with geographical and weather factors was created using all mRWIS data collected on Alberta highways. To assess the validity and feasibility of the model, sRWIS data were substituted into the model to generate friction estimates, which were then compared to the original mRWIS measured values. The rest of the report uses this highway 43 segment as the main study area. In part two, spatially discontinuous sRWIS data were interpolated using one of the most adopted kriging variants, called Ordinary Kriging (OK). The interpolated environmental values were then inputted into the model developed in part one to generate spatially continuous friction estimates. In the final part of the study, the friction estimates were visualized as a friction prediction road map. We then categorized the friction estimates as either risky or non-risky as the general public may not understand the theory behind friction coefficients. Based on the risk classification, the estimation accuracy was calculated through a confusion matrix to determine the accuracy of the models developed herein. Frictions that were both measured and estimated to be at risk were marked as True Risky (TR), while those that were not at risk were marked as True Non-risky (TN), and the corresponding other two types are False Risky (FR) and False Non-risky (FN). The accuracy was then calculated by dividing the sum of TR and TN by all instances.

The overall workflow and key steps are illustrated in Figure 2.

4.1. Regression Tree

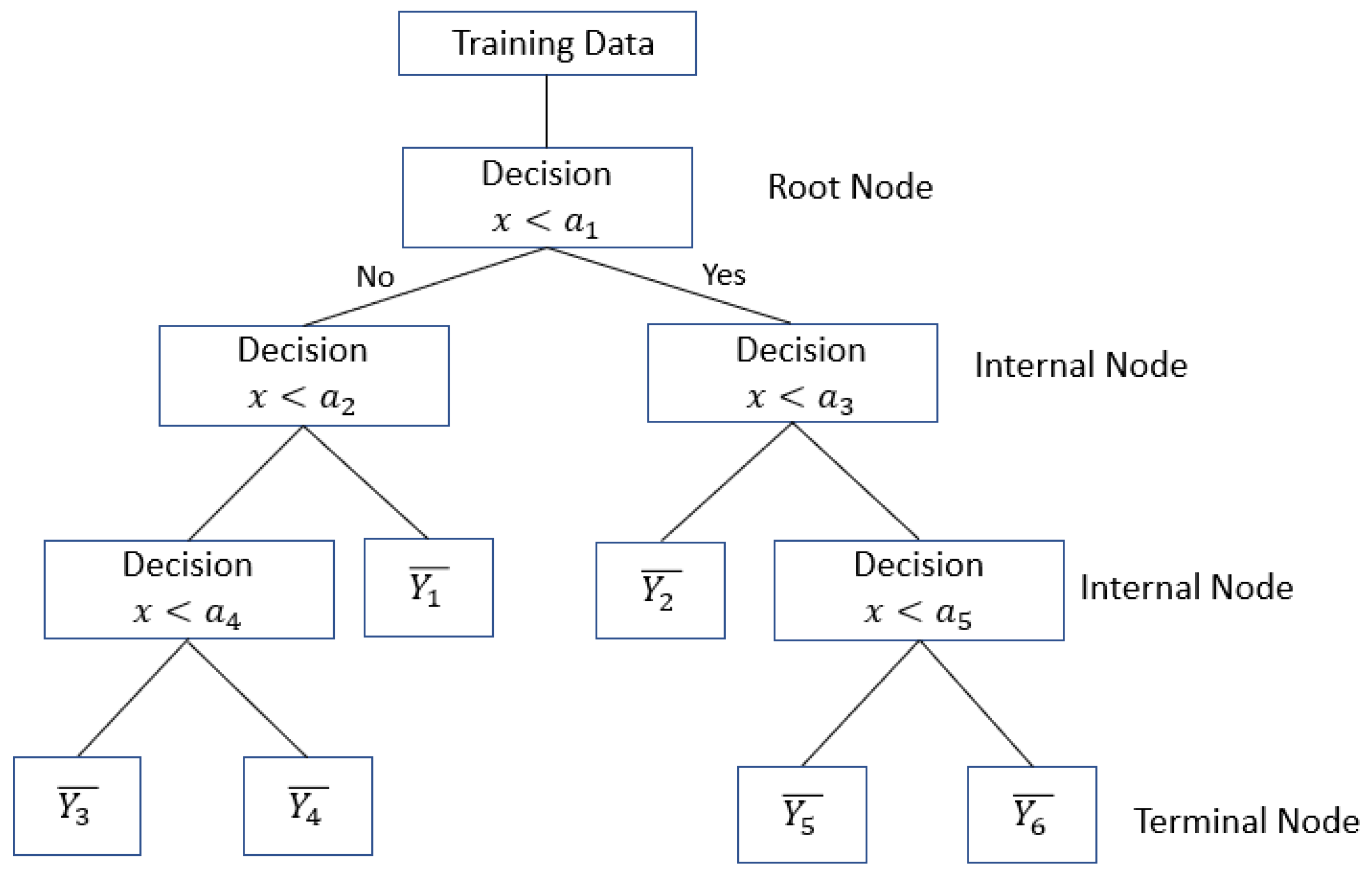
The modeling technique used in this study is the regression tree. As the name suggests, this method models the relationship between inputs and outputs similar to tree growth, as shown in Figure 3. The dataset is separated into two subsets at the root node according to different conditions. Data that satisfies the corresponding condition flows to the following internal node, where another condition exists to split the data further. Eventually, the tree will stop growing because of growth restrictions. The main advantages of using a regression tree are that it is intuitive, non-parametric, and the decision criteria are visible and easy to interpret.

The splits of regression tree are determined by a traverse approach with least square error criterion. The decision condition at each node, including an input feature and a split value, is selected by calculating the minimum residual sum of squares between observations and the mean. This process is expressed as Equations (1) and (2).

$$mi{n}_{j,s}\left[mi{n}_{c1}{\sum }_{x_i\in R_1\left(j,s\right)}{\left(y_i-c_1\right)}^2+mi{n}_{c2}{\sum }_{x_i\in R_2\left(j,s\right)}{\left(y_i-c_2\right)}^2\right],$$

(1)

$$c_m=ave(y_i|x_i\in R_m)$$

(2)

where $j$ is the split feature, $s$ is the split value, $R_1 and R_2$ are subsets divided by condition $\left(j,s\right)$, $c_m$ is the mean of subset $R_m$, $x_i and y_i$ are observations.

Despite its many advantages, the regression tree has an inherent flaw; it is prone to overfitting. As such, model parameters should be tuned carefully to avoid this issue, which are maximum depth, minimum samples split, and minimum samples leaf. Maximum depth refers to the model complexity. The deeper the tree, the more information it captures. Minimum sample split determines the minimum number of samples that are required to split an internal node; a split will not happen if there are less than a certain number of records specified by this parameter. Finally, the minimum samples leaf determines the minimum number of samples at the leaf node. To determine reasonable values for these parameters, the grid search algorithm was applied, which is an exhaustive search method that iterates through all possible parameter candidates to find the most optimal configuration. In this study, we used $r^2$ as the performance selection criteria based on prior studies [25,26].

4.2. Kriging Interpolation

The goal of spatial interpolation is to estimate values at unsampled points using observed data points. Among the many spatial interpolation methods available, kriging has been shown to produce the most accurate estimates [27,28,29]. The kriging estimates consist of deterministic trends and residuals. Ordinary Kriging (OK) [30] is one variant of kriging that is considered the most widely employed among all the Kriging methods due to its simplicity and high accuracy. For this reason, OK has been selected in this study. OK assumes an unknown but constant mean over the area. This model can be expressed as Equation (3).

$$Z\left(s\right)=\mu +\epsilon \left(s\right)$$

(3)

where μ is the unknown constant, and $\epsilon \left(s\right)$ is the residual. Similar to Inverse Distance Weighting (IDW) method, weights are needed in kriging to estimate values at unknown points. However, the difference is that the primary assumption of kriging is spatial autocorrelation, implying an internal spatial relationship between sample points. Kriging weights therefore depend on both the distance between observations and prediction location and the overall spatial arrangement of the observations. Hence, the objective of OK interpolation is to determine the optimal kriging weights that minimize the estimation variance. The OK estimate is calculated by Equation (4):

$$\widehat{Z}\left(s\right)=\mu +{\displaystyle \sum }_{i=1}^N{\lambda }_i\left[Z\left(s_i\right)-m\left(s_i\right)\right]$$

(4)

where $\widehat{Z}\left(s\right)$ is OK estimate, $Z\left(s_i\right)$ is the observation at location $s_i$, ${\lambda }_i$ is the unknown Kriging weight for the observation at location $s_i$, $s$ is the location for estimation, $N$ is the number of observations, and $m\left(s_i\right)$ is the expected values of $Z\left(s_i\right)$.

Semivariance represents the reciprocal of the spatial autocorrelation, which is calculated using Equation (5).

$$\gamma \left(h\right)=\frac{1}{2}{\left[z\left(x_i\right)-z\left(x_j\right)\right]}^2$$

(5)

where $\gamma \left(h\right)$ is the semivariance between sample points $x_i$ and $x_j$ in $h$ distance, and $z$ is the feature value. An empirical semivariogram is generated using Equation (5) to explore the spatial autocorrelation pattern of the observations. Afterward, several theoretical models are considered to fit the empirical semivariogram model. These include circular, spherical, exponential, gaussian, and linear models. The fitted semivariogram model provides three spatial parameters: sill, range, and nugget [28]. The sill is the semivariance at which the model begins to plateau, and the range is the lag distance where the semivariance reaches the sill, beyond which the spatial autocorrelation is considered non-existent. Finally, the nugget is the spatial variability at a distance smaller than the shortest distance between observations, often termed measurement error.

5. Case Study

5.1. Road Friction Estimation Model

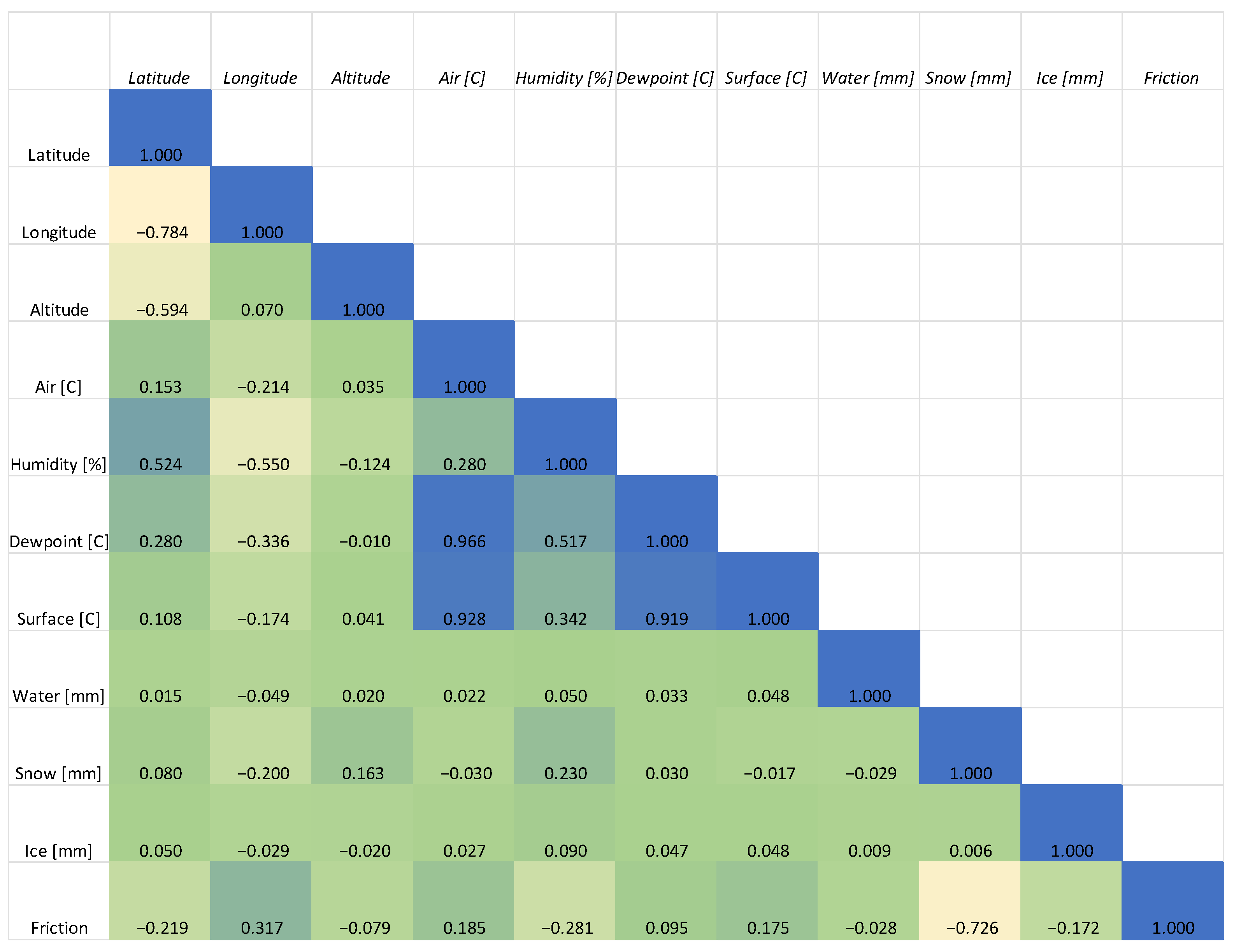
Before calibrating the model, it is essential to select a predictor with a strong relationship to friction. Thus, a correlation matrix was generated with all the potential predictors to find the relationships between each variable pairing (see Figure 4).

From the correlation matrix, snow depth has the strongest correlation with friction at −0.73, which intuitively makes sense as road surface slipperiness increases as snow layers get thicker. However, sRWIS in this study area does not collect snow depth values, so it cannot be implemented in the model. Longitude has the second highest correlation at 0.32, suggesting that the friction values generally increase with longitude. Relative humidity and latitude also have a strong but negative correlation with friction, meaning that the increase in these values lead to a reduction in friction, which is logically consistent. Air and surface temperature have a similar positive correlation with friction. Other than the factors previously mentioned, there are some factors with weak correlations less than 0.10: dewpoint temperature, altitude, and water depth. These highly correlated variables are then inputted in a stepwise manner based on the correlation matrix to calibrate the regression tree model. Since variables with low correlation (less than 0.1) contribute little to improving model accuracy, dewpoint temperature and water depth were omitted. Nevertheless, we kept altitude as it is a geographic predictor. To summarize, the model has road friction as the target variable and longitude, latitude, altitude, air temperature, relative humidity, and surface temperature as predictor variables.

For model calibration, the mRWIS data was randomly split into a training set with 74,480 data points and a testing set containing the remaining data. After finetuning, the following parameters were chosen: max depth of 26, minimum samples leaf of 2, and minimum samples split of 7. The model’s accuracy reached 93.3%, suggesting that the model’s performance was more than adequate. The validity of the model was then tested by making friction estimates using sRWIS measured predictor values and then comparing the predictions to the mRWIS measured friction values. This validation process requires using friction measurements close to the sRWIS station. In addition, the collected data needs to satisfy temporal consistency. Otherwise, the predictor variable values from sRWIS may differ significantly from the mRWIS due to potential spatial heterogeneity. Figure 5 illustrates the friction estimates from the four sRWIS stations along with its actual measurement from the nearby mRWIS. As shown, the estimations are fairly close to the measured values, especially for station AB_DOT_3-06, where the estimation error is only 0.005 with station AB_DOT_43-08’s estimation error being relatively higher at 0.14.

5.2. Spatial Interpolation via Ordinary Kriging

This step is the generation of spatially continuous friction estimates to fill in the gaps between stations, providing greater details on the distribution of road surface friction values. In particular, the proposed method takes friction values measured at an sRWIS location and interpolate friction records between each pair of sRWIS using previously developed tree-based friction model. In this study, spatial interpolation using Ordinary Kriging (OK) was performed to estimate the weather information in-between sRWIS stations.

As mentioned earlier, the estimation results between sRWIS and mRWIS are not identical. To properly evaluate the model performance and measure the estimation error of the model, the impact of the data inconsistency should be eliminated or at least minimized. This requires us to create a surrogate sRWIS by averaging the data collected from an mRWIS taken within a pre-defined buffer zone road surface (i.e., 400 m in our case upon reviewing the similarity of measured values) around an actual sRWIS. Doing so will remove the inherent measurement inconsistencies between the two RWIS types, allowing for more accurate and fair model validation. A total of 39 mobile data points were selected as testing points to evaluate the model and interpolation process. OK was then applied to air temperature (AT), surface temperature (ST), and relative humidity (RH) using Esri’s ArcGIS [31,32,33], which can tune the semivariogram parameters automatically via its built-in model optimization function. The semivariogram parameters from the optimized models for each weather factor are listed below (see Figure 6).

The semivariogram values for each of the three environmental factors provide insight into their spatial autocorrelation. For air temperature (AT), the nugget is zero, indicating that there is no inherent measurement error found, a rare but ideal outcome. The range and sill indicate that autocorrelation exists until 43 km and the maximum semivariance is 0.604. Relative humidity (RH) also has a small nugget that is approximately 0, a long range of almost 30 km, and a large sill of 12. As for the surface temperature (ST), it has a relatively large nugget value, a small range, and a small sill at 0.226, 240 m, and 0.433, respectively. The parameter values for ST make sense as they are significantly influenced by the local ground radiation, surrounding vegetation, solar exposure, and the amount of traffic driving over that location. The differences between the semivariograms are also intuitive as the atmospheric variables (air temperature and relative humidity) tend to be more stable over larger expanses than ground-based variables. The constructed semivariogram model values were then used to estimate each weather factor along the highway segment. The interpolated estimates were then compared to the observed values from the mRWIS and plotted in Figure 7 and their associated descriptive statics are provided in

Table 1. Descriptive statistics of weather parameters.

	Air Temperature		Relative Humidity		Surface Temperature
	Measured	Predicted	Measured	Predicted	Measured	Predicted
Mean	−2.49	−2.47	89.37	89.65	−3.45	−3.38
Std. Dev.	1.05	0.93	2.10	1.33	1.36	1.18
Min	−5.00	−4.10	84.00	86.00	−9.30	−7.57
Max	0.70	−1.40	97.00	93.00	−1.50	−2.20
Obs.	1588		1588		1588

.

Based on the interpolated vs. observed plots shown above, it can be asserted that OK was able to capture general variations over large distances (20 km) with some sections having less accurate predictions, possibly due to inherent local variations. An example of this limitation is seen between 3 km (where AD_DOT_43-14 locates) and 20 km. Actual AT and ST values fluctuate drastically with peaks, and RH trends opposite, while their predicted values follow a similar trend but are much smoother. This is because kriging produces smooth estimates by taking an average to offset the variation between high and low values.

5.3. Road Friction Estimation

To estimate the road friction throughout the area, the spatially interpolated weather factors and geographic features generated in the previous step were inputted into the regression tree model to produce friction estimates for the entire study area. Estimations were made at 20 m resolution. However even at high accuracy the model can hardly predict exact the same value as measured, so the estimates were aggregated every 1.0 km intervals on the road to reduce variance and make the results more realistic when plotted. A comparison plot between the estimated and actual friction is shown in Figure 8.

Figure 8 suggests that the estimated and measured friction curves closely resemble one another, especially at the 16 km to 61 km and the 111 km to 121 km segments. However, there are also regions with moderate differences, such as the 0 km to 11 km stretch. Minor discrepancies like this are likely because the input variable themselves are not measured values but estimates with error. The predicted air and surface temperature were lower than the actual measurements, while the estimated relative humidity was higher than the measured values. Since friction is positively correlated with temperature and negatively correlated with humidity, the estimated friction is lower than the actual value. The differences seen at 70 km to 76 km can be similarly explained except in the opposite direction.

While most discrepancies can be explained as a product of interpolation error propagating from the previous step, for locations between 85 km and 94 km, the difference is quite significant and cannot be attributed to predictor interpolation error. Deeper scrutiny revealed that the measured snow depth drastically changes within this region, from 1.2 mm to 0 mm. This 1.2 mm difference represents a change from being snow-covered to bare pavement due to snow depth information being not accounted for in the modeling process as sRWIS does not collect snow depth data. The same logic can be applied to 89 km, where the snow depth increased by 1 mm, resulting in a sharp friction value drop. Likewise, at the 91 km to 94 km section, where snow depth fluctuates between 0.4 mm and 1 mm, a similar friction fluctuation between 0.2 and 0.6 was observed. Based on these observations, snow depth accumulation may be a strong indicator of friction values. Nonetheless, the OK interpolation model developed has proven to capture the general road surface conditions patterns with help of just four sRWIS data points—the first of its kind in existing literature.

5.4. Road Risk Identification

5.4.1. Binary System

Providing only friction values has little meaning to the general public as it is challenging for them to grasp the safety implications between the friction values. For this reason, we simplify our friction outputs by classifying them as either risky or non-risky for the purpose of creating a color-coded risk map. Previous studies have suggested several cutoff values for when friction values are considered unsafe, which can range from 0.3 to 0.5 [34,35,36,37,38]. In this study, we consider three cutoffs within this interval: 0.3, 0.4, and 0.5 to categorize respective driving risks. The estimated road risk accuracies calculated at $Threshold=0.3, 0.4, and 0.5$ are $84.25\%, 89.76\%, and 88.98\%$, respectively. Regardless of the selected threshold, the accuracy of road risk estimation is near 90%; hence, our developed model is highly accurate.

Figure 9 illustrates the risk map at the three different thresholds based on measured and predicted friction. The risky segments are marked in red, and the non-risky sections are marked in green. Between the three risk maps of predicted friction, the identified risky sections are remarkably similar, with the only exception being two short road sections identified as risky when 0.4 and 0.5 are used as the threshold. Compared to the risk map generated with the ground truth (measured values), our predicted risk map is more conservative as it increases the length of the road segments considered risky. Although we would like our predictions to be identical to the observed, it is inevitable that errors will persist. In this case, it is much better to have false positives where non-risky are reported as risky than the reverse; the repercussions associated with reporting a risky road as non-risky are significantly higher.

5.4.2. Three-Category System

The benefit of using a binary classification system is that it is easy to understand, but this benefit comes at the cost of reducing the amount of information presented. Although general road users may appreciate its simplicity, maintenance personnel may desire more detailed information. Hence, we increased the risk categories to three to give a more comprehensive view of RSC along the road network. The three-category system is as follows: friction below 0.3 is high risk, medium risk is between 0.3 and 0.5, and low risk is above 0.5—intervals that have been generally accepted and thus used in existing literature.

Figure 10 illustrates the risk warning map of measured and predicted friction under this classification system, with red, amber, and green representing high, medium, and low risk, respectively. The accuracy based on this classification is 77.95%, which was lower than the binary system, but the model still had acceptable performance. Most of the prediction errors (18.90%) are False Risky (FR), where non-risky road sections are classified as risky, implying that our model is conservative in its predictions, which does not compromise safety.

The color-coded map provides a risk level along the select highway segments, which can be highly informative in practical applications. For instance, by providing real-time road condition estimations via online platforms (e.g., 511), trip makers will be able to adjust their travel plans and divert accordingly to avoid potential accidents and traffic delays. Likewise, this tool, once refined and tested with more data, can also be integrated into vehicle to everything (V2X) technologies [39,40,41] to provide real-time road surface conditions information for improved safety before, during, and after inclement weather events. Such information can also be utilized by winter road maintenance personnel as the maps would provide information pertaining to dangerous road sections so that maintenance vehicles could be dispatched in a more efficient and timely manner to perform location-specific and targeted maintenance operations to ensure the safety and mobility of the winter travelling public.

6. Conclusions

Road slipperiness is a safety hazard that increases the risk of collisions and reduces overall network efficiency. Having a good assessment of the friction levels throughout a network can provide maintenance personnel with valuable information to streamline their tasks. The general public can also use the same information to plan their trips to avoid high-risk road sections. However, measuring friction is often done manually and takes significant time and effort. Thus, this study looks to make use of existing RWIS infrastructure to make estimates of road friction levels throughout a network without the need for manual inspection.

In this study, we developed a road friction estimation model and then combined it with spatial interpolation to maximize its estimation potential. The model made use of weather and geographic predictors already being collected by existing RWIS installations to showcase the model’s applicability and the usefulness of an RWIS network. A case study was carried out on a segment of Alberta Provincial Highway 43 in Alberta, Canada, to demonstrate the feasibility of the proposed method and to illustrate friction variation throughout a road segment. The main findings are as follows:

• A friction estimation model was calibrated using the regression tree algorithms, with weather and geographic factors as input features. The correlation matrix suggested road friction is positively correlated with air temperature, surface temperature, and longitude; and negatively correlated with relative humidity, latitude, and altitude. The features at decision nodes shown in the model visualization were in the same order as the correlation rank. The high model accuracy rate of 93.3% shows that road friction can be explained by weather and geography.
• Ordinary Kriging, a geostatistical interpolation method, was employed to predict features at unsampled locations between sRWIS stations. The OK interpolations were similar mRWIS measurements despite certain discrepancies due to the omission of snow depth and predictor estimation error.
• Road risk map was produced based on estimated road friction and defined risk level. OK was adopted to generate continuous weather information. These interpolated weather data was then inputted into the friction estimation model to obtain a road friction map. Risk thresholds of 0.3, 0.4, and 0.5 were chosen to categorize friction as risky and non-risky. The validation accuracy reached 84.25%, 89.76%, and 88.98% for three different thresholds in increasing order.
• By increasing the number of risk categories to three, high (<0.3), medium (0.3–0.5), and low (>0.5), we were able to generate a more comprehensive risk map with a 77.95% accuracy. The prediction errors consisted mostly of False Risky (18.90%) and low False Non-risky (3.15%), indicating our developed model is conservative and advantageous from a safety perspective.
• The results obtained show that the proposed framework is robust and feasible. By generating a road friction estimation map, maintenance departments can deliver more comprehensive assessments of road conditions to road users and make their own operation more efficient.

However, this study is not without its limitations. The most evident one is the availability of dataset. The dataset used in this study does not capture parameters including snow depth, which could potentially contribute to improving the model performance. As mentioned earlier, the absence or presence of snow on the road surface has a strong correlation with road friction, meaning friction notably decreases with increasing snow depth and vice versa. In addition, there is a lack of consideration of traffic attributes, as heat from heavy traffic is known to increase road surface temperature and thus affect road surface conditions (e.g., making snow-covered roads slushy). Furthermore, limited sample size results in the insufficient spatial coverage of the data, thereby restricting model performance to local areas with reduced transferability potential. Although geographical characteristics have been taken into consideration to improve the spatial representation of variables under investigation, use of more datasets covering large areas could further improve the conclusiveness as well as the transferability of the findings documented herein.

Future research is therefore required to address the limitations mentioned above. First, the study area can be expanded to include wider spatial coverage and more available factors such as snow depth which is a measurable factor in sRWIS, although not available in this study area. Hence, it is critical to implement more spatiotemporally comprehensive datasets that can capture the diversity of geographical and topographical characteristics, and how they would affect road surface conditions. In addition, traffic volume and winter road maintenance activities should be considered to account for the influence of human activities. Likewise, more advanced variants of kriging interpolation techniques such as network kriging or regression kriging should be adopted to test and further improve interpolation accuracy. Lastly, sensitivity analysis should be performed to examine the effects other external factors (e.g., sample size, model parameters, etc.) have on model outcome.”