Deployment of an Automated Method Verification-Graphical User Interface (MV-GUI) Software

Abstract

Clinical laboratories frequently conduct method verification studies to ensure that the process meets quality standards for its intended use, such as patient testing. They play a pivotal role in healthcare, but issues such as accurate statistical assessment and reporting of verification data often make these studies challenging. Missteps can lead to false conclusions about method performance, risking patient safety or leading to incorrect diagnoses. Despite a requirement for accredited labs to document method performance, existing solutions are often expensive and complex. Addressing these issues, we present Method Verification-Graphical User Interface (MV-GUI), a software package designed for ease of use. It is platform-independent, capable of statistical analysis, and generates accreditation-ready reports swiftly and efficiently. Users can input patient data from one or more .CSV files, and MV-GUI will produce comprehensive reports, including statistical comparison tables, regression plots, and Bland–Altman plots. While method validation, which establishes the performance of new diagnostic tools, remains a crucial concern for manufacturers, MV-GUI primarily streamlines the method verification process. The software aids both medical practitioners and researchers and is designed to be user-friendly, even for non-experienced users. Requiring no internet connection, MV-GUI can operate in restricted IT environments, making method verification widely accessible and efficient.

1. Introduction

Method verification is described as a one-time process completed to assess the performance attributes of a test system prior to its usage in clinical routine [1]. It is usually carried out in clinical laboratories, especially when a clinical laboratory buys new equipment or procedure, to ensure that it is performing according to the manufacturer’s specifications.

Conversely, method validation is associated with the assessment of the performance of novel diagnostic instruments. These may include internally devised analyte-specific procedures, reagents, or self-developed laboratory information systems [1]. For approval from regulatory bodies such as the US Food and Drug Administration (US FDA [2]), Die Schweizerische Kommission für Qualitätssicherung im medizinischen Labor (QUALAB [3]), Clinical and Laboratory Standards Institute (CLSI [4]), conformité européenne (CE [5]: French for “European conformity”), and others, manufacturers are obliged to validate their devices and procedures before market release [6].

Method verification in a clinical laboratory is very important [7] as it (a) ensures the accuracy and reliability of test results, thus avoiding incorrect test results that could lead to misdiagnosis and have serious consequences for patients, (b) maintains the credibility of the laboratory by consistently obtaining reliable results and thus gaining the trust of healthcare providers and patients.

The method verification routine follows several crucial steps, recommended in most guidelines [8]. They are:

• Reviewing the method in terms of its purpose, sample preparation, instrumentation, and procedure.
• Planning and setting up the method verification experiment according to instructions, with necessary calculations or preparations.
• Analyzing collected data to ascertain if the method performs as expected and fulfills acceptance criteria [1,8,9,10,11,12].
• Establishing quality control procedures for ensuring consistently accurate results, complemented by ongoing monitoring.
• Documenting the entire method verification process—from purpose to samples, results, and adjustments—for quality control and regulatory compliance.

Different types of statistical methods are employed to assess method verification [13], particularly for steps 3 and 4. However, the minimum criteria often involve accuracy (trueness/result uncertainty), precision, and reportable range [14,15].

Numerous statistical methods of varying complexity are employed, including but not limited to:

• Simple descriptive statistics such as mean, median, variance, and standard deviation, which provides a quick overview of data.
• Coefficient of Variation (CV), a measure of the relative precision of a method.
• D’Agostino–Pearson test, a statistical test assessing whether a set of measurements follows a normal distribution [16].
• Bias, a measure of the systematic error in a measurement method.
• Measurement uncertainty, an estimate of the range within which the true value of the measure is likely to lie.
• Correlation methods such as Spearman, Pearson, and Kendall’s tau, used to evaluate the association between two measurement methods.
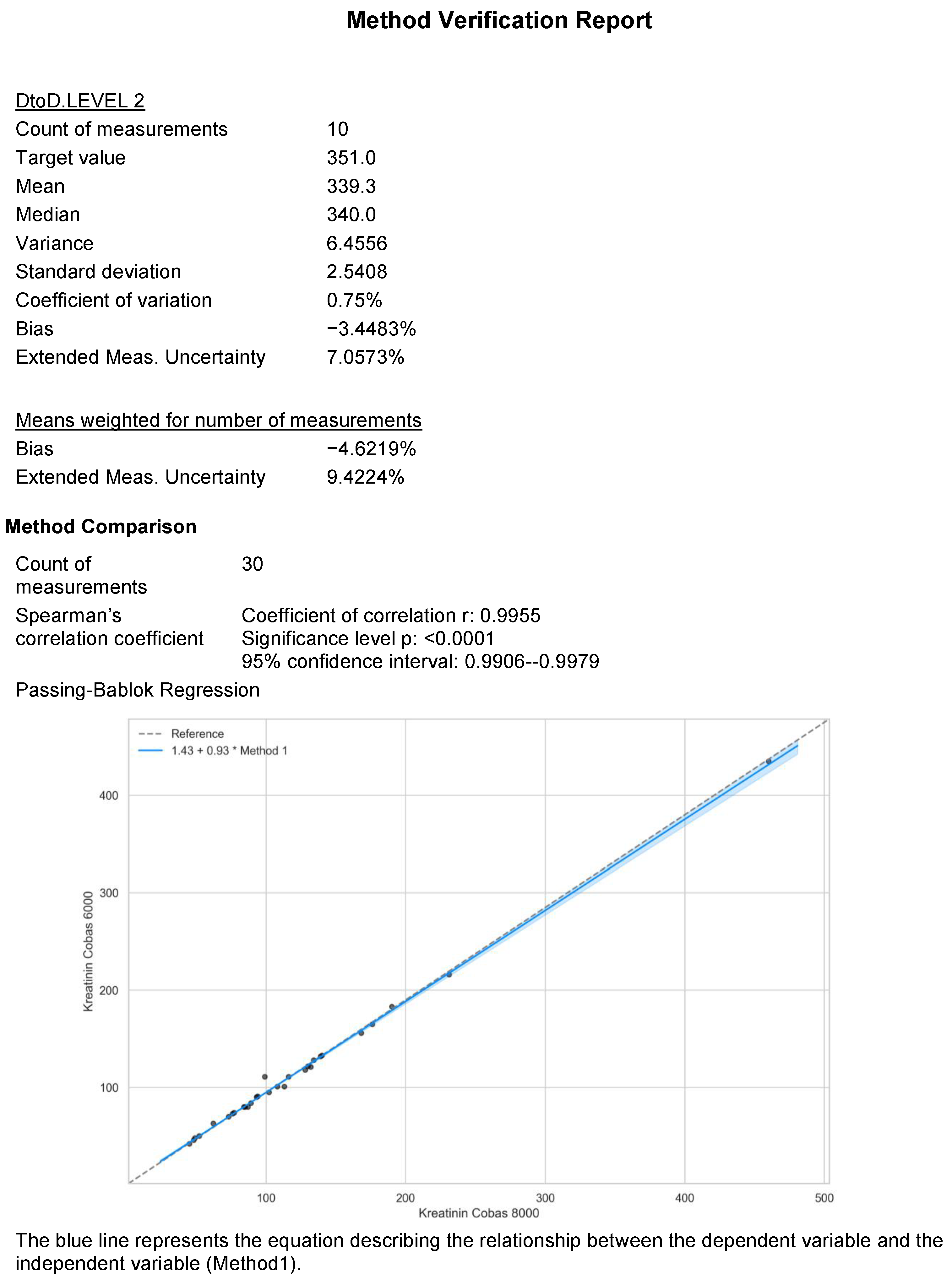
• Scatter plots, which visualize the relationship between two measurement methods, and Passing–Bablok regression, used to fit a line of best fit to the data in the scatter plot.
• Difference plots using Bland–Altman, a technique for evaluating the agreement between two measurement methods.

The outcomes from the aforementioned steps are meticulously documented in a comprehensive report. This report provides an overview of the method verification process, highlighting steps ensuring accuracy and reliability, actions addressing identified issues, and implications of the verification results for patient care.

The application of statistical methods in practice often requires various computer applications. Although numerous statistical analysis tools are readily available, a limited number of pharmaceutical/medical researchers and practitioners have the time and/or financial resources to proficiently learn to use applications such as SAS, Stata, and MedCalc, or to master statistical computing using open-source software packages such as R and Python [17]. Commercial software platforms such as labanalytics.de and analyse-it.com provide a vast array of features and functionality, yet their use is gated by their purchase requirement. Consequently, medical professionals and researchers in the pharmaceutical field tend to favor open-access graphical user interfaces, which are readily accessible at no cost. Commercial software can pose limitations, particularly for individuals or organizations operating on limited budgets. Hence, the provision of open-access software emerges as a highly sought-after solution for these practitioners and researchers who require efficient and affordable data analysis methods.

Within this framework, our study introduces an initiative to automate the third, fourth, and fifth steps of the method verification routine. We have built a standalone Graphical User Interface (GUI) with a statistical backend that is proficient in performing statistical analyses, generating regression and Bland–Altman plots, and producing reports prepared for accreditation. This significantly expedites the process of method verification. It is essential to underscore that the designed software package specifically caters to method verification routines and is not configured for method validation, which requires adaptable statistics that present challenges for automation.

2. Materials and Methods

2.1. MV-GUI User Interface

The MV-GUI has been meticulously designed to provide an easy-to-use platform to streamline the process of method verification. As demonstrated in Figure 1, MV-GUI boasts a single-page layout for easy navigation and comprehension. It offers two main tabs: ‘Select .CSV file/s’ to choose input files and a ‘Show report’ tab for report visualization. The user has the flexibility to select one or multiple .CSV files containing experimental data.

Upon selecting a single file that is pre-filled with the respective data, the backend Python script extracts necessary information, performs necessary calculations, and presents the result on the GUI panel. For multiple files, a report is generated for each without a GUI display. The ‘Show report’ tab allows the user to view any previously prepared .PDF report on the GUI panel.

Statistical Analysis

Statistical analysis is a crucial component of the method verification process, allowing us to quantitively assess the performance of the method. This analysis operates in the backend of our software, utilizing a Python script (‘main.py’) that executes a series of statistical calculations and tests.

The first set of calculations includes the mean, median, and variance of the measurement data. These simple descriptive statistics provide a quick overview of the central tendency and dispersion in the data, which are fundamental elements for understanding the behavior of the method.

The software then calculates the Coefficient of Variation (CV), which is a measure of the relative precision of a method. The CV is particularly useful in method verification as it provides insight into the repeatability and reproducibility of the method, hence its reliability.

Furthermore, the software performs the D’Agostino–Pearson test, a robust statistical test that assesses whether a set of measurements follows a normal distribution. This information is critical for method verification as many statistical tests and procedures assume a normal distribution of the data.

The Python script also calculates the standard deviation, a measure of the dispersion or variability in the data. It complements the mean by providing an understanding of the spread of the data points around the mean. Moreover, the bias is computed to measure the systematic error in a measurement method. In contrast, the measurement uncertainty gives an estimate of the range within which the true value of the measure is likely to lie.

In terms of correlational analysis, the software calculates correlation and confidence intervals using Spearman, Pearson, or Kendall’s tau coefficients. Correlation methods are used to evaluate the degree of association between two measurement methods, offering insights into their agreement.

To provide a graphical representation of the relationship between two measurement methods, the software generates scatter plots using Passing–Bablok regression. In addition, it creates difference plots using the Bland–Altman technique. These plots are instrumental in visualizing the agreement between the two measurement methods, aiding the interpretation of the statistical analysis results.

Altogether, these statistical analyses provide a comprehensive assessment of the method’s performance attributes, facilitating its verification. By automating these analyses, our software simplifies the method verification process, making it more efficient and accessible to clinical laboratories.

2.2. MV-GUI Design Philosophy

The core design philosophy of MV-GUI rests on simplicity and usability. An intuitive, easy-to-use GUI eliminates the need for extensive documentation or prior knowledge. It minimizes the learning curve and maximizes productivity.

Portability is also a vital aspect of the design philosophy. It refers to the ease with which a program written for one computer system can be readily used on another system. Open-source software trumps proprietary software in portability as it allows developers and researchers to examine, repurpose, and contribute to the product’s development, making computational methods more accessible to a wider audience.

Hence, the MV-GUI has been designed using open-source programs such as Python and Tkinter, keeping it minimalistic with just two tabs: one to select the .CSV file with the experimental values and the other to display the .PDF reports.

2.3. Implementation Details

MV-GUI is delivered as a plug-and-play software package available in .APP (Figure 2) and .EXE (Figure 3) formats for macOS and Windows, respectively. Upon double-clicking these files, the GUI opens up and allows the user to enter the essential information.

The backend Python script performs the required statistical analyses for method verification. The summary of the statistical tools utilized for method verification in our platform is listed in

Table 1. Summary of the statistical tools utilized in the script.

Statistical Tool	Where Used in Script	Description
Descriptive Statistics (Mean, Median, Variance, Standard Deviation, Coefficient of Variation)	Series.fmean(), Series.fmedian(), Series.fvar(), Series.fstd(), Series.fcv()	Calculates the central tendency, dispersion, and relative variability of a series.
Bias and Measurement Uncertainty Calculation	Series.fbias(), Series.fmu()	Computes systematic deviation from a target value and estimates the expected deviation from the true value.
Normality Tests (D’Agostino–Pearson, Kolmogorov–Smirnov, Shapiro–Wilk)	Series.fnt(), Series.fks(), Series.fsw()	Assesses if a series follows a specific (usually Gaussian) distribution.
Q-Q Plot	Series.fqqplot()	Visual tool to inspect the normality of a series.
Comparative Analysis (Passing–Bablok Regression, Bland–Altman Plot)	Comparison.fpb(), Comparison.fba()	Analyzes the agreement and robustness to outliers between two series.
Aggregate Analysis (Sample-Size Weighted Mean of Bias and Measurement Uncertainty)	MethodEvaluation.fwbiasmu()	Aggregates bias and measurement uncertainty using sample size weights.
Correlation Analysis (Pearson, Spearman, Kendall Tau) and Significance Testing (p-Value, Confidence Interval)	Correlation.regression_ci() with method = ‘pearson’, ‘spearman’, ‘kendall’	Measures the relationship between two series, calculates its significance and determines the confidence interval.

.

The Python backend script utilizes several open-source libraries, including NumPy [18] for mathematical computations, Pandas [19,20] for data manipulation and analysis, Seaborn [21] and matplotlib [22] for data visualization, SciPy for scientific computations, Tkinter [23] for GUI development, tkPDFViewer (https://pypi.org/project/tkPDFViewer/, accessed on 26 June 2023) to embed .PDF files into the Tkinter GUI, and Docxtpl (https://docxtpl.readthedocs.io/en/latest/, accessed on 26 June 2023) to read, write, and create subdocuments.

2.3.1. Recommendations for Correlation Methods

Pearson, Spearman, and Kendall are three different correlation indices used to measure the relationship between variables, each serving a unique purpose depending on the specific attributes of the given data. The use-cases, assumptions, strengths, and limitations of these indices are summarized in

Table 2. Comparison of Pearson, Spearman, and Kendall Correlation Coefficients.

Correlation Coefficient	Appropriate Usage	Assumptions	Advantages	Drawbacks
Pearson’s r	When variables are continuous, and the aim is to measure the linear relationship between them.	Assumes that the relationship between variables is linear and that the data are normally distributed.	Widely used and easily interpretable. Measures the strength and direction of the linear relationship between variables.	Assumes a linear relationship and is sensitive to outliers.
Spearman’s rho	When data are ordinal or not normally distributed, and the aim is to measure the monotonic relationship between variables.	Assumes that the relationship between variables is monotonic (i.e., variables tend to change together, but not necessarily at a constant rate).	Can capture non-linear relationships and is robust to outliers. Suitable for ranked or ordinal data.	Ignores the magnitude of differences between data points, focusing only on their rank orders.
Kendall’s tau	When data are ordinal or not normally distributed, and the aim is to measure the strength and direction of the rank-order relationship between variables.	Assumes that the relationship between variables is monotonic.	Suitable for ranked or ordinal data and is robust to outliers. Measures the concordance between variables.	Does not capture the magnitude of differences between data points.

.

The recommendation stands that the Pearson correlation method is suitable for continuous variables that exhibit a linear relationship. The Spearman correlation method, on the other hand, should be employed for ordinal or non-normally distributed data that demonstrates a monotonic relationship. The Kendall correlation method proves ideal for ordinal or non-normally distributed data where the primary interest lies in the rank-order relationship. The best selection of a correlation method ultimately rests on the characteristics of the data and the specific relationship that needs to be assessed.

For practical numerical examples, we direct readers to standard biostatistics textbooks and online resources [24,25].

2.3.2. Estimation of Bias and Measurement Uncertainty

Estimation of Bias: The bias in the predictive model was quantified as the percentage deviation of the mean of the predictions from a specified target value. This was computed using the following equation:

$$\mathrm{bias}=100-\left(\frac{100\times \mathrm{Target}}{\mathrm{mean} \left(\mathrm{Predictions}\right)}\right)$$

(1)

In this equation, ‘Predictions’ refers to the array of values generated by the model, and ‘Target’ represents the desired or true value. The bias provides an average measure of the systematic error inherent in the model’s predictions, with a zero bias indicating a perfect match between the mean prediction and the target on average. A positive bias suggests a systematic underestimation by the model, while a negative bias implies a systematic overestimation.

Assessment of Measurement Uncertainty: The measurement uncertainty, or the variability of the model’s predictions, was evaluated by considering the coefficient of variation and the bias of the model. This was calculated using:

$$\mathrm{measurement}\_\mathrm{uncertainty}=k\times \sqrt{{(100\times \mathrm{cv})}^2+{\left(\mathrm{bias}\right)}^2}$$

(2)

Here, ‘cv’ denotes the coefficient of variation, calculated as the ratio of the standard deviation to the mean of the predictions. ‘bias’ is as defined above, and ‘k’ is a coverage factor (commonly set to 2 for 95% confidence, known as “expanded uncertainty”).

The measurement uncertainty provides an estimate of the dispersion or variability in the model’s predictions, with a lower value indicating higher precision of the model. The calculation assumes that the residuals (Predictions-Target) are normally distributed and independent.

2.4. Deployment

2.4.1. Windows

To bundle the GUI into an executable (*.EXE) file, we employed an open-source tool named PyInstaller, which packages a Python program and all its dependencies into a single executable file that does not require a Python interpreter or any additional modules.

2.4.2. macOS

For macOS, the py2app tool was used to package the GUI into an application file (*.APP) that can be executed on macOS. It is a Python setuptools command that helps create standalone application bundles and plugins from Python scripts.

2.5. Input .CSV File

The anonymized sample .CSV file Figure 4 is a crucial input for the MV-GUI, which is used to evaluate the generation of reports. The .CSV file contains important information about the sample IDs and the matching values for each analyte, which is used to generate the report.

The first column in the .CSV file is the patient ID, which represents the unique identifier for each patient measurement (not necessarily the patients themselves due to anonymization reasons). The second and third columns represent the analyte levels measured by two clinical analyzers to be compared (in our example, creatinine measured on different instruments).

The assessment of measurement accuracy and reliability is crucial in any experiment. To achieve this, the control material provided at three different levels of concentration, representing low, medium, and high, respectively, is measured in each analytical run. These levels are denoted as “Level 1”, “Level 2”, and “Level 3”.

To verify the measurement results, the variability within a single run is evaluated through repeating the measurement of the same sample. This within-run variability, also known as series variability, refers to the differences in the measurement results obtained from repeating the measurement within a single run.

In addition to the within-run verification, the control samples are also measured over a consecutive period of several days (Day-to-Day, [DtoD]) to assess the variability between multiple runs. This is referred to as between-run variability and results in the measurement values being recorded as “DtoD Level 1”, “DtoD Level 2”, and “DtoD Level 3” after a sequence of days. These values are reflected in the corresponding columns in the .CSV file. The number of samples used in both series and DtoD measurements should be minimally 10 (depending on the accreditation needs), but additional samples can be used to improve the results, at the cost of increased expense. Be aware to use no special glyphs and note decimals as separated by point.

The method, platform, and unit columns in the .CSV file refer to the method used in the experiment, the platform used to measure the values, and the unit in which the values are measured, respectively. The material column refers to the biological material used in the method verification experiment.

To generate accreditation-ready reports using MV-GUI, the operator must first select the .CSV file with the filled columns for each sample. Then, the MV-GUI will perform the analysis in the background and present the report to the operator with accompanying plots.

2.6. Running MV-GUI

To run the MV-GUI, the operator must have access to a filled .CSV file as displayed in supplementary Figure 4. The operator clicks on the “Select .CSV file” button and chooses the filled .CSV file. The MV-GUI will then run the analysis in the backend and generate the report, which is presented to the operator in the form of plots on the MV-GUI interface.

The generated report (Figure 5) provides a visual representation of the measurement comparison between the two methods. The report includes plots that represent the measurement values for each patient and the corresponding comparison between the two methods.

The report also provides numerical values such as mean, standard deviation, and coefficient of variation (CV) for each method. These values provide important information about the accuracy and precision of the methods being compared.

In addition to the numerical values, the report also includes graphical representations of the comparison, such as Bland–Altman plot and Passing–Bablok regression analysis plot. The Bland–Altman plot shows the difference between the two methods against their average, and the Passing–Bablok regression analysis plot shows the slope and intercept of the regression line. These plots help to determine the agreement between the two methods and to identify any systematic biases.

The report also includes an overall conclusion that summarizes the findings from the comparison. The conclusion provides important information about the performance of the methods and the level of agreement between them.

Overall, the MV-GUI report contains a comprehensive and visual representation of the measurement comparison between the two methods, making it easier for the operator to interpret the results and to make informed decisions.

2.7. Comparison with Existing Tools

There are several existing tools that perform calculations similar to our software package, and it is essential to discuss them for a comprehensive understanding of the current landscape of method verification tools. Two such R packages include MethComp and SimplyAgree.

MethComp [26] is a package that provides an array of functions for comparing two methods of measurements. It provides a user-friendly interface and detailed output, enabling users to easily interpret the results of the comparison. Similarly, SimplyAgree [27] is another package that focuses on the agreement between different methods of measurement and provides statistical tests to evaluate the agreement. Both of these packages have robust functionality and provide a range of output options that can be easily integrated into reports.

While these tools offer valuable services, our software package provides a more specialized approach specifically tailored to method verification routines. Our software package streamlines the process by automating steps 3, 4, and 5 of the method verification routine, making it an efficient solution for practitioners who need to carry out these routines on a regular basis.

2.8. Outlook

In terms of future upgrades, our team is currently exploring options for expanding the functionality of the GUI to include additional indices and statistical performance indicators to address a wider range of lab accreditation needs, also for method validation (cf. CLSI, RiLiBÄK, etc.) [10], the possibility to append the method package insert as .PDF, and the possibility to enter data directly into the GUI without the need for a .CSV file.

We are particularly keen on incorporating additional indices, such as the Total Deviation Index (TDI) and Concordance Correlation Coefficient (CCC), which are already available in MethComp and SimplyAgree, among others. By incorporating these indices into our software, we hope to provide a more comprehensive solution for method verification routines that meet the diverse needs of our users.

It is important to clarify that these upgrades would be intended to enhance the existing functionality of the software rather than transform it into a tool for method validation. As stated earlier, method validation requires adaptable statistics that present challenges for automation. Therefore, while we strive to improve and expand our software, we remain committed to our original goal: to provide an efficient, user-friendly tool for method verification.

3. Discussion

The laborious task of accurately assessing and recording the analytical performance of laboratory techniques poses a significant challenge in clinical testing [28]. Given the stringent mandates by accreditation bodies, laboratories often grapple with the complexity and resource intensiveness associated with these evaluation procedures. It is imperative, therefore, to have tools that can streamline this process, bolster accuracy, and improve productivity.

In this context, the MV-GUI, an open-source graphical user interface with a statistical backend, emerges as a highly effective solution. The design and development of MV-GUI have been shaped by a keen understanding of the clinical testing environment and its inherent challenges. With its minimalist and user-friendly layout, the MV-GUI significantly reduces the learning curve, enabling laboratory personnel to focus on core operations rather than tool operation, thus maximizing productivity.

While acknowledging the presence of other R packages, such as MethComp [26] and SimplyAgree [27], which perform similar calculations, we argue that our software package delivers a more specialized approach designed explicitly for method verification routines. Although MethComp and SimplyAgree offer robust functionality, the MV-GUI’s specialized focus on method verification routines provides a more streamlined user experience.

Moreover, the platform-neutral design of MV-GUI allows for its wide-scale adoption. By supporting both Windows and macOS operating systems, the software extends its reach to a greater number of users. This feature, coupled with the ease of modification of scripts and GUI, allows for future expansions and upgrades aligning with the users’ needs.

While MV-GUI currently focuses on method verification routines, future iterations will enhance statistical indicators to broaden laboratory accreditation support. This improvement aligns with the need to address method evaluation challenges, such as standardization of terminology, selection of analytical performance specifications, experimental design, sample requirements, statistical assessment, and reporting [29].

Furthermore, the MV-GUI addresses the importance of detecting and monitoring lot-to-lot variations in reagents, as undetected biases can have severe implications for patient care [28,30,31]. By providing a comprehensive method evaluation solution, the MV-GUI aids in identifying and addressing such biases through its statistical analysis capabilities. This aligns with the need for more publications that objectively assess statistical approaches and provide guidance for optimal methods under different circumstances [29].

In conclusion, the MV-GUI represents an effective, user-friendly, and cost-efficient solution for assessing and recording the analytical performance of clinical testing techniques. By addressing the challenges faced in method evaluation, facilitating reproducibility and reuse of research code, and providing comprehensive statistical analysis capabilities, the MV-GUI serves as an indispensable tool in the dynamic and stringent environment of laboratory testing [29,32,33]. Its potential for future enhancements and adaptability to different operating systems further solidify its value in the field of clinical laboratory medicine [29,33].

4. Conclusions

In the field of clinical laboratory testing, it is of utmost importance to accurately assess and record the analytical performance of all techniques used. This is a mandatory requirement for accredited labs, both before the initial deployment of the techniques and throughout their continuous operation. The procedure for evaluating analytical performance can be time-consuming and complex, and it is crucial to have a clear, simple, and cost-effective solution that can simplify the process.

To address this need, we have developed an open-source graphical user interface (GUI) with a statistical backend known as MV-GUI. This platform-neutral software solution is user-friendly and enables labs to produce accreditation-ready reports with just a few clicks. MV-GUI supports both Windows and macOS operating systems, making it accessible to a wide range of users. Additionally, the scripts and GUI are flexible and can be easily modified, allowing for future updates and new capabilities to be added over time. With MV-GUI, the process of assessing and recording analytical performance can be streamlined, saving time and resources for labs while ensuring the accuracy of their results.