Meal and Physical Activity Detection from Free-Living Data for Discovering Disturbance Patterns of Glucose Levels in People with Diabetes

Abstract

Objective: The interpretation of time series data collected in free-living has gained importance in chronic disease management. Some data are collected objectively from sensors and some are estimated and entered by the individual. In type 1 diabetes (T1D), blood glucose concentration (BGC) data measured by continuous glucose monitoring (CGM) systems and insulin doses administered can be used to detect the occurrences of meals and physical activities and generate the personal daily living patterns for use in automated insulin delivery (AID). Methods: Two challenges in time-series data collected in daily living are addressed: data quality improvement and the detection of unannounced disturbances of BGC. CGM data have missing values for varying periods of time and outliers. People may neglect reporting their meal and physical activity information. In this work, novel methods for preprocessing real-world data collected from people with T1D and the detection of meal and exercise events are presented. Four recurrent neural network (RNN) models are investigated to detect the occurrences of meals and physical activities disjointly or concurrently. Results: RNNs with long short-term memory (LSTM) with 1D convolution layers and bidirectional LSTM with 1D convolution layers have average accuracy scores of 92.32% and 92.29%, and outperform other RNN models. The F1 scores for each individual range from 96.06% to 91.41% for these two RNNs. Conclusions: RNNs with LSTM and 1D convolution layers and bidirectional LSTM with 1D convolution layers provide accurate personalized information about the daily routines of individuals. Significance: Capturing daily behavior patterns enables more accurate future BGC predictions in AID systems and improves BGC regulation.

1. Introduction

Time series data are widely used in many fields, and various data-driven modeling techniques are developed to represent the dynamic characteristics of systems and forecast the future behavior. The growing research in artificial intelligence has provided powerful machine learning (ML) techniques to contribute to data-driven model development. Real-world data provide several challenges to modeling and forecasting, such as missing values and outliers. Such imperfections in data can reduce the accuracy of ML and the models developed. This necessitates data preprocessing for the imputation of missing values, down- and up-sampling, and data reconciliation. Data preprocessing is a laborious and time-consuming effort since big data are usually stacked on a large scale [1]. When models are used for forecasting, the accuracy of forecasts improve if the effects of future possible disturbances based on behavior patterns extracted from historical data are incorporated in the forecasts. This paper focuses on these two problems and investigates the benefits of preprocessing the real-world data and the performance of different recurrent neural network (RNN) models for detecting various events that affect blood glucose concentration (BGC) in people with type 1 diabetes (T1D). The behavior patterns detected are used for more accurate predictions of future BGC variations, which can be used for warnings and for increasing the effectiveness of automated insulin delivery (AID) systems.

Time series data captured in daily living of people with chronic conditions have many of these challenges to modeling, detection, and forecasting. Focusing on people with T1D, the medical objective is to forecast the BGC of a person with T1D and prevent the excursion of BGC outside a “desired range” (70–180 mg/dL) to reduce the probability of hypo- and hyperglycemia events. In recent years, the number of people with diabetes has grown rapidly around the world, reaching pandemic levels [2,3]. Advances in continuous glucose monitoring (CGM) systems, insulin pump and insulin pen technologies, and in novel insulin formulations has enabled many powerful treatment options [4,5,6,7,8,9]. The current treatment options available to people with T1D range from manual insulin injections to AID. Manual injection (insulin bolus) doses are computed based on the person’s characteristics and the properties of the meal consumed. Current AID systems necessitate the manual entry of meal information to give insulin boluses for mitigating the effects of meal on the BGC. A manual adjustment of the basal insulin dose and increasing the BGC target level and/or consumption of snacks are the options to mitigate the effects of physical activity. Some people may forget to make these manual entries and a system that can nudge them to provide appropriate information can reduce the extreme excursions in BGC. Commercially available AID systems are hybrid closed-loop systems, and they require these manual entries by the user. AID systems, also called artificial pancreas (AP), consist of a CGM, an insulin pump, and a closed-loop control algorithm that manipulates the insulin infusion rate delivered by the pump based on the recent CGM values reported [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. More advanced AID systems that use a multivariable approach [10,24,25,26] use additional inputs from wearable devices (such as wristbands) to automatically detect the occurrence of physical activity and incorporate this information to the automated control algorithms for a fully automated AID system [27]. Most AID systems use model predictive control techniques that predict future BGC values in making their insulin dosing decisions. Knowing the habits of the individual AID user improves the control decisions since the prediction accuracy of the future BGC trajectories can explicitly incorporate the future potential disturbances to the BGC, such as meals and physical activities, that will occur with high likelihood during the future BGC prediction window [24,26]. Consequently, the detection of meal and physical activity events from historical free-living data of a person with T1D will provide useful information for decision making by both the individual and by the AID system.

CGM systems report subcutaneous glucose concentration to infer BGC with a sampling rate of 5 min. Self-reported meal and physical activity data are often based on diary entries. Physical activity data can also be captured by wearable devices. The variables reported by wearable devices may have artifacts, noise, missing values, and outliers. The data used in this work include only CGM values, insulin dosing information, and diary entries of meals and physical activities.

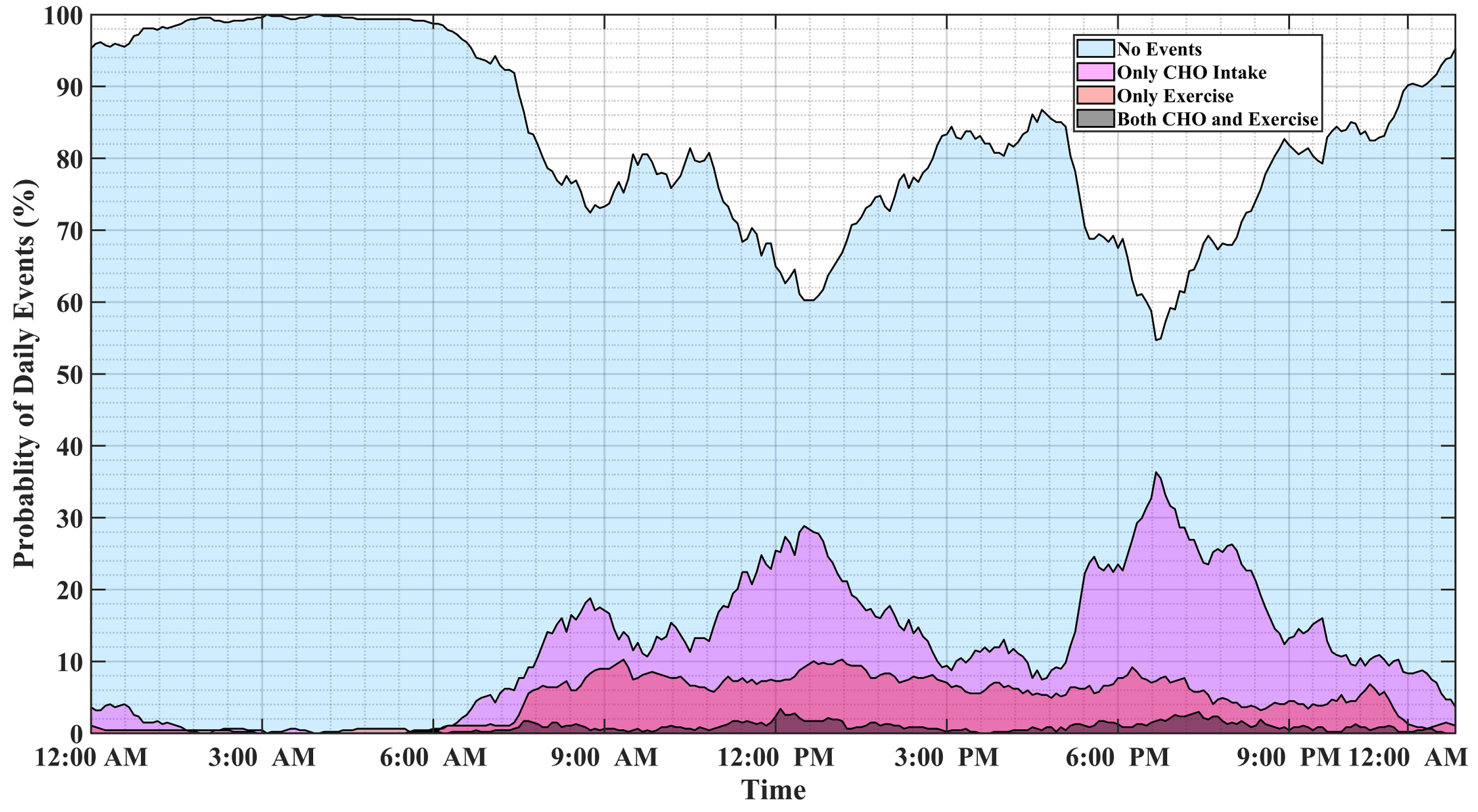
Analyzing long-term data of people with T1D indicates that individuals tend to repeat daily habitual behaviors. Figure 1 illustrates the probability of physical activity and meal (indicated as carbohydrate intake) events, either simultaneously or disjointly, for 15 months of self-reported CGM, meal, insulin pump, and physical activity data of individuals with T1D. Major factors affecting BGC variations usually occur at specific time windows and conditions, and some combinations of events are mutually exclusive. For example, insulin-bolusing and physical activity are less likely to occur simultaneously or during hypoglycemia episodes, since people do not exercise when their BGC is low. People may have different patterns of behavior during the work week versus weekends or holidays. Predicting the probabilities of exercise, meal consumption, and their concurrent occurrence based on historical data using ML can provide important information on the behavior patterns for making medical therapy decisions in diabetes.

Motivated by the above considerations, this work develops a framework for predicting the probabilities of meal and physical activity events, including their independent and simultaneous occurrences. A framework is built to handle the inconsistencies and complexities of real-world data, including missing data, outlier removal, feature extraction, and data augmentation. Four different recurrent neural network (RNN) models are developed and evaluated for estimating the probability of events causing large variations in BGC. The advent of deep neural networks (NNs) and their advances have paved the way for processing and analyzing various types of information, namely: time-series, spatial, and time-series–spatial data. Long short-term memory (LSTM) NN models are specific sub-categories of recurrent NNs introduced to reduce the computational burden of storing information over extended time intervals [28,29]. LSTMs take advantage of nonlinear dynamic modeling without knowing time-dependency information in the data. Moreover, their multi-step-ahead prediction capability makes them an appropriate choice for detecting upcoming events and disturbances that can deteriorate the accuracy of model predictions.

The main contributions of this work are the development of NN models capable of estimating the occurrences of meals and physical activities without requiring additional bio-signals from wearable devices, and the integration of convolution layers with LSTM that enable the NN to accurately estimate the output from glucose–insulin input data. The proposed RNN models can be integrated with the control algorithm of an AID system to enhance its performance by readjusting the conservativeness and aggressiveness of the AID system.

The remainder of this paper is organized as follows: the next section provides a short description of the data collected from people with T1D. The preprocessing step, including outlier removal, data imputation, and feature extraction is presented in Section 3. Section 4 presents various RNN configurations used in this study. A case study with real-world data and a discussion of the results are presented in Section 5 and Section 6, respectively. Finally, Section 6 provides the conclusions.

2. Free-Living, Self-Reported Dataset of People with T1D

A total of 300 self-collected T1D datasets were made available for research, and each dataset represents a unique individual. Among all of the datasets, 50 T1D datasets include CGM-sensor–insulin-pump recordings and exercise information such as the time, type, and duration of physical activity recorded from either open or closed-loop insulin-pump–sensor data. Meal information is reported as the amount of carbohydrates (CHO) consumed in the meal as estimated by the subject. An over or underestimation of CHO in meals is common.

The subjects with T1D selected for this study used insulin-pump–CGM-sensor therapy for up to two years, and some of them have lived with diabetes for more than fifty years.

Table 1. The general demographic information of 11 subjects with T1D and the durations of recorded samples.

Subject	Gender	Age	Duration of Data 1	Missing Samples (%)	Max Gap Size 2
1	M	36	283 days	12.36%	273
2	M	33	368 days	7.11%	71
3	F	72	280 days	1.10%	28
4	M	43	468 days	10.03%	435
5	F	52	655 days	4.91%	233
6	F	26	206 days	14.45%	107
7	M	51	278 days	6.12%	34
8	-	41	390 days	8.87%	177
9	-	42	279 days	19.70%	311
10	M	27	695 days	14.32%	571
11	F	35	413 days	8.97%	147

¹ The duration of data is calculated after imputation of missing data and counting gaps between samples. ² Number of samples, sampling time 5 min.

and

Table 2. The name and the definition of measured variables.

Variable/Symbol	Definition	Units
	Continuous glucose monitoring values sampled
CGM	every five minutes	mmol/L
Smbg	Self-monitored BGC for sensor	mmol/L
	calibration
Rate ($In{s}_{Basal}$)	The basal insulin rate	unit/h
Bolus ($In{s}_{Bolus}$)	The actual delivered amount of normal bolus insulin	unit
		Format:
Time	UTC time stamp	yyyy-mm-yy hh:mm:ss
	The actual duration of a suspend, basal, or
Duration	dual/square bolus	milliseconds
Activity.name	The type of physical activity	-
Activity.duration ($AD$)	The duration of a physical activity	milliseconds
Distance.value ($DV$)	The value of the distance traveled	miles
Energy.value ($EV$)	The amount of energy spent during activity	kilocalories
Nutrition.carbohydrate	The carbohydrates entered in a health
(CHO)	kit food entry	grams

summarize the demographic information of the selected subjects and the definition of the variables collected, respectively. Separate RNN models were developed for each person in order to capture personalized patterns of meal consumption and physical activity.

3. Data Preprocessing

This is a computational study for the development of detection and classification of infrequent events (eating, exercising) that affect the main variable of interest in people with diabetes: their blood glucose concentrations. It is based on data collected from patients in free living; hence, it contains many windows of data with missing values and outliers. Using real-world data for developing models usually has numerous challenges: (i) the datasets can be noisy and incomplete; (ii) there may be duplicate CGM samples in some of the datasets; (iii) inconsistencies exist in the sampling rate of CGM and insulin values; (iv) gaps in the time and date can be found due to insulin pump or CGM sensor disconnection. Therefore, the datasets need to be preprocessed before using them for model development.

3.1. Sample Imputation

Estimating missing data is an important step before analyzing the data [30]. Missing data are substituted with reasonable estimates (imputation) [31]. In dealing with time-series data such as CGM, observations are sorted according to their chronological order. Therefore, the variable “Time”, described in Table 2, is converted to “Unix time-stamp”, samples are sorted in ascending order of “Unix time-stamp”, and gaps without observations are filled with pump–sensor samples labeled as “missing values”.

Administered basal insulin is a piecewise constant variable and its amount is calculated by the AID system or by predefined insulin injection scenarios. Applying a simple forward or backward imputation for basal insulin with gaps in duration lasting a maximum of two hours gives reasonable reconstructed values for the missing observations. Gaps lasting more than two hours in missing recordings are imputed with basal insulin values recorded in the previous day at the same time, knowing that insulin injection scenarios usually follow a daily pattern [32].

The variable “Bolus” is a sparse variable (usually nonzero only at times of meals) and its missing samples were imputed with the median imputation approach, considering that the bolus injection policy is infrequently altered. Similarly, missing recordings of variables “Nutrition.carbohydrate”, “Smbg”, “Duration”, “Activity.duration”, and “Distance.value” were imputed with the median strategy. A multivariate strategy that uses CGM, total injected insulin, “Nutrition.carbohydrate”, the “Energy.value”, and “Activity.duration” was employed to impute missing CGM values.

This choice of variables has to do with the dynamic relationship between CGM and the amount of carbohydrate intake, the duration and the intensity of physical activity, and the total injected insulin. Estimates of missing CGM samples were obtained by performing probabilistic principal component analysis (PPCA) on the lagged matrices of the CGM data. PPCA is an extension of principal component analysis, where the Gaussian conditional distribution of the latent variables is assumed [33]. This formulation of the PPCA facilitates tackling the problem of missing values in the data through the maximum likelihood estimation of the mean and variance of the original data. Before performing PPCA on the feature variables, the lagged array of each feature variable, ${\mathcal{X}}_{k,j},k\in \{CGM,Ins,CHO,EV,AD\}$, at the jth sampling index was constructed from the past two hours of observations as:

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{k,j}={\left[\begin{array}{cc}{X}_{k,j},X_{k,j-1}\cdots & X_{k,j-24}\end{array}\right]}_{1\times 25},k\in \{CGM,Ins,CHO,EV,AD\}\hfill \\ \hfill & X_j={[{\mathcal{X}}_{1,j},\cdots ,{\mathcal{X}}_{k,j}\cdots ,{\mathcal{X}}_{M,j}]}^T,X={\left[\begin{array}{c}{X}_1,\cdots ,X_N\end{array}\right]}_{M\times N}\hfill \end{array}$$

(1)

For an observed set of feature variables $X_j$, let ${\mathcal{T}}_j={[{\mathcal{T}}_{1,j},\cdots ,{\mathcal{T}}_{q,j}]}^T$ be its q-dimensional ($q\le M$) Gaussian latent transform [34] such that

$$X_{i,j}=W_i{\mathcal{T}}_j+{\mu }_i+{ϵ}_{i,j}$$

(2)

where $W_i=[W_{i,1},\cdots ,W_{i,q}]\in {\mathbb{R}}^q$ and $\underline{\mu }={[{\mu }_1,\cdots ,{\mu }_M]}^T\in {\mathbb{R}}^M$ represent the ith row of the loading matrix $W\in {\mathbb{R}}^{M\times q}$ and mean value of the data. ${ϵ}_{i,j}\in \mathbb{R}$ is also the measurement noise with the probability distribution

$$p\left({ϵ}_{i,j}\right|{\sigma }^2)=\mathcal{N}\left({ϵ}_{i,j}\right|0,{\sigma }^2).$$

(3)

Based on the Gaussian distribution assumption of ${\mathcal{T}}_j$ and the Gaussian probability distribution of ${ϵ}_{i,j}$, one can deduce that

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & p\left({\mathcal{T}}_j\right)=\mathcal{N}\left({\mathcal{T}}_j\right|0,I_q)\hfill \\ \hfill & p\left(X_{i,j}\right|{\mu }_i,W_i,{\sigma }^2)=\mathcal{N}\left(X_{i,j}\right|{\mu }_i,W_i{W}_i^T+{\sigma }^2)\hfill \\ \hfill & p\left(X_{i,j}\right|{\mathcal{T}}_j,{\mu }_i,W_i,{\sigma }^2)=\mathcal{N}\left(X_{i,j}\right|W_i{\mathcal{T}}_j+{\mu }_i,{\sigma }^2)\hfill \end{array}\end{array}\right..$$

(4)

The joint probability distribution $p(X_{i,j},{\mathcal{T}}_j,{\mu }_i,W_i,{\sigma }^2)$ can be derived from (4) and Bayes’ joint probability rule as

$$p(X_{i,j},{\mathcal{T}}_j,{\mu }_i,W_i,{\sigma }^2)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{\frac{M}{2}}}exp\frac{{(X_{i,j}-W_i{\mathcal{T}}_j-{\mu }_i)}^2}{-2{\sigma }^2}\frac{1}{{\left(2\pi \right)}^{\frac{q}{2}}}exp\frac{-{\mathcal{T}}_j^T{\mathcal{T}}_j}{2}$$

(5)

Define the set $\eta =\left\{(i,j)\right|1\le i\le M,1\le j\le N,X_{i,j}\ne NaN\}$. The log-likelihood of the joint multivariate Gaussian probability distribution of (5) is calculated over all available observations as

$$\begin{array}{cc}\hfill ln\left(p(X_{i,j},{\mathcal{T}}_j|{\mu }_i,W_i,{\sigma }^2)\right)& =\underset{i,j\in \eta }{\sum \sum }[ln\left(p\left(X_{i,j}\right|{\mathcal{T}}_j,{\mu }_i,W_i,{\sigma }^2)\right)+lnp\left({\mathcal{T}}_j\right)]\hfill \\ \hfill & =\underset{i,j\in \eta }{\sum \sum }\frac{-M}{2}ln\left(2\pi {\sigma }^2\right)-\frac{q}{2}ln\left(2\pi \right)-\frac{{(X_{i,j}-W_i{\mathcal{T}}_j-{\mu }_i)}^2}{2{\sigma }^2}-\frac{{\mathcal{T}}_j^T{\mathcal{T}}_j}{2}\hfill \end{array}$$

(6)

where the log-likelihood (6) is defined for all available observations $X_{i,j},i,j\in \eta$. By applying the expectation operation with respect to the posterior probability distribution over all latent variables ${\mathcal{T}}_j,j\in {\eta }_i$, where ${\eta }_i=\left\{j\right|1\le j\le N,X_{i,j}\ne NaN\}$, (6) becomes

$$\begin{array}{cc}\hfill \mathbb{E}\left\{\mathcal{L}\right\}=& -\underset{i,j\in \eta }{\sum \sum }\frac{M}{2}ln\left({\sigma }^2\right)+\frac{1}{2}\mathbb{E}\left\{{\mathcal{T}}_j^T{\mathcal{T}}_j\right\}+\frac{1}{2{\sigma }^2}{(X_{i,j}-{\mu }_i)}^2\hfill \\ \hfill & -\frac{1}{{\sigma }^2}\mathbb{E}\left\{{\mathcal{T}}_j^T\right\}{W}_i^T(X_{i,j}-{\mu }_i)+\frac{1}{2{\sigma }^2}\mathbb{E}\left\{{\mathcal{T}}_j^T{\mathcal{T}}_j\right\}{W}_i{W}_i^T\hfill \end{array}$$

(7)

Maximizing (7) is feasible by setting all partial derivatives $\frac{\partial \mathbb{E}\left\{\mathcal{L}\right\}}{\partial {\sigma }^2}$, $\frac{\partial \mathbb{E}\left\{\mathcal{L}\right\}}{\partial {\mu }_i^2}$, and $\frac{\partial \mathbb{E}\left\{\mathcal{L}\right\}}{\partial W_i^2},i=1,\cdots ,M,j=1,\cdots ,N$ to zero [34].

$$\begin{array}{cc}\hfill & Cva{r}_{{\mathcal{T}}_j}=\frac{{\sigma }^2}{({\sigma }^2{I}_q+{\sum }_{i\in {\eta }_j}{W}_i{W}_i^T)}\hfill \\ \hfill & {\mu }_{{\mathcal{T}}_j}=\frac{Cva{r}_{{\mathcal{T}}_j}}{{\sigma }^2}\sum _{i\in {\eta }_j}{W}_i^T(X_{i,j}-{\mu }_i)\hfill \\ \hfill & {\mu }_i=\frac{1}{|{\eta }_i|}\sum _{j\in {\eta }_i}[X_{i,j}-W_i{\mu }_{{\mathcal{T}}_j}]\hfill \\ \hfill & W_i=\frac{1}{{\sum }_{j\in {\eta }_i}[{\mu }_{{\mathcal{T}}_j}{\mu }_{{\mathcal{T}}_j}^T+Cva{r}_{{\mathcal{T}}_j}]}\sum _{j\in {\eta }_i}{\mu }_{{\mathcal{T}}_j}(X_{i,j}-{\mu }_i)\hfill \\ \hfill & {\sigma }^2=\frac{1}{\left|\eta \right|}\sum _{i,j\in \eta }[{(X_{i,j}-W_i{\mu }_{{\mathcal{T}}_j}-{\mu }_i)}^2+W_{i}Cva{r}_{{\mathcal{T}}_j}{W}_i^T]\hfill \end{array}$$

(8)

Parameters ${\mu }_i$, ${\sigma }^2$, and $W_i$ in (8) are updated recursively until they converge to their final values. The final estimation of missing CGM samples is obtained by performing a diagonal averaging of the reconstructed lagged matrix $\widehat{X}\in {\mathbb{R}}^{M\times N}$ over rows/columns filled with CGM values. Long gaps in CGM recordings might exist in the data, and imputing their values causes problems in accuracy and reliability. Therefore, CGM gaps of no more than twenty-five consecutive missing samples (approximately two hours) are imputed by PPCA.

3.2. Outlier Removal

Signal reconciliation and outlier removal are necessary to avoid misleading interpretation of data and biased results, and to improve the quality of CGM observations. As a simple outlier removal approach for a variable with Gaussian distribution, observations outside $\pm 2.72$ standard deviations from the mean, known as inner Tukey fences, can be labeled as outliers and extreme values [35]. The probability distribution of the CGM data shows a skewed distribution compared to the Gaussian probability distribution. Thus, labeling samples as outliers only based on their probability of occurrence is not the proper way of removing extreme values from the CGM data since it can cause a loss of useful CGM information, specifically during hypoglycemia ($CGM<70$ mg/dL) and hyperglycemia ($CGM>180$ mg/dL) events. As another alternative, extreme values and spikes in the CGM data can be labeled from the prior knowledge and by utilizing other feature variables, namely: “Smbg”, “Nutrition.carbohydrate”, “Bolus”, and “Activity.duration”. Algorithm 1 is proposed to remove outliers from CGM values. Usually, BGC is slightly different from the recordings of the CGM signal because of the delay between BGC and the subcutaneous glucose concentration measured by the CGM device and sensor noise. The noisy signal can deteriorate the performance of data-driven models. Therefore, Algorithm 2, which is based on eigendecomposition of the Hankel matrix of CGM values, is used to reduce the noise in the CGM recordings.

Algorithm 1: Outlier rejection from CGM readings

1: procedureOutlierrejection ($CGM$,$Smbg$,$CHO$,$AD$,$In{s}_{Bolus}$) 2:     for $i=1:N$do      ▹ Removing samples outside of the calibration range 3:         if $CG{M}_k>400$ mg/dL or $CG{M}_k<0$ mg/dL then 4:            $CG{M}_k\leftarrow NaN$ 5:         end if 6:     end for 7:     for $i=2:N$ do 8:         $\Delta CG{M}_k\leftarrow CG{M}_k-CG{M}_{k-1}$ 9:         if $\Delta CG{M}_k>30\mathrm{mg}/\mathrm{dL}$ & all $\left(\{CH{O}_k,\cdots ,CH{O}_{k-9}\}==0\right)$ then 10:            $CG{M}_k\leftarrow \mathrm{NaN}$ 11:         end if 12:         if $\Delta CG{M}_k<30\mathrm{mg}/\mathrm{dL}$ & all $\left(\{In{s}_{Bolus,k},\cdots ,In{s}_{Bolus,k-6}\}==0\right)$ then 13:            $CG{M}_k\leftarrow \mathrm{NaN}$ 14:         end if 15:         if $\Delta CG{M}_k<30\mathrm{mg}/\mathrm{dL}$ & all $\left(\{A{D}_k,\cdots ,A{D}_{k-6}\}==0\right)$ then 16:            $CG{M}_k\leftarrow \mathrm{NaN}$ 17:         end if 18:         if $Smb{g}_k\ne \mathrm{NaN}$ & $CG{M}_k\ne \mathrm{NaN}$ & abs$\left(Smb{g}_k-CG{M}_k\right)$$>18$ mg/dL then 19:            $CG{M}_k\leftarrow \mathrm{NaN}$ 20:         end if 21:     end for 22:     return $CGM$ 23: end procedure

Algorithm 2: Smoothing CGM recordings

1: procedurecgmdenoising ($CGM$)            ▹ Smoothing CGM recordings 2:     $Q_i=[CG{M}_d,\cdots ,CG{M}_{d+q_i-1}]$   ▹$Q_i\in {\mathbb{R}}^{q_i}$ is ith consecutive CGM recordings 3:     $q_i\leftarrow \left|Q_i\right|$, $p_i\leftarrow floor\left(\frac{q_i}{2}\right)$, $w_i\leftarrow q_i-p_i+1$ 4:     $[U_i,S_i,V_i]=SVD\left(A_i\right)$       ▹$A_i\in {\mathbb{R}}^{w_i\times p_i}$ is the Hankel matrix made of $Q_i$ 5:     ${\widehat{S}}_i\leftarrow zeros(p_i,p_i)$ 6:     $\eta \leftarrow \frac{cumsum\left([s_1,\cdots ,s_{p_i}]\right)}{sum\left([s_1,\cdots ,s_{p_i}]\right)}$      ▹$s_j>0$ are eigenvalues of $S_i$ in descending order 7:     for j=1:$p_i$ do 8:         if ${\eta }_j>0.95$ then 9:            ${\widehat{S}}_i(j,j)\leftarrow 0$ 10:         else 11:            ${\widehat{S}}_i(j,j)\leftarrow S_i(j,j)$ 12:         end if 13:     end for 14:     ${\widehat{A}}_i=U_i{\widehat{S}}_i{V}_i^T$ 15:     ${\widehat{Q}}_i\leftarrow$ Diagonalaveraging$\left({\widehat{A}}_i\right)$       ▹${\widehat{Q}}_i=\left[\begin{array}{c}C\widehat{G}{M}_d,\cdots ,C\widehat{G}{M}_{d+q_i-1}\end{array}\right]$ 16:     return $C\widehat{G}M$ 17: end procedure

3.3. Feature Extraction

Converting raw data into informative feature variables or extracting new features is an essential step of data preprocessing. In this study, four groups of feature variables, including frequency domain, statistical domain, nonlinear domain, and model-based features, were calculated and added to each dataset to enhance the prediction power of models. The summarized description of each group of features and the number of past samples required for their calculation are listed in

Table 3. The type and definition of the extracted feature variables and the length of time window required for their calculations.

Domain	Feature Description	No. of Required Samples
	First derivative calculated by 4th backward differences	5
Time	Second derivative calculated by 4th backward differences	6
	Sign-product of the 1st and the 2nd derivatives	6
Nonlinear	Magnitude-product of the 1st and the 2nd derivatives	6
	Statistical measures, namely mean, variance, median, etc.,
	of windowed CGM values	24
	Pair-wise covariance and correlation coefficient between CGM
Statistical	and its 1st and 2nd derivatives	24
	The magnitudes and frequencies of three dominant peaks in
Frequency	the power spectrum of CGM	288
Model-based	Plasma insulin concentration (PIC) and gut absorption rate ($U_g$) [40,41].	1

.

A qualitative trend analysis of variables can extract different patterns caused by external factors within a specified time [36,37]. A pairwise multiplication of the sign and magnitude of the first and second derivatives of CGM values indicates the carbohydrate intake [38,39], exogenous insulin injection, and physical activity. Therefore, the first and second derivatives of CGM values, calculated by the fourth-order backward difference method, were added as feature variables. The sign and magnitude product of the first and second derivatives of CGM, their covariance, Pearson correlation coefficient, and Gaussian kernel similarity were extracted. Statistical feature variables, e.g., mean, standard deviation, variance, skewness, etc., were obtained from the specified time window of CGM values. Similar to the first and second derivatives of CGM values, a set of feature variables, including covariance and correlation coefficients, from pairs of CGM values and derivatives was extracted and augmented to the data.

As a result of the daily repetition in the trends of CGM and glycemic events and the longer time window of CGM values, samples collected during the last twenty-four hours were used for frequency-domain feature extraction. Therefore, magnitudes and frequencies of the top three dominant peaks in the power spectrum of CGM values, conveying past long-term variation of the BGC, were included in the set of feature maps.

The plasma insulin concentration (PIC) is another feature variable that informs about the carbohydrate intake information and exogenous insulin administration. PIC accounts for the accumulation of subcutaneously injected insulin within the bloodstream, which is gradually consumed by the body to enable the absorption of carbohydrates released from the gastrointestinal track to various cells and tissues. Usually, dynamic physiological models are used to describe and model the glucose and insulin concentration dynamics in diabetes. The main idea of estimating PIC from physiological models stems from predicting the intermediate state variables of physiological models by designing a state observer and utilizing the total infused insulin and carbohydrate intake as model inputs, and CGM values as the output of the model [40,41,42]. In this work, the estimation of the PIC and glucose appearance rate were obtained from a physiological model known as Hovorka’s model [43]. Equation (9) presents this nonlinear physiological (compartment) model:

$$\begin{array}{cc}\hfill & \frac{d{S}_1\left(t\right)}{dt}=Ins\left(t\right)-\frac{S_1\left(t\right)}{t_{max,I}}\hfill \\ \hfill & \frac{d{S}_2\left(t\right)}{dt}=\frac{S_1\left(t\right)}{t_{max,I}}-\frac{S_2\left(t\right)}{t_{max,I}}\hfill \\ \hfill & \frac{dI\left(t\right)}{dt}=\frac{S_2\left(t\right)}{t_{max,I}{V}_I}-K_{e}I\left(t\right)\hfill \\ \hfill & \frac{d{x}_1\left(t\right)}{dt}=k_{b,1}I\left(t\right)-k_{a,1}{x}_1\left(t\right)\hfill \\ \hfill & \frac{d{x}_2\left(t\right)}{dt}=k_{b,2}I\left(t\right)-k_{a,2}{x}_2\left(t\right)\hfill \\ \hfill & \frac{d{x}_3\left(t\right)}{dt}=k_{b,3}I\left(t\right)-k_{a,3}{x}_3\left(t\right)\hfill \\ \hfill & \frac{d{Q}_1\left(t\right)}{dt}=U_g\left(t\right)-F_{0,1}^c\left(t\right)-F_R\left(t\right)-x_1\left(t\right)Q_1\left(t\right)+k_{12}{Q}_2\left(t\right)+EG{P}_0(1-x_3\left(t\right))\hfill \\ \hfill & \frac{d{Q}_2\left(t\right)}{dt}=x_1\left(t\right)Q_1\left(t\right)-(k_{12}+x_2\left(t\right))Q_2\left(t\right)\hfill \\ \hfill & \frac{d{G}_{sub}\left(t\right)}{dt}=\frac{1}{\tau }\left(\frac{Q_1\left(t\right)}{V_g}-G_{sub}\left(t\right)\right)\hfill \end{array}$$

(9)

Model (9) comprises four sub-models, describing the action of insulin on glucose dynamics, the insulin absorption dynamics, plasma–interstitial-tissue glucose concentration dynamics, and the blood glucose dynamics.The state variables of (9), the nominal values of the parameters, and their units are listed in

Table 4. The description of variables and parameters and the nominal values of parameters in Hovorka’s model [43].

Variable/Parameter	Description	Value/Unit
	Two-compartment chain representing absorption
$S_1\left(t\right),S_2\left(t\right)$	of subcutaneously administered short-acting insulin	mU
$Ins\left(t\right)$	Subcutaneously infused insulin	mU min${}^{-1}$
$I\left(t\right)$	Plasma insulin concentration (PIC)	mU L${}^{-1}$
$x_1\left(t\right)$	The remote effect of insulin on glucose distribution	min${}^{-1}$
$x_2\left(t\right)$	The remote effect of insulin on glucose disposal	min${}^{-1}$
	The remote effect of insulin on
$x_3\left(t\right)$	endogenous glucose production (EGP)	min${}^{-1}$
$Q_1\left(t\right)$	The mass of glucose in accessible compartments	mmol
$Q_2\left(t\right)$	The mass of glucose in non-accessible compartments	mmol
$G_{sub}\left(t\right)$	Measurable subcutaneous glucose concentration	mmol L${}^{-1}$
$U_G\left(t\right)$	Gut absorption rate	mmol min${}^{-1}$
$K_e$	The fractional elimination rate of PIC	0.138 min${}^{-1}$
$k_{a,1}$		0.006 min${}^{-1}$
$k_{a,2}$		0.06 min${}^{-1}$
$k_{a,3}$	The deactivation rate constants	0.03 min${}^{-1}$
$S_{ID}^f$	The sensitivity of insulin disposal	0.00082 L min${}^{-1}$ mU${}^{-1}$
$S_{IT}^f$	The sensitivity of insulin distribution	0.00512 L min${}^{-1}$ mU${}^{-1}$
$S_{IE}^f$	The sensitivity of EGP	0.052 L mU${}^{-1}$
$k_{b,1}$		$k_{a,1}\times S_{IT}^f$
$k_{b,2}$		$k_{a,2}\times S_{ID}^f$
$k_{b,3}$	The activation rate constants	$k_{a,3}\times S_{IE}^f$
	EGP extrapolated to	0.0161
$EG{P}_0$	zero insulin concentration	mmol kg${}^{-1}$ min${}^{-1}$
	The transfer rate constant from the non-accessible
$k_{12}$	to the accessible compartment	0.066 min${}^{-1}$
	The time constant of subcutaneous
$\tau$	glucose concentration dynamic	min
	The glucose distribution volume
$V_g$	in the accessible compartment	$0.16\times BW\left(L\right)$
	The insulin distribution volume
$V_I$	in the accessible compartment	$0.12\times BW\left(L\right)$
	The renal glucose clearance above
$F_R\left(t\right)$	the glucose threshold of 9 mmol L${}^{-1}$	$\left\{\begin{array}{c}0.003(G_{sub}-9),G_{sub}\ge 9\\ 0,G_{sub}<9\end{array}\right.$
		0.0097
$F_{01}$	Non-insulin-dependent glucose flux	mmol kg${}^{-1}$ min${}^{-1}$
	The total non-insulin-dependent
$F_{0,1}^c\left(t\right)$	glucose flux (mmol min${}^{-1}$)	$\left\{\begin{array}{c}{F}_{01},G_{sub}\ge 4.5\\ F_{01}(G_{sub}/4.5),G_{sub}<4.5\end{array}\right.$

[43].

Body weight has a significant effect on the variations in the PIC and other state variables as it is used for determining the amount of exogenous insulin to be infused. Although estimating body weight as an augmented state variable of the insulin-CGM model is an effective strategy to cope with the problem of unavailable demographic information, estimating body weight from the total amount of daily administered insulin is a more reliable approach. As reported in various studies, the total daily injected insulin can have a range of 0.4–1.0 units kg${}^{-1}$ day${}^{-1}$[44,45,46]. A fair estimation of body weight can be obtained by calculating the most common amount of injected basal/bolus insulin for each subject and using a conversion factor of 0.5 units kg${}^{-1}$ day${}^{-1}$ as a rule of thumb to estimate the body weight.

The insulin–glucose dynamics (9) in discrete-time format are given by

$$\begin{array}{cc}\hfill & X_{k+1}^{\prime }=f^{\prime }(X_k^{\prime },U_k)+G_k{\omega }_k,{\omega }_k\approx N(0,Q)\hfill \\ \hfill & Y_k^{\prime }=h^{\prime }\left(X_k^{\prime }\right)+{\nu }_k,{\nu }_k\approx N(0,R)\hfill \end{array}$$

(10)

where $X_k^{\prime }=[S_{1,k},S_{2,k},I_k,x_{1,k},x_{2,k}{x}_{3,k},Q_{1,k},Q_{2,k},G_{sub,k},t_{max,I,k},k_{e,k},U_{G,k}]\in {\mathcal{R}}^{n_x}$ denotes the extended state variables and $U_k$ is the total injected exogenous insulin. Symbols ${\omega }_k$ and ${\nu }_k$ denote zero-mean Gaussian random process and measurement noises (respectively), representing any other uncertainty and model mismatch that are not taken into account. Further, $Q\in {\mathcal{R}}^{n_x\times n_x}$ and $R\in \mathcal{R}$ represent the positive definite system uncertainty and measurement noise covariance matrices, respectively.

Tracking the dynamics of the internal state variables of the model (10) is feasible by using a class of sequential Monte Carlo algorithms known as particle filters. A generic form of the particle filter algorithm proposed by [47] with an efficient adaptive Metropolis–Hastings resampling strategy developed in [48] was employed to predict the trajectory of the PIC and other state variables. In order to avoid any misleading state estimations, each state variable was subjected to a constraint to maintain all estimations within meaningful intervals [41].

3.4. Feature Selection and Dimensionality Reduction

Reducing the number of redundant feature variables lowers the computational burden of their extraction and hinders over-parameterized modeling. In this work, a two-step feature selection procedure was used to obtain the optimal subset of feature variables that boost the efficiency of the classifier the most. In the first step, the deviance statistic test was performed to filter out features with low significance (p-value > 0.05). In the second step, the training split of all datasets was used in the wrapper feature selection strategy to maximize the accuracy of the classifier in estimating the glycemic events. A sequential floating forward selection (SFFS) approach [49] was applied on a random forest estimator with thirty decision tree classifiers with a maximum depth of six layers to sort out features with the most predictive power in descending order. Consequently, the top twenty feature variables with the highest contribution to the classification accuracy enhancement were used for model development.

4. Detection and Classification Methods

Detecting the occurrence of events causing large glycemic variations requires solving a supervised classification problem. Hence, all samples required labeling using the information provided in the datasets, specifically using variables “Activity.duration” and “Nutrition.carbohydrate”. In order to determine the index sets of each class, let N be the total number of samples and $T\left(k\right)=ceil\left(AD\left(k\right)/(3\times {10}^5)\right)$ be the sample duration of physical activity at each sampling time k. Define sets of sample indexes as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}Label.Inde{x}_{\left\{1,1\right\}}:=& \left\{i\right|k\le i\le k+T\left(k\right)-1,k=1,\cdots ,N,T\left(k\right)\ne 0,\\ & Nutrition.carbohydrate\left(j\right)\ne 0,j=k+1,\cdots ,k+T\left(k\right)\}\\ Label.Inde{x}_{\left\{0,1\right\}}:=& \left\{i\right|k\le i\le k+T\left(k\right)-1,k=1,\cdots ,N,T\left(k\right)\ne 0,\\ & Nutrition.carbohydrate\left(j\right)=0,j=k+1,\cdots ,k+T\left(k\right)\}\\ Label.Inde{x}_{\left\{1,0\right\}}:=& \left\{k\right|1\le k\le N,T\left(k\right)=0,Nutrition.carbohydrate\left(k\right)\ne 0\}\\ Label.Inde{x}_{\left\{0,0\right\}}:=& \left\{k\right|1\le k\le N,T\left(k\right)=0,Nutrition.carbohydrate\left(k\right)=0\}\end{array}\right.\end{array}$$

(11)

The label indexes defined by (11) corresponds to classes “Meal and Exercise”, “no Meal but Exercise”, “no Exercise but Meal”, “neither Meal nor Exercise”, respectively.

Four different configurations of the RNN models were studied to assess the accuracy and performance of each in estimating the joint probability of the carbohydrate intake and physical activity. All four models used 24 past samples of the selected feature variables, and event estimations were performed one sample backward. Estimating the co-occurrences of the external disturbances should be performed at least one step backward as the effect of disturbance variables needs to be seen first, before parameter adjustment and event prediction can be made.

Since the imputation of gaps with a high number of consecutive missing values adversely affects the prediction of meal–exercise classes, all remaining samples with missing values after the data imputation step were excluded from parameter optimization. Excluding missing values inside the input tensor can be carried out either by using a placeholder for missing samples and filtering samples through masking layer or by manually removing incomplete samples.

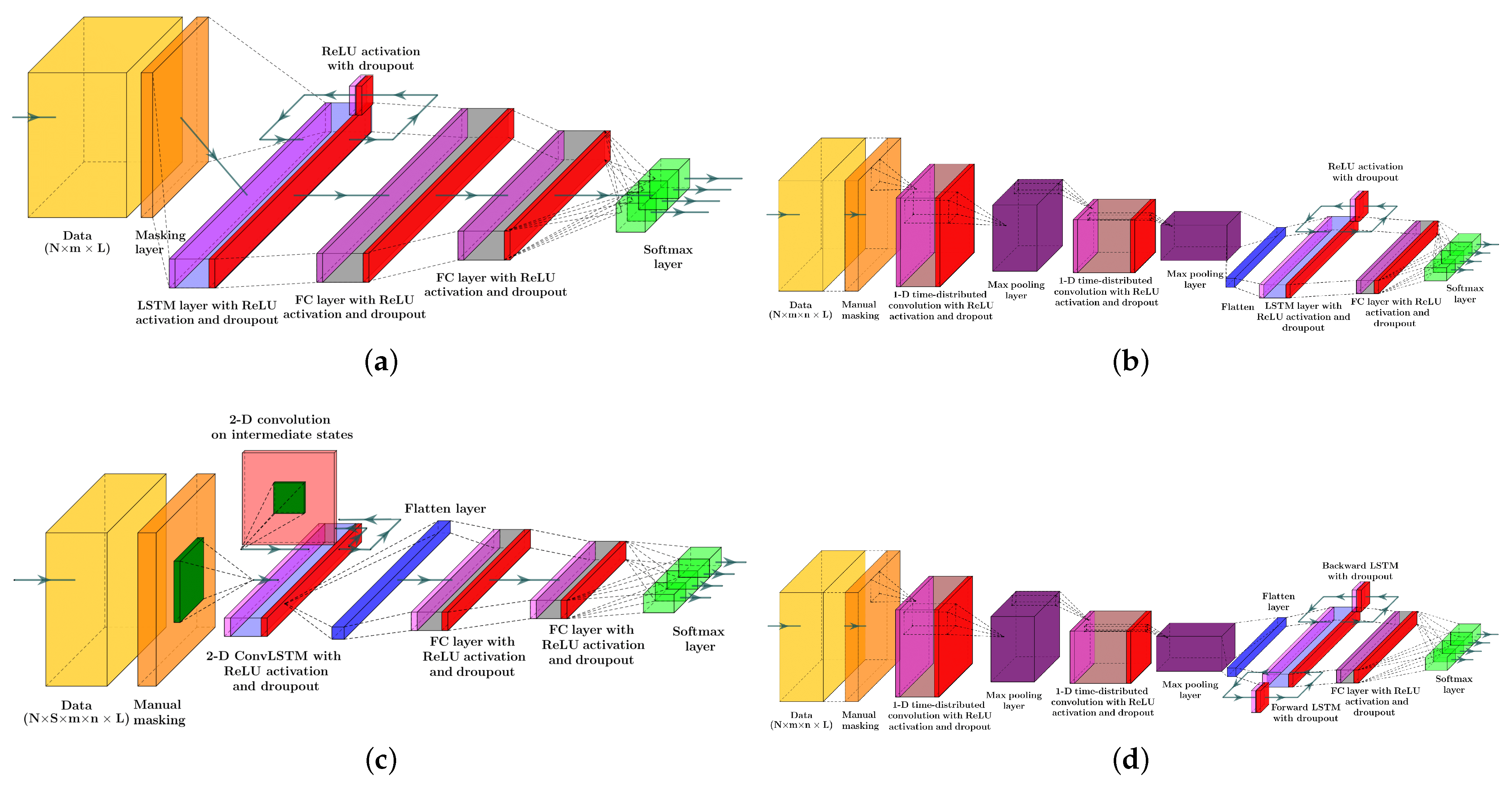
Each recurrent NN models used in this study encompasses a type of LSTM units [50] (see Figure 2) to capture the time-dependent patterns in the data. The first NN model consists of a masking layer to filter out unimputed samples, followed by a LSTM layer, two dense layers, and a softmax layer to estimate the probability of each class. The LSTM and dense layers undergo training with dropout and parameter regularization strategies to avoid the drastic growth of hyperparameters. Additionally, the recurrent information stream in the LSTM layer was randomly ignored in the calculation at each run. At each layer of the network, the magnitude of both weights and intercept coefficients was penalized by adding a $L_1$ regularizer term to the loss function. The rectified linear unit (ReLu) activation function was chosen as a nonlinear component in all layers. The input variables of the regular LSTM network will have the shape of $N\times m\times L$, which denotes the size of samples, the size of lagged samples, and the number of feature variables, respectively.

The second model encompasses a series of two 1D convolution layers, each one followed by a max pool layer for downsampling feature maps. The output of the second max pool layer was flattened to achieve a time-series extracted feature to feed to to the LSTM layer. A dense layer after LSTM was added to the model and the joint probability of events was estimated by calculating the output of the softmax layer. Like the first RNN model, the ReLU activation function was employed in all layers to capture the nonlinearity in the data. A $L_1$ regularization method was applied to all hyperparameters of the model. Adding convolution layers with repeated operations to an RNN model paves the way for extracting features for the sequence regression or classification problem. This approach has shown a breakthrough in visual time-series prediction from the sequence of images or videos for various problems, such as activity recognition, textual description, and audio and word sequence prediction [51,52]. Time-distributed convolution layers scan and elicit features from each block of the sequence of the data [53]. Therefore, each sample was reshaped into $m\times n\times L$, with $n=1$ blocks at each sample.

The third classifier has a 2D convolutional LSTM (ConvLSTM) layer, one dropout layer, two dense layers, and a softmax layer for the probability estimation of each class from the sequences of data. A two-dimensional ConvLSTM structure was designed to capture both temporal and spatial correlation in the data, moving pictures in particular, by employing a convolution operation in both input-to-state and state-to-state transitions [50]. In comparison to a regular LSTM cell, ConvLSTMs perform the convolution operation by an internal multiplication of inputs and hidden states into kernel filter matrices (Figure 2c). Similar to previously discussed models, the $L_1$ regularization constraint and ReLU activation function were considered in constructing the ConvLSTM model. A two-dimensional ConvLSTM import sample of spatiotemporal data in the format of $m\times s\times n\times L$, where $s=1$ and $n=1$, stands for the size of the rows and columns of each tensor, and $L=20$ is the number of channels/features on the data [54].

Finally, the last model comprises two 1D convolution layers, two max pooling layers, a flatten layer, a bidirectional LSTM (Bi-LSTM) layer, a dense layer, and a soft max layer to predict classes. Bi-LSTM units capture the dependency in the sequence of the data in two directions. Hence, as a comparison to a regular LSTM memory unit, Bi-LSTM requires reversely duplicating the same LSTM unit and employing a merging strategy to calculate the output of the cell [55]. The use of this approach was primarily observed in speech recognition tasks, where, instead of real-time interpretation, the whole sequence of the data was analyzed and its superior performance over the regular LSTM was justified [56]. The joint estimation of glycemic events was made one step backward. Therefore, the whole sequence of features were recorded first, and the use of an RNN model with Bi-LSTM units for the detection of unannounced disturbances was quite justifiable. The tensor of input data is similar to LSTM with 1D convolutional layers. Figure 2 is the schematic diagram of a regular LSTM, a Bi-LSTM, and a ConvLSTM unit.

Figure 3 depicts the structure of the four RNN models to estimate the probability of meal consumption, physical activity, and their concurrent occurrence. The main difference between models (a) and (b) in Figure 3 is the convolution and max-pooling layers added before the LSTM layer to extract features map from time series data. Although adding convolutional blocks to an RNN model increases the number of learnable parameters, including weights, biases, and kernel filters, calculating temporal feature maps from input data better discriminates the target classes.

5. Case Study

Eleven datasets containing CGM-sensor–insulin-pump, physical activity, and carbohydrate intake information were selected randomly from subject records for a case study. Data imputation and reconciliation, RNN training, and an evaluation of the results were conducted individually for each subject. Hence, the RNN models were personalized, using only that person’s data. All datasets were preprocessed by the procedure elaborated on in the data preprocessing section and feature variables were rescaled to have zero-mean and unit variance. Stratified six-fold cross-validation was applied to 87.5% of samples of each dataset to reduce the variance of predictions. Weight values proportional to the inversion of class sizes were assigned to the corresponding samples to avoid biased predictions caused by imbalanced samples in each class. In order to better assess the performance of each model and to avoid the effects of randomization in the initialization step of the back propagation algorithm, each model was trained five times with different random seeds. Hyperparameters of all models were obtained through an adaptive moment estimation (Adam) optimization algorithm, and 2% of the training sample size was chosen as the size of the training batches. In model training with different random seeds, the number of adjustable parameters, including weights, biases, the size and number of filter kernels, and the learning rate remained constant.

One difficulty associated with convolution layers in models (b) and (d) is the optimization of the hyperparameters of the convolutional layers. Usually, RNN models with convolution layers require a relatively high computation time. As a solution, learning rates with small values are preferred for networks with convolutional layers since they lead to a more optimal solution compared to large learning weights, which may result in non-optimality and instability.

The data preprocessing part of the work was conducted in a Matlab 2019a environment, and Keras/Keras-gpu 2.3.1 were used to construct and train all RNN models. Keras is a high-class API library with Tensorflow as the backend; all are available in the Python environment. We used two computational resources for data preparations and model training.

Table 5. Hardware specifications.

	Data Preprocessing Task	Model Training Task
CPU Model	Intel i9 9900 k	Intel i7 8700 k
CPU Frequency	3.6–5.0 GHz	3.7–4.7 GHz
Threads	16	12
RAM Capacity	64 GB (DDR IV)	32 GB (DDR IV)
Graphics Processor	RTX 2080 Ti × 2	GTX 1050 Ti (GDDR5)
Graphics Memory	11 GB	4 GB
Clock Frequency	1545–1750 MHz	1290–1392 MHz
Cuda Kernels	4352	768

provides the details of hardware resources.

6. Discussion of Results

Each classifier was evaluated by testing a 12.5% split of all sensor and insulin pump recordings for each subject, corresponding to 3–12 weeks of data for a subject. The average and the standard deviation of performance indexes are reported in

Table 6. The average performance indexes of LSTM, LSTM with 1D convolution layers, 2D ConvLSTM, and Bi-LSTM with 1D convolution layers RNN models for the event detection problem. Standard deviations are given in parentheses and values with bold notation denote the highest performance indexes.

Subject No./Model	Total Accuracy (%)	Weighted Recall (%)	Weighted Precision (%)	Weighted F1 Score (%)
	92.03 (0.37)	92.03 (0.37)	94.59 (0.29)	93.06 (0.30)
	94.61 (0.15)	94.61 (0.15)	97.67 (0.20)	96.06 (0.13)
	89.89 (0.27)	89.89 (0.27)	94.36 (0.16)	91.73 (0.13)
1$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	94.72 (0.31)	94.72 (0.31)	96.85 (0.34)	95.68 (0.29)
	93.17 (0.21)	93.17 (0.21)	96.17 (0.09)	94.37 (0.10)
	94.69 (0.33)	94.69 (0.33)	96.58 (0.20)	95.31 (0.16)
	91.29 (0.38)	91.29 (0.38)	95.90 (0.20)	93.20 (0.17)
2$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	93.56 (0.21)	93.56 (0.21)	96.99 (0.25)	95.17 (0.11)
	89.93 (0.22)	89.93 (0.22)	93.98 (0.24)	91.38 (0.22)
	88.98 (0.28)	88.98 (0.28)	93.53 (0.09)	90.61 (0.22)
	88.40 (0.25)	88.40 (0.25)	93.13 (0.12)	90.21 (0.11)
3$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	89.98 (0.17)	89.98 (0.17)	93.87 (0.05)	91.41 (0.10)
	92.55 (0.27)	92.55 (0.27)	95.49 (0.09)	93.48 (0.17)
	94.67 (0.31)	94.67 (0.31)	96.62 (0.17)	95.34 (0.22)
	88.87 (0.33)	88.87 (0.33)	94.61 (0.16)	90.93 (0.16)
4$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	94.49 (0.28)	94.49 (0.28)	96.47 (0.25)	95.13 (0.15)
	94.41 (0.21)	94.41 (0.21)	96.46 (0.10)	95.18 (0.13)
	91.65 (0.26)	91.65 (0.26)	96.16 (0.12)	93.38 (0.22)
	89.81 (0.18)	89.81 (0.18)	95.62 (0.10)	92.02 (0.17)
5$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	92.66 (0.21)	92.66 (0.21)	96.93 (0.28)	94.73 (0.20)
	94.50 (0.27)	94.50 (0.27)	95.15 (0.22)	94.78 (0.15)
	95.67 (0.26)	95.67 (0.26)	96.69 (0.09)	95.04 (0.14)
	91.10 (0.25)	91.10 (0.25)	94.37 (0.10)	92.60 (0.16)
6$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	95.86 (0.17)	95.86 (0.17)	96.72 (0.21)	96.26 (0.11)
	91.81 (0.22)	91.81 (0.22)	95.43 (0.22)	93.31 (0.16)
	89.85 (0.22)	89.85 (0.22)	94.19 (0.17)	91.68 (0.14)
	87.47 (0.27)	87.47 (0.27)	99.83 (0.22)	93.15 (0.18)
7$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	90.03 (0.24)	90.03 (0.24)	95.01 (0.16)	92.32 (0.17)
	89.19 (0.22)	89.19 (0.22)	99.68(0.27)	94.13 (0.16)
	90.99 (0.18)	90.99 (0.18)	97.68 (0.19)	94.11 (0.20)
	83.92 (0.28)	83.92 (0.28)	94.60 (0.33)	88.73 (0.12)
8$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	91.42 (0.30)	91.42 (0.30)	95.17 (0.37)	93.12 (0.12)
	92.70 (0.18)	92.70 (0.18)	96.53 (0.28)	94.10 (0.12)
	93.10 (0.32)	93.10 (0.32)	95.70 (0.31)	94.10 (0.30)
	91.56 (0.34)	91.56 (0.34)	94.81 (0.30)	93.10 (0.31)
9$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	93.33 (0.27)	93.33 (0.27)	97.24 (0.21)	95.21 (0.22)
	89.30 (0.34)	89.30 (0.34)	95.57 (0.08)	91.73 (0.22)
	91.89 (0.25)	91.89 (0.25)	96.14 (0.08)	93.65 (0.12)
	85.87 (0.27)	85.87 (0.27)	95.69 (0.08)	89.73 (0.22)
10$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	89.51 (0.25)	89.51 (0.25)	96.11 (0.03)	92.30 (0.17)
	87.17 (0.44)	87.17 (0.44)	92.26 (0.12)	89.10 (0.23)
	89.41 (0.35)	89.41 (0.35)	94.39 (0.06)	91.19 (0.23)
	86.90 (0.29)	86.90 (0.29)	94.84 (0.21)	90.05 (0.25)
11$\left\{\begin{array}{c}LSTM\\ LSTM\left(1DConvolution\right)\\ 2DConvLSTM\\ Bi-LSTM\left(1DConvolution\right)\end{array}\right.$	89.62 (0.15)	89.62 (0.15)	96.51 (0.13)	92.64 (0.14)

. The lowest performance indexes were achieved by 2D ConvLSTM models. Bi-LSTM with 1D convolution layer RNN models achieve the highest accuracy for six subjects out of eleven, and LSTM with 1D convolution RNN for three subjects. Bi-LSTM with 1D convolution layer RNN models outperformed other models for four subjects, with weighted F1 scores ranging from 91.41–96.26%. Similarly, LSTM models with 1D convolution layers achieved the highest weighted F1 score for another four subjects, with score values within 93.65–96.06%. Glycemic events for the rest of the three subjects showed to be better predicted by regular LSTM models, with a weighted F1 score between 93.31–95.18%. This indicates that 1D convolution improves both the accuracy and F1 scores for most of the subjects. Based on the number of adjustable parameters for the four different RNN models used for a specific subject, LSTMs are the most computational demanding blocks in the model. To assess the computational load of developing the various RNN models, we compared the number of learnable parameters (details provided in Supplementary Materials). These values can be highly informative, as the number of dropouts in each model and the number of learnable parameters at each epoch (iteration) are invariant.

A comparison between 1D conv-LSTM and 1D-Bi-LSTM for one randomly selected subject shows that the number of learnable parameters increases by at least 54%, mainly stemming from an extra embedded LSTM in the bidirectional layer (Table S1). While comparing adjustable parameters may not be the most accurate way of determining the computational loads for training the models, they provide a good reference to compare the computational burden of different RNN models.

Figure 4 displays a random day selected from the test data to compare the effectiveness of each RNN model in detecting meal and exercise disturbances. Among four possible realizations for the occurrence of events, detecting joint events, $Clas{s}_{1,1}$, is more challenging as it usually shows overlaps with $Clas{s}_{0,1}$ and $Clas{s}_{1,0}$. Another reason for the lower detection is the lack of enough information on $Clas{s}_{1,1}$, knowing that people would usually rather have a small snack before and after exercise sessions over having a rescue carbohydrate during physical activity. Furthermore, the AID systems used by subjects automatically record only CGM and insulin infusion values, and meal and physical activity sessions need to be manually entered to the device, which is, at times, an action that may be forgotten by the subject. Meal consumption and physical activity are two prominent disturbances that disrupt BGC regulation, but their opposite effect on BGC makes the prediction of $Clas{s}_{1,1}$ less critical than each of meal intake or only physical activity classes.

The confusion matrices of the classification results for one of the subjects (No. 2) are summarized in

Table 7. Confusion matrices calculated from the predicted and actual classes of testing samples collected from Subject 2.

		Actual						Actual
		Class{0,0}	Class{0,1}	Class{1,0}	Class{1,1}			Class{0,0}	Class{0,1}	Class{1,0}	Class{1,1}
Predicted	Class{0,0}	11,154	12	46	2	Predicted	Class{0,0}	11,297	14	8	1
	Class{0,1}	310	598	2	0		Class{0,1}	274	596	2	2
	Class{1,0}	263	21	593	1		Class{1,0}	311	8	655	1
	Class{1,1}	217	5	27	6		Class{1,1}	62	18	3	5
(a) LSTM						(b) LSTM (1D Convolution)
		Actual						Actual
		Class{0,0}	Class{0,1}	Class{1,0}	Class{1,1}			Class{0,0}	Class{0,1}	Class{1,0}	Class{1,1}
Predicted	Class{0,0}	10,984	14	29	1	Predicted	Class{0,0}	11,324	14	29	1
	Class{0,1}	560	574	16	2		Class{0,1}	110	537	16	2
	Class{1,0}	157	6	541	2		Class{1,0}	257	6	538	2
	Class{1,1}	243	42	82	4		Class{1,1}	253	79	85	4
(c) 2D ConvLSTM						(d) Bi-LSTM (1D Convolution)

. As can be observed from Figure 4 and Table 7, detecting $Clas{s}_{0,1}$ (physical activity) is more challenging in comparison to the carbohydrate intake ($Clas{s}_{1,0}$) and $Clas{s}_{0,0}$ (no meal or exercise). One reason for this difficulty is the lack of biosignal information, such as 3D accelerometer, blood volume pulse, and heart rate data. Some erroneous detections, such as confusing meals and exercise, are dangerous, since meals necessitate an insulin bolus while exercise lowers BGC, and the elimination of insulin infusion and/or increase in target BGC are needed. RNNs with LSTM and 1D convolution layers provide the best overall performance in minimizing such confusions: two meals events are classified as exercise (0.003%) and eight exercise events are classified as meals (0.125%).

Two limitations of the study are the quality and accuracy of data collected in free living and the variables that are measured. As stated in the Introduction and Data Preprocessing sections, the missing data in the time series of CGM readings is one limitation that we addressed by developing data preprocessing techniques. The second limitation is the number of variables that are measured. In this data set, there are only CGM and insulin pump data and the voluntary information provided by the patients about meal consumption and exercising. This information is usually incomplete (sometimes people may forget or have no time to enter this information). These events can be captured objectively by other measurements from wearable devices. Such data were not available in this data set and limited the accuracy of the results, especially when the meal and exercise occurred concurrently.

The proportion of correctly detected exercise and meal events to all actual exercise and meal events for all subjects reveals that a series of convolution–max-pooling layers could elicit informative feature maps for classification efficiently. Although augmented features, such as the first and second derivatives of CGM and PIC, enhance the prediction power of the NN models, the secondary feature maps, extracted from all primary features, show to be a better fit for this classification problem. In addition, repeated 1D kernel filters in convolution layers better suit the time-series nature of the data, as opposed to extracting feature maps by utilizing 2D convolution filters on the data.

7. Conclusions

This work focuses on developing RNN models for detection and classification tasks using time series data containing missing and erroneous values. The first modeling issue arose from the quality of the recorded data in free living. An outlier rejection algorithm was developed based on multivariable statistical analysis and signal denoising by decomposition of the Hankel matrix of CGM recordings. A multivariate approach based on PPCA for CGM sample imputation was used to keep the harmony and relationship among the variables. The second issue addressed is the detection of events that affect the behavior of dynamic systems and the classification of these events. Four different RNN models were developed to detect meal and exercise events in the daily lives of individuals with T1D. The results indicate that models with 1D convolution layers can classify events better than regular LSTM RNN and 2D ConvLSTM RNN models, with very low confusion between the events that may cause dangerous situations by prompting erroneous interventions, such as giving insulin boluses during exercise.